Рефераты по сексологии
Рефераты по информатике программированию
Рефераты по биологии
Рефераты по экономике
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Рефераты по авиации и космонавтике
Рефераты по административному праву
Рефераты по безопасности жизнедеятельности
Рефераты по арбитражному процессу
Рефераты по архитектуре
Рефераты по астрономии
Рефераты по банковскому делу
Рефераты по биржевому делу
Рефераты по ботанике и сельскому хозяйству
Рефераты по бухгалтерскому учету и аудиту
Рефераты по валютным отношениям
Рефераты по ветеринарии
Рефераты для военной кафедры
Рефераты по географии
Рефераты по геодезии
Рефераты по геологии
Рефераты по геополитике
Рефераты по государству и праву
Рефераты по гражданскому праву и процессу
Рефераты по делопроизводству
Рефераты по кредитованию
Рефераты по естествознанию
Рефераты по истории техники
Рефераты по журналистике
Рефераты по зоологии
Рефераты по инвестициям
Рефераты по информатике
Исторические личности
Рефераты по кибернетике
Рефераты по коммуникации и связи
Курсовая работа: Зубчатые и червячные передачи
Курсовая работа: Зубчатые и червячные передачи
ЗУБЧАТЫЕ ПЕРЕДАЧИ
1. Условия работоспособности зубьев
Меньшее из пары зубчатых колес называется шестерней (z1), большее – колесом (z2). Параметры, относящиеся к шестерне, обозначают с индексом «1», к колесу – с индексом «2». Термин «зубчатое колесо» относят как к шестерне, так и к колесу.
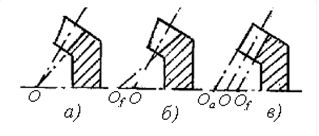
На рис. 1 изображены направления наклонов линий зубьев и их названия: а) прямые зубья; б) правый наклон; в) левый наклон; г) шевронный наклон.
Рис.1
|
|
|
|
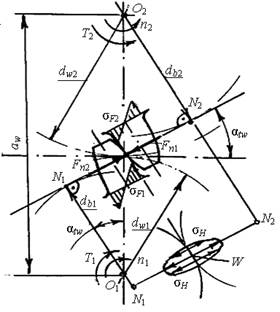
Рис. 2
При передаче вращающего момента Т в зацеплении (рис. 2) действует нормальная сила Fn = 2000 Т // db_(db = dwcosαtw – диаметр основной окружности, где dw – диаметр начальной окружности; α tw – угол зацепления), направленная по линии зацепления N1N2.
По отношению к зубу колеса сила Fn2 активна, т.е. движущая, и направлена в сторону вращения z2, по отношению к зубу z1 сила Fn1 реактивна (сила сопротивления колеса) и направлена против вращения шестерни. По закону Ньютона Fn1 = Fn2 = Fn.
Деформацию зубьев под действием силы Fn рассматривают как сжатие двух цилиндров в плоскости зацепления задача Герца с первоначальным контактом по линии.
Кроме того, относительно заделки ножки зуба сила Fn действует на некотором плече, что вызывает изгибающий момент в основании зуба.
За счет скольжения поверхностей зубьев между ними возникает сила трения Ff = fFn, где f – коэффициент трения скольжения.
Зуб испытывает сложное напряженное состояние. Решающее влияние на его работоспособность оказывают два основных напряжения: контактное σН и изгиба σF (“F” - Foot – ножка). Эти напряжения переменные, изменяются по отнулевому циклу и приводят к усталостному разрушению зубьев. Число циклов изменения напряжений σН и σF за один оборот равно с, где с – число зацеплений фиксированного зуба за один оборот.
Суммарное число циклов изменения напряжений за весь срок службы
NΣ = 60nсLh, где Lh – ресурс в часах.
2. Материалы зубчатых передач
Важнейшими критериями при выборе материалов являются масса и габариты передачи. Наименьшую массу имеют стальные зубчатые колеса. Причем, масса и габариты тем меньше, чем выше твердость поверхности зубьев.
Границей качественных свойств зубьев является твердость поверхности Н0, равная 350 НВ:
1. При Н0 ≤ 350 НВ зубья подвергают улучшению или нормализации до нарезания зубьев. Применяют в единичном и мелкосерийном производствах при отсутствии жестких требований к габаритам и массе передачи (например, стационарные машины и механизмы). Зубья из улучшенных сталей хорошо прирабатываются, не подвержены хрупкому разрушению, но имеют ограниченную нагрузочную способность.
2. Высокую твердость Н0 > 350 НВ (45…63 HRC) получают применением поверхностного термического или химико-термического упрочнения предварительно улучшенных зубчатых колес: поверхностной закалки (чаще ТВЧ – токами высокой частоты), цементации и нитроцементации с закалкой, азотирования. Упрочнение проводят после нарезания зубьев, а после него – шлифование или полирование зубьев.
Применяют в массовом и крупносерийном производствах или в любом при наличии жестких требований к габаритам и массе (например, в передачах транспортных машин).
Зубья с твердостью Н0 ≥ 56 HRC называют высокотвердыми.
Твердые зубья (Н0 > 45 HRC) плохо прирабатываются.
Для обеспечения одинаковой долговечности материал шестерни z1 должен иметь более высокие механические свойства, чем колеса z2, так как при σН – const зубья z1 в “и” – раз чаще входят в зацепление (N1 > N2), что приводит к их большей усталости.
Практикой рекомендуются соотношения твердостей:
а) для прямозубых передач Н01 – Н02 ≥ (20…30) НВ;
б) для передач косозубых, шевронных, с круговым зубом с целью повышения прирабатываемости и нагрузочной способности Н01 – Н02 ≥ (100…150) НВ;
в) для твердых передач (Н0 ≥ 45 HRC) Н01 ≈ Н02 .
3. Характерные виды разрушения зубьев
Выход зубьев из строя может вызываться:
а) многократно повторяющимися переменными напряжениями σН и σF, приводящими к усталостным разрушениям;
б) чрезмерными единичными перегрузками, вызывающими пластические деформации или хрупкие поломки зубьев.
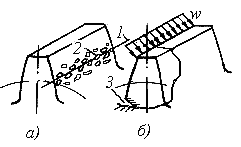
1. Усталостное выкрашивание рабочих поверхностей зубьев
Причина контактные напряжения σН и трение. Это основной вид разрушения закрытых передач (редукторов). Зубья в работе разделены слоем масла, износ их мал. Передача длительное время работает до появления на поверхности микротрещин из-за микронеровностей или других дефектов. Масло под давлением запрессовывается в трещины и способствует выкрашиванию (вырову) частиц металла.
|
Рис.3
Разрушение начинается вблизи полюсной линии 1 (рис. 3, а), где имеют место наибольшие нагрузка Fn (зона однопарного зацепления) и сила трения Ff. Поверхность зуба покрывается «раковинами», «оспинами» 2. Глубина раковин около 0,2 мм. В мягких передачах (Н0 < 350 НВ) в результате приработки наблюдается ограниченное (начальное) выкрашивание. В твердых передачах (Н0 > 350 НВ) – выкрашивание прогрессирующее.
2. Заедание зубьев наблюдается в высоконагруженных и высокоскоростных зубчатых, а также червячных передачах.
В местах контакта из-за трения развивается высокая температура, способствующая снижению вязкости масла, разрыву масляной пленки и образованию металлического контакта зубьев. Происходит молекулярное сцепление (микросварка) частиц металла. Растет сопротивление вращению, наросты металла на зубьях задирают рабочие поверхности сопряженных зубьев.
3. Поломка зубьев. Причина – напряжение изгиба σF. Это основной вид разрушения высокотвердых (Н0 ≥ 56 HRC) и открытых передач.
В открытых передачах в результате плохой смазки и абразивного истирания поверхностей зубьев от грязи выкрашивание не успевает развиться, но уменьшаются размеры сечений зубьев, растут напряжения изгиба σF. Возрастают зазоры, удары, шум. Усталостная поломка в этом случае связана с развитием трещин 3 на растянутой стороне ножки зуба (рис.3, б). В высокотвердых передачах зубья хрупкие, поверхность их имеет хорошее сопротивление выкрашиванию, но хуже противостоит прогрессирующему трещинообразованию в основании зуба.
Смятие рабочих поверхностей (пластические сдвиги) или хрупкое разрушение (Н0 ≥ 56 HRC) зубьев при кратковременных значительных перегрузках или ударном приложении нагрузки.
5. Отслаивание твердого поверхностного слоя при значительных контактных напряжениях и зарождении усталостных трещин в глубине под упрочненным слоем.
4. Расчетная нагрузка
1. Коэффициенты расчетной нагрузки
В теоретических передачах определяется номинальная нагрузка:
Рnom; Tnom = 9550
Рnom / n; Fnom = 2000Tnom / d.
При работе в зубчатом зацеплении возникают дополнительные нагрузки, вызываемые условиями нагружения, погрешностями изготовления, деформациями зубьев, валов и опор.
В расчетах это учитывают введением коэффициента нагрузки K, определяя расчетную нагрузку: Q = KQnom, где Q – любой вид нагрузки;
K = KAKβKVKα;
здесь KA, коэффициент внешней динамической нагрузки, учитывает влияние неравномерности нагружения двигателя и рабочего органа при их совместной работе с передачей;
Kβ – коэффициент неравномерности распределения нагрузки по длине контактных линий. Отклонение положения контактных линий обусловлено
погрешностями изготовления передачи, упругими деформациями зубьев, валов, опор, зазорами в подшипниках;
KV – коэффициент внутренней динамической нагрузки. Внутренняя динамическая нагрузка связана с ударами зубьев на входе в зацепление вследствие ошибок изготовления шага и деформации зубьев.
Kα – коэффициент распределения нагрузки между парами зубьев. Неравномерность распределения нагрузки между зубьями зависит от погрешностей изготовления, в результате чего при контакте одной пары зубьев в другой паре возможен зазор. При деформировании зубьев зазор может быть выбран, но при этом неравномерность распределения нагрузки неизбежна.
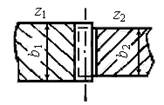
Рис.4
Цилиндрические зубчатые передачи специально не регулируют. Для перекрытия возможных осевых погрешностей расположения z1 и z2 при монтаже передачи шестерню z1 (рис. 4) выполняют шире колеса (b1 > b2) по двум причинам:
1. Для равномерного износа ширины колеса b2, так как твердость Н01 > Н02;
2. Расход металла на изготовление передачи меньше, так как объем шестерни V1 меньше, чем колеса V2.
Ширина b1 = b2 + (3…5) мм. Рабочая ширина зубчатого венца bW = b2.
Подробности о коэффициентах расчетной нагрузки см. в [1…3].
2. Точность зубчатых передач
|
Предусмотрено 12 степеней точности. Наиболее часто применяют 6-ю (высокоточные передачи), 7-ю (нормальная точность – передачи с повышенными скоростями), 8-ю (пониженная точность) степени.
Для каждой степени точности установлены три нормы:
– кинематической точности (регламентирует разность между действительным и номинальным углами поворота ведомого зубчатого колеса передачи);
– плавности работы (регламентирует колебания скорости вращения);
– контакта зубьев (регламентирует пятно прилегания поверхностей зубьев в собранной передаче).
Независимо от степеней точности стандартизирован боковой зазор зубчатой передачи. Боковой зазор необходим для предотвращения заклинивания зубьев вследствие их расширения от нагрева при работе, для размещения смазки и обеспечения свободного вращения колес. Обозначение: Н, Е, D, С, В, А
(Н – нулевой зазор…, В – нормальный, А – широкий). Чаще всего применяют сопряжения В и С (уменьшенный зазор в реверсивных передачах).
Примеры обозначения степеней точности передач редукторов в документации:
8-7-7-С ГОСТ 1643-81 – допуски цилиндрической передачи: кинематической точности по 8-й степени, плавности работы и контакта зубьев по 7-й степени точности, боковой зазор С;
7-В ГОСТ 1758-81 – допуски конической передачи: все нормы по 7-й степени точности, боковой зазор В.
5. Цилиндрические зубчатые передачи
5.1 Силы в зацеплении
Силы принято определять в полюсе W (рис.5) зацепления.
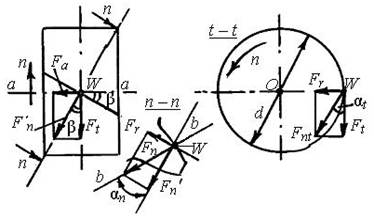
Рис.5
По линии зацепления b b (рис. 5) действует нормальная сила Fn. Для удобства расчетов силу Fn принято раскладывать на три составляющие:
1) Ft – окружная сила, направленная по касательной к делительным окружностям. Это основная, движущая, полезная сила. На колесе z2 Ft совпадает с направлением вращения n2. На шестерне z1 F направлена против вращения n1.
Следовательно, на рис. 5 дана схема сил для шестерни:
Ft = 2000Т / d, (1)
где Т – Н∙м; d – мм;
2) Fr – радиальная сила, направленная по линии центров (радиусам). Для внешнего зацепления – к оси вращения, для внутреннего – от оси.
В торцовой плоскости t t (рис. 5) имеем
Fr = tgαt, (2)
где αt – делительный угол профиля в торцовой плоскости: tgαt = tgαn / cosβ; αn– нормальный угол зацепления, β – угол наклона зубьев. В практических расче-тах αt ≈ αn =20°.
3) Fa – осевая сила, направленная параллельно оси а – а зубчатого коле-
са. Силы Ft и Fа как составляющие нормальной силы Fn′, всегда находятся вне линии зуба (рис. 5). В делительной плоскости:
Fа = Fttgβ. (3)
Необходимый в дальнейших расчетах основной угол наклона зуба
βb (в основной плоскости зацепления b) определяется как βb = arcsin(sinβcosαn).
Полная нормальная сила (рис. 5):
Fn = Fnt / cosβb = Ft / (cosαtcosβb). (4)
Для прямозубых передач во всех формулах β = βb = 0; αt = αn = α;
Ft = 2000T / d; Fr = Fttgα; Fa = 0; Fn = Ft / cosα.
Недостатком косозубых передач является наличие осевых сил Fа, которые дополнительно нагружают опоры валов, усложняя их конструкцию.
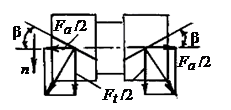
Рис. 6
В косозубых передачах углы β ограничены в пределах 8…18°.
Указанный недостаток устранен в шевронной передаче, которая представляет собой сдвоенную косозубую с противоположным наклоном зубьев на полушевронах. Из рис. 6 видно, что осевые силы Fа /2 взаимоуравновешены.
5.2. Расчет на сопротивление контактной усталости
Косые зубья цилиндрических колес нарезают тем же инструментом, что и прямые, установленным относительно заготовки под углом β.
Расчет на прочность принято вести для прямозубой передачи. Для этого все зубчатые и червячные передачи приводятся к эквивалентным прямозубым цилиндрическим.
Эквивалентные параметры косозубого цилиндрического колеса (приведение рассматривалось в курсе "Теория машин и механизмов"): делительный диаметр dv = d / cos2β; эквивалентное число зубьев zv = z / cosβ, где z – действительное число зубьев косозубого колеса.
С увеличением β эквивалентные параметры возрастают, способствуя повышению прочности передачи. Вследствие того, что косой зуб входит в зацепление не сразу всей длиной, он лучше прирабатывается, а большее число пар зубьев в зацеплении снижает шум и динамические нагрузки. Чем больше угол β, тем выше плавность зацепления.
Контактная прочность (σН ≤ σНР) является основным критерием работоспособности большинства зубчатых передач.
Расчет производят в полюсе W (рис. 7), где имеет место наибольшая нагрузка (зона однопарного зацепления) и начинается усталостное выкрашивание зубьев.
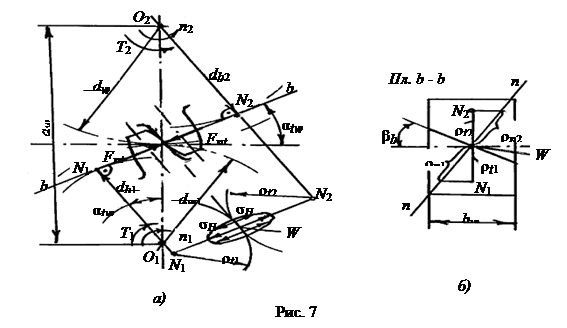
Контакт зубьев рассматривают как сжатие двух цилиндров в плоскостях n и b
Контакт зубьев рассматривают как сжатие двух цилиндров в плоскостях n с нормальными радиусами кривизны ρn1 и ρn2. Используют формулу Герца для первоначального контакта по линии:
σН = ZE(wHn / ρnv)1/2 ≤ σНP. (5)
Напряжения σН одинаковы для зубьев z1 и z2. Оценку сопротивления контактной усталости производят по расчетной величине допускаемого напряжения σНР.
В формуле (5): ZE = (1 / {π[(1 – ν12) / E1 + (1 – ν22) / E2]})1/2 –
– коэффициент механических свойств материалов z1 и z2: Е – модуль упругости; ν1, 2 – коэффициенты Пуассона. Для стали Е1 = Е2 = 2,1∙105 МПа, ν1 = ν2 = 0,3 и ZЕ =191,6 МПа1/2;
wHn = FnKH / lΣ – удельная нормальная расчетная нагрузка (на единицу длины lΣ контактных линий), Н/мм, где KH – коэффициент нагрузки; Fn – нормальная сила.
Вспомним, что lΣ = bwεα / cosβb, где εα – торцовый коэффициент перекрытия; Fn = Ft / (cosαtcosβb). Тогда получим wHn = FtKH / (bwεαcosα
1 / ρnv = 1 / ρn1 ± 1 / ρn2 – приведенная кривизна зубьев в нормальной плоскости, 1/мм.
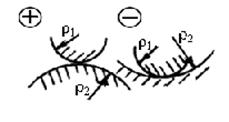
Рис. 8
Знак плюс принимают при контакте двух выпуклых тел (рис. 8), минус – выпукло (ρ1)-вогнутых (ρ2) тел (например, внутреннее зацепление).
|
Нормальные радиусы кривизны (рис. 7, б) ρn = ρt / cosβb, где из ΔONW (рис. 7, а) торцовый радиус ρt = dwsin αtw / 2. |
Выразив 1 / ρnv через параметры передачи,
получим 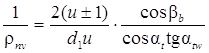 , где d1 – делительный диаметр
шестерни z1.
, где d1 – делительный диаметр
шестерни z1.
Подставив wHn и 1 / ρnv в формулу (5) и
обозначив Zε = ![]() коэффициент, учитывающий суммарную длину контактных линий (для прямых зубьев Zε =
коэффициент, учитывающий суммарную длину контактных линий (для прямых зубьев Zε = ![]() );
);
ZH = 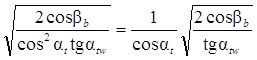 – коэффициент, учитывающий форму
сопряженных поверхностей зубьев в полюсе W, получим решение в форме
ГОСТ 21354-87:
– коэффициент, учитывающий форму
сопряженных поверхностей зубьев в полюсе W, получим решение в форме
ГОСТ 21354-87:
σН = ZEZεZH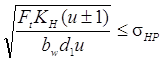 , (6)
, (6)
где знак плюс для внешнего зацепления; минус – для внутреннего.
Это формула для проверочного расчета активных поверхностей зубьев цилиндрических передач на сопротивление контактной усталости с целью предотвращения поверхностного выкрашивания.
В проектировочном расчете из условия контактной прочности определяют межосевое расстояние аw основной габаритный размер передачи.
Для этого в формуле (6) принимают ZE = 191,6 МПа1/2, в среднем εα =
= 1,6 и Zε = 0,8 – косые и шевронные зубья (β ≠ 0), Zε = 0,9 – прямые зубья (β = 0); αt = αtw = αn = 20°, ZН = 2,5 – прямые зубья, ZН = 2,46 – косые (β = 10О) зубья. Вводят коэффициент рабочей ширины ψba зубчатого венца по межосевому расстоянию: ψba = bw / аw , заменяя bw = ψbaаw. Диаметр d1 = 2аw / (u ± 1). Окружная сила Ft = 2000T1 / d1. Тогда будем иметь
аw′ = Ка(и ± 1)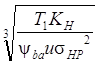 , (7)
, (7)
где Ка = ZEZεZH![]() , при β ≠ 0 Ка = 410 МПа1/3, при
β = 0 Ка = 450 МПа1/3.
, при β ≠ 0 Ка = 410 МПа1/3, при
β = 0 Ка = 450 МПа1/3.
В формуле (7) аw′, мм, Т1 , Н∙м, σНР , МПа.
Расчетное значение аw′ округляют до аw в ближайшую большую сторону:
– для стандартных передач по ГОСТ 2185-66 (по ряду чисел Ra20);
– для нестандартных передач возможно округление до числа, кратного пяти.
Формула (7) главная для проектировочного расчета закрытых цилиндрических передач с целью предотвращения усталостного выкрашивания поверхностей зубьев.
5.3 Расчет на сопротивление изгибной усталости
1. Прямозубая передача
Приняты следующие допущения:
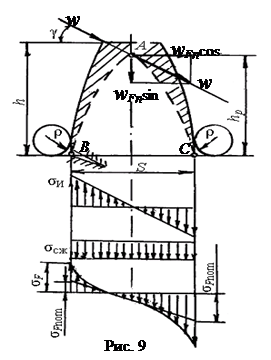
1. Нагрузка передается одной парой зубьев (lΣ = bw) и приложена к вершине зуба по линии зацепления N1N2 под углом γ (γ > αtw) (рис. 9).
2. Зуб рассматривается как вписанная в него консольная балка АВС параболического профиля, имеющая равное сопротивление изгибу в сечениях по высоте hp.
Удельная линейная расчетная нагрузка wFn = Fn / lΣ = FtKF / (bwcosα), где KF – коэффициент нагрузки при расчете на изгиб (KF = KАKFβKFvKFα). Нагрузка FtKF / bw = wFt – удельная окружная и wFn = wFt / cosα. Нагрузка wFn переносится в точку А и раскладывается на составляющие wFncosγ и wFnsinγ.
В заделке ВС балки возникают напряжения изгиба σи = wFncosγ∙hp / W и сжатия σсж = wFnsinγ / A, где W – момент сопротивления изгибу сечения ВС; А – площадь сечения ВС при его ширине, равной единице (bw = 1 мм так как нагрузка wFn единичная) и длине s; W = 1∙s2 / 6 и А = 1∙s.
|
Суммарные номинальные напряжения (рис. 9): – в точке В σFnomB = σи – σсж ≤ £ σFР (растяжение); – в точке С σFnomС = σи + σсж ≤ £ σFР (сжатие). Несмотря на то, что максимальные напряжения возникают в точке С – сжатия ножки зуба, усталостные трещины и разрушение зубьев начинаются на растянутой стороне в точке В. Расчет ведут по напряжениям σFnomB растянутой стороны. Расчетное сечение ВС расположено в зоне концентрации напряжений, вызванной изменением формы выкружкой (галтелью) радиуса ρ на переходной поверхности. Это учитывается коэффициентом концентрации напряжений ασ. Местное напряжение изгиба σF = ασσFnomB.. |
|
Раскрывая последнюю формулу в точке В, будем иметь
σF = 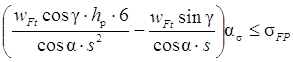 .
.
Исходя из геометрического подобия зубьев разных модулей, плечо hp и толщину s выражают через модуль m: hp = μm, s = λm, где μ и λ коэффициенты, учитывающие форму зуба.
Тогда σF = 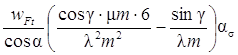 .
.
Введя YFS = 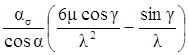 – коэффициент, учитывающий форму зуба и
концентрацию напряжений, получим
– коэффициент, учитывающий форму зуба и
концентрацию напряжений, получим
σF = wFtYFS / m ≤ σFP. (8)Величины YFS приведены в литературе в виде графиков или таблиц.
Подставляя значение wFt в формулу (8), получим формулу для проверочного расчета прямых зубьев на сопротивление усталости при изгибе:
σF = FtKFYFS / (bwm) ≤ σFP. (9)
2. Косозубая передача
Специфика косозубой передачи определяет следующие дополнительные отличия:
1. Наклон контактных линий к основанию зуба учитывается коэффициентом: Yβ = 1 εββ0 / 120 ≥ 0,7,
где εβ – коэффициент осевого перекрытия зубьев.
2. Лучшая прирабатываемость и большее перекрытие зубьев – Yε = 1 / εα.
3. Коэффициент YFS определяют в зависимости от эквивалентного числа зубьев zv = z / cos3β.
Расчетная формула (9) для косозубых передач примет вид:
σF = FtKFYFSYβYε / (bwm) ≤ σFP.(10)
Расчет на изгиб ведут по тому зубу, у которого меньше отношение σFР / YFS.
Если известно σF1, то σF2 = σF1YFS2 / YFS1.
3. Определение модуля передачи
Модуль m = P / π, где шаг Р = πd / z, введен для того. чтобы избавиться от иррационального числа π (m = d / z).
а) Закрытые передачи
Модуль определяют из условия равнопрочности зубьев по усталостному выкрашиванию и изгибу, т.е. через аw и bw:
m′ ≥ 103∙Т1(и ± 1)KFYFSYβYε / (аwbwσFР). (11)
Модуль m′ округляют по ГОСТ 9563-60 до ближайшего большего значения с предпочтением первого ряда. В силовых передачах mn ≥ 1,5 мм.
б) Открытые и высокотвердые (Н0 ≥ 56 HRC) передачи
Для этих передач изгибная прочность является основным критерием работоспособности. Их проектировочный расчет начинают с определения модуля из условий изгиба:
m′ ≥ Кm [T1KFβYFS1 / (ψbd z12σFP1)]1/3, (12)
где Кm = 12,6 – для прямозубых передач; Кm = 10 – для косозубых передач. Числом зубьев z1 и коэффициентом ψbd следует задаваться.
Модуль m′ округляют по ГОСТ 9563-60. Для силовых передач m ≥ 1,5 мм.
6. Конические зубчатые передачи
6.1. Основные параметры
Конические зубчатые передачи применяют для передачи энергии между пересекающимися осями валов. Наибольшее применение имеют ортогональные передачи с межосевым углом Σ = 90° (рис. 10).
Конические колеса бывают с прямыми (в открытых передачах) и круговыми (в редукторах) зубьями. Круговые зубья очерчены линиями по дугам окружности.
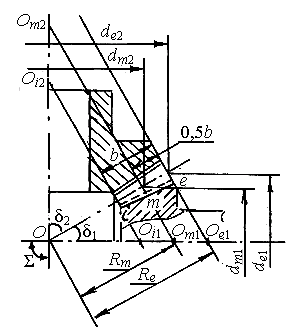
Конуса с вершиной в точке О являются основными (рис.10). Внешние и внутренние торцы на конических зубчатых колесах формируют внешними (вершины Ое) и внутренними (вершины Оi) дополнительными конусами, образующие которых перпендикулярны образующей делительного конуса.
|
Расстояние между внешним (параметры обозначают с индексом е) и внутренним (параметры – с индексом i) дополнительными конусами определяет ширину b венца. На длине 0,5b расположен средний дополнительный конус с вершиной Оm (параметры – с индексом m). Расстояние от вершины О по образующей делительного конуса до внешнего торца е называют внешним конусным расстоянием Re , до середины ширины венца – средним конусным расстоянием Rm (рис. 10). Пересечения делительного конуса с дополнительными конусами определяют диаметры делительных окружностей ко-нического зубчатого колеса: de – внешний, dm – средний, di – внутренний делительные диаметры.- |
Рис. 10 |
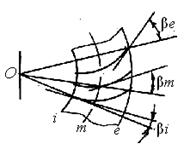
Угол наклона зубьев β определяют (рис. 11) углом между лучом, проведенным из вершины О, и касательной к линии зуба в рассматриваемой точке зуба. Для прямых зубьев β = 0. У круговых зубьев угол β переменный:
βe > βm > βi. За расчетный принимают угол βm в среднем сечении.
|
Рис. 11 |
Рис. 12 Лучше всего зарекомендовали себя передачи с круговыми зубьями с углом βm = 35°. |
Наличие угла наклона повышает плавность работы, контактную и изгибную прочность, уменьшает шум, но увеличивает нагрузки на опоры и валы.
Зубья конических колес в зависимости от изменения размеров их нормальных сечений по длине выполняют в виде трех осевых форм (рис. 12).
Осевая форма I - пропорционально понижающиеся зубья (рис. 12, а). Вершины конусов делительного и впадин совпадают, высота ножки зуба пропорциональна конусному расстоянию. Применяют для прямых зубьев.
Осевая форма II – нормально сужающиеся зубья (рис. 12, б). Вершина конуса впадин Оf расположена так, что ширина дна впадины колеса постоянна, а толщина зуба по делительному конусу пропорциональна конусному расстоянию. Эта форма позволяет одним инструментом обрабатывать сразу обе грани зубьев, повышая производительность. Является основной для колес с круговыми зубьями, особенно в массовом производстве.
Осевая форма III – равновысокие зубья (рис.12, в). Образующие конусов делительного, впадин и вершин параллельны. Высота зуба постоянна по всей длине. Применяют для передач с межосевым углом Σ меньше 40° и круговыми зубьями при (z12 + z22)1/2 ≥ 60.
За расчетное сечение конической передачи принято среднее сечение m.
Для удобства измерения размеры конических колес принято определять по внешнему торцу е зуба.
Различают внешний окружной модуль mtе, средний окружной модуль mtm (для прямых зубьев), средний нормальный модуль круговых зубьев mnm.
Связь между модулями:
mtе = mtm / (1 – 0,5Кbe); mtе = mnm / [(1 – 0,5Кbe)cosβm];
mnm = mtе(1 – 0,5 Кbe) cosβm,
где Кbe = b / Re – коэффициент ширины зубчатого венца по внешнему конусному расстоянию; принимают Кbe ≤ 0,3. Для большинства передач Кbe = 0,285;
βm – угол наклона зуба в среднем сечении.
Для прямых зубьев стандартным (ГОСТ 9563-60) является модуль mtе. В передачах с круговыми зубьями допускается не округлять модули по стандарту, так как одной и той же зуборезной головкой можно нарезать зубья в определенном интервале модуля за счет наладки резцов в головке. Модуль следует вычислять с точностью 0,0001 мм.
Диаметры делительных окружностей:
de = mtеz; dm = mtmz = mnmz / cosβm .
Внешнее конусное расстояние
Re = [(0,5de1)2 + (0,5de2)2]1/2 = 0,5de1(1 + u2)1/2.
Ширина зубчатого венца
b = Кbe Re = 0,285∙0,5de1(1 + u2)1/2 = 0,143de1(1 + u2)1/2.
Передаточное число
и = de2 / de1 = dm2 / dm1 = z2 / z1 = 2Resinδ2 / (2Resinδ1) = sinδ2 / sinδ1.
При δ1 + δ2 = 90О, где δ – углы делительных конусов, имеем δ1 = 90О δ2 и тогда и = tgδ2. Так же δ2 = 90О – δ1 и и = сtgδ1.
Для передачи с круговыми зубьями профили зубьев конических колес в среднем нормальном сечении близки к профилям зубьев эквивалентных цилиндрических прямозубых колес. Приведение к последним осуществляют в два этапа:
1. К эквивалентным цилиндрическим косозубым колесам с углом наклона зубьев βm;
2. От них к эквивалентным прямозубым цилиндрическим колесам.
Из-за двойного приведения параметры называют биэквивалентными:
mv = mnm; bv = b; dvnm = dm / (cosδcos2βm); zvnm = z / (cosδcos3βm);
иv = zvnm2 / zvnm1 = z2cosδ1cos3βm / (z1cosδ2cos3βm) = (z2 / z1)tgδ2 = u2.
Для прямых зубьев в приведенных формулах следует принять βm= 0.
6.2 Силы в зацеплении
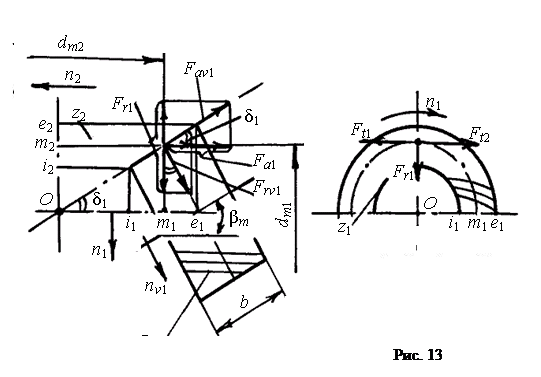 |
1. Окружная сила (рис. 13) Ft = 2000Т / dm.
2. Радиальная сила на шестерне Fr1, равная осевой силе на колесе Fа2:
Fr1 = Fа2 = Ft (tgαncosδ1 m sinβmsinδ1) / cosβm. (13)
3. Осевая сила на шестерне Fа1, равная радиальной силе на колесе Fr2:
Fа1 = Fr2 = Ft (tgαnsinδ1 ± sinβmcosδ1) / cosβm, (14)
где в формулах (13) и (14) αn – средний нормальный угол зацепления (αn ≈ 20°); βm = 35° – средний угол наклона зуба; δ1 – угол делительного конуса шестерни.
Знаки в скобках:
если смотреть с вершины делительного конуса О, то при совпадении вращения и наклона зубьев верхние знаки, при отсутствии совпадения – нижние.
Знаки результата:
во избежание заклинивания зубьев при значительных зазорах в подшипниках необходимо обеспечить направление осевой силы Fа1 от вершины к внешнему торцу е1, т.е. сила Fа1 должна быть положительной. Это возможно при совпадении вращения и наклона зубьев.
Нормальная сила в зацеплении Fn = Ft / (cosαncosβm).
Для прямых зубьев в формулах сил следует положить βm = 0:
1) Ft1 = Ft2 = 2000Т / dm; 2) Fr1 = Fа2 = Fttgα cosδ1;
3) Fа1 = Fr2 = Fttgα sinδ1; 4) Fn = Ft / cosα.
6.3 Расчет на сопротивление контактной усталости
Исходной является формула (6), которая в параметрах эквивалентной цилиндрической прямозубой передачи имеет вид:
σН = ZEZHZε[FtKH (uv + 1) / (bvdv1uvUН)]1/2,(15)
где UН – коэффициент, учитывающий влияние на несущую способность вида конической передачи: для прямых зубьев UН = 0,85; для круговых зубьев UН является функцией передаточного числа и твердости зубьев (UН > 1). Нагрузочная способность передачи с круговыми зубьями в 1,4…1,5 раза выше, чем с прямыми.
Подставив в формулу (15) значения параметров, после преобразования получим формулу для проверочного расчета стальных конических зубчатых передач на сопротивление контактной усталости при Кbe = 0,285:
σН = 6,7∙104[T2КHu / (U H dе23)]1/2 ≤ σHP,(16)
где КН = KAKНβКНV – коэффициент нагрузки.
По ГОСТ 12289-76 стандартными являются dе2, и, b.
Поэтому в проектировочном расчете по формуле (16) целесообразно определять внешний делительный диаметр колеса
dе2′ = 1650[T2КHu / (U HσHP2)]1/3,
где T2 , Н∙м; σНР , МПа; dе2′, мм .
Диаметр dе2′ округляют в большую сторону по ГОСТ 12289-76 (Ra 20).
7. Расчет на сопротивление усталости при изгибе
Расчет ведут по зубу шестерни.
Исходной является формула (9) для эквивалентной прямозубой цилиндрической передачи, которая для зубьев конической передачи будет иметь вид:
σF1 = Ft КFYFS1 / (bmnmUF) ≤ σFP1; σF2 = σF1YFS2 / YFS1 ≤ σFP2, (17)
где КF = KAKFβКFV – коэффициент нагрузки на изгиб; UF – коэффициент, учитывающий влияние вида конической передачи при изгибе (для прямых зубьев UF = 0,85); YFS – коэффициент формы зуба: определяется по формуле (графикам) для прямозубых цилиндрических передач в зависимости от zvnm = z / (cosδcos3βm).
В проектировочном расчете открытых или закрытых высокотвердых передач (HRC > 56) из условий изгиба (формула (17)) определяют модуль:
mte′ = 14[T1КFYFS1 / (ψmUFz1σFP1)]1/3,
где ψm = b / mte – коэффициент ширины венца по внешнему модулю.
Величинами ψm и z1 следует предварительно задаваться. Модуль mte′ округляют по ГОСТ 9563-60 в большую сторону.
В силовых передачах mte ≥ 1,5…2 мм.
ЧЕРВЯЧНЫЕ ПЕРЕДАЧИ
1. Общие сведения
Червяк (z1)1 (рис. 5.1) – это винт с трапецеидальной или близкой к ней резьбой. Червячное колесо (z2) 2 – косозубое цилиндрическое колесо с вогнутыми по длине зубьями.
Червячная передача – зубчато-винтовая передача с преобразованием движения по принципу винтовой пары. Направление витков червяка и зубьев колеса одинаковое. Ведущим является червяк. Вращение определяется по типу завинчивания винта и гайки. При этом направление вращения колеса зависит от расположения червяка (верхний, нижний).
Тип передачи определяют по червяку.
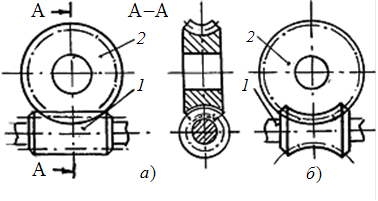
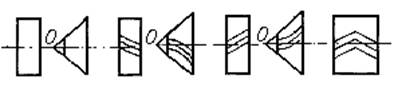
В зависимости от формы внешней поверхности червяка передачи бывают с цилиндрическим 1 (рис. 5.1, а) или глобоидным 1 (рис. 5.1, б) червяком.
|
Рис. 5.1
На практике в основном применяют передачи с цилиндрическими червяками.
В зависимости от способов нарезания винтовой поверхности червяка различают линейчатые (винтовые поверхности могут быть образованы прямой линией) и нелинейчатые червяки.
Нарезание линейчатых червяков осуществляют прямолинейной кромкой резца на токарно-винторезных станках. Это архимедов (его обозначают ZA), конволютный (ZN) и эвольвентный червяки (ZI).
Нелинейчатые червяки нарезают дисковыми фрезами конусной (червяки ZK) или тороидальной (червяки ZT) формы. Витки нелинейчатых червяков во всех сечениях имеют криволинейный профиль: в нормальном к витку сечении выпуклый, в осевом сечении - вогнутый.
Для силовых передач следует применять эвольвентные и нелинейчатые червяки.
В червячных передачах стандартным (ГОСТ 19672-74) является осевой модуль.
На работоспособность червячной передачи сильно влияет жесткость червяка. Для исключения маложестких червяков введен стандартный параметр q – коэффициент диаметра червяка: q = 8; 10; 12,5; 16; 20; 25.
Диаметр делительной окружности, где толщина витка равна ширине впадины, червяка: d1 = mq.
Число заходов (витков) червяка z1 = 1, 2 и колеса d2 = mz2.
|
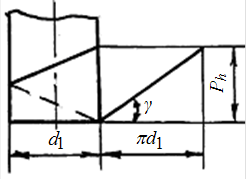
Рис. 5.2 |
Угол a профиля: для червяков ZA, ZN, ZI a = 20°; для ZT a = 22°. Делительный угол g подъема витка червяка (рис. 5.2): tg g = Ph / (pd1), где Ph = Pz1 – ход витка, Р – шаг червяка; tg g = pmz1 / / (pmq) = z1 / q. Зубья червячных колес нарезают червячными фрезами, которые являются копи- ями червяков с режущими кромками на витках |
||
|
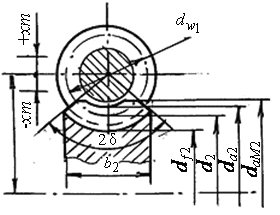
Рис. 5.3 |
и имеют больший (на два размера радиального зазора в зацеплении) наружный диаметр. Заготовка колеса и фреза совершают те же движения, какие имеют червячное колесо и червяк при работе. Основные геометрические размеры венца червячного колеса определяют в среднем его сечении (рис.5.3). Во избежание подреза ножки зуба при нарезании число зубьев z2 принимают больше 28; максимально 80. Оптимальным является z2 = 32…71. Диаметр делительной окружности |
Межосевое расстояние червячной передачи a = 0,5(d1 + d2) = 0,5m(q + z1).
Передаточное число u = z2 / z1. Так как z1 = 1, 2 и 4, z2 = 28…80, то в одной паре можно получить u = 7…80.
Для сокращения номенклатуры червячных фрез (копии червяков) по ГОСТ 2144 – 93 стандартизованы параметры: u, aw, m, q, z1, z2.
С целью вписания передачи с произвольно заданным передаточным числом u в стандартное межосевое расстояние aw выполняют смещение (xm) фрезы при нарезании зубьев колеса (рис. 5.3):
aw = a + xm; aw = 0,5m(q + z2 + 2x), (5.1)
отсюда x = (aw / m) – 0,5(q + z2).
Если a = aw, то x = 0 – передача без смещения. Предпочтительны положительные смещения – повышается прочность зубьев колеса.
Рекомендуют для передач с червяками:
1) ZA, ZN, ZI –1 £ x £ + 1 (предпочтительно x = 0,5). Из формулы (5.1) следует, что при aw = const за счет смещения в пределах x = ± 1 можем иметь z2 = z2ГОСТ m 2, т.е. стандартное число зубьев z2ГОСТ можем изменять в пределах двух зубьев, что позволяет варьировать u = z2 / z1, отличая его от стандартного.
2) ZT 1,0 £ x £ 1,4 (предпочтительно x = 1,1…1,2).
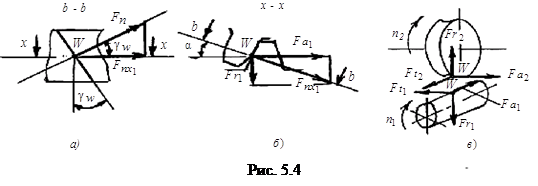
2. Силы в зацеплении
В плоскости зацепления b b (рис. 5.4, а) на витки червяка и зубья колеса действует нормальная сила Fn.
|
|
Ее осевую составляющую Fnx1 раскладываем в осевой плоскости x – x (рис. 5.4, б) червяка на осевую Fa1 и радиальную Fr1 силы. Окружная сила Ft1 = = 2000T1 / dw1 направлена против вращения n1 червяка (рис. 5.4, в – на рис. z1 и z2 условно разнесены). По отношению к зубу колеса Ft1 = Fa2 является осевой силой. Окружная сила Ft2 = 2000T2 / d2 , где T2 = T1uh (h – КПД передачи), направлена в сторону вращения n2 колеса. Для червяка Ft2 = Fa1 является осевой силой, радиальные силы Fr1 = Fr2 = Ft2tga (рис. 5.4, б). Нормальная сила (рис. 5.4, а, б) Fn = Ft2 / (cosacosgw), где gw – угол подъема червяка со смещением.
3. Материалы червячных передач
Вследствие больших скоростей скольжения материалы червячных пар должны иметь антифрикционные свойства и в то же время достаточную прочность.
Червяки изготавливают из среднеуглеродистых сталей марок 45, 50, 40Х, 40ХН с поверхностной закалкой до твердости (45…54) HRC с последующим шлифованием. Хорошо зарекомендовали себя червяки из цементуемых сталей 18ХГТ, 20ХНМ с закалкой до твердости (56…63) HRC.
Материалы зубчатых венцов червячных колес разделены на три группы.
Группа I (наилучшая). Оловянные бронзы (Бр010Ф1, Бр010Н1Ф1, Бр06Ц6С3 и др.) применяют при скоростях скольжения vS = 5…25 м/с. Эти бронзы дефицитны и дороги.
Группа II. Безоловянные бронзы (БрА9Ж4, БрА9Ж3Л и др.) и латуни (Л58Мц2С2 и др.) применяют при vS до 3…5 м/с.
Группа III. Серые чугуны (СЧ15, СЧ18 и др.) применяют при vS £ ≤ 2…3 м/с.
Для выбора материала колеса предварительно определяют скорость vS скольжения, м/с:
vS = 4,5×10 – 4n1(T2)1/3.
В случае применения бронзы или латуни червячные колеса выполняют сборными: центр (ступица с диском) из чугуна или стали и на нем венец из бронзы или латуни.
4. Расчет на прочность
В червячных передачах наиболее опасно усталостное выкрашивание рабочих поверхностей зубьев колеса. Вследствие больших vS и неблагоприятных условий смазки возможно заедание контактирующих поверхностей, когда образуются участки микросварки с резким повышением коэффициента трения и вырывом частиц бронзы (латуни) – как бы «намазывание» их на червяк. Наросты на витках червяка резко повышают изнашивание зубьев колеса. После изнашивания может происходить излом зубьев червячных колес.
Расчет на сопротивление контактной усталости – основной вид расчета, определяющий размеры передачи; проводится с целью предотвращения усталостного выкрашивания и заедания зубьев.
Расчет выполняют по контактным напряжениям sH для зубьев колеса, как выполненных из менее прочного материала, чем стальные витки червяка:
sH = (5350q1 / z2){[(z2 + q1) / (awq1)]3T2KH}1/2 £ sНР , (5.2)
где q1 = q + 2x – коэффициент диаметра червяка со смещением; KH = KHbKHv – коэффициент нагрузки.
Для передач с нелинейчатыми червяками (ZT, ZK) число 5350 в формуле (5.2) следует заменить на 4340.
Формула проектировочного расчета червячных передач:
aw¢ ³ Ka(KHT2 / s2НР)1/3 , (5.3)
где Ka = 610 для линейчатых (ZA, ZN, ZI) и Ka = 530 – для нелинейчатых червяков.
Расчетное значение aw¢ округляют до ближайшего большего по ГОСТ 2144-93. По этому стандарту в зависимости от u и aw уточняют модуль m (m¢ = = 2aw / (q + z2)), q и находят коэффициент смещения x (по формуле (5.1)).
Расчет на изгиб является проверочным по формуле
sF = 1540T2KFYF2cosgw / [(q + 2x)z2m3] £ sFР2, (5.4)
где KF = KFbKFv – коэффициент нагрузки при расчете на изгиб; YF2 – коэффициент формы зуба колеса, его выбирают по таблице для червячных передач в зависимости от эквивалентного числа зубьев: zv2 = z2 / cos3gw.
С целью предотвращения недопустимой концентрации нагрузки в зоне зацепления, что существенно ухудшает работу передачи, ограничивают величину прогиба f в среднем между опорами червяка сечении:
f = (Ft12 + Fr12)1/2l3 / (48EJф) £ [f],
где Ft1, Fr1 – соответственно окружная и радиальная силы на червяке; l – расстояние между опорами червяка (в предварительных расчетах можно принимать l = (1…0,9)d2); Е – модуль упругости стали; Jф фиктивный момент инерции некоторого цилиндрического стержня, эквивалентного червяку по прогибу; [f] = (0,005…0,008)m – допускаемый прогиб, мм.
5. Тепловой расчет
Червячные передачи из-за высокого скольжения и низкого КПД работают с большим тепловыделением.
Нагрев масла выше допустимой температуры [t°]М приводит к снижению его вязкости, потере защитных свойств, разрушению масляной пленки и возможности заедания в передаче.
Тепловой расчет червячной передачи производят на основе теплового баланса, т.е. равенства тепловыделения Qвыд и теплоотдачи Qотд. Из условия
Qвыд = Qотд определяют допустимую температуру tМ масла в корпусе при непрерывной работе и естественном охлаждении
tМ = t0 + 103(1 – h)Р1 / [KTA(1 + y)] £ [t]M,
где t0 – температура воздуха вне корпуса (обычно t0 = 20°C); h - КПД передачи; Р1 – мощность на червяке, кВт; А площадь поверхности редуктора, м2. Поверхность днища не учитывают, так как она не обтекается свободно воздухом; y – коэффициент, учитывающий отвод тепла от днища редуктора в основание; КТ – коэффициент теплоотдачи (тепловой поток в секунду с 1 м2 при перепаде температуры в 1°С) зависит от материала корпуса и скорости циркуляции воздуха. Для чугунного корпуса при естественном охлаждении КТ = 12……18 Вт/(м2×°С).В зависимости от марки масла [t]M = 90…110°С.
Если при расчете получится tМ > [t]M, то необходимо:
1) на корпусе предусмотреть охлаждающие ребра. В расчете дополнительно к площади А учитывают 50% поверхности ребер;
© 2010 Интернет База Рефератов