
Рефераты по сексологии
Рефераты по информатике программированию
Рефераты по биологии
Рефераты по экономике
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Рефераты по авиации и космонавтике
Рефераты по административному праву
Рефераты по безопасности жизнедеятельности
Рефераты по арбитражному процессу
Рефераты по архитектуре
Рефераты по астрономии
Рефераты по банковскому делу
Рефераты по биржевому делу
Рефераты по ботанике и сельскому хозяйству
Рефераты по бухгалтерскому учету и аудиту
Рефераты по валютным отношениям
Рефераты по ветеринарии
Рефераты для военной кафедры
Рефераты по географии
Рефераты по геодезии
Рефераты по геологии
Рефераты по геополитике
Рефераты по государству и праву
Рефераты по гражданскому праву и процессу
Рефераты по делопроизводству
Рефераты по кредитованию
Рефераты по естествознанию
Рефераты по истории техники
Рефераты по журналистике
Рефераты по зоологии
Рефераты по инвестициям
Рефераты по информатике
Исторические личности
Рефераты по кибернетике
Рефераты по коммуникации и связи
Контрольная работа: Моделирование экономических систем
Контрольная работа: Моделирование экономических систем
Задание 1
Раскрыть сущность экономико-математической модели. Привести классификацию экономико-математических моделей; дать понятие экономико-математического моделирования и рассмотреть его этапы.
С понятием «моделирование экономических систем» (а также математических и др.) связаны два класса задач:
задачи анализа, когда система подвергается глубокому изучению ее свойств, структуры и параметров, то есть исследуется предметная область будущего моделирования.
Задачи, связанные с задачами синтеза (получения ЭММ данной системы).
Модель – изображение, представление объекта, системы, процесса в некоторой форме, отличной от реального существования.
Различают физическое и математическое моделирование.
Классификация моделей:
— вещественные
— символьные
— словесно-описательные
1. математические
2. аналитические
· имитационные
· структурные
= формальные
= функциональные
Этапы практического моделирования
1. Анализ экономической системы, ее идентификация и определение достаточной структуры для моделирования.
2. Синтез и построение модели с учетом ее особенностей и математической спецификации.
3. Верификация модели и уточнение ее параметров
4. Уточнение всех параметров системы и соответствие параметров модели, их необходимая валидация (исправление, корректирование).
Задание 3
В качестве примера построим модель оптимального размещения активов для некоторого гипотетического банка, работающего более двух лет, баланс которого приводится в таблицах ниже.
Пассив баланса
| Наименование статей баланса | Сумма, млн. руб. | Риск одновременного снятия, % |
| Средства банков на корреспондентских счетах | 5,1 | 25 |
| Кредиты и депозиты банков (включая НБ РБ) | ||
|
Кредитные ресурсы, полученные от других банков, депозиты других банков до востребования |
2,8 | 55 |
|
Кредитные ресурсы, полученные от других банков, и депозиты других банков с договорными сроками |
3,4 | 0 |
| Средства клиентов | ||
|
Остатки на текущих (расчетных) счетах юридических и физических лиц |
196 | 25 |
| Вклады (депозиты) юридических и физических лиц: | ||
| до востребования | 5,8 | 25 |
| с договорными сроками | 85 | |
| Прочие пассивы | 7,6 | |
| Итого пассивов | 305,7 | |
| Собственный капитал банка | 68 |
Актив баланса
| Наименование статей баланса | Сумма, млн. руб. | Доход-ность, % | Степень риска, % | Ликвид-ность, % |
| Касса и приравненные к ней средства |
х1 |
0 | 0 | 100 |
| Средства на корреспондентских счетах в банках | ||||
| Средства в НБ РБ |
х2 |
0 | 0 | 100 |
| Средства в банках стран – членов ОЭСР до востребования |
х3 |
5 | 30 | 75 |
|
Средства в банках стран, не являющихся членами ОЭСР, до востребования |
х4 |
7 | 65 | 55 |
| Обязательные резервы в НБРБ | 33,5 | 0 | 0 | 0 |
| Кредиты и депозиты банкам | ||||
|
Кредиты банкам-резидентам РБ под обеспечение государственных ценных бумаг РБ в бел. руб. |
х5 |
32 | 0 | 100 |
| Депозиты в банках-резидентах РБ под гарантии НБ РБ |
х6 |
25 | 0 | 100 |
| Кредиты юридическим и физическим лицам: | ||||
|
обеспеченные залогом ценных бумаг, эмитированных юридическими лицами |
х7 |
38 | 100 | 0 |
| обеспеченные гарантийными депозитами в бел. руб. и СКВ |
х8 |
33 | 0 | 0 |
| обеспеченные залогом имущества |
х9 |
39 | 100 | 0 |
| обеспеченные гарантиями и поручительствами юридических лиц |
х10 |
34 | 100 | 0 |
| Государственные ценные бумаги РБ, номинированные в бел. руб. |
х11 |
25 | 0 | 100 |
| Основные средства и нематериальные активы | 12,4 | 0 | 100 | 0 |
Запишем целевую функцию, в данной модели представляющую процентный доход банка от размещения активов, который следует максимизировать:
f(x)= 0,05х3 + 0,07х4 + 0,32х5 + 0,25х6 + 0,38х7 + 0,33х8 + 0,39х9 +
+ 0,34х10 + 0,25х11→max
Первое ограничение следует из условия баланса: сумма активных статей баланса должна быть равна сумме пассивных его статей + собственный капитал
х1 + х2 + х3 + х4 + 33,5 + х5 + х6 + х7 + х8 + х9 + х10 + х11 + 12,4 = 373,7
Второе ограничение следует из норматива по достаточности капитала, при этом предположим, что R = 0
![]()
Третье ограничение следует из норматива мгновенной ликвидности, которое представляет собой отношение балансовых сумм активов и пассивов до востребования и с просроченными сроками:
![]()
Четвертое ограничение следует из норматива краткосрочной ликвидности, которое представляет соотношение фактической и требуемой ликвидности:
![]()
Пятое ограничение запишем исходя из минимально допустимого значения соотношения ликвидных и суммарных активов баланса:
![]()
Шестое ограничение следует из ограниченности совокупной суммы крупных рисков.
Пусть х5≥0,1×68 и х6≥0,1×68, тогда
х5 + х6≤6×68
Седьмое ограничение следует из ограниченности средств, размещенных в банках стран — не членов ОЭСР
х4≤68
Далее запишем ограничения, вытекающие из норматива максимального размера риска на одного клиента, считая для простоты, что одна статья баланса соответствует одному клиенту:
х3≤0,25×68;
х4≤0,25×68; х5≤0,25×68;
х6≤0,25×68; х7≤0,25×68; х8≤0,25×68;
х9≤0,25×68; х10≤0,25×68
![]() В завершение напишем условие
неотрицательности:
В завершение напишем условие
неотрицательности:
хj ≥ 0, j = 1,11![]()
Таким образом, все вышеперечисленные ограничения представляют собой модель оптимального распределения активов банка с рассмотренным выше балансом.
Задание 4
Построить уравнение регрессии, описывающее зависимость прибыли банка (у) от объема межбанковских кредитов и депозитов (х), оценить ее качество и степень зависимости. С помощью построенной регрессии прогнозировать, какой будет средняя прибыль банка при достижении объема межбанковских кредитов и депозитов величины 53 млн. руб.
| № банка | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Кредиты и депозиты | 18 | 23 | 28 | 29 | 34 | 36 | 37 | 42 | 44 | 45 | 49 | 50 |
| Прибыль | 12 | 17 | 15 | 25 | 20 | 32 | 25 | 35 | 30 | 40 | 41 | 45 |
Решение
Информацию, представленную в исходных данных представим графически:
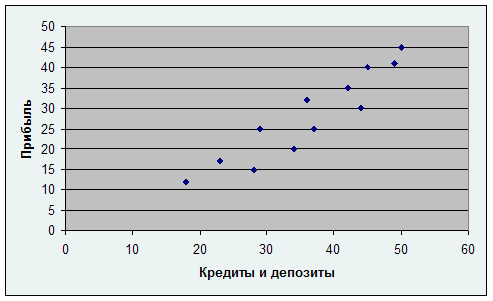
Из диаграммы рассеяния видно, что зависимость между прибылью банка и объемом межбанковских кредитов и депозитов носит линейный характер. Кроме того, исследуется зависимость прибыли банка только от одного фактора — объема межбанковских кредитов и депозитов, поэтому регрессию будем строить в виде
у = а + bх
т.е. это будет простая линейная регрессия. Для расчета ее параметров воспользуемся известными формулами:
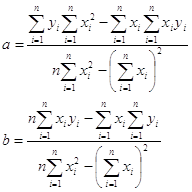
Для этого в рабочей таблице рассчитаем нужные суммы:
| i |
xi |
yi |
xiyi |
xi2 |
yi2 |
| 1 | 18 | 12 | 216 | 324 | 144 |
| 2 | 23 | 17 | 391 | 529 | 289 |
| 3 | 28 | 15 | 420 | 784 | 225 |
| 4 | 29 | 25 | 725 | 841 | 625 |
| 5 | 34 | 20 | 680 | 1156 | 400 |
| 6 | 36 | 32 | 1152 | 1296 | 1024 |
| 7 | 37 | 25 | 925 | 1369 | 625 |
| 8 | 42 | 35 | 1470 | 1764 | 1225 |
| 9 | 44 | 30 | 1320 | 1936 | 900 |
| 10 | 45 | 40 | 1800 | 2025 | 1600 |
| 11 | 49 | 41 | 2009 | 2401 | 1681 |
| 12 | 50 | 45 | 2250 | 2500 | 2025 |
| ∑ | 435 | 337 | 13358 | 16925 | 10763 |
Подставим результаты, полученные в таблице в формулы:
![]()
![]()
Таким образом, уравнение регрессии, описывающее зависимость между прибылью банка и объемом межбанковских кредитов и депозитов, имеет вид:
у = –7,71 + 0,987х
Оценим качество построенной регрессии. Для этого рассчитаем коэффициент детерминации, используя формулу:
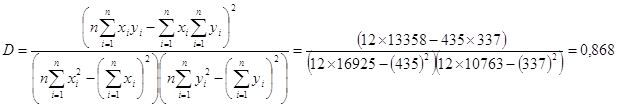
Значение коэффициента детерминации достаточно близко к единице, поэтому качество построенной регрессии хорошее. Можно утверждать, что изменение прибыли банка на 86,8% зависит от изменения межбанковских кредитов и депозитов, и на 13,2% – от прочих факторов.
Степень зависимости между исследуемыми показателями оценивается на основании коэффициента корреляции:
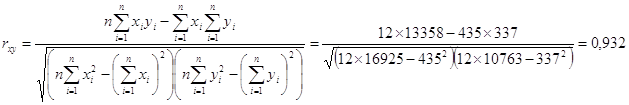
Коэффициент корреляции близок к единице, поэтому имеем достаточно сильную линейную зависимость между прибылью банка и объемом межбанковских кредитов и депозитов.
Так как качество построенной регрессии хорошее, ее можно использовать для прогнозирования. Подставим прогнозное значение хпр = 53 в построенное уравнение регрессии:
упр = –7,71 + 0,987×53 = 44,623 (млн. руб.)
Таким образом, если объем межбанковских кредитов и депозитов достигнет 53 млн. руб., то средняя прибыль коммерческого банка составит 44 млн. 623 тыс. руб.
Задание 5
За компаниями A, B и С проводились наблюдения в течение трех периодов. Данные в процентах приводятся в таблице ниже. Оценить ожидаемую доходность и риск каждой акции, на основании этих оценок дать сравнительную характеристику. Рассчитать ковариации доходностей акций друг с другом. Дать определение эффективного портфеля ценных бумаг и построить модели, позволяющие определить структуру эффективных портфелей.
| Период наблюдения | Доходность компании А | Доходность компании В | Доходность компании С |
| 1 | 27 | 25 | 22 |
| 2 | 30 | 20 | 18 |
| 3 | 33 | 26 | 16 |
Решение
Оценим ожидаемую доходность каждой акции:
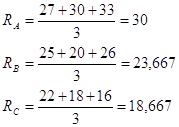
Оценим риск каждой акции, который выражается вариацией:
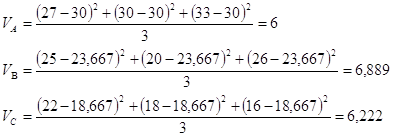
Из приведенных расчетов следует, что самыми привлекательными для инвестора ценными бумагами являются акции компании А, так как они имеют самую высокую ожидаемую доходность и наименьший риск. Если же сравнить между собой компании В и С, то акции компании В имеют несколько большую ожидаемую доходность, но и больший риск, поэтому выбор зависит от отношения инвестора к риску.
Рассчитаем ковариации доходностей акций друг с другом:
![]()
![]()
![]()
Из расчетов видно, что ковариация доходностей компаний А и С отрицательна, т.е. зависимость между доходностями акций этих компаний обратная, под воздействием одних и тех же факторов доходности меняются в разных направлениях. Ковариации доходностей акций компаний А и В, В и С положительные, что свидетельствует о прямой зависимости между доходностями акций этих компаний, под воздействием одних и тех же факторов доходности меняются в одном направлении.
Дадим определение эффективного портфеля. Портфель, имеющий минимальный риск при заданном уровне ожидаемой доходности или максимальную ожидаемую доходность при заданном уровне риска, называется эффективным.
пусть хА, хВ, хС — доли капитала инвестора, вложенные в акции компаний А, В, С соответственно. Сумма долей равна единице, т.е.:
хА + хВ + хС = 1
Так как риск портфеля, составленного из акций компаний А, В и С, выражается формулой:
![]()
а ожидаемая доходность этого же портфеля выражается формулой
![]()
![]() то, подставляя рассчитанные значения вариаций, ковариаций, получаем
модели, определяющие структуру эффективных портфелей:
то, подставляя рассчитанные значения вариаций, ковариаций, получаем
модели, определяющие структуру эффективных портфелей:
![]()
![]()
хА + хВ + хС = 1
![]()
![]()
![]()
хА + хВ + хС = 1
Задание 6
Руководство одного из банков решило разместить ресурсы в операциях с процентным арбитражем с целью получения прибыли от разницы процентных ставок на различных кредитных рынках с учетом изменения валютных курсов. Для проведения операций с процентным арбитражем на домашнем кредитном рынке было приобретено 500000 рос. руб. под 7,5% годовых на месяц. На момент начала операции наиболее привлекательными для банка оказались кредитный рынок США и еврорынок. Процентная ставка по вкладам на месяц на кредитном рынке США равнялась 7,75% годовых, а на еврорынке по вкладам в евро на месяц 7,7% годовых. Соотношение курсов валют было следующее: RUR/€ = 37,7 руб., RUR/$ = 27,8 руб. Через месяц на момент окончания операции прогнозируются следующие курсы валют: с вероятностью 0,4 RUR/ = 36,3 руб., RUR/$ = 28,2 руб., с вероятностью 0,6 RUR/€ = 38,2 руб., RUR/$ = 26,6 руб. Определить наилучшую стратегию размещения ресурсов сроком на один месяц, используя критерии Вальда, Гурвица и Байеса.
Решение
В данной задаче выделяются 2 игрока: руководство банка, принимающее решения, и природа — рынок валют. Предположим, что руководство банка определило для себя три стратегии:
А1 — разместить 500000 руб. на еврорынке;
А2— разместить 500000 руб. на рынке США;
А3— разместить 250000 руб. на рынке США и 250000 руб. на еврорынке.
У природы будут две стратегии, соответствующие двум прогнозам курсов. Для определения наилучшей стратегии построим платежную матрицу. Ее размерность будет 3×2 в соответствии с количеством стратегий.
Элементы платежной матрицы будут равны прибыли, которую получит банк в каждой из возможных ситуаций.
Рассчитаем элемент платежной матрицы а 11:
1. Конвертируем валюту:
500000/37,7 = 13262,6 €
2. Вкладываем получившуюся в валюте сумму на соответствующем рынке на месяц:
13262,6×(1+0,077/12) = 13347,7 €
3. Конвертируем полученную сумму в рубли соответственно стратегии природы:
13347,7×36,3 = 484,521 руб.
4. Рассчитаем сумму, которую нужно вернуть через месяц на домашнем рынке:
500000×(1+0,075/12) = 503125 руб.
5. Находим чистый доход от операции
484521,6 – 503125 = –18603,4 руб.
Аналогично рассчитываются все остальные элементы платежной матрицы. В результате расчетов она принимает вид:
| П1 | П2 | |
| A1 | -18603,45 | 6757,18 |
| A2 | 7344,87 | -21617,96 |
| A3 | 5629,29 | 7430,39 |
Для выбора лучшей стратегии воспользуемся следующими критериями:
1. Критерий Вальда — критерий крайнего пессимизма. Наилучшая, по Вальду, стратегия — соответствующая наибольшему из наименьших выигрышей. Наилучшей, по Вальду, будет стратегия А3, т.е. разместив по 250000 тыс. руб. на рынках США и Европы, банк получит прибыль не менее, чем на 5629,29 руб.
2. Критерий Сэвиджа — критерий минимального риска. Наилучшей, по Сэвиджу, считается стратегия, соответствующая наименьшему из наибольших рисков. Для ее определения построим дополнительную матрицу R:
| П1 | П2 | |
| A1 | 25948,32 | 673,20 |
| A2 | 0,00 | 29048,34 |
| A3 | 1715,59 | 0,00 |
Стратегия А3 соответствует минимальному из максимальных рисков, т.е. наилучшей, по Сэвиджу будет вложение по 250000 руб. на обоих рынках.
3. Критерий Гурвица — критерий пессимизма-оптимизма. Параметр γ в нашем случае равен 0,4. Рассчитаем числа и выберем из них максимальное:
a1 = 0,4×(-18603,45) + 0,6×6757,18 = -3387,07
a2 = 0,4× (-21617,96) + 0,6×7344,87 = -4240,26
a3 = 0,4×5629,29 + 0,6×7430,39 = 6709,95
Таким образом при γ = 0,4, если руководство банка настроено оптимистично оно принимает решение вложить по 250000 руб. на обоих рынках.
4.Критерий Байеса — используется тогда, когда известны вероятности состояний природы. Такая ситуация называется ситуацией риска. Наилучшей, по Байесу, стратегией считается соответствующая наибольшему ожидаемому выигрышу. Рассчитаем а1, а2, а3:
a1 = 0,4× (-18603,45) + 0,6× 6757,18 = -3387,07
a2 = 0,4×7344,87 + 0,6× (-21617,96) = -10032,82
a3 = 0,4×5629,29 + 0,6×7430,39 = 6709,95
Наилучшей, по Байесу, стратегией будет стратегия А3.
Задание 7
Компания рассматривает строительство филиалов в четырех местах, соответственно имеются четыре проекта, продолжительностью 5 лет. Первоначальные инвестиции и доходы по годам приведены в таблице исходных данных. Инвестиционные возможности компании ограничены. В силу определенных соображений сумма расстояний от компании до филиалов не должна превышать 450 км. Из-за ограниченности фонда заработной платы общее число работников филиала на должно превышать 450 человек. Совместное строительство филиалов не допускается, так как они располагаются достаточно близко друг к другу.
Построить модель оптимального распределения инвестиций по проектам, в качестве критерия оптимальности использовать сумму NPV проектов. Ставка дисконта равна 15%.
| Номер проекта |
I0 |
Доходы по годам | ||||
| первый | второй | третий | четвертый | пятый | ||
| первый | 1250 | -200 | 600 | 1200 | 1300 | 1400 |
| второй | 1300 | 100 | 830 | 700 | 570 | 720 |
| третий | 1400 | 500 | 250 | 400 | 320 | 710 |
| четвертый | 2200 | -330 | 1000 | 1150 | 1600 | 1800 |
Решение
Для расчета NPV будем использовать следующую формулу:
![]() i = 1,2,3,4
i = 1,2,3,4
Отсюда:
NPV1 = 1258,12
NPV2 = 558,68
NPV3 = 22,78
NPV4 = 835,05
Введем переменные. Пусть хi, i = 1,2,3,4 характеризует i-й проект и может принимать только 2 значения — 0 или 1. Если хi = 0, это значит, что i-й проект не следует инвестировать. Если хi = 1, то i-й проект следует инвестировать.
Используя введенные переменные запишем целевую функцию:
NPV = 1258,12х1 + 558,68х2 + 22,78х3 + 835,05х4
Теперь запишем ограничения, которые вытекают из условий задачи.
Первое ограничение следует из ограниченности инвестиционных возможностей компании:
1250х1 + 1300х2 + 1400х3 + 2200х4≤5600
Второе ограничение следует из того, что в первом году некоторые проекты еще не требуют инвестиций, которые должны быть покрыты доходами от других проектов:
-200х1 + 100х2 + 500х3 - 300х4≥0
Далее запишем ограничение, вытекающее из ограниченности суммы расстояний:
100х1 + 90х2 + 120х3 + 160х4≤450
Аналогично запишем ограничение, которое следует из того, что общее количество работников филиалов ограничено:
100х1 + 120х2 + 120х3 + 150х4≤450
Наконец, запишем условие того, что второй и третий филиалы одновременно строить нельзя:
х2 + х3 ≤1
![]() Модель оптимального распределения инвестиций по проектам состоит в
максимизации целевой функции при ограничениях, т.е.
Модель оптимального распределения инвестиций по проектам состоит в
максимизации целевой функции при ограничениях, т.е.
NPV = 1258,12х1 + 558,68х2 + 22,78х3 + 835,05х4 (max)
1250х1 + 1300х2 + 1400х3 + 2200х4≤5600
-200х1 + 100х2 + 500х3 - 300х4≥0
100х1 + 90х2 + 120х3 + 160х4≤450
100х1 + 120х2 + 120х3 + 150х4≤450
х2 + х3 ≤1
![]() 0, если i-й проект не
инвестировать
0, если i-й проект не
инвестировать
xi =
1, если i-й проект инвестировать, i=1,2,3,4
© 2010 Интернет База Рефератов