Рефераты по сексологии
Рефераты по информатике программированию
Рефераты по биологии
Рефераты по экономике
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Рефераты по авиации и космонавтике
Рефераты по административному праву
Рефераты по безопасности жизнедеятельности
Рефераты по арбитражному процессу
Рефераты по архитектуре
Рефераты по астрономии
Рефераты по банковскому делу
Рефераты по биржевому делу
Рефераты по ботанике и сельскому хозяйству
Рефераты по бухгалтерскому учету и аудиту
Рефераты по валютным отношениям
Рефераты по ветеринарии
Рефераты для военной кафедры
Рефераты по географии
Рефераты по геодезии
Рефераты по геологии
Рефераты по геополитике
Рефераты по государству и праву
Рефераты по гражданскому праву и процессу
Рефераты по делопроизводству
Рефераты по кредитованию
Рефераты по естествознанию
Рефераты по истории техники
Рефераты по журналистике
Рефераты по зоологии
Рефераты по инвестициям
Рефераты по информатике
Исторические личности
Рефераты по кибернетике
Рефераты по коммуникации и связи
Контрольная работа: Эконометрика
Контрольная работа: Эконометрика
Контрольная работа
По эконометрики
Обзор корреляционного поля
Эти данные скорее всего можно аппроксимировать при помощи линейной регрессии вида ŷ = а - b·x, как самой простой.
Рассчитаем необходимые суммы и запишем их в таблице № 1:
Таблица №1:
|
i |
x |
y |
x² |
y² |
x·y |
ŷ |
e |
e² |
A(%) |
| 2,5 | 69 | 6,25 | 4761 | 172,5 | 66,40 | 2,60 | 6,75 | 3,76 | |
| 2 | 3 | 65 | 9 | 4225 | 195 | 64,85 | 0,15 | 0,02 | 0,23 |
| 3 | 3,4 | 63 | 11,56 | 3969 | 214,2 | 63,61 | -0,61 | 0,37 | 0,97 |
| 4 | 4,1 | 59 | 16,81 | 3481 | 241,9 | 61,44 | -2,44 | 5,94 | 4,13 |
| 5 | 5 | 57 | 25 | 3249 | 285 | 58,65 | -1,65 | 2,71 | 2,89 |
| 6 | 6,3 | 55 | 39,69 | 3025 | 346,5 | 54,61 | 0,39 | 0,15 | 0,70 |
| 7 | 7 | 54 | 49 | 2916 | 378 | 52,44 | 1,56 | 2,43 | 2,89 |
|
Сумма: |
31,3 | 422 | 157,31 | 25626 | 1833,1 | 422,00 | 0,00 | 18,38 | 15,57 |
|
Среднее: |
4,471 | 60,286 | 22,473 | 3660,857 | 261,871 | - | - | - | 2,22% |
Ковариация между y и x рассчитывается по формуле ![]() ,
где
,
где ![]() ,
, ![]() ,
, ![]() . Дисперсия и среднее
квадратическое отклонение для x
и y находим по формулам:
. Дисперсия и среднее
квадратическое отклонение для x
и y находим по формулам:
![]() = 2,479,
= 2,479, ![]() =
26,490,
=
26,490, ![]() 1,575,
1,575, ![]() 5,147.
5,147.
![]() = -7,692 / 2,479 = -3,103;
= -7,692 / 2,479 = -3,103; ![]() = 60,286 + 3,103 · 4,471 =
74,159
= 60,286 + 3,103 · 4,471 =
74,159
Получили уравнение регрессии: ŷ = 74,159 - 3,103·х (округлено до сотых).
Оцениваем качество полученной линейной модели:
а) TSS = 25624 - (31,3²) : 7 = 185,492;
RSS = TSS - ESS =
185,429 - 18,38 = 176,051, где ESS = ![]() = 18,38 (в таблице №1); F - статистика = RSS · (n - m - 1)
: ESS = 176,051 · ·5 :18,38 = 45,45.
= 18,38 (в таблице №1); F - статистика = RSS · (n - m - 1)
: ESS = 176,051 · ·5 :18,38 = 45,45.
Табличное значение на 1% уровне значимости равно 16,26 (см. таблицу распределения Фишера - Снедекора). Фактическое значение F - статистики больше табличного на 1% уровне значимости, следовательно уравнение регрессии в целом значимо и на 5% уровне значимости.
б) Средняя ошибка аппроксимации равна (ΣА)/7 = ((ΣIy-ŷI: y) · 100%) / 7 = 15,57 / 7 = =2,22%, что говорит о хорошей аппроксимации зависимости моделью (2,22% < 6%).
Вывод: модель получилась приемлемая (в смысле аппроксимации).
в) Коэффициент корреляции
находим по формуле: ![]() = -0,949: сильная
обратная линейная зависимость.
= -0,949: сильная
обратная линейная зависимость.
г) Коэффициент детерминации
находим следующим образом: ![]() = 0,901
или вариация x определяет вариацию y на 90,1%.
= 0,901
или вариация x определяет вариацию y на 90,1%.
Проверка на соответствие условиям теоремы Гаусса - Маркова
а) По таблице №2 рассчитаем статистику Дарбина - Уотсона:
Таблица №2
|
i |
e² |
e |
ei-1 |
(ei-ei-1)² |
|
| 1 | 6,75 | 2,60 | - | - | |
| 2 | 0,02 | 0,15 | 2,598 | 5,996 | |
| 3 | 0,37 | -0,61 | 0,149 | 0,576 | |
| 4 | 5,94 | -2,44 | -0,610 | 3,342 | |
| 5 | 2,71 | -1,65 | -2,438 | 0,628 | |
| 6 | 0,15 | 0,39 | -1,646 | 4,134 | |
| 7 | 2,43 | 1,56 | 0,388 | 1,373 | |
| Итого: | 18,38 | - | -1,559 | 16,050 |
Полученное значение
попадает в область неопределённости: DW ![]() (0,7; 1,35). Это значит, что для прояснения вопроса
относительно автокорреляции остатков необходимо дальнейшее исследование ряда
остатков другими методами, в которых отсутствует зона неопределённости.
(0,7; 1,35). Это значит, что для прояснения вопроса
относительно автокорреляции остатков необходимо дальнейшее исследование ряда
остатков другими методами, в которых отсутствует зона неопределённости.
б) Воспользуемся тестом серий Бройша - Годфри:
Таблица №3
|
t |
et |
et-1 |
e²t-1 |
et·et-1 |
êt |
(y-bx)² |
| 1 | 2,598 | 0,149 | 0,022 | 0,387 | 0,074 | 6,371 |
| 2 | 0,149 | -0,610 | 0,372 | -0,091 | -0,302 | 0,204 |
| 3 | -0,610 | -2,438 | 5,944 | 1,487 | -1,208 | 0,358 |
| 4 | -2,438 | -1,646 | 2,709 | 4,013 | -0,816 | 2,632 |
| 5 | -1,646 | 0,388 | 0,151 | -0,639 | 0,192 | 3,379 |
| 6 | 0,388 | 1,559 | 2,430 | 0,605 | 0,773 | 0,148 |
| Итого: |
-1,559 |
-2,598 |
11,628 |
5,763 |
-1,287 | 13,092 |
На основании полученных данных построим уравнение регрессии без свободного члена вида ŷ=b·x. При этом стандартная ошибка коэффициента регрессии b, рассчитанная по формуле:
![]() ,
,
![]() ,
, ![]() = 1,181,
= 1,181,
что меньше значения t табл. =2,57. Это означает, что автокорреляция первого уровня отсутствует.
Однако следует отметить, что и тест Дарбина - Уотсона и тест серий Бройша - Годфри применяются только для выборок достаточно большого размера[1], в то время как предложенная нам для анализа выборка состоит только лишь из семи значений.
в) При помощи критерия серий проверим случайность распределения уровней ряда остатков. С 95% вероятностью распределение ряда остатков считается случайным, если одновременно выполняются два неравенства:
1) 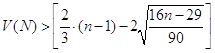
общее число серий должно
быть больше двух, и 2) ![]() -
максимальная длина серии должна быть строго меньше пяти.
-
максимальная длина серии должна быть строго меньше пяти.
Данные для расчётов получаем из таблицы № 4.
Таблица № 4. Критерий серий линейная модель не проходит:
|
ei |
ei - ei-1 |
серии |
Число серий = 2, Продолжительность самой длинной серии равна 3. 2 = хотя 3 < 5. Значит уровни распределены не случайно. |
| 0,149 | -2,449 | + | |
| -0,610 | -0,759 | + | |
| -2,438 | -1,828 | + | |
| -1,646 | 0,792 | - | |
| 0,388 | 2,033 | - | |
| 1,559 | 1,172 | - |
г) Соответствие ряда остатков нормальному закону распределения проверяем, используем RS-критерий:
![]() = 2,63, где
= 2,63, где 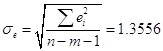 .
.
Значение нашего RS-критерия для 7 наблюдений практически попадает в интервал [2,67 3,69], (для 10 наблюдений) хотя и этот критерий определён для выборок более 10 единиц.
д) При помощи теста ранговой корреляции Спирмена определяем отсутствие или наличие гетероскедастичности.
Таблица № 5.
|
Ранг Х |
Х |
I ei I |
Ранг еi |
Di |
D²i |
Коэффициент ранговой кореляции
определяется по формуле: |
| 1 | 2,5 | 2,60 | 7 | -6 | 36 | |
| 2 | 3 | 0,15 | 4 | -2 | 4 | |
| 3 | 3,4 | 0,61 | 3 | 0 | 0 | |
| 4 | 4,1 | 2,44 | 1 | 3 | 9 | |
| 5 | 5 | 1,65 | 2 | 3 | 9 | |
| 6 | 6,3 | 0,39 | 5 | 1 | 1 | |
| 7 | 7 | 1,56 | 6 | 1 | 1 |
Так как абсолютное
значение статистики коэффициента ранговой корелляции ![]() =0,175 оказалась
значительно меньше табличного значения
=0,175 оказалась
значительно меньше табличного значения ![]() ,
то гетероскедастичность отсутствует.
,
то гетероскедастичность отсутствует.
Вывод: линейная модель не соответствует всем предпосылкам регрессионного анализа (условиям теоремы Гаусса-Маркова) и, хотя она пригодна для прогнозирования, но возникает вопрос о её значимости.
Доверительные интервалы для параметра b регрессии
Стандартные ошибки для параметров регрессии находим по формулам:
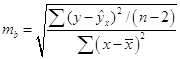 = 0,46,
= 0,46,
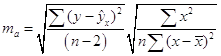 = 2,18.
= 2,18.
Проверим на
статистическую значимость коэффициент b модели, для чего рассчитаем t-статистику по формуле ![]() . Полученная t-статистика равна -6,742, что по
модулю больше табличного значения t =
2,57. Экономически этот параметр интерпретируется так: при изменении дохода потребителей
на одну единицу объёмы продаж изменятся на -3,103 ед.
. Полученная t-статистика равна -6,742, что по
модулю больше табличного значения t =
2,57. Экономически этот параметр интерпретируется так: при изменении дохода потребителей
на одну единицу объёмы продаж изменятся на -3,103 ед.
Проверим на
статистическую значимость коэффициент a модели, для чего рассчитаем t-статистику по формуле ![]() . Полученная t-статистика равна 33,992, что больше
табличного значения t = 2,57. Доверительный
интервал параметра b
определяем по формуле:
. Полученная t-статистика равна 33,992, что больше
табличного значения t = 2,57. Доверительный
интервал параметра b
определяем по формуле:
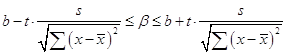 ;
;
s = 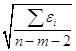 = 1,917,
= 1,917,
Доверительный интервал
параметра b составляет ![]() ; или
; или ![]() (
tтабл. = 2.57, Δ = 2,57 · 0,4602 =
1,1827).
(
tтабл. = 2.57, Δ = 2,57 · 0,4602 =
1,1827).
Проведённый анализ коэффициентов регрессии говорит о том, что параметры регрессии значимы, кроме того и уравнение регрессии в целом значимо на 1% уровне значимости (cм. выше). Это позволяет использовать построенную нами модель для получения прогнозов.
Точечный и интервальный прогнозы
Вначале находим точечный
прогноз для значения х, на 25% превышающего среднее значение ![]() = 4,47 ( т.е. при
= 4,47 ( т.е. при ![]() = 5,589),
= 5,589), ![]() . Тогда стандартная ошибка
прогноза составит:
. Тогда стандартная ошибка
прогноза составит:
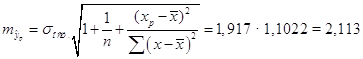 ,
,
tтабл. = 2.57, Δ = 2,57 · 2,18 = 5,604.
Интервальный прогноз для
точечного прогноза при ![]() = 5,589 (
= 5,589 (![]() ) составит:
) составит: ![]() или
или ![]() .
.
[1] Кристофер Доугерти. Введение в эконометрику. М.: Инфра М, 2001. С. 238.
© 2010 Интернет База Рефератов
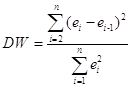 =16,050 : 18,38 = 0,8734.
=16,050 : 18,38 = 0,8734.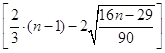 = [2.079] = 2. (не
выполняется),
= [2.079] = 2. (не
выполняется),