Контрольная работа: Парная и множественная регрессия и корреляция

1. Парная линейная регрессия и корреляция

Цель работы - овладеть навыками определения параметров линейной регрессии и корреляции с использованием формул и табличного процессора MS Excel.

1.1 Решение задач с использованием формул

1.1.1 Параметры a и b линейной регрессии

рассчитываются с помощью метода наименьших квадратов. Для этого составим систему нормальных уравнений (1).

По исходным данным определим , , , , в расчетной таблице 1.

Таблица 1 Расчет показателей парной линейной регрессии и корреляции

№				2	2
1	9.8	10.2	99.96	96.04	104.04	9.847	0.035	0.125	-1.575
2	11.3	10.1	114.13	127.69	102.01	10.088	0.001	0.000	11.300
3	11.5	10.1	116.15	132.25	102.01	10.120	-0.002	0.000	11.500
4	11.3	9.2	103.96	127.69	84.64	10.088	-0.096	0.788	11.300
5	10.9	10.7	116.63	118.81	114.49	10.023	0.063	0.458	10.900
6	11.4	9	102.6	129.96	81	10.104	-0.123	1.218	11.400
7	12.6	10.4	131.04	158.76	108.16	10.297	0.010	0.011	12.409
8	12.2	11.1	135.42	148.84	123.21	10.232	0.078	0.753	12.164
Итого	91	80.8	919.89	1040.04	819.56	80.797	-0.034	3.353	79.397
Среднее	11.375	10.1	114.986	130.005	102.445	10.100	-0.004	´	´

Система нормальных уравнений составит:

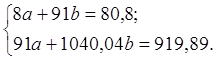
Решив систему, получим: a = 8,2717; b = 0,1607.

Уравнение линейной регрессии имеет вид:

Параметры уравнения можно определить и по следующим формулам:

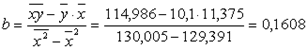
= 10,1 – 0,1608. 11,375= 8,2709

Величина коэффициента регрессии b = 0,1607 означает, что с ростом среднедушевых доходов на 1 тыс. руб. общий коэффициент рождаемости увеличится в среднем на 0,1607 раз.

1.1.2 Средний коэффициент эластичности для линейной регрессии находится по формуле:

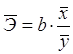
0,181

При увеличении величины среднедушевого дохода на 1%, общий коэффициент рождаемости в среднем увеличится на 0,181%.

1.1.3 Линейный коэффициент парной корреляции (r) определяется по формуле:

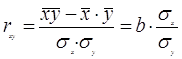где средние квадратические отклонения:

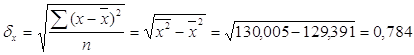
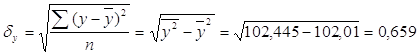
тогда , значит связь между среднедушевым доходом и рождаемостью очень слабая.

1.1.4 Определим коэффициент детерминации:

Таким образом, вариация величины рождаемости на 3,6% зависит от вариации уровня среднедушевых доходов населения, а на остальные (100%-3,6%) 96,4% − от вариации факторов, не включенных в модель.

Подставляя в уравнение регрессии фактические значения x, определим теоретические (расчетные) значения (таблица 1) и найдем величину средней ошибки аппроксимации ():

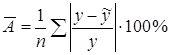==0,425

Так как допустимый предел значений не более 8-10%, качество модели по данному показателю удовлетворительное. Однако средняя ошибка аппроксимации не является главным критерием оценки значимости модели.

С помощью F−критерия Фишера оценим статистическую надежность результатов регрессионного моделирования:

Fфакт==.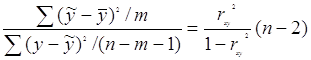

Fтабл = 5,99 при .

Так как Fфакт < Fтабл, уравнение регрессии не значимо, статистически не надежно.

1.2 Решение задачи с помощью MS Excel

1.2.1 Параметры линейной регрессии

можно определить с помощью встроенной статистической функции ЛИНЕЙН MS Excel. Порядок вычисления следующий:

1) ввожу исходные данные (рисунок 1).

2) выделяю область пустых ячеек 5´2 (5 строк, 2 столбца) с целью вывода результатов регрессионной статистики или область 1´2 для получения только оценок коэффициентов регрессии;

3) активизирую Мастер функций любым из способов:

а) в главном меню выбираю Вставка / Функция;

б) на панели инструментов Стандартная щелкаю по кнопке Вставка функции;

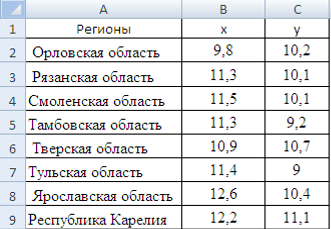
Рисунок 1 Ввод данных для корреляционно-регрессионного анализа

4) в окне «Категория» выбераю Статистические, в окне «Функция» ЛИНЕЙН. Щелкаю по кнопке ОК (рисунок 2);

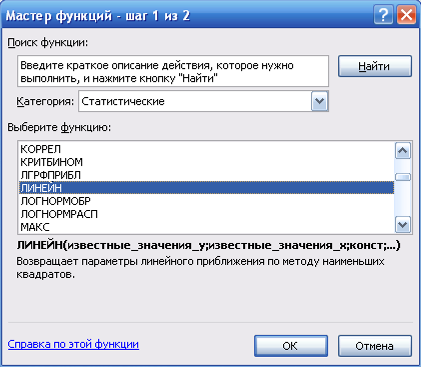
Рисунок 2 Диалоговое окно Мастер функций

5) заполняю аргументы функции (рисунок 3):

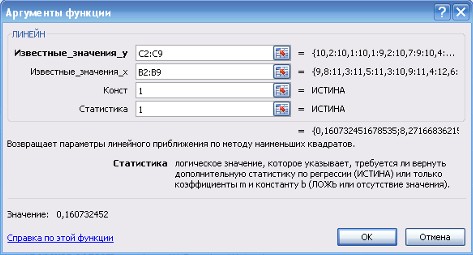
Рисунок 3 Диалоговое окно Аргументы функции

Щелкаю по кнопке ОК;

6) в левой верхней ячейке выделенной области появился первый элемент итоговой таблицы. Чтобы раскрыть всю таблицу, нажимаю на клавишу <F2>, а затем – на комбинацию клавиш <CTRL> + <SHIFT> + <ENTER>.

Дополнительная регрессионная статистика будет выводиться в порядке, указанном в следующей схеме:

Значение коэффициента b	Значение коэффициента a
Среднеквадратическое отклонение b	Среднеквадратическое отклонение a
Коэффициент детерминации R2	Среднеквадратическое отклонение y
F – статистика	Число степеней свободы
Регрессионная сумма квадратов	Остаточная сумма квадратов

Результаты вычислений функции ЛИНЕЙН представлены на рисунке 4.

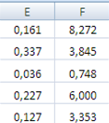
Рисунок 4 Результаты вычислений функции ЛИНЕЙН

1.2.2 С помощью инструмента анализа данных Регрессия, помимо результатов регрессионной статистики, дисперсионного анализа и доверительных интервалов, можно получить остатки и графики подбора линии регрессии, остатков и нормальной вероятности. Порядок действий следующий:

1) проверяю доступ к пакету анализа. В главном меню последовательно выбераю Сервис / Настройки. Устанавливаю флажок Пакет анализа;

2) в главном меню выбираю Сервис / Анализ данных / Регрессия. Щелкаю по кнопке ОК;

3) после вызова режима Регрессия на экране появляется диалоговое окно (рисунок 5), в котором задаются следующие параметры:

Рисунок 5 Диалоговое окно режима Регрессия

Результаты регрессионного анализа для исходных данных представлены на рисунке 6.

Вывод итогов

Регрессионная статистика
Множественный R	0,19101862
R-квадрат	0,03648811
Нормированный R-квадрат	-0,1240972
Стандартная ошибка	0,74755394
Наблюдения	8

Дисперсионный анализ

	df	SS	MS	F	Значимость F
Регрессия	1	0,12697864	0,126978637	0,2272195	0,6504571
Остаток	6	3,35302136	0,558836894
Итого	7	3,48

	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%
Y-пересечение	8,271668362	3,844685341	2,151455224	0,07495556	1,135937744	17,67927447
Переменная X 1	0,160732452	0,337194727	0,476675461	0,6504571	0,664353319	0,985818223

Вывод остатка

Наблюдение	Предсказанное Y	Остатки	Стандартные остатки
1	9,846846389	0,353153611	0,510263509
2	10,08794507	0,012054934	0,017417896
3	10,12009156	-0,020091556	-0,029029827
4	10,08794507	-0,887945066	-1,28297135
5	10,02365209	0,676347915	0,977239505
6	10,10401831	-1,104018311	-1,595170599
7	10,29689725	0,103102747	0,148970781
8	10,23260427	0,867395727	1,253280084

2. Нелинейные модели регрессии и их линеаризация

Цель работы: ознакомиться с методикой расчета показателей парной нелинейной регрессии и корреляции, овладеть приемами построения нелинейных регрессионных моделей с помощью MS Exсel.

РЕШЕНИЕ:

2.1.1 Регрессия в виде степенной функции имеет вид:

Для оценки параметров модели линеаризую (привожу к линейному виду) модель путем логарифмирования: .

Обозначаю lny =Y, lna =A, lnx =X.

Тогда получаю: Y=A+bX.

Для расчетов составляю с помощью MS Excel вспомогательную таблицу, в которой рассчитаю натуральные логарифмы с помощью математической функции LN (рисунок 7).

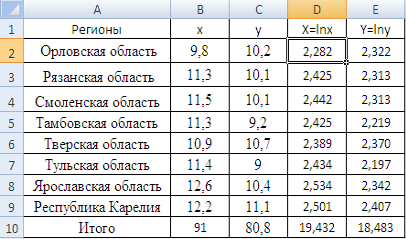
Рисунок 7 Расчет натуральных логарифмов

Далее с помощью инструмента Регрессия рассчитываю параметры уравнения (рисунки 8, 9).

Рисунок 8 Диалоговое окно Регрессия

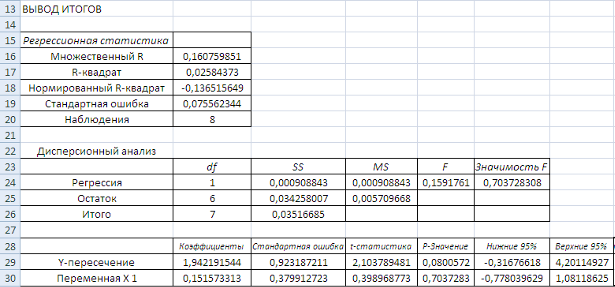
Рисунок 9 Результаты расчета параметров степенной функции

Таким образом, уравнение регрессии имеет вид:

Выполнив потенцирование, получим:

Параметр b=0,151 означает коэффициент эластичности, который показывает, что с ростом величины среднедушевых доходов населения на 1% общий коэффициент рождаемости увеличится в среднем на 0,151%.

2.1.2 Регрессия в виде экспоненты имеет вид:

. (13)

Для оценки ее параметров необходимо привести уравнение к линейному виду:

Для расчета параметров экспоненциальной прямой можно воспользоваться статистической функцией ЛГРФПРИБЛ MS Excel. Результаты вычислений представлены на рисунке 10.

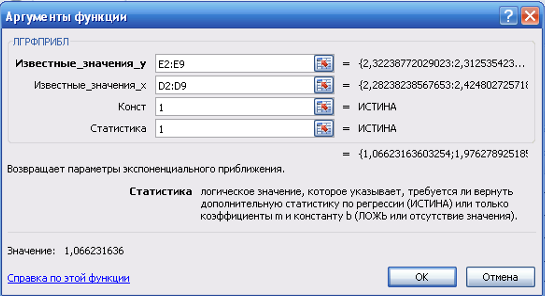
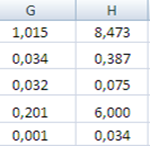
Рисунок 10 Результаты вычислений параметров экспоненциальной функции

Таким образом, уравнение регрессии в виде экспоненты имеет вид:

2.1.3 Регрессия в виде равносторонней гиперболы имеет вид:

чтобы оценить параметры a и b, привожу модель к линейному виду, заменив

Тогда

Результаты замены представлены на рисунке 11.

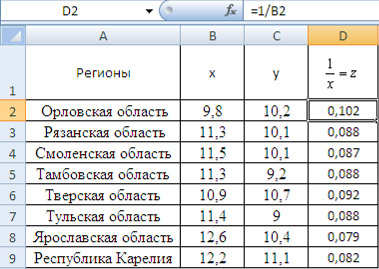
Рисунок 11 Вспомогательная таблица для расчета параметров гиперболы

Далее с помощью инструмента Регрессия рассчитываю параметры уравнения. Результаты расчета представлены на рисунке 12.

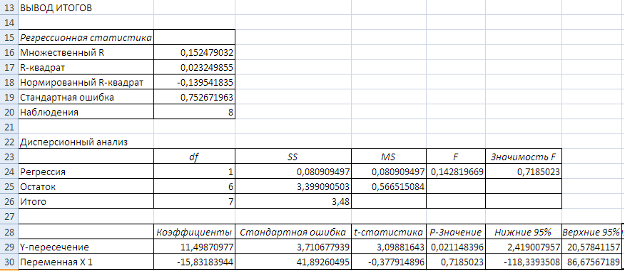
Рисунок 12 Результаты вычислений параметров гиперболической функции

Выберем наилучшую модель, для чего объединим результаты построения парных регрессий в одной таблице 3.

Все уравнения регрессии достаточно хорошо описывают исходные данные.

Таблица 3 Результаты корреляционно-регрессионного анализа

Уравнение регрессии	Коэффициент корреляции	Коэффициент детерминации	F-критерий Фишера
	0,659	0,036	0,227
	0,161	0,026	0,159
	0,179	0,032	0,201
	0,152	0,023	0,143

Предпочтение можно отдать линейной функции, для которой значения коэффициентов корреляции и детерминации и F-критериев Фишера наибольшие.

3. Множественная регрессия

Цель работы – овладеть методикой построения линейных моделей множественной регрессии, оценки их существенности и значимости, расчетом показателей множественной регрессии и корреляции.

Постановка задачи. По данным изучаемых регионов (таблица 1) изучить зависимость общего коэффициента рождаемости () от уровня бедности, % () и среднедушевого дохода, тыс. руб. ().

Таблица 1 Исходные данные для корреляционно-регрессионного анализа

Регион	x1	x2	y
1Орловская область	7,2	19,9	9,6
2 Рязанская область	8,1	17,1	9,4
3 Смоленская область	8,4	17,4	9,6
4 Тамбовская область	8,6	13,5	8,9
5 Тверская область	8,6	14,8	10,2
6 Тульская область	8,4	14,2	8,4
7 Ярославская область	9,9	15,1	9,9
8 Республика Карелия	10,1	17	10,6
9 Республика Коми	16,2	14,5	11,9
10 Архангельская область	11,6	16,1	11,9
11 Вологодская область	10,5	14,8	11,6
12 Калининградская область	11,4	12,4	10,9
13 Ленинградская область	10,6	12,6	8,3
14 Мурманская область	15,2	15,5	10,3
15 Новгородская область	8,6	20,3	10,7
16 Псковская область	7,9	17,1	9,7
17 Республика Адыгея	5,8	30,4	11,8
18 Республика Дагестан	8	13,8	17
19 Респ-ка Ингушетия	4	44,8	16,7
20 Кабардино-Балкарская Республика	6,6	18,3	12,8
21 Респ-ка Калмыкия	4,5	44,2	14,5
22 Карачаево-Черкесская Республика	6,9	18,3	14,2
23 Республика Северная Осетия - Алания	7,9	12,9	13,6
24 Чеченская Республикака	…	...	27,1
25 Краснодарский край	9,8	19,2	11,3

4. Оценка параметров уравнения множественной регрессии

4.1 Оценка параметров с помощью метода определителей

Параметры уравнения множественной регрессии оцениваются, как и в парной регрессии, методом наименьших квадратов (МНК). При его применении строится система нормальных уравнений, решение которой и позволяет получить оценки параметров регрессии.

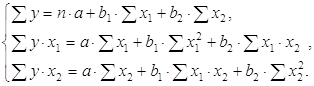
Для оценки параметров уравнения множественной регрессии построим с помощью MS Excel вспомогательную таблицу 2.

Таблица 2 Вспомогательная таблица для расчета параметров уравнения множественной регрессии

№
1	7,2	19,9	9,6	51,8	143,28	396,01	69,12	191,04	92,16
2	8,1	17,1	9,4	65,6	138,51	292,41	76,14	160,74	88,36
3	8,4	17,4	9,6	70,6	146,16	302,76	80,64	167,04	92,16
4	8,6	13,5	8,9	74	116,1	182,25	76,54	120,15	79,21
5	8,6	14,8	10,2	74	127,28	219,04	87,72	150,96	104,04
6	8,4	14,2	8,4	70,6	119,28	201,64	70,56	119,28	70,56
7	9,9	15,1	9,9	98	149,49	228,01	98,01	149,49	98,01
8	10,1	17	10,6	102	171,7	289	107,06	180,2	112,36
9	16,2	14,5	11,9	262	234,9	210,25	192,78	172,55	141,61
10	11,6	16,1	11,9	135	186,76	259,21	138,04	191,59	141,61
11	10,5	14,8	11,6	110	155,4	219,04	121,8	171,68	134,56
12	11,4	12,4	10,9	130	141,36	153,76	124,26	135,16	118,81
13	10,6	12,6	8,3	112	133,56	158,76	87,98	104,58	68,89
14	15,2	15,5	10,3	231	235,6	240,25	156,56	159,65	106,09
15	8,6	20,3	10,7	74	174,58	412,09	92,02	217,21	114,49
16	7,9	17,1	9,7	62,4	135,09	292,41	76,63	165,87	94,09
17	5,8	30,4	11,8	33,6	176,32	924,16	68,44	358,72	139,24
18	8	13,8	17	64	110,4	190,44	136	234,6	289
19	4	44,8	16,7	16	179,2	2007	66,8	748,16	278,89
20	6,6	18,3	12,8	43,6	120,78	334,89	84,48	234,24	163,84
21	4,5	44,2	14,5	20,3	198,9	1953,6	65,25	640,9	210,25
22	6,9	18,3	14,2	47,6	126,27	334,89	97,98	259,86	201,64
23	7,9	12,9	13,6	62,4	101,91	166,41	107,44	175,44	184,96
24	9,8	19,2	11,3	96	188,16	368,64	110,74	216,96	127,69
Итого	214,8	454,2	273,8	2107	3711	10337	2393	5426,07	3252,5
Среднее	8,592	18,2	10,95	84,3	148,44	413,48	95,72	217,043	130,1

На основе расчетов, представленных в таблице 2, получили следующую систему:

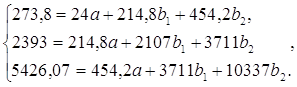
Решаем систему с помощью метода определителей. При этом:

где − определитель системы;

− частные определители.

В результате расчета определителей получили следующие значения:

∆=4702879,56;

∆а=45336681,238, ,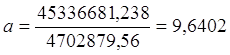

∆b1=–326370,8088, ,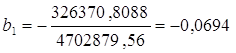

∆b2=593730,7872, .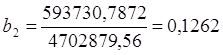

Уравнение множественной регрессии имеет вид:

=9,6402-0,0694х1+0,1262х2.

Таким образом, при увеличении уровня бедности на 1%, общий коэффициент рождаемости в изучаемых регионах снизится на 0,0694 раз, а при увеличении среднедушевого дохода на 1000 руб., общий коэффициент рождаемости увеличится на 0,1262 раз.

4.2 Построение уравнения регрессии в стандартизованном масштабе

Параметры множественной регрессии можно определить другим способом, когда на основе матрицы парных коэффициентов корреляции строится уравнение регрессии в стандартизованном масштабе:

Применяя МНК к уравнению множественной регрессии в стандартизованном масштабе, после соответствующих преобразований получим систему нормальных уравнений вида:

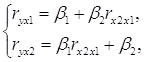
где rух1, rух2 – парные коэффициенты корреляции.

Парные коэффициенты корреляции найдем по формулам:

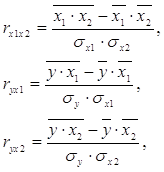
где

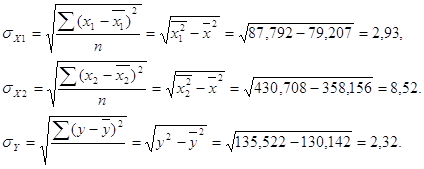
Система уравнений имеет вид:

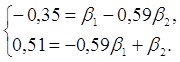
Решив систему методом определителей, получили формулы:

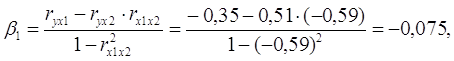
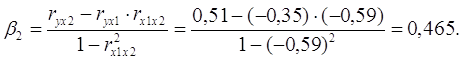
Уравнение в стандартизированном масштабе имеет вид:

Таким образом, с ростом уровня бедности на 1 сигму при неизменном среднедушевом доходе населения, общий коэффициент рождаемости уменьшится на 0,075 сигмы; а с увеличением среднедушевого дохода населения на 1 сигму при неизменном уровне бедности, общий коэффициент рождаемости возрастет на 0,465 сигмы.

Во множественной регрессии коэффициенты «чистой» регрессии bi связаны со стандартизованными коэффициентами регрессии βi следующим образом:

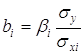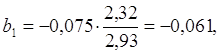
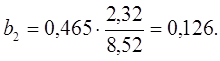
5. Частные уравнения регрессии

5.1 Построение частных уравнений регрессии

Частные уравнения регрессии связывают результативный признак с соответствующими факторами х при закреплении других учитываемых во множественной регрессии факторов на среднем уровне. Частные уравнения имеют вид:

В отличие от парной регрессии частные уравнения регрессии характеризуют изолированное влияние фактора на результат, т.к. другие факторы закреплены на неизменном уровне.

В данной задаче частные уравнения имеют вид:

5.2 Определение частных коэффициентов эластичности

На основе частных уравнений регрессии можно определить частные коэффициенты эластичности для каждого региона по формуле:

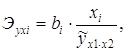
Рассчитаем частные коэффициенты эластичности для Калининградской и Ленинградской областей.

Для Калининградской области х1=11,4, х2=12,4, тогда:

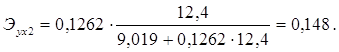
Для Ленинградской области х1 =10,6, х2=12,6:

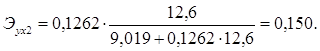
Таким образом, в Калининградской области при увеличении уровня бедности на 1%, общий коэффициент рождаемости сократится на 0,07%, а при увеличении среднедушевых доходов на 1%, общий коэффициент рождаемости возрастет на 0,148%. В Ленинградской области при увеличении уровня бедности на 1%, общий коэффициент рождаемости сократится на 0,065%, а при увеличении среднедушевых доходов на 1%, общий коэффициент рождаемости возрастет на 0,15%.

5.3 Определение средних коэффициентов эластичности

Средние по совокупности показатели эластичности находим по формуле:

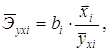
Для данной задачи они окажутся равными:

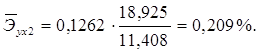
Таким образом, с ростом уровня бедности на 1%, общий коэффициент рождаемости в среднем по совокупности сократится на 0,054% при неизменном среднедушевом доходе. При увеличении среднедушевого дохода на 1%, общий коэффициент рождаемости в среднем по изучаемой совокупности возрастет на 0,209% при неизменном уровне бедности.

6. Множественная корреляция

6.1 Коэффициент множественной корреляции

Практическая значимость уравнения множественной регрессии оценивается с помощью показателя множественной корреляции и его квадрата коэффициента детерминации. Показатель множественной корреляции характеризует тесноту связи рассматриваемого набора факторов с исследуемым признаком, т.е. оценивает тесноту связи совместного влияния факторов на результат.

Величина индекса множественной корреляции должна быть больше или равна максимальному парному индексу корреляции. При линейной зависимости признаков формула индекса корреляции может быть представлена следующим выражением:

Ryx1x2 =.

Таким образом, связь общего коэффициента рождаемости с уровнем бедности и среднедушевым доходом слабая.

6.2 Определение совокупного коэффициента корреляции через матрицу парных коэффициентов корреляции

При линейной зависимости совокупный коэффициент корреляции можно также определить через матрицу парных коэффициентов корреляции:

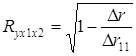Для уравнения

определитель матрицы коэффициентов парной корреляции принимает вид:

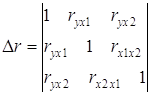
Определитель более низкого порядка ∆r11 остается, когда вычеркиваются из матрицы коэффициентов парной корреляции первый столбец и первая строка, что соответствует матрице коэффициентов парной корреляции между факторами:

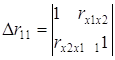В данной задаче ∆r =0,4799, ∆r11= 0,6519.

Тогда

6.3 Определение коэффициента детерминации (скорректированного, нескорректированного)

Качество построенной модели в целом оценивает коэффициент детерминации. Коэффициент множественной детерминации рассчитывается как квадрат индекса множественной корреляции:

Скорректированный индекс множественной детерминации содержит поправку на число степеней свободы и рассчитывается по формуле:

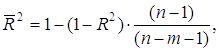
Таким образом, вариация общего коэффициента рождаемости на 27,9% (21% - при скорректированном индексе детерминации) зависит от вариации уровня бедности и среднедушевого дохода, а на остальные 72,1% (79%) от других факторов, не включенных в модель.

6.4 Частные коэффициенты корреляции

Частные коэффициенты корреляции характеризуют тесноту связи между результатом и соответствующим фактором при устранении влияния других факторов, включенных в модель. Формула коэффициента частной корреляции, выраженная через показатель детерминации, для х1 принимает вид:

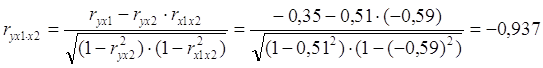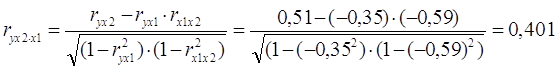Таким образом, при закреплении фактора х2 на постоянном уровне (элиминировании) корреляция у и х1 равна -0,937, то есть связь обратная сильная. При закреплении фактора х1 на постоянном уровне корреляция у и х2 равна 0,401, то есть связь прямая слабая.

7. Оценка надежности результатов множественной регрессии и корреляции

7.1 Оценка значимости уравнения с помощью F-критерия Фишера

Значимость уравнения множественной регрессии в целом, оценивается с помощью F-критерия Фишера по формуле:

При этом выдвигается гипотеза о статистической незначимости уравнения регрессии и показателя тесноты связи.

Fтабл. =4,32 (при k1=m=2 и k2=n-m-1=24-2-1=21.

Так как Fфакт. < Fтабл, то гипотезу (Н0) принимаем. С вероятностью 95% делаем вывод о статистической не значимости уравнения в целом и показателя тесноты связи, которые сформировались под неслучайным воздействием факторов х1, х2.

7.2 Расчет частных F-критериев

Частные F-критерии оценивают статистическую значимость присутствия факторов х1 и х2 в уравнении множественной регрессии, оценивают целесообразность включения в уравнение одного фактора после другого фактора, т.е. Fх1 оценивает целесообразность включения в уравнение фактора х1 после того, как в него был включен фактор х2. Соответственно, Fx2 указывает на целесообразность включения в модель фактора х2 после фактора х1. Определим частные F-критерии для факторов х1 и х2 по формулам:

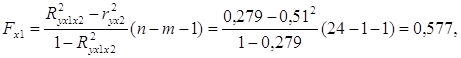
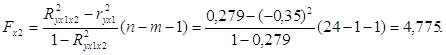
Fтабл. = 4,32.

Таким образом, низкое значение Fх1факт. свидетельствует о нецелесообразности включения в модель фактора х1 (уровень бедгости). Включение же фактора х2 в модель статистически целесообразно. Это означает, что парная регрессионная модель зависимости общего коэффициента рождаемости от среднедушевого дохода является достаточно статистически значимой, надежной и нет необходимости улучшать ее, включая дополнительный фактор х1.

7.3 Оценка значимости коэффициентов чистой регрессии по t-критерию Стьюдента

Частный F-критерий оценивает значимость коэффициентов чистой регрессии:

tтабл.=2,0796.

Так как tb1 < tтабл., то фактор х1 статистически незначим, а так как tb2> tтабл., то фактор х2 статистически значим.

8. Результаты регрессионного анализа в Excel

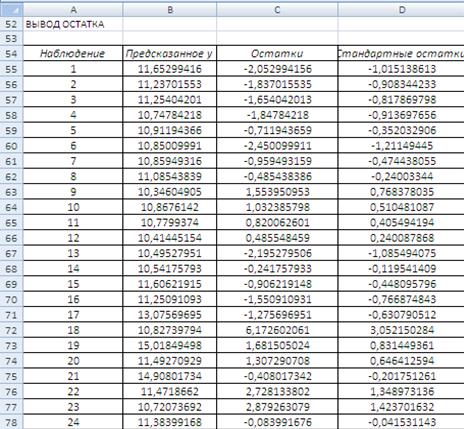
Рисунок 1 Результат применения инструмента Регрессия