
Рефераты по сексологии
Рефераты по информатике программированию
Рефераты по биологии
Рефераты по экономике
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Рефераты по авиации и космонавтике
Рефераты по административному праву
Рефераты по безопасности жизнедеятельности
Рефераты по арбитражному процессу
Рефераты по архитектуре
Рефераты по астрономии
Рефераты по банковскому делу
Рефераты по биржевому делу
Рефераты по ботанике и сельскому хозяйству
Рефераты по бухгалтерскому учету и аудиту
Рефераты по валютным отношениям
Рефераты по ветеринарии
Рефераты для военной кафедры
Рефераты по географии
Рефераты по геодезии
Рефераты по геологии
Рефераты по геополитике
Рефераты по государству и праву
Рефераты по гражданскому праву и процессу
Рефераты по делопроизводству
Рефераты по кредитованию
Рефераты по естествознанию
Рефераты по истории техники
Рефераты по журналистике
Рефераты по зоологии
Рефераты по инвестициям
Рефераты по информатике
Исторические личности
Рефераты по кибернетике
Рефераты по коммуникации и связи
Контрольная работа: Парная регрессия
Контрольная работа: Парная регрессия
Смысл регрессионного анализа – построение функциональных зависимостей между двумя группами переменных величин Х1, Х2, … Хр и Y. При этом речь идет о влиянии переменных Х (это будут аргументы функций) на значения переменной Y (значение функции). Переменные Х мы будем называть факторами, а Y – откликом.
Наиболее простой случай – установление зависимости одного отклика y от одного фактора х. Такой случай называется парной (простой) регрессией.
Парная регрессия – уравнение связи двух переменных у и x:
![]() ,
,
где у – зависимая переменная (результативный признак);
х – независимая, объясняющая переменная (признак-фактор).
Различают линейные и нелинейные регрессии.
Линейная регрессия:![]() .
.
Нелинейные регрессии делятся на два класса: регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам, и регрессии, нелинейные по оцениваемым параметрам.
Регрессии, нелинейные по объясняющим переменным:
• полиномы разных степеней ![]()
•равносторонняя гипербола ![]()
Регрессии, нелинейные по оцениваемым параметрам:
•
степенная ![]() ;
;
•
показательная ![]()
•
экспоненциальная ![]()
Построение уравнения регрессии сводится к оценке ее параметров.
Для оценки параметров регрессий, линейных по параметрам, используют метод
наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров,
при которых сумма квадратов отклонений фактических значений результативного
признака у от теоретических ![]() минимальна, т.е.
минимальна, т.е.
![]()
Для линейных и нелинейных уравнений, приводимых к линейным, решается следующая система относительно а и b:
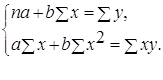
Можно воспользоваться готовыми формулами, которые вытекают из этой системы:
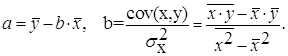
Тесноту связи изучаемых явлений оценивает линейный коэффициент
парной корреляции ![]() для линейной регрессии
для линейной регрессии ![]()
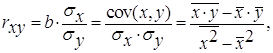
и индекс корреляции ![]() - для нелинейной регрессии
(
- для нелинейной регрессии
(![]() ):
):
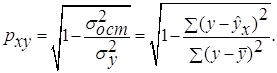
Оценку качества построенной модели даст коэффициент (индекс) детерминации, а также средняя ошибка аппроксимации.
Средняя ошибка аппроксимации – среднее отклонение расчетных значений от фактических:
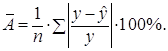
Допустимый предел значений ![]() – не
более 8 – 10%.
– не
более 8 – 10%.
Средний коэффициент эластичности ![]() показывает, на сколько процентов в
среднем по совокупности изменится результат у от своей средней величины
при изменении фактора x на 1% от своего среднего
значения:
показывает, на сколько процентов в
среднем по совокупности изменится результат у от своей средней величины
при изменении фактора x на 1% от своего среднего
значения:
![]()
Задача дисперсионного анализа состоит в анализе дисперсии зависимой переменной:
![]()
где ![]() – общая сумма квадратов отклонений;
– общая сумма квадратов отклонений;
![]() – сумма квадратов отклонений, обусловленная
регрессией («объясненная» или «факторная»);
– сумма квадратов отклонений, обусловленная
регрессией («объясненная» или «факторная»);
![]() – остаточная сумма квадратов отклонений.
– остаточная сумма квадратов отклонений.
Долю дисперсии, объясняемую регрессией, в общей дисперсии результативного признака у характеризует коэффициент (индекс) детерминации R2:
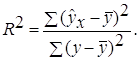
Коэффициент детерминации – квадрат коэффициента или индекса корреляции.
F-тест – оценивание качества уравнения регрессии – состоит в проверке гипотезы Но о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического Fфакт и критического (табличного) Fтабл значений F-критерия Фишера. Fфакт определяется из соотношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы:
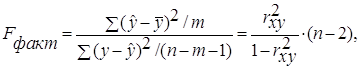
п – число единиц совокупности;
т – число параметров при переменных х.
Fтабл – это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости а. Уровень значимости а – вероятность отвергнуть правильную гипотезу при условии, что она верна. Обычно а принимается равной 0,05 или 0,01.
Если Fтабл < Fфакт, то H0 – гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность. Если Fтабл > Fфакт, то гипотеза Н0 не отклоняется и признается статистическая незначимость, ненадежность уравнения регрессии.
Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитываются t-критерий Стьюдента и доверительные интервалы каждого из показателей. Выдвигается гипотеза Н0 о случайной природе показателей, т.е. о незначимом их отличии от нуля. Оценка значимости коэффициентов регрессии и корреляции с помощью f-критерия Стьюдента проводится путем сопоставления их значений с величиной случайной ошибки:
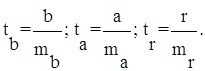
Случайные ошибки параметров линейной регрессии и коэффициента корреляции определяются по формулам:
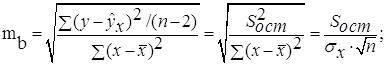
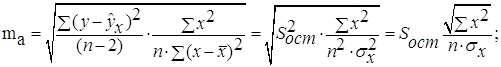
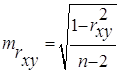
Сравнивая фактическое и критическое (табличное) значения t-статистики – tтабл и tфакт – принимаем или отвергаем гипотезу Hо.
Связь между F-критерием Фишера и t-статистикой Стьюдента выражается равенством
![]()
Если tтабл < tфакт, то Hо отклоняется, т.е. а, b и ![]() не случайно отличаются от
нуля и сформировались под влиянием систематически действующего фактора х. Если
tтабл > tфакт, то гипотеза Но
не отклоняется и признается случайная природа формирования a, b или
не случайно отличаются от
нуля и сформировались под влиянием систематически действующего фактора х. Если
tтабл > tфакт, то гипотеза Но
не отклоняется и признается случайная природа формирования a, b или ![]() .
.
Для расчета доверительного интервала определяем предельную ошибку ∆ для каждого показателя:
![]()
Формулы для расчета доверительных интервалов имеют следующий вид:
![]()
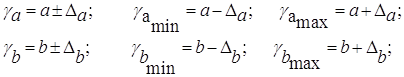
Если в границы доверительного интервала попадает ноль, т.е. нижняя граница отрицательна, а верхняя положительна, то оцениваемый параметр принимается нулевым, так как он не может одновременно принимать и положительное, и отрицательное значения.
Прогнозное значение ![]() определяется
путем подстановки в уравнение регрессии
определяется
путем подстановки в уравнение регрессии ![]() соответствующего
(прогнозного) значения
соответствующего
(прогнозного) значения ![]() . Вычисляется средняя стандартная
ошибка прогноза
. Вычисляется средняя стандартная
ошибка прогноза ![]() :
:
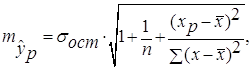 где
где 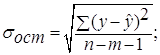
и строится доверительный интервал прогноза:
![]() где
где ![]()
Задача:
По 22 регионам страны изучается зависимость розничной продажи телевизоров, y от среднедушевых денежных доходов в месяц, x (табл. 1):
| № региона | X | Y |
| 1,000 | 2,800 | 28,000 |
| 2,000 | 2,400 | 21,300 |
| 3,000 | 2,100 | 21,000 |
| 4,000 | 2,600 | 23,300 |
| 5,000 | 1,700 | 15,800 |
| 6,000 | 2,500 | 21,900 |
| 7,000 | 2,400 | 20,000 |
| 8,000 | 2,600 | 22,000 |
| 9,000 | 2,800 | 23,900 |
| 10,000 | 2,600 | 26,000 |
| 11,000 | 2,600 | 24,600 |
| 12,000 | 2,500 | 21,000 |
| 13,000 | 2,900 | 27,000 |
| 14,000 | 2,600 | 21,000 |
| 15,000 | 2,200 | 24,000 |
| 16,000 | 2,600 | 34,000 |
| 17,000 | 3,300 | 31,900 |
| 19,000 | 3,900 | 33,000 |
| 20,000 | 4,600 | 35,400 |
| 21,000 | 3,700 | 34,000 |
| 22,000 | 3,400 | 31,000 |
Задание
1. Постройте поле корреляции и сформулируйте гипотезу о форме связи.
2. Рассчитайте параметры уравнений линейной, степенной, экспоненциальной, полулогарифмической, обратной, гиперболической парной регрессий.
3. Оцените тесноту связи с помощью показателей корреляции и детерминации.
4. С помощью среднего (общего) коэффициента эластичности дайте сравнительную оценку силы связи фактора с результатом.
5. Качество уравнений оцените с помощью средней ошибки аппроксимации.
6. С помощью F-критерия Фишера определите статистическую надежность результатов регрессионного моделирования. Выберите лучшее уравнение регрессии и дайте его обоснование.
7. Рассчитайте прогнозное значение результата по линейному уравнению регрессии, если прогнозное значение фактора увеличится на 7% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости α=0,05.
8. Оцените полученные результаты, выводы оформите в аналитической записке.
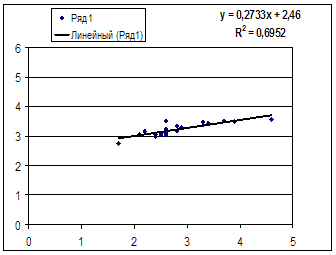
1. Поле корреляции для:
· Линейной регрессии y=a+b*x:
·
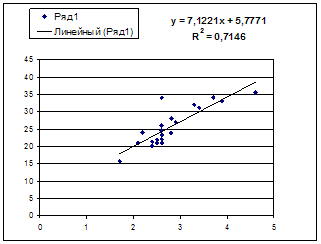
Гипотеза о форме связи: чем больше размер среднедушевого денежного дохода в месяц (факторный признак), тем больше при прочих равных условиях розничная продажа телевизоров (результативный признак). В данной модели параметр b называется коэффициентом регрессии и показывает, насколько в среднем отклоняется величина результативного признака у при отклонении величины факторного признаках на одну единицу.
·
Степенной регрессии ![]() :
:
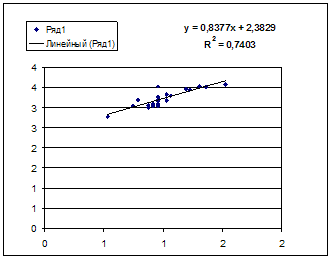
Гипотеза о форме связи: степенная функция имеет вид Y=axb.
Параметр b степенного уравнения называется показателем эластичности и указывает, на сколько процентов изменится у при возрастании х на 1%. При х = 1 a = Y.
·
Экспоненциальная регрессия ![]() :
:
·
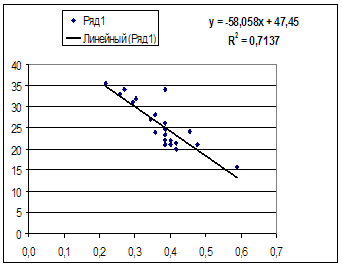
Равносторонняя гипербола 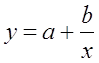 :
:
Гипотеза о форме связи: В ряде случаев обратная связь между факторным и результативным признаками может быть выражена уравнением гиперболы: Y=a+b/x.
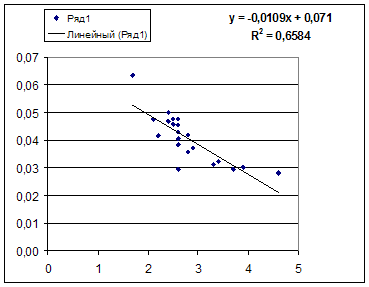
·
Обратная гипербола 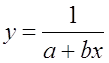 :
:
·
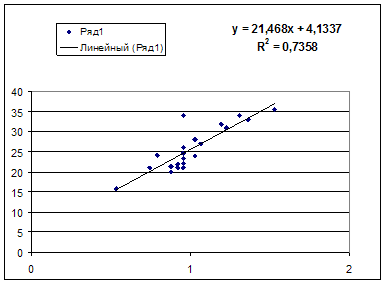
Полулогарифмическая регрессия ![]() :
:
2. Рассчитайте параметры уравнений линейной, степенной, экспоненциальной, полулогарифмической, обратной, гиперболической парной регрессий.
· Рассчитаем параметры уравнений линейной парной регрессии. Для расчета параметров a и b линейной регрессии y=a+b*x решаем систему нормальных уравнений относительно a и b:
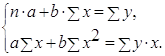
По исходным данным рассчитываем ∑y, ∑x, ∑yx, ∑x2, ∑y2 (табл. 2):
| № региона | X | Y | XY | X^2 | Y^2 | Y^cp | Y-Y^cp | Ai |
| 1 | 2,800 | 28,000 | 78,400 | 7,840 | 784,000 | 25,719 | 2,281 | 0,081 |
| 2 | 2,400 | 21,300 | 51,120 | 5,760 | 453,690 | 22,870 | -1,570 | 0,074 |
| 3 | 2,100 | 21,000 | 44,100 | 4,410 | 441,000 | 20,734 | 0,266 | 0,013 |
| 4 | 2,600 | 23,300 | 60,580 | 6,760 | 542,890 | 24,295 | -0,995 | 0,043 |
| 5 | 1,700 | 15,800 | 26,860 | 2,890 | 249,640 | 17,885 | -2,085 | 0,132 |
| 6 | 2,500 | 21,900 | 54,750 | 6,250 | 479,610 | 23,582 | -1,682 | 0,077 |
| 7 | 2,400 | 20,000 | 48,000 | 5,760 | 400,000 | 22,870 | -2,870 | 0,144 |
| 8 | 2,600 | 22,000 | 57,200 | 6,760 | 484,000 | 24,295 | -2,295 | 0,104 |
| 9 | 2,800 | 23,900 | 66,920 | 7,840 | 571,210 | 25,719 | -1,819 | 0,076 |
| 10 | 2,600 | 26,000 | 67,600 | 6,760 | 676,000 | 24,295 | 1,705 | 0,066 |
| 11 | 2,600 | 24,600 | 63,960 | 6,760 | 605,160 | 24,295 | 0,305 | 0,012 |
| 12 | 2,500 | 21,000 | 52,500 | 6,250 | 441,000 | 23,582 | -2,582 | 0,123 |
| 13 | 2,900 | 27,000 | 78,300 | 8,410 | 729,000 | 26,431 | 0,569 | 0,021 |
| 14 | 2,600 | 21,000 | 54,600 | 6,760 | 441,000 | 24,295 | -3,295 | 0,157 |
| 15 | 2,200 | 24,000 | 52,800 | 4,840 | 576,000 | 21,446 | 2,554 | 0,106 |
| 16 | 2,600 | 34,000 | 88,400 | 6,760 | 1156,000 | 24,295 | 9,705 | 0,285 |
| 17 | 3,300 | 31,900 | 105,270 | 10,890 | 1017,610 | 29,280 | 2,620 | 0,082 |
| 19 | 3,900 | 33,000 | 128,700 | 15,210 | 1089,000 | 33,553 | -0,553 | 0,017 |
| 20 | 4,600 | 35,400 | 162,840 | 21,160 | 1253,160 | 38,539 | -3,139 | 0,089 |
| 21 | 3,700 | 34,000 | 125,800 | 13,690 | 1156,000 | 32,129 | 1,871 | 0,055 |
| 22 | 3,400 | 31,000 | 105,400 | 11,560 | 961,000 | 29,992 | 1,008 | 0,033 |
| Итого | 58,800 | 540,100 | 1574,100 | 173,320 | 14506,970 | 540,100 | 0,000 | |
| сред значение | 2,800 | 25,719 | 74,957 | 8,253 | 690,808 | 0,085 | ||
| станд. откл | 0,643 | 5,417 |
Система нормальных уравнений составит:
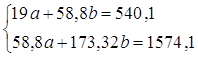
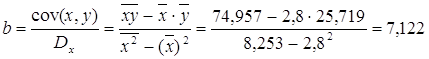
![]()
![]() Ур-ие регрессии: = 5,777+7,122∙x. Данное уравнение показывает, что с
увеличением среднедушевого денежного дохода в месяц
на 1 тыс. руб. доля розничных продаж телевизоров повышается в среднем на 7,12%.
Ур-ие регрессии: = 5,777+7,122∙x. Данное уравнение показывает, что с
увеличением среднедушевого денежного дохода в месяц
на 1 тыс. руб. доля розничных продаж телевизоров повышается в среднем на 7,12%.
·
Рассчитаем параметры уравнений степенной парной регрессии.
Построению степенной модели ![]() предшествует процедура
линеаризации переменных. В примере линеаризация производится путем
логарифмирования обеих частей уравнения:
предшествует процедура
линеаризации переменных. В примере линеаризация производится путем
логарифмирования обеих частей уравнения:
![]() где
где ![]()
Для расчетов используем данные табл. 3:
| № рег | X | Y | XY | X^2 | Y^2 | Yp^cp | y^cp |
| 1 | 1,030 | 3,332 | 3,431 | 1,060 | 11,104 | 3,245 | 25,67072 |
| 2 | 0,875 | 3,059 | 2,678 | 0,766 | 9,356 | 3,116 | 22,56102 |
| 3 | 0,742 | 3,045 | 2,259 | 0,550 | 9,269 | 3,004 | 20,17348 |
| 4 | 0,956 | 3,148 | 3,008 | 0,913 | 9,913 | 3,183 | 24,12559 |
| 5 | 0,531 | 2,760 | 1,465 | 0,282 | 7,618 | 2,827 | 16,90081 |
| 6 | 0,916 | 3,086 | 2,828 | 0,840 | 9,526 | 3,150 | 23,34585 |
| 7 | 0,875 | 2,996 | 2,623 | 0,766 | 8,974 | 3,116 | 22,56102 |
| 8 | 0,956 | 3,091 | 2,954 | 0,913 | 9,555 | 3,183 | 24,12559 |
| 9 | 1,030 | 3,174 | 3,268 | 1,060 | 10,074 | 3,245 | 25,67072 |
| 10 | 0,956 | 3,258 | 3,113 | 0,913 | 10,615 | 3,183 | 24,12559 |
| 11 | 0,956 | 3,203 | 3,060 | 0,913 | 10,258 | 3,183 | 24,12559 |
| 12 | 0,916 | 3,045 | 2,790 | 0,840 | 9,269 | 3,150 | 23,34585 |
| 13 | 1,065 | 3,296 | 3,509 | 1,134 | 10,863 | 3,275 | 26,4365 |
| 14 | 0,956 | 3,045 | 2,909 | 0,913 | 9,269 | 3,183 | 24,12559 |
| 15 | 0,788 | 3,178 | 2,506 | 0,622 | 10,100 | 3,043 | 20,97512 |
| 16 | 0,956 | 3,526 | 3,369 | 0,913 | 12,435 | 3,183 | 24,12559 |
| 17 | 1,194 | 3,463 | 4,134 | 1,425 | 11,990 | 3,383 | 29,4585 |
| 19 | 1,361 | 3,497 | 4,759 | 1,852 | 12,226 | 3,523 | 33,88317 |
| 20 | 1,526 | 3,567 | 5,443 | 2,329 | 12,721 | 3,661 | 38,90802 |
| 21 | 1,308 | 3,526 | 4,614 | 1,712 | 12,435 | 3,479 | 32,42145 |
| 22 | 1,224 | 3,434 | 4,202 | 1,498 | 11,792 | 3,408 | 30,20445 |
| итого | 21,115 | 67,727 | 68,921 | 22,214 | 219,361 | 67,727 | 537,270 |
| сред зн | 1,005 | 3,225 | 3,282 | 1,058 | 10,446 | 3,225 | |
| стан откл | 0,216 | 0,211 |
Рассчитаем С и b:
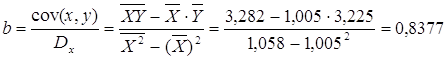
![]()
Получим линейное уравнение: ![]() . Выполнив
его потенцирование, получим:
. Выполнив
его потенцирование, получим: ![]()
Подставляя в данное уравнение фактические значения х, получаем теоретические значения результата y.
·
Рассчитаем параметры уравнений экспоненциальной парной регрессии.
Построению экспоненциальной модели ![]() предшествует процедура
линеаризации переменных. В примере линеаризация производится путем
логарифмирования обеих частей уравнения:
предшествует процедура
линеаризации переменных. В примере линеаризация производится путем
логарифмирования обеих частей уравнения:
![]() где
где ![]()
Для расчетов используем данные табл. 4:
| № региона | X | Y | XY | X^2 | Y^2 | Yp | y^cp |
| 1 | 2,800 | 3,332 | 9,330 | 7,840 | 11,104 | 3,225 | 25,156 |
| 2 | 2,400 | 3,059 | 7,341 | 5,760 | 9,356 | 3,116 | 22,552 |
| 3 | 2,100 | 3,045 | 6,393 | 4,410 | 9,269 | 3,034 | 20,777 |
| 4 | 2,600 | 3,148 | 8,186 | 6,760 | 9,913 | 3,170 | 23,818 |
| 5 | 1,700 | 2,760 | 4,692 | 2,890 | 7,618 | 2,925 | 18,625 |
| 6 | 2,500 | 3,086 | 7,716 | 6,250 | 9,526 | 3,143 | 23,176 |
| 7 | 2,400 | 2,996 | 7,190 | 5,760 | 8,974 | 3,116 | 22,552 |
| 8 | 2,600 | 3,091 | 8,037 | 6,760 | 9,555 | 3,170 | 23,818 |
| 9 | 2,800 | 3,174 | 8,887 | 7,840 | 10,074 | 3,225 | 25,156 |
| 10 | 2,600 | 3,258 | 8,471 | 6,760 | 10,615 | 3,170 | 23,818 |
| 11 | 2,600 | 3,203 | 8,327 | 6,760 | 10,258 | 3,170 | 23,818 |
| 12 | 2,500 | 3,045 | 7,611 | 6,250 | 9,269 | 3,143 | 23,176 |
| 13 | 2,900 | 3,296 | 9,558 | 8,410 | 10,863 | 3,252 | 25,853 |
| 14 | 2,600 | 3,045 | 7,916 | 6,760 | 9,269 | 3,170 | 23,818 |
| 15 | 2,200 | 3,178 | 6,992 | 4,840 | 10,100 | 3,061 | 21,352 |
| 16 | 2,600 | 3,526 | 9,169 | 6,760 | 12,435 | 3,170 | 23,818 |
| 17 | 3,300 | 3,463 | 11,427 | 10,890 | 11,990 | 3,362 | 28,839 |
| 19 | 3,900 | 3,497 | 13,636 | 15,210 | 12,226 | 3,526 | 33,978 |
| 20 | 4,600 | 3,567 | 16,407 | 21,160 | 12,721 | 3,717 | 41,140 |
| 21 | 3,700 | 3,526 | 13,048 | 13,690 | 12,435 | 3,471 | 32,170 |
| 22 | 3,400 | 3,434 | 11,676 | 11,560 | 11,792 | 3,389 | 29,638 |
| Итого | 58,800 | 67,727 | 192,008 | 173,320 | 219,361 | 67,727 | 537,053 |
| сред зн | 2,800 | 3,225 | 9,143 | 8,253 | 10,446 | ||
| стан откл | 0,643 | 0,211 |
Рассчитаем С и b:
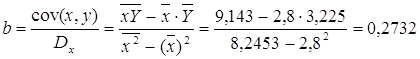
![]()
Получим линейное уравнение: ![]() . Выполнив
его потенцирование, получим:
. Выполнив
его потенцирование, получим: ![]()
Для расчета
теоретических значений y подставим в уравнение ![]() значения x.
значения x.
·
Рассчитаем параметры уравнений полулогарифмической парной
регрессии. Построению полулогарифмической модели ![]() предшествует
процедура линеаризации переменных. В примере линеаризация производится путем
замены:
предшествует
процедура линеаризации переменных. В примере линеаризация производится путем
замены:
![]() где
где ![]()
Для расчетов используем данные табл. 5:
| № региона | X | Y | XY | X^2 | Y^2 | y^cp |
| 1 | 1,030 | 28,000 | 28,829 | 1,060 | 784,000 | 26,238 |
| 2 | 0,875 | 21,300 | 18,647 | 0,766 | 453,690 | 22,928 |
| 3 | 0,742 | 21,000 | 15,581 | 0,550 | 441,000 | 20,062 |
| 4 | 0,956 | 23,300 | 22,263 | 0,913 | 542,890 | 24,647 |
| 5 | 0,531 | 15,800 | 8,384 | 0,282 | 249,640 | 15,525 |
| 6 | 0,916 | 21,900 | 20,067 | 0,840 | 479,610 | 23,805 |
| 7 | 0,875 | 20,000 | 17,509 | 0,766 | 400,000 | 22,928 |
| 8 | 0,956 | 22,000 | 21,021 | 0,913 | 484,000 | 24,647 |
| 9 | 1,030 | 23,900 | 24,608 | 1,060 | 571,210 | 26,238 |
| 10 | 0,956 | 26,000 | 24,843 | 0,913 | 676,000 | 24,647 |
| 11 | 0,956 | 24,600 | 23,506 | 0,913 | 605,160 | 24,647 |
| 12 | 0,916 | 21,000 | 19,242 | 0,840 | 441,000 | 23,805 |
| 13 | 1,065 | 27,000 | 28,747 | 1,134 | 729,000 | 26,991 |
| 14 | 0,956 | 21,000 | 20,066 | 0,913 | 441,000 | 24,647 |
| 15 | 0,788 | 24,000 | 18,923 | 0,622 | 576,000 | 21,060 |
| 16 | 0,956 | 34,000 | 32,487 | 0,913 | 1156,000 | 24,647 |
| 17 | 1,194 | 31,900 | 38,086 | 1,425 | 1017,610 | 29,765 |
| 19 | 1,361 | 33,000 | 44,912 | 1,852 | 1089,000 | 33,351 |
| 20 | 1,526 | 35,400 | 54,022 | 2,329 | 1253,160 | 36,895 |
| 21 | 1,308 | 34,000 | 44,483 | 1,712 | 1156,000 | 32,221 |
| 22 | 1,224 | 31,000 | 37,937 | 1,498 | 961,000 | 30,406 |
| Итого | 21,115 | 540,100 | 564,166 | 22,214 | 14506,970 | 540,100 |
| сред зн | 1,005 | 25,719 | 26,865 | 1,058 | 690,808 | |
| стан откл | 0,216 | 5,417 |
Рассчитаем a и b:
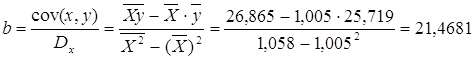
![]()
Получим линейное уравнение: ![]() .
.
·
Рассчитаем параметры уравнений обратной парной регрессии. Для
оценки параметров приведем обратную модель 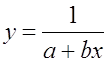 к
линейному виду, заменив
к
линейному виду, заменив ![]() , тогда
, тогда ![]()
Для расчетов используем данные табл. 6:
| № региона | X | Y | XY | X^2 | Y^2 | Y^cp |
| 1 | 2,800 | 0,036 | 0,100 | 7,840 | 0,001 | 24,605 |
| 2 | 2,400 | 0,047 | 0,113 | 5,760 | 0,002 | 22,230 |
| 3 | 2,100 | 0,048 | 0,100 | 4,410 | 0,002 | 20,729 |
| 4 | 2,600 | 0,043 | 0,112 | 6,760 | 0,002 | 23,357 |
| 5 | 1,700 | 0,063 | 0,108 | 2,890 | 0,004 | 19,017 |
| 6 | 2,500 | 0,046 | 0,114 | 6,250 | 0,002 | 22,780 |
| 7 | 2,400 | 0,050 | 0,120 | 5,760 | 0,003 | 22,230 |
| 8 | 2,600 | 0,045 | 0,118 | 6,760 | 0,002 | 23,357 |
| 9 | 2,800 | 0,042 | 0,117 | 7,840 | 0,002 | 24,605 |
| 10 | 2,600 | 0,038 | 0,100 | 6,760 | 0,001 | 23,357 |
| 11 | 2,600 | 0,041 | 0,106 | 6,760 | 0,002 | 23,357 |
| 12 | 2,500 | 0,048 | 0,119 | 6,250 | 0,002 | 22,780 |
| 13 | 2,900 | 0,037 | 0,107 | 8,410 | 0,001 | 25,280 |
| 14 | 2,600 | 0,048 | 0,124 | 6,760 | 0,002 | 23,357 |
| 15 | 2,200 | 0,042 | 0,092 | 4,840 | 0,002 | 21,206 |
| 16 | 2,600 | 0,029 | 0,076 | 6,760 | 0,001 | 23,357 |
| 17 | 3,300 | 0,031 | 0,103 | 10,890 | 0,001 | 28,398 |
| 19 | 3,900 | 0,030 | 0,118 | 15,210 | 0,001 | 34,844 |
| 20 | 4,600 | 0,028 | 0,130 | 21,160 | 0,001 | 47,393 |
| 21 | 3,700 | 0,029 | 0,109 | 13,690 | 0,001 | 32,393 |
| 22 | 3,400 | 0,032 | 0,110 | 11,560 | 0,001 | 29,301 |
| Итого | 58,800 | 0,853 | 2,296 | 173,320 | 0,036 | 537,933 |
| сред знач | 2,800 | 0,041 | 0,109 | 8,253 | 0,002 | |
| стан отклон | 0,643 | 0,009 |
Рассчитаем a и b:
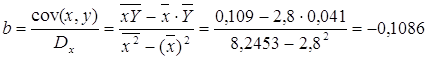
![]()
Получим линейное уравнение: ![]() . Выполнив
его потенцирование, получим:
. Выполнив
его потенцирование, получим: 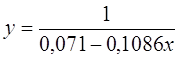
Для расчета
теоретических значений y подставим в уравнение ![]() значения
x.
значения
x.
·
Рассчитаем параметры уравнений равносторонней гиперболы парной
регрессии. Для оценки параметров приведем модель равносторонней гиперболы 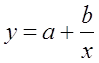 к линейному виду, заменив
к линейному виду, заменив ![]() , тогда
, тогда ![]()
Для расчетов используем данные табл. 7:
| № региона | X=1/z | Y | XY | X^2 | Y^2 | Y^cp |
| 1 | 0,357 | 28,000 | 10,000 | 0,128 | 784,000 | 26,715 |
| 2 | 0,417 | 21,300 | 8,875 | 0,174 | 453,690 | 23,259 |
| 3 | 0,476 | 21,000 | 10,000 | 0,227 | 441,000 | 19,804 |
| 4 | 0,385 | 23,300 | 8,962 | 0,148 | 542,890 | 25,120 |
| 5 | 0,588 | 15,800 | 9,294 | 0,346 | 249,640 | 13,298 |
| 6 | 0,400 | 21,900 | 8,760 | 0,160 | 479,610 | 24,227 |
| 7 | 0,417 | 20,000 | 8,333 | 0,174 | 400,000 | 23,259 |
| 8 | 0,385 | 22,000 | 8,462 | 0,148 | 484,000 | 25,120 |
| 9 | 0,357 | 23,900 | 8,536 | 0,128 | 571,210 | 26,715 |
| 10 | 0,385 | 26,000 | 10,000 | 0,148 | 676,000 | 25,120 |
| 11 | 0,385 | 24,600 | 9,462 | 0,148 | 605,160 | 25,120 |
| 12 | 0,400 | 21,000 | 8,400 | 0,160 | 441,000 | 24,227 |
| 13 | 0,345 | 27,000 | 9,310 | 0,119 | 729,000 | 27,430 |
| 14 | 0,385 | 21,000 | 8,077 | 0,148 | 441,000 | 25,120 |
| 15 | 0,455 | 24,000 | 10,909 | 0,207 | 576,000 | 21,060 |
| 16 | 0,385 | 34,000 | 13,077 | 0,148 | 1156,000 | 25,120 |
| 17 | 0,303 | 31,900 | 9,667 | 0,092 | 1017,610 | 29,857 |
| 19 | 0,256 | 33,000 | 8,462 | 0,066 | 1089,000 | 32,564 |
| 20 | 0,217 | 35,400 | 7,696 | 0,047 | 1253,160 | 34,829 |
| 21 | 0,270 | 34,000 | 9,189 | 0,073 | 1156,000 | 31,759 |
| 22 | 0,294 | 31,000 | 9,118 | 0,087 | 961,000 | 30,374 |
| Итого | 7,860 | 540,100 | 194,587 | 3,073 | 14506,970 | 540,100 |
| сред знач | 0,374 | 25,719 | 9,266 | 0,146 | 1318,815 | |
| стан отклон | 0,079 | 25,639 |
Рассчитаем a и b:
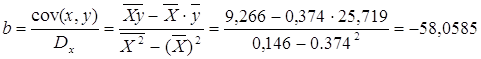
![]()
Получим линейное уравнение: ![]() . Получим
уравнение регрессии:
. Получим
уравнение регрессии: 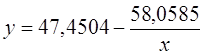 .
.
3. Оценка тесноты связи с помощью показателей корреляции и детерминации:
·
Линейная модель. Тесноту линейной связи оценит коэффициент
корреляции. Был получен следующий коэффициент корреляции rxy=b![]() =7,122*
=7,122*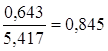 , что говорит о прямой сильной связи фактора
и результата. Коэффициент детерминации r²xy=(0,845)²=0,715. Это
означает, что 71,5% вариации результативного признака (розничная продажа телевизоров, у) объясняется вариацией
фактора х – среднедушевой денежный доход в месяц.
, что говорит о прямой сильной связи фактора
и результата. Коэффициент детерминации r²xy=(0,845)²=0,715. Это
означает, что 71,5% вариации результативного признака (розничная продажа телевизоров, у) объясняется вариацией
фактора х – среднедушевой денежный доход в месяц.
·
Степенная модель. Тесноту нелинейной связи оценит индекс
корреляции. Был получен следующий индекс корреляции 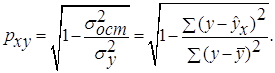 =
=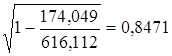 , что говорит о очень сильной тесной связи, но немного больше чем
в линейной модели. Коэффициент детерминации r²xy=0,7175. Это означает, что 71,75%
вариации результативного признака (розничная
продажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в
месяц.
, что говорит о очень сильной тесной связи, но немного больше чем
в линейной модели. Коэффициент детерминации r²xy=0,7175. Это означает, что 71,75%
вариации результативного признака (розничная
продажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в
месяц.
· Экспоненциальная модель. Был получен следующий индекс корреляции ρxy=0,8124, что говорит о том, что связь прямая и очень сильная, но немного слабее, чем в линейной и степенной моделях. Коэффициент детерминации r²xy=0,66. Это означает, что 66% вариации результативного признака (розничная продажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.
· Полулогарифмическая модель. Был получен следующий индекс корреляции ρxy=0,8578, что говорит о том, что связь прямая и очень сильная, но немного больше чем в предыдущих моделях. Коэффициент детерминации r²xy=0,7358. Это означает, что 73,58% вариации результативного признака (розничная продажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.
· Гиперболическая модель. Был получен следующий индекс корреляции ρxy=0,8448 и коэффициент корреляции rxy=-0,1784 что говорит о том, что связь обратная очень сильная. Коэффициент детерминации r²xy=0,7358. Это означает, что 73,5% вариации результативного признака (розничная продажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.
· Обратная модель. Был получен следующий индекс корреляции ρxy=0,8114 и коэффициент корреляции rxy=-0,8120, что говорит о том, что связь обратная очень сильная. Коэффициент детерминации r²xy=0,6584. Это означает, что 65,84% вариации результативного признака (розничная продажа телевизоров, у) объясняется вариацией фактора х – среднедушевой денежный доход в месяц.
Вывод: по полулогарифмическому уравнению получена наибольшая оценка тесноты связи: ρxy=0,8578 (по сравнению с линейной, степенной, экспоненциальной, гиперболической, обратной регрессиями).
4. С помощью среднего (общего) коэффициента эластичности дайте сравнительную оценку силы связи фактора с результатом.
Рассчитаем коэффициент эластичности для линейной модели:
· Для уравнения прямой: y = 5,777+7,122∙x
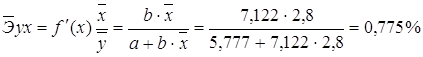
·
Для уравнения степенной модели ![]() :
:
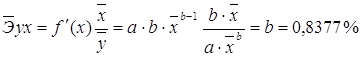
·
Для уравнения экспоненциальной модели![]() :
:
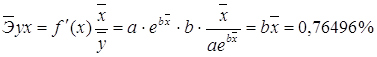
Для
уравнения полулогарифмической модели ![]() :
:
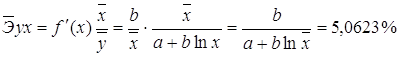
·
Для уравнения обратной
гиперболической модели 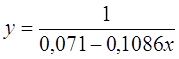 :
:
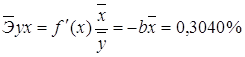
·
Для уравнения равносторонней
гиперболической модели 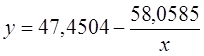 :
:
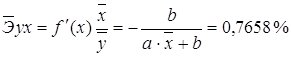
Сравнивая значения ![]() , характеризуем оценку силы связи фактора с
результатом:
, характеризуем оценку силы связи фактора с
результатом:
·
![]()
·
![]()
·
![]()
·
![]()
·
![]()
·
![]()
Известно, что коэффициент эластичности показывает связь между фактором и результатом, т.е. на сколько% изменится результат y от своей средней величины при изменении фактора х на 1% от своего среднего значения. В данном примере получилось, что самая большая сила связи между фактором и результатом в полулогарифмической модели, слабая сила связи в обратной гиперболической модели.
5. Оценка качества уравнений с помощью средней ошибки аппроксимации.
Подставляя в уравнение регрессии фактические значения х, определим
теоретические (расчетные) значения ![]() . Найдем величину
средней ошибки аппроксимации
. Найдем величину
средней ошибки аппроксимации ![]() :
:
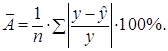
В среднем расчетные значения отклоняются от фактических на:
·
Линейная регрессия. ![]() =
=![]() *100%= 8,5%, что говорит о повышенной ошибке аппроксимации, но в
допустимых пределах.
*100%= 8,5%, что говорит о повышенной ошибке аппроксимации, но в
допустимых пределах.
Качество построенной модели оценивается как хорошее, так как ![]() не превышает 8 -10%.
не превышает 8 -10%.
·
Степенная регрессия. ![]() =
=![]() *100%= 8,2%, что говорит о повышенной ошибке аппроксимации, но в
допустимых пределах.
*100%= 8,2%, что говорит о повышенной ошибке аппроксимации, но в
допустимых пределах.
Качество построенной модели оценивается как хорошее, так как ![]() не превышает 8 -10%.
не превышает 8 -10%.
·
Экспоненциальная регрессия. ![]() =
=![]() *100%= 9%, что говорит о повышенной ошибке аппроксимации, но в
допустимых пределах.
*100%= 9%, что говорит о повышенной ошибке аппроксимации, но в
допустимых пределах.
Качество построенной модели оценивается как хорошее, так как ![]() не превышает 8 -10%.
не превышает 8 -10%.
·
Полулогарифмическая регрессия. ![]() =
=![]() *100%= 7,9 что говорит о повышенной ошибке аппроксимации, но в
допустимых пределах.
*100%= 7,9 что говорит о повышенной ошибке аппроксимации, но в
допустимых пределах.
Качество построенной модели оценивается как хорошее, так как ![]() не превышает 8 -10%.
не превышает 8 -10%.
·
Гиперболическая регрессия. ![]() =
=![]() *100%= 9,3 что говорит о повышенной ошибке аппроксимации, но в
допустимых пределах.
*100%= 9,3 что говорит о повышенной ошибке аппроксимации, но в
допустимых пределах.
Качество построенной модели оценивается как хорошее, так как ![]() не превышает 8 -10%.
не превышает 8 -10%.
·
Обратная регрессия. ![]() =
=![]() *100%= 9,9 3 что говорит о повышенной ошибке аппроксимации, но в
допустимых пределах.
*100%= 9,9 3 что говорит о повышенной ошибке аппроксимации, но в
допустимых пределах.
Качество построенной модели оценивается как хорошее, так как ![]() не превышает 8 -10%.
не превышает 8 -10%.
6. Рассчитаем F-критерий:
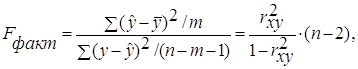
·
Линейная регрессия. ![]() =
= 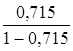 *19= 47,579
*19= 47,579
где ![]() =4,38<
=4,38< ![]()
·
Степенная регрессия. ![]() =
=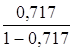 *19= 48,257
*19= 48,257
где ![]() =4,38<
=4,38< ![]()
·
Экспоненциальная регрессия. ![]() =
=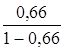 *19= 36,878
*19= 36,878
где ![]() =4,38<
=4,38< ![]()
·
Полулогарифмическая регрессия. ![]() =
=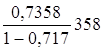 *19= 52,9232
*19= 52,9232
где ![]() =4,38<
=4,38< ![]()
·
Гиперболическая регрессия. ![]() =
=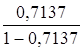 *19= 47,357
*19= 47,357
где ![]() =4,38<
=4,38< ![]()
·
Обратная регрессия. ![]() =
=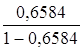 *19= 36,627
*19= 36,627
где ![]() =4,38<
=4,38< ![]()
Для всех регрессий ![]() =4,38<
=4,38< ![]() , из чего
следует, что уравнения регрессии статистически значимы.
, из чего
следует, что уравнения регрессии статистически значимы.
Вывод: ![]() остается
на допустимом уровне для всех уравнений регрессий.
остается
на допустимом уровне для всех уравнений регрессий.
| А | R^2 | Fфакт | |
| Линейная модель | 8,5 | 0,714 | 47,500 |
| Степенная модель | 8,2 | 0,718 | 48,250 |
| Полулогарифмическая модель | 7,9 | 0,736 | 52,920 |
| Экспоненциальная модель | 9,0 | 0,660 | 36,870 |
| Равносторонняя гипербола | 9,3 | 0,714 | 47,350 |
| Обратная гипербола | 9,9 | 0,453 | 15,700 |
Все уравнения регрессии достаточно хорошо описывают исходные данные. Некоторое предпочтение можно отдать полулогарифмической функции, для которой значение R^2 наибольшее, а ошибка аппроксимации – наименьшая
7. Рассчитаем прогнозное значение результата по линейному уравнению регрессии, если прогнозное значение фактора увеличится на 7% от его среднего уровня. Определим доверительный интервал прогноза для уровня значимости α=0,05:
Прогнозное значение ![]() определяется путем подстановки в уравнение регрессии
определяется путем подстановки в уравнение регрессии ![]() соответствующего (прогнозного) значения
соответствующего (прогнозного) значения ![]() .
.
![]() 5,777+7,122*2,996=27,114
5,777+7,122*2,996=27,114
где ![]() =
= ![]() =2,8*1,07=2,996
=2,8*1,07=2,996
Средняя стандартная ошибка прогноза ![]() :
:
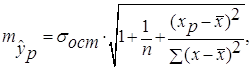 =
=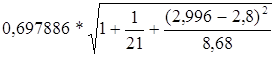 =3,12
=3,12
где 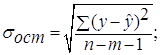 =
=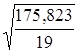 =0,697886
=0,697886
Предельная ошибка прогноза:
![]()
![]()
![]()
Доверительный интервал прогноза
![]() где
где ![]()
![]() =27,11
=27,11![]() 6,53;
6,53;
![]()
![]() 27,11–6,53 = 20,58
27,11–6,53 = 20,58
27,11+6,53 = 33,64
Выполненный прогноз среднедушевых
денежных доходов в месяц, x оказался надежным (р = 1 – α
= 1 – 0,05 = 0,95), но неточным, так как диапазон верхней и нижней границ
доверительного интервала ![]() составляет 2,09 раза:
составляет 2,09 раза:
![]() =
=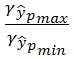 =
=![]() =1,63
=1,63
© 2010 Интернет База Рефератов