
Рефераты по сексологии
Рефераты по информатике программированию
Рефераты по биологии
Рефераты по экономике
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Рефераты по авиации и космонавтике
Рефераты по административному праву
Рефераты по безопасности жизнедеятельности
Рефераты по арбитражному процессу
Рефераты по архитектуре
Рефераты по астрономии
Рефераты по банковскому делу
Рефераты по биржевому делу
Рефераты по ботанике и сельскому хозяйству
Рефераты по бухгалтерскому учету и аудиту
Рефераты по валютным отношениям
Рефераты по ветеринарии
Рефераты для военной кафедры
Рефераты по географии
Рефераты по геодезии
Рефераты по геологии
Рефераты по геополитике
Рефераты по государству и праву
Рефераты по гражданскому праву и процессу
Рефераты по делопроизводству
Рефераты по кредитованию
Рефераты по естествознанию
Рефераты по истории техники
Рефераты по журналистике
Рефераты по зоологии
Рефераты по инвестициям
Рефераты по информатике
Исторические личности
Рефераты по кибернетике
Рефераты по коммуникации и связи
Контрольная работа: Расчет вероятностей событий
Контрольная работа: Расчет вероятностей событий
Какова вероятность того, что наудачу взятое натуральное число не делится:
а) ни на два, ни на три;
б) на два или на три?
Решение:
Пусть А – событие, что натуральное число делится на 2→ p(A)=1/2 (каждое второе натуральное число кратно 2)
В-событие, что натуральное число делится на 3
p(В)=1/3 (каждое третье натуральное число кратно 3)
а) С – событие, что наудачу взятое натуральное число не делится ни на
два, ни на три ![]()
Вероятность произведения двух независимых событий А и В равна произведению их вероятностей
Тогда вероятность события С:
![]()
Т.е. пять из шести натуральных чисел не делится ни на 2 ни на 3
б) D – событие, что наудачу взятое натуральное число не делится на 2
или на 3 ![]() .
.
Вероятность суммы двух несовместных событий А и В равна сумме вероятностей этих событий
Тогда вероятность события D:
![]() .
.
Т.е. одно из трех натуральных чисел не делится на 2 или на 3
Задание №2
В ружейной пирамиде имеются винтовки двух систем: одна винтовка типа 1 и две винтовки типа 2. Вероятность попасть в мишень при выстреле из винтовки типа 1 равна р1, из винтовки типа 2 – р2.
Стрелок производит 7 выстрелов из наудачу взятой винтовки. Чему равна вероятность того, что мишень окажется поражённой не менее пяти раз?
Решение:
А – событие, что поражена мишень
Пусть событие Н1 – винтовка I типа; событие Н2 – винтовка II типа.
![]() и
и ![]()
А/Н1 – мишень поражена при выстреле из винтовки I типа
А/Н2 – мишень поражена при выстреле из винтовки II типа
![]()
![]()
Для
нахождения вероятности ![]() применяют формулу
применяют формулу
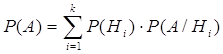
![]()
2. Рn (k) – вероятность, что в n испытаниях событие
наступит k раз находится по формуле Бернулли 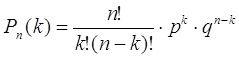 .
.
Вероятность события, что мишень окажется поражённой не менее пяти раз, если произведено 7 выстрелов из наудачу взятой винтовки.
![]()
![]()
Задание №3
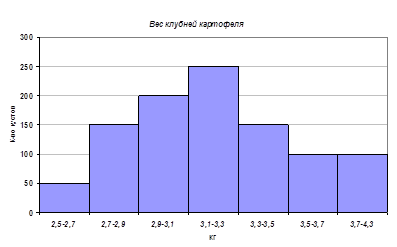
При измерении урожайности картофеля вес клубней в одном кусте распределился по интервалам следующим образом:
| Х(кг) | 2,5–2,7 | 2,7–2,9 | 2,9–3,1 | 3,1–3,3 | 3,3–3,5 | 3,5–3,7 | 3,7–4,3 |
| К-во кустов | 50 | 150 | 200 | 250 | 150 | 100 | 100 |
Построить гистограмму и найти средний вес одного куста.
Решение:
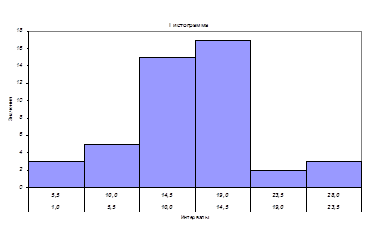
Гистограмма
служит для изображения интервальных рядов и представляет собой ступенчатую
фигуру из прямоугольников с основаниями, равными интервалам значений признака ![]() , и высотами, равными
частотам
, и высотами, равными
частотам ![]() интервалов.
интервалов.
Для расчета среднего веса одного куста воспользуемся формулой средней арифметической.
Средней арифметической дискретного вариационного ряда ![]() называется отношение суммы
произведений вариантов на соответствующие частоты к объему совокупности:
называется отношение суммы
произведений вариантов на соответствующие частоты к объему совокупности:
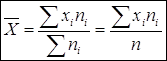
где ![]() - варианты дискретного ряда
или середины интервалов вариационного ряда,
- варианты дискретного ряда
или середины интервалов вариационного ряда, ![]() -
соответствующие им частоты.
-
соответствующие им частоты.
Для каждого
интервала найдем середины по формуле ![]() .
.
| Х(кг) | 2,5–2,7 | 2,7–2,9 | 2,9–3,1 | 3,1–3,3 | 3,3–3,5 | 3,5–3,7 | 3,7–4,3 |
|
|
2,6 | 2,8 | 3 | 3,2 | 3,4 | 3,6 | 4 |
| К-во кустов | 50 | 150 | 200 | 250 | 150 | 100 | 100 |
![]()
![]()
Ответ: средний вес одного куста составляет 3,22 кг.
По следующим данным построить интервальный вариационный ряд и гистограмму: 24, 14, 15, 26, 16, 17, 14, 15, 1, 11, 14, 12, 16, 17, 13, 10, 11, 12, 13, 15, 14, 10, 11, 14, 7, 15, 14, 15, 15, 14, 15, 14, 2, 5, 18, 19, 16, 17, 9, 10, 18, 19, 20, 22, 28.
Найти среднее значение, дисперсию и стандартное отклонение.
Решение:
1. Проранжируем[1] исходный ряд, подсчитаем частоту вариантов. Получим вариационный ряд
2. Для определения числа групп воспользуемся формулой Стерджесса:
n = 1+3,322 * lgN
где n – число групп, N =45 – число единиц совокупности
Для данных задачи n = 1 + 3,322*lg 45 = 1 + 3,322 * 1,65 = 6б49 » 6 групп
Величина интервала представляет собой разность между максимальным и минимальным значением признака в каждой группе.
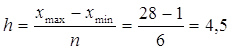
3. Выполним промежуточные вычисления во вспомогательной таблице и определим значения числовых характеристик:
Середины
интервалов 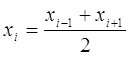
Средняя
арифметическая 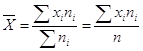 где
где ![]() -
варианты дискретного ряда или середины интервалов вариационного ряда,
-
варианты дискретного ряда или середины интервалов вариационного ряда, ![]() - соответствующие им частоты.
- соответствующие им частоты.
Дисперсия 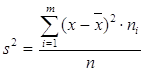 .
.
Среднее
квадратическое отклонение 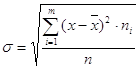 .
.
| № |
Значения |
группы | Интервалы | Частота | |||
| 1 |
1 |
нач |
кон |
||||
| 2 |
2 |
1 | 1,0 | 5,5 |
3 |
||
| 3 |
5 |
2 | 5,5 | 10,0 |
5 |
||
| 4 |
7 |
3 | 10,0 | 14,5 |
15 |
||
| 5 |
9 |
4 | 14,5 | 19,0 |
17 |
||
| 6 |
10 |
5 | 19,0 | 23,5 |
2 |
||
| 7 |
10 |
6 | 23,5 | 28,0 |
3 |
||
| 8 |
10 |
||||||
| 9 |
11 |
||||||
| 10 |
11 |
||||||
| 11 |
11 |
||||||
| 12 |
12 |
||||||
| 13 |
12 |
||||||
| 14 |
13 |
||||||
| 15 |
13 |
||||||
| 16 |
14 |
||||||
| 17 |
14 |
||||||
| 18 |
14 |
||||||
| 19 |
14 |
||||||
| 20 |
14 |
||||||
| 21 |
14 |
||||||
| 22 |
14 |
||||||
| 23 |
14 |
||||||
| 24 |
15 |
||||||
| 25 |
15 |
||||||
| 26 |
15 |
||||||
| 27 |
15 |
||||||
| 28 |
15 |
||||||
| 29 |
15 |
||||||
| 30 |
15 |
||||||
| 31 |
16 |
||||||
| 32 |
16 |
||||||
| 33 |
16 |
||||||
| 34 |
17 |
||||||
| 35 |
17 |
||||||
| 36 |
17 |
||||||
| 37 |
18 |
||||||
| 38 |
18 |
||||||
| 39 |
19 |
||||||
| 40 |
19 |
||||||
| 41 |
20 |
||||||
| 42 |
22 |
x min |
1 |
||||
| 43 |
24 |
x max |
28 |
||||
| 44 |
26 |
h |
4,5 |
||||
| 45 |
28 |
||||||
| группы | Интервалы | Частота |
Промежуточные вычисления |
|||||
|
нач |
кон |
сер |
ni |
xcp*ni |
(x-Xcp) |
(x-Xcp)2 |
ni*(x-Xcp)2 |
|
| 1 | 1,0 | 5,5 | 3,25 |
3 |
9,75 | -10,9 | 118,81 | 356,43 |
| 2 | 5,5 | 10,0 | 7,75 |
5 |
38,75 | -6,4 | 40,96 | 204,80 |
| 3 | 10,0 | 14,5 | 12,25 |
15 |
183,75 | -1,9 | 3,61 | 54,15 |
| 4 | 14,5 | 19,0 | 16,75 |
17 |
284,75 | 2,6 | 6,76 | 114,92 |
| 5 | 19,0 | 23,5 | 21,25 |
2 |
42,50 | 7,1 | 50,41 | 100,82 |
| 6 | 23,5 | 28,0 | 25,75 |
3 |
77,25 | 11,6 | 134,56 | 403,68 |
|
|
45 | 636,75 |
|
1234,80 |
||||
|
|
14,15 |
S2 |
27,44 |
|||||
| |
5,24 |
|||||||
Среднее
значение 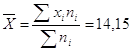
Дисперсия 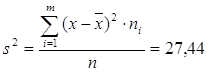
Среднее
квадратическое отклонение 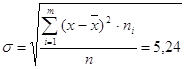
Ответ: ![]() ,
, ![]() ,
, ![]()
Некоторая случайная величина подчиняется закону нормального распределения с математическим ожиданием 50 и дисперсией 36. Найти вероятность того, что отдельное значение случайной величины заключено в интервале от 40 до 60.
Решение:
Пусть X – случайная величина подчиняется закону нормального распределения
По условию ![]() и
и ![]()
Найти: ![]()
Для нормального распределения СВ X
![]()
![]()
где Ф(Х) – функция Лапласа, дифференциальная функция нормального
закона имеет вид 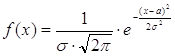 .
.
Значения Ф(Х) – табулированы
Ответ: ![]()
Задание №6
Определить вероятность того, что истинное значение расстояния отличается от среднего (1000 м), полученного в 100 опытах, не более, чем на 5 м, если стандартное отклонение 25 м.
Решение:
Пусть X – случайная величина расстояния, м
По условию ![]()
![]()
![]()
![]()
Найти: ![]()
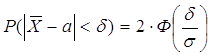
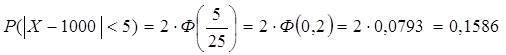
Ответ: ![]()
Задание №7
При измерении дальности расстояния дальномеры дали различные показания так, что среднее расстояние оказалось 1000 м с выборочной дисперсией 36 м2. В каких пределах находится истинное расстояние с вероятностью 80%, если произведено 11 измерений.
Решение:
По условию задана выборка объемом ![]() и дисперсия нормально
распределенной СВ X 36. Найдено выборочное среднее
и дисперсия нормально
распределенной СВ X 36. Найдено выборочное среднее ![]() .
Требуется найти доверительный интервал для неизвестного математического
ожидания
.
Требуется найти доверительный интервал для неизвестного математического
ожидания ![]() , если доверительная вероятность
должна быть равна
, если доверительная вероятность
должна быть равна ![]()
1. Доверительный интервал имеет общий вид![]()
2. По условию ![]()
![]()
![]()
![]()
![]() находим из решения
уравнения
находим из решения
уравнения
![]() →
→ ![]() →
→ ![]()
используя таблицу значений функции Лапласа ![]()
3. Находим значения концов доверительного интервала
![]() .
.
![]() .
.
Т.о., искомый доверительный интервал ![]() , т.е.
, т.е. ![]()
Ответ: ![]()
Задание №8
При определении массы пяти таблеток лекарственного вещества получены следующие результаты: 0,148; 0,149; 0,151; 0,153; 0,155 (г). Найти ошибку в определении массы таблетки с вероятностью 80%.
Решение:
| xi | 1 | 2 | 3 | 4 | 5 |
| mi | 0,148 | 0,149 | 0,151 | 0,153 | 0,155 |
Вычислим
ошибку в определении массы таблетки с вероятностью 80% по формуле: 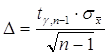 - предельная ошибка малой
выборки.
- предельная ошибка малой
выборки.
Учитывая, что ![]() определим
определим
![]() табулированные значения
табулированные значения ![]() - критерия Стьюдента.
- критерия Стьюдента.
![]()
![]()
![]()
![]() .
.
Таким образом,
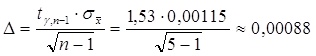 .
.
Ответ: Ошибка в определении массы таблетки с вероятностью 80% составляет 0,00088
Задание №9
При изменении скорости реакции 2-х человек провели по сто опытов и получили следующие данные: Xср = 100 мс, дисперсия средних равна 9 мс2, Yср = 110 мс, дисперсия средних равна 16 мс2.
Проверить гипотезу о равенстве математических ожиданий двух нормальных распределений для уровня значимости 0,02.
Решение:
Пусть ![]() - гипотеза, математические
ожидания двух нормальных распределений для случайных величин X и Y равны.
- гипотеза, математические
ожидания двух нормальных распределений для случайных величин X и Y равны.
При
достаточно больших объемах выборки выборочные средние ![]() и
и ![]() имеют приближенно
нормальный закон распределения с математическим ожиданием
имеют приближенно
нормальный закон распределения с математическим ожиданием ![]() и дисперсией
и дисперсией 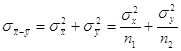 .
.
При
выполнении гипотезы ![]() статистика
статистика
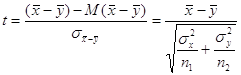 имеет стандартное нормальное распределение
N (0; 1)
имеет стандартное нормальное распределение
N (0; 1)
По данным задачи
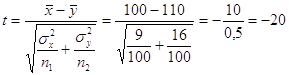
В случае
конкурирующей гипотезы ![]() выбирают
одностороннюю критическую область, и критическое значение статистики находят из
условия
выбирают
одностороннюю критическую область, и критическое значение статистики находят из
условия ![]()
Т.о. ![]()
Табулированное
значение ![]()
Если
фактические наблюдаемое значение статистики t больше критического tкр,
определенного на уровне значимости a (по абсолютной величине),
т.е. ![]() , то гипотеза
, то гипотеза ![]() отвергается, в противном
случае – гипотеза
отвергается, в противном
случае – гипотеза ![]() не противоречит
имеющимся наблюдениям.
не противоречит
имеющимся наблюдениям.
Т.к.
наблюдаемое значение статистики ![]() , а
критическое значение
, а
критическое значение ![]() , то в силу
условия
, то в силу
условия ![]() →
→![]() делаем ввод, что гипотеза
делаем ввод, что гипотеза ![]() отвергается, т.е.
математические ожидания двух нормальных распределений для случайных величин X и
Y не равны.
отвергается, т.е.
математические ожидания двух нормальных распределений для случайных величин X и
Y не равны.
Оцените достоверность различия продолжительности жизни мужчин (X) и женщин (Y) для уровня значимости 0,10:
X |
60 | 65 | 66 | 70 | 64 |
| Y | 72 | 71 | 80 | 78 | 69 |
Решение:
Пусть ![]() - гипотеза, достоверность
различия в продолжительности жизни мужчин и женщин на уровне значимости 0,10
- гипотеза, достоверность
различия в продолжительности жизни мужчин и женщин на уровне значимости 0,10
Вычислим ![]() и
и ![]()
![]()
![]()
При
выполнении гипотезы ![]() статистика
статистика 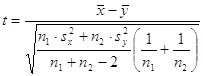 .
.
где ![]() и
и ![]()
|
X |
60 | 65 | 66 | 70 | 64 |
|
|
Y |
72 | 71 | 80 | 78 | 69 |
|
|
|
25 | 0 | 1 | 25 | 1 |
52 |
|
|
4 | 9 | 36 | 16 | 25 |
90 |
|
|
13 |
|||||
|
|
22,5 |
|||||
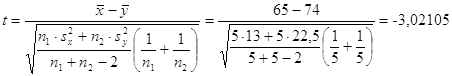
Критическое
значение статистики находят из условия ![]() .
.
Т.о. ![]() .
.
Табулированное
значение ![]() .
.
Т.к.
наблюдаемое значение статистики ![]() , а
критическое значение
, а
критическое значение ![]() то в силу
условия
то в силу
условия ![]() делаем ввод, что гипотеза
делаем ввод, что гипотеза ![]() отвергается, т.е. достоверность
различия продолжительности жизни мужчин (X) и женщин (Y) для уровня значимости
0,10 не подтверждается.
отвергается, т.е. достоверность
различия продолжительности жизни мужчин (X) и женщин (Y) для уровня значимости
0,10 не подтверждается.
Задание №11
По данным наблюдений за последние 5 лет составили таблицу урожайности пшеницы и числа дождливых дней за вегетативный период:
| Ц/ га | 10 | 15 | 6 | 20 | 9 |
| Число дождливых дней | 14 | 20 | 6 | 20 | 10 |
Коррелируют ли данные величины?
Решение:
Для оценки тесноты корреляционной зависимости между величинами Y и X используется коэффициент корреляции – показатель тесноты линейной связи.
![]()
![]() (
(![]() )
)
![]() (
(![]() )
)
Свойства коэффициента корреляции:
1 0 Коэффициент корреляции удовлетворяет неравенству ![]() .
.
2 0 В зависимости от близости r к единице различают связь слабую, умеренную, заметную, достаточно тесную, тесную и весьма тесную
Оценка тесноты линейной связи (шкала Чаддока)
|
Значение ½r½ |
0–0,1 |
0,1–0,3 |
0,3–0,5 |
0,5–0,7 |
0,7–0,9 |
0,9–0,99 |
1 |
|
Теснота линейной связи |
Нет связи |
Слабая | Умеренная | Заметная | Высокая | Очень высокая | Функциональная |
|
Значение R |
Связь |
Интерпретация связи |
| R = 0 | Отсутствует | Отсутствует линейная связь между х и у |
| 0<R < 1 | Прямая | С увеличением х величина у в среднем увеличивается и наоборот |
| -1<R<0 | Обратная | С увеличением х величина у в среднем уменьшается и наоборот |
| R =+1 R = -1 | Функциональная | Каждому значению х соответствует одно строго определенное значение величины у и наоборот |
| Ц/га | Число дождливых дней | Промежуточные вычисления | |||
| № |
Y |
X |
Y*X |
Y2 |
X2 |
|
1 |
10 | 14 | 140 | 100 | 196 |
|
2 |
15 | 20 | 300 | 225 | 400 |
|
3 |
6 | 6 | 36 | 36 | 36 |
|
4 |
20 | 20 | 400 | 400 | 400 |
|
5 |
9 | 10 | 90 | 81 | 100 |
|
S |
60 | 70 | 966 | 842 | 1132 |
|
Средние |
12 |
14 |
193,2 |
168,4 |
226,4 |
|
Sx2 |
30,4 |
||||
|
Sy2 |
24,4 |
||||
|
Sx |
5,51 |
||||
|
Sy |
4,94 |
||||
|
r |
0,925 |
||||
Таким образом, коэффициент корреляции r=0,925, следовательно, можно сделать вывод, что между двумя факторами присутствует связь прямая и очень тесная.
Ответ: данные величины коррелируют.
Задание №12
По данным таблицы сделайте прогноз значения X, если Y = 3.
| X | 4 | 2 | 3 | 7 | 5 | 6 | 3 |
| Y | 2 | 7 | 4 | 6 | 5 | 2 | 1 |
Решение:
1. Определим и оценим тесноту корреляционной зависимости
между величинами Y и X с помощью коэффициента корреляции ![]() .
.
| Промежуточные вычисления | Уравнение регрессии | |||||
| № |
Y |
X |
Y*X |
Y2 |
X2 |
|
|
1 |
2 | 4 | 8 | 4 | 16 | 3,853 |
|
2 |
7 | 2 | 14 | 49 | 4 | 3,824 |
|
3 |
4 | 3 | 12 | 16 | 9 | 3,838 |
|
4 |
6 | 7 | 42 | 36 | 49 | 3,897 |
|
5 |
5 | 5 | 25 | 25 | 25 | 3,868 |
|
6 |
2 | 6 | 12 | 4 | 36 | 3,882 |
|
7 |
1 | 3 | 3 | 1 | 9 | 3,838 |
|
S |
27 |
30 |
116 |
135 |
148 |
3,84 |
|
Средние |
3,86 |
4,29 |
16,57 |
19,29 |
21,14 |
|
|
Sx |
1,67 |
a |
3,794 |
|||
|
Sy |
2,10 |
b |
0,015 |
|||
|
r |
0,012 |
|||||
Коэффициент корреляции r=0,012, следовательно можно сделать вывод, что между двумя факторами связь прямая, но очень слабая (почти отсутствует).
Уравнение
регрессии выбирают по возможности простым, и оно, как правило, лишь приближенно
описывает зависимость между значениями x одного признака и
соответствующими средними значениями другого признака ![]() .
.
Наиболее простой и употребляемый вид зависимости – линейная зависимость. Она определяется уравнением линейной регрессии.
В
рассматриваемом примере предположим, что эмпирическая линия регрессии
приближается к прямой, и, следовательно, теоретическая линия регрессии может
быть представлена уравнением вида: ![]() и
изображается на графике в виде прямой регрессии. Уравнение регрессии называется
выборочным, поскольку его параметры a и b находятся по
результатам выборки (хi, уi), i=1,2,… n,
причем наилучшим образом в смысле метода наименьших квадратов. Сущность метода
заключается в том, чтобы была наименьшей сумма квадратов отклонений наблюдаемых
значений уi от соответствующих значений
и
изображается на графике в виде прямой регрессии. Уравнение регрессии называется
выборочным, поскольку его параметры a и b находятся по
результатам выборки (хi, уi), i=1,2,… n,
причем наилучшим образом в смысле метода наименьших квадратов. Сущность метода
заключается в том, чтобы была наименьшей сумма квадратов отклонений наблюдаемых
значений уi от соответствующих значений ![]() , вычисленных по уравнению
регрессии
, вычисленных по уравнению
регрессии![]() , то есть
, то есть ![]()
Для нахождения параметров а и b уравнения регрессии используем метод наименьших квадратов. Для этого составим и решим систему линейных уравнений:
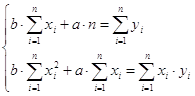 →
→ 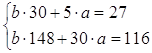
Решив систему уравнений, получим следующие значения параметров
a=3,794.
b=0,015.
Уравнение линейной регрессии ![]() .
.
Прогноз значения X, если Y = 3 при линейной зависимости
![]()
Список литературы
1. Адрухаев Х.М. Сборник задач по теории вероятностей./ Под ред. Проф. А.С. Солодовникова. – М.: Высшая школа, 2005.
2. Горелова Г.В. Теория вероятностей и математическая статистика в примерах и задачах с применением MS Excel. /Под ред. Г.В. Гореловой, И.А. Кацко. – Ростов н/Д: Феникс, 2006.
3. Информатика и математика для юристов. /Под ред. Проф. Х.А. Адриашина, проф. С.Я. Казанцева. М.: Юнити-Дана, Закон и право, 2003
4. Ковбаса С.И., Ивановский В.Б. Теория вероятностей и математическая статистика: Учебное пособие для экономистов. – СПб.: Альфа, 2001.
5. Кремер Н.Ш. Теория вероятностей и математическая статистика: Учебник. – М.: ЮНИТИ-ДАНА, 2007.
6. Ниворожкина Л.И., Морозова З.А. Основы статистики с элементами теории вероятностей для экономистов: Руководство для решения задач. – Ростов н/Д: Феникс, 1999 г. Информатика
7. Пехлецкий И.Д. Математика. / Под ред. И.Д. Пехлецкого. – М.: Издательский центр «Академия», 2003.
8. Пугачев В.С. Теория вероятностей и математическая статистика: Учебное пособие. – М.: ФИЗМАТЛИТ, 2002.
9. Сборник задач по теории вероятностей, математической статистике и теории случайных чисел: Учебное пособие. /Под общ. Ред. А.А. Свешникова. – СПб: Издательство «Лань», 2007.
[1] Ранжирование – операция, заключенная в расположении значений признака по возрастанию
© 2010 Интернет База Рефератов