
Рефераты по сексологии
Рефераты по информатике программированию
Рефераты по биологии
Рефераты по экономике
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Рефераты по авиации и космонавтике
Рефераты по административному праву
Рефераты по безопасности жизнедеятельности
Рефераты по арбитражному процессу
Рефераты по архитектуре
Рефераты по астрономии
Рефераты по банковскому делу
Рефераты по биржевому делу
Рефераты по ботанике и сельскому хозяйству
Рефераты по бухгалтерскому учету и аудиту
Рефераты по валютным отношениям
Рефераты по ветеринарии
Рефераты для военной кафедры
Рефераты по географии
Рефераты по геодезии
Рефераты по геологии
Рефераты по геополитике
Рефераты по государству и праву
Рефераты по гражданскому праву и процессу
Рефераты по делопроизводству
Рефераты по кредитованию
Рефераты по естествознанию
Рефераты по истории техники
Рефераты по журналистике
Рефераты по зоологии
Рефераты по инвестициям
Рефераты по информатике
Исторические личности
Рефераты по кибернетике
Рефераты по коммуникации и связи
Контрольная работа: Вычисление показателей вариации
Контрольная работа: Вычисление показателей вариации
Контрольная работа
по курсу: Статистика
Раздел "Общая теория статистики"
Задача 1
| Стаж, число лет | Рабочий,№ п/п | Число рабочих | Месячная з/пл (тыс. руб) |
| До 5,0 | 1,6,7,4,16,14 | 6 | 750,752,762,764,778,782 |
| 5,0 - 9,0 | 17,5,2,18, 19, 20,13 | 7 | 775,770,762,785,790,798,787 |
| Более 9,0 | 3,15,12,10,11,9,8 | 7 | 795,790,788,811,796,810,818 |
Решение. Признаком в данной задаче является общий стаж рабочего, а частотами соответственно количество рабочих, имеющих тот или иной стаж. Ряд распределения - интервальный, причем первый и последний интервал - открытые.
Если интервалы открыты, то по правилам принимаем величину первого интервала равной второму, а последнего предпоследнему. Так как имеются и значения признака и частоты, то средний стаж находим по формуле средней арифметической взвешенной. А так как ряд интервальный, то в качестве значения признака в каждой группе берём середины интервала
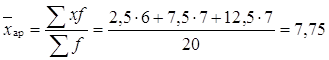
Для решения задачи и вычисления заданных показателей, построим вспомогательную таблицу.
| № п/п |
x |
||
| 1 | 750 | ||
|
2 3 4 5 6 |
752 762 764 778 782 |
||
| Итого: | 4588 | ||
| 5,0 - 9,0 | |||
| 1 | 775 | ||
|
2 3 4 5 6 7 |
770 762 785 790 798 787 |
||
| Итого: | 5467 | ||
| Более 9,0 | |||
|
1 2 |
795 790 |
|||
| 3 | 788 | |||
| 4 | 811 | |
|
5 6 7 |
796 810 818 |
| Итого: | 5608 | |||
| Всего: | 15663 |
Среднюю заработную плату по каждой группе и для всех рабочих определяем по формуле средней арифметической простой:
![]()
Задача 2
Решение: 1) Вычислим средний процент выполнения плана по выпуску продукции
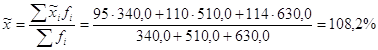 .
.
2) Абсолютный прирост показывает насколько изменился текущий уровень по сравнению с предыдущим или базисным и определяется как разность двух уровней
![]() .
.
∆3=630,0 - 510,0 =120,0
Задача 3
Решение. В задаче значения
признака имеют различную численность, поэтому значения, ![]() , d,
, d, ![]() ,
, ![]() , V
должны вычисляться как средние взвешенные величины. Для вычисления показателей
вариации проводим дополнительные расчеты.
, V
должны вычисляться как средние взвешенные величины. Для вычисления показателей
вариации проводим дополнительные расчеты.
| x | f | xf |
(x - |
(x - |
(x - |
(x - |
| 3000 | 1 | 3000 | -1770 | -1770 | 3132900 | 3132900 |
| 3500 | 2 | 7000 | -1270 | -2540 | 1612900 | 3225800 |
| 4000 | 8 | 32000 | -770 | -6160 | 592900 | 4743200 |
| 4500 | 42 | 189000 | -270 | -11340 | 72900 | 3061800 |
| 5000 | 30 | 150000 | 230 | 6900 | 52900 | 1587000 |
| 5500 | 12 | 66000 | 730 | 8760 | 532900 | 6394800 |
| 6000 | 5 | 30000 | 1230 | 6150 | 1512900 | 7564500 |
| Итого | 100 | 477000 | 29710000 |
а) Среднее время горения электролампы определяется по формуле
![]()
б) Дисперсия, взвешенная по частоте вариантов, равна
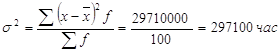 2.
2.
Среднее квадратичное отклонение равно:
![]() .
.
2) коэффициент вариации составляет
![]() .
.
3) Решение. Для определения моды определяем модальный интервал. Им является интервал 25-30 лет, так как его частота наибольшая (1054), тогда
Мо![]()
Для определения медианы тоже необходимо определить медианный интервал. Медианным интервалом является интервал 4000-4500, так как он является первым интервалом, накопленная частота которого превышает полусумму частот (100: 2=50). Тогда медиана определится как:
Ме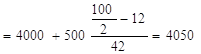 час
час
Задача 4
Решение.
Абсолютный прирост показывает, насколько изменился текущий уровень по сравнению с предыдущим или базисным и определяется как разность двух уровней
![]() .
.
Темп роста показывает, во сколько раз текущий уровень больше предыдущего или базисного, и определяется как отношение двух уровней, выраженное в процентах:
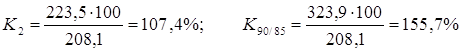 .
.
Темп прироста показывает, на сколько процентов увеличился текущий уровень по сравнению с текущим или базисным и определяется как разность соответствующего темпа роста и 100%:
![]() .
.
Абсолютное значение 1% прироста определяется как отношение абсолютного прироста к темпу прироста:
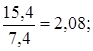 и т.д.
и т.д.
Среднегодовой темп роста рассчитывается по формуле средней геометрической
![]() .
.
Среднегодовой темп прироста равен среднегодовому темпу роста минус 100%, т.е.1,12% - 100% = - 98,88%
| Год |
тыс. шт. |
Абсолютные приросты, тыс. шт. | Темпы роста, % | Темпы прироста,% |
Абсолютное значение 1% прироста, тыс. шт. |
|||
| цепные | базисные | цепные | базис-ные | цеп-ные | базис-ные | |||
| 1985 | 208,1 | - | - | - | - | - | - | - |
| 1986 | 223,5 | 15,4 | 15,4 | 107,4 | 107,4 | 7,4 | 7,4 | 2,08 |
| 1987 | 237,5 | 14 | 29,4 | 106,3 | 114,1 | 6,3 | 14,1 | 2,2 |
| 1988 | 274,6 | 37,1 | 66,5 | 115,7 | 132 | 15,7 | 32 | 2,3 |
|
1989 1990 |
285,5 323,9 |
10,9 38,4 |
77,4 115,8 |
104 113,5 |
137,2 155,7 |
4 13,5 |
37,2 55,7 |
2,7 2,8 |
Среднегодовой абсолютный прирост исчисляется по формуле средней арифметической простой и равен
![]() руб.
руб.
Среднегодовой абсолютный прирост можно вычислить и таким образом:
![]() руб.
руб.
Начальный уровень (величина первого члена ряда) - 4140, конечный - 5426. Средний уровень ряда определяется по формуле простой средней арифметической, так как ряд периодический
![]() руб.
руб.
Задача 5
Решение.
Решение.
Рассчитываем индекс физического объема:
Iq=![]()
![]()
Рассчитываем индекс себестоимости объема:
Ip=![]()
![]()
Агрегатные индексы затрат на производство продукции, себестоимости и физического объема:
Iq=![]()
![]()
Ip=![]()
![]()
Средние затраты рассчитываем при помощи средней арифметической взвешенной, затем найдем индекс переменного состава:
In. c=![]()
![]()
![]()
![]() 0=
0=![]()
![]()
![]()
![]() 1=
1=![]()
![]()
Динамика средней себестоимости складывается под влиянием двух факторов: изменения себестоимости на отдельных предприятиях и от структуры производства продукции отрасли.
Рассчитаем индекс себестоимости постоянного состава:
Iср. с=![]()
![]()
Таким образом, в результате повышения себестоимости единицы продукции на обоих предприятиях средняя цена выросла на 18,7%
Определим влияние на среднюю цену структурных сдвигов:
Iстр. сдв=

За изучаемый период, структура производства практически не изменилась, поэтому изменение средней цены произошло целиком за счет влияния первого фактора, т. е изменения себестоимости на производство продукции на каждом предприятии. Правильность расчетов подтверждает проверка через взаимосвязь индексов
In. c=Iф. с*Iстр. сдв=1,187*1=1,187
© 2010 Интернет База Рефератов