
Рефераты по сексологии
Рефераты по информатике программированию
Рефераты по биологии
Рефераты по экономике
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Рефераты по авиации и космонавтике
Рефераты по административному праву
Рефераты по безопасности жизнедеятельности
Рефераты по арбитражному процессу
Рефераты по архитектуре
Рефераты по астрономии
Рефераты по банковскому делу
Рефераты по биржевому делу
Рефераты по ботанике и сельскому хозяйству
Рефераты по бухгалтерскому учету и аудиту
Рефераты по валютным отношениям
Рефераты по ветеринарии
Рефераты для военной кафедры
Рефераты по географии
Рефераты по геодезии
Рефераты по геологии
Рефераты по геополитике
Рефераты по государству и праву
Рефераты по гражданскому праву и процессу
Рефераты по делопроизводству
Рефераты по кредитованию
Рефераты по естествознанию
Рефераты по истории техники
Рефераты по журналистике
Рефераты по зоологии
Рефераты по инвестициям
Рефераты по информатике
Исторические личности
Рефераты по кибернетике
Рефераты по коммуникации и связи
Курсовая работа: Применение индексного метода при анализе цен
Курсовая работа: Применение индексного метода при анализе цен
Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
Амурский государственный университет
(ГОУ ВПО «АмГУ»)
КУРСОВАЯ РАБОТА.
на тему: Применение индексного метода при анализе цен
По дисциплине Статистика
Исполнитель
Студентка 534 группы О.Е.Штейникова
Руководитель
Ассистент . К.Д.Шубина
Нормоконтроль
Ассистент Н.Н. Медзяловская
Благовещенск 2006
РЕФЕРАТ
Курсовая работа содержит 43 страницы, 8 таблиц, 3 рисунка, 10 источников.
Цена, статистика цен, классификация цен, средние цены, показатели динамики цен, показатели вариации, индексный метод анализа цен, корреляционно-регрессионный анализ.
Цель работы состоит в том, чтобы изучить индексный метод анализа цен. В работе изложены понятие и сущность цен, классификация цен, изучены основные показатели статистики цен, а также рассмотрен индексный метод анализа цен. В практической части рассчитаны все показатели на основе реальных цен, сделаны выводы на основании расчетов.
Объектом исследования является реально существующее предприятие МП ГУКС, осуществляющее свою деятельность на строительном рынке города Благовещенска.
1 ТЕОРЕТИЧЕСКИЕ ОСНОВЫ СТАТИСТИЧЕСКОГО ИЗУЧЕНИЯ
ЦЕН
1.1 Понятие цены
Цена - многофункциональное экономическое явление, ведущая рыночная категория. Изменение цены часто влечет за собой серьезнейшие социальные, экономические, а также политические последствия. Поэтому во всесторонней и объективной информации о ценах, в глубоком анализе закономерностей и тенденций их изменения заинтересовано все общество, а не только властные структуры и маркетинговые службы.
Цена - сумма денег, уплачиваемая за единицу товара, эквивалент обмена товара на деньги /7, с.266 /. Цена- это выражение стоимости товара в денежных единицах определенной валюты за количественную единицу товара в конкретных условиях места и времени /1, с.88/.
Цены, процессы их образования и изменения представляют собой предмет статистического исследования. Статистика цен - самостоятельный блок, входящий как составная часть в статистику рынка и соответственно в социально-экономическую статистику. Поэтому в органах государственной статистики сформирована самостоятельная служба статистики цен. Сложились уже и альтернативные службы статистики цен /7, с.266/.
Категория цен связана с функционированием товарно-денежных отношений. В условиях развитого рынка цена характеризует не только те затраты на производство и реализацию товара, которые произведены, но и признаваемые общественно обоснованными с учетом спроса.
При помощи цен определяются, прогнозируются и анализируются хозяйственные пропорции, эффективность производства, выгодность продукции для производителей и потребителей. Ценой измеряется эквивалентность обмена во внутренних и внешних экономических связях, между промышленностью и сельским хозяйством, предприятиями и организациями. От уровня и динамики цен на товары зависит уровень жизни населения. В цене, таким образом, фокусируются экономические и социальные проблемы общества.
Цена выполняет учетную, стимулирующую и распределительную функции.
Учетная функция позволяет оценить затраты и результаты производства.
Стимулирующая функция призвана активизировать научно-технический прогресс, повысить ресурсосбережение, эффективность производства и качество продукции.
Распределительная функция предусматривает учет в цене акциза на отдельные группы и виды товаров, налога на добавленную стоимость и других форм централизованного чистого дохода, который поступает в федеральный и местный бюджеты. С помощью этой функции цены решаются социальные задачи /3, с.369/.
Рыночная цена выполняет различные функции. Цена - это посредник и соизмеритель при обмене товаров на деньги. Цена - важный показатель конъюнктуры рынка, фактор уровня, структуры и соотношения спроса и предложения, территориального размещения производства. Цена - инструмент образования прибыли и управления эффективностью, фактор налогообложения. Цена - это главная составляющая инфляционных процессов, средство влияния на инвестиционную политику (повышение цен часто ведет к росту привлекательности инвестиций). Цена - мощный фактор уровня жизни населения, влияющий на рынок труда, объем и структуру потребления, уровень реальных доходов различных социальных групп. И наконец, цена - это орудие конкурентной борьбы /8, с.267/.
Цены классифицируют по различным направлениям.
1. По сферам товарного обслуживания:
- оптовые цены, по которым предприятия реализуют в больших объемах продукцию промышленно-технического и потребительского назначения (между отраслями внутри оптовой сферы и из оптовой в розничную). При наличии разветвленной сети потребления товара оптимизировать продажу позволяют посреднические оптовые фирмы или организации (снабженческо-сбытовые организации, товарные биржи). При отсутствии потребности в посредниках поставщики и потребители устанавливают прямые хозяйственные связи;
- розничные цены, по которым товары реализуются конечному потребителю (в основном населению) в ограниченном количестве;
- закупочные цены, по которым государство покупает продукцию у сельскохозяйственных предприятий (фермеров);
- цены и тарифы на услуги. Тарифы могут относиться к сфере оптовой торговли (например, грузовые транспортные тарифы, фрахт) и розничной (пассажирские тарифы) /7, с.271/.
2. По способу отражения транспортных расходов:
- цены франко-отправления (на товары ограниченного производства и разветвленной сети потребления), включающие транспортные издержки до пункта магистрального транспорта (порта, железнодорожной станции), расходы на остальной путь покрывает покупатель;
- цены франко-назначения, включающие транспортные расходы до пункта назначения.
3. По формам продаж:
- контрактные (договорные) цены - цены фактической договоренности между продавцом и покупателем;
- биржевые котировки - это уровень цены товара, реализуемого через биржу. Цена биржевого товара складывается из биржевой котировки и надбавки (скидки) за качество, удаленность от места поставки;
- цены ярмарок и выставок (часто льготные);
- аукционные цены, отражающие ход продаж на аукционах (различают стартовые цены и продажные)
Аукционы (публичные торги) бывают трех типов:
1. С повышением цены (товар продают по цене, наиболее высокой из предложенных покупателями).
2. Вейлинговые торги (цена предложения наивысшая, на экране-циферблате стрелки имеют обратный ход, покупатель нажатием кнопки определяет устраивающую его цену).
3. С подачей заявок в запечатанных конвертах, при этом отсутствует возможность сравнения с запросами других покупателей.
4. По стадиям продажи:
- цены предложения (цены продавца, или стартовые), по которым продавец желает продать товар. Как правило, это верхний предел диапазона возможных цен этого товара (за исключением аукционных и цен подряда), который корректируется в ходе переговоров с покупателем. Для некоторых товаров (машин, оборудования) цены предложения - единственный источник информации об уровне цен на рынке;
- цены спроса, по которым покупатель заинтересован приобрести товар;
- цены реализации (сделки, продажи, покупки) - фактические, или номинальные, цены. Их следует отличать от реальных, соотнесенных с уровнем дохода общества или общим уровнем цен /7, с.272/.
5. По степени регулирования:
- жестко фиксированные (основной тип цен в условиях административно-командной экономики);
- регулируемые (допускаются изменения в определенных пределах, устанавливаются государством, как правило, на продукты повышенного социального назначения);
- свободные (не подвержены прямому вмешательству, формируются в соответствии с конъюнктурой рынка).
6. По степени устойчивости во времени:
- твердые: устанавливаются при заключении договора на весь срок действия;
- подвижные: зафиксированная в договоре цена меняется в момент поставки, если изменилась рыночная цена товара, установленная по оговоренному в контракте источнику;
- скользящие: в договоре устанавливается исходная цена и оговаривается порядок (формула) внесения поправок в случае изменения стоимости ценообразующих факторов. Скользящие цены применяются к товарам, требующим длительного срока изготовления;
- с последующей фиксацией: в договоре определяются условия фиксации и принцип определения уровня цены: периодичность фиксации, база фиксации, сроки согласования и осуществления фиксации.
В качестве базовой цены, ориентира для внесения поправок или фиксации уровня цены при заключении сделки используются:
1. Расчетные цены, которые обосновываются поставщиком для каждого конкретного заказа с учетом его технических и коммерческих условий.
2. Справочные цены, публикуемые в справочниках, каталогах, периодических изданиях. Как правило, это средние цены фактических сделок за определенный период, экспертные оценки, биржевые котировки, цены предложений крупных фирм и т. д.
3. Цены прейскурантов и ценников. Прейскуранты выпускаются, как правило, производителем для готовых изделий, рассылаются клиентам, включают цены для конечных пользователей, стабильные скидки в разрезе всей или части товарной номенклатуры фирмы. При необходимости частого изменения цен прейскуранты дополняются вкладышами с коэффициентами изменений.
Кроме перечисленных выделяют и другие виды цен, например:
- трансфертные (внутрифирменные - для обмена между цехами одного предприятия, дочерними фирмами, заграничными филиалами, конфиденциальны);
- мировые (выступают в качестве условной средней стоимости товаров, реализуемых в нескольких странах, на практике, как правило, модальные, т. е. цены отдельных стран - основных производителей товара) /7, с.273/.
Задачи статистики цен:
- регистрация цен, наблюдение за их изменением;
- анализ уровня цен, его дифференциации;
- характеристика структуры цен;
- изучение соотношений цен различных товаров, субрынков и перекрестной эластичности цен;
- оценка, анализ и моделирование колеблемости, цикличности и сезонности цен;
- региональный анализ цен;
- анализ и моделирование динамики цен;
- выявление и моделирование факторов, влияющих на уровень, вариацию и динамику цен;
- изучение конъюнктуры рынка;
- прогнозирование цен /10, с.104/.
1.2 Показатели статистики цен
Решение совокупности современных задач, предъявляемых статистике цен, предполагает построение и совершенствование системы статистических показателей, в составе можно предусмотреть выделение нескольких самостоятельных групп показателей. Важнейшие группы системы показателей статистики цен: показатели уровня цен, показатели структуры цены, показатели рядов динамики цен, показатели вариации цен и индексы цен /9, с.536/.
Средняя цена – это обобщающая характеристика уровня цен на одноименные товары и услуги /5, с.245/. Средние цены рассчитываются с помощью средней арифметической.
Средняя арифметическая простая:
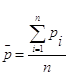 (1)
(1)
где pi – цена,
n – число цен совокупности.
Средняя арифметическая взвешенная:
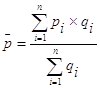 (2)
(2)
где qi – объем продаж.
Показатели вариации используются для измерения степени колеблемости отдельных значений признака от средней. Основные показатели: размах колебаний, дисперсия, среднее квадратическое отклонение и коэффициент вариации /6, с.5/.
Размах колебаний (размах вариации):
![]() (3)
(3)
где pmax – максимальное значение цены,
pmin - минимальное значение цены.
Величина показателя зависит от величины только двух крайних вариант и не учитывает степени колеблемости основной массы членов ряда /4, с.74/.
Дисперсия – это средняя арифметическая квадратов отклонений отдельных значений признака от средней арифметической. В зависимости от исходных данных дисперсия вычисляется по формуле средней арифметической простой или взвешенной.
Дисперсия простая:
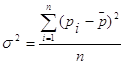 (4)
(4)
где ![]() - среднее значение цены,
- среднее значение цены,
n - количество цен совокупности.
Дисперсия взвешенная:
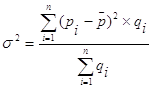 (5)
(5)
Среднее квадратическое отклонение представляет собой корень квадратный из дисперсии /6, с.5/.
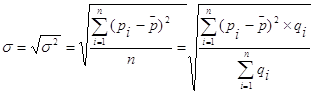 (6)
(6)
В отличие от дисперсии среднее квадратическое отклонение является абсолютной мерой вариации признака в совокупности и выражается в единицах измерения варьирующего признака (в рублях, процентах, тоннах и т.д.).
Для сравнения размеров вариации различных признаков, а также для сравнения степени вариации одноименных признаков в нескольких совокупностях и исчисляется относительный показатель вариации – коэффициент вариации, который представляет собой процентное соотношение среднего квадратического отклонения к средней арифметической.
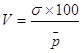 (7)
(7)
По величине коэффициента вариации можно судить о степени вариации признака, а следовательно, об однородности состава совокупности. Чем больше его величина, тем больше разброс значений признака вокруг средней, тем менее однородна совокупность по составу /6, с.6/. Совокупность считается однородной, если коэффициент вариации не превышает 33 % /4, с.77/.
Ряды динамики характеризуют изменение цены во времени. Для анализа рядов динамики рассчитываются: абсолютные приросты, темпы роста, темпы прироста, абсолютное значение одного процента.
Абсолютный прирост показывает на сколько в абсолютном выражении уровень текущего периода больше (или меньше) базисного (предыдущего).
Базисный абсолютный прирост:
![]() (8)
(8)
где pi – цена текущего периода,
pб – цена базисного периода.
Цепной абсолютный прирост:
![]() (9)
(9)
где pi-1 – цена предыдущего периода.
Темп роста – это коэффициент роста, выраженный в процентах. Он показывает, сколько процентов уровень текущего периода составляет по отношению к уровню базисного периода.
Базисный темп роста:
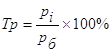 (10)
(10)
Цепной темп роста:
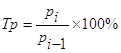 (11)
(11)
Темп прироста показывает, на сколько процентов уровень текущего периода больше (или меньше) уровня базисного периода.
![]() (12)
(12)
Абсолютное значение одного процента – это одна сотая часть базиса уровня и отношения абсолютного прироста к соответствующему темпу роста или одна сотая часть предыдущего уровня /4, с.218/.
![]() (13)
(13)
Средний абсолютный прирост исчисляется как средняя арифметическая простая цепных приростов:
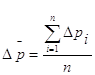 (14)
(14)
где n – число абсолютных приростов.
Средний темп роста исчисляется по формуле средней геометрической из цепных коэффициентов роста.
![]() (15)
(15)
Средний темп прироста исчисляется следующим образом /6, с.8/.
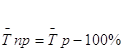 (16)
(16)
Средняя величина абсолютного значения одного процента прироста исчисляется следующим образом /4, с.220/.
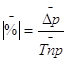 (17)
(17)
Эта система показателей статистики цен позволяет полностью изучить цены, их влияние на экономико-социальные процессы и решать задачи, предъявляемые статистике цен /9, с.537/.
1.3 Методы расчета и анализа индексов цен
Индексный метод является основным методом всестороннего статистического исследования цен.
Индекс цен - относительный показатель выраженный в коэффициентах или процентах, характеризующий изменение цен во времени или в пространстве /9, с.554/.
Сравнение цен одного товара осуществляется с помощью индивидуального (однотоварного) индекса цен:
![]()
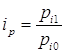 (18)
(18)
где pi1 – цена на товар в текущем периоде,
pi0 – цена на товар в базисном периоде /4, с.272/.
Индивидуальные индексы характеризуют динамику цены конкретного товара /9, с.555/.
Основной формой индекса цен для совокупности разнородных товаров является агрегатный индекс. Цены различных товаров (например, кондитерских изделий и компьютеров) складывать бессмысленно. Несуммируемость элементов совокупности преодолевается путем взвешивания каждой цены по количеству проданных товаров. Сумма произведений цен товаров на их количество составляет товарооборот совокупности товаров. Чтобы выявить непосредственно изменение цен, необходимо зафиксировать показатели количества на одном из уровней.
Базисного периода времени (формула Ласпейреса)
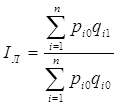 (19)
(19)
где qi0 – объем продаж в базисном периоде,
qi1 – объем продаж в текущем периоде.
Текущего периода времени (формула Пааше)
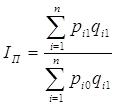 .
(20)
.
(20)
Четкость интерпретации, экономический смысл и удобство практического расчета формулы Ласпейреса сделали ее самой популярной в мире для расчета индекса потребительских цен, который показывает, во сколько раз изменились бы потребительские расходы в текущем периоде по сравнению с базисным, если бы при изменении цен уровень потребления оставался прежним. Такой расчет корректен при отсутствии значительных количественных и качественных изменений в структуре потребления (во времени и по территории, если индекс рассчитывается для нескольких регионов) /7, с.304/.
Изучение динамики розничных цен (например, для получения дефлятора, позволяющего рассчитать стоимостные показатели отчетного периода в сопоставимых ценах) должно быть максимально приближено к совокупности товаров, произведенных в отчетном периоде. Результат расчета по формуле Пааше показывает, во сколько раз сумма фактических затрат населения на покупку товаров больше (меньше) суммы денег, которую население должно было бы заплатить за эти же товары, если бы цены оставались на уровне базисного периода.
Статистическим анализом доказано, что в долговременном аспекте формула Пааше занижает реальное изменение цен вследствие общественной отрицательной корреляции (относительный вес товара падает, если цена его возрастает).
Доказано, что наилучший линейный индекс лежит между индексами, вычисленными по формулам Ласпейреса и Пааше. Зарубежные статистики пытались найти компромиссную формулу.
Формула Эджворта - Маршалла:
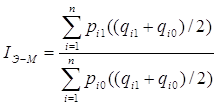 (21)
(21)
Формула улавливает сдвиги в структуре покупок, но привязана к условной структуре товарооборота, не характерной ни для одного реального периода, не имеет прямого экономического смысла. Ее расчет встречает препятствия в сборе материалов /7, с.305/.
Наиболее удачным компромиссом многие экономисты считают «идеальный» индекс Фишера.
![]() (22)
(22)
Он оценивает не только набор товаров базисного периода по ценам текущего, но и набор товаров текущего периода по ценам базисного. Применяется в случае трудностей с выбором весов или значительного изменения структуры весов.
Индексы при систематическом расчете из года в год образуют индексные ряды. Различают базисные ряды (цены каждого года сравниваются с ценами года, принятого за базу) и цепные (характеризующие изменение цен по сравнению с предыдущим годом). Веса индексов ряда могут быть постоянными (на уровне одного года), и тогда произведение цепных индексов даст базисный индекс.
Применение системы переменных весов (по количеству товаров отчетного года) в индексном ряду цен порождает ошибку при переходе от цепных индексов к базисным и обратно, так как позитивна корреляция между текущим изменением цен и прошлым изменением количества проданных товаров. Эта ошибка мала, если корреляционная связь между изменением цен и количества проданного товара незначительна. На практике система цепных индексов (достоинство - сокращает период сравнения, ограничивает круг несопоставимых товаров) используется для коротких периодов, затем осуществляется поправка по формуле базисного периода, так как за длительный период ошибка накапливается /7, с.306/.
Индексный метод широко применяется также для изучения динамики средних величин и выявления факторов, влияющих на динамику средних. С этой целью исчисляется система взаимосвязанных индексов: переменного, постоянного состава и структурных сдвигов.
Индекс переменного состава представляет собой соотношение двух взвешенных средних величин с переменными весами, характеризующие изменение индексируемого показателя.
Индекс переменного состава для цены имеет следующий вид /6, с.10/.
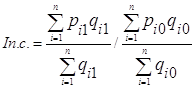 (23)
(23)
Величина этого индекса характеризует изменение цены за счет двух факторов – уровня цен и структуры продаж /2, с.134/.
Индекс фиксированного (постоянного) состава представляет собой отношение средних с одними и теми же весами. Для цены он может быть записан следующим образом /6, с.10/.
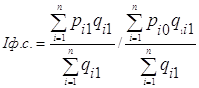 (24)
(24)
Индекс постоянного состава учитывает изменение средних цен за счет уровня цен.
Индекс структурных сдвигов характеризует влияние структуры продаж на изменение средней цены и рассчитывается по формуле /2, с.134/.
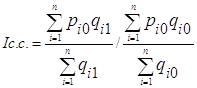 (25)
(25)
Система взаимосвязанных индексов имеет вид /6, с.10/.
![]() (26)
(26)
Численные значения индексов, рассчитанных по различным формулам на основе одних и тех же данных, отличаются и порой значительно, особенно в годы резких изменений уровня цен и связанного с этим изменения структуры спроса. Отдать предпочтение одной формуле трудно: разные цели диктуют применение индексных форм, имеющих разный экономический смысл. Отказ от концепции единственного индекса цен в пользу концепции системы индексов позволит дать обобщающую характеристику и оценку основных причин изменения розничных цен. Но поскольку все же индексный метод не универсален, а отражает лишь тенденцию движения цен, то нельзя требовать большей определенности от рассчитанных индексов. Кроме того, на чистоту результатов огромное влияние оказывает достоверность исходных материалов, особенно ошибка выборки, степень представительности товаров, включенных в расчет /7, с.310/.
2 СТАТИСТИЧЕСКИЙ АНАЛИЗ ЦЕН МП ГУКС ИНДЕКСНЫМ
МЕТОДОМ
2.1 Краткая характеристика МП ГУКС
Официальное полное название организации - Муниципальное предприятие «Городское управление капитального строительства» (в дальнейшем МП ГУКС).
По роду деятельности МП ГУКС является предприятием, оказывающим услуги по выполнению функций заказчика по строительству объектов различного назначения: жилищное строительство, объектов социально-культурного назначения, коммунального хозяйства и др. Управление контролирует и координирует процесс строительства от самого начала, т.е. с момента поступления заказа на строительство того или иного объекта и до самого его завершения ввода в эксплуатацию.
Отдел капитального строительства Благовещенского горисполкома, правопреемником которого является МП ГУКС, был образован в 1957 году. В связи со значительным увеличением объемов строительства выполняемых за счет средств бюджета города, области и федерации, отдел капитального строительства в 1972 году был преобразован в Управление капитального строительства Благовещенского горисполкома.
За 47 лет деятельности с момента образования управлением построено более 1 миллиона 300 тысяч квадратных метров общей площади жилья или 6 квадратных метров на каждого жителя города.
Введено в эксплуатацию 23 школы на 18 тысяч учащихся, 17 детских садов на 5 тысяч мест. Управлением внесен большой вклад в развитие материальной базы здравоохранения города и области: построено более десяти больниц на 2,5 тысячи коек и поликлиник на 4,5 тысячи посещений, в том числе: комплекс областной клинической больницы, мощностью 1080 коек и 1100 посещений, 1-ая, 2-ая, 3-я и 4-я городские больницы, родильный дом на 130 коек, дом ребенка на 150 мест, здания станции переливания крови и скорой помощи, туберкулезного и кожно-венерологического диспансера, инфекционная больница, 3-я городская и стоматологическая поликлиники, здание предприятия по ремонту медицинской техники.
Управление капитального строительства выступало заказчиком многих Административных зданий города: управления Госстраха, штаба гражданской обороны, областного суда, администрации г. Благовещенска.
Построено большое количество объектов коммунального и гостиничного хозяйства, более 180 километров магистральных коммуникаций канализации, водопровода, теплотрасс, водозаборные сооружения на реках Амур и Зея, городские очистные сооружения, крытый рынок, гостиницы «Амур», «Зея», «Юбилейная», троллейбусное депо, тяговые подстанции и контактные сети электротранспорта, несколько котельных, два здания автоматических телефонных станций, стадион «Амур», плавательный бассейн, дома престарелых и ветеранов и ряд других объектов отраслей народного хозяйства.
Строительство жилья в настоящее время осуществляется в соответствии с договорами долевого строительства, заключенными с отдельными гражданами, предприятиями и организациями.
Целями предприятия являются получение прибыли от производства и реализации продукции и товаров, выполнения работ и оказания услуг и выполнения городских и областных социально-экономических заказов, удовлетворение общественных потребностей.
В данной работе анализу подлежит многоквартирный жилой дом в квартале 407, который входит в состав микрорайона № 2.
2.2 Анализ средней цены
Для расчета показателей необходимы данные цен одного квадратного метра и количество проданных квадратных метров. Эти данные представлены в таблицах 1 и 2.
Таблица 1 – Цена одного квадратного метра жилья в многоквартирном жилом доме в 407 квартале.
В тысячах рублей
| Период | Однокомнатные | Двухкомнатные | Трехкомнатные | ||||||
| Первый этаж |
Средний этаж |
Последний этаж |
Первый этаж |
Средний этаж |
Последний этаж |
Первый этаж |
Средний этаж |
Последний этаж |
|
| 3 кв. 2005 | 19,70 | 19,92 | 19,47 | 18,66 | 18,89 | 18,44 | 17,63 | 17,86 | 17,40 |
| 4 кв. 2005 | 21,65 | 21,90 | 21,41 | 20,52 | 20,77 | 20,27 | 19,38 | 19,63 | 19,13 |
| 1 кв. 2006 | 23,61 | 23,88 | 23,34 | 22,37 | 22,64 | 22,10 | 21,13 | 21,40 | 20,86 |
| 2 кв. 2006 | 25,57 | 25,86 | 25,27 | 24,23 | 24,52 | 23,93 | 22,88 | 23,18 | 22,59 |
| 3 кв. 2006 | 27,53 | 27,84 | 27,21 | 26,08 | 26,40 | 25,76 | 24,64 | 24,95 | 24,32 |
Таблица 2 – Количество проданных квадратных метров в многоквартирном жилом доме в 407 квартале.
В квадратных метрах
| Период | Однокомнатные | Двухкомнатные | Трехкомнатные | ||||||
| Первый этаж |
Средний этаж |
Последний этаж |
Первый этаж |
Средний этаж |
Последний этаж |
Первый этаж |
Средний этаж |
Последний этаж |
|
| 3 кв. 2005 | 38 | 190 | - | 57,6 | 230,4 | - | 81,6 | 244,8 | - |
| 4 кв. 2005 | 38 | 76 | 38 | 57,6 | 172,8 | 57,6 | 81,6 | 244,8 | 81,6 |
| 1 кв. 2006 | - | 76 | 38 | 115,2 | 172,8 | 57,6 | 81,6 | 244,8 | 81,6 |
| 2 кв. 2006 | 38 | - | 76 | 115,2 | - | 172,8 | 163,2 | 81,6 | 81,6 |
| 3 кв. 2006 | 38 | 38 | - | - | - | 57,6 | 81,6 | - | 81,6 |
По формуле (2) средней арифметической взвешенной рассчитаем средние цены одного квадратного метра жилья в многоквартирном доме в 407 квартале.
Для однокомнатных квартир:
![]() тыс. руб.
тыс. руб.
Средняя цена одного квадратного метра в однокомнатной квартире в третьем квартале 2005 года составила 19,88 тысяч рублей.
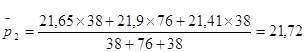 тыс. руб.
тыс. руб.
Средняя цена одного квадратного метра в однокомнатной квартире в четвертом квартале 2005 года составила 21,72 тысячи рублей.
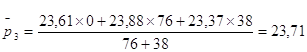 тыс. руб.
тыс. руб.
Средняя цена одного квадратного метра в однокомнатной квартире в первом квартале 2006 года составила 23,71 тысячи рублей.
![]() тыс. руб.
тыс. руб.
Средняя цена одного квадратного метра в однокомнатной квартире во втором квартале 2006 года составила 25,37 тысяч рублей.
![]() тыс. руб.
тыс. руб.
Средняя цена одного квадратного метра в однокомнатной квартире в третьем квартале 2006 года составила 27,69 тысяч рублей.
Для двухкомнатных квартир:
![]() тыс. руб.
тыс. руб.
Средняя цена одного квадратного метра в двухкомнатной квартире в третьем квартале 2005 года составила 18,84 тысячи рублей.
![]() тыс. руб.
тыс. руб.
Средняя цена одного квадратного метра в двухкомнатной квартире в четвертом квартале 2005 года составила 20,62 тысячи рублей.
![]() тыс. руб.
тыс. руб.
Средняя цена одного квадратного метра в двухкомнатной квартире в первом квартале 2006 года составила 22,17 тысяч рублей.
![]() тыс. руб.
тыс. руб.
Средняя цена одного квадратного метра в двухкомнатной квартире во втором квартале 2006 года составила 24,05 тысяч рублей.
![]() тыс. руб.
тыс. руб.
Средняя цена одного квадратного метра в двухкомнатной квартире в третьем квартале 2006 года составила 25,76 тысяч рублей.
Для трехкомнатных квартир:
![]() тыс. руб.
тыс. руб.
Средняя цена одного квадратного метра в трехкомнатной квартире в третьем квартале 2005 года составила 17,80 тысяч рублей.
![]() тыс. руб.
тыс. руб.
Средняя цена одного квадратного метра в трехкомнатной квартире в четвертом квартале 2005 года составила 19,48 тысяч рублей.
![]() тыс. руб.
тыс. руб.
Средняя цена одного квадратного метра в трехкомнатной квартире в первом квартале 2006 года составила 21,24 тысяч рублей.
![]() тыс. руб.
тыс. руб.
Средняя цена одного квадратного метра в трехкомнатной квартире во втором квартале 2006 года составила 22,88 тысяч рублей.
![]() тыс. руб.
тыс. руб.
Средняя цена одного квадратного метра в трехкомнатной квартире в третьем квартале 2006 года составила 24,48 тысяч рублей.
Результаты расчетов сведены в таблицы 3.
Таблица 3 – Средняя цена одного квадратного метра жилья в многоквартирном жилом доме в 407 квартале.
В тысячах рублей
| Период | Однокомнатные | Двухкомнатные | Трехкомнатные |
| 3 кв. 2005 | 19,88 | 18,84 | 17,80 |
| 4 кв. 2005 | 21,72 | 20,62 | 19,48 |
| 1 кв. 2006 | 23,71 | 22,17 | 21.24 |
| 2 кв. 2006 | 25,37 | 24,05 | 22,88 |
| 3 кв. 2006 | 27,69 | 25,76 | 24,48 |
В таблице 4 представлены данные общего количества квадратных метров по периодам для однокомнатных, двухкомнатных и трехкомнатных квартир.
Таблица 4 – Общее количество проданных квадратных метров в многоквартирном жилом доме в 407 квартале по кварталам.
В квадратных метрах
| Период | Однокомнатные | Двухкомнатные | Трехкомнатные |
| 3 кв. 2005 | 228 | 288 | 326,4 |
| 4 кв. 2005 | 152 | 288 | 408 |
| 1 кв. 2006 | 114 | 345,6 | 408 |
| 2 кв. 2006 | 114 | 288 | 326,4 |
| 3 кв. 2006 | 76 | 57,6 | 163,2 |
В дальнейших расчетах будут использоваться данные таблиц 3 и 4.
2.3 Анализ динамики цен
В анализе динамики цен рассчитаем абсолютные приросты, темпы роста, темпы прироста, абсолютное значение одного процента и их средние для однокомнатных, двухкомнатных и трехкомнатных квартир.
Для однокомнатных квартир:
По формулам (8) и (9) определим базисные и цепные абсолютные приросты цен (в расчетах используем значения средних цен).
Базисные абсолютные приросты:
![]() тыс. руб.
тыс. руб.
![]() тыс. руб.
тыс. руб.
![]() тыс. руб.
тыс. руб.
![]() тыс. руб.
тыс. руб.
Цепные абсолютные приросты:
![]() тыс. руб.
тыс. руб.
![]() тыс. руб.
тыс. руб.
![]() тыс. руб.
тыс. руб.
![]() тыс. руб.
тыс. руб.
По формуле (14) определим средний абсолютный прирост.
![]() тыс. руб.
тыс. руб.
Анализируя расчеты видно, что наблюдается динамика роста цен на однокомнатные квартиры в среднем на 1,95 тысяч рублей.
По формулам (10) и (11) определим базисные и цепные темпы роста цен.
Базисные темпы роста:
![]() %
%
![]() %
%
![]() %
%
![]() %
%
Цепные темпы роста:
![]() %
%
![]() %
%
![]() %
%
![]() %
%
По формуле (15) определим средний темп роста.
![]() %
%
Таким образом, на основании расчетов уровень цен однокомнатных квартир текущего периода по отношению к предыдущему в среднем составляет 108,6 %.
По формуле (12) определим базисные и цепные темпы прироста цен.
Базисные темпы прироста:
![]() %
%
![]() %
%
![]() %
%
![]() %
%
Цепные темпы прироста:
![]() %
%
![]() %
%
![]() %
%
![]() %
%
По формуле (16) определим средний темп прироста.
![]() %
%
Анализируя расчеты можно сделать вывод, что в среднем на 8,6 % уровень текущих цен больше предыдущего уровня цен, наблюдается динамика роста цен на однокомнатные квартиры.
По формуле (13) определим абсолютное значение одного процента цены.
![]() тыс. руб.
тыс. руб.
![]() тыс. руб.
тыс. руб.
![]() тыс. руб.
тыс. руб.
![]() тыс. руб.
тыс. руб.
По формуле (17) определим среднюю величину абсолютного значения одного процента прироста.
![]() тыс. руб.
тыс. руб.
Средняя величина абсолютного значения одного процента прироста цены равна 0,2267 тысяч рублей.
Таким образом, результаты расчетов сведем в таблицу 5.
Таблица 5 – Показатели динамики цен однокомнатных квартир в многоквартирном жилом доме в 407 квартале
| Период | Абсолютный прирост, тыс. руб. | Темп роста, % | Темп прироста, % | Абсолютное значение одного процента, тыс. руб. | ||||
| цепной | базисный | цепной | базисный | цепной | базисный | |||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 3 кв. 2005 | - | - | - | - | - | - | - | |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 4 кв. 2005 | 1,84 | 1,84 | 109,3 | 109,3 | 9,3 | 9,3 | 0,1988 | |
| 1 кв. 2006 | 3,83 | 1,99 | 119,3 | 109,2 | 19,3 | 9,2 | 0,2172 | |
| 2 кв. 2006 | 5,49 | 1,66 | 127,6 | 107,0 | 27,6 | 7,0 | 0,2371 | |
| 3 кв. 200 | 7,81 | 2,32 | 139,3 | 109,1 | 39,3 | 9,1 | 0,2537 | |
Для двухкомнатных и трехкомнатных квартир показатели динамики рассчитываются аналогично расчетам для однокомнатных квартир. Результаты расчетов сведем в таблицы 6 и 7.
Таблица 6 – Показатели динамики цен двухкомнатных квартир в многоквартирном жилом доме в 407 квартале
| Период | Абсолютный прирост, тыс. руб. | Темп роста, % | Темп прироста, % | Абсолютное значение одного процента, тыс. руб. | ||||
| цепной | базисный | цепной | базисный | цепной | базисный | |||
| 3 кв. 2005 | - | - | - | - | - | - | - | |
| 4 кв. 2005 | 1,78 | 1,78 | 109,4 | 109,4 | 9,4 | 9,4 | 0,1884 | |
| 1 кв. 2006 | 3,33 | 1,55 | 117,7 | 107,5 | 17,7 | 7,5 | 0,2062 | |
| 2 кв. 2006 | 5,21 | 1,88 | 127,7 | 108,5 | 27,7 | 8,5 | 0,2217 | |
| 3 кв. 2006 | 6,92 | 1,71 | 136,7 | 107,1 | 36,7 | 7,1 | 0,2405 | |
Средние значения показателей динамики для двухкомнатных квартир:
![]() тыс.
руб.
тыс.
руб.
Анализируя расчеты видно, что наблюдается динамика роста цен на двухкомнатные квартиры в среднем на 1,73 тысяч рублей.
![]() %
%
Таким образом, на основании расчетов уровень цен двухкомнатных квартир текущего периода по отношению к предыдущему в среднем составляет 108,1 %.
![]() %
%
Анализируя расчеты можно сделать вывод, что в среднем на 8,1 % уровень текущих цен больше предыдущего уровня цен, наблюдается динамика роста цен на двухкомнатные квартиры.
![]() тыс. руб.
тыс. руб.
Средняя величина абсолютного значения одного процента прироста цены равна 0,2136 тысяч рублей.
Таблица 7 – Показатели динамики цен трехкомнатных квартир в многоквартирном жилом доме в 407 квартале
| Период | Абсолютный прирост, тыс. руб. | Темп роста, % | Темп прироста, % | Абсолютное значение одного процента, тыс. руб. | ||||
| цепной | базисный | цепной | базисный | цепной | базисный | |||
| 3 кв. 2005 | - | - | - | - | - | - | - | |
| 4 кв. 2005 | 1,68 | 1,68 | 109,4 | 109,4 | 9,4 | 9,4 | 0,1780 | |
| 1 кв. 2006 | 3,44 | 1,76 | 119,3 | 109,0 | 19,3 | 9,0 | 0,1948 | |
| 2 кв. 2006 | 5,08 | 1,64 | 128,5 | 107,7 | 28,5 | 7,7 | 0,2124 | |
| 3 кв. 2006 | 6,68 | 1,60 | 137,5 | 107,0 | 37,5 | 7,0 | 0,2288 | |
Средние значения показателей динамики для трехкомнатных квартир:
![]() тыс.
руб.
тыс.
руб.
Анализируя расчеты видно, что наблюдается динамика роста цен на трехкомнатные квартиры в среднем на 1,67 тысяч рублей.
![]() %
%
Таким образом, на основании расчетов уровень цен трехкомнатных квартир текущего периода по отношению к предыдущему в среднем составляет 108,3 %.
![]() %
%
Анализируя расчеты можно сделать вывод, что в среднем на 8,3 % уровень текущих цен больше предыдущего уровня цен, наблюдается динамика роста цен на трехкомнатные квартиры.
![]() тыс. руб.
тыс. руб.
Средняя величина абсолютного значения одного процента прироста цены равна 0,2012 тысяч рублей.
2.4 Анализ цен показателями вариации
Рассчитаем основные показатели вариации: размах колебаний, дисперсию, среднее квадратическое отклонение и коэффициент вариации для однокомнатных, двухкомнатных и трехкомнатных квартир.
Для однокомнатных квартир:
По формуле (3) определим размах колебаний.
![]() тыс. руб.
тыс. руб.
Разница между максимальным и минимальным значением цен на однокомнатные квартиры составляет 7,81 тысяч рублей.
По формуле (5) определим дисперсию. Для расчета дисперсии необходимо знать среднее значение цены, которое определяется по формуле (2) средней арифметической взвешенной.
![]() тыс. руб.
тыс. руб.
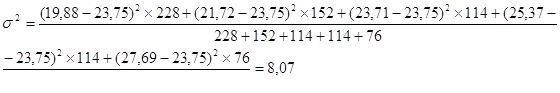
По формуле (6) вычислим среднее квадратическое отклонение.
![]() тыс. руб.
тыс. руб.
Индивидуальные значения цен на однокомнатные квартиры отличаются в среднем от средней арифметической цены на 2,84 тысяч рублей.
По формуле (7) определим коэффициент вариации.
![]() %
%
Значение коэффициента вариации (11,96 %) свидетельствует о том, что совокупность цен на однокомнатные квартиры однородна.
Расчеты показателей вариации для двухкомнатных и трехкомнатных квартир аналогичны расчетам показателей для однокомнатных квартир.
Для двухкомнатных квартир:
![]() тыс. руб.
тыс. руб.
![]()
![]() тыс. руб.
тыс. руб.
Индивидуальные значения цен на двухкомнатные квартиры отличаются в среднем от средней арифметической цены на 2,05 тысяч рублей.
![]() %
%
Значение коэффициента вариации (9,5 %) свидетельствует о том, что совокупность цен на двухкомнатные квартиры однородна.
Для трехкомнатных квартир:
![]() тыс. руб.
тыс. руб.
![]()
![]() тыс. руб.
тыс. руб.
Индивидуальные значения цен на трехкомнатные квартиры отличаются в среднем от средней арифметической цены на 1,8 тысяч рублей.
![]() %
%
Значение коэффициента вариации (8,9 %) свидетельствует о том, что совокупность цен на трехкомнатные квартиры однородна.
2.5 Применение индексного метода анализа цен
По формуле (19) рассчитаем цепные и базисные индексы цен Ласпейреса.
Цепные индексы цен Ласпейреса:
![]()
![]()
![]()
![]()
Зная, что произведение соответствующих цепных индексов
равно базисному индексу, рассчитаем базисные индексы. ![]()
Базисные индексы цен Ласпейреса:
![]()
![]()
![]()
![]()
Анализируя расчеты можно сделать вывод, что идет тенденция снижения количества проданных квадратных метров, увеличение наблюдается только в первом квартале 2006 года по сравнению с третьем и четвертым кварталами 2005 года.
По формуле (20) рассчитаем цепные и базисные индексы цен Пааше.
Цепные индексы цен Пааше:
![]()
![]()
![]()
![]()
Базисные индексы цен Пааше:
![]()
![]()
![]()
![]()
Анализируя расчеты можно сделать вывод, что идет тенденция увеличения цены на один квадратный метр. Это говорит о том, что растут затраты населения на покупку квартир.
По формуле (21) рассчитаем цепные и базисные индексы цен Эджворта – Маршалла.
Цепные индексы цен Эджворта – Маршалла:
![]()
![]()
![]()
![]()
Базисные индексы цен Эджворта – Маршалла:
![]()
![]()
![]()
![]()
Анализируя расчеты можно сделать вывод, что идет тенденция увеличения величины индексов цен Эджворта – Маршалла.
По формуле (22) рассчитаем цепные и базисные индексы цен Фишера.
Цепные индексы цен Фишера:
![]()
![]()
![]()
![]()
Базисные индексы цен Фишера:
![]()
![]()
![]()
![]()
Анализируя расчеты можно сделать вывод, что идет тенденция снижения величины индексов цен Фишера.
По формуле (23) рассчитаем базисные и цепные индексы переменного состава.
Цепные индексы цен переменного состава:
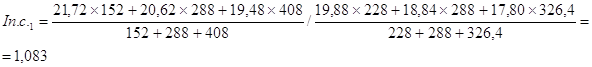
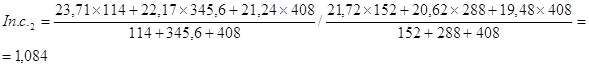
Остальные цепные индексы переменного состава рассчитываются аналогично.
![]()
![]()
Базисные индексы цен переменного состава.
![]()
![]()
![]()
![]()
Таким образом, на основании расчетов можно сделать вывод, что наблюдается динамика увеличения средних цен и следовательно увеличение затрат населения из-за изменения объем продаж квадратных метров и уровня цен на один квадратный метр.
По формуле (24) рассчитаем цепные и базисные индексы цен фиксированного состава.
Цепные индексы цен фиксированного состава:
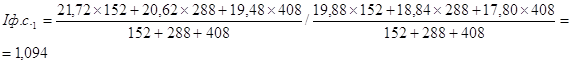
Остальные цепные индексы цен фиксированного состава рассчитываются аналогично.
![]()
![]()
![]()
Базисные индексы цен фиксированного состава:
![]()
![]()
![]()
![]()
Таким образом, на основании расчетов можно сделать вывод, что наблюдается динамика увеличения затрат населения из-за изменения уровня цен на один квадратный метр, при неизменной структуре продаж.
По формуле (25) рассчитаем цепные и базисные индексы цен структурных сдвигов.
Цепные индексы цен структурных сдвигов:
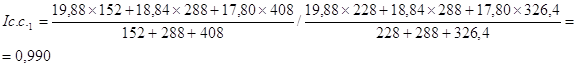
Остальные цепные индексы цен структурных сдвигов рассчитываются аналогично.
![]()
![]()
![]()
Базисные индексы цен структурных сдвигов:
![]()
![]()
![]()
![]()
Анализируя расчеты можно сделать вывод, что динамика затрат населения почти меняется из-за изменения структуры продажи, при неизменных уровнях цен.
С помощью формулы (26) проверим правильность расчетов индексов цен переменного состава, фиксированного состава и структурных сдвигов.
![]()
![]()
![]()
![]()
Из расчетов видно, что значения равны вычисленным ранее индексов цен переменного состава, следовательно, расчеты индексов переменного состава, фиксированного состава и структурных сдвигов верны.
2.6 Корреляционно-регрессионный анализ цен
При корреляционно-регрессионном анализе необходимо знать уравнение регрессии и рассчитать коэффициент корреляции.
Уравнение регрессии является уравнением прямой и записывается следующим образом:
![]() (27)
(27)
где yх – теоретические значения результативного признака,
х – индивидуальные значения факторного признака,
а0, а1 - параметры уравнения прямой.
Параметры уравнения прямой определяются следующим образом:
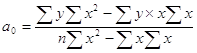 (28)
(28)
где n число значений признака.
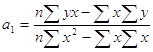 (29)
(29)
В уравнение прямой параметр a0 экономического смысла не имеет. Параметр а1 является коэффициентом регрессии и показывает изменение результативного признака при изменение факторного признака на единицу.
Линейный коэффициент корреляции применяется для измерения тесноты связи и вычисляется следующим образом:
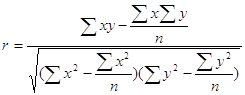 (30)
(30)
Для расчета уравнения необходимы значения факторного признака, которым в нашем случае является среднедушевой доход населения. Данные среднедушевого дохода представлены в таблице 8.
Таблица 8 – Среднедушевой доход населения
В рублях
| 3 кв. 2005 | 4 кв. 2005 | 1 кв. 2006 | 2 кв. 2006 | 3 кв. 2006 |
| 6323,3 | 7237,5 | 5699,5 | 7008,7 | 6871,4 |
По формулам (28) и (29) рассчитаем параметры а0 и а1, а также коэффициент корреляции r и построим графики для наглядности для однокомнатных, двухкомнатных и трехкомнатных квартир.
Для однокомнатных квартир:
а0 =16941, 2
а1 =1,02
yх=16941,2+1,02х
r=0,206
По коэффициенту корреляции видно, что цены на однокомнатные квартиры мало зависят от среднедушевого дохода.
Построим два графика зависимости. Первый, зависимость средних цен на однокомнатные квартиры от среднедушевого дохода, второй, график уравнения регрессии, которые изображены на рисунке 1.
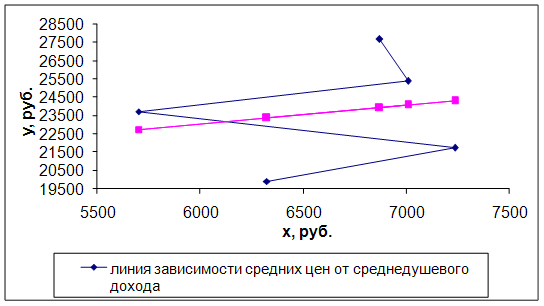
Рисунок 1 – График зависимости средних цен на однокомнатные квартиры от среднедушевого дохода и график уравнения регрессии
Для двухкомнатных квартир:
а0 =15102,3
а1 =1,08
yх=15102,3+1,08х
r=0,246
По коэффициенту корреляции видно, что цены на двухкомнатные квартиры мало зависят от среднедушевого дохода.
Графики зависимости цен на двухкомнатные квартиры от среднедушевого дохода представлены на рисунке 2.
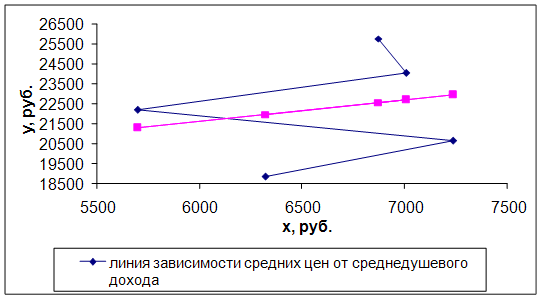
Рисунок 2 – График зависимости средних цен на двухкомнатные квартиры от среднедушевого дохода и график уравнения регрессии
Для трехкомнатных квартир:
а0 =15163,6
а1 =0,91
yх=15102,3+1,08х
r=0,212
По коэффициенту корреляции видно, что цены на трехкомнатные квартиры мало зависят от среднедушевого дохода.
Графики зависимости цен на трехкомнатные квартиры от среднедушевого дохода представлены на рисунке 3.
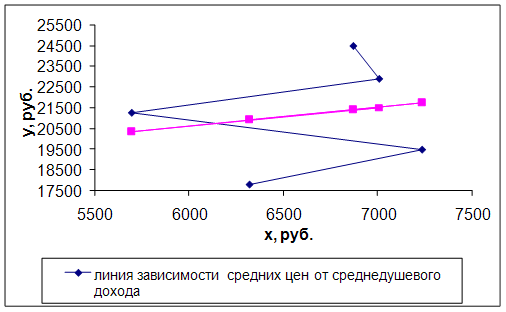
Рисунок 3 – График зависимости средних цен на трехкомнатные квартиры от среднедушевого дохода и график уравнения регрессии
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1 Бурцева С.А. Статистика финансов: Учеб.: Рек. УМО вузов / С.А. Бурцева.-М.: Финансы и статистика, 2004.-288с.
2 Голуб Л.А. Социально-экономическая статистика: Учеб. пособие для студ. вузов: Рек. Мин. обр. РФ / Л.А. Голуб.- М.: Владос, 2001.-271с.
3 Гусаров В.М. Статистика: Учеб. пособие для вузов / В.М. Гусаров.- М.: ЮНИТИ-ДАНА, 2003.-463с.
4 Ефимова М.Р. Практикум по общей теории статистики: Учеб. пособие / М.Р. Ефимова, О.И. Ганченко, Е.В. Петрова.-2-е изд., перераб. и доп..- М.: Финансы и статистика, 2005.-336с.
5 Статистика: Учеб. пособие / А.В. Багат, М.М. Конкина, В.М. Симчера и др.; Под ред. В.М. Симчеры.- М.: Финансы и статистика, 2005.-368с
6 Статистика: Практикум для студентов экономических специальностей заочной формы обучения / Составители В.З. Григорьева, С.С. Донецкая, Н.В. Смолина.- Благовещенск: Амурский гос. ун-т, 2000.- 24с.
7 Статистика рынка товаров и услуг: Учеб.: Доп. Мин. обр. РФ / Ред. И.К. Беляевский.- 2-е изд., перераб. и доп..- М.: Финансы и статистика, 2002.-656с. 8 Статистика финансов: Учеб.: Рек. Мин. обр. РФ / Ред. М.Г. Назарова.- М.: Омега-Л, 2005,461с.
9 Статистика финансов: Учеб.: Рек. Мин. обр. РФ / Ред. В.Н. Салин.- 2-е изд..- М.: Финансы и статистика, 2003.-815с.
10 Ярных Э.А. Статистика финансов предприятия торговли: Учеб. пособие: Рек. Мин. обр. РФ / Э.А. Ярных.-2-е изд., перераб. и доп..- М.: Финансы и статистика, 2005.-216с.
ЗАКЛЮЧЕНИЕ
Поставленные цель и задачи можно считать достигнутыми. В курсовой работе был освещен теоретический материал, отражены аспекты статистики цен. Все полученные знания и методика использования индексного метода были успешно применены на практике, что позволило на примере оригинальных данных понять всю важность и значимость данной тематики в современной экономике.
В работе на примере строительного предприятия МП ГУКС были рассчитаны все основные показатели статистики цен. В первую очередь были определены средние цены, на основании которых были произведены все остальные расчеты. Далее были изучены показатели рядов динамики, в результате можно сделать вывод, что средние цены на один квадратный метр однокомнатных, двухкомнатных, трехкомнатных квартир в многоквартирном жилом доме в 407 квартале с каждым кварталом времени увеличиваются в среднем на 1,95 тысяч рублей. Это говорит о том, что расходы населения на покупку квартиры растут.
Изученные показатели вариации говорят о том, что совокупность цен на один квадратный метр однокомнатных, двухкомнатных, трехкомнатных квартир однородна, следовательно, средние цены в полном объеме описывают особенности цен всей совокупности. Индексный метод показал, что увеличение расходов населения на покупку квартиры идет вследствие увеличения уровня цен, и влияние изменений структуры продаж не значительно. Были рассчитаны все основные индексы цен: Пааше, Ласпейреса, Эджворта – Маршалла, Фишера, переменного состава, фиксированного состава и структурных сдвигов.
С помощью корреляционно-регрессионного анализа была изучена взаимосвязь средних цен на один квадратный метр и среднедушевого дохода населения. На основании расчета коэффициента корреляции можно сделать вывод, что цены мало зависят от среднедушевого дохода населения.
© 2010 Интернет База Рефератов