
Рефераты по сексологии
Рефераты по информатике программированию
Рефераты по биологии
Рефераты по экономике
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Рефераты по авиации и космонавтике
Рефераты по административному праву
Рефераты по безопасности жизнедеятельности
Рефераты по арбитражному процессу
Рефераты по архитектуре
Рефераты по астрономии
Рефераты по банковскому делу
Рефераты по биржевому делу
Рефераты по ботанике и сельскому хозяйству
Рефераты по бухгалтерскому учету и аудиту
Рефераты по валютным отношениям
Рефераты по ветеринарии
Рефераты для военной кафедры
Рефераты по географии
Рефераты по геодезии
Рефераты по геологии
Рефераты по геополитике
Рефераты по государству и праву
Рефераты по гражданскому праву и процессу
Рефераты по делопроизводству
Рефераты по кредитованию
Рефераты по естествознанию
Рефераты по истории техники
Рефераты по журналистике
Рефераты по зоологии
Рефераты по инвестициям
Рефераты по информатике
Исторические личности
Рефераты по кибернетике
Рефераты по коммуникации и связи
Курсовая работа: Регрессионный анализ. Транспортная задача
Курсовая работа: Регрессионный анализ. Транспортная задача
Регрессионный анализ
Задача
Некоторая фирма занимается поставками различных грузов на короткие расстояния внутри города. Необходимо оценить стоимость таких услуг, зависящую от затрачиваемого на поставку времени. В качестве наиболее важного фактора, влияющего на время доставки, выбрано пройденное расстояние. Были собраны исходные данные о десяти поставках (табл.).
| Расстояние, км | 3,5 | 2,4 | 4,9 | 4,2 | 3,0 | 1,3 | 1,0 | 3,0 | 1,5 | 4,1 |
| Время, мин | 16 | 13 | 19 | 18 | 12 | 11 | 8 | 14 | 9 | 16 |
Постройте график исходных данных, определите по нему характер зависимости между расстоянием и потраченным временем, постройте уравнение регрессии, проанализируйте силу регрессионной связи и сделайте прогноз поездки на 2 км.
Решение
Для расчёта стоимости услуг, зависящих от затрачиваемого на поставку времени, вычислим суммы (рис. 1):
| t | y(t) |
|
||||||||||||
|
|
|
|
|
|
|
||||||||
| 1 | 3,50 | 16,00 | 12,25 | 56,00 | 256,00 | 15,22 | 2,63 | |||||||
| 2 | 2,40 | 13,00 | 5,76 | 31,20 | 169,00 | 12,30 | 1,70 | |||||||
| 3 | 4,90 | 19,00 | 24,01 | 93,10 | 361,00 | 18,95 | 28,58 | |||||||
| 4 | 4,20 | 18,00 | 17,64 | 75,60 | 324,00 | 17,08 | 12,14 | |||||||
| 5 | 3,00 | 12,00 | 9,00 | 36,00 | 144,00 | 13,89 | 0,09 | |||||||
| 6 | 1,30 | 11,00 | 1,69 | 14,30 | 121,00 | 9,37 | 17,88 | |||||||
| 7 | 1,00 | 8,00 | 1,00 | 8,00 | 64,00 | 8,57 | 25,27 | |||||||
| 8 | 3,00 | 14,00 | 9,00 | 42,00 | 196,00 | 13,89 | 0,09 | |||||||
| 9 | 1,50 | 9,00 | 2,25 | 13,50 | 81,00 | 9,90 | 13,67 | |||||||
| 10 | 4,10 | 16,00 | 16,81 | 65,60 | 256,00 | 16,82 | 10,36 | |||||||
| сумма |
|
|
|
|
|
|
|
|||||||
| 13,60 | ||||||||||||||
| a1 = | 2,66 | |||||||||||||
| a0 = | 5,91 | |||||||||||||
| r2 = | 0,92 | 91,83% | ||||||||||||
| 8,17 |
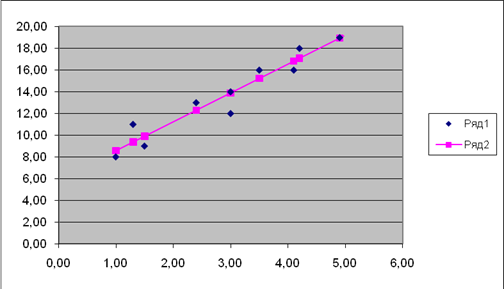
Рис .1 - График исходных данных
Вывод: существует сильная связь между исходными данными.
Задача
В таблице приведены данные по объемам собранного урожая овощей из тепличного хозяйства за последний год (по месяцам), а также данные о затраченной электроэнергии, воде и удобрениях.
| Месяц | Объем собранного урожая | Факторы, влияющие на урожай | ||
| Электроэнергия, кВт | Удобрения, тонн | Вода, литр | ||
|
t |
y |
x1 |
x2 |
x3 |
| январь | 140 | 165 | 138 | 134 |
| февраль | 138 | 164 | 139 | 128 |
| март | 158 | 158 | 157 | 168 |
| апрель | 144 | 159 | 142 | 147 |
| май | 142 | 148 | 144 | 146 |
| июнь | 134 | 152 | 136 | 140 |
| июль | 122 | 143 | 122,5 | 132 |
| август | 125 | 146 | 128 | 135 |
| сентябрь | 124 | 148 | 119 | 125 |
| октябрь | 138 | 150 | 142 | 126 |
| ноябрь | 157 | 156 | 159 | 143 |
| декабрь | 161 | 160 | 164 | 150 |
Необходимо определить степень влияния каждого отдельного фактора на результат (объем урожая). Для этого необходимо построить графики исходных данных, построить уравнения регрессии, проанализировать силу регрессионной связи (по коэффициенту детерминации) и сделать прогноз урожая по двум-трем значениям (в пределах прогноза исходных данных).
Решение
Строим графики исходных данных (рис. 2, 3):
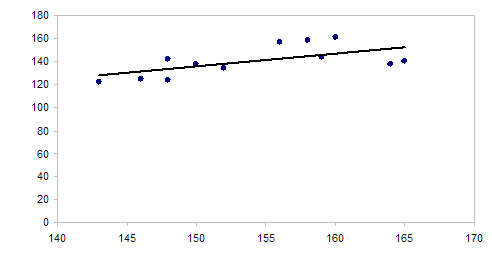
Рис. 2 - График зависимости урожая от удобрения
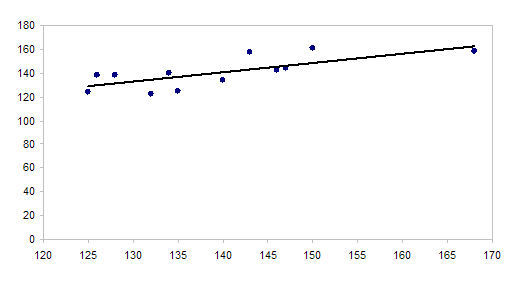
Рис. 3 - График зависимости урожая от воды
Численные коэффициенты функции регрессии для первой зависимости:
Численные коэффициенты функции регрессии
|
X1i |
Yi |
X1i² |
X1i Yi |
Yi ² |
Yi p |
(Yi p -y)² |
(Yi -y)² |
| 165 | 140 | 27225 | 23100 | 19600 | 152,5778 | 151,9747 | 0,0625 |
| 164 | 138 | 26896 | 22632 | 19044 | 151,4485 | 125,4073 | 5,0625 |
| 158 | 158 | 24964 | 24964 | 24964 | 144,673 | 19,56251 | 315,0625 |
| 159 | 144 | 25281 | 22896 | 20736 | 145,8022 | 30,82711 | 14,0625 |
| 148 | 142 | 21904 | 21016 | 20164 | 133,3803 | 47,19267 | 3,0625 |
| 152 | 134 | 23104 | 20368 | 17956 | 137,8974 | 5,534888 | 39,0625 |
| 143 | 122 | 20449 | 17446 | 14884 | 127,734 | 156,6506 | 333,0625 |
| 146 | 125 | 21316 | 18250 | 15625 | 131,1218 | 83,32442 | 232,5625 |
| 148 | 124 | 21904 | 18352 | 15376 | 133,3803 | 47,19267 | 264,0625 |
| 150 | 138 | 22500 | 20700 | 19044 | 135,6388 | 21,26283 | 5,0625 |
| 156 | 157 | 24336 | 24492 | 24649 | 142,4144 | 4,684729 | 280,5625 |
| 160 | 161 | 25600 | 25760 | 25921 | 146,9315 | 44,64219 | 430,5625 |
| 1849 | 1683 | 285479 | 259976 | 237963 | 738,2566 | 1922,25 | |
| Среднее значение | 140,25 |
Коэффициент детерминации r2=0,384059.
Коэффициент детерминации низкий поэтому модель не адекватна.
Численные коэффициенты функции регрессии для первой зависимости, представляем расчеты виде таблицы:
Численные коэффициенты функции регрессии
|
X2i |
Yi |
X2i² |
X2i Yi |
Yi ² |
Yi p |
(Yi p -y)² |
(Yi -y)² |
| 138 | 140 | 19044 | 19320 | 19600 | 137,5802 | 7,127725 | 0,0625 |
| 139 | 138 | 19321 | 19182 | 19044 | 138,5088 | 3,031641 | 5,0625 |
| 157 | 158 | 24649 | 24806 | 24964 | 155,224 | 224,2202 | 315,0625 |
| 142 | 144 | 20164 | 20448 | 20736 | 141,2947 | 1,091391 | 14,0625 |
| 144 | 142 | 20736 | 20448 | 20164 | 143,1519 | 8,421225 | 3,0625 |
| 136 | 134 | 18496 | 18224 | 17956 | 135,723 | 20,49389 | 39,0625 |
| 122,5 | 122 | 15006,25 | 14945 | 14884 | 123,1866 | 291,1588 | 333,0625 |
| 128 | 125 | 16384 | 16000 | 15625 | 128,294 | 142,9452 | 232,5625 |
| 119 | 124 | 14161 | 14756 | 15376 | 119,9365 | 412,64 | 264,0625 |
| 142 | 138 | 20164 | 19596 | 19044 | 141,2947 | 1,091391 | 5,0625 |
| 159 | 157 | 25281 | 24963 | 24649 | 157,0812 | 283,29 | 280,5625 |
| 164 | 161 | 26896 | 26404 | 25921 | 161,7243 | 461,1463 | 430,5625 |
| 1690,5 | 1683 | 240302,3 | 239092 | 237963 | 1856,658 | 1922,25 | |
| Среднее значение | 140,25 |
Коэффициенты регрессии сдвиг а0 и наклон а1 прямой у:
| a0= | 9,430782 |
| a1= | 0,928619 |
Коэффициент детерминации r2=0,965877.
Коэффициент детерминации высокий, поэтому модель адекватна и можно делать прогноз.
Прогноз на три шага вперед y13=120.9, y14=154.3, y15=142.2.
Численные коэффициенты функции регрессии для первой зависимости, представляем расчеты виде таблицы:
Численные коэффициенты функции регрессии
|
X3i |
Yi |
X3i² |
X3i Yi |
Yi ² |
Yi p |
(Yi p -y)² |
(Yi -y)² |
| 134 | 140 | 17956 | 18760 | 19600 | 135,8979 | 18,94079 | 0,0625 |
| 128 | 138 | 16384 | 17664 | 19044 | 131,1502 | 82,80727 | 5,0625 |
| 168 | 158 | 28224 | 26544 | 24964 | 162,8018 | 508,5838 | 315,0625 |
| 147 | 144 | 21609 | 21168 | 20736 | 146,1847 | 35,22048 | 14,0625 |
| 146 | 142 | 21316 | 20732 | 20164 | 145,3934 | 26,4545 | 3,0625 |
| 140 | 134 | 19600 | 18760 | 17956 | 140,6456 | 0,156535 | 39,0625 |
| 132 | 122 | 17424 | 16104 | 14884 | 134,3153 | 35,22048 | 333,0625 |
| 135 | 125 | 18225 | 16875 | 15625 | 136,6892 | 12,67937 | 232,5625 |
| 125 | 124 | 15625 | 15500 | 15376 | 128,7763 | 131,6463 | 264,0625 |
| 126 | 138 | 15876 | 17388 | 19044 | 129,5676 | 114,1144 | 5,0625 |
| 143 | 157 | 20449 | 22451 | 24649 | 143,0195 | 7,670238 | 280,5625 |
| 150 | 161 | 22500 | 24150 | 25921 | 148,5586 | 69,03215 | 430,5625 |
| 1674 | 1683 | 235188 | 236096 | 237963 | 1042,526 | 1922,25 | |
| Среднее значение | 140,25 |
Коэффициенты регрессии сдвиг а0 и наклон а1 прямой у:
| a0= | 29,86486 |
| a1= | 0,791291 |
Коэффициент детерминации r2=0,542347.
Коэффициент детерминации низкий, поэтому модель не адекватна.
Задача
Санаторный комплекс ежегодно заключает с пекарней договор на выпечку хлеба сорта С1. Чтобы полностью использовать свои производственные мощности пекарня также выпекает хлеб сорта С2, который пускает в свободную продажу. В таблице приведены данные выпуска хлеба (тыс. шт.) пекарней за последний год
| Месяц | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|
С1 |
1 | 2,3 | 1,5 | 0,5 | 4 | 5 | 2 | 3,5 | 1 | 4,5 | 2,5 | 1,5 |
|
С2 |
9 | 6,5 | 8,1 | 8,7 | 4 | 0,2 | 7,6 | 5 | 8,7 | 2 | 7 | 8,4 |
Проанализируйте график исходных данных и постройте регрессионную модель функции производственных возможностей пекарни. Проверьте удовлетворительность модели и сделайте прогноз выпуска хлеба С2, если санаторный комплекс сделает заказ хлеба С1 3 тысячи булок.
Решение
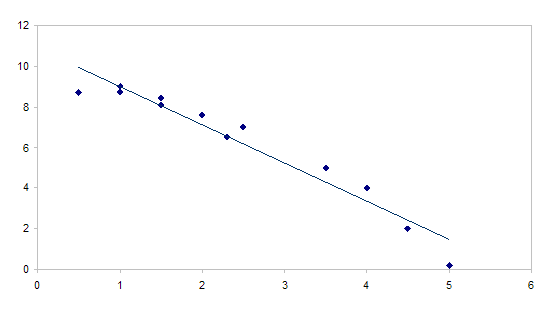
Рис. 4 - График исходных данных
Суммы, необходимые для расчета коэффициентов линейной регрессии и коэффициента детерминации вычислим с помощью таблицы, учитывая данные зависимости объема собранного урожая от количества электроэнергии.
| x | y |
x2 |
xy |
yp |
(yp-ycp)2 |
(y-ycp)2 |
| 1 | 9 | 1 | 9 | 8.981453 | 7.370065 | 7.471111 |
| 2.3 | 6.5 | 5.29 | 14.95 | 6.533438 | 0.071167 | 0.054444 |
| 1.5 | 8.1 | 2.25 | 12.15 | 8.039909 | 3.144387 | 3.361111 |
| 0.5 | 8.7 | 0.25 | 4.35 | 9.922997 | 13.36875 | 5.921111 |
| 4 | 4 | 16 | 16 | 3.332187 | 8.611173 | 5.137778 |
| 5 | 0.2 | 25 | 1 | 1.449098 | 23.20897 | 36.80444 |
| 2 | 7.6 | 4 | 15.2 | 7.098364 | 0.691721 | 1.777778 |
| 3.5 | 5 | 12.25 | 17.5 | 4.273731 | 3.971792 | 1.604444 |
| 1 | 8.7 | 1 | 8.7 | 8.981453 | 7.370065 | 5.921111 |
| 4.5 | 2 | 20.25 | 9 | 2.390642 | 15.02356 | 18.20444 |
| 2.5 | 7 | 6.25 | 17.5 | 6.15682 | 0.012066 | 0.537778 |
| 1.5 | 8.4 | 2.25 | 12.6 | 8.039909 | 3.144387 | 4.551111 |
| å=29.3 | å=75.2 | å=95.79 | å=137.95 | å=85.98811 | å=91.34667 |
Находим коэффициенты регрессии — сдвиг а0 и наклон а1 прямой у:
| a0= | 10,86454 |
| a1= | -1,88309 |
Коэффициент детерминации r2=0,941338.
Коэффициент детерминации высокий поэтому модель адекватна и можно делать прогноз.
Если санаторный комплекс сделает заказ хлеба С1 3 тысячи булок, то прогноз С2 =-1,88309*3000+10,86454=5215,7.
Транспортная задача
Задача
Заводы некоторой автомобильной фирмы расположены в городах А, В и С. Основные центры распределения продукции сосредоточены в городах D и E. Объемы производства указанных трех заводов равняются 1000, 1300 и 1200 автомобилей ежеквартально.
Величины квартального спроса в центрах распределения составляют 2300 и 1400 автомобилей соответственно.
Стоимости перевозки автомобилей по железной дороге по каждому из возможных маршрутов приведены в таблице
Стоимость перевозки автомобилей, руб./шт.
| D | E | |
| А | 80 | 215 |
| В | 100 | 108 |
| С | 102 | 68 |
Постройте математическую модель, позволяющую определить количество автомобилей, перевозимых из каждого завода в каждый центр распределения, таким образом, чтобы общие транспортные расходы были минимальны.
Задаем целевую функцию и ограничения с помощью «Поиска решений»:
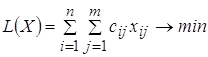 ;
;
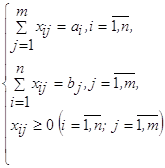
Получаем:
| Стоимость перевозки автомобилей, руб./шт | ||||
| D | Е |
V |
Издержки | |
| А | 80 | 215 | 1000 | |
| В | 100 | 108 | 1300 | |
| С | 102 | 68 | 1200 | |
| Спрос | 2300 | 1400 | 291600 | |
| Продукция | ||||
| D | Е | Сумма | ||
| А | 1000 | 0 | 1000 | |
| В | 1300 | 0 | 1300 | |
| С | 0 | 1200 | 1200 | |
| Y | 0 | 200 | 200 | |
| Сумма | 2300 | 1400 | ||
Задача
Постройте транспортную модель для исходных данных задачи 2.1 при условии, что квартальный спрос в пункте распределения D упал до 1900 автомобилей, а выпуск на заводе В увеличился до 1500 автомобилей за квартал.
Решение
Задаем целевую функцию и ограничения с помощью «Поиска решений»:
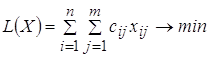 ;
;
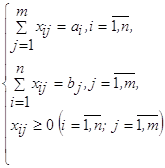
Получаем:
|
Стоимость перевозки автомобилей, руб./шт |
|||||
| D | Е | F |
V |
Издержки | |
| А | 80 | 215 | 0 | 1000 | |
| В | 100 | 108 | 0 | 1500 | |
| С | 102 | 68 | 0 | 1200 | |
| Спрос | 1900 | 1400 | 400 | 273200 | |
| Продукция | |||||
| D | Е | F | Сумма | ||
| А | 1000 | 0 | 0 | 1000 | |
| В | 900 | 200 | 400 | 1500 | |
| С | 0 | 1200 | 0 | 1200 | |
| Сумма | 1900 | 1400 | 400 | ||
Задача
Три электрогенерирующие станции мощностью 25, 40 и 30 миллионов кВт×ч поставляют электроэнергию в три города. Максимальная потребность в электроэнергии этих городов оценивается в 30, 35 и 24 миллионов кВт×ч. Цены за миллион кВт-ч в данных городах приведены в табл. 4.4.
Стоимость за электроэнергию, руб. /млн. кВтч
| Города | ||||
|
1 |
2 |
3 |
||
| Станция |
1 |
600 | 700 | 400 |
|
2 |
320 | 300 | 350 | |
|
3 |
500 | 480 | 450 | |
В августе на 20% возрастает потребность в электроэнергии в каждом из трех городов. Недостаток электроэнергии могут восполнить из другой электросети по цене 1000 за 1 миллион кВт-ч. Но третий город не может подключиться к альтернативной электросети. Электрогенерирующие станции планируют разработать наиболее экономичный план распределения электроэнергии и восполнения ее недостатка в августе. Сформулируйте эту задачу в виде транспортной модели.
Решение
Задаем целевую функцию и ограничения с помощью «Поиска решений»:
![]() ;
;
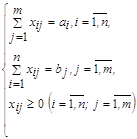
Получаем:
| Стоимость за электроэнергию, руб. /млн. кВтч | ||||||
| Города | Издержки | |||||
| 1 | 2 | 3 | Мощность | |||
| Станция | 1 | 600 | 700 | 400 | 25 | |
| 2 | 320 | 300 | 350 | 40 | ||
| 3 | 500 | 480 | 450 | 30 | ||
| 4 | 1000 | 1000 | 10000 | 12 | ||
| Потребление | 36 | 42 | 29 | 48570 | ||
| Города | ||||||
| 1 | 2 | 3 | Сумма | |||
| Станция | 1 | 0 | 0 | 25 | 25 | |
| 2 | 24 | 16 | 0 | 40 | ||
| 3 | 0 | 26 | 4 | 30 | ||
| 4 | 12 | 0 | 0 | 12 | ||
| Сумма | 36 | 42 | 29 | |||
Задача
Найти тремя методами опорный план ТЗ, в которой запасы на трех складах равны 210, 170, 65 ед. продукции, потребности четырех магазинов равны 125, 90, 130, 100 ед. продукции, тарифы перевозки в рублях за единицу продукции следующие:

Решение
Проверка сбалансированности задачи показывает, что суммарный объем запасов равен суммарному объему потребностей, т.е. введение фиктивных столбцов или строк не потребуется
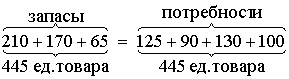
Результаты нахождения опорного плана различными методами представлены в табл.
Транспортная таблица с опорным планом северо-западного угла
|
Пункты отправления, |
Пункты потребления, |
Запасы, ед. продукции | |||
|
|
|
|
|
||
|
|
125 5 |
85 8 |
1 | 2 | 210/85/0 |
|
|
2 |
5 5 |
130 4 |
35 9 |
170/165/35/0 |
|
|
9 | 2 | 3 |
65 1 |
65/0 |
|
Потребность, ед. продукции |
125/0 | 90/5/0 | 130/0 | 100/65/0 | |
Опорный план ![]() ,
найденный методом северо-западного угла
,
найденный методом северо-западного угла
 [ед.товара]
[ед.товара]
Соответствующая ЦФ (общие затраты на перевозку)
![]() [руб.].
[руб.].
Транспортная таблица с опорным планом минимального элемента
|
Пункты отправления, |
Пункты потребления, |
Запасы, ед. продукции | |||
|
|
|
|
|
||
|
|
5 |
45 8 |
130 1 |
35 2 |
210/80/45/0 |
|
|
125 2 |
45 5 |
4 | 9 | 170/45/0 |
|
|
9 | 2 | 3 |
65 1 |
65/0 |
|
Потребность, ед. продукции |
125/0 | 90/45/0 | 130/0 | 100/35/0 | |
Опорный план ![]() ,
найденный методом минимального элемента
,
найденный методом минимального элемента
 [ед.товара]
[ед.товара]
![]() [руб.]
[руб.]
Транспортная таблица с опорным планом Фогеля
|
|
|
|
|
|
Штрафы строк, |
||||
|
|
5 | 8 |
110 1 |
100 2 |
210/110/0 | 1 | 1 | 1 |
7 |
|
|
125 2 |
25 5 |
20 4 |
9 | 170/45/25/0 | 2 | 1 | 1 | 1 |
|
|
9 |
65 2 |
3 | 1 | 65/0 | 1 | 1 | – | – |
|
|
125/0 | 90/25/0 | 130/20/0 | 100/0 | |||||
|
Штрафы столбцов, |
3 |
3 | 2 | 1 | |||||
| – |
3 |
2 | 1 | ||||||
| – | 3 | 3 |
7 |
||||||
| – | 3 | 3 | – | ||||||
На первом шаге нахождения опорного плана методом Фогеля возникает ситуация равенства значений максимальных штрафов транспортной матрицы
![]()
Минимальные тарифы в этих столбцах также совпадают
![]() .
.
Поэтому необходимо
сравнить суммарные штрафы ![]() клеток (2,1) и (3,2)
клеток (2,1) и (3,2)
![]() ;
;
![]() .
.
Т.к. ![]() , то
выбираем на первом шаге для заполнения клетку (2,1).
, то
выбираем на первом шаге для заполнения клетку (2,1).
Опорный план ![]()
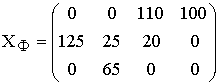 [ед.товара],
[ед.товара], ![]() [руб.]
[руб.]
Задача
Найти тремя методами опорный план ТЗ, в которой запасы на трех складах равны 160, 140, 170 ед. продукции, потребности четырех магазинов равны 120, 50, 200, 110 ед. продукции, тарифы перевозки в рублях за единицу продукции следующие:
Решение
Суммарный объем запасов равен суммарному объему потребностей
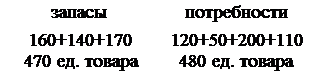 |
Транспортная таблица с опорным планом северо-западного угла
|
Пункты отправления, |
Пункты потребления, |
Запасы, ед. продукции | |||
|
|
|
|
|
||
|
|
120 7 |
40 8 |
1 | 2 | 160/40/0 |
|
|
4 |
10 5 |
130 9 |
8 | 140/130/0 |
|
|
9 | 2 |
70 3 |
100 6 |
170/100/0 |
| фиктивный склад | 0 | 0 | 0 |
10 0 |
10/0 |
|
Потребность, ед. продукции |
120/0 | 50/10/0 | 200/70/0 | 110/10/0 | |
Опорный план ![]() , найденный
методом северо-западного угла [ед.товара].
, найденный
методом северо-западного угла [ед.товара].

Соответствующая ЦФ (общие затраты на перевозку)
![]()
Транспортная таблица с опорным планом минимального элемента
|
Пункты отправления, |
Пункты потребления, |
Запасы, ед. продукции | |||
|
|
|
|
|
||
|
|
7 | 8 |
160 1 |
2 | 160/0 |
|
|
110 4 |
5 | 9 |
30 8 |
140/30/0 |
|
|
9 |
50 2 |
40 3 |
80 6 |
170/120/80/0 |
| фиктивный склад |
10 0 |
0 | 0 | 0 | 10/0 |
|
Потребность, ед. продукции |
120/110/0 | 50/0 | 200/40/0 | 110/30/0 | |
Опорный план ![]() , найденный
методом минимального элемента
, найденный
методом минимального элемента
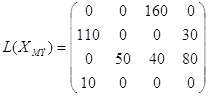
![]()
Транспортная таблица с опорным планом Фогеля
|
|
|
|
|
|
Штрафы строк, |
||||||
|
|
7 | 8 |
50 1 |
110 2 |
160/50/0 | 1 | 1 | 6 |
- |
- |
- |
|
|
110 4 |
30 5 |
9 | 8 | 140/110/0 | 1 | 1 | 1 | 1 | 1 | 1 |
|
|
9 |
20 2 |
150 3 |
6 | 170/20/0 | 1 | 1 | 1 | 1 |
7 |
- |
| фикт. |
10 0 |
0 | 0 | 0 | 10/0 | 0 | - | - | - |
- |
- |
|
|
120/110/0 | 50/30/0 | 200/150/0 | 110/0 | |||||||
|
Штрафы столбцов, |
4 |
2 | 1 | 2 | |||||||
| 3 | 3 | 2 |
4 |
||||||||
| 3 | 3 | 2 |
- |
||||||||
| 5 | 3 |
6 |
– | ||||||||
| 5 | 3 |
- |
- | ||||||||
| 4 |
5 |
- |
- | ||||||||
Опорный план ![]() , найденный
методом Фогеля [ед.товара],
, найденный
методом Фогеля [ед.товара],
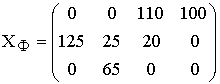
![]()
Задача
Некоторая фирма производит автомобили четырех различных марок М1, М2, М3, М4. Завод в городе А производит только автомобили марок М3, M4, в городе В – только автомобили марок М1, М2, M4, а в городе С – только автомобили марок М1, М2. Ежеквартальные объемы выпуска каждого завода и величины спроса в каждом пункте распределения приведены в таблице 1.3. Постройте соответствующую модель экономичных перевозок и определите целевую функцию по двум вариантам:
каждому виду продукции должна соответствовать одна транспортная матрица;
• все виды продукции представлены в одной общей матрице с использованием запрещающих тарифов в клетках, связывающих разные виды продукции.
Объемы производства заводов и спроса пунктов распределения автомобилей, шт/квартал
| Марка автомобиля | ||||
|
M1 |
M2 |
M3 |
M4 |
|
| Заводы | ||||
| А | — |
— |
700 | 300 |
| В | 500 | 600 | — | 400 |
| С | 800 | 400 | — | — |
| Пункты распределения | ||||
| D | 700 | 500 | 500 | 600 |
| Е | 600 | 500 | 200 | 100 |
Стоимость перевозки автомобилей, руб./шт
| D | Е | |
| А | 80 | 215 |
| В | 100 | 108 |
| С | 102 | 68 |
Решение:
Составляем для каждого вида продукции транспортную матрицу:
Транспортная матрица для первого вида продукции:
| D | Е | Объем | |
| А | 0 | 0 | 0 |
| В | 100 | 108 | 500 |
| С | 102 | 68 | 800 |
| Спрос | 700 | 600 | |
| издержки | 111200 | ||
| D | Е | Сумма | |
| А | 0 | 0 | 0 |
| В | 500 | 0 | 500 |
| С | 200 | 600 | 800 |
| Сумма | 700 | 600 | |
Транспортная матрица для второго вида продукции:
| D | Е | Объем | |
| А | 0 | 0 | 0 |
| В | 100 | 108 | 600 |
| С | 102 | 68 | 400 |
| Спрос | 500 | 500 | |
| издержки | 88000 | ||
| D | Е | Сумма | |
| А | 0 | 0 | 0 |
| В | 500 | 100 | 600 |
| С | 0 | 400 | 400 |
| Сумма | 500 | 500 | |
Транспортная матрица для третьего вида продукции:
| D | Е | Объем | |
| А | 80 | 215 | 700 |
| В | 0 | 0 | 0 |
| С | 0 | 0 | 0 |
| Спрос | 500 | 200 | |
| издержки | 83000 | ||
| D | Е | Сумма | |
| А | 500 | 200 | 700 |
| В | 0 | 0 | 0 |
| С | 0 | 0 | 0 |
| Сумма | 500 | 200 | |
Транспортная матрица для четвертого вида продукции:
| D | Е | Объем | |
| А | 80 | 215 | 300 |
| В | 100 | 108 | 400 |
| С | 0 | 0 | 0 |
| Спрос | 600 | 100 | |
| издержки | 64800 | ||
| D | Е | Сумма | |
| А | 300 | 0 | 300 |
| В | 300 | 100 | 400 |
| С | 0 | 0 | 0 |
| Сумма | 600 | 100 | |
Целевая функция равна сумме издержек по каждому виду продукции 347000.
Объединяем все виды продукции в одной общей матрице и с помощью «Поиска решений» находим оптимальный план и целевую функцию:
| D1 | E1 | D2 | E2 | D3 | E3 | D4 | E4 | производство | |||||||||||
| A3 | 10000 | 10000 | 10000 | 10000 | 80 | 215 | 10000 | 10000 | 700 | ||||||||||
| A4 | 10000 | 10000 | 10000 | 10000 | 10000 | 10000 | 80 | 215 | 300 | ||||||||||
| B1 | 100 | 108 | 10000 | 10000 | 10000 | 10000 | 10000 | 10000 | 500 | ||||||||||
| B2 | 10000 | 10000 | 100 | 108 | 10000 | 10000 | 10000 | 10000 | 600 | ||||||||||
| B4 | 10000 | 10000 | 10000 | 10000 | 10000 | 10000 | 100 | 108 | 400 | ||||||||||
| C1 | 102 | 68 | 10000 | 10000 | 10000 | 10000 | 10000 | 10000 | 800 | ||||||||||
| C2 | 10000 | 10000 | 102 | 68 | 10000 | 10000 | 10000 | 10000 | 400 | ||||||||||
| спрос | 700 | 600 | 500 | 500 | 500 | 200 | 600 | 100 |
347000 |
||||||||||
| D1 | E1 | D2 | E2 | D3 | E3 | D4 | E4 |
|
|||||||||||
| A3 | 0 | 0 | 0 | 0 | 500 | 200 | 0 | 0 | 700 |
|
|||||||||
| A4 | 0 | 0 | 0 | 0 | 0 | 0 | 300 | 0 | 300 |
|
|||||||||
| B1 | 500 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 500 |
|
|||||||||
| B2 | 0 | 0 | 500 | 100 | 0 | 0 | 0 | 0 | 600 |
|
|||||||||
| B4 | 0 | 0 | 0 | 0 | 0 | 0 | 300 | 100 | 400 |
|
|||||||||
| C1 | 200 | 600 | 0 | 0 | 0 | 0 | 0 | 0 | 800 |
|
|||||||||
| C2 | 0 | 0 | 0 | 400 | 0 | 0 | 0 | 0 | 400 |
|
|||||||||
| 700 | 600 | 500 | 500 | 500 | 200 | 600 | 100 |
|
|||||||||||
Задача о назначениях
Задача
а). Строительной компании «Спецстройкурнож» необходимо выполнить бетонные работы на 4 строящихся объектах. В фирме имеется 4 бригады бетонщиков, которые могут выполнить эту работу. Бригадиры каждой бригады побывали на объектах, оценили объемы работ и рассчитали сроки, за которые они могут выполнить работы.
| Бригада | Объект | |||
| 1 | 2 | 3 | 4 | |
| №1 | 30 | 40 | 50 | 60 |
| №2 | 36 | 41 | 52 | 58 |
| №3 | 28 | 44 | 49 | 57 |
| №4 | 35 | 39 | 49 | 63 |
Перед руководством фирмы стоит задача распределения бригад по объектам таким образом, чтобы суммарный срок выполнения всех работ был минимальным. Поскольку количества бригад и объектов одинаковы, следовательно, имеем сбалансированную задачу о назначениях.
Решение
С помощью «Поиска решения» распределяем бригады по объектам таким образом, чтобы суммарный срок выполнения всех работ был минимальным.
| Бригада | Объект | |||
| 1 | 2 | 3 | 4 | |
| №1 | 30 | 40 | 50 | 60 |
| №2 | 36 | 41 | 52 | 58 |
| №3 | 28 | 44 | 49 | 57 |
| №4 | 35 | 39 | 49 | 63 |
|
целевая функция |
175 |
|||
| Бригада | Объект | |||
| 1 | 2 | 3 | 4 | |
| №1 | 0 | 1 | 0 | 0 |
| №2 | 0 | 0 | 0 | 1 |
| №3 | 1 | 0 | 0 | 0 |
| №4 | 0 | 0 | 1 | 0 |
| ∑ | 1 | 1 | 1 | 1 |
б). Несбалансированная задача. Пока руководство фирмы «Спецстройизбкурнож» решало, какую бригаду бетонщиков послать на какой объект, освободилась от работ на предыдущем объекте еще одна бригада и выразила готовность также подключиться к работе на одном из четырех объектов. Бригадир этой бригады оценил работы на каждом объекте и подсчитал, что работы на первом объекте его бригада выполнит за 29 рабочих дней, на втором объекте за 40 дней, на третьем объекте за 48 дней и на четвертом – за 59 дней
Решение
С помощью «Поиска решений» распределяем бригады по объектам таким образом, чтобы суммарный срок выполнения всех работ был минимальным.
| Бригада | Объект | |||
| 1 | 2 | 3 | 4 | |
| №1 | 30 | 40 | 50 | 60 |
| №2 | 36 | 41 | 52 | 58 |
| №3 | 28 | 44 | 49 | 57 |
| №4 | 35 | 39 | 49 | 63 |
| №5 | 29 | 40 | 48 | 59 |
|
цел. функция |
173 |
|||
| Бригада | Объект | |||
| 1 | 2 | 3 | 4 | |
| №1 | 0 | 0 | 0 | 0 |
| №2 | 0 | 0 | 0 | 1 |
| №3 | 1 | 0 | 0 | 0 |
| №4 | 0 | 1 | 0 | 0 |
| №5 | 0 | 0 | 1 | 0 |
| ∑ | 1 | 1 | 1 | 1 |
Общая распределительная задача линейного программирования
Задача
На фабрике эксплуатируются три типа ткацких станков, которые могут выпускать четыре вида тканей. Известны следующие данные о производственном процессе:
производительности станков по каждому виду ткани, м/ч
 ;
;
себестоимость тканей, руб./м
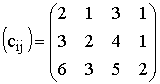 ;
;
фонды рабочего времени
станков (![]() ):
90, 220, 180 ч;
):
90, 220, 180 ч;
планируемый объем выпуска
тканей (![]() ):
1200, 900, 1800, 840 м.
):
1200, 900, 1800, 840 м.
Требуется распределить выпуск ткани по станкам с целью минимизации общей себестоимости производства ткани.
Решение
|
|||||||||||||||||||||
| 1.1 |
|
||||||||||||||||||||
| 1 | 1 | 1 | 1 |
|
|||||||||||||||||
|
ai |
0,5 | 0,5 | 0,5 | 0,5 |
|
||||||||||||||||
| 0,33333 | 0,33333 | 0,33333 | 0,3333 |
|
|||||||||||||||||
|
|||||||||||||||||||||
| 1.2 |
|
||||||||||||||||||||
| 90 | 1 | 90 |
|
||||||||||||||||||
| 220 | * | 0,5 | = | 110 |
|
||||||||||||||||
| 180 | 0,33333 | 60 |
|
||||||||||||||||||
|
|||||||||||||||||||||
| 1.3 |
|
||||||||||||||||||||
| 24 | 30 | 18 | 42 |
|
|||||||||||||||||
|
bj |
12 | 15 | 9 | 21 |
|
||||||||||||||||
| 8 | 10 | 6 | 14 |
|
|||||||||||||||||
| 1200 | 900 | 1800 | 840 |
|
|||||||||||||||||
|
|||||||||||||||||||||
| bj' | 50 | 30 | 100 | 20 |
|
||||||||||||||||
| b(фиктив)' | 60 |
|
|||||||||||||||||||
|
|||||||||||||||||||||
| 1.4 |
|
||||||||||||||||||||
| 2 | 1 | 3 | 1 |
|
|||||||||||||||||
|
cij |
3 | 2 | 4 | 1 | * | 24 | 30 | 18 | 42 |
|
|||||||||||
| 6 | 3 | 5 | 2 |
|
|||||||||||||||||
|
|||||||||||||||||||||
| 48 | 30 | 54 | 42 |
|
|||||||||||||||||
| = | 72 | 60 | 72 | 42 |
|
||||||||||||||||
| 144 | 90 | 90 | 84 |
|
|||||||||||||||||
|
|||||||||||||||||||||
| 2. |
ai |
bj |
|
||||||||||||||||||
| 90 | 50 |
|
|||||||||||||||||||
| 110 | 30 |
|
|||||||||||||||||||
| 60 | 100 |
|
|||||||||||||||||||
| 260 | 20 |
|
|||||||||||||||||||
| 60 |
|
||||||||||||||||||||
| 260 |
|
||||||||||||||||||||
|
|||||||||||||||||||||
| 3. |
|
||||||||||||||||||||
| 48 | 30 | 54 | 42 | 0 | 90 |
|
|||||||||||||||
| 72 | 60 | 72 | 42 | 0 | 110 |
|
|||||||||||||||
| 144 | 90 | 90 | 84 | 0 | 60 |
|
|||||||||||||||
| 50 | 30 | 100 | 20 | 60 |
|
||||||||||||||||
|
|||||||||||||||||||||
| 50 | 30 | 10 | 0 | 0 |
|
||||||||||||||||
| 0 | 0 | 90 | 20 | 0 | Поиск оптимального решения |
|
|||||||||||||||
| 0 | 0 | 0 | 0 | 60 |
|
||||||||||||||||
| 4. | |||||||||||||||||||||
| 50 | 30 | 10 | 0 | 0 | 1 | ||||||||||||||||
|
xij |
0 | 0 | 90 | 20 | 0 | / | 0,5 | = | |||||||||||||
| 0 | 0 | 0 | 0 | 60 | 0,3333 | ||||||||||||||||
| 50 | 30 | 10 | 0 | 0 | |||||||||||||||||
| = | 0 | 0 | 180 | 40 | 0 | ||||||||||||||||
| 0 | 0 | 0 | 0 | 180 | |||||||||||||||||
| 5. | |||||||||||||||||||||
| 50 | 30 | 10 | 0 | 0 | 24 | 30 | 18 | 42 | 0 | ||||||||||||
| 0 | 0 | 180 | 40 | 0 | * | 12 | 15 | 9 | 21 | 0 | |||||||||||
| 0 | 0 | 0 | 0 | 180 | 8 | 10 | 6 | 14 | 0 | ||||||||||||
| 1200 | 900 | 180 | 0 | 0 | 2 | 1 | 3 | 1 | 0 | ||||||||||||
| 0 | 0 | 1620 | 840 | 0 | * | 3 | 2 | 4 | 1 | 0 | |||||||||||
| 0 | 0 | 0 | 0 | 0 | 6 | 3 | 5 | 2 | 0 | ||||||||||||
| 2400 | 900 | 540 | 0 | ||||||||||||||||||
| 0 | 0 | 6480 | 840 | L(x)= | 11160 | ||||||||||||||||
| 0 | 0 | 0 | 0 | ||||||||||||||||||
Задача
Некоторая фирма содержит три магазина, которым еженедельно следует доставлять товар: первому магазину – 1050 кг сыра, второму – 600 мешков муки, третьему – 2400 упаковок сока. Товары доставляются грузовыми машинами четырех транспортных предприятий. Количество машин на этих предприятиях составляет 65, 40, 45 и 20 машин. Все машины имеют различную грузоподъемность [ед. тов. / маш.], в зависимости от типа машины и типа перевозимого груза
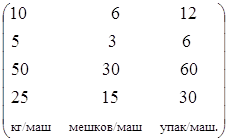
Стоимости использования машин [руб. / маш.] в зависимости от дальности перевозки и емкости машины равны
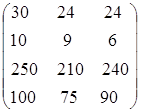 .
.
Организуйте экономичную перевозку товаров (при решении используйте метод северо-западного угла).
Решение:
| Этапы решения распределительной задачи: | |||||||||||
| 1.1 | |||||||||||
| 0,2 | 0,2 | 0,2 | |||||||||
|
ai |
0,1 | 0,1 | 0,1 | ||||||||
| 1 | 1 | 1 | |||||||||
| 0,5 | 0,5 | 0,5 | |||||||||
| 1.2 | |||||||||||
| 65 | 0,2 | 13 | |||||||||
| 40 | * | 0,1 | = | 4 | |||||||
| 45 | 1 | 45 | |||||||||
| 20 | 0,5 | 10 | |||||||||
| 1.3 | |||||||||||
| 10 | 6 | 12 | |||||||||
|
bj |
5 | 3 | 6 | ||||||||
| 50 | 30 | 60 | |||||||||
| 25 | 15 | 30 | |||||||||
| 1050 | 600 | 2400 | |||||||||
|
bj |
21 | 20 | 40 | ||||||||
| a фикт | 9 | ||||||||||
| 1.4 | |||||||||||
| 30 | 24 | 24 | 1500 | 720 | 1440 | ||||||
|
cij |
10 | 9 | 6 | * | 50 | 30 | 60 | = | 500 | 270 | 360 |
| 250 | 210 | 240 | 12500 | 6300 | 14400 | ||||||
| 100 | 75 | 90 | 5000 | 2250 | 5400 | ||||||
| 2. |
ai |
bj |
|||||||||
| 13 | 21 | ||||||||||
| 4 | 20 | ||||||||||
| 45 | 40 | ||||||||||
| 10 | 81 | ||||||||||
| 9 | |||||||||||
| 81 | |||||||||||
| 3. | |||||||||||
| 1500 | 720 | 1440 | 13 | ||||||||
| 500 | 270 | 360 | 4 | ||||||||
| 12500 | 6300 | 14400 | 45 | ||||||||
| 5000 | 2250 | 5400 | 10 | ||||||||
| 0 | 0 | 0 | 9 | ||||||||
| 21 | 20 | 40 | |||||||||
| 13 | 0 | 0 | |||||||||
| 4 | 0 | 0 | |||||||||
| 4 | 20 | 21 | Поиск оптимального решения | ||||||||
| 0 | 0 | 10 | |||||||||
| 0 | 0 | 9 | |||||||||
| 4. | 13 | 0 | 0 | 0,2 | 65 | 0 | 0 | ||||
| 4 | 0 | 0 | 0,1 | 40 | 0 | 0 | |||||
|
xij |
4 | 20 | 21 | / | 1 | = | 4 | 20 | 21 | ||
| 0 | 0 | 10 | 0,5 | 0 | 0 | 20 | |||||
| 0 | 0 | 9 | 0 | 0 | 0 | 0 | |||||
| 5. | |||||||||||
| 65 | 0 | 0 | 10 | 6 | 12 | 650 | 0 | 0 | |||
| 40 | 0 | 0 | 5 | 3 | 6 | 200 | 0 | 0 | |||
| 4 | 20 | 21 | * | 50 | 30 | 60 | = | 200 | 600 | 1260 | |
| 0 | 0 | 20 | 25 | 15 | 30 | 0 | 0 | 600 | |||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||
| 650 | 0 | 0 | 30 | 24 | 24 | 19500 | 0 | 0 | |||
| 200 | 0 | 0 | 10 | 9 | 6 | 2000 | 0 | 0 | |||
| 200 | 600 | 1260 | * | 250 | 210 | 240 | = | 50000 | 1E+05 | 3E+05 | |
| 0 | 0 | 600 | 100 | 75 | 90 | 0 | 0 | 54000 | |||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||
| L(x)= | 553900 | ||||||||||
Модели управления запасами
Задача
Объем продажи некоторого магазина составляет в год 500 упаковок супа в пакетах. Величина спроса равномерно распределяется в течение года. Цена покупки одного пакета равна 2 руб. За доставку заказа владелец магазина должен заплатить 10 руб. Время доставки заказа от поставщика составляет 12 рабочих дней (при 6-дневной рабочей неделе). По оценкам специалистов, издержки хранения в год составляют 40 коп. за один пакет. Необходимо определить: сколько пакетов должен заказывать владелец магазина для одной поставки; частоту заказов; точку заказа. Магазин работает 300 дней в году.
Постройте график затрат Q [10; 200] с учетом затрат владельца магазина на закупку пакетов супа у поставщика. Графически определите наиболее выгодный объем заказа.
Решение
Пусть Q - размер
заказа; T=300 - продолжительность периода планирования; D=500
- величина спроса за период планирования; К=10 - издержки одного
заказа (стоимость доставки); ![]() - удельные издержки
хранения за период; с=2 — цена продукта. Тогда:
- удельные издержки
хранения за период; с=2 — цена продукта. Тогда:
Издержки
заказа за период планирования:![]() ;
;
Издержки
хранения за период планирования : ![]() ;
;
Издержки
на закупку товара: ![]() .
.
При этом
совокупные издержки: 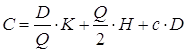 .
.
Формула совокупных издержек:
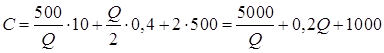 .
.
Для нахождения наименьшего значения функции С найдем ее производную и прировняем ее к нулю.
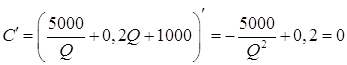
Отсюда
получаем: ![]() .
.
Оптимальное число заказов:
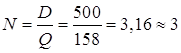 .
.
Число дней между заказами:
![]() дней.
дней.
Так как длина интервала между поставками равна 100 дней, а время доставки – 12 дней, то заказ нужно возобновить, когда уровень запаса достаточен для удовлетворения потребностей на 12 рабочих дней.
Так как
ежедневная потребность равна 500/300=1,67 упаковок супа в день, то заказы
должны делаться регулярно при достижении уровня запаса ![]() пачек
супа.
пачек
супа.
График затрат Q [10; 200] с учетом затрат владельца магазина на закупку пакетов супа у поставщика (рис. 5):
![]()
![]()
|
|
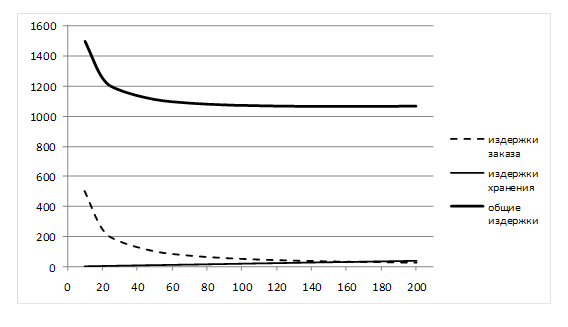
Рис. 5
Оптимальный размер заказа (точка пересечения графиков издержек заказа и издержек хранения) приблизительно равен 158 пакетов супа.
Величина общих годовых издержек составит примерно 1060 руб.
Задача
На некотором станке производятся детали в количестве 2000 штук в месяц. Эти детали используются для производства продукции на другом станке с интенсивностью 500 шт. в месяц. По оценкам специалистов компании, издержки хранения составляют 50 коп. в год за одну деталь. Стоимость производства одной детали равна 2,50 руб., а стоимость на подготовку производства составляет 1000 руб. Каким должен быть размер партии деталей, производимой на первом станке, с какой частотой следует запускать производство этих партий?
Решение
Для начала определяем сколько производит первый и второй станки за год деталей:
первый станок = 2000*12=24000;
второй станок = 500 * 12 = 6000.
Затем по формулам модели Уилсона находим, оптимальный план, частоту заказов и общие издержки.
![]()
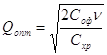
![]()
![]()
Qопт=5656,85
С=2121,32
τ месс=11,31
Задача
Фирма может производить изделие или покупать его. Если фирма сама выпускает изделие, то каждый запуск его в производство обходится в 20 руб. Интенсивность производства составляет 120 шт. в день. Если изделие закупается, то затраты на осуществление заказа равны 15 руб. Затраты на содержание изделия в запасе независимо от того, закупается оно или производится, равны 2 коп. в день. Потребление изделия фирмой оценивается в 26 000 шт. в год.
Предполагая, что фирма работает без дефицита, определите, что выгоднее: закупать или производить изделие (в месяце 22 рабочих дня).
Подтвердите свое решение графически, для этого на одном рисунке постройте графики общих затрат фирмы для случаев покупки и производства изделий.
Решение
Производство изделий:
Обозначим Q -
размер выпускаемой партии; D=26000 шт. - величина спроса в год; ![]() шт. – величина спроса в день;
шт. – величина спроса в день; ![]() шт. - интенсивность производства; К=20
руб. – стоимость каждого запуска изделия в производство;
шт. - интенсивность производства; К=20
руб. – стоимость каждого запуска изделия в производство; ![]() руб. - издержки хранения за год.
Тогда:
руб. - издержки хранения за год.
Тогда:
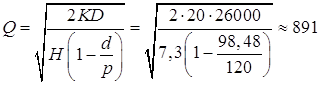 шт.
шт.
Cовокупные издержки:
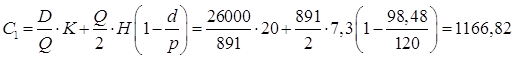 руб.
руб.
Покупка изделий
Обозначим Q -
размер приобретаемой партии; D=26000 шт. - величина спроса в год; К=15
руб. – стоимость каждой покупки; ![]() руб.
- издержки хранения за год. Тогда:
руб.
- издержки хранения за год. Тогда:
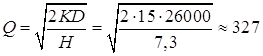 шт.
шт.
Совокупные издержки:
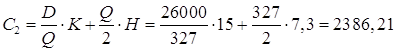 руб.
руб.
|
|
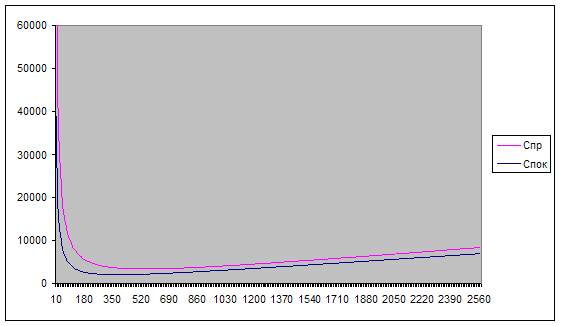
Рис. 6 - Графики общих затрат фирмы для случаев покупки и производства изделий
Вывод: выгоднее производить изделия, чем покупать их.
Задача
При строительстве участка автодороги длиной 500 м используют гравий, расход которого составляет 120 кг/м. Сроки строительства составляют 17 дней. Работа идет в одну смену. Расход гравия равномерный. Гравий доставляется грузовыми машинами, емкостью 7 т, в течение 4 часов. Затраты на один рейс грузовика равны 15 руб. Затраты на хранение гравия на месте строительства составляют 1 руб. 10 коп. в сутки за тонну.
Определить: оптимальный объем заказа, количество грузовых машин, используемых для доставки, период поставок, точку заказа, затраты за всю стройку. Постройте график двух последних циклов изменения запаса гравия на месте строительства.
Решение
Пусть Q –
оптимальный объем заказа; D=![]() т - величина спроса за
период строительства; К=
т - величина спроса за
период строительства; К=![]() руб. - издержки
одного заказа (здесь 7 - грузоподъемность машины);
руб. - издержки
одного заказа (здесь 7 - грузоподъемность машины); ![]() руб.
- удельные издержки хранения за период; Т=17 дней – период
планирования;
руб.
- удельные издержки хранения за период; Т=17 дней – период
планирования; ![]() сут. (принимаем время смены 8
часов). Тогда:
сут. (принимаем время смены 8
часов). Тогда:
Издержки
заказа за период планирования :![]() ;
;
Издержки
хранения за период планирования:![]() .
.
Оптимальный размер заказа составит:
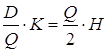 или
или 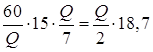 , откуда
, откуда  т.
т.
Количество
грузовых машин равно ![]() ед.
ед.
Период
поставок: 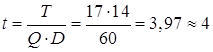 дня.
дня.
Точка
заказа: ![]() т.
т.
Затраты на всю стройку составят:
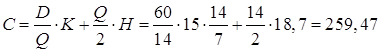 руб.
руб.
Так как период поставок равен 4 дня, а время работы равно 17 дней, получим 4 полные поставки и в 16-й день еще одну машину с гравием.
Задача
Пусть затраты на заказ равны 10 руб., затраты на хранение продукции 1 руб. в сутки, интенсивность потребления товара 5 шт. в день, цена товара – 2руб. за штуку, а при объеме закупки 15 шт. и более- 1руб.
Определите оптимальный размер заказа, цену покупки и затраты на управление запасами. Постройте график общих затрат.
Пусть Q - размер
заказа; ![]() - величина потребления за день; К=10
- издержки одного заказа; h=1 - удельные издержки хранения за день; сi
цена продукта при соответствующем размере заказа.
- величина потребления за день; К=10
- издержки одного заказа; h=1 - удельные издержки хранения за день; сi
цена продукта при соответствующем размере заказа.
Издержки
заказа за период планирования: ![]() ;
;
Издержки
хранения за период планирования: ![]() ;
;
Издержки
на закупку товара:![]() .
.
Совокупные издержки:
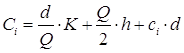 .
.
При размере заказа менее 15 шт формула совокупных издержек запишется в виде:
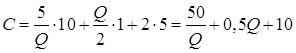 .
.
Для нахождения наименьшего значения функции С находим ее производную и прировняем ее к нулю.
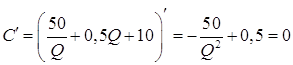
![]() .
.
Аналогично находим при заказе 15 шт. и более:
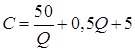 ;
; 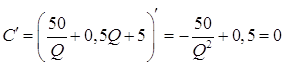 ;
; ![]() .
.
![]()
Общие издержки для каждого размера заказа и вида скидок с выбором наименьшего значения:
| Размер заказа | Менее 15 шт. | 15 шт. и более |
| Цена 1 шт., руб. | 2 | 1 |
| Размер заказа, шт. | 10 | 15 |
| Издержки заказа, руб. | 5 | 3,33 |
| Издержки хранения, руб. | 5 | 7,5 |
| Издержки на закупку товара, руб. | 10 | 5 |
| Общие затраты, руб. | 20 | 15,83 |
Выбираем размер заказа,
минимизирующий общие годовые издержки. Заказ в размере 15 шт. будет
минимизировать общие затраты, оптимальный размер заказа ![]() шт.
шт.
При этом цена покупки
составит ![]() руб., затраты на управление запасами составят
руб., затраты на управление запасами составят
![]() руб.
руб.
График общих
|
|
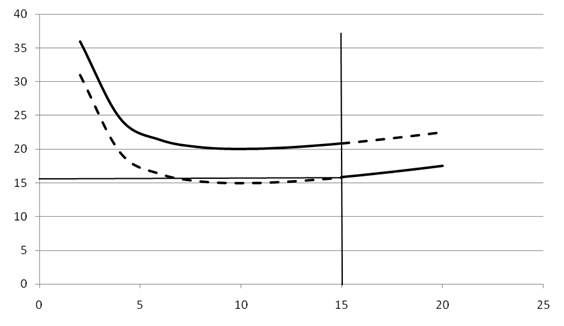
Рис.7
Задача
Рассмотрим задачу 5.1. Пусть поставщик супа в пакетах предоставляет следующие скидки
| Размер заказа | Цена, руб./шт. |
| 1-199 | 2 |
| 200-499 | 1,96 (2% скидки) |
| 500 и более | 1,92 (4% скидки) |
Следует ли владельцу магазина воспользоваться одной из скидок, предоставляемых поставщиком? Каковы при этом будут размер заказа и общие затраты на управление запасами? Постройте график общих затрат.
Решение
Пусть Q - размер заказа; T=300 - продолжительность периода планирования; D=500 - величина спроса за период планирования; К=10 - издержки одного заказа; Н=0,4 - удельные издержки хранения за период; сi — цена продукта при соответствующем размере заказа. Тогда:
Издержки
заказа за период планирования: ![]() ;
;
Издержки
хранения за период планирования : ![]() ;
;
Издержки
на закупку товара : ![]() .
.
Совокупные издержки:
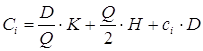 .
.
Оптимальный заказ:
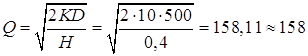 .
.
Поэтому
для первого уровня цен принимаем ![]() ; для других цен -
; для других цен - ![]()
![]() . Рассчитываем общие
издержки для каждого размера заказа и вида скидок, а затем выбрать наименьшее
значение.
. Рассчитываем общие
издержки для каждого размера заказа и вида скидок, а затем выбрать наименьшее
значение.
| Размер заказа | 1-199 | 200-499 | 500 и более |
| Цена пакета, руб. | 2 | 1,96 | 1,92 |
| Размер заказа, шт. | 158 | 200 | 500 |
| Издержки заказа за год, руб. | 31,65 | 25,0 | 10 |
| Издержки хранения за год, руб. | 31,6 | 40 | 100 |
| Издержки на закупку товара за год, руб. | 1000 | 980 | 960 |
| Совокупные издержки, руб. | 1063,25 | 1045,0 | 1070,0 |
Выберем тот размер
заказа, который минимизирует общие годовые издержки. Из таблицы видно, что
заказ в размере 200 пакетов супа будет минимизировать совокупные издержки,
следовательно, оптимальный размер заказа ![]() пакетов.
пакетов.
При этом совокупные
издержки за год составят ![]() руб.
руб.
![]()
![]()
![]()
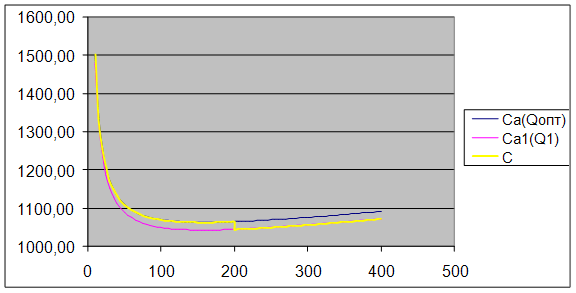
Рис. 8 - График общих затрат
Задача
Какое количество товара заказывать и по какой цене, каковы затраты при оптимальной организации управления запасами? Известно, что n =240 шт./дн.; С0= 30 руб.; Сh = 3 руб./шт.дн.; a = 6 руб./шт.; a1 = 5 руб./шт.; a2 =3 руб./шт.; Qp1= 50 шт.; QP2 =500 шт.
Решение
Пусть Q - размер
заказа; v=240 шт./дн. - величина спроса за
период планирования; С0=30 руб. - издержки одного
заказа; ![]() руб./шт.дн. - удельные
издержки хранения за период; сi — цена продукта при
соответствующем размере заказа. Тогда:
руб./шт.дн. - удельные
издержки хранения за период; сi — цена продукта при
соответствующем размере заказа. Тогда:
Издержки
заказа за период планирования: ![]() ;
;
Издержки
хранения за период планирования: ![]() ;
;
Издержки
на закупку товара:![]() .
.
Совокупные издержки:
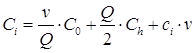 .
.
Оптимальный заказ:
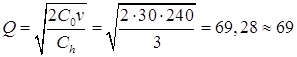 .
.
Поэтому
для первого уровня цен принимаем ![]() ; для других цен -
; для других цен - ![]()
![]() . Далее рассчитаем общие
издержки для каждого размера заказа и вида скидок, а затем выбрать наименьшее
значение.
. Далее рассчитаем общие
издержки для каждого размера заказа и вида скидок, а затем выбрать наименьшее
значение.
| Размер заказа | 1-49 | 50-499 | 500 и более |
| Цена ед. товара, руб. | 6 | 5 | 3 |
| Размер заказа, шт. | 49 | 69 | 500 |
| Издержки заказа, руб. | 146,94 | 104,35 | 14,40 |
| Издержки хранения, руб. | 73,50 | 103,50 | 750,00 |
| Издержки на закупку товара, руб. | 1440,00 | 1200,00 | 720,00 |
| Совокупные издержки, руб. | 1660,44 | 1407,85 | 1484,40 |
Выберем тот размер
заказа, который минимизирует общие издержки. Из таблицы видно, что заказ в
размере 69 единиц товара будет минимизировать совокупные издержки,
следовательно, оптимальный размер заказа ![]() .
.
Вывод: совокупные издержки 1407,85 руб.
Расчет и анализ сетевых моделей
1. Рассчитайте табличным методом представленный сетевой график. Определите критический путь.
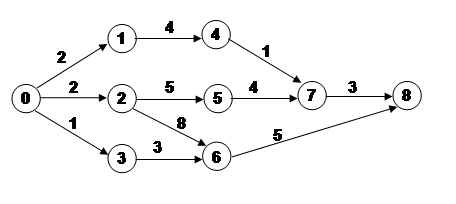
Решение
Расчёты сетевого графика табличным методом приведены в таблице:
| hi | i | j | РН | tij | РО | ПО | tij | ПН | Rij | rij |
| - | 0 | 1 | 0 | 2 | 2 | 7 | 2 | 5 | 5 | 0 |
| - | 0 | 2 | 0 | 2 | 2 | 2 | 2 | 0 | 0 | 0 |
| - | 0 | 3 | 0 | 1 | 1 | 7 | 1 | 6 | 6 | 0 |
| 1 | 1 | 4 | 2 | 4 | 6 | 11 | 4 | 7 | 5 | 0 |
| 1 | 2 | 5 | 2 | 5 | 7 | 8 | 5 | 3 | 1 | 0 |
| 1 | 2 | 6 | 2 | 8 | 10 | 10 | 8 | 2 | 0 | 0 |
| 1 | 3 | 6 | 1 | 3 | 4 | 10 | 3 | 7 | 6 | 6 |
| 1 | 4 | 7 | 6 | 1 | 7 | 12 | 1 | 11 | 5 | 4 |
| 1 | 5 | 7 | 7 | 4 | 11 | 12 | 4 | 8 | 1 | 0 |
| 2 | 6 | 8 | 10 | 5 | 15 | 15 | 5 | 10 | 0 | 0 |
| 2 | 7 | 8 | 11 | 3 | 14 | 15 | 3 | 12 | 1 | 1 |
| 2 | 8 | - | 15 | - | 15 | 15 | - | 15 | 0 | 0 |
Критический путь: 0-2-6-8
2. Рассчитайте табличным методом представленный сетевой график.. Определите критический путь.
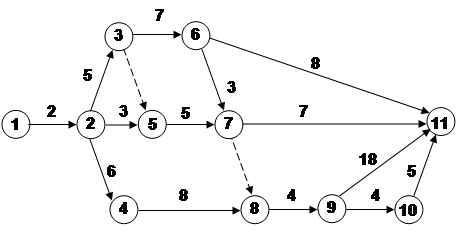 |
Решение
Расчёты сетевого графика табличным методом приведены в таблице:
| hi | i | j | РН | tij | РО | ПО | tij | ПН | Rij | rij |
| - | 1 | 2 | 0 | 2 | 2 | 2 | 2 | 0 | 0 | 0 |
| 1 | 2 | 3 | 2 | 5 | 7 | 7 | 5 | 2 | 0 | 0 |
| 1 | 2 | 4 | 2 | 6 | 8 | 9 | 6 | 3 | 1 | 0 |
| 1 | 2 | 5 | 2 | 3 | 5 | 12 | 3 | 9 | 7 | 2 |
| 1 | 3 | 5 | 7 | 0 | 7 | 12 | 0 | 12 | 5 | 0 |
| 1 | 3 | 6 | 7 | 7 | 14 | 14 | 7 | 7 | 0 | 0 |
| 1 | 4 | 8 | 8 | 8 | 16 | 17 | 8 | 9 | 1 | 1 |
| 2 | 5 | 7 | 7 | 5 | 12 | 17 | 5 | 12 | 3 | 5 |
| 1 | 6 | 7 | 14 | 3 | 17 | 17 | 3 | 14 | 0 | 0 |
| 1 | 6 | 11 | 14 | 8 | 22 | 39 | 8 | 31 | 17 | 17 |
| 2 | 7 | 8 | 17 | 0 | 17 | 17 | 0 | 17 | 0 | 0 |
| 2 | 7 | 11 | 17 | 7 | 24 | 39 | 7 | 32 | 15 | 15 |
| 2 | 8 | 9 | 17 | 4 | 21 | 21 | 4 | 17 | 0 | 0 |
| 1 | 9 | 10 | 21 | 4 | 25 | 34 | 4 | 30 | 9 | 0 |
| 1 | 9 | 11 | 21 | 18 | 39 | 39 | 18 | 21 | 0 | 0 |
| 1 | 10 | 11 | 25 | 5 | 30 | 39 | 5 | 34 | 9 | 9 |
| 4 | 11 | - | 39 | - | 39 | 39 | - | 39 | 0 | 0 |
Критический путь: 1-2-3-6-7-8-9-11
3. Рассчитайте табличным методом представленный сетевой график. Определите критический путь.
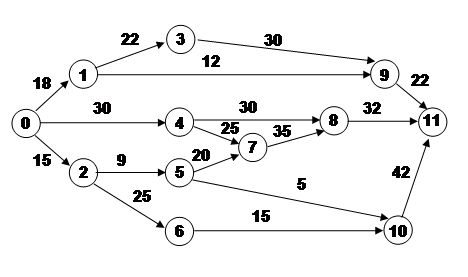
Решение
Расчеты сетевого графика табличным методом приведены в таблице:
| hi | i | j | РН | tij | РО | ПО | tij | ПН | Rij | rij |
| - | 0 | 1 | 0 | 18 | 18 | 48 | 18 | 30 | 30 | 0 |
| - | 0 | 2 | 0 | 15 | 15 | 26 | 15 | 11 | 11 | 0 |
| - | 0 | 4 | 0 | 30 | 30 | 30 | 30 | 0 | 0 | 0 |
| 1 | 1 | 3 | 18 | 22 | 40 | 70 | 22 | 48 | 30 | 0 |
| 1 | 1 | 9 | 18 | 12 | 30 | 100 | 12 | 88 | 70 | 52 |
| 1 | 2 | 5 | 15 | 9 | 24 | 35 | 9 | 26 | 9 | 0 |
| 1 | 2 | 6 | 15 | 15 | 40 | 62 | 15 | 40 | 25 | 0 |
| 1 | 3 | 9 | 40 | 30 | 70 | 100 | 30 | 70 | 30 | 0 |
| 1 | 4 | 7 | 30 | 25 | 55 | 55 | 25 | 30 | 0 | 0 |
| 1 | 4 | 8 | 30 | 30 | 60 | 90 | 30 | 60 | 30 | 30 |
| 1 | 5 | 7 | 24 | 20 | 44 | 55 | 20 | 35 | 11 | 11 |
| 1 | 5 | 10 | 24 | 5 | 29 | 80 | 5 | 75 | 51 | 26 |
| 1 | 6 | 10 | 40 | 15 | 55 | 80 | 15 | 65 | 25 | 0 |
| 2 | 7 | 8 | 55 | 35 | 90 | 90 | 35 | 55 | 0 | 0 |
| 2 | 8 | 11 | 90 | 32 | 122 | 122 | 32 | 90 | 0 | 0 |
| 2 | 9 | 11 | 70 | 22 | 99 | 122 | 22 | 100 | 30 | 23 |
| 2 | 10 | 11 | 55 | 42 | 97 | 122 | 42 | 80 | 25 | 25 |
| 3 | 11 | - | 122 | - | 122 | 122 | - | 122 | - | - |
Критический путь: 0-4-7-8-11
4.Рассчитайте секторным методом представленный сетевой график. Определите критический путь.
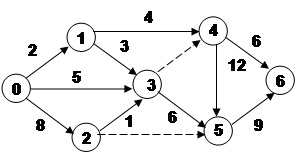 |
Решение
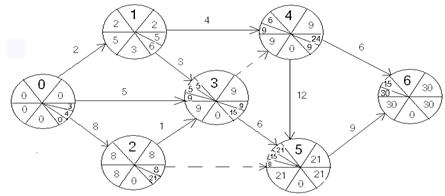
Критический путь 0-2-3-4-5-6
5. Рассчитайте представленный сетевой график методом диагональной таблицы. Определите критический путь.
Решение
Расчёты сетевого графика методом диагональной таблицы:
| Ti P | i/j | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0 | 0 | 2 | |||||||||
| 2 | 1 | 3 | 8 | 6 | 4 | 7 | |||||
| 5 | 2 | 4 | |||||||||
| 10 | 3 | 2 | |||||||||
| 8 | 4 | 11 | |||||||||
| 6 | 5 | 10 | |||||||||
| 9 | 6 | 7 | |||||||||
| 12 | 7 | 4 | |||||||||
| 19 | 8 | 5 | |||||||||
| 24 | 9 | ||||||||||
| TiП | 0 | 2 | 8 | 13 | 8 | 9 | 12 | 15 | 19 | 24 | |
| Ti P | 0 | 2 | 5 | 10 | 8 | 6 | 9 | 12 | 19 | 24 | |
| r | 0 | 0 | 3 | 3 | 0 | 3 | 3 | 3 | 0 | 0 |
Критический путь: 0-1-4-8-9
6. Рассчитайте представленный сетевой график методом диагональной таблицы. Определите критический путь.
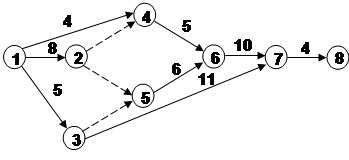 |
Решение
Расчёты методом диагональной таблицы:
| Ti P | i/j | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 0 | 1 | 8 | 5 | 4 | |||||
| 8 | 2 | 0 | 0 | ||||||
| 5 | 3 | 0 | 11 | ||||||
| 8 | 4 | 5 | |||||||
| 8 | 5 | 6 | |||||||
| 14 | 6 | 10 | |||||||
| 24 | 7 | 4 | |||||||
| 28 | 8 | ||||||||
| TiП | 0 | 8 | 8 | 9 | 8 | 14 | 24 | 28 | |
| Ti P | 0 | 8 | 5 | 8 | 8 | 14 | 24 | 28 | |
| r | 0 | 0 | 3 | 1 | 0 | 0 | 0 | 0 |
Критический путь:1-2-5-6-7-8
© 2010 Интернет База Рефератов