
Рефераты по сексологии
Рефераты по информатике программированию
Рефераты по биологии
Рефераты по экономике
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Рефераты по авиации и космонавтике
Рефераты по административному праву
Рефераты по безопасности жизнедеятельности
Рефераты по арбитражному процессу
Рефераты по архитектуре
Рефераты по астрономии
Рефераты по банковскому делу
Рефераты по биржевому делу
Рефераты по ботанике и сельскому хозяйству
Рефераты по бухгалтерскому учету и аудиту
Рефераты по валютным отношениям
Рефераты по ветеринарии
Рефераты для военной кафедры
Рефераты по географии
Рефераты по геодезии
Рефераты по геологии
Рефераты по геополитике
Рефераты по государству и праву
Рефераты по гражданскому праву и процессу
Рефераты по делопроизводству
Рефераты по кредитованию
Рефераты по естествознанию
Рефераты по истории техники
Рефераты по журналистике
Рефераты по зоологии
Рефераты по инвестициям
Рефераты по информатике
Исторические личности
Рефераты по кибернетике
Рефераты по коммуникации и связи
Реферат: Зведення та групування даних
Реферат: Зведення та групування даних
Зведення та групування даних
За даними бюджетних обстежень 20 домогосподарств ( наведені в таблиці ) згрупувати домогосподарства за кількістю членів та загальним грошовим доходом, побудувати комбінаційне групування за вказаними ознаками, побудувати аналітичне групування , яке б характеризувало зв’язок між середньодушовим доходом та кількістю членів домогосподарств та типологічне групування, виділивши групи бідних, середніх та заможних домогосподарств.
Таблиця 1.
| Порядковий номер домогосподарства | Кількість членів домогосподарства | Загальний грошовий доход, включаючи трансферти, гр. од. | Середньодушовий доход, гр. од. |
|
Гр. 1 |
Гр. 2 |
Гр. 3 |
Гр. 4 |
| 1 | 2 | 185 | 92,5 |
| 2 | 3 | 268 | 89,3 |
| 3 | 4 | 539 | 134,7 |
| 4 | 2 | 193 | 96,5 |
| 5 | 3 | 473 | 157,6 |
| 6 | 3 | 324 | 108,0 |
| 7 | 4 | 710 | 177,5 |
| 8 | 3 | 172 | 57,3 |
| 9 | 4 | 248 | 62,0 |
| 10 | 2 | 350 | 175,0 |
| 11 | 3 | 516 | 172,0 |
| 12 | 3 | 374 | 124,7 |
| 13 | 4 | 450 | 112,5 |
| 14 | 3 | 603 | 201,0 |
| 15 | 3 | 229 | 76,3 |
| 16 | 2 | 368 | 184,0 |
| 17 | 4 | 313 | 78,3 |
| 18 | 3 | 346 | 115,3 |
| 19 | 3 | 447 | 149,0 |
| 20 | 4 | 392 | 98,0 |
Розв’язання.
Кількість членів домогосподарств є дискретною ознакою групування зводиться до підрахунку числа домогосподарств для кожного значення ознаки. Число груп визначається кількістю різних значень ознаки: 2, 3, 4. Слід відмітити, що різних значень ознаки не багато, тому кожне наступне значення визначатиме групу. Результати групування представимо в таблиці 2.
Таблиця 2.
| Чисельність членів домогосподарства | Кількість домогосподарств | В % до підсумку |
|
Гр. 1 |
Гр. 2 |
Гр. 3 =(гр. 2 : 20) . 100 |
| 2 | 4 | 20 |
| 3 | 10 | 50 |
| 4 | 6 | 30 |
| В цілому | 20 | 100 |
Грошовий місячний дохід – ознака неперервна, межі її варіац досить широкі – від 172 до 710 грн. од., а тому доцільно складати інтервальний ряд розподілу, враховуючи характер розподілу. Визначимо етапи проведення групування.
1. За формулою Стерджеса ![]() ,
де N – кількість спостережень визначимо
необхідну кількість груп:
,
де N – кількість спостережень визначимо
необхідну кількість груп: ![]()
2. Обчислимо ширину інтервалу за формулою ![]()
3. Знайдемо межі інтервалів за формулами![]() ,
, ![]() . Дані запишемо в таблиці.
. Дані запишемо в таблиці.
Таблиця 3.
| Загальний грошовий доход домогосподарства, гр. од. | Кількість домогосподарств | В % до підсумку |
|
Гр. 1 |
Гр. 2 |
Гр. 3 =(гр. 2 : 20) . 100 |
| 172 – 279,6 | 6 | 30 |
| 279,6 - 387,2 | 6 | 30 |
| 387,2 – 494,8 | 4 | 20 |
| 494,8 - 602,4 | 2 | 10 |
| 602,4 - 710 | 2 | 10 |
| В цілому | 20 | 100 |
Слід зазначити, що нижні межі інтервалів ми будемо включати до інтервалу, а верхні – ні. В інтервал 602,4 – 710 включаємо обидві межі.
В багатьох випадках кількість інтервалів та ширину інтервалу дослідник визначає сам. Інтервали можуть бути відкритими та закритими.
Наприклад, виконаємо теж завдання, але сформуємо чотири нтервали: До 200; 200 – 400; 400 – 600; 600 і більше.
Таблиця 4.
| Загальний грошовий доход домогосподарства, гр. од. | Кількість домогосподарств | В % до підсумку |
|
Гр. 1 |
Гр. 2 |
Гр. 3 =(гр. 2 : 20) . 100 |
| До 200 | 3 | 15 |
| 200 400 | 10 | 50 |
| 400 – 600 | 5 | 25 |
| 600 більше | 2 | 10 |
| В цілому | 20 | 100 |
Групування домогосподарств одночасно за двома ознаками да комбінаційний розподіл. В таблиці підметом буде групування за факторною ознакою (в даному випадку - за кількістю членів домогосподарств), а групи за результативною ознакою (загальний грошовий дохід ) розмістимо вгорі.
Таблиця 5.
| Чисельність членів домогосподарства | Загальний грошовий доход домогосподарства, гр. од. | В цілому | |||
| До 200 | 200 - 400 | 400 - 600 | 600 і більше | ||
| 2 | 2 | 2 | - | - | 4 |
| 3 | 1 | 5 | 3 | 1 | 10 |
| 4 | - | 3 | 2 | 1 | 6 |
| В цілому | 3 | 10 | 5 | 2 | 20 |
Для побудови даного групування необхідно підрахувати кількість домогосподарств, які одночасно належать до певної групи за факторною ознакою та до тієї чи іншої групи за результативною ознакою. В нашому випадку ми маємо, наприклад, 5 домогосподарств, кількість членів яких дорівнює 3 загальний грошовий дохід яких не менше 200 і не більше 400 гр. од. і т. д.
Розміщення частот таблиці у напрямку з верхнього лівого кута у нижній правий вказує на наявність прямого зв’язку між факторною та результативною ознакою, в нашому випадку – між чисельністю членів домогосподарств та загальним грошовим доходом домогосподарств.
Розміщення частот таблиці у напрямку з нижнього лівого кута у верхній правий вказує на наявність зворотного зв’язку між факторною та результативною ознакою.
Виявити наявність та напрямок зв’язку між двома ознаками можна за допомогою аналітичного групування. Для його побудови знайдемо середн значення результативної ознаки в кожній групі за факторною ознакою. Результати представимо в таблиці 6.
Таблиця 6.
| Чисельність членів домогосподарства | Кількість домогосподарств | Сумарна кількість членів домогосподарств | Дохід за місяць, гр. од. | ||
| Загальний грошовий | У середньому | ||||
| На одне домогосподарство | На одного члена домогосподарства | ||||
|
Гр. 1 |
Гр. 2 |
Гр. 3 = гр. 1 . гр. 2 |
Гр. 4 |
Гр. 5 = гр. 4 : гр. 2 |
Гр. 4 = гр. 4 : гр. 3 |
| 2 | 4 | 8 | 1096 | 274,0 | 137,0 |
| 3 | 10 | 30 | 3752 | 375,2 | 125,1 |
| 4 | 6 | 24 | 2652 | 442,0 | 110,5 |
| В цілому | 20 | 62 | 7500 | 375,0 | 121,0 |
За даними таблиці 6 із збільшенням кількості членів домогосподарства зростає середній дохід на одне домогосподарство, але середньодушовий дохід зменшується.
Паралельне зіставлення групових значень факторної та результативної ознак да можливість визначити не лише напрямок зв’язку, а й інтенсивність змін результативної ознаки. За умови рівномірного нарощування значень факторно ознаки різниця між груповими середніми результативної ознаки використовується для оцінки ефекту впливу фактора на результат. Ефект впливу другої групи 125,1 137,0 = - 11,9 гр. од.; третьої групи 110,5 – 125,1 = - 14,6 гр. од., тобто нтенсивність впливу фактора на результат зростає.
Згідно з методикою Європейської комісії ООН до бідних
віднесено домогосподарства, середньодушовий доход яких не перевищує 2/3
середньодушового рівня за сукупністю в цілому. До середнього прошарку віднесено
домогосподарства, середньодушовий доход яких знаходиться в інтервалі![]() Домогосподарства із
середньодушовим доходом
Домогосподарства із
середньодушовим доходом ![]() більше ідентифікуються як заможні. В нашому випадку межею бідності є
більше ідентифікуються як заможні. В нашому випадку межею бідності є ![]() гр. од. До середнього
прошарку віднесемо домогосподарства, середньодушовий доход яких належить
нтервалу 121 ± 121/3, тобто від 181 до 161 гр. од. Домогосподарства з
середньодушовим доходом 161 гр. од. І більше ідентифікуються як заможні.
гр. од. До середнього
прошарку віднесемо домогосподарства, середньодушовий доход яких належить
нтервалу 121 ± 121/3, тобто від 181 до 161 гр. од. Домогосподарства з
середньодушовим доходом 161 гр. од. І більше ідентифікуються як заможні.
Таблиця 7.
| Середньодушовий дохід, гр. од. | Кількість | Загальний грошовий дохід домогосподарств, гр. од. | Середньодушовий дохід, гр. од. | |
| домогосподарств | членів домогосподарств | |||
|
Гр. 1 |
Гр. 2 |
Гр. 3 |
Гр. 4 |
Гр. 5 = гр. 4 : гр. 3 |
| До 81 | 4 | 14 | 962 | 68,7 |
| 81 161 | 11 | 34 | 3991 | 117,4 |
| 161 більше | 5 | 14 | 2547 | 181,9 |
| За сукупністю в цілому | 20 | 62 | 7500 | 121,0 |
За результатами групування середньодушовий дохід в групах становить: 181,9; 117,4; 68,7 гр. од., тобто дохід заможних домогосподарств в 2,6 рази перевищує дохід бідних.
Статистичні показники
1. Маємо дані про попит та пропозицію на ринку праці служби зайнятості у I півріччі 1998 та 1999 років за категоріями працівників та службовців.
Таблиця 8.
| Категор працівників | Середньоспискова кількість незайнятих громадян, тис. осіб | Середньомісячна кількість вільних робочих місць та вакантних посад, тис. осіб | ||
| 1998 | 1999 | 1998 | 1999 | |
|
Гр. 1 |
Гр. 2 |
Гр. 3 |
Гр. 4 |
Гр. 5 |
| Робітники | 34,1 | 33,0 | 155,8 | 126,9 |
| Службовці | 21,3 | 20,8 | 9,6 | 13,2 |
| Всього | 55,4 | 53,8 | 165,4 | 140,1 |
Визначити:
a) зміну чисельності незайнятих громадян та вільних робочих місць та вакантних посад за допомогою відносних і абсолютних показників динаміки;
b) структуру попиту та пропозиції на ринку праці служби зайнятості та її зміни за допомогою абсолютних і відносних показників;
c) показники координації для характеристики співвідношення попиту та пропозиції.
Обчисленні показники звести до окремих таблиць проаналізувати.
Розв’язання.
Величина
абсолютного приросту за суміжні періоди чи моменти часу обчислюється за
формулою: ![]() ,
,
де
![]() - абсолютний приріст, уt
- будь-який рівень ряду, починаючи з другого, уt-1 -
рівень, що передує уt . Це ланцюгові абсолютні прирости.
- абсолютний приріст, уt
- будь-який рівень ряду, починаючи з другого, уt-1 -
рівень, що передує уt . Це ланцюгові абсолютні прирости.
Базисн
абсолютні прирости - це прирости за період у цілому, вони визначаються за
формулою: ![]() , де
, де ![]() - абсолютний приріст, yt
- рівень ряду, y0 - значення показника, взяте за
базисне. Базисні темпи росту:
- абсолютний приріст, yt
- рівень ряду, y0 - значення показника, взяте за
базисне. Базисні темпи росту: ![]() ;
ланцюгові темпи росту:
;
ланцюгові темпи росту: ![]() .
.
Відносні величини структури характеризують склад сукупності, х обчислюють діленням обсягу кожної частини сукупності на обсяг сукупності в цілому. Виражаються в коефіцієнтах або у відсотках. Зміни в структур характеризують структурні зрушення. Вони показують на скільки процентних пунктів змінилась частка певної частини сукупності в даному періоді порівняно з попереднім.
Відносні величини координації характеризують співвідношення частин досліджуваної сукупності, які показують, у скільки разів порівнювана частина сукупності більша або менша частини, що приймається за базу порівняння. Вибір бази порівняння довільний. В даному випадку ми розраховуємо скільки незайнятих громадян припадає на 100 вільних робочих місць.
Таблиця 9.
| Категор працівників | Середньоспискова кількість незайнятих громадян, тис. осіб | Абсолютний приріст, тис. осіб | Темп росту | Структура незайнятих громадян, % до підсумку | Структурні зрушення, п.п. | ||
| 1998 | 1999 | ∆ |
k |
1998 | 1999 | ||
|
Гр. 1 |
Гр. 2 |
Гр. 3 |
Гр. 4 = гр. 3 – гр. 2 |
Гр. 5 =(гр. 3 : гр. 2 ) . 100 |
Гр. 6 =(гр. 2 : 55,4 ) . 100 |
Гр. 7 =(гр. 3 : 53,8 ) . 100 |
Гр. 8 =(гр. 7 : гр. 6 ) |
|
Робітники, ст. 1 |
34,1 | 33,0 | -1,1 | 96,77 | 61,55 | 61,34 | -0,21 |
|
Службовці, ст. 2 |
21,3 | 20,8 | -0,5 | 97,65 | 38,45 | 38,66 | 0,21 |
|
Всього, ст. 3 |
55,4 | 53,8 | -1,6 | 97,11 | 100,00 | 100,00 | 0,00 |
Таблиця 10.
| Категор працівників | Середньомісячна кількість вільних робочих місць та вакантних посад, тис. осіб | Абсолютний приріст, тис. осіб | Темп росту | Структура середньомісячної кількості вільних робочих місць та вакантних посад, % до підсумку | Структурні зрушення, п.п. | Відносні величини координації, чисельність незайнятих громадян на 100 вільних робочих місць | |||
| 1998 | 1999 | ∆ |
k |
1998 | 1999 | 1998 | 1999 | ||
|
Гр. 1 |
Гр. 2 |
Гр. 3 |
Гр. 4 = гр. 3 – гр. 2 |
Гр. 5 =(гр. 3 : гр. 2 ) . 100 |
Гр. 6 =(гр. 2 : 55,4 ) . 100 |
Гр. 7 =(гр. 3 : 53,8 ) . 100 |
Гр. 8 =(гр. 7 : гр. 6 ) |
Гр. 9 |
Гр. 10 |
|
Робітники, ст. 1 |
155,8 | 126,9 | -28,9 | 81,45 | 94,20 | 90,58 | -3,62 | 22 | 26 |
|
Службовці, ст. 2 |
9,6 | 13,2 | 3,6 | 137,50 | 5,80 | 9,42 | 3,62 | 222 | 158 |
|
Всього, ст. 3 |
165,4 | 140,1 | -25,3 | 84,70 | 100,00 | 100,00 | 0,00 | 33 | 38 |
Гр. 9 =((ст. 1; 2; 3, гр. 2(таб. 9.)) : ((ст. 1; 2; 3, гр. 2(таб. 10))) . 100; гр. 10 =((ст. 1; 2; 3, гр. 3(таб. 9.)) : ((ст. 1; 2; 3, гр. 3(таб. 10))) . 100.
2. За трьома районами міста є наступні дані на кінець 2003 року:
Таблиця 11.
| Район міста | Кількість банків | Середнє число вкладів | Середній розмір вкладу, грн. |
|
Гр. 1 |
Гр. 2 |
Гр. 3 |
Гр. 4 |
| 1 | 5 | 1500 | 400 |
| 2 | 6 | 1000 | 450 |
| 3 | 4 | 2000 | 500 |
Визначити в цілому по місту:
a) середню кількість банків;
b) середн число вкладів в банки;
c) середній розмір вкладу;
d) середню суму вкладів в банках.
Розв’язання.
В даному випадку середні значення показників обчислюватимемо за формулами середньо арифметичної. Для розв’язання задачі в кожному випадку починатимемо з логічно формули розрахунку середньої.
![]()
![]()
![]()
![]()
При розрахунку трьох останніх показників ми використали формулу середньо арифметичної зваженої. Для розрахунку середнього числа вкладів в банках в якості ваги ми використали кількість вкладів в одному банку.
4. Залишки обігових коштів на початок місяця становили тис. гр. од. :
січень ___________________1400; лютий___________________1550; березень___________________1270; квітень___________________1300.
Визначити середньомісячний залишок обігових коштів.
Розв’язання.
В цій задачі використаємо формулу середньої хронологічної, оскільки маємо показники моментні ( залишки обігових коштів на початок місяця ).
Середн значення моментного показника розраховується за формулою хронологічно середньої:
![]() .
.
5. Податкова дисципліна підприємств різних видів діяльності характеризується даними:
Таблиці 12.
| Вид діяльності | Кількість підприємців, як сплачують податки | |
| Всього, чол. | % до всіх зареєстрованих | |
| Виробнича | 18 | 60 |
| Торгівельна | 28 | 70 |
| Посередницька | 44 | 55 |
Визначити у середньому за всіма видами діяльності частку підприємців, які сплачують податки.
Розв’язання.
Запишемо логічну формулу: 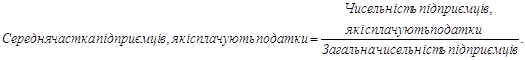
Але ми не маємо даних щодо загальної чисельності підприємців.
Тобто використати середню арифметичну ми не можемо. В цьому випадку потрібно
застосувати формулу середньої гармонічної: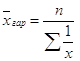 або
або
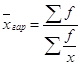 .
.
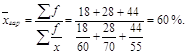
6. У таблиці наведений розподіл населення України за рівнем середньодушового сукупного доходу у 1998 р.
Таблиця 13.
| Усе населення, млн. | 50,3 |
| У тому числі із середньодушовим доходом на місяць, грн. | |
| До 30,0 | 0,6 |
| 30,1 – 60,0 | 7,3 |
| 60,1 – 90,0 | 14,2 |
| 90,1 – 120,0 | 12,0 |
| 120,1 – 150,0 | 7,0 |
| 150,1 – 180,0 | 3,9 |
| 180,1 – 210,0 | 2,3 |
| 210,1 – 240,0 | 1,1 |
| 240,1 – 270,0 | 0,8 |
| 270,1 – 300,0 | 0,4 |
| Понад 300,0 | 0,7 |
Обчислити показники, що характеризують центр розподілу: середній рівень доходу, модальний та медіанний дохід.
Розв’язання.
Обчислення середньої арифметичної інтервального ряду розподілу:
1. якщо варіаційний інтервальний ряд розподілу має відкриті інтервали, то, перш за все, х треба закрити за розмірами інтервалів, розташованих поруч.
2. знаходимо середину інтервалів: до нижньої границі інтервалу додаємо верхню і ділимо на 2.
3. знаходимо середню, використовуючи замість середньої величини за кожною групою середину нтервалу.
Таблиця 14.
| Середина інтервалу | Чисельність населення, млн. | Сукупний дохід, млн. грн. | Кумулятивна частота |
| 15,05 | 0,6 | 9,03 | 0,6 |
| 45,05 | 7,3 | 328,865 | 7,9 |
| 75,05 | 14,2 | 1065,71 | 22,1 |
| 105,05 | 12 | 1260,6 | 34,1 |
| 135,05 | 7 | 945,35 | 41,1 |
| 165,05 | 3,9 | 643,695 | 45 |
| 195,05 | 2,3 | 448,615 | 47,3 |
| 225,05 | 1,1 | 247,555 | 48,4 |
| 255,05 | 0,8 | 204,04 | 49,2 |
| 285,05 | 0,4 | 114,02 | 49,6 |
| 315,05 | 0,7 | 220,535 | 50,3 |
| Разом | 50,3 | 5488 | - |
Середній рівень доходу: ![]()
Модальний дохід: ![]()
Медіанний дохід: ![]()
Модальний інтервал - ( 60,1 – 90,1 ), медіанний інтервал –
( 90,1 – 120,1 ). Середньодушовий дохід складає 109,11 грн., переважна частина населення мала дохід на душу населення 82,77 грн., а половина всього населення мала середньодушовий дохід менший 90,35 грн.
Показники варіації
Кредитні ставки комерційних банків під короткострокові позики становили:
Таблиця 15.
| Кредитна ставка, % | Сума наданих кредитів, млн. гр. од. | |
| I квартал | II квартал | |
|
До 35 35 – 45 45 – 55 55 і більше |
11 5 8 6 |
6 8 10 6 |
| Разом | 30 | 30 |
За кожний квартал визначити середню кредитну ставку, середн лінійне відхилення, дисперсію та середньоквадратичне відхилення.
Порівняти варіацію кредитної ставки комерційних банків в I та II кварталі.
Розв’язання.
Наведемо необхідні для розрахунку формули:
Середня арифметична 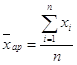 або
або
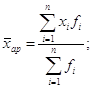 середнє лінійне відхилення
середнє лінійне відхилення
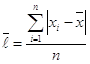 або
або 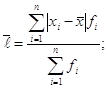 дисперсія
дисперсія 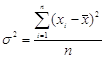 або
або 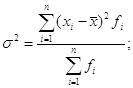 середньоквадратичне
відхилення
середньоквадратичне
відхилення![]() коефіцієнт варіації
коефіцієнт варіації ![]()
Таблиця 16.
| I квартал | II квартал | ||||||||||||
| Кредитна ставка, % |
Сума наданих кредитів, млн. гр. од. fi |
Кредитна ставка, % |
Середня кредитна ставка, % xi |
xifi |
|xi –x |fi |
(xi –x)2fi |
Кредитна ставка, % |
Сума наданих кредитів, млн. гр. од. fi |
Кредитна ставка, % |
Середня кредитна ставка, % xi |
xifi |
|xi –x |fi |
(xi –x)2fi |
|
Гр. 1 |
Гр. 2 |
Гр. 3 |
Гр. 4 |
Гр. 5 = гр. 2 . гр. 4 |
Гр. 6 |
Гр. 7 |
Гр. 8 |
Гр. 9 |
Гр. 10 |
Гр. 11 |
Гр. 12 = гр. 9 . гр. 11 |
Гр. 13 |
Гр. 14 |
| До 35 | 11 | 25-35 | 30 | 330,00 | 143,00 | 1859,00 | До 35 | 6 | 25-35 | 30 | 180,00 | 92,00 | 1410,67 |
| 35 – 45 | 5 | 35-45 | 40 | 200,00 | 15,00 | 45,00 | 35 – 45 | 8 | 35-45 | 40 | 320,00 | 42,67 | 227,56 |
| 45 – 55 | 8 | 45-55 | 50 | 400,00 | 56,00 | 392,00 | 45 – 55 | 10 | 45-55 | 50 | 500,00 | 46,67 | 217,78 |
| 55 і більше | 6 | 55-65 | 60 | 360,00 | 102,00 | 1734,00 | 55 і більше | 6 | 55-65 | 60 | 360,00 | 88,00 | 1290,67 |
| Разом | 30 | - | - | 1290,00 | 316,00 | 4030,00 | Разом | 30 | - | - | 1360,00 | 269,33 | 3146,67 |
I квартал: 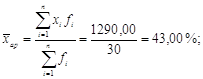
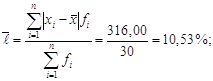
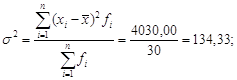
![]()
![]()
II квартал: 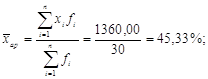
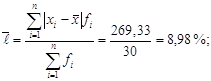
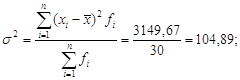
![]()
![]()
Варіація кредитної ставки в II кварталі менша, оскільки значення коефіцієнта варіації в II кварталі менше.
Вибіркове спостереження
1. За результатами обстеження 100 зареєстрованих безробітних ( 2 % вибірка ), з яких 40 проходять перенавчання за новою професією, середня тривалість перерви в роботі становить 3 місяці, а дисперсія дорівнює 2,25. Визначити довірчий нтервал середньої тривалості перерви в роботі та частки безробітних, як проходять перенавчання за новою професією та відносні похибки цих показників.
Розв’язання.
Визначимо меж середньої тривалості перерви в роботі з імовірністю 0,954 ( t = 2).
Гранична похибка ![]() , де
, де ![]()
![]() Довірчий інтервал
Довірчий інтервал ![]() , тобто
, тобто ![]()
Це дає підставу стверджувати з імовірністю 0,954, що середня тривалість перерви в робот становить не менш як 2,7 і не більш як 3,3 місяця.
Для того, щоб визначити граничну похибку частки безробітних, які перенавчаються, обчислимо дисперсію частки: σ2 = 0,4(1-0,4)=0,24. Частка р = 40 / 100 = 0,4.
Гранична похибка ![]() Довірчий інтервал
Довірчий інтервал ![]()
Отже, з такою самою імовірністю можна стверджувати, що частка безробітних, як перенавчаються, у генеральній сукупності становить не менше як 20,2 % і не більш як 39,8 %.
Відносна похибка
середньої тривалості перерви в роботі ![]()
Відносна похибка
частки безробітних, які перенавчаються, становить ![]() Таким чином, відносна
похибка частки більш ніж в два рази перевищує похибку середньої перерви в
роботі.
Таким чином, відносна
похибка частки більш ніж в два рази перевищує похибку середньої перерви в
роботі.
2. На лісовому масиві в 400 га передбачається визначити загальний запас деревини. Пробні площі становлять 0,1 га. За даними попередніх обстежень дисперсія виходу деревини з 0,1 га становила 9. Скільки пробних площ необхідно обстежити, щоб похибка вибірки з імовірністю 0,954 не перевищила 1 м3 ?
Розв’язання.
Всього на даному
масиві 4000 ділянок. Достатній обсяг вибірки пробних ділянок визначимо,
виразивши з формули граничної похибки невідомий показник: ![]()
Методи аналізу взаємозв’язків
1. Маємо дані щодо кредитового обороту обласних філій банку та кількості їх клієнтів. Керівництво банку вважає, що між цими показниками снує певна залежність, і хоче знати, як функціонально кредитовий оборот філ залежить від кількості клієнтів банку. Потрібно перевірити, чи лінійною залежність між даними показниками, побудувати модель лінійної парної регресії, яка б характеризувала дану залежність, а також:
а) виконати перевірку статистичної значимості оцінок параметрів, знайдених за методом найменших квадратів, та знайти інтервали довіри для параметрів b0,b1;
б) знайти коефіцієнти еластичності, пояснити їх зміст;
в) знайти коефіцієнти кореляції та детермінації, за допомогою знайдених коефіцієнтів описати вплив розглядуваного фактору на результат;
г) виконати перевірку моделі на адекватність;
д) знайти нтервальні прогнози індивідуального значення для будь-якого значення незалежної змінної.
Для десяти філій маємо зафіксовані значення показників y, x :
Таблиця 17.
|
Обласні філіїї банку |
Кредитовий оборот, млн. грн., у |
Чисельність клієнтів банку, х |
| 1 | 7,4 | 6 |
| 2 | 7,2 | 5 |
| 3 | 8,6 | 7 |
| 4 | 9,5 | 8 |
| 5 | 4,6 | 4 |
| 6 | 7,3 | 5 |
| 7 | 8,6 | 7 |
| 8 | 9,8 | 7 |
| 9 | 7 | 4 |
| 10 | 4,8 | 3 |
Розв'язання.
Важливою задачею є вибір раціонального типу регресійно моделі. Конкретна аналітична форма зв’язку між економічними показниками згідно з простою регресійною моделлю вибирається на підставі змістовного тлумачення цього зв’язку.
Якщо регресійна модель вимірює зв’язок між двома змінними, то кожну пару спостережень над цими змінними можна зобразити у двовимірній системі координат:
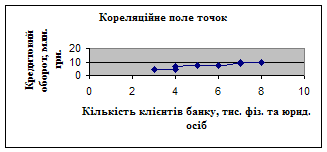
Аналіз зображеної множини точок дозволяє зробити висновок про наявність лінійного зв’язку між кількістю клієнтів банку та кредитовим оборотом, тобто для характеристики дано залежності варто обрати лінійну функцію.
Нехай залежність між кредитовим оборотом та чисельністю клієнтів банку описується простою лінійною моделлю y=β0+β1x+u, де y- кредитовий оборот; х - чисельність клієнтів банку; u – стохастична складова, яка вводиться до моделі з метою урахувати наявність впливу факторів, які не входять до моделі, β0 , β1 –параметри моделі .
Згідно з гіпотезою про лінійний зв’язок через кореляційне поле точок можна провести принаймні кілька прямих ліній, які різняться своїми параметрами b0 та b1. Щоб певна пряма адекватно описувала фактичну залежність, необхідно обрати такий метод оцінювання параметрів моделі, щоб відхилення фактичних значень від розрахункових били мінімальними.
У цьому раз
мінімізації підлягає сума квадратів відхилень: ![]() Це є сутністю методу
найменших квадратів.
Це є сутністю методу
найменших квадратів.
Розрахунков
значення кредитового обороту можна знайти, скориставшись такою моделлю парної лінійної регресії: ![]() =b0+b1x.
=b0+b1x.
Щоб оцінити параметри моделі b0 та b1 методом 1МНК, запишемо систему нормальних рівнянь
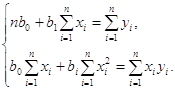
Параметри регрес розраховуються за формулами:
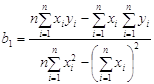 ,
, ![]()
Параметр b1 вказує на скільки одиниць у середньому зміниться у зі зміною х на одиницю, а параметр b0 – чому дорівнює у, якщо х=0 ( при умові, що змінна х може набувати нульових значень ).
Необхідні розрахунки:
Таблиця 18.
|
Обласні філії банку |
Кредитовий оборот, млн. грн., у |
Чисельність клієнтів банку, х |
х*у |
х2 |
урозр. |
(y-y розр.)2 |
(x-xсер)2 |
(y-yсер.)2 |
(x-xсер)(у-усер) |
(yрозр.-yсер.)2 |
| 1 | 7,4 | 6 | 44,4 | 36 | 7,8705 | 0,221363 | 0,16 | 0,0064 | -0,032 | 0,15249025 |
| 2 | 7,2 | 5 | 36 | 25 | 6,8943 | 0,093476 | 0,36 | 0,0784 | 0,168 | 0,34304449 |
| 3 | 8,6 | 7 | 60,2 | 49 | 8,8467 | 0,060871 | 1,96 | 1,2544 | 1,568 | 1,86786889 |
| 4 | 9,5 | 8 | 76 | 64 | 9,823 | 0,104297 | 5,76 | 4,0804 | 4,848 | 5,489649 |
| 5 | 4,6 | 4 | 18,4 | 16 | 5,918 | 1,73721 | 2,56 | 8,2944 | 4,608 | 2,439844 |
| 6 | 7,3 | 5 | 36,5 | 25 | 6,8943 | 0,164623 | 0,36 | 0,0324 | 0,108 | 0,34304449 |
| 7 | 8,6 | 7 | 60,2 | 49 | 8,8467 | 0,060871 | 1,96 | 1,2544 | 1,568 | 1,86786889 |
| 8 | 9,8 | 7 | 68,6 | 49 | 8,8467 | 0,90874 | 1,96 | 5,3824 | 3,248 | 1,86786889 |
| 9 | 7 | 4 | 28 | 16 | 5,918 | 1,170653 | 2,56 | 0,2304 | 0,768 | 2,439844 |
| 10 | 4,8 | 3 | 14,4 | 9 | 4,9418 | 0,020108 | 6,76 | 7,1824 | 6,968 | 6,44245924 |
| Сума | 74,8 | 56 | 442,7 | 338 | 4,542213 | 24,4 | 27,796 | 23,82 | 23,25398214 |
Маємо: ![]()
Модель лінійно парної регресії має вигляд: у=0,98х+2. Оскільки вільний член b0=2≠0, то величина кредитового обороту не строго пропорційною до кількості клієнтів банку. Кількісна оцінка параметра b1=0,98 показує, що граничне збільшення кредитового обороту при зростанні чисельності клієнтів банку на одного становить 0,98 млн. грн.
Еластичність
кредитового обороту щодо кількості клієнтів банку визначається коефіцієнтом
еластичності ![]()
Значення цього коефіцієнта слід тлумачити так: при збільшенні кількості клієнтів банку на 1% кредитовий оборот гранично зросте на 0,73 %.
Параметри регресії у невеликих за обсягом сукупностях здатні до випадкових коливань. Тому здійснимо перевірку їх істотності або статистичної значимості за допомогою t –критерію Стьюдента:
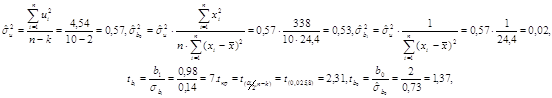
де ![]() оцінки дисперсій помилок та
параметрів відповідно;
оцінки дисперсій помилок та
параметрів відповідно; ![]() значення критерію
для кожного з параметрів.
значення критерію
для кожного з параметрів.
Критичне значення критерію Стьюдента для рівня значимості α=0,05 ( задається дослідником ) та n-k=10-2 ступенів вільності ( k – кількість параметрів ) знаходимо за допомогою таблиць t – розподілу Стьюдента. Оскільки tкр .< tфак. , то коефіцієнт регрес вважається статистично значимим, тобто з ймовірністю 0, 95 вплив чисельност клієнтів банку на кредитовий оборот визнається істотним.
Для перетину b0 критичне значення більше фактичного значення критерію Стьюдента, тобто оцінка перетину статистично не значима.
Для того, щоб визначити, як оцінки параметрів пов’язані з параметрами, потрібно побудувати нтервали довіри для параметрів узагальненої регресійної моделі, тобто нтервали в які з заданою ймовірністю потрапляють їхні оцінки.
Довірчі меж
коефіцієнта регресії : ![]() з
ймовірністю 0,95.
з
ймовірністю 0,95.
Довірчі меж
вільного члена: ![]() зі ймовірністю 0,95.
зі ймовірністю 0,95.
Щоб відповісти на питання наскільки значним є вплив змінної х на у, знайдемо значення коефіцієнта кореляції, значення якого знаходиться між –1 та +1:
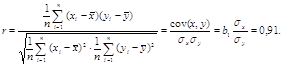
Значення лінійного коефіцієнта кореляції 0,91 близьке до одиниці, тому можна зробити висновок про досить тісний прямий ( r >0 ) зв’язок між кількістю клієнтів банку та величиною кредитового обороту.
Загальну дисперсію результативної ознаки можна розкласти на дві частини - дисперсію, що пояснює регресію, та дисперсію помилок:
![]()
Поділивши обидв частини на загальну дисперсію, отримаємо:
![]()
Перша частина цього виразу являє собою частину дисперсії, яку не можна пояснити через регресійний зв’язок, друга - частину дисперсії, яку можна пояснити, виходячи з регресії. Вона називається коефіцієнтом детермінації і використовується як критерій адекватності моделі, бо є мірою пояснювальної сили незалежної змінної:
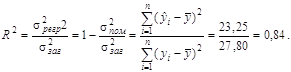
Постільки
значення коефіцієнта детермінації близьке до одиниці, то можна вважати, що
побудована модель адекватна тобто зв’язок між кредитовим оборотом та
чисельністю клієнтів банку істотний. (![]() ).
).
Інший критерій стотності зв’язку – критерій Фішера. Він використовується найчастіше і да відповідь на питання щодо адекватності моделі, коли значення коефіцієнта детермінації має не явно виражене граничне значення, наприклад, 0,5: 0,45: 0,44 н.
Перевірка модел на адекватність за F – критерієм Фішера складається з таких етапів:
1.
Розраховуємо
величину F – критерію: ![]()
В цій формулі n, k – кількість спостережень та кількість параметрів відповідно.
2. Задаємо рівень значимості, наприклад, α =0,05. Тобто, ми вважаємо, що можлива помилка для нас становить 0,05, це означає, що ми можемо помилитися не більш, ніж у 5% випадків, а в 95% випадків наші висновки будуть правильними.
3. На цьому етапі за статистичними таблицями F – розподілу Фішера з ( k-1, n-k) ступенями вільності та рівнем значимості 100(1-α)% знаходимо критичне значення : Fкр=5,32,
4. Оскільки, Fкр<Fфакт, то зі ймовірністю 0,95 ми стверджуємо, що побудована нами модель є адекватною тобто зв’язок істотний.
2. За даними про рівень ефективності економіки та надійність ділового партнерства для семи країн східної Європи оцінити щільність зв’язку між цими ознаками.
Таблиця 19.
| Країна | A | B | C | D | K | M | P | |
| Інтегральн показники |
Ефективність економіки ( max = 10 ) |
5,9 | 7,1 | 4,2 | 3,4 | 4,9 | 2,7 | 2,9 |
|
Надійність ділового партнерства ( max = 100 ) |
54,9 | 54,8 | 45,3 | 36,9 | 35,8 | 26,4 | 24,8 | |
Розв’язання.
Для оцінки щільності зв'язку між ознаками порядкової (рангової) шкали використовують коефіцієнт рангової кореляції r , який за змістом ідентичний лінійному коефіцієнту кореляції. Найбільш поширена формула Спірмена
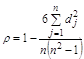 ,
де dj
відхилення рангів факторної (Rx)
та результативної (Ry)
ознак; n
кількість рангів.
,
де dj
відхилення рангів факторної (Rx)
та результативної (Ry)
ознак; n
кількість рангів.
Визначимо
для кожної країни значення рангів таким чином, щоб ранг країни з найменшим
значенням показника був присвоєний найнижчий ранг і т. д. В нашому випадку сума
квадратів відхилень рангів становить ![]() ,
а коефіцієнт рангової кореляції
,
а коефіцієнт рангової кореляції
![]()
Таблиця 20.
| Країна | Інтегральні показники. | Ранги показників |
Відхилення рангів, dj |
|
|||
| Ефективності економіки (max = 10 ) | Надійності ділового партнерства (mах = 100 ) |
Rx |
Ry |
||||
| А | 5,9 | 54,9 | 6 | 7 | 1 | 1 | |
| В | 7,1 | 54,8 | 7 | 6 | 1 | 1 | |
| С | 4,2 | 45,3 | 4 | 5 | -1 | 1 | |
| D | 3,4 | 36,9 | 3 | 4 | -1 | 1 | |
| К | 4,9 | 35,8 | 5 | 3 | 2 | 4 | |
| М | 2,7 | 26,4 | 1 | 2 | -1 | 1 | |
| Р | 2,9 | 24,8 | 2 | 1 | 1 | 1 | |
| Разом | - | - | - | - | 0 | 10 | |
Значення
коефіцієнта рангової кореляції свідчить про наявність прямого і досить
помітного зв'язку між зазначеними параметрами ризику іноземного інвестування
економіки. Критичне значення коефіцієнта рангової кореляції для α =0,05 та
n=7 становить ![]() , що значно менше
фактичного. Отже, істотність зв'язку доведена з імовірністю 0,95.
, що значно менше
фактичного. Отже, істотність зв'язку доведена з імовірністю 0,95.
3. За даними опитування 200 інвесторів побудовано комбінаційний розподіл респондентів за віком та схильністю до ризику. До групи ризикових віднесено респондентів, які мають намір придбати цінні папери, незважаючи на ризик, обережні не уявляють ризику без гарантій, не ризикові уникають ризику взагалі.
Таблиця 21.
| Вік, років | Тип нвестора | Разом | ||
| Ризиковий | Обережний | Не ризиковий | ||
| До 30 | 24 | 12 | 4 | 40 |
| 30 50 | 20 | 50 | 30 | 100 |
| 50 старші | 6 | 18 | 36 | 60 |
| Разом | 50 | 80 | 70 | 200 |
Проаналізувати комбінаційний розподіл робітників, оцінити щільність зв’язку між віком нвесторів та схильністю до ризику за допомогою коефіцієнта взаємної спряженості. Перевірити істотність зв’язку з імовірністю 0,95, зробити висновок.
Розв’язання.
Концентрація частот навколо діагоналі з верхнього лівого кута у правий нижній свідчить про наявність стохастичного зв’язку.
Для
оцінки щільності зв’язку обчислимо коефіцієнт спряженості Чупрова, тому що
кількість груп за факторною ознакою – віком та результативною – тип інвестора
щодо схильності до ризику однакова: mx
= 3, my
= 3. Обчислимо значення квадратичної спряженості Пірсона ![]() :
:
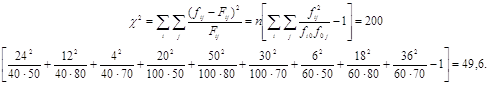
Фактичне значення показника значно перевищує критичне, яке ми знайдемо за таблицями для заданої імовірності 0,95 та числа ступенів свободи
k
= ( mx
1 )( my
1 ) = ( 3 – 1 )( 3 – 1 ) = 4 ![]() Отже,
стотність зв’язку між віком респондентів та схильністю їх до ризику доведена з
мовірністю 0,95.
Отже,
стотність зв’язку між віком респондентів та схильністю їх до ризику доведена з
мовірністю 0,95.
Коефіцієнт
взаємної спряженості: ![]() тобто
зв’язок між ознаками помірний.
тобто
зв’язок між ознаками помірний.
Ряди динаміки
1. Вивантаження вагонів за відділенням залізниці (тис. ум. ваг.) характеризується даними:
Таблиця 22.
| Місяці | Вивантажено | Місяці | Вивантажено |
| Січень | 40,4 | Липень | 40,8 |
| Лютий | 36,3 | Серпень | 44,8 |
| Березень | 40,6 | Вересень | 49,4 |
| Квітень | 38,0 | Жовтень | 48,9 |
| Травень | 42,2 | Листопад | 46,4 |
| Червень | 48,5 | Грудень | 40,2 |
Провести згладжування ряду динаміки методом тричленної та чотиричленної плинно середньої. Зробити висновок про тенденцію обсягів вивантаження вагонів за відділенням залізниці.
Розв’язання.
Тенденція - деякий загальний напрямок розвитку. Очевидно, що в окремі місяці вивантаження вагонів зменшувалося в порівнянні з раніше досягнутим рівнем.
Для виявлення загальної тенденції розвитку іноді використовують так звані плинн середні, тобто середні укрупнених інтервалів, утворених шляхом послідовного виключення початкового члена інтервалу і заміни його черговим членом ряду динаміки.
Рухлив тричленні середні вивантаження вагонів за відділенням залізниці ( тис. ум. ваг. ):
Таблиця 23.
| Місяці | Вивантажено | Плинна тримісячна сума | Плинна середня |
| Січень | 40,4 | - | - |
| Лютий | 36,3 | 117,3 | 39,1 |
| Березень | 40,6 | 114,9 | 38,3 |
| Квітень | 38 | 120,8 | 40,3 |
| Травень | 42,2 | 128,7 | 42,9 |
| Червень | 48,5 | 131,5 | 43,8 |
| Липень | 40,8 | 134,1 | 44,7 |
| Серпень | 44,8 | 135 | 45,0 |
| Вересень | 49,4 | 142,1 | 47,4 |
| Жовтень | 47,9 | 143,7 | 47,9 |
| Листопад | 46,4 | 139,5 | 46,5 |
| Грудень | 45,2 | - | - |
У даному прикладі як укрупнений інтервал узятий період у три місяці. Перша рухлива середня розрахована з даних про вивантаження вагонів за січень, лютий, березень, друга - з даних за лютий, березень, квітень і т. д. Конкретн значення рухливих середніх відносять до середини інтервалу. Новий ряд динаміки чітко показує, що обсяг вивантаження вагонів поступово збільшується, чого не можна було сказати на основі місячних даних.
| Місяці | Вивантажено | Плинн чотиричленні суми | Плинн чотиричленні середні | Центрован плинні середні |
| Січень | 40,4 | - | - | - |
| Лютий | 36,3 | - | - | - |
| Березень | 40,6 | 155,3 | 38,8 | 39,1 |
| Квітень | 38,0 | 157,1 | 39,3 | 40,8 |
| Травень | 42,2 | 169,3 | 42,3 | 42,4 |
| Червень | 48,5 | 169,5 | 42,4 | 43,2 |
| Липень | 40,8 | 176,3 | 44,1 | 45,0 |
| Серпень | 44,8 | 183,5 | 45,9 | 45,8 |
| Вересень | 49,4 | 182,9 | 45,7 | 46,4 |
| Жовтень | 47,9 | 188,5 | 47,1 | 47,2 |
| Листопад | 46,4 | 188,9 | 47,2 | - |
| Грудень | 45,2 | - | - | - |
Таблиця 24.
При парному числі членів ряду, що входять в укрупнений інтервал, середина його не збігається з конкретним періодом чи датою. Так, при чотиричленному інтервал середина першого буде знаходитися між другим і третім членами ряду, середина другого між третім і четвертим і т.д.
При розрахунку рухливих середніх з парного числа членів ряду виконується так зване центрування рухливих середніх, тобто віднесення їх до визначеного періоду чи дати. З цією метою з рухливих середніх обчислюються у свою чергу рухлив двочленні середні. Середина цього нового інтервалу, що охоплює первинні рухлив середні, обчислені з парного числа членів ряду динаміки, завжди збігається з конкретним періодом чи датою.
В цьому випадку новий ряд динаміки також показує, що обсяг вивантаження вагонів поступово збільшується.
2. Динаміка експорту цукру ( тис. т ) характеризується даними:
Таблиця 25.
| Рік | 1999 | 2000 | 2001 | 2002 | 2003 |
| Експорт, тис. т | 37 | 39 | 43 | 48 | 52 |
a) описати тенденцію зростання експорту цукру лінійним трендом, пояснити зміст параметрів трендового рівняння;
b) припустивши, що виявлена тенденція збережеться, визначити очікувані обсяги експорту в 2004 році;
c) з мовірністю 0,95 визначити довірчі інтервали прогнозного рівня.
Розв’язання.
Більш вживаним прийомом вивчення загальної тенденції в рядах динаміки є аналітичне вирівнювання. При вивченні загальної тенденції методом аналітичного вирівнювання виходять з того, що зміни рівнів ряду динаміки можуть бути з тим чи іншим ступенем точності наближення виражені визначеними математичними функціями. В нашому прикладі ми побудуємо лінійний тренд, який характеризуватиме тенденцію зміни експорту цукру.
Лінійний тренд має вигляд уt=a+bt, де уt - рівні ряду, звільнені від коливань, вирівняні по прямій; а - початковий рівень ряду в момент чи період, прийнятий за початок відліку часу; b - середній абсолютний приріст (середня зміна за одиницю часу), константа тренда.
Розраховуються параметри трендових рівнянь методом найменших квадратів. Для лінійної функц параметри знаходять із системи рівнянь:
![]() ,
,
![]() .
.
Система рівнянь спрощується, якщо початок відліку часу (t =0) перенести в середину динамічного ряду. Тоді значення t , розміщені вище середини, будуть негативними, а нижче - позитивними. При непарному числі членів ряду змінної t присвоюється значення з інтервалом одиниця: -2, -1, 0, 1, 2; при парному - з інтервалом два: -5, -3, -1, 1, 3, 5. В розглядуваному приклад п’ять рівнів ряду, тому маємо наступні розрахунки:
Таблиця 26.
| Рік | Експорт, тис. т |
t |
tyt |
yрозр.t |
( yt - yрозр.t )2 |
| 1999 | 37 | -2 | -74 | 36 | 1 |
| 2000 | 39 | -1 | -39 | 39,9 | 0,81 |
| 2001 | 43 | 0 | 0 | 43,8 | 0,64 |
| 2002 | 48 | 1 | 48 | 47,7 | 0,09 |
| 2003 | 52 | 2 | 104 | 51,6 | 0,16 |
| Сума | 219 | 0 | 39 | 219 | 2,7 |
В
обох випадках åt = 0, а система
рівнянь приймає вид: ![]() ,
, ![]() .
.
Значення
![]() можна визначити за
формулою для непарної кількості членів ряду
можна визначити за
формулою для непарної кількості членів ряду
![]() Звідси,
Звідси, ![]() ,
, ![]()
Отже,
![]() тобто середній рівень
експорту цукру становив 43,8 тис. т. Щорічно експорт цукру зростає у середньому
на 3,9 тис. т. За умови, що комплекс причин, який формує тенденцію, ближчим
часом не зміниться, можна продовжити тенденцію за межі динамічного ряду.
Очікуваний обсяг експорту цукру в 2004 році становить у2004 =
43,8 + 3,9 . 3 = 55,5 тис. т.
тобто середній рівень
експорту цукру становив 43,8 тис. т. Щорічно експорт цукру зростає у середньому
на 3,9 тис. т. За умови, що комплекс причин, який формує тенденцію, ближчим
часом не зміниться, можна продовжити тенденцію за межі динамічного ряду.
Очікуваний обсяг експорту цукру в 2004 році становить у2004 =
43,8 + 3,9 . 3 = 55,5 тис. т.
Це
точкова оцінка прогнозу. Інтервальна оцінка прогнозу, тобто довірчі інтервали,
визначаються з деякою імовірністю за формулою ![]() ±
tsp, де sp - помилка прогнозу, t
- довірче число (відношення Стьюдента), v - період випередження.
±
tsp, де sp - помилка прогнозу, t
- довірче число (відношення Стьюдента), v - період випередження.
Помилка
прогнозу для обсягу експорту цукру в 2004 році: ![]() ,
,
де
![]() - оцінка дисперс
залишків, n - кількість спостережень, k
- кількість параметрів рівняння.
- оцінка дисперс
залишків, n - кількість спостережень, k
- кількість параметрів рівняння.
Критичне
значення двостороннього t
критерію для імовірност
0,95 та числа ступенів свободи ( n
2 ) = 5 – 2 = 3 становить ![]()
tsp = 3,18 . 1,38 = 4,39 довірчий інтервал прогнозного рівня 55,5 ± 4,39 тис. т. Це означає, що в 2004 році можна з імовірністю 0,95 очікувати обсяг експорту цукру не менше 51,11 тис. т але не більше 59,89 тис. т.
Індекси
1. Маємо дані за споживчим ринком міста про середні ціни та обсяги реалізації продукції:
Таблиця 27.
| Місяць | Товар А | Товар В | ||
| Ціна за одиницю, грн. | Кількість проданого товару, кг | Ціна за одиницю, грн. | Кількість проданого товару, кг | |
| Березень | 1,5 | 5000 | 3,8 | 4000 |
| Квітень | 1,4 | 6000 | 3,9 | 4500 |
Обчислити:
a) ндивідуальн ндекси цін на кожний товар;
b) загальн ндекси цін, обсягів та товарообігу на всі товари в цілому, причому перші два за схемами індексів Пааше та Ласпейреса;
c) показати взаємозв’язок індексів;
d) абсолютний приріст товарообігу в цілому та за рахунок факторів: рівня цін та обсягів реалізованих товарів.
Розв’язання.
Для розвязання задачі перенесемо дані таблицю 17 в таблицю 18. Туди ж записуватимемо розрахункові дані, необхідні для обчислення індексів.
Таблиця 28.
| Товар | Ціна за одиницю, грн. | Кількість проданого товару, кг |
p0q0 |
p1q1 |
p0q1 |
p1q0 |
||
| Березень | Квітень | Березень | Квітень | |||||
|
p0 |
p1 |
q0 |
q1 |
|||||
|
Гр. 1 |
Гр. 2 |
Гр. 3 |
Гр. 4 |
Гр. 5 |
Гр. 6 = гр. 2 . гр. 4 |
Гр. 7 = гр. 3 . гр. 5 |
Гр. 8 = гр. 2 . гр. 5 |
Гр. 9 = гр. 3 . гр. 4 |
| А | 1,5 | 1,4 | 5000 | 6000 | 7500 | 8400 | 9000 | 7000 |
| В | 3,8 | 3,9 | 4000 | 4500 | 15200 | 17550 | 17100 | 15600 |
| Всього | - | - | 9000 | 10500 | 22700 | 25950 | 26100 | 22600 |
Індивідуальн
ндекси цін на кожний товар: ![]()
Ціна товару А в квітні порівняно з березнем зменшилася на 7 %, тоді як ціна товару В зросла на 3 %.
Загальний індекс
товарообігу ![]()
Загальний індекс
цін на обидва товари в цілому за схемою індексів Пааше: ![]()
В загальному ціни зменшилися на 0,6 %.
Загальний індекс
цін на обидва товари в цілому за схемою індексів Ласпейреса: ![]()
В загальному ціни зменшилися на 0,4 %.
Загальний індекс
обсягу реалізованих товарів в цілому за схемою індексів Пааше: ![]()
В загальному обсяг реалізації збільшився на 14,8 %.
Загальний
ндекс обсягу реалізованих товарів в цілому за схемою індексів Ласпейреса: ![]()
В загальному обсяг реалізації збільшився на 15,0 %.
В даному приклад ндекси Ласпейреса мають дещо більше значення ніж індекси Пааше.
Відомо, що ![]() Індекс товарообігу
дорівнює добутку індексу цін, розрахованому як індекс Пааше, та індексу обсягу,
розрахованому як індекс Ласпейреса, і навпаки. Перевірте це самостійно.
Індекс товарообігу
дорівнює добутку індексу цін, розрахованому як індекс Пааше, та індексу обсягу,
розрахованому як індекс Ласпейреса, і навпаки. Перевірте це самостійно.
Абсолютну зміну товарообігу в цілому та за рахунок факторів можна як різницю між чисельником та знаменником відповідного індексу.
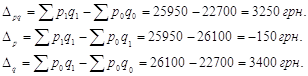
За рахунок зміни цін на товари величина товарообігу зменшилась на 150 грн., а за рахунок зміни обсягів - збільшилася на 3400 грн., що в загальному склало збільшення товарообігу на 3250 грн.
2. Дані про динаміку випуску та цін трьох товарів – представників продукції галузі вміщено в таблиці:
Таблиця 29.
| Товари - представники | Приріст цін, % | Вартість випуску, тис. грн. | |
| 1996 | 1999 | ||
| А | +5,0 | 1000 | 1600 |
| В | +1,5 | 1500 | 1100 |
| С | +3,5 | 3000 | 2500 |
Знайти:
a) зведен ндекси цін та обсягів за трьома товарами;
b) середньорічний приріст цін у цілому за трьома товарами.
Розв’язання.
Таблиця 30.
| Товари - представники | Приріст цін, % |
Індекси цін
|
Вартість випуску, тис. грн. | |
|
1996
|
1999
|
|||
| А | +5,0 | 1,05 | 1000 | 1600 |
| В | +1,5 | 1,015 | 1500 | 1100 |
| С | +3,5 | 1,035 | 3000 | 2500 |
| Всього | - | - | 4500 | 5200 |
Використаємо для обчислення індексу цін формулу середньозваженого гармонічного індексу:
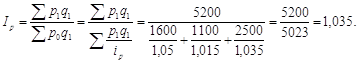 Отже, ціни зросли на 3,5 %.
Отже, ціни зросли на 3,5 %.
![]() Вартість товарів збільшилась на 15,6
5. Використовуючи зв’язок між індексами, знайдемо індекс обсягу:
Вартість товарів збільшилась на 15,6
5. Використовуючи зв’язок між індексами, знайдемо індекс обсягу:
![]() Обсяги товарів збільшились на 11,6
5. Цей індекс можна було знайти як середній арифметичний індекс з
ндивідуальних індексів обсягу для кожного товару з вагами – товарообігом
базисного періоду. Проте нам не відомі індивідуальні індекси обсягів, і для обчислення
шуканої величини ми використовуємо зв’язок між індексами.
Обсяги товарів збільшились на 11,6
5. Цей індекс можна було знайти як середній арифметичний індекс з
ндивідуальних індексів обсягу для кожного товару з вагами – товарообігом
базисного періоду. Проте нам не відомі індивідуальні індекси обсягів, і для обчислення
шуканої величини ми використовуємо зв’язок між індексами.
Середній
темп приросту: ![]() де
де 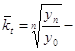 середньорічний темп росту.
Період з 1996 по 1999 рік складається з трьох років, тобто n
=3, підкореневий вираз – базисний темп росту цін, в
якості якого ми використовуємо обчислений індекс – 1,035. Таким чином,
середньорічний темп росту.
Період з 1996 по 1999 рік складається з трьох років, тобто n
=3, підкореневий вираз – базисний темп росту цін, в
якості якого ми використовуємо обчислений індекс – 1,035. Таким чином,
![]() В середньому з кожним роком
ціни зростали на 1,153 %.
В середньому з кожним роком
ціни зростали на 1,153 %.
3. За наведеними в таблиці даними обчислити:
a) ндекси середньої матеріаломісткості продукції змінного та фіксованого складу;
b) ндекс впливу структурних зрушень;
c) зміну загального обсягу матеріальних витрат і в тому числі за рахунок окремих факторів.
Таблиця 31.
| Показники | Підприємство № 1 | Підприємство № 2 | ||
| Базисний період | Звітний період | Базисний період | Звітний період | |
| 1. Вартість виробленої продукції, тис. грн. | 582,8 | 570,1 | 633,4 | 712,5 |
| 2. Матеріальн витрати, тис. грн. | 376,2 | 342,4 | 410,2 | 541,6 |
Розв’язання.
Таблиця 32.
| Підприємства | Вартість вироблено продукції, тис грн. | Матеріальні витрати, тис грн. | Матеріаломісткість виробленої продукції, грн. |
MM0.Q1 |
|||
|
базисний, Q0 |
звітний, Q1 |
базисний, M0 |
звітний, M1 |
базисний, MM0 |
звітний, MM1 |
||
| № 1 | 582,8 | 570,1 | 376,2 | 410,2 | 0,65 | 0,72 | 368,00 |
| № 2 | 633,4 | 712,5 | 342,4 | 541,6 | 0,54 | 0,76 | 385,16 |
| Разом | 1216,2 | 1282,6 | 718,6 | 951,8 | - | - | 753,16 |
Спочатку обчислимо матеріаломісткість, розділивши величину матеріальних витрат на вартість виробленої продукції. Дані розрахунків запишемо в таблицю.
![]()
![]()
![]()
![]() тис грн. )
тис грн. )
![]() тис грн. )
тис грн. )
![]() тис грн. )
тис грн. )
Середня матеріаломісткість продукції збільшилась на 25,6 %, за рахунок збільшення матеріаломісткості на окремих підприємствах – на 26,4 %, а за рахунок змін в обсягах виробництва – на 0,6 % зменшилася. При цьому в цілому матеріальн витрати збільшилися на 233,2 тис грн., за рахунок збільшення матеріаломісткост на 198, 6 тис грн., а за рахунок змін обсягів виробництва – на 34, 6 тис грн.
© 2010 Интернет База Рефератов