Шпаргалка: Принципы организации государственной статистики

1. Предмет и метод статистики. Основные черты предмета

статистики. История развития

Количественные изменения общественных явлений и процессов в неразрывной связи с их качественным содержанием и изучает статистика как наука.

Предметом статистики выступают размеры и количественные соотношения качественно определенных социально-экономических явлений, закономерности их связи и развития в конкретных условиях места и времени.

Свой предмет статистика изучает методом обобщающих показателей.

В определении предмета статистики подчеркивается несколько характерных особенностей статистики как науки. Статистика изучает:

• массовые общественные явления при помощи статистических показателей (численность населения)

• количественную сторону массовых общественных явлений и дает количественное, цифровое освещение общественных явлений;

• количественную сторону общественных явлений в неразрывной связи с их качественным содержанием;

• количественную сторону общественных явлений в конкретных условиях места и времени (динамику численности населения)

• количественные связи между общественными явлениями, с помощью специальной методологии.

Термин «статистика» происходит от латинского слова status, что в Средние века означало политическое состояние государства. В науку этот термин введен немецким ученым Готфридом Ахенвалем (1719 — 1772 гг.), и означал он тогда государствоведение.

Г. Ахенваль с 1746 г. начал читать впервые в Марбургском, а затем в Геттенгенском университетах новую учебную дисциплину, которую он и назвал статистикой. Основным содержанием этого курса было описание политического состояния и достопримечательностей государства.

Первой особенностью статистики как науки является то, что исследуются не отдельные факты, а массовые социально-экономические явления и процессы, выступающие как множества отдельных фактов, обладающих как индивидуальными, так и общими признаками

Второй особенностью статистики как науки является то, что она изучает прежде всего количественную сторону общественных явлений и процессов в конкретных условиях места и времени

Третья особенность статистики заключается в том, что она характеризует структуру общественных явлений. Структура - это внутреннее строение массовых явлений, т. е. внутреннее строение статистического множества. Статистика должна эту структуру обнаружить, выразить и отразить с помощью статистических показателей.

Четвертая особенность – изменения в простарнстве выявляются посредством анализа структуры общественного явления, а изменения уровня и структуры явления исследуются во времени, т. е. в динамике.

Выявление связей является пятой особенностью статистики как науки.

2. Основные понятия и категории статистики. Особенности

статистической методологии. Методы статистики

Статистика оперирует определенными категориями, т. е. понятиями, отражающими существенные, всеобщие свойства и основные отношения явлений действительности.

Статистическая совокупность — это множество единиц (объектов, явлений), объединенных единой закономерностью и варьирующих в пределах общего качества.

Под единицами совокупности понимаются ее неделимые первичные элементы, выражающие ее качественную однородность, т. е. являющиеся носителями признаков.

Под качественной однородностью единиц совокупности понимается сходство единиц (объектов, явлений) по каким-либо существенным признакам, но различающихся по каким-либо другим признакам.

Признак - показатель, характеризующий некоторое свойство объекта совокупности, рассматриваемый как случайная величина.

Вариация различия в значениях того или иного признака у отдельных единиц, входящих в данную совокупность.

Признаки, характеризующие статистическую совокупность, взаимосвязаны между собой, поэтому следует различать факторные (признаки- факторы) и результативные признаки.

Факторные признаки — это независимые признаки, оказывающие влияние на другие, связанные с ними признаки.

Результативные признаки — это зависимые признаки, которые изменяются под влиянием факторных признаков.

Статистический показатель — это количественно-качественная обобщающая характеристика какого-то свойства группы единиц или совокупности в целом.

Величина — характеристика объекта или явления материального мира, общая в качественном отношении, но индивидуальная для каждого из них в количественном отношении.

Значение конкретной величины — это ее оценка, выражаемая произведением отвлеченного числа на принятую для данной величины единицу. Значение показателя является функцией пространства и времени.

Система статистических показателей — это совокупность взаимосвязанных показателей, объективно отражающая существующие между явлениями взаимосвязи.

Статистическое исследование состоит из трех основных стадий:

1) статистическое наблюдение; 2) первичная обработка, сводка и группировка результатов наблюдения; 3) анализ полученных сводных материалов.

Статистическое наблюдение - научно организованный сбор сведений об изучаемых социально-экономических процессах или явлениях.

Метод статистических группировок и таблиц представляет собой комплекс последовательных действий по обобщению конкретных единичных фактов, образующих совокупность в целях выявления типичных черт и закономерностей, присущих изучаемому явлению в целом.

Статистический анализ является заключительной стадией статистического исследования.

Выделяют следующие основные этапы анализа:

1) констатация фактов и их оценка; 2) установление характерных черт и причин явления; 3) сопоставление явления с другими, принятыми за базу сравнения - нормативными, плановыми и прочими явлениями; 4) формулирование гипотез, выводов и предположений; 5) статистическая проверка выдвинутых гипотез с помощью специальных статистических показателей

3. Принципы организации государственной статистики в

Российской Федерации

В основу организации статистической работы в России положены следующие принципы:

1) централизованное руководство статистикой;

2) единые организационное строение и методология;

3) неразрывная связь статистических органов с органами государственного управления.

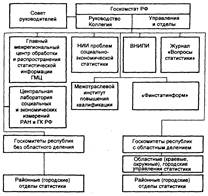
В соответствии с Положением о Государственном комитете РФ по статистике, утвержденным постановлением Правительства РФ от 9 июля 1994 г., определено создание Государственного комитета Российской Федерации по статистике (Госкомстат России), который является федеральным органом исполнительной власти, осуществляющим руководство российской статистикой.

В соответствии с государственным устройством и административно-территориальными образованиями Российской Федерации создана единая система государственной статистики, которая проводит работу по единым плану и методологии. Методология статистических показателей, формы, методы сбора и обработки статистических данных, устанавливаемые Госкомстатом России, являются официальными статистическими стандартами Российской Федерации.

Система государственной статистики находится в ведении Правительства РФ и ему подотчетна, что обеспечивает неразрывную связь с органами государственного управления.

4. Статистическое наблюдение, формы, виды статистического

наблюдения. Особенности отчетности.

Статистическое наблюдение - массовое, планомерное, научно организованное наблюдение за явлениями социальной и экономической жизни, которое заключается в регистрации признаков, отобранных у каждой единицы совокупности.

Цель наблюдения - получение достоверной информации для выявления закономерностей развития явлений и процессов.

Объект наблюдения — статистическая совокупность, в которой проистекают исследуемые социально-экономические явления и процессы.

Единица наблюдения - составной элемент объекта, являющийся носителем признаков, подлежащих регистрации.

Отчетная единица - субъект, от которого поступают данные о единице наблюдения.

Программа наблюдения - перечень признаков (или вопросов), подлежащих регистрации в процессе наблюдения.

Статистический формуляр - документ единого образца, содержащий программу и результаты наблюдения.

Критический момент (дата) - день года, час дня, по состоянию на который должна быть проведена регистрация признаков по каждой единице исследуемой совокупности.

Срок (период) наблюдения - время, в течение которого происходит заполнение статистических формуляров.

Отчетность - основная форма статистического наблюдения, с помощью которой статистические органы в определенные сроки получают от предприятий, учреждений и организаций необходимые данные в виде установленных в законном порядке отчетных документов, скрепляемых подписями лиц, ответственных за их предоставление и достоверность собираемых сведений.

Перепись - специально организованное наблюдение, повторяющееся, как правило, через равные промежутки времени, с целью получения данных о численности, составе и состоянии объекта статистического наблюдения по ряду признаков.

Регистровое наблюдение - форма непрерывного статистического наблюдения за долговременными процессами, имеющими фиксированное начало, стадию развития и фиксированный конец.

Непосредственное наблюдение - регистраторы путем непосредственного замера, взвешивания, подсчета или проверки работы и так далее устанавливают факт, подлежащий регистрации, и на этом основании производят записи в формуляре наблюдения.

Документальный способ наблюдения — основан на использовании в качестве источника статистической информации различного рода документов, как правило, учетного характера.

Опрос - способ наблюдения, при котором наблюдаемые сведения получают со слов респондента.

Текущее наблюдение - наблюдение, когда изменения в отношении изучаемых явлений фиксируются по мере их наступления.

Единовременное обследование - сведения даются о количественных характеристиках какого-либо явления или процесса в момент его исследования.

Сплошное наблюдение - получение информации о всех единицах исследуемой совокупности.

Несплошное наблюдение - обследованию подлежит лишь часть единиц изучаемой совокупности.

Точность статистического наблюдения - степень соответствия величин какого-либо показателя, определяемого по материалам статистического наблюдения, действительной его величине.

Ошибка наблюдения - расхождение между расчетным и действительным значением изучаемых величин

5 Унифицированные формы федерального статистического

наблюдения. Статистические показатели, характеризующие

экономическую деятельность организаций

В отечественной статистике используются три организационные формы (типы) статистического наблюдения:

• отчетность (предприятий, организаций, учреждений и т. п.);

• специально организованное статистическое наблюдение (переписи, единовременные учеты, обследования сплошного и несплошного характера);

• регистры.

Отчетность - это основная форма статистического наблюдения, с помощью которой статистические органы в определенные сроки получают от предприятий, учреждений и организаций необходимые данные в виде установленных в законном порядке отчетных документов, скрепляемых подписями лиц, ответственных за их предоставление и достоверность собираемых сведений. Таким образом, отчетность - это официальный документ, содержащий статистические сведения о работе предприятия, учреждения, организации и т. п.

Перепись - специально организованное наблюдение проводится с целью получения сведений, отсутствующих в отчетности, или для проверки ее данных. Наиболее простым примером такого наблюдения является перепись. Российская практическая статистика проводит переписи населения, материальных ресурсов, многолетних насаждений, неустановленного оборудования, строек незавершенного строительства, оборудования и др.

Перепись — это специально организованное наблюдение, повторяющееся, как правило, через равные промежутки времени, с целью получения данных о численности, составе и состоянии объекта статистического наблюдения по ряду признаков.

Регистровое наблюдение - это форма непрерывного статистического наблюдения за долговременными процессами, имеющими фиксированное начало, стадию развития и фиксированный конец. Оно основано на ведении статистического регистра. Регистр представляет собой систему, постоянно следящую за состоянием единицы наблюдения и оценивающую силу воздействия различных факторов на изучаемые показатели. В регистре каждая единица наблюдения характеризуется совокупностью показателей. Одни из них остаются неизменными в течение всего времени наблюдения и регистрируются один раз; другие показатели, периодичность изменения которых неизвестна, обновляются по мере изменения; третьи - представляют собой динамические ряды показателей с заранее известным периодом обновления.

Предприятие это самостоятельный хозяйствующий субъект, созданный для организации предпринимательской деятельности, экономическими целями которого являются обеспечение общественных потребностей и извлечение прибыли

На предприятии в натуральном выражении могут быть учтены, как правило, все виды выпускаемой продукции.

В статистике широко используется система стоимостных показателей продукции предприятия : валовая, товарная, реализованная продукция, чистая продукция; каждый из них носит определенный экономический смысл, имеет свою методику расчета в различных отраслях материального производства.

Валовая продукция (ВП) предприятия - стоимость всех готовых изделий и полуфабрикатов, изготовленных в отчетном периоде из своего материала и материала заказчика, а также стоимость выполненных работ за вычетом стоимости готовых изделий и полуфабрикатов собственной выработки, потребленных в производстве. Валовая продукция предприятия характеризует конечные результаты производственной деятельности предприятия и не включает повторного счета стоимости одних и тех же изделий внутри предприятия.

Товарная продукция предприятия, или как ее называют в настоящее время, объем продукции (работ, услуг) (ОП) представляет собой показатель, характеризующий продукцию, произведенную Для реализации на сторону, т.е. за пределы предприятия. Она может быть определена на основе валовой продукции путем вычитания из последней тех элементов, которые не могут быть реализованы (стоимость изменения остатков незавершенного производства и полуфабрикатов). Объем продукции (ОП) промышленного предприятия определяется по заводскому методу без стоимости внутризаводского оборота, т.е. без стоимости той части выработанных или готовых изделий и полуфабрикатов, которая и пользуется внутри данного предприятия на собственные промышленно-производственные нужды.

Стоимость продукции (работ, услуг) определяется в отпускных ценах предприятия без налога на добавленную стоимость и акциза:

а) в фактических действующих ценах; б) в фиксированных (сопоставимых) ценах.

Реализованная продукция (РП) — отгруженная покупателям

(заказчикам) и оплаченная ими в данном периоде (предъявлены расчетные документы).

Чистая продукция (ЧП) представляет собой стоимость, вновь созданную трудом в той или иной сфере материального производства. В отечественной практике рассчитывается как разность между объемами валовой продукции и материальными (производственными) затратами (МЗ) (сырье, материалы, топливо, энергия, амортизационные отчисления) в ценах конечного потребления (действующих и сопоставимых):

ЧП = ВП - МЗ.

6Сводка и группировка статистических данных. Виды

статистических группировок

Сводка - комплекс последовательных операций по обобщению конкретных единичных факторов для выявления типичных черт и закономерностей, присущих изучаемому явлению в целом.

Группировка - расчленение множества единиц изучаемой совокупности на группы по определенным, существенным для них признакам.

Типологическая группировка - разделение исследуемой качественно разнородной совокупности на классы, социально-экономические типы, однородные группы единиц в соответствии с правилами научной группировки.

Структурная группировка - разделение однородной совокупности на группы, характеризующие ее структуру по какому-либо варьирующему признаку.

Аналитическая группировка - группировка, выявляющая взаимосвязи между изучаемыми явлениями и их признаками.

Группировочный признак - признак, по которому производится разбиение единиц совокупности на отдельные группы.

Классификация - систематическое распределение явлений и объектов на определенные группы, классы, разряды на основании их сходства и различия.

Интервал - значения варьирующего признака, лежащие в определенных границах.

Величина интервала - разность между верхней и нижней границами интервала.

Открытые интервалы - интервалы, у которых указана только одна граница.

Закрытые интервалы - интервалы, у которых обозначены обе границы.

Ряд распределения - упорядоченное распределение единиц совокупности на группы по определенному варьирующему признаку.

Атрибутивный ряд распределения - ряд, построенный по качественному признаку.

Вариационный ряд распределения - ряд, построенный по количественному признаку.

Варианты - отдельные значения признака, которые он принимает в вариационном ряду.

Частоты - выраженные в долях единицы или в процентах к итогу значения изучаемого признака.

Дискретный вариационный ряд - распределение единиц совокупности по дискретному признаку.

Интервальный вариационный ряд - ряд, который отражает непрерывную вариацию признака.

Вторичная группировка - операция по образованию новых групп на основе ранее построенной группировки.

7 Принципы построения статистических группировок и

классификаций. Ряды распределения и группировки

Группировочным признаком называется признак, по которому проводится разбивка единиц совокупности на отдельные группы. Его часто называют основанием группировки. От правильного выбора группировочного признака зависят выводы, которые получают в результате статистического исследования.

В качестве основания группировки следует использовать существенные признаки. В каждом конкретном исследовании включение признака в состав группировочных должно быть теоретически обосновано. Только на базе теоретического анализа экономических законов развития исследуемого явления можно правильно определить состав признаков.

В основание группировки могут быть положены как количественные, так и качественные признаки. Первые имеют числовое выражение (объем торгов, курс доллара в рублях, возраст человека, денежный доход семьи и т. д.), а вторые отражают состояние единицы совокупности (пол человека, его национальность, семейное положение, отраслевая принадлежность предприятия, его форма собственности и организационно-правовая форма и т. Д.).

После определения основания группировки следует решить вопрос о количестве групп, на которые надо разбить исследуемую совокупность.

Число групп зависит от задач исследования и вида признака, положенного в основание группировки, численности совокупности, степени вариации признака.

Единицы анализируемого объекта могут быть разбиты по одному и тому же признаку на разное число групп. Например, при группировке населения по возрасту с целью определения трудовых ресурсов страны все население в практической статистике делится на три группы: население моложе трудоспособного возраста, трудоспособное население и население старше трудоспособного возраста. Если же анализируется продолжительность жизни, то строится более детальная группировка и выделяются пятигодичные группы.

При построении группировки по качественному признаку групп, как правило, будет столько, сколько имеется градаций, видов, состояний у этого признака. Например, в случае проведения группировки населения по полу можно образовать только две группы: мужчины и женщины. Если проводится группировка производства товаров народного потребления по экономическим районам, то вся исследуемая совокупность делится на 11 групп: именно на столько экономических районов поделена территория страны.

Классификацией называется систематизированное распределение явлений и объектов на определенные группы, классы, разряды на основании их сходства и различия.

Отличительной чертой классификации является, во-первых, то, что в основу ее кладется качественный признак. Во-вторых, классификации стандартны. Они устанавливаются органами государственной и международной статистики. Если в каждом конкретном исследовании строится своя группировка, то классификация едина для любого исследования независимо от того, проводят ли его органы государственной статистики или другие учреждения и ведомства (министерства, налоговые органы и т. п.). В-третьих, классификации устойчивы. Они остаются неизменными в течение длительного времени. Однако если появляются новые группы единиц, их классы, разряды, то в классификации вносятся соответствующие изменения и дополнения.

Классификация, предопределяя важнейшие признаки группировки единиц совокупности, является основой группировок. В классификации точно определены всевозможные группы и имеются подробные указатели, которые помогают отнести любую единицу объекта в ту или иную группу в каждом конкретном случае.

Статистический ряд распределения представляет собой упорядоченное распределение единиц изучаемой совокупности на группы по определенному варьирующему признаку. Он характеризует состав (структуру) изучаемого явления, позволяет судить об однородности совокупности, закономерности распределения и границах варьирования единиц совокупности.

Ряды распределения, построенные по атрибутивным признакам (в порядке возрастания или убывания наблюденных знаний), называются атрибутивными. Примером атрибутивных рядов могут служить распределения населения по полу, занятости, национальности, профессии и т.д.

Ряды распределения, построенные по количественному признаку, называются вариационными. Например, распределение населения по возрасту, рабочих — по стажу работы, заработной плате и т.д.

Атрибутивный ряд распределения - ряд, построенный по качественному признаку.

Вариационный ряд распределения - ряд, построенный по количественному признаку.

Варианты - отдельные значения признака, которые он принимает в вариационном ряду.

Частоты - выраженные в долях единицы или в процентах к итогу значения изучаемого признака.

Дискретный вариационный ряд - распределение единиц совокупности по дискретному признаку.

Интервальный вариационный ряд - ряд, который отражает непрерывную вариацию признака.

Вторичная группировка - операция по образованию новых групп на основе ранее построенной группировки

8. Общее понятие о классификациях, группировках и

номенклатурах, их роль в статистическом исследовании.

Важнейшие экономические группировки

Группировки как метод исследования широко используются в практике статистики.

При анализе формирования рыночных отношений большое значение имеет группировка предприятий по численности занятых в отраслях производственной и непроизводственной сфер с обязательным выделением группы малых предприятий, группировка предприятий по формам собственности, организационно-правовым формам.

Большое значение играет и группировка по экономическому назначению продукции. Так, при анализе продукции промышленности используют группировку, позволяющую выделить из всего объема продукции производство средств производства и | производство предметов потребления.

В статистике розничной торговли используется группировка товаров на продовольственные и непродовольственные, в статистике сельского хозяйства - группировка продукции на продукцию растениеводства и животноводства, а внутри этих групп - деление продукции по ведущим производственным направлениям.

Среди группировок, применяемых отечественной статистикой, особое место принадлежит группировке по отраслям народного хозяйства. Она используется при анализе валового внутреннего продукта, валового национального дохода, капитальных вложений и ввода в действие основных фондов, структуры ввоза и вывоза продукции.

Кроме группировок в практической статистике широко применяются классификации. Существует много различных классификаций. В макроэкономической статистике применяют классификацию отраслей народного хозяйства, основных фондов; в статистике капитального строительства - классификацию капитальных вложений и строительных машин; в статистике труда - классификацию профессий, а в статистике внешней торговли - классификацию, называемую «Товарная номенклатура внешнеэкономической деятельности».

На этапе перехода от одной формы хозяйствования к другой возникла потребность в новых классификаторах, таких, как классификатор форм собственности и организационно-правовых форм хозяйствующих субъектов.

Группировка — расчленение множества единиц изучаемой совокупности на группы по определенным, существенным для них признакам.

Типологическая группировка — разделение исследуемой качественно разнородной совокупности на классы, социально-экономические типы, однородные группы единиц в соответствии с правилами научной группировки.

Группировочный признак — признак, по которому производится разбиение единиц совокупности на отдельные группы.

9. Абсолютные величины, их виды и способы получения. Значение

абсолютных величин. Единицы измерения абсолютных величин

Абсолютными в статистике называются суммарные обобщающие показатели, характеризующие размеры (уровни, объемы) общественных явлений в конкретных условиях места и времени. Они характеризуют экономическую мощь страны и социальную жизнь населения (ВВП, ВНП, ВНД, реальные располагаемые денежные доходы населения, объемы промышленного и сельскохозяйственного производства, объем выпуска важнейших видов продукции).

Различают два вида абсолютных величин: индивидуальные и суммарные.

Индивидуальными называют абсолютные величины, характеризующие размеры признака у отдельных единиц совокупности (например, размер заработной платы отдельного работника, вклада гражданина в определенном банке и т.д.). Они получаются непосредственно в процессе статистического наблюдения и фиксируются в первичных учетных документах.

Суммарные абсолютные величины характеризуют итоговую величину признака по определенной совокупности объектов, охваченных статистическим наблюдением. Они являются суммой количества единиц изучаемой совокупности (численность совокупности) или суммой значений варьирующего признака всех единиц совокупности (объем варьирующего признака).

Абсолютные статистические величины представляют собой именованные числа, т. е. имеют какую-либо единицу измерения.

В зависимости от сущности исследуемого социально-экономического явления абсолютные статистические величины выражаются в натуральных, стоимостных и трудовых единицах измерения. Абсолютные статистические величины могут быть как положительными (доходы), так и отрицательными (убытки, потери).

Натуральные единицы измерения в свою очередь могут быть простыми (тонны, штуки, метры, литры) и сложными, являющимися комбинацией нескольких разноименных величин (грузооборот железнодорожного транспорта выражается в тонно-километрах, производство электроэнергии — в киловатт-часах, затраты труда — в человеко-часах, человеко-днях). В статистике применяют и абсолютные показатели, выраженные в условно-натуральных единицах измерения (например, разные виды топлива пересчитываются в условное топливо, тракторный парк — в эталонные тракторы).

Стоимостные единицы измерения используются, например, для выражения объема разнородной продукции в стоимостной (денежной) форме рублях. В стоимостных единицах выражают валовой выпуск продукции, доходы населения и др.

При использовании стоимостных измерителей принимают во внимание изменение цен с течением времени. Этот недостаток стоимостных измерителей преодолевают применением «неизменных» или «сопоставимых» цен одного и того же периода.

В трудовых единицах измерения (человеко-днях, человеко-часах) учитываются общие затраты труда на предприятии, трудоемкость отдельных операций технологического цикла.

10. Относительные величины, их сущность и формы выражения.

Выбор базы относительной величины. Виды относительных

величин, методы расчета

Относительная величина — это обобщающий показатель, который представляет собой частное от деления одного абсолютного показателя на другой и дает числовую меру соотношения между ними.

Основное условие правильного расчета относительной величины — сопоставимость сравниваемых показателей и наличие реальных связей между изучаемыми явлениями.

Величина, с которой производится сравнение (знаменатель дроби), обычно называется базой сравнения или основанием.

В зависимости от выбора базы сравнения относительный показатель может быть представлен в различных долях единицы: десятых; сотых (т. е. процентах); тысячных (десятая часть процента называется промилле); десятитысячных (сотая часть процента называется продецимилле).

Сопоставляемые величины могут быть как одноименными, так и разноименными (в последнем случае их наименования образуются от наименований сравниваемых величин, например, руб./чел.; ц/га; руб./м2).

По своему содержанию относительные величины подразделяются на виды: относительные величины динамики, планового задания, структуры, интенсивности, уровня экономического развития, координации и сравнения.

Относительная величина динамики (i) рассчитывается как отношение уровня признака в определенный период или момент времени к уровню этого же признака в предшествующий период или момент времени, т. е. она характеризует изменение уровня какого-либо явления во времени. Относительные величины динамики называют темпами роста. Выбор базы сравнения при исчислении относительных показателей динамики определяется целью исследования.

Относительная величина планового задания (iпл 3) рассчитывается как отношение уровня, запланированного на предстоящий период, к уровню, фактически сложившемуся в этом периоде

Относительная величина выполнения плана (iвьп.пл.) представляет собой отношение фактически достигнутого в данном периоде уровня к запланированному:

Относительные величины динамики, планового задания и выполнения плана связаны соотношением:

Относительными величинами структуры называются показатели, характеризующие долю отдельных частей изучаемой совокупности во всем ее объеме. Они рассчитываются путем деления численности единиц в отдельных частях совокупности на общую численность единиц совокупности (или объем явления). Выражаются они простым кратным отношением или в процентах. В качестве примера относительных величин структуры могут служить данные об удельном весе городского населения в общей численности населения России: в 1913 г. — 18%, в 1999 г. — 73%.

Относительными величинами интенсивности называют показатели, характеризующие степень распространения или уровень развития того или иного явления в определенной среде. Они вычисляются путем сравнения разноименных величин, находящихся в определенной связи между собой. Эти показатели обычно определяются в расчете на 100, 1000 и т.д. единиц изучаемой совокупности (на 100 га земли, на 1000 человек населения и т.д.) и являются именованными числами

11. Средние величины в статистике. Виды средних и методика их

расчета

Средней величиной называется обобщающий показатель, характеризующий типичный уровень явления в конкретных условиях места и времени, отражающий величину варьирующего признака в расчете на единицу качественно однородной совокупности.

Вычисление среднего — один из распространенных приемов обобщения; средний показатель отражает то общее, что характерно (типично) для всех единиц изучаемой совокупности, в то же время он игнорирует различия отдельных единиц.

Средняя отражает характерный, типичный, реальный уровень изучаемых явлений, характеризует эти уровни и их изменения во времени и в пространстве.

Средняя - это сводная характеристика закономерностей процесса в тех условиях, в которых он протекает.

Выбор вида средней определяется экономическим содержанием определенного показателя и исходных данных. В каждом конкретном случае применяется одна из средних величин: арифметическая, гармоническая, геометрическая, квадратическая, кубическая и т.д.

Перечисленные средние относятся к классу степенных средних и объединяются общей формулой (при различных значениях т):

При m = -1 — средняя гармоническая; при т = 0 — средняя геометрическая хг ; при т = 1 — средняя арифметическая хар ; при т = 2 — средняя квадратическая хквадр; при т = 3 — средняя кубическая хкуб.

При использовании одних и тех же исходных данных, чем больше т в формуле, тем больше значение средней величины:

Это свойство степенных средних возрастать с повышением показателя степени определяющей функции называется в статистике правилом мажорантности средних.

12. Средняя арифметическая простая и взвешенная. Условия

применения. Вычисление средней арифметической по данным

интервального ряда

Средняя арифметическая применяется в тех случаях, когда объем варьирующего признака для всей совокупности является суммой значений признаков отдельных ее единиц. Для общественных явлений характерна аддитивность (суммарность) объемов варьирующего признака, этим определяется область применения средней арифметической и объясняется ее распространенность как обобщающего показателя.

Средняя арифметическая простая равна простой сумме отдельных значений осредняемого признака, деленной на общее число этих значений (она применяется в тех случаях, когда имеются несгруппированные индивидуальные значения признака):

Средняя из вариантов, которые повторяются различное число раз, или, как говорят, имеют различный вес, называется взвешенной.

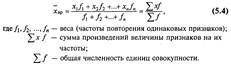
Cредняя гармоническая средняя взвешенная из варьирующих обратных значений признака. Она является преобразованной формой арифметической средней и тождественна ей. Вместо гармонической всегда можно рассчитать среднюю арифметическую, но для этого сначала нужно определить веса отдельных значений признака, скрытые в весах средней гармонической.

13. Средняя гармоническая. Методика расчета, формулы и условия

применения средней гармонической

Таким образом, средняя гармоническая применяется тогда, когда неизвестны действительные веса f, а известно w = xf, т.е. в тех случаях, когда средняя предназначается для расчета сумм слагаемых, обратно пропорциональных величине данного признака, когда суммированию подлежат не сами варианты, а обратные им величины.

В тех случаях, когда вес каждого варианта равен единице (индивидуальные значения обратного признака встречаются по одному разу), применяется средняя гармоническая простая, исчисляемая по формуле:

14. Средние структурные величины, методика их расчета.

Cтруктурные средние применяются для изучения внутреннего строения и структуры рядов распределения значений признака. К таким показателям относятся мода и медиана.

Мода — значение случайной величины, встречающееся с наибольшей вероятностью в дискретном вариационном ряду вариант, имеющий наибольшую частоту.

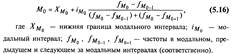
Медиана Ме — это вариант, который находится в середине вариационного ряда. Медиана делит ряд на две равные (по числу единиц) части — со значениями признака меньше медианы и со значениями признака больше медианы. Чтобы найти медиану, необходимо отыскать значение признака, которое ра-ходится в середине упорядоченного ряда. В ранжированных рядах несгруппированных данных нахождение медианы сводится к отысканию порядкового номера медианы.

15. Вариация и задачи ее статистического изучения. Основные

показатели вариации, их достоинства и значение.

Вариация - колеблемость, многообразие, изменяемость величины признака у отдельных единиц совокупности.

Вариация даёт возможность оценить степень воздействия на данный признак других варьирующих признаков, установить, например, какие факторы и в какой степени влияют на смертность населения, финансовое положение предприятий, урожайность пшеницы и т. п.

Вариация существует в пространстве и во времени. Под вариацией в пространстве понимается колеблемость значений признака по отдельным территориям.

Объективно существует также вариация во времени. Под ней подразумевают изменение значений признака в различные периоды (или моменты) времени. Так, со временем изменяются средняя продолжительность жизни, срок службы товаров длительного пользования, мнения людей и т. д.

Показатели вариации делятся на две группы: абсолютные и относительные. К абсолютным относятся размах вариации, среднее линейное отклонение, дисперсия и среднее квадратическое отклонение. Вторая группа показателей вычисляется как отношение абсолютных показателей вариации к средней арифметической (или медиане). Относительными показателями вариации являются коэффициенты осцилляции, вариации, относительное линейное отклонение и др.

Самым простым абсолютным показателем является размах вариации (R).

Размах показывает, насколько велико различие между единицами совокупности, имеющими самое маленькое и самое большое значение признака.

Знание подобного рода величин необходимо в практической и хозяйственной деятельности, а также в научных исследованиях.

Например, размах вариации применяется при контроле качества продукции для определения влияния систематически действующих причин на производственный процесс. Для этого отбирают через определенные промежутки времени несколько деталей и производят их измерение. Рассчитав по данным этих выборок показатели размаха вариации, на основе сопоставления результатов вычислений судят об устойчивости режима производственного процесса.

В учебной литературе по статистике обычно указывается, что размах имеет существенный недостаток. Его величина всецело зависит от крайних значений признака, и он не учитывает всех изменений варьирующего признака в пределах совокупности.

Этот упрек в адрес размаха вариации является не совсем верным. Какой же это недостаток, когда именно в этом заключается суть показателя.

К недостаткам размаха вариации можно отнести то обстоятельство, что очень низкое и очень высокое значения признака по сравнению с основной массой его значений в совокупности могут быть обусловлены какими-либо сугубо случайными обстоятельствами (т. е. эти значения являются аномальными в совокупности).

Условия существования и развития отдельных единиц совокупности в определенной степени различны, что сказывается и на различии значений у них взятого нами признака. Средняя величина отражает эти средние условия.

Среднее линейное отклонение дает обобщенную характеристику степени колеблемости признака в совокупности. Однако при его исчислении приходится допускать некорректные с точки зрения математики действия, нарушать законы алгебры, что побудило математиков и статистиков искать иной способ оценки вариации для того, чтобы иметь дело только с положительными величинами. Самый простой выход - возвести все отклонения во вторую степень.

Полученная мера вариации называется дисперсией, a корень квадратный из дисперсии - средним квадратическим отклонением. Эти показатели являются общепринятыми мерами вариации и часто используются в статистических исследованиях, а также в технике, биологии и других отраслях знаний. Данные показатели нашли также свое широкое применение в международной практике учета и статистического анализа, в частности в системе национального счетоводства.

Дисперсия есть средняя величина квадратов отклонений.

Среднее квадратическое отклонение - это обобщающая характеристика размеров вариации признака в совокупности. Оно выражается в тех же единицах измерения, что и признак (в метрах, тоннах, рублях, процентах и т. д.).

16. Понятие вариации и ее значение. Статистическое изучение

вариации признаков.

Вариация - колеблемость, многообразие, изменяемость величины признака у отдельных единиц совокупности.

Вариация порождается комплексом условий, действующих на совокупность и ее единицы. Например, вариация оценок на экзамене в вузе порождается, в частности, различными способностями студентов, временем, затрачиваемым ими на самостоятельную работу, различием социально-бытовых условий и т. д. Именно вариация и предопределяет необходимость статистики. Если бы все студенты получали одинаковые оценки или, например, семьи имели одинаковые доходы, то необходимость в статистическом исследовании отпала бы.

Исследование вариации в статистике имеет важное значение. Вариация даёт возможность оценить степень воздействия на данный признак других варьирующих признаков, установить, например, какие факторы и в какой степени влияют на смертность населения, финансовое положение предприятий, урожайность пшеницы и т. п. Определение вариации необходимо при организации выборочного наблюдения, построении статистических моделей разработке материалов экспертных опросов и во многих других случаях.

По степени вариации можно судить о многих сторонах процесса развития изучаемых явлений, в частности об однородности совокупности, устойчивости индивидуальных значений признака, типичности средней, о взаимосвязи между признаками одного и того же явления и признаками разных явлений. Статистические показатели, характеризующие вариацию, широко применяются в практической деятельности, например для оценки ритмичности работы промышленных предприятий, контроля за ходом других производственных процессов, устойчивости урожайности сельскохозяйственных культур тех или иных сортов или одного и того же сорта в определенных почвенно-климатических условиях. На основе показателей вариации в статистике разрабатываются другие показатели и методы изучения явлений и процессов общественной жизни - показатели тесноты связи между явлениями и их признаками, показатели оценки точности выборочного наблюдения.

17. Абсолютные и относительные показатели вариации, сущность и

значение, методика расчета

К абсолютным показателям вариации относятся размах вариации, среднее линейное отклонение, среднее квадратическое отклонение, дисперсия и среднее квадратическое отклонение.

Относительные показатели вариации - это коэффициенты осцилляции, вариации, относительное линейное отклонение и др.

Размах вариации - разность между наибольшим и наименьшим значениями варьирующего признака.

Среднее линейное отклонение - средняя арифметическая из абсолютных значений отклонений вариант признака от их средней.

Дисперсия - средний квадрат отклонений индивидуальных значений признака от их средней величины.

Среднее квадратическое отклонение рассчитывается как корень квадратный из дисперсии. Среднее квадратическое отклонение, дисперсия и среднее линейное отклонение могут определяться по формулам простой и взвешенной (в зависимости от исходных данных).

Коэффициент осцилляции - процентное отношение размаха вариации к средней величине признака.

Самым простым абсолютным показателем является размах вариации (R).

Размах вариации применяется при контроле качества продукции для определения влияния систематически действующих причин на производственный процесс. Для этого отбирают через определенные промежутки времени несколько деталей и производят их измерение. Рассчитав по данным этих выборок показатели размаха вариации, на основе сопоставления результатов вычислений судят об устойчивости режима производственного процесса.

Дисперсия есть средняя величина квадратов отклонений.

Различают следующие относительные показатели вариации (V):

Наиболее часто в практических расчетах применяется показатель относительной вариации - коэффициент вариации

18. Вариация альтернативного признака. Расчет дисперсии по

разным способам.

Среди множества варьирующих признаков, изучаемых статистикой, существуют признаки, которыми обладают одни единицы совокупности и не обладают другие. Эти признаки называются альтернативными. Примером таких признаков являются: наличие бракованной продукции, ученая степень у преподавателя вуза, работа по полученной специальности и т. д. Вариация альтернативного признака количественно проявляется в значении нуля у единиц, которые этим признаком не обладают, или единицы у тех, которые данный признак имеют.

Пусть р - доля единиц в совокупности, обладающих данным признаком (р = m/n); q - доля единиц, не обладающих данным признаком, причем р + q = 1. Альтернативный признак принимает всего два значения - 0 и 1 с весами соответственно q и р. Исчислим среднее значение альтернативного признака по формуле средней арифметической:

Дисперсия альтернативного признака определяется по формуле:

Таким образом, дисперсия альтернативного признака равна произведению доли на дополняющее эту долю до единицы число. Корень квадратный из этого показателя соответствует среднему квадратическому отклонению альтернативного признака.

Показатели вариации альтернативных признаков широко используются в статистике, в частности при проектировании выборочного наблюдения, обработке данных социологических обследований, статистическом контроле качества продукции, в ряде других случаев.

19. Правило сложения дисперсий. Дисперсионный факторный

анализ.

Бывает необходимо проследить количественные изменения признака по группам, на которые разделяется совокупность, а также и между группами. Такое изучение вариации достигается посредством вычисления и анализа различных видов дисперсии.

Выделяют дисперсию общую, межгрупповую и внутригрупповую. Общая дисперсия измеряет вариацию признака во всей совокупности под влиянием всех факторов, обусловивших эту вариацию:

Существует закон, связывающий три вида дисперсии. Общая дисперсия равна сумме средней из внутригрупповых и межгрупповой дисперсий:

Данное соотношение называют правилом сложения дисперсий. Согласно этому правилу, общая дисперсия, возникающая под действием всех факторов, равна сумме дисперсии, появляющейся под влиянием всех прочих факторов, и дисперсии, возникающей за счет группировочного признака.

Зная любые два вида дисперсий, можно определить или проверить правильность расчета третьего вида.

20. Динамический ряд, его элементы. Виды рядов динамики.

Правила построения динамических рядов

Ряд динамики (или динамический ряд) представляет собой ряд расположенных в хронологической последовательности числовых значений статистического показателя, характеризующих изменение общественных явлений во времени.

В каждом ряду динамики имеются два основных элемента: время t и конкретное значение показателя (уровень ряда) у.

Уровни ряда — это показатели, числовые значения которых составляют динамический ряд. Время — это моменты или периоды, к которым относятся уровни.

Построение и анализ рядов динамики позволяют выявить и измерить закономерности развития общественных явлений во времени. Эти закономерности не проявляются четко на каждом конкретном уровне, а лишь в тенденции, в достаточно длительной динамике. На основную закономерность динамики накладываются другие, прежде всего случайные, иногда сезонные влияния. Выявление основной тенденции в изменении уровней, именуемой трендом, является одной из главных задач анализа рядов динамики.

По времени, отраженному в динамических рядах, они разделяются на моментные и интервальные.

Моментным рядом динамики называется такой ряд, уровни которого характеризуют состояние явления на определенные даты (моменты времени).

Интервальным (периодическим) рядом динамики называется такой ряд, уровни которого характеризуют размер явления за конкретный период времени (год, квартал, месяц).

Уровни в динамическом ряду, могут быть представлены абсолютными, средними или относительными величинами.

По расстоянию между уровнями ряды динамики подразделяются на ряды с равностоящими и неравностоящими уровнями по времени

При построении динамических рядов необходимо соблюдать определенные правила: основным условием для получения правильных выводов при анализе рядов динамики и прогнозировании его уровней является сопоставимость уровней динамического ряда между собой.

Статистические данные должны быть сопоставимы по территории, кругу охватываемых объектов, единицам измерения, времени регистрации, ценам, методологии расчета и др.

Сопоставимость по территории предполагает одни и те же границы территории.

Сопоставимость по кругу охватываемых объектов означает сравнение совокупностей с равным числом элементов.

При этом нужно иметь в виду, что сопоставляемые показатели динамического ряда должны быть однородны по экономическому содержанию и границам объекта, который они характеризуют (однородность может быть обеспечена одинаковой полнотой охвата разных частей явления).

Сопоставимость по времени регистрации для интервальных рядов обеспечивается равенством периодов времени, за которые приводятся данные.

Сопоставимость по ценам. При проведении к сопоставимому виду продукции, измеренной в стоимостных (ценностных) показателях, трудность заключается в том, что, во-первых, с течением времени происходит непрерывное изменение цен, а во-вторых, существует несколько видов цен.

Сопоставимость по методологии расчета. При определении уровней динамического ряда необходимо использовать единую методологию их расчета.

21. Показатели анализа ряда динамики. Средние показатели ряда

динамики.

Анализ интенсивности изменения во времени осуществляется с помощью показателей, получаемых в результате сравнения уровней, к таким показателям относятся: абсолютный прирост, темп роста, темп прироста, абсолютное значение одного процента прироста.

Система средних показателей включает средний уровень ряда, средний абсолютный прирост, средний темп роста, средний темп прироста.

Показатели анализа динамики могут вычисляться на постоянной и переменных базах сравнения. При этом принято называть сравниваемый уровень отчетным, а уровень, с которым производится сравнение, — базисным.

Для расчета показателей анализа динамики на постоянной базе каждый уровень рада сравнивается с одним и тем же базисным уровнем. В качестве базисного выбирается либо начальный уровень в раду динамики, либо уровень, с которого начинается какой-то новый этап развития явления. Исчисляемые при этом показатели называются базисными.

Для расчета показателей анализа динамики на переменной базе каждый последующий уровень рада сравнивается с предыдущим. Вычисленные таким образом показатели анализа динамики называются цепными.

Важнейшим статистическим показателем анализа динамики является абсолютный прирост (сокращение), т.е. абсолютное изменение, характеризующее увеличение или уменьшение уровня рада за определенный промежуток времени. Абсолютный прирост с переменной базой называют скоростью роста.

Цепные и базисные абсолютные приросты связаны между собой: сумма последовательных цепных абсолютных приростов равна базисному, т. е. общему приросту за весь промежуток времени.

Для обобщающей характеристики динамики исследуемого явления определяют средние показатели: средние уровни ряда и средние показатели изменения уровней ряда.

Средний уровень ряда характеризует обобщённую величину абсолютных уровней. Он рассчитывается по средней хронологической, т. е. по средней исчисленной из значений, изменяющихся во времени.

Для интервальных рядов динамики из абсолютных уровней средний уровень за период времени определяется по формуле средней арифметической:

• при равных интервалах применяется средняя арифметическая простая:

Обобщающий показатель скорости изменения уровней во времени — средний абсолютный прирост (убыль), представляющий собой обобщенную характеристику индивидуальных абсолютных приростов ряда динамики. По цепным данным об абсолютных приростах за ряд лет можно рассчитать средний абсолютный прирост как среднюю арифметическую простую.

22. Показатели интенсивности изменения уровня ряда:

абсолютный прирост, темп роста, темп прироста, абсолютное

значение одного процента прироста. Цепной и базисный способ

расчета.

При изучении динамики общественных явлений возникает проблема описания интенсивности изменения и расчета средних показателей динамики.

Коэффициент роста (снижения) показывает, во сколько раз сравниваемый уровень больше уровня, с которым производится сравнение (если этот коэффициент больше единицы) или какую часть уровня, с которым производится сравнение, составляет сравниваемый уровень (если он меньше единицы). Темп роста всегда представляет собой положительное число.

Темп прироста (сокращения) можно получить и из темпа роста, выраженного в процентах, если из него вычесть 100%. Коэффициент прироста получается вычитанием единицы из коэффициента роста.

При анализе динамики развития следует также знать, какие абсолютные значения скрываются за темпами роста и прироста. Сравнение абсолютного прироста и темпа прироста за одни и те же периоды времени показывает, что при снижении (замедлении) темпов прироста абсолютный прирост не всегда уменьшается, в отдельных случаях он может возрастать. Поэтому, чтобы правильно оценить значение полученного темпа прироста, его рассматривают в сопоставлении с показателем абсолютного прироста. Результат выражают показателем, который называют абсолютным значением (содержанием) одного процента прироста и рассчитывают как отношение абсолютного прироста к темпу прироста за тот же период времени, %:

23. Средние показатели ряда динамики: средний уровень ряда,

средний абсолютный прирост, средний темп роста и прироста. Их

расчет.

Методы расчета среднего уровня интервального и моментного рядов динамики различны.

• при равных интервалах применяется средняя арифметическая простая:

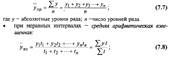
Средний уровень моментного ряда динамики с равностоящими уровнями определяется по формуле средней хронологической моментного ряда:

Средний уровень моментных рядов с неравностоящими уровнями определяется по формуле средней хронологической взвешенной:

Средний абсолютный прирост определим через накопленный (базисный) абсолютный прирост. Для случая равных интервалов применим следующую формулу:

где т число уровней ряда динамики в изучаемом периоде, включая базисный.

Сводной обобщающей характеристикой интенсивности изменения уровней ряда динамики служит средний темп роста (снижения), показывающий, во сколько раз в среднем за единицу времени изменяется уровень ряда динамики.

Средний темп роста (снижения) - обобщенная характеристика индивидуальных темпов роста ряда динамики.

Средний темп роста представляет собой средний коэффициент роста, выраженный в процентах, то для равностоящих рядов динамики расчеты по средней геометрической сводятся к исчислению средних коэффициентов роста из цепных коэффициентов роста (по «цепному способу»):

Средние темпы прироста (сокращения) рассчитываются на основе средних темпов роста, вычитанием из последних 100 %. Соответственно при исчислении средних коэффициентов прироста из значений коэффициентов роста вычитается единица:

24. Методы сглаживания рядов динамики. Сущность метода

укрупнения интервалов и метода скользящей средней.

Аналитическое выравнивание ряда динамики.

Основной тенденцией развития (трендом) называется плавное и устойчивое изменение уровня явления во времени, свободное от случайных колебаний.

Задача состоит в том, чтобы выявить общую тенденцию в изменении уровней ряда, освобожденную от действия различных случайных факторов. С этой целью ряды динамики подвергаются обработке методами укрупнения интервалов, скользящей средней и аналитического выравнивания.

Одним из наиболее простых методов изучения основной тенденции в рядах динамики является укрупнение интервалов. Он основан на укрупнении периодов времени, к которым относятся уровни ряда динамики (одновременно уменьшается количество интервалов).

Выявление основной тенденции может осуществляться также методом скользящей (подвижной) средней. Сущность его заключается в том, что исчисляется средний уровень из определенного числа, обычно нечетного (3, 5, 7 и т.д.), первых по счету уровней ряда, затем — из такого же числа уровней, но начиная со второго по счету, далее — начиная с третьего и т.д. Таким образом, средняя как бы «скользит» по ряду динамики, передвигаясь на один срок.

Недостатком сглаживания ряда является «укорачивание» сглаженного ряда по сравнению с фактическим, а следовательно, потеря информации.

Рассмотренные приемы сглаживания динамических рядов (укрупнение интервалов и метод скользящей средней) дают возможность определить лишь общую тенденцию развития явления, более или менее освобожденную от случайных и волнообразных колебаний. Однако получить обобщенную статистическую модель тренда посредством этих методов нельзя.

Для того чтобы дать количественную модель, выражающую основную тенденцию изменения уровней динамического ряда во времени, используется аналитическое выравнивание ряда динамики.

Основным содержанием метода аналитического выравнивания в рядах динамики является то, что общая тенденция развития рассчитывается как функция времени:

где yt — уровни динамического ряда, вычисленные по соответствующему аналитическому уравнению на момент времени.

Определение теоретических (расчетных) уровней yt производится на основе так называемой адекватной математической модели, которая наилучшим образом отображает (аппроксимирует) основную тенденцию ряда динамики.

Выбор типа модели зависит от цели исследования и должен быть основан на теоретическом анализе, выявляющем характер развития явления, а также на графическом изображении ряда динамики (линейной диаграмме).

Например, простейшими моделями (формулами), выражающими тенденцию развития, являются:

В тех случаях, когда требуется особо точное изучение тенденции развития (например, модели тренда для прогнозирования), при выборе вида адекватной функции можно использовать специальные критерии математической статистики.

Расчет параметров функции обычно производится методом наименьших, квадратов, в котором в качестве решения принимается точка минимума суммы квадратов отклонений между теоретическими и эмпиричесими уровнями:

Выравнивание по прямой используется, как правило, в тех случаях, когда абсолютные приросты практически постоянны, т. е. когда уровни изменяются в арифметической профессии (или близко к ней).

Выравнивание по показательной функции используется в тех случаях, когда ряд отражает развитие в геометрической профессии, т. е. когда цепные коэффициенты роста практически постоянны.

25. Статистическое изучение сезонных колебаний в ряде динамики;

индексы сезонности.

При сравнении квартальных и месячных данных многих социально-экономических явлений часто обнаруживаются периодические колебания, возникающие под влиянием смены времен года. Они являются результатом влияния природно-климатических условий, общих экономических факторов, а также многочисленных и разнообразных факторов, которые часто являются регулируемыми.

В статистике периодические колебания, которые имеют определенный и постоянный период, равный годовому промежутку, носят название «сезонные колебания» или «сезонные волны», а динамический ряд в этом случае называют сезонным рядом динамики.

Индексами сезонности являются процентные отношения фактических (эмпирических) внутригрупповых уровней к теоретическим (расчетным) уровням, выступающим в качестве базы сравнения.

Для того чтобы выявить устойчивую сезонную волну, на которой не отражались бы случайные условия одного года, индексы сезонности вычисляют по данным за несколько лет (не менее трех), распределенным по месяцам.

Если ряд динамики не содержит ярко выраженной тенденции в развитии, то индексы сезонности вычисляются непосредственно по эмпирическим данным без их предварительного выравнивания.

Для каждого месяца рассчитывается средняя величина уровня, например за три года, затем вычисляется среднемесячный уровень для всего ряда у . После чего определяется показатель сезонной волны - индекс сезонности Is как процентное отношение средних для каждого месяца к общему среднемесячному уровню ряда, %:

где уi - средний уровень для каждого месяца (минимум за три года); у — среднемесячный уровень для всего ряда.

Когда уровень проявляет тенденцию к росту или снижению, то отклонения от постоянного среднего уровня могут исказить сезонные колебания. В таких случаях фактические данные сопоставляются с выравненными, т. е. полученными аналитическим выравниванием.

Формулу для расчета индекса сезонности, %, в этом случае можно записать так: