
Рефераты по сексологии
Рефераты по информатике программированию
Рефераты по биологии
Рефераты по экономике
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Рефераты по авиации и космонавтике
Рефераты по административному праву
Рефераты по безопасности жизнедеятельности
Рефераты по арбитражному процессу
Рефераты по архитектуре
Рефераты по астрономии
Рефераты по банковскому делу
Рефераты по биржевому делу
Рефераты по ботанике и сельскому хозяйству
Рефераты по бухгалтерскому учету и аудиту
Рефераты по валютным отношениям
Рефераты по ветеринарии
Рефераты для военной кафедры
Рефераты по географии
Рефераты по геодезии
Рефераты по геологии
Рефераты по геополитике
Рефераты по государству и праву
Рефераты по гражданскому праву и процессу
Рефераты по делопроизводству
Рефераты по кредитованию
Рефераты по естествознанию
Рефераты по истории техники
Рефераты по журналистике
Рефераты по зоологии
Рефераты по инвестициям
Рефераты по информатике
Исторические личности
Рефераты по кибернетике
Рефераты по коммуникации и связи
Контрольная работа: Исследование частотных характеристик типовых динамических звеньев
Контрольная работа: Исследование частотных характеристик типовых динамических звеньев
Министерство образования и науки Украины
Донбасская Государственная Машиностроительная Академия
Кафедра АПП
Лабораторная работа
по дисциплине
Теория автоматического управления
Тема
Исследование частотных характеристик типовых динамических звеньев
Краматорск
Задание
Таблица 1
| № п/п | Параметры динамических звеньев | ||||||
| Безынерцион. | Апериодич. 1-го порядка | Апериодич. 2-го порядка | Колебательное | Реальные дифференцирующие и интегрирующие, звено запаздывания | |||
| K | T, с | T1, с | T2, с | T, с | ξ | T, с | |
| 14 | 25-37 | 0.06 – 0.5 | 0.26 | 0.06 – 0.5 | 0.06 – 0.5 | 0.1-0.9 | 0.06 – 0.5 |
1. Исследование безынерционного звена
1.1 Исследование частотных характеристик безынерционного звена
Для исследования частотных характеристик безынерционного звена в прикладном пакете Proteus\ISIS составляем структурную схему, представленную на рисунке 1 для трех значений K:
![]() .
.
ЛАЧХ звеньев представлены на рисунке 2, графики переходной функции – на рисунке 3.
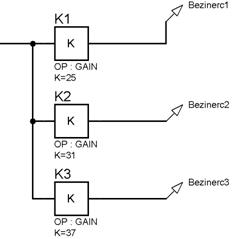
Рисунок 1 – Структурная схема для исследования безынерционного звена
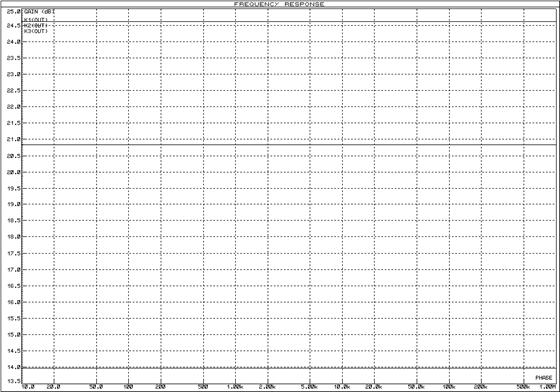
Рисунок 2 – ЛАЧХ безынерционных звеньев
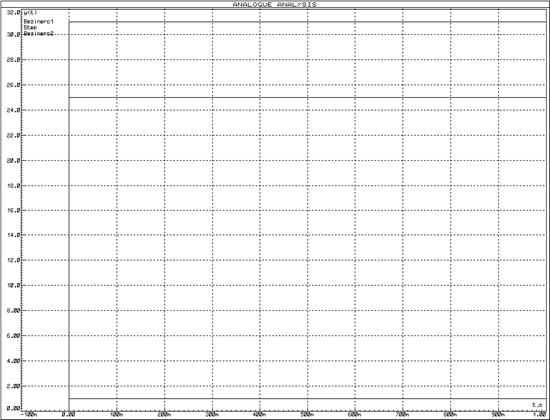
Рисунок 3 – Переходные функции безынерционных звеньев
1.2 Реализация безынерционного звена
Реализуем безынерционное
звено с коэффициентом усиления ![]() на
операционных усилителях (рисунки 4 и 7). ЛАЧХ и ЛФЧХ инвертирующего и
неинвертирующего усилителей представлены на рисунках 5 и 8, переходные функции
на рисунках 6 и 9. Для сравнения частотных характеристик идеальных и реальных
звеньев изобразим их ЛЧХ в совмещенных координатах (рисунок 10).
на
операционных усилителях (рисунки 4 и 7). ЛАЧХ и ЛФЧХ инвертирующего и
неинвертирующего усилителей представлены на рисунках 5 и 8, переходные функции
на рисунках 6 и 9. Для сравнения частотных характеристик идеальных и реальных
звеньев изобразим их ЛЧХ в совмещенных координатах (рисунок 10).
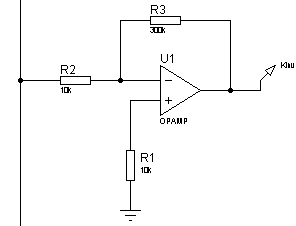
Рисунок 4 – Электрическая принципиальная схема
инвертирующего усилителя с коэффициентом усиления ![]()
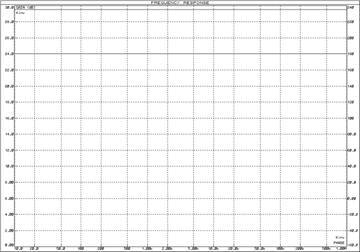
Рисунок 5 – ЛАЧХ и ЛФЧХ инвертирующего усилителя
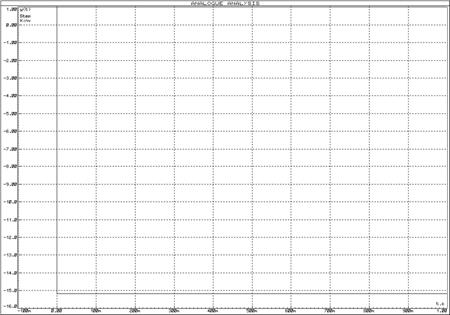
а)
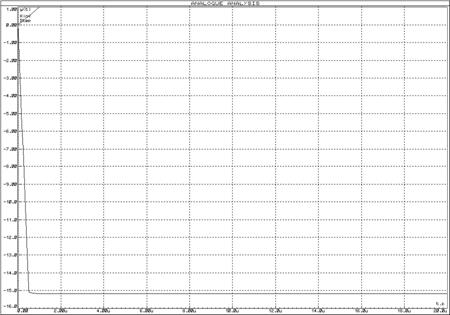
б)
Рисунок 6 – Переходные функции идеального безынерционного звена и инвертирующего усилителя
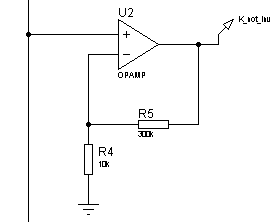
Рисунок 7 – Электрическая принципиальная схема
неинвертирующего усилителя с коэффициентом усиления ![]()
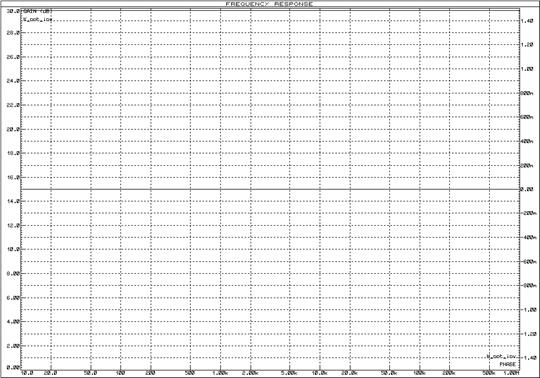
Рисунок 8 – ЛАЧХ и ЛФЧХ неинвертирующего усилителя
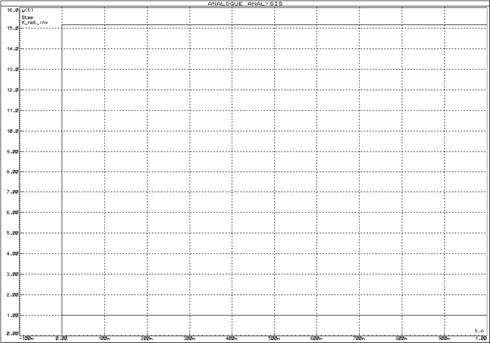
а)
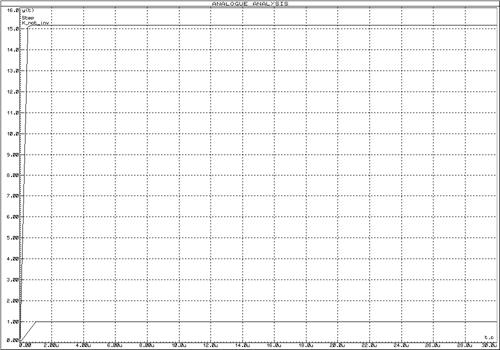
б)
Рисунок 9 – Переходные функции идеального безынерционного звена и неинвертирующего усилителя
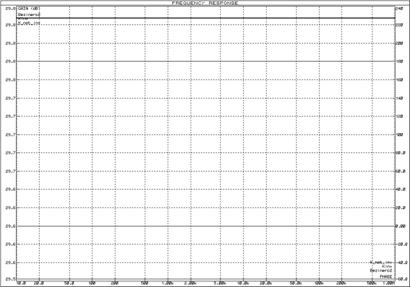
Рисунок 10 – ЛАЧХ и ЛФЧХ идеального безынерционного звена, инвертирующего усилителя и неинвертирующего усилителя
При рассмотрении частотных и временных характеристик безынерционных звеньев можно сделать следующие выводы:
· при прохождении через безынерционный элемент амплитуда и фаза выходного сигнала не зависит от частоты входного сигнала
· при увеличении (уменьшении) коэффициента усиления ЛАЧХ увеличивается (уменьшается) во столько же раз, а ЛФЧХ не меняется.
2. Исследование апериодического звена 1-го порядка
a. Исследование частотных характеристик апериодического звена 1-го порядка
Для исследования
частотных характеристик апериодического звена 1-го порядка в прикладном
пакете Proteus\ISIS составляем структурную схему, представленную на
рисунке 11, для трех значений ![]() :
:
![]() .
.
Логарифмические частотные характеристики апериодических звеньев представлены на рисунке 12, графики переходной функции – на рисунке 13.
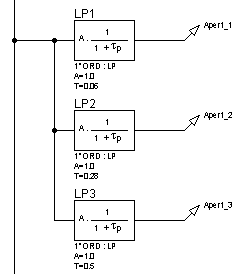
Рисунок 11 – Структурная схема для исследования апериодических звеньев 1-го порядка
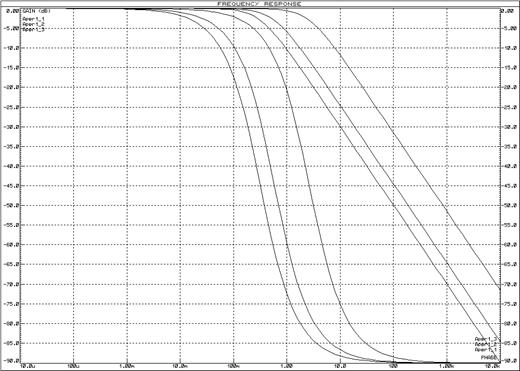
Рисунок 12 – Логарифмические частотные характеристики апериодических звеньев 1-го порядка
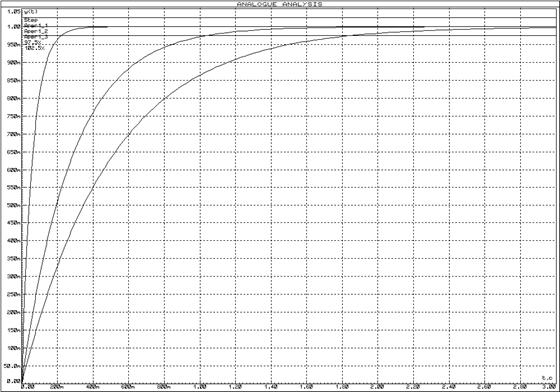
Рисунок 13 – Переходные функции апериодических звеньев 1-го порядка
b. Реализация апериодического звена 1-го порядка
Реализуем апериодическое
звено 1-го порядка с постоянной времени ![]() на
на
![]() -цепочке и на
-цепочке и на ![]() -цепочке (рисунок 14). ЛАЧХ
и ЛФЧХ
-цепочке (рисунок 14). ЛАЧХ
и ЛФЧХ ![]() -цепочки и на
-цепочки и на![]() -цепочки представлены на
рисунке 15, а и 15, б. Для сравнения частотных характеристик идеальных и
реальных апериодических звеньев изобразим их ЛЧХ в совмещенных координатах
(рисунок 15, в).
-цепочки представлены на
рисунке 15, а и 15, б. Для сравнения частотных характеристик идеальных и
реальных апериодических звеньев изобразим их ЛЧХ в совмещенных координатах
(рисунок 15, в).
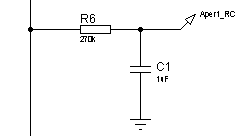
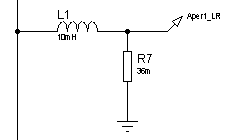
а)б)
а) ![]() -цепочка;
-цепочка;
б) ![]() -цепочка
-цепочка
Рисунок 14 – Электрическая принципиальная схема
апериодических звеньев 1-го порядка с постоянной времени ![]()
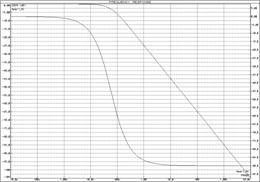
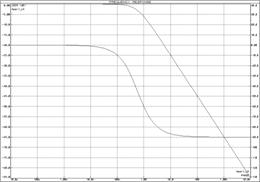
а) б)
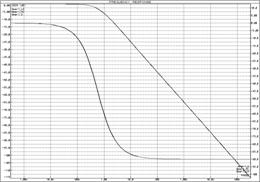
в)
Рисунок 15 – ЛАЧХ и ЛФЧХ апериодических звеньев
а) ![]() -цепочка; б)
-цепочка; б) ![]() -цепочка; в) совмещенные
ЛЧХ идеального апериодического звена,
-цепочка; в) совмещенные
ЛЧХ идеального апериодического звена, ![]() -цепочка
и
-цепочка
и ![]() -цепочка
-цепочка
При анализе частотных характеристик апериодических звеньев 1-го порядка можно сделать следующие выводы:
· увеличение (уменьшение) постоянной времени звена приводит к сдвигу ЛАЧХ и ЛФЧХ влево (вправо).
·
чем меньше
постоянная времени Т, тем шире полоса пропускания (т.к.![]() ~
~![]() ).
).
· при уменьшении постоянной времени уменьшается время переходного процесса и наоборот.
· чем меньше постоянная времени, тем меньше время переходного процесса и шире полоса пропускания, следовательно, чем меньше время переходного процесса, тем шире полоса пропускания.
·
если на график
ЛАЧХ заменить ломаной кривой и из точки ''разлома'' опустить прямую на ось ![]() , то это и будет сопрягающая
частота. Постоянную времени можно определить, зная сопрягающую частоту
, то это и будет сопрягающая
частота. Постоянную времени можно определить, зная сопрягающую частоту ![]() :
: ![]() .
.
c. Исследование частотных характеристик апериодического звена 2-го порядка
Для исследования
частотных характеристик апериодического звена 2-го порядка в прикладном
пакете Proteus\ISIS составляем структурную схему, представленную на рисунке
16, при неизменной первой постоянной времени ![]() и
для трех значений
и
для трех значений ![]() :
:
![]() .
.
Логарифмические частотные характеристики апериодических звеньев 2-го порядка представлены на рисунке 17, графики переходной функции – на рисунке 18.
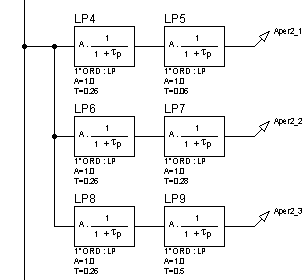
Рисунок 16 – Структурная схема для исследования апериодических звеньев 2-го порядка
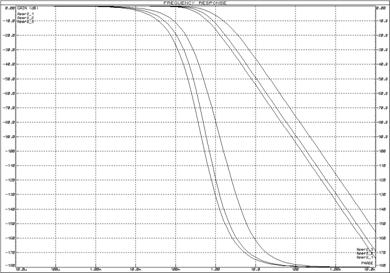
Рисунок 17 – Логарифмические частотные характеристики апериодических звеньев 2-го порядка
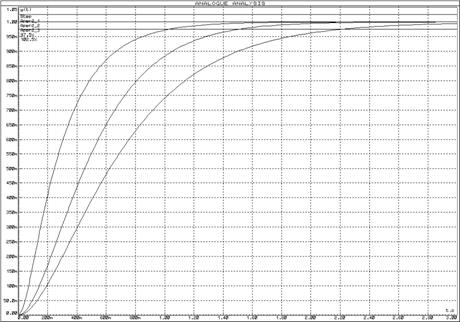
Рисунок 18 – Переходные функции апериодических звеньев 2-го порядка
d. Реализация апериодического звена 2-го порядка
Попробуем реализовать
апериодическое звено 2-го порядка с постоянными времени ![]() и
и ![]() на двух последовательно
соединенных
на двух последовательно
соединенных ![]() -цепочках, отдельно каждая
из которых представляет собой апериодическое звено 1-го порядка (рисунок 19).
ЛАЧХ и ЛФЧХ данного звена и необходимого апериодического звена 2-го порядка
представлены на рисунке 20, а, а их переходные функции – на рисунке 20, б.
-цепочках, отдельно каждая
из которых представляет собой апериодическое звено 1-го порядка (рисунок 19).
ЛАЧХ и ЛФЧХ данного звена и необходимого апериодического звена 2-го порядка
представлены на рисунке 20, а, а их переходные функции – на рисунке 20, б.
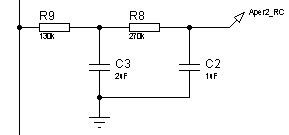
Рисунок 19 – Электрическая принципиальная схема
двух последовательно соединенных апериодических звеньев 1-го порядка с
постоянными времени ![]() и
и ![]()
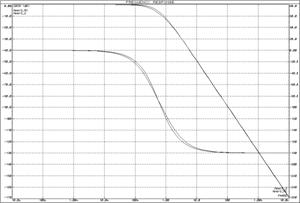
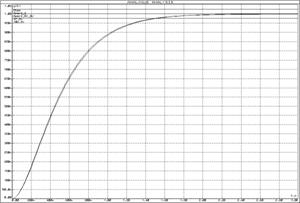
а)б)
а) ЛАЧХ и ЛФЧХ; б) переходная функция
Рисунок 20 – Характеристики последовательно
соединенных ![]() -цепочек
-цепочек
Реализуем апериодическое
звено 2-го порядка с постоянными времени ![]() и
и
![]() на двух последовательно
соединенных
на двух последовательно
соединенных ![]() -цепочках, разделенных
промежуточным (разделяющим, развязывающим) усилителем (повторителем) (рисунок
21). ЛАЧХ и ЛФЧХ данного звена и необходимого апериодического звена 2-го
порядка представлены на рисунке 22, а, а их переходные функции – на рисунке 22,
б.
-цепочках, разделенных
промежуточным (разделяющим, развязывающим) усилителем (повторителем) (рисунок
21). ЛАЧХ и ЛФЧХ данного звена и необходимого апериодического звена 2-го
порядка представлены на рисунке 22, а, а их переходные функции – на рисунке 22,
б.
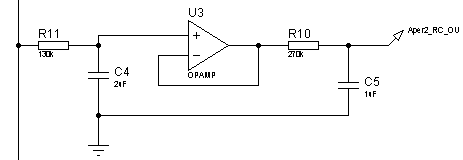
Рисунок 21 – Электрическая принципиальная схема
двух ![]() -цепочек с постоянными
времени
-цепочек с постоянными
времени ![]() и
и ![]() , разделенных операционным
усилителем
, разделенных операционным
усилителем
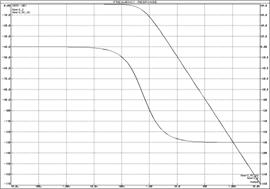
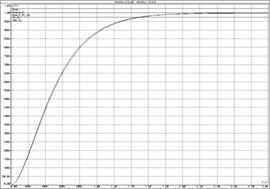
а) б)
а) ЛАЧХ и ЛФЧХ;
б) переходная функция
Рисунок 22 – Характеристики последовательно
соединенных ![]() -цепочек с разделительным
усилителем
-цепочек с разделительным
усилителем
При анализе частотных характеристик апериодических звеньев 2-го порядка можно сделать следующие выводы:
· увеличение (уменьшение) постоянной времени звена приводит к сдвигу ЛАЧХ и ЛФЧХ влево (вправо).
· увеличение (уменьшение) постоянной времени звена приводит к увеличению (уменьшению) времени переходного процесса.
· на полосу пропускания большее влияние оказывает большая постоянная времени
· при увеличении постоянной времени звена время переходного процесса увеличивается, а полоса пропускания уменьшается, следовательно, при увеличении времени переходного процесса полоса пропускания уменьшается и наоборот.
e. Аппроксимация апериодического звена 2-го порядка звеном 1-го порядка
Ввиду того, что
апериодическое звено 2-го порядка можно аппроксимировать звеном 1-го порядка,
если одна постоянная времени намного превышает вторую (![]() в 10 раз), сравним
характеристики звена с постоянными времени
в 10 раз), сравним
характеристики звена с постоянными времени ![]() и
и
![]() со звеном 1-го порядка,
изображенным на рисунке 23.
со звеном 1-го порядка,
изображенным на рисунке 23.
Аппроксимация апериодического звена 2-го порядка звеном 1-го порядка
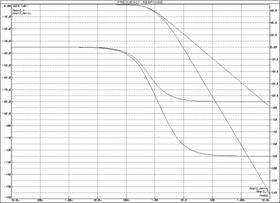
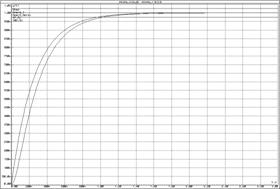
а) б)
а) ЛАЧХ и ЛФЧХ;б) переходные функции
Рисунок 24 – Характеристики апериодического звена 2-го порядка и инерционного звена
При анализе характеристик апериодических звеньев (рисунок 24) можно сделать следующие выводы:
· апериодическое звено 2-го порядка можно аппроксимировать апериодическим звеном 1-го порядка, если первая постоянная времени намного меньше второй, т.к. в таком случае влияние первой экспоненты на форму выходного сигнала несущественно.
Исследование колебательного звена
При исследовании
колебательного звена необходимо пронаблюдать за характером его частотных
характеристик при изменении постоянной времени и декремента затухания в
пределах, указанных в индивидуальном задании. Т.е. необходимо исследовать
частотные характеристики при постоянных времени ![]() и декременте затухания
и декременте затухания ![]() .
.
f. Исследование частотных характеристик
колебательного звена при изменении постоянной времени (![]() ) и неизменном декременте
затухания (
) и неизменном декременте
затухания (![]() )
)
Для исследования
колебательного звена при изменении постоянной времени (![]() ) и неизменном декременте
затухания в прикладном пакете Proteus\ISIS составляем структурную схему,
представленную на рисунке 25. Логарифмические частотные характеристики
колебательного звена представлены на рисунке 26, графики переходной функции
на рисунке 27.
) и неизменном декременте
затухания в прикладном пакете Proteus\ISIS составляем структурную схему,
представленную на рисунке 25. Логарифмические частотные характеристики
колебательного звена представлены на рисунке 26, графики переходной функции
на рисунке 27.
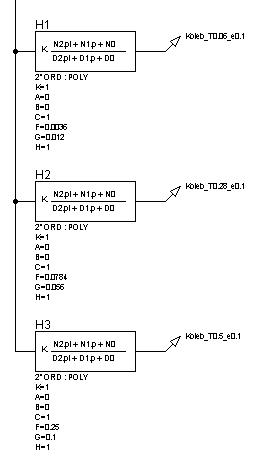
Рисунок 25 – Структурная схема для исследования
колебательных звеньев при изменении постоянной времени (![]() ) и неизменном декременте
затухания (
) и неизменном декременте
затухания (![]() )
)
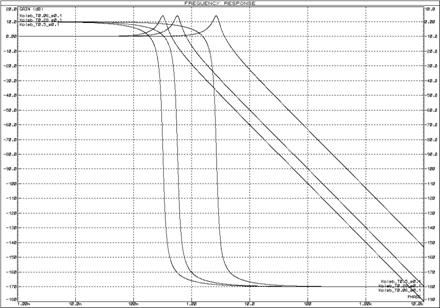
Рисунок 26 – Логарифмические частотные
характеристики колебательных звеньев при изменении постоянной времени (![]() ) и неизменном декременте
затухания (
) и неизменном декременте
затухания (![]() )
)
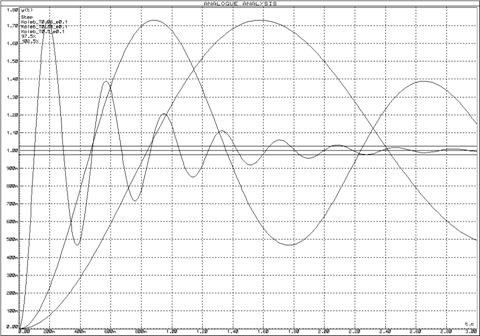
Рисунок 27 – Переходные функции колебательных
звеньев при изменении постоянной времени (![]() )
и неизменном декременте затухания (
)
и неизменном декременте затухания (![]() )
)
g. Исследование частотных характеристик
колебательного звена при изменении постоянной времени (![]() ) и неизменном коэффициенте
демпфирования (
) и неизменном коэффициенте
демпфирования (![]() )
)
Для исследования
колебательного звена при изменении постоянной времени (![]() ) и неизменном декременте
затухания (
) и неизменном декременте
затухания (![]() ) в
прикладном пакете Proteus\ISIS составляем структурную схему,
представленную на рисунке 28. Логарифмические частотные характеристики
колебательного звена представлены на рисунке 29, графики переходной функции
на рисунке 30.
) в
прикладном пакете Proteus\ISIS составляем структурную схему,
представленную на рисунке 28. Логарифмические частотные характеристики
колебательного звена представлены на рисунке 29, графики переходной функции
на рисунке 30.
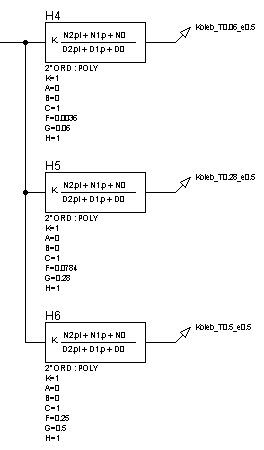
Рисунок 28 – Структурная схема для исследования
колебательных звеньев при изменении постоянной времени (![]() ) и неизменном декременте
затухания (
) и неизменном декременте
затухания (![]() )
)
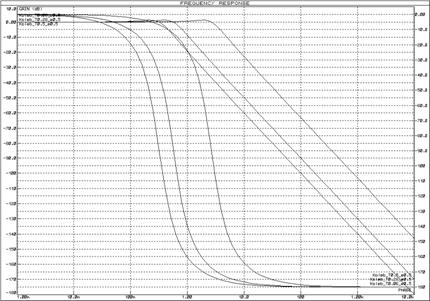
Рисунок 29 – Логарифмические частотные
характеристики колебательных звеньев при изменении постоянной времени (![]() ) и неизменном декременте
затухания (
) и неизменном декременте
затухания (![]() )
)
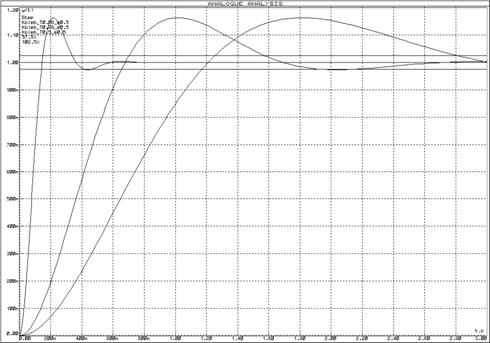
Рисунок 30 – Переходные функции колебательных
звеньев при изменении постоянной времени (![]() )
и неизменном декременте затухания (
)
и неизменном декременте затухания (![]() )
)
h. Исследование частотных характеристик
колебательного звена при неизмененной постоянной времени (![]() ) и изменении декремента
затухания (
) и изменении декремента
затухания (![]() ).
).
Для исследования
колебательного звена при неизмененной постоянной времени (![]() ) и изменении коэффициента
демпфирования (
) и изменении коэффициента
демпфирования (![]() ) в
прикладном пакете Proteus\ISIS составляем структурную схему,
представленную на рисунке 31. Логарифмические частотные характеристики
колебательного звена представлены на рисунке 32, графики переходной функции
на рисунке 33.
) в
прикладном пакете Proteus\ISIS составляем структурную схему,
представленную на рисунке 31. Логарифмические частотные характеристики
колебательного звена представлены на рисунке 32, графики переходной функции
на рисунке 33.
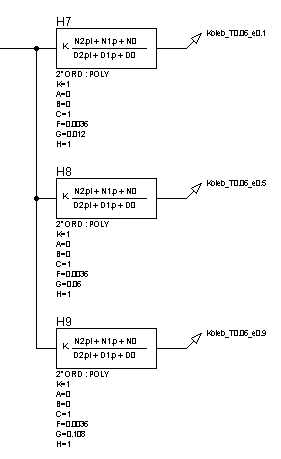
Рисунок 31 – Структурная схема для исследования
колебательного звена при неизмененной постоянной времени (![]() ) и изменении декремента
затухания (
) и изменении декремента
затухания (![]() )
)
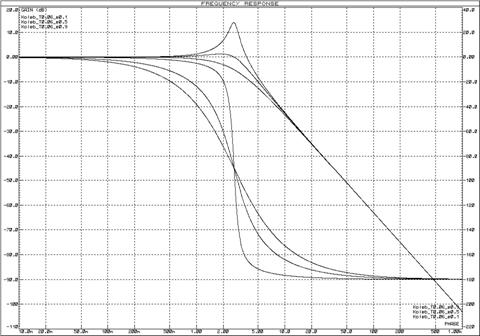
Рисунок 32 – Логарифмические частотные
характеристики колебательных звеньев при изменении постоянной времени (![]() ) и неизменном декременте
затухания (
) и неизменном декременте
затухания (![]() )
)
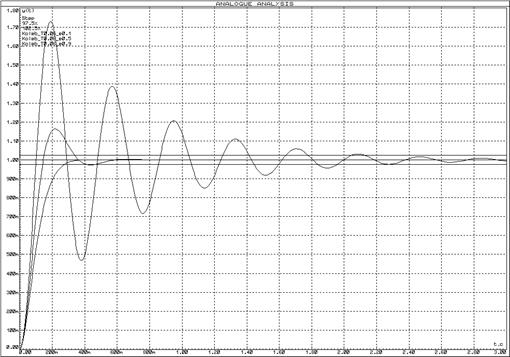
Рисунок 33 – Переходные функции колебательного
звена при неизмененной постоянной времени (![]() )
и изменении декремента затухания (
)
и изменении декремента затухания (![]() )
)
i. Реализация колебательного звена
Реализуем колебательное
звено с постоянной времени ![]() и
коэффициентом демпфирования
и
коэффициентом демпфирования ![]() на
на ![]() -контуре (рисунок 34). ЛАЧХ
и ЛФЧХ данного звена и необходимого колебательного звена представлены на
рисунке 35, а, а их переходные функции – на рисунке 35, б.
-контуре (рисунок 34). ЛАЧХ
и ЛФЧХ данного звена и необходимого колебательного звена представлены на
рисунке 35, а, а их переходные функции – на рисунке 35, б.
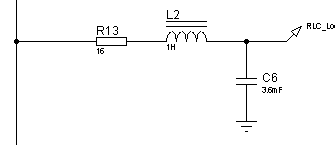
Рисунок 34 – Электрическая принципиальная схема
колебательного ![]() -контура
-контура
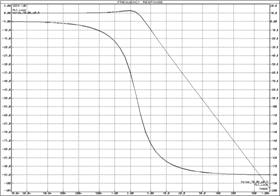
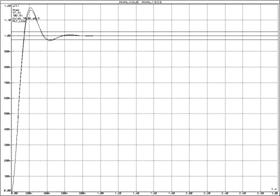
а) б)
а) ЛАЧХ и ЛФЧХ;б) переходная функция
Рисунок 35 – Характеристики колебательного
звена и ![]() -контура
-контура
При анализе графиков частотных характеристик и переходных процессов (рисунок 35) колебательных звеньев можно сделать следующие выводы:
· увеличение (уменьшение) постоянной времени звена при неизменном декременте затухания приводит к сдвигу частотных характеристик влево (вправо).
· при неизменном коэффициенте демпфирования увеличение постоянной времени звена приводит к сужению полосы пропускания; колебательность переходного процесса не меняется.
· при неизменной постоянной времени увеличение (уменьшение) коэффициента демпфирования приводит к уменьшению (увеличению) колебательности переходного процесса и к более плавной ЛФЧХ.
· при неизменной постоянной времени увеличение (уменьшение) коэффициента демпфирования приводит к уменьшению (увеличению) перерегулирования, сужению (расширению) полосы пропускания и уменьшению (увеличению) колебательности.
3. Исследование дифференцирующих звеньев
a. Исследование частотных характеристик идеального дифференцирующего звена
Для исследования частотных характеристик идеального дифференцирующего звена в прикладном пакете Proteus\ISIS составляем структурную схему, представленную на рисунке 36. Логарифмические частотные характеристики идеального дифференцирующего звена представлены на рисунке 37, график переходной функции на рисунке 38.
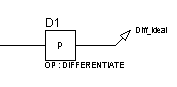
Рисунок 36 – Структурная схема для исследования идеального дифференцирующего звена
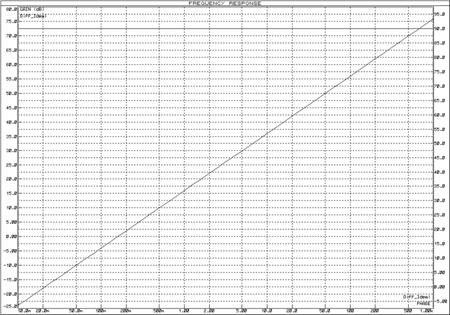
Рисунок 37 – Логарифмические частотные характеристики идеального дифференцирующего звена
Рисунок 38 – Переходная функция идеального дифференцирующего звена
b. Реализация идеального дифференцирующего звена
Реализуем идеальное дифференцирующее звено схемой, изображенной на рисунке 39. ЛАЧХ и ЛФЧХ дифференцирующего звена представлены на рисунках 40 и 41, переходная функция на рисунке 42.
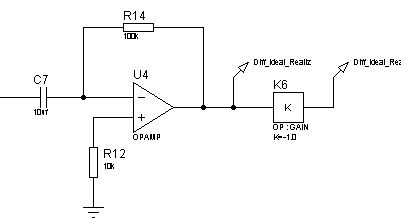
Рисунок 39 – Электрическая принципиальная схема дифференцирующего звена
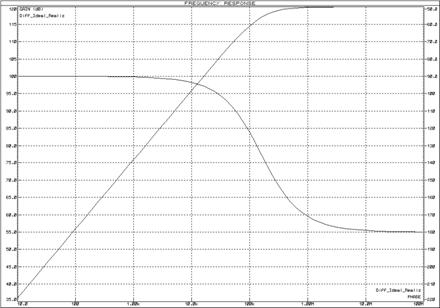
Рисунок 40 – ЛАЧХ и ЛФЧХ дифференцирующего звена
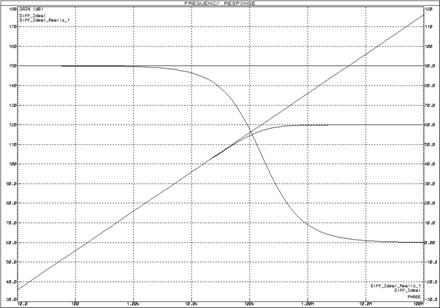
Рисунок 41 – ЛАЧХ и ЛФЧХ дифференцирующего звена с инвертором
а)
б)
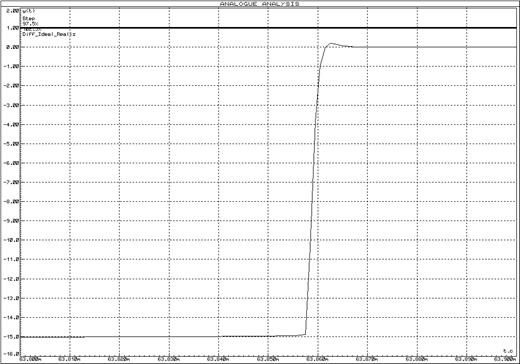
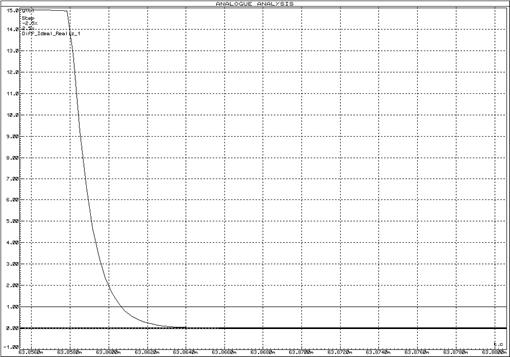
Рисунок 42 – Переходная функция схемы реализации идеального дифференцирующего звена
c. Исследование частотных характеристик реального дифференцирующего звена
Для исследования частотных характеристик реального дифференцирующего звена в прикладном пакете Proteus\ISIS составляем структурную схему, представленную на рисунке 43. Логарифмические частотные характеристики реального дифференцирующего звена представлены на рисунке 44, переходные функции – на рисунке 45.
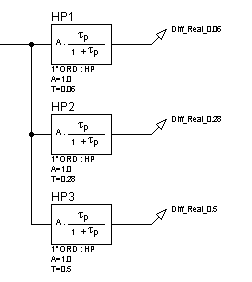
Рисунок 43 – Структурная схема для исследования реального дифференцирующего звена
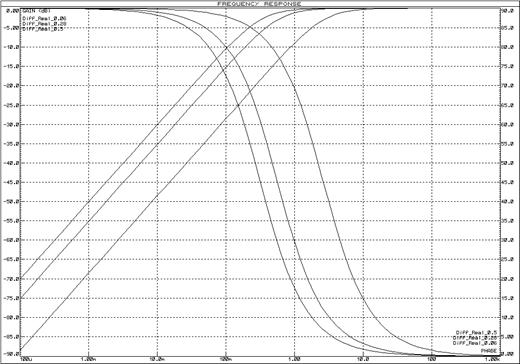
Рисунок 44 – Логарифмические частотные характеристики реального дифференцирующего звена
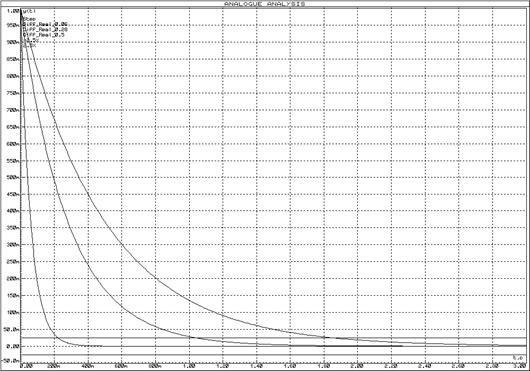
Рисунок 45 – Переходные функции реального дифференцирующего звена
d. Реализация реального дифференцирующего звена
Реализуем реальное дифференцирующее звено с помощью схем, изображенных на рисунке 46. ЛАЧХ и ЛФЧХ дифференцирующего звена представлены на рисунках 47, переходные функции – на рисунке 48.
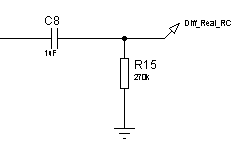
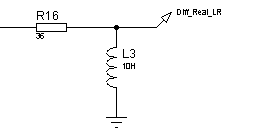
а)б)
а) ![]() -цепочка;б)
-цепочка;б) ![]() -цепочка
-цепочка
Рисунок 46 – Электрические принципиальные схемы реального дифференцирующего звена
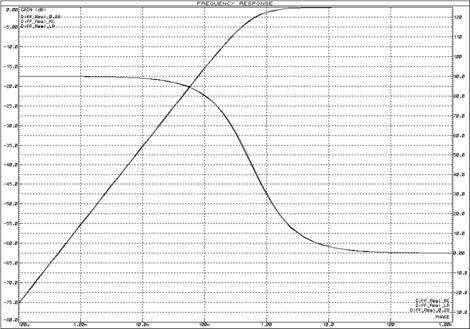
Рисунок 47 – ЛАЧХ и ЛФЧХ схем реализации дифференцирующего звена
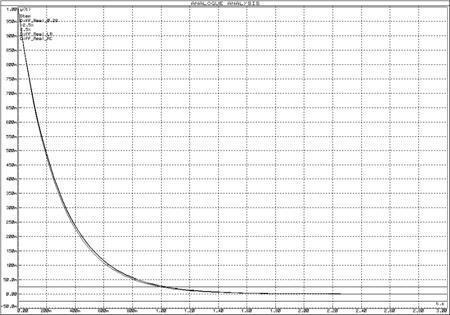
Рисунок 48 – Переходная функция схемы реального дифференцирующего звена
4. Исследование интегрирующих звеньев
a. Исследование частотных характеристик идеального интегрирующего звена
Для исследования частотных характеристик идеального интегрирующего звена в прикладном пакете Proteus\ISIS составляем структурную схему, представленную на рисунке 49. Логарифмические частотные характеристики идеального интегрирующего звена представлены на рисунке 50, график переходной функции – на рисунке 51.
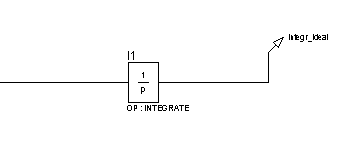
Рисунок 49 – Структурная схема для исследования идеального интегрирующего звена
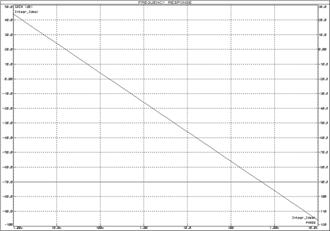
Рисунок 50 – Логарифмические частотные характеристики идеального интегрирующего звена
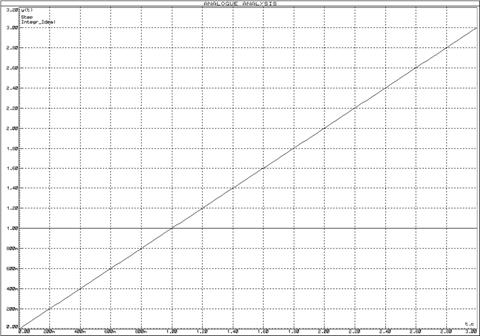
Рисунок 51 – Переходная функция идеального интегрирующего звена
b. Реализация идеального интегрирующего звена
Реализуем идеальное интегрирующее звено схемой, изображенной на рисунке 52. ЛАЧХ и ЛФЧХ интегрирующего звена представлены на рисунках 53 и 54, переходная функция – на рисунке 55.
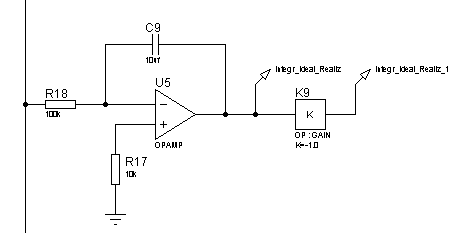
Рисунок 52 – Электрическая принципиальная схема интегрирующего звена
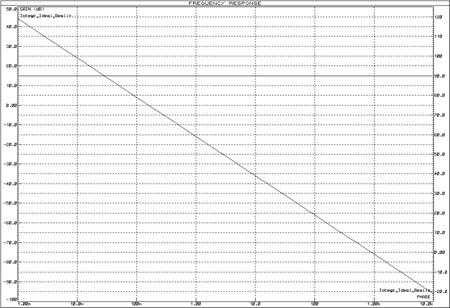
Рисунок 53 – ЛАЧХ и ЛФЧХ интегрирующего звена
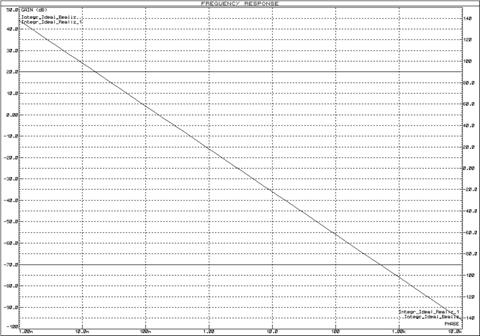
Рисунок 54 – ЛАЧХ и ЛФЧХ интегрирующего звена с инвертором
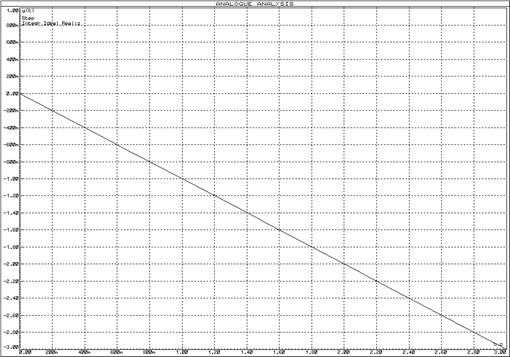
Рисунок 55 – Переходная функция схемы реализации идеального интегрирующего звена
c. Исследование частотных характеристик реального интегрирующего звена
Для исследования частотных характеристик реального интегрирующего звена в прикладном пакете Proteus\ISIS составляем структурную схему, представленную на рисунке 56. Логарифмические частотные характеристики реального интегрирующего звена представлены на рисунке 57, переходные функции – на рисунке 58.
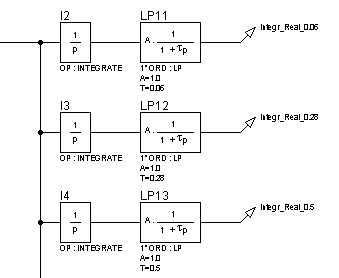
Рисунок 56 – Структурная схема для исследования реального интегрирующего звена
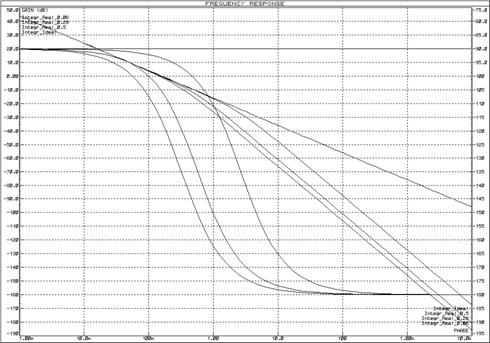
Рисунок 57 – Логарифмические частотные характеристики реального интегрирующего звена
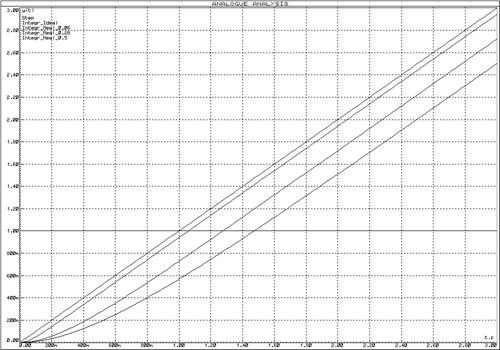
Рисунок 58 – Переходные функции реального интегрирующего звена
При анализе частотных и переходных характеристик реального интегрирующего звена и его реализации можно сделать следующие выводы:
5. Исследование изодромного звена
Изодромное звено можно условно представить в виде совокупности двух звеньев, действующих параллельно, - идеального интегрирующего и безынерционного. Поэтому данное звено совмещает полезные качества обоих звеньев и часто используется в качестве регулирующего устройства ПИ-регулятора (пропорционально-интегрального регулятора).
a. Исследование частотных характеристик изодромного звена
Для исследования частотных характеристик изодромного звена в прикладном пакете Proteus\ISIS составляем структурную схему, представленную на рисунке 59. Логарифмические частотные характеристики изодромного звена представлены на рисунке 60.
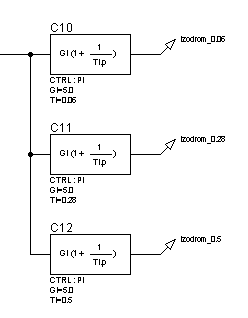
Рисунок 59 – Структурная схема для исследования изодромного звена
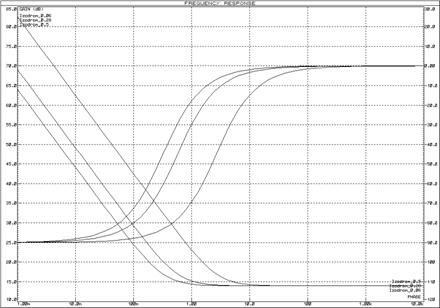
Рисунок 60 – Логарифмические частотные характеристики изодромного звена
b. Реализация изодромного звена
Реализуем изодромное звено схемой, изображенной на рисунке 61. ЛАЧХ и ЛФЧХ интегрирующего звена представлены на рисунках 62 и 63, переходная функция – на рисунке 64.
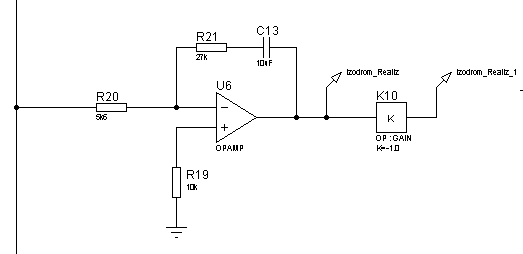
Рисунок 61 – Электрическая принципиальная схема изодромного звена
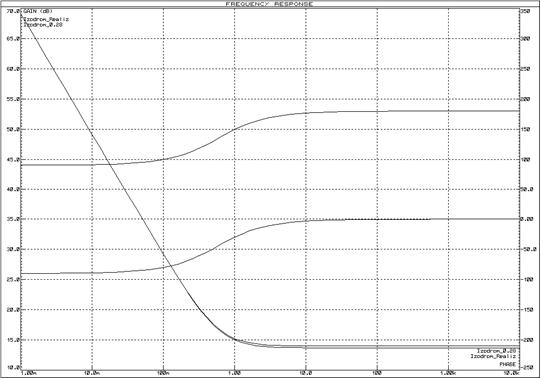
Рисунок 62 – ЛАЧХ и ЛФЧХ изодромного звена
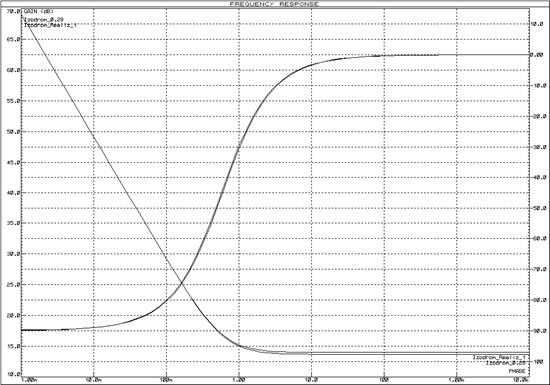
Рисунок 63 – ЛАЧХ и ЛФЧХ изодромного звена с инвертором
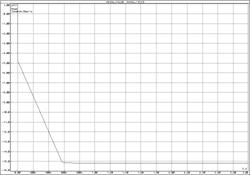
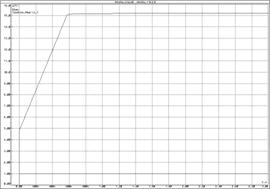
а) б)
а) без инвертора;
б) с инвертором
Рисунок 64 – Переходная функция изодромного звена
6. Исследование звена запаздывания
Для исследования частотных характеристик звена запаздывания в прикладном пакете Proteus\ISIS составляем структурную схему, представленную на рисунке 65. Логарифмические частотные характеристики изодромного звена представлены на рисунке 66, переходные характеристики – на рисунке 67.
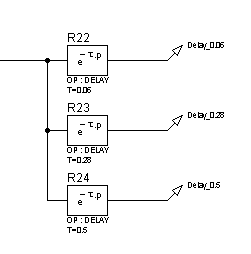
Рисунок 65 – Структурная схема для исследования звена запаздывания
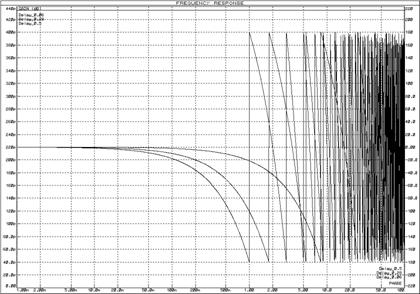
Рисунок 66 – Логарифмические частотные характеристики звена запаздывания
Рисунок 67 – Переходные функции звена запаздывания
© 2010 Интернет База Рефератов