
Рефераты по сексологии
Рефераты по информатике программированию
Рефераты по биологии
Рефераты по экономике
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Рефераты по авиации и космонавтике
Рефераты по административному праву
Рефераты по безопасности жизнедеятельности
Рефераты по арбитражному процессу
Рефераты по архитектуре
Рефераты по астрономии
Рефераты по банковскому делу
Рефераты по биржевому делу
Рефераты по ботанике и сельскому хозяйству
Рефераты по бухгалтерскому учету и аудиту
Рефераты по валютным отношениям
Рефераты по ветеринарии
Рефераты для военной кафедры
Рефераты по географии
Рефераты по геодезии
Рефераты по геологии
Рефераты по геополитике
Рефераты по государству и праву
Рефераты по гражданскому праву и процессу
Рефераты по делопроизводству
Рефераты по кредитованию
Рефераты по естествознанию
Рефераты по истории техники
Рефераты по журналистике
Рефераты по зоологии
Рефераты по инвестициям
Рефераты по информатике
Исторические личности
Рефераты по кибернетике
Рефераты по коммуникации и связи
Контрольная работа: Программа имитационного моделирования работы банка
Контрольная работа: Программа имитационного моделирования работы банка
Программа имитационного моделирования работы банка
Содержание
6. ПРИЛОЖЕНИЕ А – «Блок-схема имитационного моделирования работы банка»_ 9
1. Постановка задачи
В современном мире гарантией эффективной работы любого предприятия служит рациональное использование денежных средств и трудового фактора. Так для расчета экономического эффекта работы банка необходимо провести имитационное моделирование на основании предварительно установленных зависимостей.
Допустим, что клиенты в банк прибывают с интервалом, исчисляемым в минутах (см. рис. 1).
|
|
|
|
|
|

Рис. 1 – «Приход клиентов в банк»
Приход клиентов в банк описывается пуассоновским потоком с интенсивностью r, который определяется следующим образом:
![]()
![]() (1.1)
(1.1)
где: r – интенсивность потока;
k – время между приходами клиентов.
Параметр k может принимать дискретные значения от нуля до бесконечности. Причем k=0 означает приход сразу двух клиентов.
Предположим, в банке
имеется N касс. Математическое ожидание обслуживания клиентов в банке обозначим
![]() . Обслуживание клиентов у
касс происходит по экспоненциальному закону распределения случайной величины
. Обслуживание клиентов у
касс происходит по экспоненциальному закону распределения случайной величины ![]() (
(![]() - время обслуживания клиентов) с плотностью
распределения
- время обслуживания клиентов) с плотностью
распределения ![]() :
:
![]()
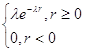 (1.2)
(1.2)
Примечание:
Если в банке есть свободные кассы, то клиент становится на обслуживание к ближайшей из них (т.е. к кассе с минимальным номером). Если все кассы заняты – клиент становится в очередь к той кассе, где очередь минимальна. Если очереди одинаковы, то клиент становится в любую из них.
Для решения поставленной задачи необходимо разработать алгоритм имитационного моделирования работы банка за восьмичасовой рабочий день. А также определить время простоя касс и количество клиентов в очереди не обслуженных на момент закрытия банка.
2. Метод решения задачи
Имитационное моделирование на ЭВМ процесса функционирования автоматизированной системы управления работой банка позволяет получить численное решение поставленной задачи. Суть рассматриваемого приближенного метода решения состоит в проведении ряда случайных испытаний вероятностной модели исследуемой системы и получении совокупности реализаций случайных процессов изменения состояния.
В результате многократной реализации случайных процессов определяются оценки вероятности тех или иных событий и средние значения случайных величин. Имитационное моделирование связано с необходимостью воспроизведения случайных событий и величин, распределенных по произвольному закону. Существует несколько способов генерации случайных величин и формирования их распределений. Модель системы управления работой банка включает в себя:
·
Приход клиентов в
банк ![]() ;
;
·
Время
обслуживания клиентов у касс ![]() .
.
По условию поставленной задачи приход клиентов в банк описывается пуассоновским потоком с интенсивностью r. Для лучшего понимания сути распределения Пуассона необходимо знать основные определения:
Интенсивность потока среднее число событий, которое появляется в единицу времени.
Поток последовательность событий, которые наступают в случайные моменты времени.
Закон распределения Пуассона выражается формулой (1.1).
Будем моделировать интервал времени между двумя последовательно зашедшими в банк клиентами методом Монте-Карло с датчиком случайных чисел на интервале [0 - 1].
Совокупность ![]() независимых случайных событий,
образующих полную группу, характеризуется вероятностями появления каждого из
событий
независимых случайных событий,
образующих полную группу, характеризуется вероятностями появления каждого из
событий ![]() , причем
, причем ![]() . Для моделирования этой
совокупности случайных событий используется генератор случайных чисел,
равномерно распределенных в интервале [0 - 1]. При делении отрезка [0 - 1] на n
частей, численно равных
. Для моделирования этой
совокупности случайных событий используется генератор случайных чисел,
равномерно распределенных в интервале [0 - 1]. При делении отрезка [0 - 1] на n
частей, численно равных ![]() ,
возникновение события
,
возникновение события ![]() устанавливается
путем определения нахождения случайного числа Х в пределах интервала при
проверке условия
устанавливается
путем определения нахождения случайного числа Х в пределах интервала при
проверке условия ![]() , где
, где ![]() изменяется от нуля до n. При
изменяется от нуля до n. При ![]() имеем
имеем ![]() ; при
; при ![]() имеем
имеем ![]() и так далее. При подстановке
и так далее. При подстановке ![]() в формулу (1.1) получим:
в формулу (1.1) получим:
![]()
![]() ;
;
![]()
![]() ;
;
![]()
![]() и так далее.
и так далее.
Причем ![]() (мин.) – максимальное количество ожидания
клиентов.
(мин.) – максимальное количество ожидания
клиентов.
Так как опыт проводится многократно, то, очевидно, что частота попадания случайных чисел на каждый из отрезков, определяющихся их длиной, и соответствует полученным вероятностям.
Моделирование времени обслуживания клиентов у касс происходит по экспоненциальному закону распределения, формула которого представлена выше (формула (1.2)).
Время обслуживания
клиентов ![]() , как и любая иная
случайная величина, описывается функцией распределения
, как и любая иная
случайная величина, описывается функцией распределения ![]() , определяемая как вероятность
, определяемая как вероятность ![]() случайного события, заключающегося в том,
что время обслуживания клиентов
случайного события, заключающегося в том,
что время обслуживания клиентов ![]() меньше некоторого заданного времени
меньше некоторого заданного времени ![]() :
:
![]()
Эта вероятность
рассматривается как функция ![]() во
всем диапазоне возможных значений величины
во
всем диапазоне возможных значений величины ![]() . Функция распределения любой случайной величины
является неубывающей функцией времени
. Функция распределения любой случайной величины
является неубывающей функцией времени ![]() . Примерный вид функции
. Примерный вид функции ![]() дан на рисунке 3.
дан на рисунке 3.
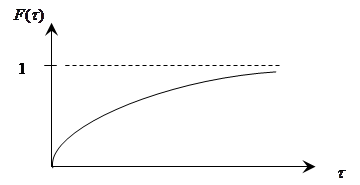 |
Рис. 3 – «Функция распределения экспоненциального закона»
Так как значения ![]() не могут быть отрицательными, то
не могут быть отрицательными, то
![]() . При
. При ![]()
![]() величина
величина ![]() стремится к единице. Таким образом, функция
распределения времени обслуживания клиентов:
стремится к единице. Таким образом, функция
распределения времени обслуживания клиентов:
![]() (1.3)
(1.3)
где ![]() - параметр распределения (среднее время
обслуживания клиентов у кассы).
- параметр распределения (среднее время
обслуживания клиентов у кассы).
Соответственно плотность распределения:
![]() (1.4)
(1.4)
Для моделирования времени
обслуживания клиента у кассы проинтегрируем функцию распределения ![]() :
:
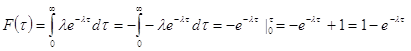
![]() (1.5)
(1.5)
От датчика случайных
чисел равномерно распределенных на интервале [0 - 1] получаем очередное число
Х, которое подставляем в формулу (1.5) и вычисляем ![]() :
:
![]()
![]() (1.6)
(1.6)
Из соотношения (1.6)
найдем ![]() соответствующее Х,
которое будем принимать за случайное число, обозначающее время обслуживания
данной кассой.
соответствующее Х,
которое будем принимать за случайное число, обозначающее время обслуживания
данной кассой.
3. ПРОГРАММНОЕ РЕШЕНИЕ
Программа имитационного моделирования работы банка написана на языке C с помощью среды разработки Borland C++ 3.1.
Исходный текст программы состоит из следующих файлов:
– main.c – содержит реализацию основных функций программы:
void ZovnVydProg (void) перерисовка интерфейса программы;
void InZminnyh (void) очистка переменных;
void Zapusk (void) прием входных данных и их обработка.
Данный файл содержит так же описание используемых глобальных переменных.
– main.h – файл содержит прототипы основных функций, реализованных в файле main.c, а так же прототипы функций вычисления, реализованных в файле engine.c;
– engine.c – файл содержит реализацию функций вычисления:
ZVIT* Obchyslennya (void) функция, содержащая основной цикл вычисления;
void KorChasuObsl (void) коррекция времени обслуживания каждого клиента;
int TObsl(void) моделирование времени обслуживания для очередного клиента;
int MinCherga (void) определение номера кассы с минимальной очередью;
void DobKlUChergy (void) постановка клиента в очередь, либо к свободной кассы;
int Ksi(void) – моделирование времени прихода очередного клиента;
4. Инструкция пользователю
1. Программа имитационного моделирования работы банка расположена по следующему адресу:
С:\П – 00 – 51\К&F\Bank.exe
2. На запрос программы:
« Введите количество касс : »
Вводим предполагаемое (данное) количество касс обслуживающих клиентов.
3. На запрос программы:
« Введите интенсивность потока r: »
Вводим r - интенсивность потока, равную среднему числу событий, которые появляются в единицу времени.
4. На запрос программы:
« Введите параметр распределения lambda: »
Вводим ![]() равное
среднему времени обслуживания клиентов у кассы.
равное
среднему времени обслуживания клиентов у кассы.
5. На запрос программы:
« Введите максимальное время ожидания клиента: »
Вводим k равное максимальному времени в минутах ожидания клиентов.
5. РУКОВОДСТВО ПРОГРАММИСТА
Несмотря на то, что программа предназначена для создания имитационной модели работы банка, она также может использоваться для других целей, к примеру, для моделирования работы магазина. Вследствие этого может возникнуть необходимость в модернизации или изменении программы.
– Для изменения продолжительности рабочего дня необходимо изменить значение константы WORK_TIME, описанную в файле engine.c;
– Для изменения закона распределения, использующегося для моделирования времени прихода следующего клиента необходимо изменить содержимое функции int Ksi(void), подставив в тело реализацию необходимого распределения;
– Для изменения закона распределения, использующегося для моделирования времени обслуживания клиента кассиром необходимо изменить содержимое функции int TObsl(void), подставив в тело реализацию необходимого распределения;
– В случае возникновения необходимости ввода времени работы банка пользователем при каждом запуске программы необходимо сделать следующие изменения:
1. Добавить название соответствующего поля ввода к массиву названия полей *ZagolPol[];
2. Добавить окно поля ввода в функцию void ZovnVydProg(void);
3. Увеличить верхнюю границу счетчика в цикле перерисовки названий полей функции void ZovnVydProg (void);
4. Добавить соответствующий обработчик в функцию void Zapusk(void);
5. В файле engine.c изменить строку #define WORK_TIME 8*60 строкой #define WORK_TIME timevar, где timevar – имя переменной, содержащей введенное пользователем время работы банка;
– В случае возникновения необходимости получения более детальной информации о работе банка необходимо добавить соответствующие переменные в структуру ZVIT и обеспечить заполнение этих переменных значениями в соответствующих функциях.
6.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|


|
|

![]()
![]()
![]()
|
|
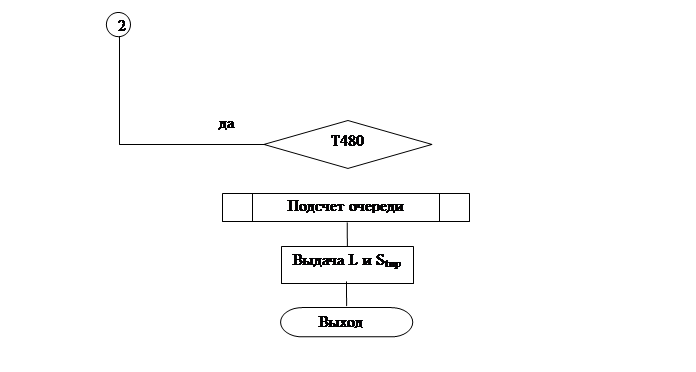
Процедура постановки клиента в очередь
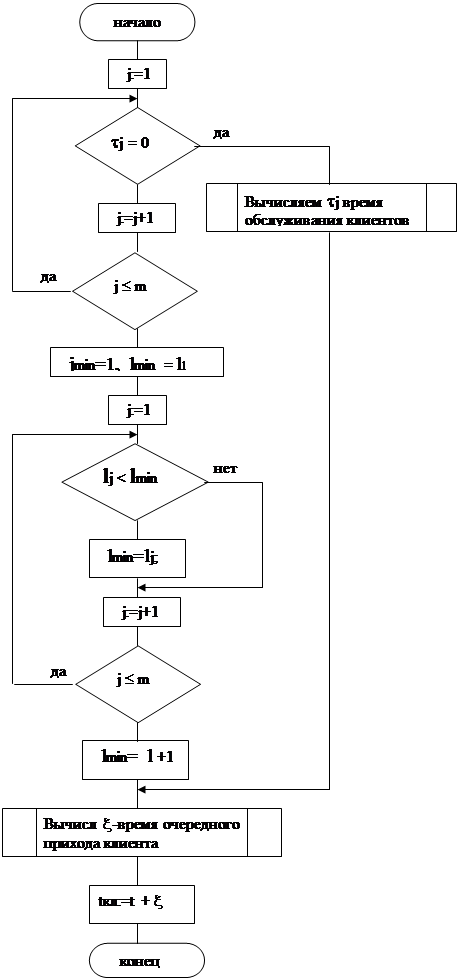
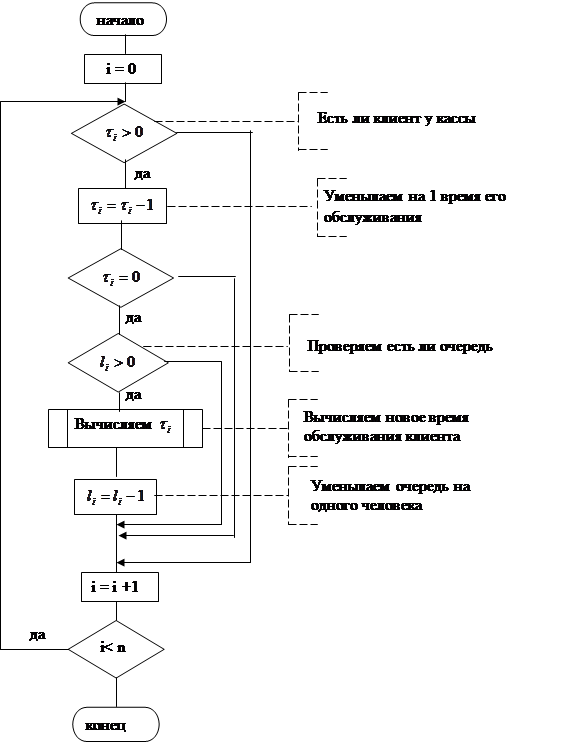
Блок схема
корректировки времени обслуживания клиентов у касс и продвижения очереди.
© 2010 Интернет База Рефератов