
Рефераты по сексологии
Рефераты по информатике программированию
Рефераты по биологии
Рефераты по экономике
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Рефераты по авиации и космонавтике
Рефераты по административному праву
Рефераты по безопасности жизнедеятельности
Рефераты по арбитражному процессу
Рефераты по архитектуре
Рефераты по астрономии
Рефераты по банковскому делу
Рефераты по биржевому делу
Рефераты по ботанике и сельскому хозяйству
Рефераты по бухгалтерскому учету и аудиту
Рефераты по валютным отношениям
Рефераты по ветеринарии
Рефераты для военной кафедры
Рефераты по географии
Рефераты по геодезии
Рефераты по геологии
Рефераты по геополитике
Рефераты по государству и праву
Рефераты по гражданскому праву и процессу
Рефераты по делопроизводству
Рефераты по кредитованию
Рефераты по естествознанию
Рефераты по истории техники
Рефераты по журналистике
Рефераты по зоологии
Рефераты по инвестициям
Рефераты по информатике
Исторические личности
Рефераты по кибернетике
Рефераты по коммуникации и связи
Контрольная работа: Вычисление наибольшей прибыли предприятия
Контрольная работа: Вычисление наибольшей прибыли предприятия
Содержание
Задача 1. 2
Задача 2. 4
Задача 3. 6
Пусть х (млн. шт.) объем производства, С(х)=2х3-7х и D(x)=2х2+9х+15 соответственно функция издержек и доход некоторой фирмы. При каком значении х фирма получит наибольшую прибыль π(х)? какова эта прибыль?
Решение
Прибыль фирмы является разницей между доходом и издержками фирмы:
![]() ,
,
![]() ,
,
![]() .
.
Найдем наибольшее
значение прибыли путем нахождения максимума функции ![]() .
.
![]()
![]()
![]() - не
удовлетворяет условию задачи,
- не
удовлетворяет условию задачи,
![]() .
.
График функции прибыли представлен на рисунке 1.
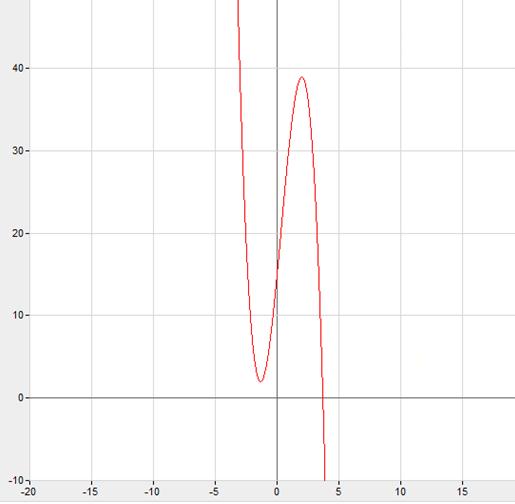
Рисунок 1 - График
функции прибыли ![]()
Как видно из рисунка 1,
функция прибыли ![]() в точке х=2 достигает
максимального значения. Следовательно, фирма получает наибольшую прибыль при
объеме производства 2 млн. шт. и эта прибыль составляет:
в точке х=2 достигает
максимального значения. Следовательно, фирма получает наибольшую прибыль при
объеме производства 2 млн. шт. и эта прибыль составляет:
![]() млн.
у.е.
млн.
у.е.
Ответ: наибольшую прибыль фирма получит при объеме производства 2 млн. шт. и эта прибыль составит 39 млн. у.е.
Заданы: функция прибыли
![]() , где х1 и х2
объемы некоторых ресурсов; цены р1=1 и р2=1 за единицу
каждого ресурса соответственно (в некоторых у.е.); бюджетное ограничение I=150
на затраты по приобретению указанных ресурсов (в тех же у.е.). При каких
значениях объемов используемых ресурсов фирма–производитель получит наибольшую
прибыль?
, где х1 и х2
объемы некоторых ресурсов; цены р1=1 и р2=1 за единицу
каждого ресурса соответственно (в некоторых у.е.); бюджетное ограничение I=150
на затраты по приобретению указанных ресурсов (в тех же у.е.). При каких
значениях объемов используемых ресурсов фирма–производитель получит наибольшую
прибыль?
Решение
Задача сводится к
поиску максимума функции ![]() при
существовании ограничения
при
существовании ограничения ![]() :
:
![]()
при ![]() .
.
![]() ,
,
![]() .
.
Найдем максимум функции графически.
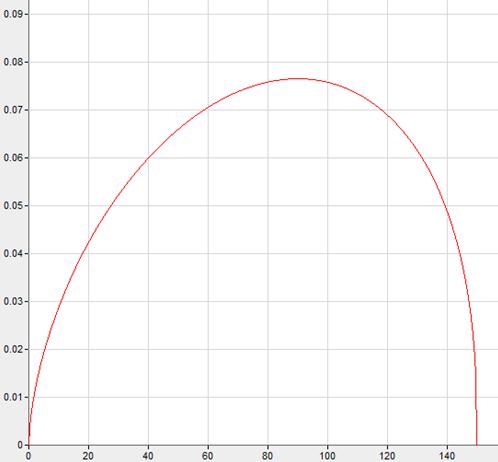
Рисунок 2 – График
функции ![]()
Как видно, функция достигает максимального значения при х1=90.
![]() ,
,
![]() .
.
Ответ: фирма–производитель получит наибольшую прибыль при объемах ресурсов х1=90 и х2=60.
Задана парная выборка из 10 пар значений случайных велbчин X и Y (таблица 1).
Таблица 1 – Исходные данные
| х | у | |
| 1 | 5 | 70 |
| 2 | 11 | 65 |
| 3 | 15 | 55 |
| 4 | 17 | 60 |
| 5 | 2 | 50 |
| 6 | 22 | 35 |
| 7 | 25 | 40 |
| 8 | 27 | 30 |
| 9 | 30 | 25 |
| 10 | 35 | 32 |
1) Изобразите корреляционное поле случайных величин X и Y.
2) Вычислите основные числовые характеристики случайных величин X и Y: их математические ожидания и дисперсии, средние квадратические отклонения и размах вариации.
3) Найдите их совместные числовые характеристики: ковариацию, коэффициент корреляции.
4) С помощью найденных характеристик составьте уравнение линейной регрессии Y на X.
5) Составьте уравнение линейной регрессии X на Y.
6) Нанесите найденные уравнения на корреляционное поле; найдите точку пересечения полученных линий регрессии.
7) Вычислите стандартные ошибки коэффициентов регрессии b0 и b1.
8) Проверьте гипотезы о статистической значимости коэффициентов регрессии b0 и b1.
9) Вычислите с надежностью 0,95 интервальные оценки коэффициентов b0 и b1 регрессии Y на X.
10) Найдите коэффициент детерминации R2 и поясните смысл полученного результата.
Решение.
1) Корреляционное поле случайных величин X и Y
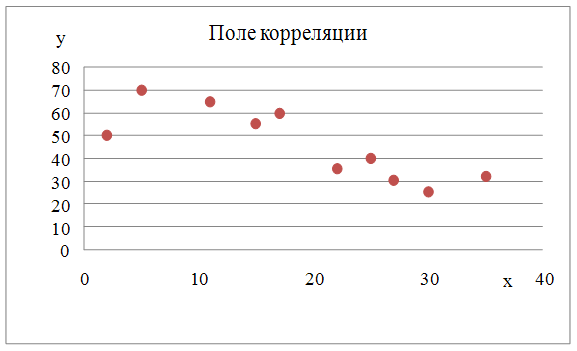
2) Основные числовые характеристики случайных величин X и Y: их математические ожидания и дисперсии, средние квадратические отклонения и размах вариации
Таблица 2 Вспомогательные расчеты
| х | у |
х2 |
y2 |
xy | |
| 1 | 5 | 70 | 25 | 4900 | 350 |
| 2 | 11 | 65 | 121 | 4225 | 715 |
| 3 | 15 | 55 | 225 | 3025 | 825 |
| 4 | 17 | 60 | 289 | 3600 | 1020 |
| 5 | 2 | 50 | 4 | 2500 | 100 |
| 6 | 22 | 35 | 484 | 1225 | 770 |
| 7 | 25 | 40 | 625 | 1600 | 1000 |
| 8 | 27 | 30 | 729 | 900 | 810 |
| 9 | 30 | 25 | 900 | 625 | 750 |
| 10 | 35 | 32 | 1225 | 1024 | 1120 |
| сумма | 189 | 462 | 4627 | 23624 | 7460 |
| средн | 18,9 | 46,2 | 462,7 | 2362,4 | 746 |
Математическое ожидание:
![]() ,
,
![]() .
.
Дисперсия:
![]() ,
,
![]() .
.
Среднеквадратическое отклонение:
![]() ,
,
![]() .
.
Размах вариации:
![]() ,
,
![]() .
.
3) Совместные числовые характеристики: ковариацию, коэффициент корреляции
Ковариация:
![]() .
.
Коэффициент корреляции:
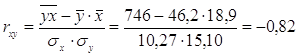 .
.
4) Уравнение линейной регрессии Y на X
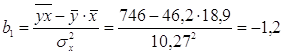 ,
,
![]() ,
,
![]() .
.
5) Уравнение линейной регрессии X на Y
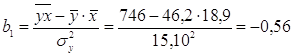 ,
,
![]() ,
,
![]() .
.
6) Нанесите найденные уравнения на корреляционное поле; найдите точку пересечения полученных линий регрессии
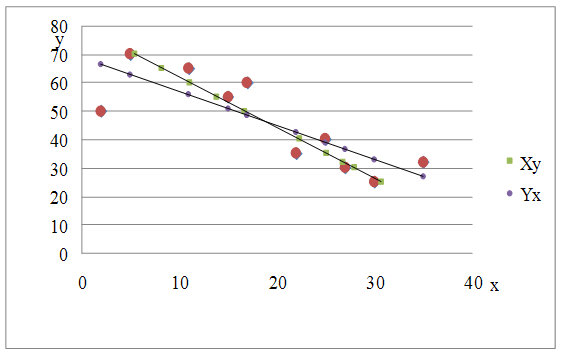
Точка пересечения (18,4;46,9).
7) Стандартные ошибки коэффициентов регрессии b0 и b1
Таблица 3 Вспомогательные расчеты
| х | у | x' | y' |
x-xcp |
y-ycp |
(x-xcp)2 |
(y-ycp)2 |
|
| 1 | 5 | 70 | 5,572 | 62,975 | -13,028 | 16,775 | 169,7288 | 281,4006 |
| 2 | 11 | 65 | 8,3645 | 55,745 | -10,2355 | 9,545 | 104,7655 | 91,10702 |
| 3 | 15 | 55 | 13,9495 | 50,925 | -4,6505 | 4,725 | 21,62715 | 22,32562 |
| 4 | 17 | 60 | 11,157 | 48,515 | -7,443 | 2,315 | 55,39825 | 5,359225 |
| 5 | 2 | 50 | 16,742 | 66,59 | -1,858 | 20,39 | 3,452164 | 415,7521 |
| 6 | 22 | 35 | 25,1195 | 42,49 | 6,5195 | -3,71 | 42,50388 | 13,7641 |
| 7 | 25 | 40 | 22,327 | 38,875 | 3,727 | -7,325 | 13,89053 | 53,65563 |
| 8 | 27 | 30 | 27,912 | 36,465 | 9,312 | -9,735 | 86,71334 | 94,77023 |
| 9 | 30 | 25 | 30,7045 | 32,85 | 12,1045 | -13,35 | 146,5189 | 178,2225 |
| 10 | 35 | 32 | 26,795 | 26,825 | 8,195 | -19,375 | 67,15803 | 375,3906 |
| сумма | 189 | 462 | 188,643 | 462,255 | 2,643 | 0,255 | 711,7565 | 1531,748 |
| средн | 18,9 | 46,2 | 18,8643 | 46,2255 | 0,2643 | 0,0255 | 71,17565 | 153,1748 |
Для линии регрессии Y на X:
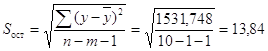 ,
,
![]() ,
,
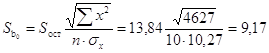 .
.
Для линии регрессии X на Y:
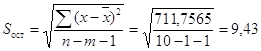 ,
,
![]() ,
,
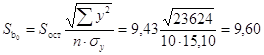 .
.
8) Проверка гипотезы о статистической значимости коэффициентов регрессии b0 и b1
Для α=0,05 и k=n-1-1=8 значение критерия Стьюдента t=2,31
Для линии регрессии Y на X:
![]() , коэффициент
значим,
, коэффициент
значим,
![]() , коэффициент
значим.
, коэффициент
значим.
Для линии регрессии X на Y:
![]() , коэффициент
значим,
, коэффициент
значим,
![]() , коэффициент
значим.
, коэффициент
значим.
9) Вычисляем с надежностью 0,95 интервальные оценки коэффициентов b0 и b1 регрессии Y на X
Доверительный интервал для b0:
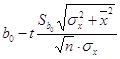 <a0<
<a0<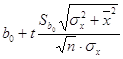 ,
,
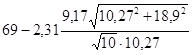 <a0<
<a0<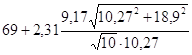 ,
,
54,97<a0<83,03.
Доверительный интервал для b1:
![]() <a1<
<a1<![]() ,
,
![]() <a1<
<a1<![]() ,
,
-1,23<a1<-1,17.
10) Коэффициент детерминации R2 :
![]() .
.
Коэффициент детерминации R2=0,6724 показывает, что вариация параметра Y на 67,24% объясняется фактором Х. Доля влияния неучтенных факторов – 32,76%.
© 2010 Интернет База Рефератов