Курсовая работа: Лисп-реализация алгоритма кодирования информации RSA

Содержание

Введение

1. Постановка задачи

2. Математические и алгоритмические основы решения задачи

3. Функциональные модели и блок-схемы решения задачи

4. Программная реализация решения задачи

5. Пример выполнения программы

Заключение

Список использованных источников и литературы

Введение

Испокон веков не было ценности большей, чем информация. ХХ век – век информатики и информатизации. Технология дает возможность передавать и хранить все большие объемы информации. Это благо имеет и оборотную сторону. Информация становится все более уязвимой по разным причинам:

возрастающие объемы хранимых и передаваемых данных;

• расширение круга пользователей, имеющих доступ к ресурсам ЭВМ, программам и данным;

• усложнение режимов эксплуатации вычислительных систем.

Поэтому все большую важность приобретает проблема защиты информации от несанкционированного доступа (НСД) при передаче и хранении. Сущность этой проблемы – постоянная борьба специалистов по защите информации со своими «оппонентами».

Для того чтобы ваша информация, пройдя шифрование, превратилась в «информационный мусор», бессмысленный набор символов для постороннего, используются специально разработанные методы – алгоритмы шифрования. Такие алгоритмы разрабатываются учеными математиками или целыми коллективами сотрудников компаний или научных центров.

Алгоритмы шифрования делятся на два больших класса: симметричные (AES, ГОСТ, Blowfish, CAST, DES) и асимметричные (RSA, El-Gamal). Симметричные алгоритмы шифрования используют один и тот же ключ для зашифровывания информации и для ее расшифровывания, а асимметричные алгоритмы используют два ключа – один для зашифровывания, другой для расшифровывания.

Если зашифрованную информацию необходимо передавать в другое место, то в этом надо передавать и ключ для расшифрования. Слабое место здесь это канал передачи данных – если он не защищенный или его прослушивают, то ключ для расшифрования может попасть к злоумышленику. Системы на ассиметричных алгоритмах лишены этого недостатка. Поскольку каждый участник такой системы обладает парой ключей: Открытым и Секретным Ключом.

Алгоритм RSA стоит у истоков асимметричной криптографии. Он был предложен тремя исследователями – математиками Рональдом Ривестом (R. Rivest), Ади Шамиром (A. Shamir) и Леонардом Адльманом (L. Adleman) в 1977–78 годах.

1. Постановка задачи

Разработать и отладить программу на языке Лисп реализующую криптографический алгоритм кодирования информации с открытым ключом – RSA.

Шифрование:

Входные данные: M сообщение, состоящее из целых чисел.

Выходные данные: T Зашифрованное сообщение.

Дешифрование:

Входные данные: T Результат шифрования.

Выходные данные: M изначальное сообщение.

Пример 1.

1. Выбираем два простых числа: p = 3557, q = 2579.

2. Вычисляем их произведение: n = p · q = 3557 · 2579 = 9173503.

3. Вычисляем функцию Эйлера: φ(n) = (p-1) (q-1) = 9167368.

4. Выбираем открытый показатель: e = 3.

5. Вычисляем секретный показатель: d = 6111579.

6. Публикуем открытый ключ: (e, n) = (3, 9173503).

7. Сохраняем секретный ключ: (d, n) = (6111579, 9173503).

8. Выбираем открытый текст: M = 127.

9. Вычисляем шифротекст: P(M) = Me mod n = 10223mod 9173503 = 116.

10.Вычислить исходное сообщение: S(C) = Cd mod n = 1166111579mod 9173503 = 1022.

Пример 2.

1. Выбираем два простых числа: p = 79, q = 71.

2. Вычисляем их произведение: n = p · q = 79 · 71 = 5609.

3. Вычисляем функцию Эйлера: φ(n) = (p-1) (q-1) = 5460.

4. Выбираем открытый показатель: e = 5363.

5. Вычисляем секретный показатель: d = 2927.

6. Публикуем открытый ключ: (e, n) = (5363, 5609).

7. Сохраняем секретный ключ: (d, n) = (2927, 5609).

8. Выбираем открытый текст: M = 23.

9. Вычисляем шифротекст: P(M) = Me mod n = 235363mod 5609 = 5348.

10.Вычислить исходное сообщение: S(C) = Cd mod n = 53482927mod 5609 = 23.

2. Математические и алгоритмические основы решения задачи

Первым этапом любого асимметричного алгоритма является создание пары ключей: открытого и закрытого и распространение открытого ключа «по всему миру». Для алгоритма RSA этап создания ключей состоит из следующих операций:

1). Выбираются два простых числа p и q

2). Вычисляется их произведение n (=p*q)

3). Выбирается произвольное число e (e<n), такое, что

НОД (e, (p-1) (q-1))=1,

то есть e должно быть взаимно простым с числом (p-1) (q-1).

4). Методом Евклида решается в целых числах уравнение

e*d+(p-1) (q-1)*y=1.

Здесь неизвестными являются переменные d и y – метод Евклида как раз и находит множество пар (d, y), каждая из которых является решением уравнения в целых числах.

5). Два числа (e, n) – публикуются как открытый ключ.

6). Число d хранится в строжайшем секрете – это и есть закрытый ключ, который позволит читать все послания, зашифрованные с помощью пары чисел (e, n).

Как же производится собственно шифрование с помощью этих чисел:

Отправитель разбивает свое сообщение на блоки, равные k=[log2(n)] бит, где квадратные скобки обозначают взятие целой части от дробного числа.

Подобный блок может быть интерпретирован как число из диапазона (0; 2k-1). Для каждого такого числа (назовем его mi) вычисляется выражение

ci=((mi)e) mod n.

Блоки ci и есть зашифрованное сообщение Их можно спокойно передавать по открытому каналу, поскольку операция возведения в степень по модулю простого числа, является необратимой математической задачей. Обратная ей задача носит название «логарифмирование в конечном поле» и является на несколько порядков более сложной задачей. То есть даже если злоумышленник знает числа e и n, то по ci прочесть исходные сообщения mi он не может никак, кроме как полным перебором mi.

А вот на приемной стороне процесс дешифрования все же возможен, и поможет нам в этом хранимое в секрете число d. Достаточно давно была доказана теорема Эйлера, частный случай которой утвержает, что если число n представимо в виде двух простых чисел p и q, то для любого x имеет место равенство

(x(p-1)(q-1)) mod n = 1.

Для дешифрования RSA-сообщений воспользуемся этой формулой. Возведем обе ее части в степень

(-y): (x(-y)(p-1)(q-1)) mod n = 1(-y) = 1.

Теперь умножим обе ее части на x:

(x(-y)(p-1)(q-1)+1) mod n = 1*x = x.

А теперь вспомним как мы создавали открытый и закрытый ключи. Мы подбирали с помощью алгоритма Евклида d такое, что

e*d+(p-1) (q-1)*y=1,

то есть

e*d=(-y) (p-1) (q-1)+1.

Следовательно, в последнем выражении предыдущего абзаца мы можем заменить показатель степени на число (e*d). Получаем

(xe*d) mod n = x.

То есть для того чтобы прочесть сообщение ci=((mi)e) mod n достаточно возвести его в степень d по модулю m:

((ci)d) mod n = ((mi)e*d) mod n = mi.

На самом деле операции возведения в степень больших чисел достаточно трудоемки для современных процессоров, даже если они производятся по оптимизированным по времени алгоритмам. Поэтому обычно весь текст сообщения кодируется обычным блочным шифром (намного более быстрым), но с использованием ключа сеанса, а вот сам ключ сеанса шифруется как раз асимметричным алгоритмом с помощью открытого ключа получателя и помещается в начало файла.

Скорость работы алгоритма RSA

Как при шифровании и расшифровке, так и при создании и проверке подписи алгоритм RSA по существу состоит из возведения в степень, которое выполняется как ряд умножений.

В практических приложениях для открытого (public) ключа обычно выбирается относительно небольшой показатель, а зачастую группы пользователей используют один и тот же открытый (public) показатель, но каждый с различным модулем. (Если открытый (public) показатель неизменен, вводятся некоторые ограничения на главные делители (факторы) модуля.) При этом шифрование данных идет быстрее чем расшифровка, а проверка подписи – быстрее чем подписание.

Если k количество битов в модуле, то в обычно используемых для RSA алгоритмах количество шагов необходимых для выполнения операции с открытым (public) ключом пропорционально второй степени k, количество шагов для операций частного (private) ключа – третьей степени k, количество шагов для операции создания ключей – четвертой степени k.

Методы «быстрого умножения» – например, методы основанные на Быстром Преобразовании Фурье (FFT Fast Fourier Transform) – выполняются меньшим количеством шагов; тем не менее они не получили широкого распространения из-за сложности программного обеспечения, а также потому, что с типичными размерами ключей они фактически работают медленнее. Однако производительность и эффективность приложений и оборудования реализующих алгоритм RSA быстро увеличиваются.

Алгоритм RSA намного медленнее чем DES и другие алгоритмы блокового шифрования. Программная реализация DES работает быстрее по крайней мере в 100 раз и от 1,000 до 10,000 в аппаратной реализации (в зависимости от конкретного устройства). Благдаря ведущимся разработкам, работа алгоритма RSA, вероятно, ускорится, но аналогично ускорится и работа алгоритмов блокового шифрования.

3. Функциональные модели и блок-схемы решения задачи

Функциональные модели и блок-схемы решения задачи представлены на рисунках 1 – 6.

Условные обозначения:

· P и Q – случайные простые числа;

· N произведение простых чисел P и Q;

· PHI – значение функции Эйлера;

· E взаимно простое число с PHI;

· PRIVATE_KEY – секретный ключ;

· LST – список простых чисел;

· NUM – число для шифрования / дешифрования;

· I, IO, I1, J, JO, R, L – рабочие переменные.

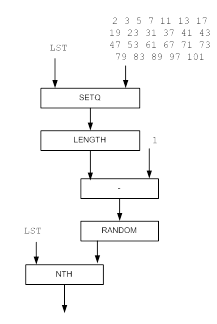
Рисунок 1 Функциональная модель решения задачи для функции SIMPLE_NUMBER

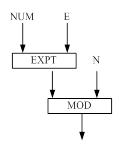
Рисунок 2 Функциональная модель решения задачи для функции ENCRYPT

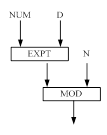
Рисунок 3 Функциональная модель решения задачи для функции DECODING

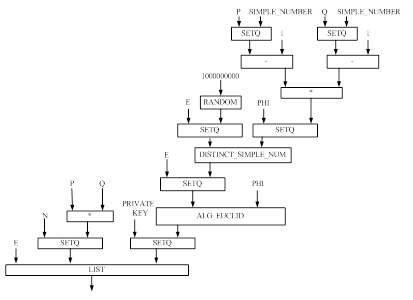
Рисунок 4 Функциональная модель решения задачи для функции RSA

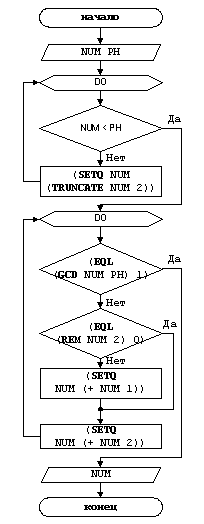
Рисунок 5 Блок-схема решения задачи для функции DISTINCT_SIMPLE_NUM

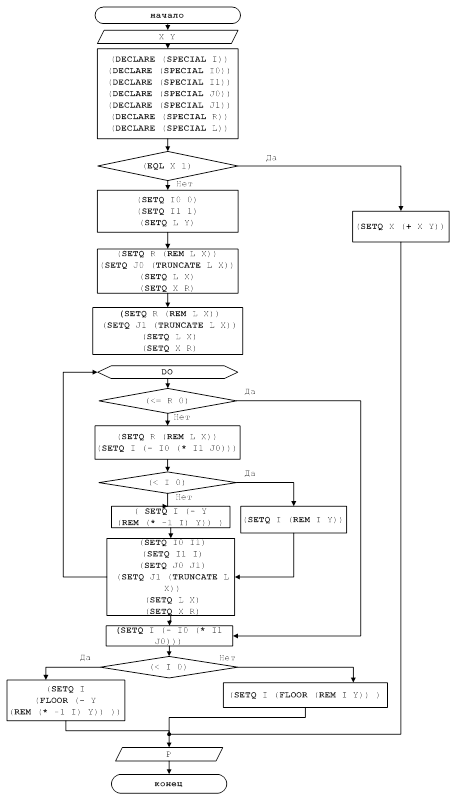
Рисунок 6 Блок-схема решения задачи для функции ALG_ EUCLID

4. Программная реализация решения задачи

; ПОИСК ВЗАИМНО ПРОСТОГО ЧИСЛА

(DEFUN DISTINCT_SIMPLE_NUM (NUM PH)

(DO

()

((< NUM PH) NUM)

; TRUNCATE – ЦЕЛОЧИСЛЕННОЕ ДЕЛЕНИЕ

(SETQ NUM (TRUNCATE NUM 2))

)

(DO

()

; GCD – НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ

((EQL (GCD NUM PH) 1) NUM)

; REM – ОСТАТОК ОТ ДЕЛЕНИЯ

(IF (EQL (REM NUM 2) 0) (SETQ NUM (+ NUM 1)))

(SETQ NUM (+ NUM 2))

)

; ГЕНЕРИРУЕМ СЛУЧАЙНОЕ ПРОСТОЕ ЧИСЛО

(DEFUN SIMPLE_NUMBER ()

; ОБЪЯВЛЕНИЕ ПЕРЕМЕННОЙ

(DECLARE (SPECIAL LST))

; СПИСОК ПРОСТЫХ ЧИСЕЛ

(SETQ LST ' (2 3 5 7 11 13 17 19 23 31 37 41 43 47 53 61 67 71 73 79 83 89 97 101))

; ВЫБИРАЕМ СЛУЧАЙНОЕ ЧИСЛО ИЗ СПСКА

(NTH (RANDOM (– (LENGTH LST) 1)) LST)

)

; РАСШИРЕННЫЙ АЛГОРИТМ ЕВКЛИДА

(DEFUN ALG_EUCLID (X Y)

; – ОБЪЯВЛЕНИЕ ПЕРЕМЕННЫХ–

(DECLARE (SPECIAL I))

(DECLARE (SPECIAL I0))

(DECLARE (SPECIAL I1))

(DECLARE (SPECIAL J0))

(DECLARE (SPECIAL J1))

(DECLARE (SPECIAL R))

(DECLARE (SPECIAL L))

;–

(IF (EQL X 1) (SETQ X (+ X Y))

; ИНАЧЕ

(PROGN

(SETQ I0 0)

(SETQ I1 1)

(SETQ L Y)

(SETQ R (REM L X))

(SETQ J0 (TRUNCATE L X))

(SETQ L X)

(SETQ X R)

(SETQ R (REM L X))

(SETQ J1 (TRUNCATE L X))

(SETQ L X)

(SETQ X R)

(DO

(())

((<= R 0) R)

(SETQ R (REM L X))

(SETQ I (– I0 (* I1 J0)))

(IF (< I 0) (SETQ I (- Y (REM (* -1 I) Y))) (SETQ I (REM I Y)))

(SETQ I0 I1)

(SETQ I1 I)

(SETQ J0 J1)

(SETQ J1 (TRUNCATE L X))

(SETQ L X)

(SETQ X R)

)

(SETQ I (– I0 (* I1 J0)))

(IF (< I 0) (SETQ I (FLOOR (- Y (REM (* -1 I) Y)))) (SETQ I (FLOOR (REM I Y))))

)

; РЕАЛИЗАЦИЯ АЛГОРИТМА RSA

(DEFUN RSA ()

; – ОБЪЯВЛЕНИЕ ПЕРЕМЕННЫХ–

(DECLARE (SPECIAL N))

(DECLARE (SPECIAL E))

(DECLARE (SPECIAL PHI))

(DECLARE (SPECIAL PRIVATE_KEY))

(DECLARE (SPECIAL P))

(DECLARE (SPECIAL Q))

;–

; ВЫБИРАЮТСЯ ДВА ПРОСТЫХ ЧИСЛА

(SETQ P (SIMPLE_NUMBER))

(SETQ Q (SIMPLE_NUMBER))

; ВЫЧИСЛЯЕМ ИХ ПРОИЗВЕДЕНИЕ

(SETQ N (* P Q))

; НАХОДИМ PHI = (P-1) (Q-1)

(SETQ PHI (* (- P 1) (- Q 1)))

; ВЫБИРАЕМ ПРОИЗВОЛЬНОЕ ЧИСЛО

(SETQ E (RANDOM 10000000000000000))

; НАХОДИМ ВЗАИМНОЕ ПРОСТОЕ E С PHI

(SETQ E (DISTINCT_SIMPLE_NUM E PHI))

; НАХОДИМ ЗАКРЫТЫЙ КЛЮЧ PRIVATE_KEY

(SETQ PRIVATE_KEY (ALG_EUCLID E PHI))

(LIST E N PRIVATE_KEY)

)

; ПОЛУЧАЕМ КЛЮЧИ

(SETQ LIST_KEY (RSA))

(SETQ E (CAR LIST_KEY))

(SETQ N (CADR LIST_KEY))

(SETQ D (CADDR LIST_KEY))

; ШИФРОВАНИЕ ЧИСЛА

(DEFUN CODING (NUM)

(MOD (EXPT NUM E) N)

)

; ДЕШИФРОВАНИЕ ЧИСЛА

(DEFUN DECODING (NUM)

(MOD (EXPT NUM D) N)

)

; ПОЛУЧАЕМ СООБЩЕНИЕ

(SETQ TEXT 0)

(SETQ INPUT (OPEN «D:\MESSAGE.TXT»:DIRECTION:INPUT))

(SETQ TEXT (READ INPUT))

(CLOSE INPUT)

; ШИФРУЕМ СООБЩЕНИЕ

(SETQ OUTPUT (OPEN «D:\CODING.TXT»:DIRECTION:OUTPUT))

(SETQ CODING_TEXT (MAPCAR 'CODING TEXT))

(PRINT (LIST 'CODING_TEXT CODING_TEXT) OUTPUT)

(PRINT (LIST 'PUBLIC_KEY (LIST E N)) OUTPUT)

(TERPRI OUTPUT)

(CLOSE OUTPUT)

; ДЕШИФРУЕМ СООБЩЕНИЕ

(SETQ OUTPUT (OPEN «D:\DECODING.TXT»:DIRECTION:OUTPUT))

(SETQ DECODING_TEXT (MAPCAR 'DECODING CODING_TEXT))

(PRINT (LIST 'DECODING_TEXT DECODING_TEXT) OUTPUT)

(TERPRI OUTPUT)

(CLOSE OUTPUT)

5. Пример выполнения программы

Пример 1

Рисунок 7. Переданное сообщение

Рисунок 8. Зашифрованное сообщение

Рисунок 9. Расшифрованное сообщение

Пример 2

Рисунок 10. Переданное сообщение

Рисунок 11. Зашифрованное сообщение

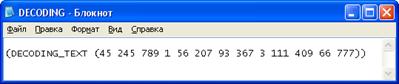
Рисунок 12. Расшифрованное сообщение

Пример 3

Рисунок 13. Переданное сообщение

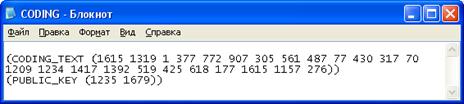
Рисунок 14. Зашифрованное сообщение

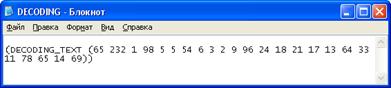
Рисунок 15. Расшифрованное сообщение

Заключение

Криптосистема RSA используется в самых различных продуктах, на различных платформах и во многих отраслях. В настоящее время криптосистема RSA встраивается во многие коммерческие продукты, число которых постоянно увеличивается. Также ее используют операционные системы Microsoft, Apple, Sun и Novell. В аппаратном исполнении RSA алгоритм применяется в защищенных телефонах, на сетевых платах Ethernet, на смарт-картах, широко используется в криптографическом оборудовании THALES (Racal). Кроме того, алгоритм входит в состав всех основных протоколов для защищенных коммуникаций Internet, в том числе S/MIME, SSL и S/WAN, а также используется во многих учреждениях, например, в правительственных службах, в большинстве корпораций, в государственных лабораториях и университетах. На осень 2000 года технологии с применением алгоритма RSA были лицензированы более чем 700 компаниями.

Итогом работы можно считать созданную функциональную модель алгоритма кодирования информации RSA. Данная модель применима к положительным целым числам.

Созданная функциональная модель и ее программная реализация могут служить органической частью решения более сложных задач.

Список использованных источников и литературы

1. Венбо Мао. Современная криптография: теория и практика. [Электронный ресурс] / Венбо Мао. – М.: Вильямс, 2005. С. 768.

2. Кландер, Л. Hacker Prof: полное руководство по безопасности компьютера. [Электронный ресурс] / Л. Кландер – М.: Попурри, 2002. С. 642.

3. Фергюсон, Н. Практическая криптография. [Текст] / Н. Фергюсон, Б. Шнайер. – М.: Диалектика, 2004. С. 432.

4. Шнайер, Б. Прикладная криптография. Протоколы, алгоритмы. [Текст] / Б. Шнайер. – М.: Триумф, 2002. С. 816