
Рефераты по сексологии
Рефераты по информатике программированию
Рефераты по биологии
Рефераты по экономике
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Рефераты по авиации и космонавтике
Рефераты по административному праву
Рефераты по безопасности жизнедеятельности
Рефераты по арбитражному процессу
Рефераты по архитектуре
Рефераты по астрономии
Рефераты по банковскому делу
Рефераты по биржевому делу
Рефераты по ботанике и сельскому хозяйству
Рефераты по бухгалтерскому учету и аудиту
Рефераты по валютным отношениям
Рефераты по ветеринарии
Рефераты для военной кафедры
Рефераты по географии
Рефераты по геодезии
Рефераты по геологии
Рефераты по геополитике
Рефераты по государству и праву
Рефераты по гражданскому праву и процессу
Рефераты по делопроизводству
Рефераты по кредитованию
Рефераты по естествознанию
Рефераты по истории техники
Рефераты по журналистике
Рефераты по зоологии
Рефераты по инвестициям
Рефераты по информатике
Исторические личности
Рефераты по кибернетике
Рефераты по коммуникации и связи
Курсовая работа: Механизм поперечно-строгального станка
Курсовая работа: Механизм поперечно-строгального станка
Кафедра «Основы проектирования машин»
Курсовая работа
Поперечно-строгальный станок
Содержание
1. Кинематический анализ рычажного механизма
1.1 Структурный анализ механизма
1.2 Определение недостающих размеров
1.3 Определение скоростей точек механизма
1.4 Определение ускорений точек механизма
1.5 Определение угловых скоростей и ускорений звеньев
1.6 Диаграммы движения выходного звена
1.7 Аналитический метод анализа рычажного механизма
2. Силовой анализ рычажного механизма
2.1 Определение сил инерции
2.2 Расчёт диады 4-5
2.3 Расчёт диады 2-3
2.4 Расчёт кривошипа
2.5 Определение уравновешивающей силы методом рычага Жуковского
2.6 Определение мощностей
2.7 Определение кинетической энергии и приведенного момента инерции механизма
2.8 Определение сил инерции
3. Геометрический расчёт прямозубой передачи. Проектирование планетарного редуктора
3.1 Геометрический расчёт прямозубой передачи
3.2 Синтез и анализ комбинированного зубчатого механизма
3.3 Построение плана скоростей и частот вращения звеньев зубчатого механизма
Список литературы
1. Кинематический анализ рычажного механизма
Исходные данные:
Ход долбяка:____________________ H=320 мм
Коэффициент производительности:_ K=1,3
Отношения длин звеньев :_________ О2О3/BO3=1,25; BC/BO3=1,8
Частота вращения кривошипа :_____ n =97 об/мин
1.1 Структурный анализ механизма
Степень подвижности механизма:
Для определения степени подвижности механизма воспользуемся формулой Чебышева.
W = 3k - 2p1 - p2
где k -число подвижных звеньев;
p1 -число одноподвижных кинематических пар;
p2 -число двухподвижных кинематических пар;
Для данного механизма: k = 5; p1 = 7; p2 = 0. Тогда
W = 3 · 5 – 2 · 7 – 0 = 1
Разложение механизма на структурные группы Ассура :
Формула строения механизма : I(0,1)®II(2,3)®II(4,5)
Вывод: механизм II класса.
1.2 Определение недостающих размеров
Угол размаха кулисы:
β = 180˚·(k-1)/(k+1) = 180˚·(1,3-1)/(1,3+1) = 23028I
Угол рабочего хода:
φpx = β +1800 = 203º
Угол холостого хода:
φxx =1800- β = 154º
O3B=160/sin11o=786.8mm
O2O3=983.5 mm
Масштабный коэффициент построения схемы:
Kl = lO1A / O1A = 0,113 / 113 = 0,001
Строим 12 планов механизма, приняв за начало отсчёта крайнее положение, соответствующее началу рабочего хода механизма.
1.3 Определение скоростей точек механизма
Определим угловую скорость ω1 кривошипа по формуле :
ω1 = (π · nкр) / 30º = (3,14 · 132) / 30º = 13,816 рад/с
Определяем скорость точки А :
VA = ω1 · lO1A = 13,816 · 0,113 = 1,561 m/c
Масштабный коэффициент для плана скоростей :
KV = VA / PVA =1,561 / 50 = 0,003 m/c·mm
Для точки А’ (внутренней пары диады) напишем систему уравнений :
VA’ = VA + VA’A
VA’ = VO2 + VA’O2
Эту систему решаем графически:
VA’ = KV · PVA = 0,003 · 50 = 1,5 m/c
Скорость точки В находим методом подобия. Для этого составляем пропорцию :
PVB / PVA’ = O2B / O2A’
PVB = (O2B / O2A’) · PVA’ = (70 / 147) · 50 = 23,8 mm
Абсолютная величина скорости точки B:
VB = KV · PVB = 0,003 · 23,8 = 0,0714 m/c
Скорость точки С определяем графически, решая систему уравнений :
![]() VC
= VB + VBC
VC
= VB + VBC
VC =VO2 + VO2B
VC = KV · PVC = 0,003 · 24 = 0,072 m/c
1.4 Определение ускорений точек механизма
Ускорение точки А :
aA = an = ω12 · lO1A = 13,8162 · 0,113 = 0,2157 m/c2
aA направлен по кривошипу к центру вращения O1
Масштабный коэффициент для плана ускорений :
KA = aA / PAA = 0,2157 / 50 = 0,004 m/c2mm
Для точки А’ напишем систему уравнений :
![]()
![]()
![]()
![]()
![]() aA
= aA + akA’A + aτA’A
aA
= aA + akA’A + aτA’A
![]()
![]()
![]()
![]() aA’ = aO2 + anA’O2 + aτA’O2
aA’ = aO2 + anA’O2 + aτA’O2
Ускорения aA’A и aA’O2 раскладываем на составляющие :
akA’A = 2VA’A · ω3 = 2 · 0,15 · 1,02 = 0,306 m/c2
anA’O2 = V2A’O2 / lA’O2 = 0,153 m/c2
aτA’A = 0 (так как движение камня по кулисе прямолинейное);
Величина
PaakA’A = akA’A / KA = 0,0306 / 0,004 = 7,7 mm
PaanA’O2 = anA’O2 / KA = 0,153 / 0,004 = 38,25 mm
Далее ускорение точки А’ находим графически:
aA’ = PAA’ · KA = 50 · 0,004 = 0,2 m/c2
Ускорение точки В находим методом подобия: PAB / PAA’ = O2B / O2A’
PAB = (O2B / O2A’) · PAA’ = (70 / 147) · 50 = 23,8 mm
Абсолютная величина ускорения точки B:
aB = PAB · KA =23,8 · 0,004 = 0,095 m/c2
Ускорение точки С определяем графически, решая систему уравнений :
![]() aC = aB + aBC +
aτB
aC = aB + aBC +
aτB
aC = aO2 + aO2C + anB
anB = V2B / lO2B = 0,07142 / 0,07 = 0,0728 m/c2
aτB = PτAB · KA = 40 · 0,004 = 0,16 m/c2
Абсолютная величина ускорения точки С равна:
aC = PAC · KA = 58 · 0,004 = 0,232 m/c2
1.5 Определение угловых скоростей и ускорений звеньев.
ω1 [C1] = ( π · nкр ) / 30º = ( 3,14 · 132 ) / 30 = 13,8 рад/с
ω3 = VA’ / lO2A’ = 1,5 / 0,147 = 10,2 рад/с
ω4 = VBC / lBC = 2,33 / 0,21 = 11,1 рад/с
ε3 = aτA’O2 / lA’O2 = 0,022 / 0,147 = 0,15 рад/с2
ε4 = aτВС / lBC = 0,16 / 0,21 = 0,76 рад/с2
| Номер звена | 1 | 2 | 3 | 4 | 5 |
| ω рад/с | 13,8 | 0 | 10,2 | 11,1 | 0 |
| ε рад/с2 | 0 | 0 | 0,15 | 0,76 | 0 |
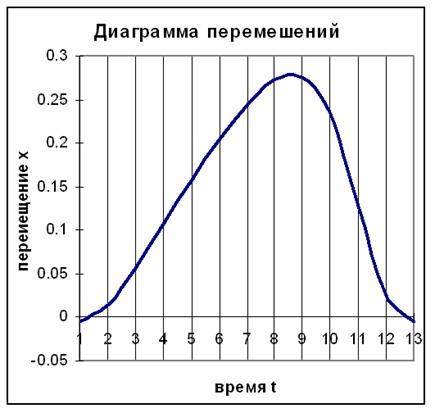
1.6 Диаграммы движения выходного звена
Диаграмму перемещения S-t строим, используя полученную из плана положений механизма траекторию движения точки С.
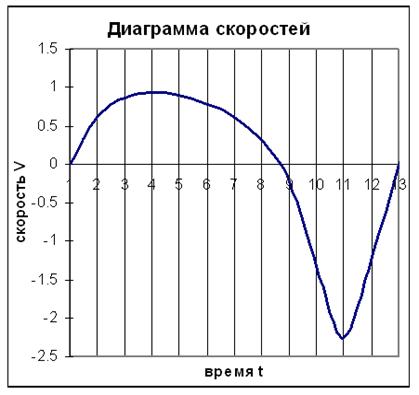
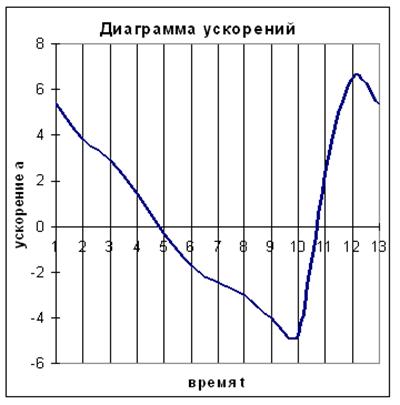
Диаграммы скоростей V-t и ускорений a-t строим методом хорд.
Масштабные коэффициенты диаграмм :
KL = 0,001 m/mm
KT = 0,005 c/mm
KV = 0,003 m/c·mm
KA = 0,004 m/c·mm2
1.7 Аналитический метод анализа рычажного механизма
Положение точки А определяется уравнениями :
ХA = r · Sin( f );
YA = e + r · cos( f ).
Угол размаха кулисы можно определить по уравнению :
f = arctg ( XA / YA ).
Скорость точки А1 , принадлежащей кривошипу 1 равна :
V = ω1 · r.
Скорость точки А3, принадлежащей кулисе 3 равна :
V = V · Cos( f – f3 ) = ω1 · r · Cos( f – f3 ).
Расстояние
AB=XA +YA=r · Sin(f) +e+2 · e · r · Cos(f)+r · Cos(f)=r+e+2 · e · r · cos( f ).
Угловая скорость кулисы :
ω = ωкр·λ·(λ+cos(f)) / (1+2λcos(f)+λ2)
Продифференцируем предыдущее уравнение по времени :
ε = ω2кр·a·r·((a2-r2)sin(f)) / (a2 + 2a·r·cos(f) + r2)2
Перемещение долбяка 5 :
X = r1 · Cos( f ) + l · Cos( arcsin((lO2B·sin (f))/lBC)).
Угол определим по формуле :
cos (f) = r/a
Скорость долбяка 5 определяется по формуле :
V = r·ωкр(sin(f) + 1/2·λ·sin2(f))
Ускорение долбяка 5:
a = r·ω2кр·(cos(f)+ λcos2(f))
Составляем программу для вычисления скоростей и ускорений долбяка 5 и для построения диаграмм скорости и ускорения долбяка 5.
Sub tron()
Dim a, e, h, r, n, w, fi, w1, alf As Double
Worksheets(1).Activate
a = Range("b2").Value
r = Range("b3").Value
n = Range("b4").Value
w1 = 3.14159265358979 * n / 30
alf = 0
h = 30 * 3.14159265358979 / 180
For n = 1 To Range("c2:c14").Count
F = Atn(r * Sin(alf) / (a + r * Cos(alf)))
fi = (180 / 3.14159265358979) * F
w = w1 * r * (r + a * Cos(alf)) / (a ^ 2 + 2 * a * r * Cos(alf) + r ^ 2)
e = w1 ^ 2 * a * r * (a ^ 2 - r ^ 2) * Sin(alf) / ((a ^ 2 + 2 * a * r * Cos(alf) + r ^ 2) ^ 2)
Range("c2:c14").Cells(n, 1) = fi
Range("c2:c14").Cells(n, 2) = w
Range("c2:c14").Cells(n, 3) = e
alfa = alf * 180 / 3.14159265358979
Range("c2:c14").Cells(n, 4) = alfa
alf = alf + h
Next n
End Sub
2. Силовой анализ рычажного механизма
2.1 Определение сил инерции
Исходные данные :
Масса кулисы 3 : m = 30 кг ;
Масса шатуна 4 : m = 10 кг ;
Масса долбяка 5 : m = 72 кг ;
Определяем веса звеньев :
G3’ = m3’ · g = 11,5 · 9,8 = 112,8519 H ;
G3” = m3” · g = 18,4845 · 9,8 = 181,104 H ;
G4 = m4 · g = 10 · 9,8 = 98 H ;
G5 = m5 · g = 72 · 9,8 = 705,6 H .
Сила полезного сопротивления : Q = 2000 H.
Вычисляем силы инерции :
U3’ = m3’ · aS3’ = 18,4845*2,56375 = 47,3896 H ;
U3” = m3“ · aS3“ = 11,5155*1,5875 = 18,28 H ;
U4 = m4 · aS4 = 10 · 2,3 = 23 H ;
U5 = m5 · aS5 = 72· 0,92= 66,24 H ;
2.2 Расчёт диады 4-5
Составляем уравнение равновесия диады:
Σ P (4 ;5) = 0 ;
R50 + Q + U5 + G5 + U4 + G4 + Rτ43 + Rn43 =0
Составим сумму моментов сил звена 4:
Σ MC ( зв.4 ) = 0
G4 · hG4 + U4 · hU4 - Rτ43 · lBC = 0;
Rτ43 = ( G4 · hG4 + U4 · hU4 ) / lBC = ( 800 · 0,052 + 14,4 · 0,131 ) / 0,21 = 57,815 (Н)
Строим план сил диады 4-5 в масштабе:
Kp = Q/Q = 2000 / 200 = 10 H/мм ;
Считаем отрезки плана сил в мм.
Q = 2000 / 10 = 200 (мм); G5 = 705,6 / 10 = 70,56 (мм); U5 = 66,24 / 10 = 6,624 (мм);
G4 = 98 / 10 =9,8 (мм); U4 = 23 / 10 = 2,3 (мм);
Из плана сил определяем реакции
R43 = R43 · Kр = 209,92 · 10 = 2099,2 Н
R50 = R50 · Kр = 104,86 · 10 = 1048,6 Н
2.3 Расчет диады 2-3
Составляем уравнение равновесия диады: Σ P (2 ;3) = 0 ;
R21 + G’3 + U’3 + G”3 + U”3 + R43 + R30 = 0
Составим сумму моментов сил звена 3:
Σ MO2 (зв.3) = 0
- R21 · lAO2 – U’3 · hU’3 + G’3 · hG’3 + G”3 · hG”3 + R34 · lO2B = 0
R21 = (– U’3 · hU’3 + G’3 · hG’3 + G”3 · hG”3 + R34 · lO2B) / lAO2 = 1403,367 (H)
Строим план сил диады 2-3, считаем отрезки плана сил:
![]()
R34 = R34 / Kp =10100 / 100 = 101 mm; U”3 = 0,32 / 100 = 0,0032 mm;
![]()
G”3 = 20 / 100 = 0,2 mm; G’3 = 50 / 100 = 0,5 mm; U’3 = 0,7 / 100 = 0,007 mm;
R21 = 4820,48 / 100 = 48,2 mm
Из плана сил определяем реакции
R30 = R30 · Kp = 104 · 100 = 684 (H)
Внутреннюю силу R23 находим из условия равновесия ползуна
Σ P(2) = 0
R23 + R21 = 0 => R23 = - R21
R23 = 1403,367 (H)
Расчет кривошипа
Составим уравнение равновесия кривошипа
![]() Σ P = 0
Σ P = 0
![]()
![]()
![]() Py + P12 + R10 = 0
Py + P12 + R10 = 0
Составим сумму моментов сил звена 1
Σ MO1(зв.1) = 0
Py = 1382,928 (H)
Строим план сил, считаем отрезки сил
2.5 Определение уравновешивающей силы методом рычага Жуковского
![]() Построим
повёрнутый на 90 градусов (в нашем случае против часовой стрелки) план
скоростей и к нему приложим все внешние силы, действующие на механизм. Составим
уравнение моментов относительно полюса :
Построим
повёрнутый на 90 градусов (в нашем случае против часовой стрелки) план
скоростей и к нему приложим все внешние силы, действующие на механизм. Составим
уравнение моментов относительно полюса :
Σ Mp = 0 ;
U3 · hU3 – U4 · hU4 – G3 · hG3 – G4 · hG4 – (Q + U5 + G5) · (h(Q + U5 + G5)) – P’y · PVa3 = 0
Отсюда P’y = 1394,788 (H)
Определяем погрешность :
S = (P’y – Py) / P’y · 100% = 0,85%
2.6 Определение мощностей
Определяем потери мощности на трение в кинематических парах.
Мощность от силы в поступательных парах :
Nп = f · R · Vотн .
N23 = f · R23 · VA’A = 4820,48 · 0,16 · 0,015 = 11,57 (Вт)
N50 = f · R50 · VC = 0,16 · 3300 · 0,072 = 38 (Вт)
Мощность привода, затрачиваемая на преодоление полезной нагрузки
NA = Q · VC = 7500 · 0,072 = 540 (Вт)
Потери на мощность во вращательных парах :
Nвр = f ‘·R · r · ωОТН
N10 = R10 · f’ · (ω1 –ω0) · r = 500 · 0,24 · 13,8 · 0,02 = 33,12 Вт
N30 = R30 · f’ · (ω3 –ω0) · r = 10400 · 0,24 · 10,2 · 0,02 = 509,2 Вт
N34 = R34 · f’ · (ω3 –ω4) · r = 10100 · 0,24 · 10,2 · 0,02 = 494,5 Вт
где f - коэффициент трения скольжения ;
f ‘= (1,2...1,5) · f - коэффициент трения скольжения приведенный ;
R - реакция в кинематической паре ;
r - радиус цапфы вала ;
Vотн и ωОТН - относительные линейная и угловая скорости звеньев, образующих пару ;
f = 0,16
f ‘ = 0,24
r = 0,02 m
Суммарная мощность :
NТР = N10 + N12 + N23 + N34 + N45 + N30 = 1086,4
Мощность привода на преодоление полезной нагрузки :
N = Q · Vв = 7500 · 0,0714 = 535,5 (Вт) .
Мгновенная потребная мощность двигателя :
N = Npy + Nтр ;
N = 540 + 1086,4 = 1626,4 (Вт)
2.7 Определение кинетической энергии и приведенного момента инерции механизма
Кинетическая энергия механизма равна сумме кинетических энергий звеньев, составляющих механизм, и рассчитывается для 3-го положения.
Тмeх = Σ Тi = Т3 + Т4 + Т5
Кинетическая энергия звена 3 рассчитывается по формуле :
Т3 = (J3 · ω3)/2 ;
J3 = J3’ + J3’’;
J3’ = (m3’ · O2A3)/3 = (5 · 0,147 )/3 = 0,245 кг·м ;
J3’’ = (m3’’ · O2B )/3 = (2 · 0,07 )/3 = 0,047 кг·м ;
J3 = 0,245 + 0,047 = 0,292 кг·м ;
Т3 = (0,292 · 10,2 )/2 = 1,5 Дж;
Кинетическая энергия звена 4 рассчитывается по формуле :
Т4 = (J4 · ω4 )/2 + (m4 · V )/2 ;
J4 = (m4 · BC )/12 = (80·0,21 )/12 = 1,4 кг·м ;
V = ω4 · BC/2 = 11,1·0,21/2 = 1,17 м/с ;
T4 = (1,4·11,1 )/2 + (80·1,17 )/2 = 54,57 Дж ;
Движение звена 5 рассматриваем как поступательное. Кинетическая энергия :
Т5 = (m5 · Vc )/2 = (140· 0,072 )/2 = 5,04 Дж ;
Тмех = Т3 + Т4 + Т5 = 1,5 + 54,57 + 5,04 = 61,11 Дж .
За звено приведения принимаем кривошип.
Jпр = (2·Tмех)/ω1 = (2·61,11)/13,816 = 8,85 кг·м ;
2.8 Определение сил инерции
Для аналитического вычисления сил инерции воспользуемся аналитическим расчётом рычажного механизма.
Ускорение
ε3 = aτA3O2 / lO2A = 12 · KA / 0,147 = 0,327
ε4 = aτCB / lCB = 40 · KA / 0,21 = 0,762
Момент
М = J · ε H·м ;
Момент инерции
J’3 = ((m · 02A2) / 12) = 0,009 кг·м;
J”3 = 0,00082 кг·м
J4 = 0,294 кг·м
Тогда М’3 = 0,009 · 0,327 = 0,003 H·м .
М”3 =0,00082 · 0,327 = 0,00027 H·м
M4 = 0,294 · 0,762 = 0,224 Н·м
Составим программу:
Sub analit()
f0 = 0.24
w1 = 13.8
e1 = 0
n = 12
l1 = 0.035
l2 = 0.21
l3 = 0.07
l4 = 0.147
h = 0.14
m2 = 7
m3 = 80
m5 = 140
lk = 0.37
Worksheets(1).Range("a1") = "результаты аналитического расчета"
Worksheets(1).Range("a2") = "начальные параметры"
Worksheets(1).Range("a3") = "f0"
Worksheets(1).Range("b3") = f0
Worksheets(1).Range("a4") = "w1"
Worksheets(1).Range("b4") = w1
Worksheets(1).Range("a5") = "e1"
Worksheets(1).Range("b5") = e1
Worksheets(1).Range("a6") = "полученные значения"
Worksheets(1).Range("a7") = "N"
Worksheets(1).Range("b7") = "S"
Worksheets(1).Range("c7") = "V"
Worksheets(1).Range("d7") = "a"
df = 2 * 3.14 / n
f1 = f0 + df
For i = 0 To n
f1 = f1 - df
Worksheets(1).Cells(i + 8, 1).Value = i
'определение углов поворота
a = l1 * Cos(f1) + 14
b = l1 * Sin(f1)
aa = (a ^ 2 + b ^ 2 + l2 ^ 2 - l3 ^ 2) / (2 * a * l2)
bb = b / a
'определение угла f2
cf2 = -((aa + bb * ((1 - aa ^ 2 + bb ^ 2))) ^ 0.5) / (1 + bb ^ 2)
tf2 = (1 / ((cf2 ^ 2) - 1)) ^ 0.5
f2 = Atn(tf2)
If cf2 < 0 Then
tf2 = -tf2
f2 = Atn(tf2) + 3.14
End If
'определение угла f3
cf3 = (a + l2 * cf2) / l3
tf3 = (1 / ((cf3 ^ 2) - 1)) ^ 0.5
f3 = Atn(tf3)
If cf3 < 0 Then
tf3 = -tf3
f3 = Atn(tf3) + 3.14
End If
'определение угловых скоростей
i31 = (l1 * Sin(f1 - f2)) / (l3 * Sin(f3 - f2))
i21 = -(l1 * Sin(f1 - f3)) / (l2 * Sin(f2 - f3))
w3 = w1 * i31
w2 = w1 * i21
'определение угловых ускорений
i131 = (l1 * Cos(f1 - f2) + i21 ^ 2 * l2 - i31 ^ 2 * l3 * Cos(f3 - f2)) / (l3 * Sin(f3 - f2))
i121 = -(l1 * Cos(f1 - f3) - i31 ^ 2 * l3 + i21 ^ 2 * l2 * Cos(f2 - f3)) / (l2 * Sin(f2 - f3))
e3 = w1 ^ 2 * i131 + e1 * i31
e2 = w1 ^ 2 * i121 + e1 * i21
'определение перемещения питателя
s = h * (Tan(0.261666) - Tan(f3 - 1.57))
Worksheets(1).Cells(i + 8, 2).Value = s
'определение скорости питателя
v = h * w3 / ((Cos(f3 - 1.57)) ^ 2)
Worksheets(1).Cells(i + 8, 3).Value = v
'определение ускорения питателя
usk = -h * (e3 * Cos(f3 - 1.57) + 2 * w3 ^ 2 * Sin(f3 - 1.57)) / ((Cos(f3 - 1.57)) ^ 3)
Worksheets(1).Cells(i + 8, 4).Value = usk
'определение ускорений звеньев
a1n = w1 ^ 2 * l1
a2n = w2 ^ 2 * l2 / 2
a2t = e2 * l2 / 2
a2 = ((a1n * Cos(f1) + a2n * Cos(f2) + a2t * Cos(f2 - 1.57)) ^ 2 + (a1n * Sin(f1) + a2n * Sin(f2) + a2t * Sin(f2 - 1.57)) ^ 2) ^ 0.5
a3n = w3 ^ 2 * (lk / 2 - l3)
a3t = e3 * (lk / 2 - l3)
a3 = (a3n ^ 2 + a3t ^ 2) ^ 0.5
a5 = usk
'определение сил и моментов инерции
Worksheets(2).Cells(i + 8, 1).Value = i
u3 = -m3 * a3
Worksheets(2).Cells(i + 8, 2).Value = u3
mu3 = -m3 * l3 ^ 2 * e3 / 12
Worksheets(2).Cells(i + 8, 3).Value = mu3
u4 = -m4 * a4
Worksheets(2).Cells(i + 8, 4).Value = u4
mu4 = -m4 * lk ^ 2 * e4 / 12
Worksheets(2).Cells(i + 8, 5).Value = mu4
u5 = -m5 * a5
Worksheets(2).Cells(i + 8, 6).Value = u5
Next i
Worksheets(2).Range("a1") = "результаты аналитического расчета"
Worksheets(2).Range("a2") = "начальные параметры"
Worksheets(2).Range("a3") = "m3"
Worksheets(2).Range("b3") = m3
Worksheets(2).Range("a4") = "m4"
Worksheets(2).Range("b4") = m4
Worksheets(2).Range("a5") = "m5"
Worksheets(2).Range("b5") = m5
Worksheets(2).Range("a6") = "полученные значения"
Worksheets(2).Range("a7") = "N"
Worksheets(2).Range("b7") = "u3"
Worksheets(2).Range("c7") = "mu3"
Worksheets(2).Range("d7") = "u4"
Worksheets(2).Range("e7") = "mu4"
Worksheets(2).Range("f7") = "u5"
End Sub
3. Геометрический расчёт прямозубой передачи. Проектирование планетарного редуктора
3.1 Геометрический расчёт прямозубой передачи
Исходные данные :
Число зубьев шестерни : Z5 = 12.
Число зубьев колеса : Z6 = 30.
Модуль зубчатых колёс : m = 6.
Коэффициент высоты головки : ha* = 1.
Коэффициент радиального зазора : с* = 0,25.
Zсум = Z5 + Z6 = 12 + 30 = 42 > 34, =>,
коэффициент смещения шестерни определяется по формуле :
Х5 = (17 – Z5)/17 =(17 – 12)/17 = 0,294
а коэффициент смещения колеса :
X6 = - Х5 = -0,294
Угол профиля исходного профиля = 20˚ .
Делительное межосевое расстояние :
а = 0,5 · m · Zсум.= 0,5 · 6 · 42 = 126 mm
Коэффициент воспринимаемого смещения:
y = 0.
Коэффициент уравнительного смещения:
y = 0.
Делительная высота головки зуба :
ha5 = m · (ha* + X5) = 6 · (1+0,294) = 7,764 мм
ha6 = m · (ha* + X6) = 6 · (1-0,294) = 4,236 мм
Делительная высота ножки зуба :
hf5 = m · (ha* + c* - X5) = 6 · (1+0,25-0,294) = 5,736 mm
hf6 = m · (ha* + c* - X6) = 6 · (1+0,25+0,294) = 9,264 mm
Высота зуба :
h = 2,25 · m = 2,25 · 6 = 13,5 мм
Делительный диаметр :
d5 = m · Z5 = 6 · 12 = 72мм
d6 = m · Z6 = 6 · 30 =180мм
Основной диаметр :
db5 = m · Z5 · Cos(α) = 6 · 12 · cos20˚ = 67,68 mm
db6 = m · Z6 · Cos(α) = 6 · 30 · cos20˚ = 169,2 mm
Диаметр вершин :
dа5 = m · Z5 + 2 · m · (ha* + X5) = 6 · 12 + 2 · 6(1+0,294) = 87,528 mm
dа6 = m · Z6 + 2 · m · (ha* + X6) = 6 · 30 + 2 · 6(1-0,294) = 188,472 mm
Диаметр впадин :
df5 = m · Z5 - 2 · m · (ha* +c* + X5) = 6 · 12 – 2 · 6(1+0,25-0,294) =60,528 mm
df6 = m · Z6 - 2 · m · (ha* +c* - X6) = 6 · 30 – 2 · 6(1+0,25-0,294) =161,472 mm
Делительная толщина зуба :
S5 = 0,5 · π · m +2 · m · X5 · tg(α ) = 11,67796 mm
S6 = 0,5 · π · m +2 · m · X6 · tg(α ) = 7,16208 mm
Толщина зуба по окружности вершин :
Sa5 =da5 · ( S5 /d5 + inv20˚ + invαa5 ) = 3,862 mm
Sa6 =da6 · ( S6 /d6 + inv20˚ + invαa6 ) = 3.7862 mm
Делительный шаг :
P = π · m = 18.84 mm
Оновной шаг :
Pb = π · m · cosα = 3,14 · 6 · 0,94 = 17.71
По результатам расчёта строим картину равносмещённого эвольвентного зацепления.
3.2 Синтез и анализ комбинированного зубчатого механизма
Исходные данные :
n = 1455 мин-1 ;
n = 97 мин-1 ;
U16 = “-”;
Z5 = 12;
Z6 = 30:
Общее передаточное отношение привода :
U16 = -(nДВ / n6) = -(n1 / n6) = -(1455 / 97) = -(5.31) .
Передаточное отношение простой ступени :
U56 = -(Z6 / Z5) = -(30/12) .
Передаточное отношение планетарной ступени :
U1H = U16 / U56 = 6.1263 .
Формула Виллиса :
UH14 = (n1 - nH)/(n4 - nH) = (U1H –1)/(0-1) = 1- U1H = 1.2
Передаточное отношение U H14 через число зубьев :
U H14 = (-Z2/Z1)/(- Z4/ Z3) = (Z2· Z4)/(Z1· Z3) = -(6/5)
Из условия соосности определяем неизвестные числа зубьев колёс :
Z1 + Z2 = Z3 + Z4 .
Принимаем : Z1 = 2 ; Z2 = 1 ; Z3 = 3 ; Z4 = 5 .
2 + 1 = 3 16
3 + 5 = 8 6
В итоге принимаем : Z1 = 32 ; Z2 = 16 ; Z3 = 18 ; Z4 = 30 .
3.3 Построение плана скоростей и частот вращения звеньев зубчатого механизма
Диаметры всех колёс :
d1 = m·Z1 = 6·32 = 192 мм ;
d2 = m·Z2 = 6·16 = 96 мм ;
d3 = m·Z3 = 6·18 = 108 мм
d4 = m·Z4 = 6·30 = 180 мм
d5 = m·Z5 = 6·12 = 72 мм
d6 = m·Z6 = 6·30 = 180 мм
Принимаем масштабный коэффициент построения схемы механизма :
КL = 0,001 м/мм ;
Определяем скорость точки, принадлежащей ведущему звену (точка А):
Va = ω1 · d = 24 м/с ;
Принимаем масштабный коэффициент построения плана скоростей :
Кv =0,4 м/(c·мм) ;
Выполняем построение плана скоростей.
Построение плана частот вращения.
Принимаем масштабный коэффициент построения плана частот вращения :
Кv =20 мин /мм ;
Выполняем построение плана частот вращения.
Значения частот, полученных графически :
n1 = 24·40 = 960 мин-1
n2 = 262·40 = 10480 мин-1
n3 = 262·40 = 10480 мин-1
n5 = 121·40 = 4840 мин-1
n6 = 37·40 = 1480 мин-1
nH = 121·40 = 4840 мин-1
Составим программу:
Sub evol()
'ввод данных
z5 = 11
z6 = 45
m = 5
h1 = 1
c = 0.25
Worksheets(3).Range("a1") = "результаты аналитического расчета"
Worksheets(3).Range("a2") = "начальные параметры"
Worksheets(3).Range("a3") = "z5"
Worksheets(3).Range("b3") = z5
Worksheets(3).Range("a4") = "z6"
Worksheets(3).Range("b4") = z6
Worksheets(3).Range("a5") = "m"
Worksheets(3).Range("b5") = m
Worksheets(3).Range("a6") = "h1"
Worksheets(3).Range("b6") = h1
Worksheets(3).Range("a7") = "c"
Worksheets(3).Range("b7") = c
For i = 1 To 21
Worksheets(3).Cells(i + 8, 1).Value = i
Next i
'вычисление
Worksheets(3).Range("b8") = "полученные значения"
Worksheets(3).Range("c8") = "шестерня 5"
Worksheets(3).Range("d8") = "колесо 6"
Worksheets(3).Range("b9") = "суммарное число зубьев z"
z = z5 + z6
Worksheets(3).Range("c9") = z
Worksheets(3).Range("b10") = "min коэффициент смещения X"
x5 = (17 - z5) / 17
x6 = -x5
Worksheets(3).Range("c10") = x5
Worksheets(3).Range("d10") = x6
Worksheets(3).Range("b11") = "угол профиля исходного контура"
v = 20
q = 0.348888
Worksheets(3).Range("c11") = v
Worksheets(3).Range("b12") = "делительное межосевое расстояние a"
a = 0.5 * m * (z5 + z6)
Worksheets(3).Range("c12") = a
Worksheets(3).Range("b13") = "inv20"
inv = 0.0149
Worksheets(3).Range("c13") = inv
Worksheets(3).Range("b14") = "межосевое расстояние aw"
Worksheets(3).Range("c14") = a
Worksheets(3).Range("b15") = "делительная высота головки зуба ha"
ha5 = m * (h1 + x5)
ha6 = m * (h1 + x6)
Worksheets(3).Range("c15") = ha5
Worksheets(3).Range("d15") = ha6
Worksheets(3).Range("b16") = "делительная высота ножки зуба hf"
hf5 = m * (h1 + c - x5)
hf6 = m * (h1 + c - x6)
Worksheets(3).Range("c16") = hf5
Worksheets(3).Range("d16") = hf6
Worksheets(3).Range("b17") = "высота зуба h"
h = ha5 + hf5
Worksheets(3).Range("c17") = h
'диаметры
Worksheets(3).Range("b18") = "делительный диаметр d"
d5 = m * z5
d6 = m * z6
Worksheets(3).Range("c18") = d5
Worksheets(3).Range("d18") = d6
Worksheets(3).Range("b19") = "основной диаметр db"
db5 = m * z5 * Cos(q)
db6 = m * z6 * Cos(q)
Worksheets(3).Range("c19") = db5
Worksheets(3).Range("d19") = db6
Worksheets(3).Range("b20") = "начальный диаметр dw"
dw5 = d5
dw6 = d6
Worksheets(3).Range("c20") = dw5
Worksheets(3).Range("d20") = dw6
Worksheets(3).Range("b21") = "диаметр вершин зубьев da"
da5 = m * z5 + 2 * m * (h1 + x5)
da6 = m * z6 + 2 * m * (h1 + x6)
Worksheets(3).Range("c21") = da5
Worksheets(3).Range("d21") = da6
Worksheets(3).Range("b22") = "диаметр впадин зубьев df"
df5 = m * z5 - 2 * m * (h1 + c - x5)
df6 = m * z6 - 2 * m * (h1 + c - x6)
Worksheets(3).Range("c22") = df5
Worksheets(3).Range("d22") = df6
Worksheets(3).Range("b23") = "делительная толщина зубьев S"
s5 = 0.5 * 3.14 * m + 2 * m * x5 * Tan(q)
s6 = 0.5 * 3.14 * m + 2 * m * x6 * Tan(q)
Worksheets(3).Range("c23") = s5
Worksheets(3).Range("d23") = s6
Worksheets(3).Range("b24") = "основная толщина зубьев Sb"
sb5 = db5 * (3.14 / (2 * z5) + 2 * x5 * Tan(q) / z5 + inv)
sb6 = db6 * (3.14 / (2 * z6) + 2 * x6 * Tan(q) / z6 + inv)
Worksheets(3).Range("c24") = sb5
Worksheets(3).Range("d24") = sb6
Worksheets(3).Range("b25") = "начальная толщина зубьев Sw"
sw5 = s5
sw6 = s6
Worksheets(3).Range("c25") = sw5
Worksheets(3).Range("d25") = sw6
Worksheets(3).Range("b26") = "делительный шаг P"
p = 3.14 * m
Worksheets(3).Range("c26") = p
Worksheets(3).Range("b27") = "основной шаг pb"
pb = 3.14 * m * Cos(q)
Worksheets(3).Range("c27") = pb
Worksheets(3).Range("b28") = "радиус кривизны галтели r"
r = 0.4 * m
Worksheets(3).Range("c28") = r
Worksheets(3).Range("b29") = "коэффициент торцевого перекрытия e"
t5 = (((da5 / db5) ^ 2) - 1) ^ 0.5
t6 = (((da6 / db6) ^ 2) - 1) ^ 0.5
e = (z5 * t5 + z6 * t6 - (z5 + z6) * Tan(q)) / (2 * 3.14)
Worksheets(3).Range("c29") = e
End Sub
Список литературы
1Алехнович В.М.”Теория механизмов и манипуляторов”. Издательство высшая школа.1985г.
2.Машков А.А.”Теория механизмов и манипуляторов”. Издательство высшая школа.1971г.
Приложение
| исходные данные | |||
| наимено- вание параметра | обозначение | единица измерения | значение |
| O1-A | r | м | 0.113 |
| О1-О2 | e | м | 0.35 |
| B-O2 | r1 | м | 0.7 |
| y | y | м | 0.14 |
| BC | l | м | 0.21 |
| w1 | w1 | с | 13.80 |
| угол размаха | b | рад | 0.87266 |
| результаты вычислений | |||
| угол поворота | перемещение | скорость | ускорение |
| 0 | -0.004922 | -0.00083 | 5.38194 |
| 0.5236 | 0.0141113 | 0.60678 | 3.80533 |
| 1.0472 | 0.0561586 | 0.865058 | 2.90399 |
| 1.5708 | 0.1068522 | 0.935913 | 1.44724 |
| 2.0944 | 0.1582127 | 0.898178 | -0.2797 |
| 2.61799 | 0.2054088 | 0.789663 | -1.6989 |
| 3.14159 | 0.2447813 | 0.613949 | -2.4693 |
| 3.66519 | 0.2716014 | 0.3239 | -2.9936 |
| 4.18879 | 0.275994 | -0.23141 | -3.9887 |
| 4.71239 | 0.235559 | -1.32772 | -4.7289 |
| 5.23599 | 0.128899 | -2.26762 | 2.34036 |
| 5.75959 | 0.0256355 | -1.20752 | 6.53008 |
| 6.28319 | -0.004922 | -0.00083 | 5.38168 |
| результаты аналитического расчета | |||||
| начальные параметры | |||||
| m3 | 6 | ||||
| m4 | 70 | ||||
| m5 | 120 | ||||
| полученные значения | |||||
| N | u3 | mu3 | u4 | mu4 | u5 |
| 0 | -57.2731 | -2.34731 | -114.527 | 17.41795 | -1.1E+07 |
| 1 | -164.798 | -6.93282 | -337.12 | 50.99269 | -1.6E+08 |
| 2 | -276.534 | -11.8008 | -569.925 | 85.85486 | -3.5E+08 |
| 3 | -274.011 | -11.6716 | -564.147 | 84.71694 | -4E+08 |
| 4 | -144.589 | -5.97045 | -293.037 | 43.71576 | -2.5E+08 |
| 5 | -14.8626 | 0.344928 | -18.0173 | -1.93163 | -5.5E+07 |
| 6 | -27.7479 | 0.975466 | -49.8168 | -7.57031 | -8453251 |
| 7 | -108.177 | -5.36884 | -240.551 | 36.11039 | -1.7E+08 |
| 8 | -270.175 | -12.9273 | -589.596 | 88.70336 | -3.8E+08 |
| 9 | -305.491 | -14.5559 | -664.985 | 100.0586 | -4.3E+08 |
| 10 | -193.961 | -9.33578 | -424.105 | 63.86084 | -2.6E+08 |
| 11 | -67.0119 | -3.22456 | -145.531 | 22.04901 | -5.8E+07 |
| 12 | -56.9106 | -2.33274 | -113.79 | 17.30617 | -1.1E+07 |
| результаты аналитического расчета | |||
| начальные параметры | |||
| z5 | 12 | ||
| z6 | 40 | ||
| m | 5 | ||
| h1 | 1 | ||
| c | 0.25 | ||
| полученные значения | шестерня 5 | колесо 6 | |
| 1 | суммарное число зубьев z | 52 | |
| 2 | min коэффициент смещения X | 0.2941177 | -0.294 |
| 3 | угол профиля исходного контура | 20 | |
| 4 | делительное межосевое расстояние a | 130 | |
| 5 | inv20 | 0.0149 | |
| 6 | межосевое расстояние aw | 130 | |
| 7 | делительная высота головки зуба ha | 6.4705887 | 3.5294 |
| 8 | делительная высота ножки зуба hf | 4.7794117 | 7.7206 |
| 9 | высота зуба h | 11.25 | |
| 10 | делительный диаметр d | 60 | 200 |
| 11 | основной диаметр db | 56.385206 | 187.95 |
| 12 | начальный диаметр dw | 60 | 200 |
| 13 | диаметр вершин зубьев da | 72.941177 | 207.06 |
| 14 | диаметр впадин зубьев df | 50.441177 | 184.56 |
| 15 | делительная толщина зубьев S | 8.9199084 | 6.7801 |
| 16 | основная толщина зубьев Sb | 9.2226541 | 9.1721 |
| 17 | начальная толщина зубьев Sw | 8.9199084 | 6.7801 |
| 18 | делительный шаг P | 15.7 | |
| 19 | основной шаг pb | 14.754129 | |
| 20 | радиус кривизны галтели r | 2 | |
| 21 | коэффициент торцевого перекрытия e | 1.5002282 | |
[C1]ω
© 2010 Интернет База Рефератов