Курсовая работа: Модель распределения ресурсов

Содержание

Введение

1. Основные понятия

1.1. Модель динамического программирования

1.2. Принцип оптимальности. Уравнение Беллмана

2. Оптимальное распределение ресурсов

2.1 Постановка задачи

2.2 Двумерная модель распределения ресурсов

2.3 Дискретная динамическая модель оптимального распределения ресурсов

2.4 Учет последействия в задачах оптимального распределения ресурсов

Заключение

Список используемых источников

Приложение 1. Листинг программы для решения задачи оптимального распределения ресурсов с заданными параметрами. Результаты работы программы

Введение

На протяжении всей своей истории люди при необходимости принимать решения прибегали к сложным ритуалам. Они устраивали торжественные церемонии, приносили в жертву животных, гадали по звездам и следили за полетом птиц. Они полагались на народные приметы и старались следовать примитивным правилам, облегчающим им трудную задачу принятия решений. В настоящее время для принятия решения используют новый и, по-видимому, более научный «ритуал», основанный на применении электронно-вычислительной машины. Без современных технических средств человеческий ум, вероятно, не может учесть многочисленные и разнообразные факторы, с которыми сталкиваются при управлении предприятием, конструировании ракеты или регулировании движения транспорта. Существующие в настоящее время многочисленные математические методы оптимизации уже достаточно развиты, что позволяет эффективно использовать возможности цифровых и гибридных вычислительных машин. Одним из этих методов является математическое программирование, включающее в себя как частный случай динамическое программирование.

Большинство практических задач имеет несколько (а некоторые, возможно, даже бесконечное число) решений. Целью оптимизации является нахождение наилучшего решения среди многих потенциально возможных в соответствии с некоторым критерием эффективности или качества. Задача, допускающая лишь одно решение, не требует оптимизации. Оптимизация может быть осуществлена при помощи многих стратегий, начиная с весьма сложных аналитических и численных математических процедур и кончая разумным применением простой арифметики.

Динамическое программирование – метод оптимизации, приспособленный к операциям, в которых процесс принятия решений может быть разбит на отдельные этапы (шаги). Такие операции называются многошаговыми.

Как раздел математического программирования, динамическое программирование (ДП) начало развиваться в 50-х годах XX в. благодаря работам Р. Беллмана и его сотрудников. Впервые этим методом решались задачи оптимального управления запасами, затем класс задач значительно расширился. Как практический метод оптимизации, метод динамического программирования стал возможен лишь при использовании современной вычислительной техники.

В основе метода динамического программирования лежит принцип оптимальности, сформулированный Беллманом. Этот принцип и идея включения конкретной задачи оптимизации в семейство аналогичных многошаговых задач приводят к рекуррентным соотношениям — функциональным уравнениям — относительно оптимального значения целевой функции. Их решение позволяет последовательно получить оптимальное управление для исходной задачи оптимизации.

1. Основные понятия

1.1 Модель динамического программирования

Дадим общее описание модели динамического программирования.

Рассматривается управляемая система, которая под влиянием управления переходит из начального состояния в конечное состояние . Предположим, что процесс управления системой можно разбить на п шагов. Пусть , ,…, — состояния системы после первого, второго,..., п-го шага. Схематически это показано на рис. 1.

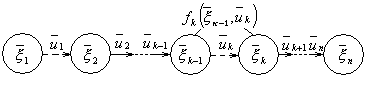
Рисунок 1

Состояние системы после k-го шага (k= 1,2 …,n) характеризуется параметрами , ,…, которые называются фазовыми координатами. Состояние можно изобразить точкой s-мерного пространства называемого фазовым пространством. Последовательное преобразование системы (по шагам) достигается с помощью некоторых мероприятий , ,…, , которые составляют управление системой , где — управление на k-м шаге, переводящее систему из состояния в состояние (рис. 1). Управление на k-ом шаге заключается в выборе значений определенных управляющих переменных* .

Предполагаем впредь, что состояние системы в конце k-го шага зависит только от предшествующего состояния системы и управления на данном шаге (рис. 1). Такое свойство получило название отсутствия последействия. Обозначим эту зависимость в виде

, (1.1)

Равенства (1.1) получили название уравнений состояний. Функции полагаем заданными.

Варьируя управление U, получим различную «эффективность» процесса**, которую будем оценивать количественно целевой функцией Z, зависящей от начального состояния системы и от выбранного управления U:

. (1.2)

Показатель эффективности k-го шага процесса управления, который зависит от состояния в начале этого шага и управления , выбранного на этом шаге, обозначим через рассматриваемой задаче пошаговой оптимизации целевая функция (1.2) должна быть аддитивной, т. е.

. (1.3)

Если свойство аддитивности целевой функции Z не выполняется, то этого иногда можно добиться некоторыми преобразованиями функции. Например, если Z— мультипликативная функция, заданная в виде , то можно рассмотреть функцию , которая является аддитивной.

Обычно условиями процесса на управление на каждом шаге накладываются некоторые ограничения. Управления, удовлетворяющие этим ограничениям называются допустимыми.

Задачу пошаговой оптимизации можно сформулировать так: определить совокупность допустимых управлении , ,…, , переводящих систему из начального состояния в конечное состояние и максимизирующих или минимизирующих показатель эффективности (1.3).

Для единообразия формулировок (но не вычислительных процедур!) в дальнейшем мы будем говорить только о задаче максимизации, имея в виду, что если необходимо минимизировать Z, то, заменив Z на Z' = —Z перейдем к максимизации Z'.

Начальное состояние и конечное состояние могут быть заданы однозначно или могут быть указаны множество начальных состояний множество конечных состояний так, что , . В последнем случае в задаче пошаговой оптимизации требуется определить совокупность допустимых управлений, переводящих систему из начального состояния в конечное состояние и максимизирующих целевую функцию (1.3). Управление, при котором достигается максимум целевой функции (1.3), называется оптимальным управлением и обозначается через .

Если переменные управления принимают дискретные значения, то модель ДП называется дискретной. Если же указанные переменные изменяются непрерывно, то модель ДП называется непрерывной. В зависимости от числа параметров состояний (s) и числа управляющих переменных на каждом шаге (r) различают одномерные и многомерные модели ДП. Число шагов в задаче может быть либо конечным, либо бесконечным.

Динамическое программирование применяется при оптимизации как детерминированных, так и стохастических процессов.

В некоторых задачах, решаемых методом ДП, процесс управления естественно разбивается на шаги. Например, при распределении на несколько лет ресурсов деятельности предприятия шагом естественно считать временной период; при распределении средств между n предприятиями номером шага естественно считать номер очередного предприятия. В других задачах разбиение на шаги вводится искусственно. Например, непрерывный управляемый процесс можно рассматривать как дискретный, условно разбив его на некоторые временные отрезки шаги. Исходя из условий каждой конкретной задачи, длину шага выбирают таким образом, чтобы на каждом шаге получить простую задачу оптимизации и обеспечить требуемую точность вычислений.

1.2 Принцип оптимальности. Уравнение Беллмана

Метод динамического программирования состоит в том, что оптимальное управление строится постепенно, шаг за шагом. На каждом шаге оптимизируется управление только этого шага. Вместе с тем на каждом шаге управление выбирается с учетом последствий, так как управление, оптимизирующее целевую функцию только для данного шага, может привести к неоптимальному эффекту всего процесса. Управление на каждом шаге должно быть оптимальным с точки зрения процесса в целом.

Иллюстрацией к сказанному выше может служить задача о выборе кратчайшего пути для перехода из точки A в точку B, если маршрут должен пройти через некоторые пункты. На рис. 2 эти пункты обозначены кружками, а соединяющие их дороги — отрезками, рядом с которыми проставлены соответствующие расстояния.

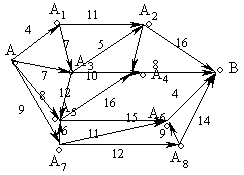
Рисунок 2

С точки зрения интересов оптимизации только каждого ближайшего шага — выбора кратчайшего пути из данной точки в соседнюю — следует двигаться по маршруту, проходящему через точки . Длина этого маршрута равна 34. Такой путь из A в B не является кратчайшим. Например, маршрут, проходящий через точки , имеет меньшую длину, равную 25. Решив эту задачу, можно убедиться, что второй путь также не является оптимальным.

Приведенный пример многошаговой операции показывает, что управление на каждом шаге надо выбирать с учетом его последствий на предстоящих шагах. Это основное правило ДП, сформулированное Р. Беллманом, называется принципом оптимальности.

Оптимальное управление обладает таким свойством, что каково бы ни было начальное состояние на любом шаге и управление, выбранное на этом шаге, последующие управления должны выбираться оптимальными относительно состояния, к которому придет система в конце данного шага.

Использование этого принципа гарантирует, что управление, выбранное на любом шаге, является не локально лучшим, а лучшим с точки зрения процесса в целом.

Так, если система в начале k-го шага находится в состоянии , и мы выбираем произвольное управление , то система придет в новое состояние , и дальнейшие управления должны выбираться оптимальными относительно состояния . Последнее означает, что при этих управлениях максимизируется показатель эффективности на последующих до конца процесса шагах k+1,...,n, т. е. величина . Показатель, характеризующий суммарную эффективность от данного k-го до последнего п-го шага, будем обозначать через , т.е. . Задача оптимизации процесса, начиная с k-го до последнего n-го шага (рис. 3), похожа на исходную при начальном состоянии системы , управлении и показателе эффективности [аналогично (1.2)]. Выбрав оптимальное управление на оставшихся п—k+l шагах, получим величину , которая зависит только от , т. е.

. (1.4)

Назовем величину условным максимумом. Если теперь мы выберем на k-м шаге некоторое произвольное управление , то система придет в состояние . Согласно принципу оптимальности, какое бы мы ни выбрали, на последующих шагах управление должно выбираться так, чтобы показатель эффективности достигал максимального значения, равного . Остается выбрать управление . Его нельзя выбирать из условия локальной максимизации показателя эффективности на данном k-м шаге, лишь бы получить . Такой подход был бы недальновидным, поскольку от выбора зависит новое состояние , а от последнего—максимально возможная эффективность, которая может быть достигнута в дальнейшем, т. е. величина . Поэтому необходимо выбирать управление так, чтобы оно в совокупности с оптимальным управлением на последующих шагах (начиная с (k+1)-го) приводило бы к общему максимуму показателя эффективности на п—k+l шагах, начиная с k-го до конца. Это положение в аналитической форме можно записать в виде следующего соотношения:

, (1.5)

получившего название основного функционального уравнения ДП, или уравнения Беллмана. Схематически соотношение (1.5) иллюстрируется на рис. 3.

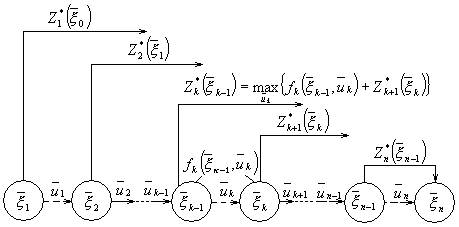
Рисунок 3

Из уравнения (1.5) может быть получена функция , если известна функция ; аналогично можно получить , если найдена и т. д., пока не будет определена величина , представляющая по определению максимальное значение показателя эффективности процесса в целом: .

Соотношения (1.5) для определения последовательности функций через получили название основных рекуррентных уравнений Беллмана.

Решая уравнение (1.5) для определения условного максимума показателя эффективности за n—k+l шагов, начиная с k-го, мы определяем соответствующее оптимальное управление , при котором этот максимум достигается. Это управление также зависит от . Будем обозначать такое управление через и называть условным оптимальным управлением на k-м шаге.

Основное значение уравнения (1.5), в котором реализована идея динамического программирования, заключается в том, что решение исходной задачи определения - максимума функции (1.2) n переменных , ,…, сводится к решению последовательности n задач, задаваемых соотношениями (1.5), каждое из которых является задачей максимизации функции одной переменной . Эти задачи оказываются взаимосвязанными, так как в соотношении (1.5) при определении учитывается найденная при решении предыдущей задачи функция .

2. Оптимальное распределение ресурсов

2.1 Постановка задачи

Класс задач, рассматриваемый в данной главе, имеет многочисленные практические приложения.

В общем виде эти задачи могут быть описаны следующим образом. Имеется некоторое количество ресурсов, под которыми можно понимать денежные средства, материальные ресурсы (например, сырье, полуфабрикаты, трудовые ресурсы, различные виды оборудования и т. п.). Эти ресурсы необходимо распределить между различными объектами их использования по отдельным промежуткам планового периода или по различным промежутками по различным объектам так, чтобы получить максимальную суммарную эффективность от выбранного способа распределения. Показателем эффективности может служить, например, прибыль, товарная продукция, фондоотдача (задачи максимизации) или суммарные затраты, себестоимость, время выполнения данного объема работ и т. п. (задачи минимизации).

Вообще говоря, подавляющее число задач математического программирования вписывается в общую постановку задачи оптимального распределения ресурсов. Естественно, что при рассмотрении моделей и вычислительных схем решения подобных задач методом ДП необходимо конкретизировать общую форму задачи распределения ресурсов.

В дальнейшем будем предполагать, что условия, необходимые для построения модели ДП, в задаче выполняются. Опишем типичную задачу распределения ресурсов в общем виде.

Задача 1. Имеется начальное количество средств , которое необходимо распределить в течение n лет между s предприятиями. Средства , выделенные в k-м году i-му предприятию, приносят доход в размере и к концу года возвращаются в количестве. В последующем распределении доход может либо участвовать (частично или полностью), либо не участвовать.

Требуется определить такой способ распределения ресурсов (количество средств, выделяемых каждому предприятию в каждом плановом году), чтобы суммарный доход от s предприятий за n лет был максимальным.

Следовательно, в качестве показателя эффективности процесса распределения ресурсов за n лет принимается суммарный доход, полученный от s предприятий:

. (2.1)

Количество ресурсов в начале k-го года будем характеризовать величиной (параметр состояния). Управление на k-м шаге состоит в выборе переменных , обозначающих ресурсы, выделяемые в k-м году i-му предприятию.

Если предположить, что доход в дальнейшем распределении не участвует, то уравнение состояния процесса имеет вид

(2.2)

Если же некоторая часть дохода участвует в дальнейшем распределении в каком-нибудь году, то к правой части равенства (2.2) прибавляется соответствующая величина.

Требуется определить ns неотрицательных переменных , удовлетворяющих условиям (2.2) и максимизирующих функцию (2.1).

Вычислительная процедура ДП начинается с введения функции , обозначающей доход, полученный за п—k+1 лет, начиная с k-го года до конца рассматриваемого периода, при оптимальном распределении средств между s предприятиями, если в k-м году распределялось средств. Функции для удовлетворяют функциональным уравнениям (1.5), которые запишутся в виде

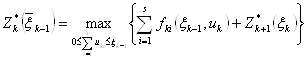(2.3)

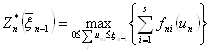
При согласно (1.5) получаем

. (2.4)

Далее необходимо последовательно решить уравнения (2.4) и (2.3) для всех возможных . Каждое из этих уравнений представляет собой задачу на оптимизацию функции, зависящей от s переменных. Таким образом, задача с ns переменными сведена к последовательности n задач, каждая из которых содержит s переменных. В этой общей постановке задача по-прежнему сложна (из-за многомерности) и упростить ее, рассматривая как ns-шаговую задачу, в данном случае нельзя. В самом деле, попробуем это сделать. Пронумеруем шаги по номерам предприятий сначала в 1-м году, затем во 2-м и т. д.:

и будем пользоваться одним параметром для характеристики остатка средств.

В течение k-го года состояние к началу любого шага (i=l, 2, .... s) определится по предыдущему состоянию с помощью простого уравнения . Однако по истечении года, т. е. к началу следующего года, к наличным средствам необходимо будет добавить средств и, следовательно, состояние в начале -го шага будет зависеть не только от предшествующего ks-го состояния, но и от всех s состояний и управлений за прошлый год. В результате мы получим процесс с последействием. Чтобы исключить последействие, приходится вводить несколько параметров состоянии; задача на каждом шаге остается по-прежнему сложной из-за многомерности.

2.2 Двумерная модель распределения ресурсов

Задача 2. Планируется деятельность двух предприятий (s=2) в течение n лет. Начальные средства составляют . Средства x, вложенные в предприятие I, приносят к концу года доход и возвращаются в размере ; аналогично, средства x, вложенные в предприятие II, дают доход и возвращаются в размере . По истечении года все оставшиеся средства заново перераспределяются между предприятиями I и II, новых средств не поступает и доход в производство не вкладывается.

Требуется найти оптимальный способ распределения имеющихся средств.

Будем рассматривать процесс распределения средств как n-шаговый, в котором номер шага соответствует номеру года. Управляемая система — два предприятия с вложенными в них средствами. Система характеризуется одним параметром состояния — количеством средств, которые следует перераспределить в начале k-го года. Переменных управления на каждом шаге две: и — количество средств, выделенных соответственно предприятию I и II. Так как средства ежегодно перераспределяются полностью, то . Для каждого шага задача становится одномерной. Обозначим через , тогда .

Показатель эффективности k-го шага равен . Это—доход, полученный от двух предприятий в течение k-го года.

Показатель эффективности задачи—доход, полученный от двух предприятий в течение n лет—составляет

. (2.5)

Уравнение состояния выражает остаток средств после k-го шага и имеет вид

. (2.6)

Пусть условный оптимальный доход, полученный от распределения средств между двумя предприятиями за п—k+1 лет, начиная с k-го года до конца рассматриваемого периода. Запишем рекуррентные соотношения для этих функций:

; (2.7)

где - определяется из уравнения состояния (2.6).

Задача 3. Решить задачу 2 при следующих условиях: ; ; ; ; ; .

Если и - средства, выделенные соответственно предприятиям I и II в k-м году, то суммарный доход, полученный от обоих предприятий, равен

а уравнение состояния (2.6) принимает вид

Основные функциональные уравнения (2.7) запишутся следующим образом:

;

Проведем этап условной оптимизации.

4-й шаг. Условный оптимальный доход равен

так как линейная относительно функция достигает максимума в конце интервала, т.е. при .

3-й шаг:

Коэффициент при отрицателен, поэтому максимум в этой линейной относительно функции достигается в начале интервала, т.е.

; .

2-й шаг:

, откуда ; .

1-й шаг:

при .

Результат условной оптимизации:

; ; ; ;

; ; ;

Перейдем к безусловной оптимизации. Полагаем ; тогда , . Зная , находим ; используя , получаем и . Аналогично , . Наконец, . Следовательно, средства по годам нужно распределить так:

	Год
Предприятие	1	2	3	4
I	0	0	0	5120
II	10000	8000	6400	0

При таком распределении средств (10000 руб.) за четыре года будет получен доход, равный .

Непрерывные модели, примером которых служит задача 3, не являются типичными в практике распределения ресурсов. В дальнейшем большинство задач будет носить дискретный характер.

2.3 Дискретная динамическая модель оптимального распределения ресурсов

При дискретном вложении ресурсов может возникнуть вопрос о выборе шага в изменении переменных управления. Этот шаг может быть задан или определяется исходя из требуемой точности вычислений и точности исходных данных. В общем случае эта задача сложна, требует интерполирования по таблицам на предыдущих шагах вычисления. Иногда предварительный анализ уравнения состояния позволяет выбрать подходящий шаг , а также установить предельные значения , для которых на каждом шаге нужно выполнить табулирование.

Рассмотрим двумерную задачу, аналогичную предыдущей, в которой строится дискретная модель ДП процесса распределения ресурсов.

Задача 3. Составить оптимальный план ежегодного распределения средств между двумя предприятиями в течение трёхлетнего планового периода при следующих условиях: 1) начальная сумма составляет 400; 2) вложенные средства в размере x приносят на предприятии I доход и возвращаются в размере 60% от x, а на предприятии II—соответственно и 20%; 3) ежегодно распределяются все наличные средства, получаемые из возвращенных средств: 4) функции и заданы в табл. 1:

Таблица 1

100

150

200

250

300

350

400

Модель динамического программирования данной задачи аналогична модели, составленной в задаче 1.

Процесс управления является трехшаговым. Параметр — средства, подлежащие распределению в k-м году (k=1, 2, 3). Переменная управления — средства, вложенные в предприятие I в k-м году. Средства, вложенные в предприятие II в k-м году, составляют . Следовательно, процесс управления на k-м шаге зависит от одного параметра (модель одномерная). Уравнение состояния запишется в виде

, (2.8)

а функциональные уравнения – в виде

, (2.9)

. (2.10)

Попытаемся определить максимально возможные значения, для которых необходимо проводить табулирование на k-м шаге (k=1, 2, 3). При из уравнения (2.8) определяем максимально возможное значение ; имеем =0,6-400= 2400 (все средства вкладываются в предприятие I). Аналогично, для получаем предельное значение . Пусть интервал изменения совпадает с табличным, т. е. =50. Составим таблицу суммарной прибыли на данном шаге: (см. табл. 2). Это облегчит дальнейшие расчеты. Так как , то клетки, расположенные по диагонали таблицы, отвечают одному и тому же значению, указанному в 1-й строке (в 1-м столбце) табл. 2. Во 2-й строке таблицы записаны значения , а во 2-м столбце — значения , взятые из табл. 1. Значения в остальных клетках таблицы получены сложением чисел и . стоящих во 2-й строке и во 2-м столбце и соответствующих столбцу и строке, на пересечении которых находится данная клетка. Например, для =150 получаем ряд чисел: 20—для x=0, у=150; 18—для x=50, y==100; 18— для x=100, y=50; 15—для x=150, y=0.

Таблица 2

x y	0	50	100	150	200	250	300	350	400
0	0	6	10	15	26	28	38	45	49
50	8	14	18	23	34	36	46	53
100	12	18	22	27	38	40	50
150	20	26	30	35	46	48
200	28	34	38	43	54
250	35	41	45	50
300	40	46	50
350	46	52
400	48

Аналогичную таблицу полезно подготовить и для расчетов по формуле (2.8). Расчет приведен в табл.3.

Таблица 3

x y	0	50	100	150	200	250	300	350	400
0	0	30	60	90	120	150	180	210	240
50	10	40	70	100	130	160	190	220
100	20	50	80	110	140	170	200
150	30	60	90	120	150	180
200	40	70	100	130	160
250	50	80	110	140
300	60	90	120
350	70	100
400	80

Проведем условную оптимизацию по обычной схеме.

3-й шаг. Основное уравнение (2.9)

решим с помощью табл. 2. Как указывалось выше, . Просмотрим числа на диагоналях, соответствующих ; 50; 100; 150 и на каждой диагонали выберем наибольшее. Это и есть . В 1-й строке находим соответствующее условное оптимальное управление. Данные оптимизации на 3-м шаге поместим в основную таблицу (табл. 4). В ней введен столбец , который в дальнейшем используется при интерполяции.

Оптимизация 2-го шага проведена в табл. 5 согласно уравнению вида (2.10):

Таблица 4 (основная)

	3-й шаг			2-й шаг

		8			10,8
50	8		50	10,8		50
		6			9,6
100	14		50	20,4		50
		6			8,0
150	20		0	28,4		100
					14
200				42,4		200
					9,2
250				51,6		200

Таблица 5

50		100			150
0	50	0	50	100	0	50	100	150
50	0	100	50	0	150	100	50	0
10	30	20	40	60	30	50	70	90
8	6	12	14	10	20	18	18	15
1,6	4,8	3,2	6,4	9,2	4,8	8	10,4	12,8
9,6	10,8	15,2	20,4	19,2	24,8	26	28,4	27,8

Продолжение

200					250
0	50	100	150	200	0	50	100	150	200	250
200	150	100	50	0	250	200	150	100	50	0
40	60	80	100	120	50	70	90	110	130	150
28	26	22	23	26	35	34	30	27	31	28
6,4	9,2	11,6	14	16,4	8	10,4	12,8	16,2	17,6	20
34,4	35,2	33,6	37	42,4	43	44,4	42.8	42,2	51,6	48

Результаты оптимизации занесены в табл. 4. Для значений, некратных 50, приведена линейная интерполяция функции в табл. 4.

Условная оптимизация 1-го шага согласно уравнению

для =400 приведена во вспомогательной табл. 6. Для значений, некратных 50, соответствующие значения функции получены интерполяцией в основной табл. 4.

Таблица 6

0	50	100	150	200	250	300	350	400
400	350	300	250	200	150	100	50	0
80	100	120	140	160	180	200	220	240
48	52	50	50	54	48	50	53	49
16,6	20,4	23,6	27,8	31,2	36,8	42,4	46,1	49,8
64,6	72,4	73,6	77,8	85,2	84,8	92,4	99,1	98,8

Перейдем к безусловной оптимизации. Из табл. 6 получаем Zmax=99,l, =350, =50. По и в табл. 3 находим =220; для этого значения из табл. 4 получаем =200. Следовательно, =20. Этому управлению в табл. 3 соответствует =124; для полученного значения из табл. 4 после интерполирования находим =24 и =100.

Итак, мы получили следующий оптимальный план распределения средств между двумя предприятиями по годам:

Предприятие	1-й год	2-й год	3-й год
I	350	200	24
II	50	20	100

При этом может быть получен максимальный доход, равный Zmax=99,l. Прямой подсчет дохода по табл. 2 для найденного оптимального управления дает 97,2. Расхождение в результатах на 1,9 (около 2%) объясняется ошибкой линейной интерполяции.

Мы рассмотрели несколько вариантов задачи оптимального распределения ресурсов. Существуют другие варианты этой задачи, особенности которых учитываются соответствующей динамической моделью.

2.4 Учет последействия в задачах оптимального распределения ресурсов

При постановке задачи оптимального распределения ресурсов мы предполагали, что доход на каждом шаге от всех предприятий и максимальный доход , начиная с k-го шага до конца планового периода, зависели только от состояния системы к k-му шагу и от управления на этом шаге, но не зависели от того, каким образом распределялись средства между предприятиями на предыдущих шагах. Однако во многих задачах оптимального распределения средств доход, полученный на k-м шаге, может оказаться зависимым и от того, какие средства и в каком количестве выделялись каждому из предприятий на предыдущих шагах, т. е. от предыстории процесса.

Таким образом, нарушается одно из условий, предъявляемых к задачам оптимизации, для того чтобы их можно было описать моделью ДП. Чтобы учесть предысторию процесса распределения ресурсов, можно увеличить число параметров состояния на каждом шаге, искусственно включив в число фазовых координат все управляющие параметры: предшествующих шагов, которые определяют последействие. Если число таких параметров велико, то схема ДП усложняется настолько, что становится практически неприменимой. В случае если размерность искусственного фазового пространства не превышает 3-4, то задачу можно решить вручную или (для большого числа шагов n) на машине.

Рассмотрим модель задачи оптимального распределения ресурсов с последействием, аналогичную задаче 2.

Задача 5. Начальные средства распределяются между двумя предприятиями в течение n лет. Доход, полученный в конце k-го года от предприятий I и II, зависит от средств и , выделенных соответственно в предприятия I и II в k-м году, и от суммы всех вложенных в предприятия I и II средств соответственно за предыдущие k—1 лет. От этих же факторов зависит и величина средств, которые возвращаются в конце каждого года и перераспределяются в очередном плановом периоде. Новые средства не поступают, доход в производство не вкладывается.

Требуется найти оптимальный способ распределения ресурсов между предприятиями I и II на n лет.

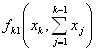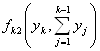
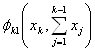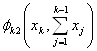Обозначим через , функции дохода, а через и — функции возврата средств для предприятии I и II соответственно.

Состояние системы в конце k-го шага удовлетворяет уравнению

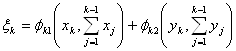, (2.11)

а доход, полученный на k-м шаге от двух предприятий, равен

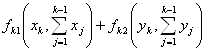. (2.12)

Величины (2.11) и (2.12) зависят не только от управления на k-м шаге, но и от всех управлении на предшествующих шагах (процесс распределения ресурсов обладает последействием).

Введем в рассмотрение две новые фазовые координаты:

, , (2.13)

полагая . Состояние системы к началу k-го шага характеризуется тремя параметрами: , , . Так как все наличные средства в k-м году полностью распределяются между предприятиями I и II, то .

Уравнение состояния имеет вид

(2.14)

а доход на k-м шаге равен

. (2.15)

Суммарный доход за n лет составляет

. (2.16)

Требуется найти неотрицательные переменные , обращающие в максимум функцию (2.16) и удовлетворяющие уравнениям (2.14) при начальных условиях , , .

Обозначим через условный максимальный доход, полученный за n—k+1 шагов, начиная с k-го до n-го включительно, при оптимальном распределении средств на этих шагах.

Функциональные уравнения (1.5) для имеют вид

;

. (2.17)

Решая последовательно уравнения (2.17) для , получим, как и выше, две последовательности значений и . Далее при начальных условиях , , , учитывая уравнение состояния (2.14), по цепочке получим оптимальное управление и :

Оптимальное управление получается по формулам , а соответствующий максимальный доход равен .

Рассмотрим, как реализуется схема ДП, учитывающая предысторию процесса, на следующей дискретной модели оптимального распределения ресурсов.

Задача 6. Средства = 6 распределяются между тремя предприятиями, принадлежащими одному объединению и связанными одним технологическим циклом так, что продукция предприятия I служит полуфабрикатом для предприятия II, и продукция первых двух предприятий служит полуфабрикатом для предприятия III. В табл. 7 заданы функции , , , характеризующие выпуск продукции в одних и тех же единицах в зависимости от вложенных средств в предприятия I, II, III соответственно. Каждому предприятию можно выделить не более 5 ед. средств, кратных .

Требуется распределить начальные средства между тремя предприятиями так, чтобы максимизировать выпуск продукции.

Запишем модель ДП задачи.

Начальное состояние =6; номер шага k—номер предприятия (k=l, 2, 3); переменные - средства, выделенные предприятиям I, II, III соответственно,— удовлетворяют условиям

. (2.18)

Таблица 7

Предприятия	Продукция		1	2	3	4	5
I			2,1	3,2	4,3	5,1	5,1
II		x1 x2	1	2	3	4	5
		0	2,2	2,8	3.1	4,3	6
		1	3,1	4.2	5,3	7,1	8
		2	3,3	4,5	6,1	7,3	-
		3	3,5	4,8	6,7	-	-
		4	5,4	5,9	-	-	-
III		x3 x1+x2	1	2	3	4	5
		0	3,4	3,8	4,2	5,0	5,0
		1	3,7	4,1	4,5	5,3	5,3
		2	3,7	4,1	4,5	5,4	-
		3	4,0	4,5	4,8	-	-
		4	4,2	4,8	-	-	-
		5	4,6	-	-	-	-
		6	-	-	-	-	-

Показатель эффективности — суммарная продукция — равен

. (2.19)

Найти переменные , удовлетворяющие условиям (2.18) и обращающие в максимум функцию (2.19).

Будем характеризовать состояние процесса распределения средств в начале k-го шага двумя параметрами: — остатком средств после выделения предыдущим k—1 предприятиям; — количеством средств, вложенных в предыдущее предприятие (). Уравнения состояний имеют вид

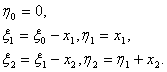(2.20)

Пусть - условный максимум продукции, выпущенной предприятиями, считая с k-го до конца. Функции при удовлетворяют уравнениям

, (2.21)

Обозначим выражения, стоящие в фигурных скобках второго и третьего уравнений (2.21), соответственно через и .

Условная оптимизация 3-го шага сводится к решению первого уравнения из (2.21). Результат ее совпадает с разделом III табл. 7 (здесь ).

Условная оптимизация 2-го шага проведена в табл. 8, при этом во втором из уравнений (2.21) состояния и выражены через и из соотношений (2.20). Условные максимумы для всех , в таблице подчеркнуты. При заполнении табл. 8 использовались разделы II и III табл. 7.

Условная оптимизация 1-го шага проведена в табл. 9 только для =6. При использовании третьего из уравнений (2.21) и выражены через и из соотношений (2.20). При расчетах в табл. 9 использовались раздел I табл. 7 и подчеркнутые значения табл. 8.

Используя результат условной оптимизации (табл. 9, 8 и раздел III табл. 7), получим оптимальное решение.

Из табл. 9 получаем Zmax=15,l; это значение достигается при . Отсюда . Из табл. 8 находим ; следовательно, . Из раздела III табл.7 определяем .

Таким образом, при распределении =(4, 1, 1) средств между тремя предприятиями может быть достигнут максимальный выпуск продукции, величина которого равна 15,1 ед.

Таблица 8



0	0	1	0	3,4	3,4	0	3,7	3,7	0	3,7	3,7	0	3,5	3,5	0	4,6	4,6
	1	0	2,2	0	2,2	3,1	0	3,1	3,3	0	5,3	4,0	0	4,0	5,4	0	5,4

	0	2	0	3,8	3,8	0	3,8	3,8	0	4,1	4,1	0	4,5	4,5	0	4,8	4,8
2	1	1	2,2	3,7	5,9	3,1	3,7	6,8	3,3	4,0	7,3	3,5	4,2	7,7	5,4	4,6	10,0
	2	0	2,8	0	2,8	4,2	0	4,2	4,5	0	4,5	4,8	0	4,8	5,9	0	5,9

	0	3	0	4,0	4,2	0	4,5	4,5	0	4,5	4,5	0	4,8	4,8
	1	2	2,2	38	6,0	3,1	4,1	7,2	3,3	4,5	7,8	3,5	4,8	8,3
3	2	1	2,8	3,7	6,5	4,2	4,0	8,2	4,5	4,2	8,7	4,8	4,6	9,4
	3	0	3,1	0	3,1	5,3	0	5,3	6,1	0	0	6,7	0	6,7


	0	4	0	5	5	0	5,3	5,3	0	5,4	5,4
	1	3	2,2	4,5	6,7	3,1	4,5	7,6	3,3	4,8	8,1
4	2	2	2,8	4,1	6,9	4,2	4,5	8,7	4,5	4,8	8,4
	3	1	3,1	4	7,1	5,3	4,2	9,5	6,1	4,6	10,7
	4	0	4,3	0	4,3	7,1	0	7,1	7,3	0	7,3

	0	5	0	5	5	0	5,3	5,3
	1	4	2,2	5,3	7,5	3,1	5,4	8,5
5	2	3	2,8	4,5	7,3	4,2	4,8	9
	3	2	3,1	4,5	7,6	5,3	4,8	10,1
	4	1	4,3	4,2	8,5	7,1	4,6	11,7
	5	0	6	0	6	8	0	8

	0	6	0	5	5
	1	5	2,2	5,3	7,5
	2	4	2,8	5,4	8,2
6	3	3	3,1	4,8	7,9
	4	2	4,3	4,8	9,1
	5	1	6	4,6	10,6
	6	0	6	0	6

Таблица 9


0	6	0	0	10,6	10,6
1	5	1	2,1	11,7	13,8
2	4	2	3,2	10,7	13,9
3	3	3	4,3	9,4	13,7
4	2	4	5,1	10	15,1
5	1	5	5,1	5,4	10,5

Заключение

В работе было рассмотрено применение динамического программирования для решения задач оптимального распределения ресурсов. Этот метод играет важную роль в решении прикладных задач различных областей науки, что обусловлено его высокой эффективностью. Однако, как и любой математический аппарат, методы динамического программирования нельзя слепо применять для решения той или иной задачи без тщательного предварительного анализа. Практическое применение данных методов требует от исследователя определенного искусства. При этом определяющее значение имеет корректное построение модели и применение подходящих численных процедур.

Список используемых источников

1. Беллман Р. Динамическое программирование. М.: ИЛ, 1960. 430 с.

2. Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся ВТУЗов. М.: Наука, 1986. 534 с.

3. Каллихман И.Л., Войтенко М.А. Динамическое программирование в примерах и задачах. М.: Высшая школа, 1979. 124 с.

4. Химмельблау Д.М. Прикладное нелинейное программирование. М.: Мир, 1975. 534с.

Приложение 1

Листинг программы для решения задачи оптимального распределения ресурсов с заданными параметрами

#include<iostream.h>

#include<conio.h>

#include<values.h>

//--------------Определяем начальные ресурсы--------------------

const ksi_0 = 6;

//--------------Класс таблицы для вывода------------------------

class Table

{

int tx, ty, c_x, new_y;

public:

Table();

void NewString(double a1, double a2, double a3,

double a4, double a5, double a6, double a7);

void EndOfTable();

};

//-------------Конструктор класса-------------------------------

Table::Table()

{

tx=1, ty=1;

c_x=77;

clrscr();

gotoxy(tx,ty);

cout << "┌";

for (int i=0;i<c_x;i++)

cout << "─";

cout << "┐";

gotoxy(tx+7,ty); cout << "┬";

gotoxy(tx+14,ty); cout << "┬";

gotoxy(tx+19,ty); cout << "┬";

gotoxy(tx+26,ty); cout << "┬";

gotoxy(tx+40,ty); cout << "┬";

gotoxy(tx+63,ty); cout << "┬";

gotoxy(tx,ty+1); cout << "│";

gotoxy(tx+2,ty+1) ; cout << "ksi1";

gotoxy(tx+7,ty+1); cout << "│";

gotoxy(tx+9,ty+1) ; cout << "eta1";

gotoxy(tx+14,ty+1); cout << "│";

gotoxy(tx+16,ty+1); cout << "x1";

gotoxy(tx+19,ty+1); cout << "│";

gotoxy(tx+21,ty+1); cout << "ksi2";

gotoxy(tx+26,ty+1); cout << "│";

gotoxy(tx+28,ty+1); cout << "f2(x2,eta1)";

gotoxy(tx+40,ty+1); cout << "│";

gotoxy(tx+42,ty+1); cout << "Z3_max(ksi2,eta1+x1)";

gotoxy(tx+63,ty+1); cout << "│";

gotoxy(tx+65,ty+1); cout << "Z2(ksi1,eta1)";

gotoxy(tx+78,ty+1); cout << "│";

gotoxy(tx,ty+2); cout << "├";

for (i=0;i<c_x;i++)

cout << "─";

cout << "┤";

gotoxy(tx+7,ty+2); cout << "┼";

gotoxy(tx+14,ty+2); cout << "┼";

gotoxy(tx+19,ty+2); cout << "┼";

gotoxy(tx+26,ty+2); cout << "┼";

gotoxy(tx+40,ty+2); cout << "┼";

gotoxy(tx+63,ty+2); cout << "┼";

new_y=ty+3;

}

//-------------Определение методов класса таблицы---------------

void Table::NewString(double a1, double a2, double a3,

double a4, double a5, double a6, double a7)

{

gotoxy(tx,new_y);

for(int i=0;i<c_x;i++)

cout << " ";

gotoxy(tx+7,ty+2); cout << "┼";

gotoxy(tx+14,ty+2); cout << "┼";

gotoxy(tx+19,ty+2); cout << "┼";

gotoxy(tx+26,ty+2); cout << "┼";

gotoxy(tx+40,ty+2); cout << "┼";

gotoxy(tx+63,ty+2); cout << "┼";

gotoxy(tx,new_y); cout << "│";

gotoxy(tx+2,new_y) ; cout << a1;

gotoxy(tx+7,new_y); cout << "│";

gotoxy(tx+9,new_y) ; cout << a2;

gotoxy(tx+14,new_y); cout << "│";

gotoxy(tx+16,new_y); cout << a3;

gotoxy(tx+19,new_y); cout << "│";

gotoxy(tx+21,new_y); cout << a4;

gotoxy(tx+26,new_y); cout << "│";

gotoxy(tx+28,new_y); cout << a5;

gotoxy(tx+40,new_y); cout << "│";

gotoxy(tx+42,new_y); cout << a6;

gotoxy(tx+63,new_y); cout << "│";

gotoxy(tx+65,new_y); cout << a7;

gotoxy(tx+78,new_y); cout << "│";

new_y++;

if(new_y>24)

{

gotoxy(tx,new_y); cout << "└";

for (int i=0;i<c_x;i++)

cout << "─";

cout << "┘";

gotoxy(tx+7,ty+2); cout << "┴";

gotoxy(tx+14,ty+2); cout << "┴";

gotoxy(tx+19,ty+2); cout << "┴";

gotoxy(tx+26,ty+2); cout << "┴";

gotoxy(tx+40,ty+2); cout << "┴";

gotoxy(tx+63,ty+2); cout << "┴";

new_y=ty+3;

}

void Table::EndOfTable()

{

int i,j;

gotoxy(tx,new_y); cout << "└";

for (i=0;i<c_x;i++)

cout << "─";

cout << "┘";

gotoxy(tx+7,ty+2); cout << "┴";

gotoxy(tx+14,ty+2); cout << "┴";

gotoxy(tx+19,ty+2); cout << "┴";

gotoxy(tx+26,ty+2); cout << "┴";

gotoxy(tx+40,ty+2); cout << "┴";

gotoxy(tx+63,ty+2); cout << "┴";

gotoxy(tx,new_y+1);

for(j=new_y+1;j<26;j++)

{

for(i=tx;i<c_x+4;i++)

{

gotoxy(i,j);

cout << " ";

}

gotoxy(1,24);

}

//------------Сообщения-----------------------------------------

void MessageSend(char *MessageForFunc)

{

cout << MessageForFunc << endl;

getch();

}

//----Определения функций, характеризующих выпуск продукции-----

double f3(int arg1, int arg2)

{

if((arg1<0 || arg1>ksi_0) || (arg2<0 || arg2>ksi_0))

return (double)MAXINT;

double Values[ksi_0+1][ksi_0+1]={ 0, 3.4, 3.8, 4.2, 5.0, 5.0, 0,

0, 3.7, 4.1, 4.5, 5.3, 5.3, 0,

0, 3.7, 4.1, 4.5, 5.4, 0, 0,

0, 4.0, 4.5, 4.8, 0, 0, 0,

0, 4.2, 4.8, 0, 0, 0, 0,

0, 4.6, 0, 0, 0, 0, 0,

0, 0, 0, 0, 0, 0, 0 };

return Values[arg2][arg1];

}

double f2(int arg1, int arg2)

{

if((arg1<0 || arg1>ksi_0) || (arg2<0 || arg2>ksi_0))

return (double)MAXINT;

double Values[ksi_0+1][ksi_0+1]={ 0, 2.2, 2.8, 3.1, 4.3, 6, 0,

0, 3.1, 4.2, 5.3, 7.1, 8, 0,

0, 3.3, 4.5, 6.1, 7.3, 0, 0,

0, 3.5, 4.8, 6.7, 0, 0, 0,

0, 5.4, 5.9, 0, 0, 0, 0,

0, 0, 0, 0, 0, 0, 0,

0, 0, 0, 0, 0, 0, 0 };

return Values[arg2][arg1];

}

double f1(int arg1)

{

if(arg1<0 || arg1>ksi_0)

return (double)MAXINT;

double Values[ksi_0+1]={ 0, 2.1, 3.2, 4.3, 5.1, 5.1, 0 };

return Values[arg1];

}

int main(void)

{

clrscr();

Table ob;

int ksi, eta, x, i, j, Indexes[6][5], IndexOfMax = -1, X_opt[3];

double Z_2[6][5], Max=0, MayBeMax=0, Z_max;

for(i=0; i<6; i++)

for(j=0; j<5; j++)

{

Z_2[i][j]=0;

Indexes[i][j]=-1;

}

for(ksi=1; ksi<7; ksi++)

{

for(eta=0; eta<5; eta++)

{

Max = MayBeMax = 0;

for(x=0; x<ksi + 1; x++)

{

if((ksi + eta) > 6)

break;

MayBeMax = f2(x, eta) + f3(ksi - x, x + eta);

if(Max < MayBeMax)

{

Max = MayBeMax;

IndexOfMax = x;

}

ob.NewString(ksi, eta, x, ksi-x, f2(x, eta), f3(ksi - x, x + eta), MayBeMax);

getch();

}

if(Max>0)

{

Z_2[ksi-1][eta] = Max;

Indexes[ksi-1][eta] = IndexOfMax;

}

ob.EndOfTable();

getch();

Max = MayBeMax = 0;

for(x = 0; x<ksi_0; x++)

{

MayBeMax = f1(x) + Z_2[ksi_0 - 1 - x][x];

if(Max < MayBeMax)

{

Max = MayBeMax;

X_opt[0] = x;

}

Z_max = Max;

X_opt[1] = Indexes[ksi_0 - 1 - X_opt[0]][X_opt[0]];

Max = MayBeMax = 0;

for(i=0; i<ksi_0 + 1; i++)

{

MayBeMax = f3(i,X_opt[0]+1);

if(Max < MayBeMax)

{

Max = MayBeMax;

X_opt[2] = i;

}

cout << "Максимальный выпуск продукции: " << Z_max << endl;

cout << "достигается при распределении средств: ";

cout << "x1=" << X_opt[0] << ", x2=" << X_opt[1] << ", x3=" << X_opt[2];

getch();

return 0;

}

Результаты работы программы

┌──┬───┬──┬──┬───────┬────────────┬───────┬

│ksi1│eta1│x1│ksi2│f2(x2,eta1)│Z3_max(ksi2,eta1+x1)│ Z2(ksi1,eta1)│

├───┴───┴──┴──┴───────┴───────────┴───────┴

│ 1 │ 0 │ 0 │ 1 │ 0 │ 3.4 │ 3.4 │

│ 1 │ 0 │ 1 │ 0 │ 2.2 │ 0 │ 2.2 │

│ 1 │ 1 │ 0 │ 1 │ 0 │ 3.7 │ 3.7 │

│ 1 │ 1 │ 1 │ 0 │ 3.1 │ 0 │ 3.1 │

│ 1 │ 2 │ 0 │ 1 │ 0 │ 3.7 │ 3.7 │

│ 1 │ 2 │ 1 │ 0 │ 3.3 │ 0 │ 3.3 │

│ 1 │ 3 │ 0 │ 1 │ 0 │ 4 │ 4 │

│ 1 │ 3 │ 1 │ 0 │ 3.5 │ 0 │ 3.5 │

│ 1 │ 4 │ 0 │ 1 │ 0 │ 4.2 │ 4.2 │

│ 1 │ 4 │ 1 │ 0 │ 5.4 │ 0 │ 5.4 │

│ 2 │ 0 │ 0 │ 2 │ 0 │ 3.8 │ 3.8 │

│ 2 │ 0 │ 1 │ 1 │ 2.2 │ 3.7 │ 5.9 │

│ 2 │ 0 │ 2 │ 0 │ 2.8 │ 0 │ 2.8 │

│ 2 │ 1 │ 0 │ 2 │ 0 │ 4.1 │ 4.1 │

│ 2 │ 1 │ 1 │ 1 │ 3.1 │ 3.7 │ 6.8 │

│ 2 │ 1 │ 2 │ 0 │ 4.2 │ 0 │ 4.2 │

│ 2 │ 2 │ 0 │ 2 │ 0 │ 4.1 │ 4.1 │

│ 2 │ 2 │ 1 │ 1 │ 3.3 │ 4 │ 7.3 │

│ 2 │ 2 │ 2 │ 0 │ 4.5 │ 0 │ 4.5 │

│ 2 │ 3 │ 0 │ 2 │ 0 │ 4.5 │ 4.5 │

│ 2 │ 3 │ 1 │ 1 │ 3.5 │ 4.2 │ 7.7 │

│ 2 │ 3 │ 2 │ 0 │ 4.8 │ 0 │ 4.8 │

│ 2 │ 4 │ 0 │ 2 │ 0 │ 4.8 │ 4.8 │

│ 2 │ 4 │ 1 │ 1 │ 5.4 │ 4.6 │ 10 │

│ 2 │ 4 │ 2 │ 0 │ 5.9 │ 0 │ 5.9 │

│ 3 │ 0 │ 0 │ 3 │ 0 │ 4.2 │ 4.2 │

│ 3 │ 0 │ 1 │ 2 │ 2.2 │ 4.1 │ 6.3 │

│ 3 │ 0 │ 2 │ 1 │ 2.8 │ 3.7 │ 6.5 │

│ 3 │ 0 │ 3 │ 0 │ 3.1 │ 0 │ 3.1 │

│ 3 │ 1 │ 0 │ 3 │ 0 │ 4.5 │ 4.5 │

│ 3 │ 1 │ 1 │ 2 │ 3.1 │ 4.1 │ 7.2 │

│ 3 │ 1 │ 2 │ 1 │ 4.2 │ 4 │ 8.2 │

│ 3 │ 1 │ 3 │ 0 │ 5.3 │ 0 │ 5.3 │

│ 3 │ 2 │ 0 │ 3 │ 0 │ 4.5 │ 4.5 │

│ 3 │ 2 │ 1 │ 2 │ 3.3 │ 4.5 │ 7.8 │

│ 3 │ 2 │ 2 │ 1 │ 4.5 │ 4.2 │ 8.7 │

│ 3 │ 2 │ 3 │ 0 │ 6.1 │ 0 │ 6.1 │

│ 3 │ 3 │ 0 │ 3 │ 0 │ 4.8 │ 4.8 │

│ 3 │ 3 │ 1 │ 2 │ 3.5 │ 4.8 │ 8.3 │

│ 3 │ 3 │ 2 │ 1 │ 4.8 │ 4.6 │ 9.4 │

│ 3 │ 3 │ 3 │ 0 │ 6.7 │ 0 │ 6.7 │

│ 4 │ 0 │ 0 │ 4 │ 0 │ 5 │ 5 │

│ 4 │ 0 │ 1 │ 3 │ 2.2 │ 4.5 │ 6.7 │

│ 4 │ 0 │ 2 │ 2 │ 2.8 │ 4.1 │ 6.9 │

│ 4 │ 0 │ 3 │ 1 │ 3.1 │ 4 │ 7.1 │

│ 4 │ 0 │ 4 │ 0 │ 4.3 │ 0 │ 4.3 │

│ 4 │ 1 │ 0 │ 4 │ 0 │ 5.3 │ 5.3 │

│ 4 │ 1 │ 1 │ 3 │ 3.1 │ 4.5 │ 7.6 │

│ 4 │ 1 │ 2 │ 2 │ 4.2 │ 4.5 │ 8.7 │

│ 4 │ 1 │ 3 │ 1 │ 5.3 │ 4.2 │ 9.5 │

│ 4 │ 1 │ 4 │ 0 │ 7.1 │ 0 │ 7.1 │

│ 4 │ 2 │ 0 │ 4 │ 0 │ 5.4 │ 5.4 │

│ 4 │ 2 │ 1 │ 3 │ 3.3 │ 4.8 │ 8.1 │

│ 4 │ 2 │ 2 │ 2 │ 4.5 │ 4.8 │ 9.3 │

│ 4 │ 2 │ 3 │ 1 │ 6.1 │ 4.6 │ 10.7 │

│ 4 │ 2 │ 4 │ 0 │ 7.3 │ 0 │ 7.3 │

│ 5 │ 0 │ 0 │ 5 │ 0 │ 5 │ 5 │

│ 5 │ 0 │ 1 │ 4 │ 2.2 │ 5.3 │ 7.5 │

│ 5 │ 0 │ 2 │ 3 │ 2.8 │ 4.5 │ 7.3 │

│ 5 │ 0 │ 3 │ 2 │ 3.1 │ 4.5 │ 7.6 │

│ 5 │ 0 │ 4 │ 1 │ 4.3 │ 4.2 │ 8.5 │

│ 5 │ 0 │ 5 │ 0 │ 6 │ 0 │ 6 │

│ 5 │ 1 │ 0 │ 5 │ 0 │ 5.3 │ 5.3 │

│ 5 │ 1 │ 1 │ 4 │ 3.1 │ 5.4 │ 8.5 │

│ 5 │ 1 │ 2 │ 3 │ 4.2 │ 4.8 │ 9 │

│ 5 │ 1 │ 3 │ 2 │ 5.3 │ 4.8 │ 10.1 │

│ 5 │ 1 │ 4 │ 1 │ 7.1 │ 4.6 │ 11.7 │

│ 5 │ 1 │ 5 │ 0 │ 8 │ 0 │ 8 │

│ 6 │ 0 │ 0 │ 6 │ 0 │ 0 │ 0 │

│ 6 │ 0 │ 1 │ 5 │ 2.2 │ 5.3 │ 7.5 │

│ 6 │ 0 │ 2 │ 4 │ 2.8 │ 5.4 │ 8.2 │

│ 6 │ 0 │ 3 │ 3 │ 3.1 │ 4.8 │ 7.9 │

│ 6 │ 0 │ 4 │ 2 │ 4.3 │ 4.8 │ 9.1 │

│ 6 │ 0 │ 5 │ 1 │ 6 │ 4.6 │ 10.6 │

│ 6 │ 0 │ 6 │ 0 │ 0 │ 0 │ 0 │

└──────────────────────────────────────────

Максимальный выпуск продукции: 15.1

достигается при распределении средств: x1=4, x2=1, x3=1

* Управление на k-м шаге может характеризоваться качественно

** Термин «эффективность» понимается как некоторая оценка результата процесса. Она может выражать собой пoкaзaтeль, который желательно максимизировать (например, прибыль, фондоотдача, производительность) или показатель, который необходимо минимизировать (например, затраты, себестоимость, потери)