Курсовая работа: Открытые сети с многорежимными стратегиями обслуживания и информационными сигналами

Курсовая работа: Открытые сети с многорежимными стратегиями обслуживания и информационными сигналами

Министерство образования Республики Беларусь

Учреждение образования

«Гомельский государственный университет им. Ф. Скорины»

Математический факультет

Кафедра ТВ и мат статистики

Курсовая работа

ОТКРЫТЫЕ СЕТИ С МНОГОРЕЖИМНЫМИ СТРАТЕГИЯМИ ОБСЛУЖИВАНИЯ И ИНФОРМАЦИОННЫМИ СИГНАЛАМИ

Исполнитель:

Студент группы М-32 Левашов А.Ю.

Научный руководитель:

Канд. физ-мат. наук, доцент

Малинковский М.Т.

Гомель 2007

СОДЕРЖАНИЕ

ПЕРЕЧЕНЬ УСЛОВНЫХ ОБОЗНАЧЕНИЙ

ВВЕДЕНИЕ

1. ОТКРЫТЫЕ СЕТИ С МНОГОРЕЖИМНЫМИ СТРАТЕГИЯМИ ОБСЛУЖИВАНИЯ И ОТРИЦАТЕЛЬНЫМИ ЗАЯВКАМИ

2. ОТКРЫТЫЕ СЕТИ С МНОГОРЕЖИМНЫМИ СТРАТЕГИЯМИ ОБСЛУЖИВАНИЯ И ИНФОРМАЦИОННЫМИ СИГНАЛАМИ ДВУХ ТИПОВ

ЗАКЛЮЧЕНИЕ

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

 - число узлов в сети массового обслуживания, размерность вектора состояний марковского процесса, описывающего сеть;

 - число заявок, циркулирующих в замкнутой сети;

 - матрица маршрутизации для открытой сети;

 - матрица маршрутизации для замкнутой сети;

 - состояние -го узла;

 - число заявок в -ом узле ( для открытой сети,  для замкнутой сети);

 - номер режима работы прибора в -м узле ;

 - состояние -го узла в момент времени ;

 - число заявок в -м узле в момент времени ;

 - номер режима работы прибора в -м узле в момент времени ;

 - состояние сети массового обслуживания;

 - марковский процесс, описывающий состояние сети массового обслуживания в момент времени ;

 - марковский процесс, описывающий состояние изолированного узла в фиктивной окружающей среде;

 - пространство состояний случайного процесса  и марковского процесса  в случае открытой сети;

 - пространство состояний случайного процесса  и марковского процесса  в случае замкнутой сети;

 - пространство состояний марковского процесса  для открытой сети и  для замкнутой сети);

 - интенсивность перехода марковского процесса с непрерывным временем и не более чем счетным пространством состояний из состояния  в состояние ;

 - интенсивность выхода марковского процесса из состояния ;

 - стационарное распределение марковского процесса .

 - стационарное распределение марковского процесса  в случае открытой сети;

 - стационарное распределение марковского процесса  в случае замкнутой сети;

 - интенсивность пуассоновского потока, поступающего в открытую сеть;

 - интенсивность пуассоновского потока положительных заявок;

 - интенсивность пуассоновского потока отрицательных заявок (сигналов);

 - интенсивность пуассоновского потока сигналов, увеличивающих номер режима;

 - интенсивность пуассоновского потока сигналов, уменьшающих номер режима;

 - интенсивность обслуживания прибором -го узла, находящегося в состоянии ;

 - интенсивность перехода прибора -го узла с режима  на режим ;

 - интенсивность перехода прибора -го узла с режима  на режим ;

 - интенсивности потоков положительных заявок, отрицательных сигналов, сигналов увеличения номера режима, сигналов уменьшения номера режима соответственно в -й узел открытой сети;

 - вероятности направления в -й узел поступающих в открытую сеть положительных заявок, отрицательных сигналов, сигналов уменьшения номера режима, сигналов увеличения номера режима соответственно;

 - вероятности для заявки, обслуженной в -м узле, перейти в -й узел с превращением ее в положительную заявку, отрицательный сигнал, сигнал уменьшения номера режима, сигнал увеличения номера режима соответственно;

 - индикатор события , равный 1, если  происходит, и равный 0, если  не происходит.

ВВЕДЕНИЕ

Важными задачами для развития современного общества являются сбор, обработка, хранение и распространение информации. Передача информации представляет собой основу для решения этих задач и потому требует тщательного изучения. Адекватное описание процесса передачи информации с помощью математических моделей может быть осуществлено в рамках теории массового обслуживания. При этом для многих реальных систем такой процесс моделируется посредством сетей массового обслуживания. Например, к указанному результату приводит математическое моделирование мультипрограммных вычислительных систем и анализ их производительности, проектирование и анализ сетей передачи данных и сетей ЭВМ.

В начале XX века датский ученый А.К.Эрланг, работавший на копенгагенской телефонной станции, поставил и решил ряд новых математическтх задач, позволивших оценивать характеристики телефонных и телеграфных линий связи. Это способствовало возникновению нового направления в теории вероятностей - теории массового обслуживания. На начальной стадии своего развития теория массового обслуживания имела дело с системами массового обслуживания, которые описываются потоками однородных заявок, поступающих в систему, процедурами обслуживания с помощью одного или нескольких каналов, процедурами формирования очередей и способами организации процесса ожидания заявок. Строгое научное описание случайных процессов в теории массового обслуживания и их всестороннее исследование впервые было осуществлено А.Я.Хинчиным. Он исследовал одноканальную систему с ожиданием, простейшим входным потоком и рекуррентным обслуживанием, установив для нее так называемый основной закон стационарной очереди: стационарное распределение числа заявок в системе совпадает с их стационарным распределением в случайные моменты ухода заявок из системы. Большой вклад в развитие теории массового обслуживания внесли Ю.К.Беляев, А.А.Боровков, Б.В.Гнеденко, Н.Джейсуолл, Дж.Р.Джексон, Ф.П.Келли, Дж.Кендалл, Дж.Ф.С.Кингмэн, Л.Клейнрок, Г.П.Климов, И.Н.Коваленко, С.Пальм, Ф.Поллачек, Ю.В.Прохоров, Дж.Риордан, Т.Саати, В.Л.Смит и др.

В 1957г. Дж.Р.Джексон впервые ввел в рассмотрение понятие открытой сети массового обслуживания ([99]), а в 1967г. Гордон и Ньюэлл ввели аналогичное понятие замкнутой сети ([91]). В отличие от системы массового обслуживания сеть представляет собой более сложное образование, состоящее из систем массового обслуживания, называемых узлами сети, которые взаимодействуют между собой с помощью некоторого вероятностного механизма. В открытых сетях заявки могут поступать извне, а также уходить из сети. В замкнутых сетях сохраняется постоянное число заявок, которые с помощью случайной маршрутизации могут перемещаться между узлами сети; при этом поступление заявок в сеть и уход заявок из сети невозможны.

Результаты Джексона и Гордона-Ньюэлла не использовались до тех пор, пока в 1971г. Ф.Р.Мур [115] не обнаружил, что замкнутые сети адекватно описывают вычислительные системы со многими ресурсами. С этого момента теория сетей обслуживания стала быстро развиваться благодаря задачам, связанным с математическим моделированием мультипрограммных вычислительных систем и анализом их производительности, с проектированием и анализом сетей передачи данных и сетей ЭВМ. Дополнительный толчок к дальнейшему развитию теории дала разработка и использование в повсеместной практике различных глобальных и локальных сетей таких, например, как EZERNET, INTERNET и т.д. Значительный вклад в развитие теории сетей внесли Г.П.Башарин, А.А.Боровков, Э.Геленбе, Дж.Джексон, В.А.Ивницкий, Ф.П.Келли, Д.Кениг, Л.Клейнрок, Ю.В.Малинковский, М.Миязава, Б.Меламед, Р.Мюнтц, С.Е.М.Перс, П.К.Поллетт, А.Н.Рыбко, Р.Серфозо, Ю.М.Сухов, П.Тейлор, А.Л.Толмачев, Д.Тоусли, П.Уиттли, Дж.Уолрэнд, Г.И.Фалин, В.Хендерсон, Х.Чао, К.Ченди, Р.Шассбергер и многие другие.

Состояние сети массового обслуживания обычно характеризуется вектором, координаты которого описывают состояния отдельных узлов сети. В силу многомерности случайного процесса состояний и статистической зависимости между координатами исследование сетей массового обслуживания на порядок сложнее, чем исследование систем массового обслуживания. Даже в случае экспоненциальных сетей, когда случайный процесс состояний является марковским, его эргодическое стационарное распределение удовлетворяет настолько сложной системе уравнений, что решить ее удается в основном только тогда, когда решение имеет форму произведеня. Множители в этом произведении зависят только от свойств индивидуальных узлов. В имеющейся литературе по стационарному распределению экспоненциальных сетей практически не рассматриваются сети с ненадежными или частично ненадежными приборами. В считанных работах рассмотрены только очень частные вырожденные случаи и то для сетей, состоящих из двух узлов. В то же время в практических ситуациях оборудование может частично или полностью выходить из строя. Например, при работе на персональном компьютере очень часто нарушаются функциональные связи между некоторыми файлами, программами или другими элементами, хотя компьютер продолжает работать. Налицо частичная потеря работоспособности, а значит, уменьшение интенсивности обслуживания.

Поэтому в данной работе предпринята попытка построения моделей, адекватно описывающих такую ситуацию. Рассмотрены экспоненциальные сети с многорежимными стратегиями обслуживания, в которых обслуживающие устройства в узлах частично ненадежны и в различных режимах функционирования работают с разными интенсивностями. Для таких сетей находится инвариантная вероятностная мера в мультипликативной форме.

Рассматривается открытая сеть массового обслуживания с экспоненциальным обслуживанием в узлах и марковской маршрутизацией, в которую поступают два независимых между собой пуассоновских стационарных потока: обычных (положительных) заявок, требующих обслуживания в узлах, и так называемых отрицательных заявок, которые не обслуживаются и могут удалять из узлов заявки (-сеть). Положительная заявка после обслуживания может с некоторой вероятностью трансформироваться в отрицательную. Однолинейные узлы могут работать в нескольких режимах, время переключения с одного режима на другой имеет показательное распределение с параметром, зависящим от состояния узла. Переключение происходит только на соседние режимы. Устанавливается условие эргодичности и находится стационарное распределение состояний сети в мультипликативной форме.

Постановка задачи.

В главе 2 рассматривалась открытая сеть с многорежимными стратегиями обслуживания, в которой приборы могут частично выходить из строя, работая при этом в "щадящем" режиме. В 4.1 рассматривается аналогичная сеть при упрощающем предположении, состоящем в том, что интенсивности обслуживания в узле не зависят от его состояния. Однако добавляется возможность поступления в сеть так называемых отрицательных заявок и возможность трансформирования обычных (положительных) заявок в отрицательные, что существенно усложняет задачу, превращая, в частности, линейные уравнения трафика в нелинейные.

В сеть, состоящую из  однолинейных узлов, поступают два независимых стационарных пуассоновских потока: положительных заявок с параметром  и отрицательных заявок с параметром . Отрицательные заявки в отличие от обычных (положительных) заявок не требуют обслуживания, а поступление отрицательной заявки в узел уменьшает число заявок в нем на единицу, если число заявок в узле больше нуля, и не производит никаких изменений, если в узле нет заявок. После указанных операций отрицательные заявки исчезают и в дальнейшем не оказывают влияния на сеть. Каждая заявка входного потока положительных заявок независимо от других заявок с вероятностью  направляется в -й узел, а каждая заявка входного потока отрицательных заявок независимо от других заявок с вероятностью  направляется в -й узел . Положительная заявка, обслуженная в -м узле, мгновенно направляется в -й узел, с вероятностью  оставаясь положительной и с вероятностью  превращаясь в отрицательную, или покидает сеть с вероятностью  В -м узле находится единственный прибор, который может работать в  режимах. Состояние -го узла характеризуется парой чисел , где  - число положительных заявок в -м узле,  - номер режима, в котором работает прибор в -м узле . Длительность обслуживания прибором -го узла положительных заявок имеет показательное распределение с параметром . Назовем 0 основным режимом работы. Время пребывания в основном режиме работы имеет показательное распределение с параметром , после чего прибор переходит в режим 1. Для состояний , у которых , время пребывания в режиме  также имеет показательное распределение, при этом с интенсивностью  прибор -го узла переходит в режим , а с интенсивностью  - в режим . Время пребывания в последнем -м режиме имеет показательное распределение с параметром , после чего прибор переходит в -й режим. Во время переключения прибора с одного режима работы на другой число заявок в узле не меняется.

Состояние сети в момент времени  будем характеризовать вектором , где  - состояние -го узла в момент времени . В соответствии с вышесказанным здесь  - число положительных заявок в -м узле в момент ,  - номер режима работы -го узла в момент . Основная цель данной работы - нахождение стационарного распределения марковского процесса .

Предположим, что все величины  строго положительны. Обозначим через  среднюю интенсивность поступления положительных заявок в -й узел, а через  среднюю интенсивность поступления отрицательных заявок в -й узел. Эти интенсивности удовлетворяют следующей системе нелинейных уравнений трафика:

Лемма 1.1 [54, C.91]. Система уравнений (4.1.1), (4.1.2) имеет решение

.

Доказательство. Так как  - непрерывная функция от  и , то доказательство следует из результата [90], полученного в этой работе с помощью теоремы Брауэра о неподвижной точке.

В дальнейшем будем предполагать, что существует решение (4.1.1),(4.1.2), для которого все . Для того, чтобы это выполнялось, надо наложить некоторые условия на маршрутизацию заявок в сети. Например, такое решение будет заведомо существовать, если при каждом  выполняется условие . На самом деле можно наложить гораздо менее жесткие условия. Всюду в дальнейшем под словами решение (4.1.1),(4.1.2) будет пониматься именно такое решение. Это предположение гарантирует неприводимость марковского процесса  на фазовом пространстве , где .

 Изолированный узел в фиктивной окружающей среде.

Рассмотрим изолированный -й узел в фиктивной окружающей среде, считая, что в него поступают два независимых пуассоновских потока: положительных заявок с параметром  и отрицательных заявок с параметром , где  и  найдены из системы уравнений трафика (4.1.1),(4.1.2). Окружающая среда является фиктивной потому, что в самой сети потоки заявок на ее узлы не являются простейшими. Необходимым и достаточным условием обратимости, а, значит, и квазиобратимости изолированного узла является условие

Действительно, модифицируя доказательство леммы 2.2, получаем, что при его выполнении произведение интенсивностей, ведущих из любого состояния в это же самое состояние по ребрам элементарного квадрата по и против часовой стрелки совпадают для марковского процесса, описывающего такой изолированный узел. Условия (4.1.3) выполняются, в частности, если интенсивности переходов из одного режима в другой не зависят от состояния узла. Обозначая через  финальные стационарные вероятности его состояний, запишем уравнения обратимости для изолированного узла:

Из этих уравнений легко определяются стационарные вероятности состояний изолированного узла в фиктивной окружающей среде:

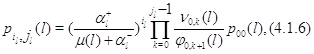
где

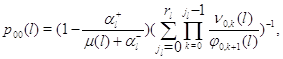
и, как всегда, предполагается, что произведение, в котором нижний индекс больше верхнего, равно 1.

Согласно эргодической теореме Фостера [82] для эргодичности марковского процесса, описывающего изолированный узел в фиктивной окружающей среде, достаточно существования нетривиального неотрицательного решения системы уравнений равновесия такого, что

Если

то в силу (4.1.6) ряд  сходится как сумма геометрической прогрессии со знаменателем, меньшим единицы. При выполнении условия

интенсивность выхода из состояния  ограничена:

Поэтому при выполнении условий

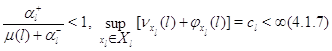
сходится ряд  и по эргодической теореме Фостера марковский процесс, описывающий изолированный узел в фиктивной окружающей среде эргодичен.

 Основной результат. Пусть  - интенсивность перехода процесса  из состояния  в состояние ,  - интенсивность его выхода из состояния ,  - вектор , у которого все  кроме  равны 0, а , и все ,  - вектор , у которого все  и все  кроме  равны 0, а . Очевидно, интенсивности перехода процесса  имеют следующий вид:

для всех иных состояний  выполняется .

Интенсивность выхода получается сложением этих интенсивностей:

Основной результат 4.1 состоит в следующем.

Теорема 1.1. [54, C.92], [55, C.180] Если для всех  выполняются условия (4.1.3) и неравенства (4.1.7), то марковский процесс  эргодичен, а его финальное стационарное распределение имеет форму произведения

где  - стационарное распределение изолированного -го узла в фиктивной окружающей среде, определяемое с помощью соотношений (4.1.6).

Доказательство. Для доказательства того, что , определенные в (4.1.15), образуют стационарное распределение марковского процесса , достаточно [94,97,103] подобрать функцию

которая удовлетворяла бы соотношениям

и

Если такие  удастся найти (см. [94,97,103]), то окажется, что  будут являться инфинитезимальными интенсивностями перехода для обращенной во времени цепи Маркова , а  - стационарными вероятностями для  и . Положим

для всех остальных состояний  положим . Для функции  соотношение (4.1.16) действительно выполняется, что легко проверяется подстановкой в него равенств (4.1.8)-(4.1.13), (4.1.18)-(4.1.23) и использования (4.1.4),(4.1.5). Остается доказать (4.1.17). Складывая (4.1.18)-(4.1.23), получим, что

Используя (4.1.1)-(4.1.2), имеем

Применяя снова (4.1.1)-(4.1.2), а также свойства индикаторов, получим

Сравнивая полученный результат с (4.1.14), делаем вывод, что  для любого состояния . Докажем, что при выполнении условий (4.1.7) марковский процесс  эргодичен. Согласно эргодической теореме Фостера [82], для этого достаточно доказать, что существует нетривиальное неотрицательное решение уравнений глобального равновесия

такое, что ряд  сходится. Складывая (4.1.16) по всем , убеждаемся, что  является решением (4.1.24). Из (4.1.14) следует, что

Поскольку ряд

распадается в произведение  рядов, каждый из которых сходится в силу условия (4.1.7) как сумма бесконечной геометрической прогрессии со знаменателем, меньшим единицы, то и сам он сходится. В силу (4.1.25) будет сходиться ряд

По эргодической теореме Фостера это означает, что марковский процесс  эргодичен. Таким образом, теорема доказана полностью.

Замечание 4.1. Если условия (4.1.3) и (4.1.7) выполнены во всех узлах, то получается простой алгоритм для нахождения стационарных вероятностей:

1. Проверяется выполнение условий (4.1.3).

2. Решается система нелинейных уравнений (4.1.1)-(4.1.2).

3. Проверяется выполнение (4.1.7).

4. Определяются  с помощью соотношений (4.1.6).

5. Находится стационарное распределение состояний сети  с помощью формулы (4.1.15).

Этот алгоритм может быть дополнен алгоритмом расчета совместного стационарного распределения чисел заявок в узлах и совместного стационарного распределения номеров режимов работы узлов, а также расчета моментов этих распределений. Если  - состояние сети, где , то через  обозначим вектор, характеризующий числа положитнльных заявок в узлах, а через  - вектор, характеризующий режимы работы в узлах. Стационарные распределения этих двух векторов обозначим соответственно  и .

Нетрудно убедиться, складывая (4.1.15) по всем возможным значениям , что совместное стационарное распределение чисел положительных заявок в узлах имеет следующую форму:

где каждый множитель имеет геометрическое распределение

Производящая функция стационарного распределения числа заявок в -м узле имеет вид

а -й факториальный момент есть

Как и следовало ожидать, в стационарном режиме среднее число положительных заявок и дисперсия числа положительных заявок в каждом узле,

стремятся к нулю, когда загрузка этого узла

Точно так же, складывая (4.1.15) по всем возможным значениям , определим совместное стационарное распределение режимов в узлах сети:

где

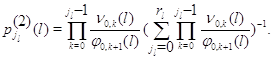
Средний номер режима работы -го узла в стационарной сети находится как

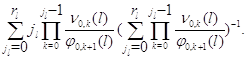
Анализ характера выходящих потоков из сети провести крайне трудно, так как эти потоки являются сложными благодаря воздействию отрицательных заявок и из-за нелинейности уравнений трафика.

В 1 исследовалось стационарное распределение марковского процесса, описывающего открытую сеть с многорежимными стратегиями обслуживания и отрицательными заявками. Здесь мы рассмотрим открытую сеть массового обслуживания, в которую наряду с отрицательными заявками, называемыми в дальнейшем отрицательными сигналами, поступает еще один вид информационных сигналов, изменяющих режим функционирования обслуживающих устройств в узлах.

На фазовом пространстве  задан многомерный марковский процесс , где , своими инфинитезимальными интенсивностями перехода: для  

для всех других состояний  предполагается, что . Интенсивность выхода получается сложением этих интенсивностей:

Этот процесс описывает сеть, состоящую из  однолинейных узлов, в которую поступают четыре независимых стационарных пуассоновских потока: положительных заявок с параметром , отрицательных сигналов с параметром , сигналов уменьшения режима с параметром , сигналов увеличения режима с параметром . Поступление отрицательного сигнала в узел уменьшает число заявок в нем на единицу, если число заявок в узле больше нуля, и не производит никаких изменений, если в узле нет заявок. Сигнал уменьшения режима при поступлении в -й узел с режимом  переводит его в режим работы , не изменяя числа заявок в узле, и не производит никаких изменений, если узел находится в режиме работы 0; сигнал увеличения режима при поступлении в -й узел с режимом  переводит его в режим работы , не изменяя числа заявок в узле, и не производит никаких изменений, если узел находится в режиме работы . После этих операций информационные сигналы пропадают, не оказывая более влияния на сеть. Поступающие положительная заявка, отрицательный сигнал, сигнал уменьшения и сигнал увеличения режима направляются в -й узел соответственно с вероятностями . Положительная заявка, обслуженная в -м узле, мгновенно направляется в -й узел, с вероятностью  оставаясь положительной, с вероятностью  превращаясь в отрицательный сигнал, с вероятностью  - в сигнал понижения режима, с вероятностью  - в сигнал повышения режима, или с вероятностью  покидает сеть . Длительность обслуживания прибором -го узла положительных заявок имеет показательное распределение с параметром . Режимы работы и интенсивности перехода с режима на режим определяются как в предыдущем разделе. Состояние сети в момент времени  описывается так же, только теперь  - число положительных заявок в -м узле в момент .

Предположим, что все величины  положительны. Пусть  - средние интенсивности поступления в -й узел положительных заявок, отрицательных сигналов, сигналов понижения и повышения режимов соответственно, удовлетворяющие системе нелинейных уравнений трафика:

Уравнения (4.2.3) имеют решение. Действительно, первые два уравнения в (4.2.3) совпадают с уравнениями трафика (4.1.1),(1.1.2), которые имеют решение . Очевидно, по найденным  из третьего и четвертого уравнений (4.2.3) однозначно определятся .

Рассмотрим изолированный -й узел в фиктивной окружающей среде, считая, что в него поступают четыре независимых пуассоновских потока: положительных заявок с параметром , отрицательных сигналов с параметром , сигналов уменьшения режима с параметром  и сигналов увеличения режима с параметром . Необходимым и достаточным условием обратимости, а, значит, и квазиобратимости изолированного узла является условие

что проверяется с помощью простой модификации доказательства леммы 2.2. Заметим, что это условие заведомо выполняется, когда интенсивности переходов с режима на режим  не зависят от состояния узла. Уравнения обратимости для изолированного узла имеют вид:

Из уравнений (4.2.5) находим

Полагая в (4.2.6)  и заменяя  на , получим:

откуда

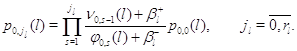
Подставляя это в (4.2.7), имеем:

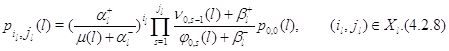
Из условия нормировки находим, что

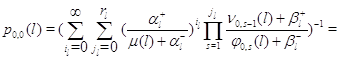
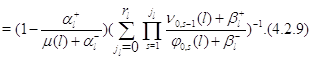
В силу теоремы Фостера [82] для эргодичности изолированного узла достаточно выполнения неравенств

Доказательство дословно повторяет то, которое использовалось при доказательстве аналогичного утверждения в 4.1.2, с заменой оценки для  следующей оценкой:

Отметим то обстоятельство, что вторая часть (4.2.10) заведомо имеет место, когда интенсивности переходов с режима на режим не зависят от состояния узла. Заметим также, что второе неравенство в (4.2.10) гарантирует регулярность марковского процесса, описывающего изолированный узел в фиктивной окружающей среде. Это означает, что за конечное время процесс не может сделать бесконечное число переходов из одного состояния в другое (моменты скачков процесса не могут иметь конечной предельной точки).

Теорема 2.2. [45, C.186] Если для всех  выполняются условия (4.2.4) и (4.2.10), то марковский процесс  эргодичен, а его стационарное распределение имеет форму произведения (4.1.15), где  определяются с помощью соотношений (4.2.8),(4.2.9).

Доказательство. Для доказательства того, что , определенные в (4.1.15),(4.2.5),(4.2.6), образуют стационарное распределение марковского процесса , достаточно [94,97,103] подобрать функцию  которая удовлетворяла бы соотношениям

Если такие  удастся найти (см. [94,97,103]), то окажется, что  будут являться инфинитезимальными интенсивностями перехода для обращенной во времени цепи Маркова , а  - стационарными вероятностями для  и . Положим

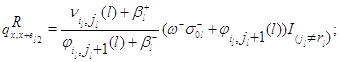
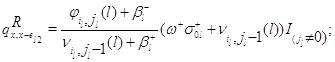
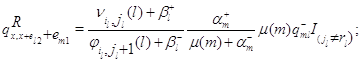
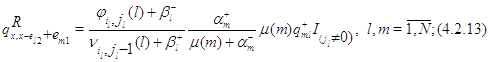
для всех остальных состояний  положим . Для функции  (4.2.11) действительно выполняется, что легко проверяется подстановкой в него равенств (4.2.1),(4.2.13) и использования (4.2.8),(4.2.9). Остается доказать (4.2.12). Складывая (4.2.13), получим, что

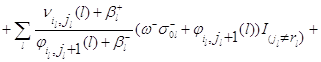
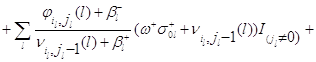
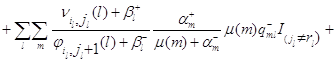
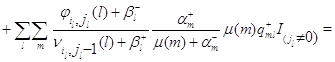
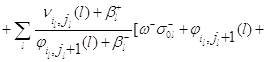
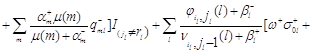
Используя (4.2.3), имеем

Применяя снова (4.2.3), свойства индикаторов и тот факт, что , получим

Сравнивая полученный результат с (4.2.2), делаем вывод, что  для любого состояния .

Докажем, что при выполнении условий (4.2.10) марковский процесс  эргодичен. Согласно эргодической теореме Фостера [82], для этого достаточно доказать, что существует нетривиальное неотрицательное решение уравнений глобального равновесия

такое, что ряд  сходится. Складывая (4.2.11) по всем , убеждаемся, что  является решением (4.2.14). Из (4.2.2) следует, что

Поскольку ряд

распадается в произведение  рядов, каждый из которых сходится в силу условия (4.2.10) как сумма бесконечной геометрической прогрессии со знаменателем, меньшим единицы, то и сам он сходится. В силу (4.2.15) будет сходиться ряд

По эргодической теореме Фостера это означает, что марковский процесс  эргодичен. Таким образом, теорема доказана полностью.

 Замечание 4.2. Если условия (4.2.4) и (4.2.10) выполнены во всех узлах, то получается следующий алгоритм для нахождения стационарных вероятностей:

1. Проверяется выполнение условий (4.2.4).

2. Решается система нелинейных уравнений (4.2.3).

3. Проверяется выполнение (4.2.10).

4. Определяются  с помощью соотношений (4.2.8), (4.2.9).

5. Находится стационарное распределение состояний сети  с помощью формулы (4.1.15).

Этот алгоритм также может быть дополнен алгоритмом расчета совместного стационарного распределения чисел заявок в узлах и совместного стационарного распределения номеров режимов работы узлов, а также расчета моментов этих распределений.

Если  - состояние сети, где , то через  обозначим вектор, характеризующий числа положитнльных заявок в узлах, а через  - вектор, характеризующий режимы работы в узлах. Стационарные распределения этих двух векторов обозначим соответственно  и .

Нетрудно убедиться, складывая (4.1.15) по всем возможным значениям , что совместное стационарное распределение чисел положительных заявок в узлах имеет следующую форму:

где каждый множитель имеет геометрическое распределение

Производящая функция стационарного распределения числа заявок в -м узле имеет вид

а -й факториальный момент есть

Как и следовало ожидать, в стационарном режиме среднее число положительных заявок и дисперсия числа положительных заявок в каждом узле,

стремятся к нулю, когда загрузка этого узла

Точно так же, складывая (4.1.15) по всем возможным значениям , определим совместное стационарное распределение режимов в узлах сети:

где

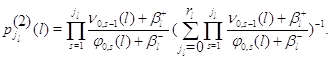
Средний номер режима работы -го узла в стационарной сети находится как

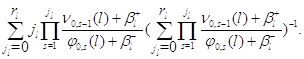
Анализ выходящих из сети потоков положительных заявок не проводился, поскольку, как и в предыдущем подразделе, такие потоки носят сложный характер из-за нелинейности уравнений трафика.

ЗАКЛЮЧЕНИЕ

В работе рассмотрена открытая сеть массового обслуживания с многорежимными стратегиями обслуживания, в которую наряду с обычными, положительными заявками поступают пуассоновские потоки информационных сигналов, оказывающих разовое воздействие на соответствующий узел сети. Интенсивность обслуживания прибором узла зависит от номера узла, но не зависит от его состояния. Предполагалось, что при помещении изолированного узла в фиктивную окружающую среду, характеризующуюся поступлением в него пуассоновских независимых потоков положительных заявок и информационных сигналов каждого типа, узел описывается обратимым марковским процессом с непрерывным временем и счетным пространством состояний. Положительная заявка после обслуживания в некотором узле может остаться положительной, а может превратиться в информационный сигнал любого из рассматриваемых типов. Рассмотрены два случая: а)кроме положительных заявок в сеть могут поступать отрицательные заявки; б)кроме положительных заявок в сеть могут поступать отрицательные сигналы, сигналы умньшения и сигналы увеличения номера режима на единицу.

Для обоих случаев составлены нелинейные уравнения трафика и доказано существование их решения, установлены достаточные условия эргодичности марковского процесса, характеризующего состояния рассматриваемых открытых сетей, и в аналитической форме найдено финальное стационарное распределение состояний этого процесса. Построен алгоритм для расчета стационарных вероятностей состояний сети.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1. Анисимов B.B., Лебедев Е.А. Стохастические сети обслуживания. Марковские модели. - Киев: Лыбидь, 1992. - 205 с.

2. Башарин Г.П., Бочаров П.П., Коган Я.А. Анализ очередей в вычислительных сетях. - М.: Наука. - 1989. - 336с.

3. Башарин Г.П., Толмачев А.Л. Некоторые результаты теории сетей массового обслуживания // Методы развития теории телетрафика. - М. - 1970. - С.52-65.

4. Башарин Г.П., Толмачев А.Л. Теория сетей массового обслуживания и ее приложения к анализу информационно-вычислительных систем // Итоги науки и техники. - М., 1983. - Т.21. - С.3-119. - (Сер. Теория вероятностей. Матем. статистика. Теор. кибернетика / ВИНИТИ).

5. Бочаров П.П., Печинкин А.В. Теория массового обслуживания: Учебник. - М.: РУДН, 1995. - 529с.

6. Гихман И.И., Скороход А.В. Введение в теорию случайных процессов. - М.: Наука, 1977. - 568с.

7. Горцев А.М., Назаров А.А., Терпугов А.Ф. Управление и адаптация в системах массового обслуживания. - Томск: ТГУ, 1978. - 208с.

8. Добрушин Р.Л., Кельберт М.Я., Рыбко А.Н., Сухов Ю.М. Качественные методы теории сетей с очередями // Препринт. -М., 1986. - 50с. - (ИППИ АН СССР).

9. Евдокимович В.Е., Малинковский Ю.В. Сети массового обслуживания с динамической маршрутизацией и динамическими вероятностными обходами узлов заявками // Проблемы передачи информации. - 2001. - Том 37, вып.3. - С.55-66.

10. Жожикашвили В.А., Вишневский В.М. Сети массового обслуживания. Теория и применение к сетям ЭВМ. - М.: Радио и связь. - 1988. - 192с.

11. Ивницкий В.А. Сети массового обслуживания и их применение в ЭВМ // Зарубежная радиоэлектроника. - 1977. - №7. - С.33-70.

12. Ивницкий В.А. Об условии независимости стационарных вероятностей состояний разомкнутой сети однолинейных систем с потерями от вида распределений длительностей обслуживания // Известия АН СССР. Техническая кибернетика. - 1981. - №4. - С.136-140.

13. Ивницкий В.А. Об условии инвариантности стационарных вероятностей для сетей массового обслуживания // Теория вероятностей и ее применения. - 1982. - Т. 27, 1. - С.188-192.

14. Ивницкий В.А. Об инвариантности стационарных вероятностей состояний для замкнутых сетей однолинейных СМО // ДАН УССР. А. - 1989. - №7. - С.8-11.

15. Ивницкий В.А. Об условии инвариантности стационарных вероятностей состояний для сетей однолинейных СМО // Теория вероятностей и ее применения. - 1989. - Т. 34, 3. - С.576-580.

16. Ивницкий В.А. Об инвариантности стационарных вероятностей состояний для сетей многолинейных систем массового обслуживания с абсолютным приоритетом поступающего требования и дообслуживанием // Исследование систем и сетей массового обслуживания: Тез. докл. 12-й Бел. зимней школы-семинара по ТМО, Гродно, янв.-февр. 1996 г. / Бел. гос. унив. - Минск, 1996. - С.36-37.

17. Кельберт М.Я., Сухов Ю.М. Математические вопросы теории сетей с очередями // Итоги науки и техники. - М., 1988. - Т.26. - С.3-96. - (Сер. Теория вероятностей. Матем. статистика. Теор. кибернетика / ВИНИТИ).

18. Кениг Д., Рыков В.В., Шмидт Ф. Стационарные системы массового обслуживания с зависимостями // Итоги науки и техники. - М., 1981. - Т.18. - С.95-186. - (Сер. Теория вероятностей. Матем. статистика. Теор. кибернетика / ВИНИТИ).

19. Клейнрок Л. Коммуникационные сети. - М.: Наука, 1970. - 255с.

20. Клейнрок Л. Вычислительные системы с очередями. - М.: Мир, 1979. - 600с.

21. Климов Г.П. Стохастические системы обслуживания. - М.: Наука, 1966. - 243с.

22. Ковалев Е.А. Сети с ненадежными каналами и резервом//Математические методы исследования сетей связи и сетей ЭВМ. Тезисы докладов VI Белорусской школы-семинара по ТМО. - Минск,1990. - С.70-71.