Рефераты по сексологии
Рефераты по информатике программированию
Рефераты по биологии
Рефераты по экономике
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Рефераты по авиации и космонавтике
Рефераты по административному праву
Рефераты по безопасности жизнедеятельности
Рефераты по арбитражному процессу
Рефераты по архитектуре
Рефераты по астрономии
Рефераты по банковскому делу
Рефераты по биржевому делу
Рефераты по ботанике и сельскому хозяйству
Рефераты по бухгалтерскому учету и аудиту
Рефераты по валютным отношениям
Рефераты по ветеринарии
Рефераты для военной кафедры
Рефераты по географии
Рефераты по геодезии
Рефераты по геологии
Рефераты по геополитике
Рефераты по государству и праву
Рефераты по гражданскому праву и процессу
Рефераты по делопроизводству
Рефераты по кредитованию
Рефераты по естествознанию
Рефераты по истории техники
Рефераты по журналистике
Рефераты по зоологии
Рефераты по инвестициям
Рефераты по информатике
Исторические личности
Рефераты по кибернетике
Рефераты по коммуникации и связи
Курсовая работа: Построение траектории Броуновского движения
Курсовая работа: Построение траектории Броуновского движения
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
«Брестский государственный университет имени А. С. Пушкина»
Кафедра информатики и прикладной математики
Курсовая работа
ПОСТРОЕНИЕ ТРАЕКТОРИИ БРОУНОВСКОГОДВИЖЕНИЯ
студентка 3 курса специальности
Александр Леонидович
ВВЕДЕНИЕ
1. СЛУЧАЙНЫЕ ФРАКТАЛЫ
1.1 Снежинка Коха
1.2 Салфетка Серпинского
1.3 Броуновское движение
2. СУТЬ БРОУНОВСКОГО ДВИЖЕНИЯ
3. ОПРЕДЕЛЕНИЕ
4. ПРОГРАММИРОВАНИЕ НА DELPHI
4.1 Код программы «Броуновское движение, как хаотичное движение частиц»
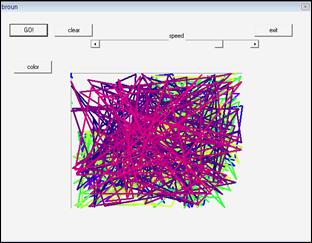
4.2 Код программы «Построение траектории броуновское движение»
ЗАКЛЮЧЕНИЕ
ЛИТЕРАТУРА
Для того чтобы раскрыть суть броуновского движения необходимо иметь понятие о хаосе и фракталах. Ведь броуновское движение, яркий пример фрактала, который впервые наблюдал в 19 веке шотландский ботаник Роберт Браун. Он же в 1827 году должным образом описал наблюдаемый эффект.
Какими же инструментами располагает теория хаоса? В первую очередь это фракталы.
Мандельброт ввел в употребление термин фрактал, основываясь на теории фрактальной (дробной) размерности Хауодорфа предложенной в 1919 году. Он отыскал нишу для имевших дурную репутацию множеств Кантора, кривых Пеано, функций Вейерштрасса и их многочисленных разновидностей, которые считались нонсенсом. Он и его ученики открыли много новых фракталов, например, фрактальное броуновское движение
Траектории частиц броуновского движения, которым занимались Роберт Броун еще в 1828 году и Альберт Эйнштейн в 1905 году, представляют собой пример фрактальных кривых, хотя их математическое описание было дано только в 1923 году Норбертом Винером. В 1890 году Пеано сконструировал свою знаменитую кривую.
Но в тоже время, как это часто случается в так называемой новой математике, открытия опираются на работы великих математиков прошлого. Исаак Ньютон понимал это, говоря «Если я и видел дальше других, то только потому, что стоял на плечах гигантов».
Изучение фракталов и хаоса открывает замечательные возможности, как в исследовании бесконечного числа приложений, так и в области чистой математики, именно поэтому, этот факт является целью написания данной работы. Здесь описывается суть броуновского движения и траектории, особенности открытия этого явления, определение (с точки зрения теории вероятности) и примеры программирования, что в свою очередь, говорит о возможности применения данного «хаоса» в различных приложениях.
Фрактальные объекты повсеместно встречаются в природе. Это модели снежинок, деревьев, кустов, листьев и тому подобных объектов. Однако фракталы, получаемые с помощью L-систем или СИФ, обладают одним явным недостатком, ограничивающим их применение для моделирования естественных объектов. Они детерминированы.
Построение этих фракталов не сводится к случайным возмущениям детерминированных фракталов. Напротив, случайный характер присущ им изначально, что связано со случайными процессами.
Основной моделью является фрактальное броуновское движение – случайный процесс, широко распространенный в природе.
Некоторые примеры фракталов:
1.1 Снежинка Коха
Снежинка Коха представляет собой линию бесконечной длины, ограничивающую конечную площадь, которая в 1.6 раза больше площади образующего ее треугольника.
Пример построения этого фрактала изображен ниже на рис.1.

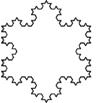


Рис.1.Снежинка Коха
Три первых шага в построении этого фрактала изображены на рис.2, а сам фрактал — на рис.3.
Число треугольных пар все меньшего и меньшего масштаба в нем бесконечно. Число черных треугольников в этом построении растет как 3n, где n — номер шага, а длина их стороны уменьшается как 2–n. Легко показать, что площадь белых пятен равна площади исходного треугольника.

Рис.2 Построение салфетки Серпинского

Рис.3. Салфетка Серпинского
Рассмотренные выше примеры фракталов относятся к так называемым точным фракталам или детерминистическим. Они все построены по вполне определенному геометрическому правилу. Помимо точных фракталов, существуют еще так называемые случайные фракталы. В расположении их элементов есть некоторая доля случайности. Простейшим случайным фракталом является траектория частицы, совершающей броуновское движение рис.4. И хотя сама траектория имеет очень сложный извилистый характер, определить ее фрактальную размерность очень просто. Для этого заметим, что если частица продиффундировала на расстояние R, то среднее число "шагов", которое она сделала, где l — характерная длина одного шага.
![]()
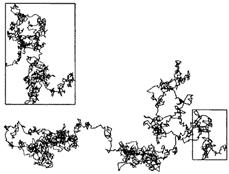
Рис. 4. Траектория движения броуновской частицы.
Это значит, что характерный размер диффузионной траектории на заданной площади пропорционален величине этой площади. То есть траектория на плоскости является достаточно густой. Это, впрочем, не означает конечности площади, заметаемой самой диффузионной кривой, из-за множества самопересечений. Можно показать, что для двумерного броуновского движения вероятность возвращения в любую, сколь угодно малую окрестность произвольно выбранной точки, равна 1. В случае же диффузии в трехмерном пространстве траектория броуновской частицы является, напротив, очень рыхлой (ее фрактальная размерность по-прежнему равна 2) и не заполняет всего предоставленного ей объема. В этом случае вероятность возврата оказывается меньше единицы.
Начало исследования броуновского движения датируется 1827 годом, когда шотландский ботаник Роберт Броун обнаружил, что мелкие частицы, взвешенные в жидкости, совершают беспорядочное непрерывное движение, которое было названо в честь своего открывателя. В 1905 году Альберт Эйнштейн объяснил это движение хаотическими столкновениями с молекулами окружающей среды.
Шотландский ботаник Роберт Броун (иногда его фамилию транскрибируют как Браун) еще при жизни как лучший знаток растений получил титул «князя ботаников». Он сделал много замечательных открытий. В 1827 Броун проводил исследования пыльцы растений. Он, в частности, интересовался, как пыльца участвует в процессе оплодотворения. Как-то он разглядывал под микроскопом выделенные из клеток пыльцы североамериканского растения Clarkia pulchella (кларкии хорошенькой) взвешенные в воде удлиненные цитоплазматические зерна. Неожиданно Броун увидел, что мельчайшие твердые крупинки, которые едва можно было разглядеть в капле воды, непрерывно дрожат и передвигаются с места на место. Он установил, что эти движения, по его словам, «не связаны ни с потоками в жидкости, ни с ее постепенным испарением, а присущи самим частичкам». Наблюдение Броуна подтвердили другие ученые. Мельчайшие частички вели себя, как живые, причем «танец» частиц ускорялся с повышением температуры и с уменьшением размера частиц и явно замедлялся при замене воды более вязкой средой. Это удивительное явление никогда не прекращалось: его можно было наблюдать сколь угодно долго. Поначалу Броун подумал даже, что в поле микроскопа действительно попали живые существа, тем более что пыльца – это мужские половые клетки растений, однако так же вели частички из мертвых растений, даже из засушенных за сто лет до этого в гербариях. Тогда Броун подумал, не есть ли это «элементарные молекулы живых существ», о которых говорил знаменитый французский естествоиспытатель Жорж Бюффон. Это предположение отпало, когда Броун начал исследовать явно неживые объекты; сначала это были очень мелкие частички угля, а также сажи и пыли лондонского воздуха, затем тонко растертые неорганические вещества: стекло, множество различных минералов. «Активные молекулы» оказались повсюду: «В каждом минерале, – писал Броун, – который мне удавалось измельчить в пыль до такой степени, чтобы она могла в течение какого-то времени быть взвешенной в воде, я находил, в больших или меньших количествах, эти молекулы».
Надо сказать, что у Броуна не было каких-то новейших микроскопов. В своей статье он специально подчеркивает, что у него были обычные двояковыпуклые линзы, которыми он пользовался в течение нескольких лет. И далее пишет: «В ходе всего исследования я продолжал использовать те же линзы, с которыми начал работу, чтобы придать больше убедительности моим утверждениям и чтобы сделать их как можно более доступными для обычных наблюдений».
Сейчас чтобы повторить наблюдение Броуна достаточно иметь не очень сильный микроскоп и рассмотреть с его помощью дым в зачерненной коробочке, освещенный через боковое отверстие лучом интенсивного света. В газе явление проявляется значительно ярче, чем в жидкости: видны рассеивающие свет маленькие клочки пепла или сажи (в зависимости от источника дыма), которые непрерывно скачут туда и сюда.
Норберт Винер в 1923 году построил первую удовлетворительную с математической точки зрения модель выборочных реализаций и доказал их «почти наверное» (на языке теории вероятностей) непрерывность.
Простейшей дискретной аппроксимацией броуновского движения служит случайное одномерное блуждание. В этом случае частица первоначально располагается в точке х0 = 0 на прямой. Частица совершает единичный шаг вправо или влево в зависимости от случайного выбора, например, бросания монеты. Случайное блуждание происходит итеративно. Для каждого п = 1,2,3,….положим, что
хn = хn-1 ± 1.
Более точным приближением
к реальному броуновскому движению является замена шагов ±1 случайными
величинами gп, имеющими гауссовское, или
нормальное распределение. После первого шага частица находится в положении ![]() 1=
1= ![]() 0 + g1, а после n шагов в положении
0 + g1, а после n шагов в положении
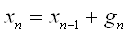 .
.
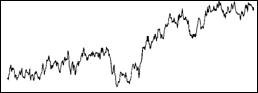
На рис.5. изображена типичная реализация гауссовского случайного блуждания.
![]()
Рис.5. График гауссовского случайного блуждания
Случайная величина X называется гауссовской, или нормальной с математическим ожиданием µ и дисперсией σ2, если она распределена, но закону:
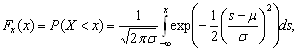
то есть её плотность вероятности f(x) имеет вид:
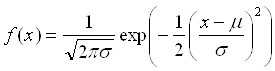 .
.
График y=f(x) напоминает
колокол рис.6. В наших приложениях математическое ожидание ![]() обычно равно нулю.
обычно равно нулю.
Гауссовское случайное блуждание легко реализуется на компьютере. Единственная сложность― необходим генератор гауссовских случайных чисел. Если имеется генератор, равномерно распределённый на отрезке [0,1] случайных чисел, то вполне приемлемое приближение можно получить, используя формулу:
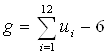 ,
,
Можно использовать и более общую формулу:
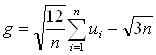 ,
,
|
0,8 |
|
|||||||||||||||||
|
0,6 |
|
|||||||||||||||||
|
|
||||||||||||||||||
|
0,4 |
|
|||||||||||||||||
|
|
||||||||||||||||||
|
0,2 |
|
|||||||||||||||||
|
|
|
|||||||||||||||||
|
0 |
|
|||||||||||||||||
|
|
||||||||||||||||||
|
-0,2 |
|
|||||||||||||||||
|
|
||||||||||||||||||
|
-0,4 |
|
|||||||||||||||||
|
|
||||||||||||||||||
|
-0,6 |
|
|||||||||||||||||
|
|
||||||||||||||||||
|
-0,8 |
|
|||||||||||||||||
|
|
||||||||||||||||||
|
|
||||||||||||||||||
| -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | |||||||||||
|
|||||||||||||||||||
Рис.6. Нормированная гауссовская кривая
Что касается броуновского движения, определенного на конечном интервале, например, на отрезке [а, Ь]. Приведенное ниже определение позволяет сфокусировать внимание на его принципиальных свойствах. Большинство утверждений о броуновском движении относится к одномерному случаю, но имеет соответствующие аналоги для случая двух и большего числа измерений. Прежде всего, нам понадобится определение гауссовского случайного процесса.
Случайный процесс X{t) называется гауссовским, если для каждого конечного набора моментов времени t1, t2, …, tn вектор ( X(t1), X(t2),… , X(tn)) имеет гауссовское распределение. Двумерный гауссовский процесс Х(х; у) определяется аналогично.
Определение: Гауссовский процесс X(t) называется одномерным броуновским движением, или винеровским процессом на интервале [а, Ь], если он обладает следующими свойствами
Х(0) = 0 и функция X(t) почти всегда непрерывна.
Свойство гауссовости приращений: случайная величина
![]()
![]()
имеет гауссовское
распределение с математическим ожиданием ![]() и
дисперсией
и
дисперсией ![]() где σ — положительная
константа, то есть
где σ — положительная
константа, то есть
P(ΔX<x)=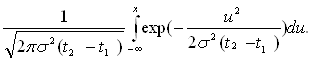
![]()
Броуновское движение, как и любой процесс с независимыми приращениями, есть Марковский процесс. Это означает, что условная вероятность события «Х(t2) достигает определённого значения при данном значении Х(t1)», где t1>t2, зависит только от t1 и t2. Эта вероятность не зависит от поведения Х(t), при t<t1, то есть в процессе случайного блуждания каждый шаг делается без какой-либо информации о том, каким образом процесс достиг текущего значения.
Условная вероятность события А при заданном событии В обозначается P(A/B). Формальное определение Марковского процесса:
![]()
Где
4. ПРОГРАММИРОВАНИЕ НА DELPHI
Delphi обусловлен как тем, что это наиболее популярная среда программирования, так и объективными несомненными достоинствами.
Среди них:
простой и мощный язык программирования Pascal;
удобная и полная объектная модель;
достаточно удобная среда разработки;
обширная объектная библиотека VCL;
мощные средства разработки приложений баз данных.
Delphi – это потомок среды программирования Turbo Pascal. Система визуального объектно-ориентированного проектирования Delphi позволяет:
Создавать законченные приложения для Windows самой различной направленности.
Быстро создавать профессионально выглядящий оконный интерфейс для любых приложений; интерфейс удовлетворяет всем требованиям Windows и автоматически настраивается на ту систему, которая установлена, поскольку использует функции, процедуры и библиотеки Windows.
Создавать свои динамически присоединяемые библиотеки компонентов, форм, функций, которые потом можно использовать из других языков программирования.
Создавать мощные системы работы с базами данных любых типов.
Формировать и печатать сложные отчеты, включающие таблицы, графики и т.п.
Создавать справочные системы, как для своих приложений, так и для любых других.
Создавать профессиональные программы установки для приложений Windows, учитывающие всю специфику и все требования операционной системы.
Интегрированная среда разработки Delphi – это среда, в которой есть все необходимое для проектирования, запуска и тестирования создаваемых приложений. Именно поэтому, учитывая особенности и характеристики данной среды, для написания программ, я выбрала Delphi.
Общее описание среды
Верхней части окна среды отображается полоса главного меню. Назначение каждого пункта меню можно уточнить в справочной системе Delphi. Для получения справки следует выбрать интересующий пункт меню и нажать клавишу F1. Выбор команды меню выполняется любым из стандартных способов: F10, Alt+горячая клавиша или щелчком мыши на нужном пункте меню.
Назначение команд меню представлены в таблице:
| Раздел меню | Назначение |
| 1) Меню File (Файл) | Разделы меню позволяют создавать новый проект, новую форму, открыть ранее созданный проект или форму, сохранить проекты или форму в файлах с заданными именами. |
| 2) Меню Edit (Правка) | Разделы этого меню позволяют выполнять обычные для приложений Windows операции с буфером обмена, а также дают возможность выравнивать группы размещенных на форме компонентов по размерам и местоположению. |
| 3) Меню Search (Поиск) | Разделы этого меню позволяют осуществлять поиск фрагментов текста, ошибок, объектов, модулей, переменных и символов в редакторе кода. |
| 4) Меню View (Вид) | Разделы этого меню позволяют вывести на экран или скрыть различные элементы среды проектирования и открыть окна, связанные с интегрированным отладчиком. |
| 5) Меню Project (Проект) | Разделы меню позволяют добавлять и удалять из проекта формы, задавать опции проекта, компилировать проект без его выполнения, дать информацию о размерах приложения. |
| 6) Меню Run (Выполнить) | Предоставляет возможность выполнять проект в нормальном или отладочном режимах, по шагам, останавливаясь в указанных точках, просматривая значения переменных и т.д. |
| 7) Меню Component (Компонент) | Содержит раскрывающееся меню, которое позволяет работать с компонентами: создавать новые компоненты, изменять палитру компонентов и т.п. |
| 8) Меню Database (База данных) | Раздел меню позволяет использовать инструментарий для работы с базами данных. |
| 9) Меню Tools (Сервис) | Включает ряд разделов, позволяющих выполнять различные вспомогательные программы: редактор изображений, программы, конфигурирующие базы данных и сети и т.п. |
| 10) Меню Windows (Окно) | Содержит список открытых окон среды и предоставляет возможность перехода из одного окна в другое. |
| 11) Меню Help (Помощь) | Содержит разделы, помогающие работать со справочной системой среды программирования Delphi. |
| 1. Палитра компонентов Standard (Стандартная) | Большинство компонентов на этой странице являются аналогами экранных элементов операционной системы Windows: меню, кнопки, полосы прокрутки, панели и т.п. Имена компонентов можно узнать из всплывающей подсказки. Назначение компонентов можно уточнить, используя систему контекстной справки Delphi. |
| 2. Палитра компонентов Additional (Дополнительная) | Содержит более развитые компоненты: а) воспроизведение звука, музыки и видео; б) отображение графической информации. |
| 3. Палитра компонентов System (Системная) | Предоставляет возможность объединять отдельные элементы, такие как списки каталогов и файлов, а также генерировать события через определенные промежутки времени. |
| 4. Палитра компонентов Win32 | Содержит компоненты, позволяющие созданным программам использовать интерфейс Windows. |
| 5. Палитра компонентов Dialogs (Диалоговая) | Содержит стандартные диалоговые окна для операций над файлами, поиска и замены текста, выбор шрифтов, цветов и т.д. |
| 6. Палитра компонентов Data Access, Data Controls (Сервис баз данных) | Использует механизм баз данных для организации доступа к файлам баз данных различных форматов. |
| 7. Палитра компонентов QReport (Отчеты) | Предоставляет компоненты для визуального проектирования отчетов баз данных. |
| 8. Палитра компонентов Servers (Сервис) | Предоставляет компоненты-наследники для доступа ко всем серверным объектам Microsoft Office. |
| 9. Палитра компонентов Samples (Примеры) | Содержит компоненты-примеры, которые можно добавлять в собственные приложения. |
| 10. Палитра компонентов Internet | Предоставляет компоненты для разработки приложений, позволяющих создавать HTML‑файлы непосредственно из файлов баз данных и других типов, взаимодействующих с другими приложениями для Интернета. |
Ниже полосы главного меню расположены две инструментальные панели. Левая панель (состоящая, в свою очередь, из трех панелей) содержит два ряда кнопок, дублирующих некоторые наиболее часто используемые команды меню (открыть, сохранить, сохранить все и т.д.). Правая панель содержит панель библиотеки визуальных компонентов (или палитра). Палитра компонентов содержит ряд страниц, закладки которых видны в ее верхней части. Страницы сгруппированы в соответствии с их смыслом и назначением. Поскольку число предоставляемых компонентов растет от версии к версии, то остановимся на основных (12 страниц).
Правее полосы главного меню располагается еще одна небольшая инструментальная панель, содержащая раскрывающийся список и две кнопки. Эта панель служит для сохранения и выбора различных конфигураций окна среды, которые можно создавать и запоминать.
Под палитрой компонентов располагается окно формы с размещенными на ней компонентами. Форма является основой почти всех приложений Delphi. Форму можно понимать как типичное окно Windows. Она обладает теми же свойствами, что и другие окна. Во время проектирования форма покрыта сеткой из точек. В узлах этой сетки размещаются те компоненты, которые помещены на форму. Во время выполнения приложения эта сетка не видна.
В основном поле окна слева находится окно Инспектора объектов, с помощью которого в дальнейшем можно задавать свойства компонентов и обработчики событий. Инспектор объектов состоит из двух страниц, каждую из которых можно использовать для определения поведения активного компонента. Первая страница – это Свойства, вторая – События.
Рассмотрим некоторые свойства любого компонента:
| Свойство | Назначение |
| Caption (надпись) | Название компонента |
| Color | Цвет поверхности компонента |
| Font Color | Цвет шрифта |
| Font Height | Высота шрифта |
| Font Name | Имя шрифта |
| Font Size | Размер шрифта |
| Style fsBold | Стиль надписи на компоненте Жирный |
| Style fsItalic | Стиль надписи на компоненте курсив |
| Style fsUnderline | Стиль надписи на компоненте подчеркивание |
| Style fsStrikeOut | Стиль надписи на компоненте зачеркивание |
Каждый компонент имеет свой набор свойств, который соответствует назначению этого компонента.
Страница Событий – вторая часть Инспектора объектов. На ней указаны все события, на которые может реагировать выбранный объект.
Одним из наиболее важных элементов среды Delphi является окно Редактора кода. Оно располагается ниже окна формы, обычно при первом взгляде на экран невидимо, т. к. его размер равен размеру формы и окно Редактора кода практически полностью перекрывается окном формы. Редактор кода является полноценным программным редактором. В заголовке окна редактора кода отображается имя текущего файла, с текстом которого производится работа (стандартное имя – Main.pas). В нижней части окна Редактора кода располагается строка состояния. В самой левой ее позиции отображается позиция курсора: номер строки и колонки.
Выше окна Инспектора объектов расположено окно Дерево объектов, которое отображает структуру компонентов приложения с точки зрения их принадлежности друг к другу.
Общая организация программы в Delphi
Программа, создаваемая в среде Delphi в процессе проектирования приложения, основана на модульном принципе. Главная программа состоит из объявления списка используемых модулей и нескольких операторов, создающих объекты для необходимых форм и запускающих приложение на выполнение. Модульность очень важна для создания надежных и относительно легко модифицируемых и сопровождаемых приложений. Четкое соблюдение принципов модульности в сочетании с принципом скрытия информации позволяет производить модификации внутри любого модуля, не затрагивая при этом остальных модулей и главную программу.
Все объекты компонентов размещаются в объектах – формах. Для каждой формы, проектируемой в приложении, Delphi создает отдельный модуль. Именно в модулях и осуществляется программирование задачи. В обработчиках событий объектов размещаются описания алгоритмов, которые в основном сводятся к обработке информации, содержащейся в свойствах одних объектов, и задании по результатам этой обработки свойств других объектов.
Структура файла главной (головной) программы приложения Delphi.
В процессе проектирования Delphi автоматически создает код головной программы и отдельных модулей. В модули вводятся собственные коды, создавая обработчики различных событий. Но головную программу, как правило, не приходится модифицировать и даже просматривать ее текст (только в исключительных случаях).
Головной файл приложения Delphi имеет следующую структуру:
Program < имя >;
{объявление подключаемых модулей, а также локальных типов, классов, констант, переменных, описание локальных функций и переменных}
Begin
{операторы тела программы}
End.
Типичная головная программа приложения имеет следующий вид:
Program Project 1;
Uses
Forms,
Unit 1 in Unit 1.pas’ {Form 1}, Unit 2 in ‘Unit 2.pas’ {Form 2};
{$R *. res}
{можно поместить описание констант, переменных, функций, процедур, доступных для использования только в пределах данного файла}
Begin
Application. Initialize;
Application. CreateForm (TForm 1, Form 1);
Application. CreateForm (TForm 2, Form 2);
Application. Run;
End.
1) Программа начинается с ключевого слова program, после которого указывается имя программы (оно совпадает с именем файла, в котором был сохранен проект). Это же имя присваивается исполняемому файлу приложения. По умолчанию используется имя Project1.
2) После заголовка в тексте программы располагается предложение:
Uses
Forms,
Unit 1 in Unit 1.pas’ {Form 1}, Unit 2 in ‘Unit 2.pas’ {Form 2};
В этом предложении перечисляются модули, загружаемые программой. Первый модуль Forms является системным, а следующие модулями разработанными самостоятельно форм. Данный пример подразумевает, что в проекте были созданы две формы с именами Form1, Form2 в модулях Unit1, Unit2. Заключенные в фигурные скобки название форм представляют собой комментарии.
3) Следующая строка текста – {$R *. res} – представляет собой директиву компилятора, связанную с использованием файлов ресурсов. Указанный файл должен быть файлом ресурсов Windows. По умолчанию используется расширение.RES для файлов ресурсов.
4) Первый оператор в теле программы Application. Initialize; – инициализирует приложение, следующий за ним оператор Application. CreateForm (TForm 1, Form 1); и Application. CreateForm (TForm 2, Form 2); – создают объекты формы1 и формы2, последний оператор Application. Run; – начинает выполнение приложения.
Общая структура файла модуля:
Unit < имя модуля >;
Interface // Открытый интерфейс модуля (могут помещаться списки подключаемых модулей, объявление типов, констант, переменных, функций и процедур, к которым будет доступ из других модулей)
Implementation // Реализация модуля (могут помещаться списки подключаемых модулей, объявление типов, констант, переменных, функций и процедур, к которым не будет доступа из других модулей)
Initialization // (Необязательный раздел операторы выполняются один раз при первом обращении к модулю)
Finalization // (Необязательный раздел операторы выполняются при любом завершении работы модуля)
End.
Рассмотрим теперь текст модуля с пустой формой:
Unit Unit1;
Interface // Открытый интерфейс модуля
Uses {Список подключаемых модулей}
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms, Dialogs;
Type {Объявление класса формы}
TForm1 = class (TForm)
Private // закрытый раздел класса
Public // открытый раздел класса
End;
VarForm 1: TForm1;
Implementation // Реализация модуля
{$R *. dfm}
End.
4.1 Код программы «Броуновское движение, как хаотичное движение частиц»
unit Unit1;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, ExtCtrls, StdCtrls, math;
type
TForm1 = class(TForm)
Label1: TLabel;
GroupBox1: TGroupBox;
Label2: TLabel;
Edit1: TEdit;
Button1: TButton;
Label3: TLabel;
Edit2: TEdit;
Label4: TLabel;
Edit3: TEdit;
Panel1: TPanel;
PaintBox: TPaintBox;
Button2: TButton;
procedure Button1Click(Sender: TObject);
procedure Button2Click(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
procedure GetData;
end;
Molecula = record
x, y:Integer; // координаты частицы
Vx, Vy: Integer; // составляющие скорости
angle: real; // угол полета
speed: byte;
end;
var
Form1: TForm1;
R, Vmax, n: integer;
mol: array [1..100] of molecula;
run: boolean;
implementation
{$R *.dfm}
procedure TForm1.GetData;
begin
R:=strtoint(Edit1.Text); // радиус чистицы
Vmax:=strtoint(Edit2.Text); // максимальная скорость движения
n:=strtoint(Edit3.Text); // количество частиц
end;
procedure TForm1.Button1Click(Sender: TObject);
var i, j: byte;
temp: integer;
begin
GetData;
// запуск движения
PaintBox.Refresh;
PaintBox.Canvas.Brush.Color:=clBlack;
PaintBox.Canvas.Pen.Color:=clBlack;
PaintBox.Canvas.Rectangle(0,0,400,400);
PaintBox.Canvas.Brush.Color:=clBlue;
PaintBox.Canvas.Pen.Color:=clBlue;
Randomize;
// определение начального положения частиц
for i:=1 to N do
begin
// начальные координаты
mol[i].x:=RandomRange(R, PaintBox.Width-R);
mol[i].y:=RandomRange(R, PaintBox.Height-R);
// начальное направление движения
mol[i].angle:=Random(360)*Pi/180;
mol[i].speed:=RandomRange(1, Vmax);
// cоставляющие движения частицы по осям
mol[i].Vx := Round(mol[i].speed * Sin(mol[i].angle));
mol[i].Vy := Round(mol[i].speed * Cos(mol[i].angle));
// вывод на экран
PaintBox.Canvas.Ellipse(mol[i].x-R, mol[i].y-R, mol[i].x+R, mol[i].y+R);
end;
Run:=True;
repeat
for i:=1 to N do
begin
// стираем молекулу
PaintBox.Canvas.Brush.Color:=clBlack;
PaintBox.Canvas.Pen.Color:=clBlack;
PaintBox.Canvas.Ellipse(mol[i].x-R, mol[i].y-R, mol[i].x+R, mol[i].y+R);
// обработка столкновения
for j:=1 to n do
if j<>i then
begin
// определяем столкновение молекулы
if sqrt(sqr(mol[i].x-mol[j].x)+sqr(mol[i].y-mol[j].y))<2*R+1 then
begin
temp:=mol[i].Vx; mol[i].Vx:=mol[j].Vx; mol[j].Vx:=temp;
temp:=mol[i].Vy; mol[i].Vy:=mol[j].Vy; mol[j].Vy:=temp;
end;
end;
// сдвигаем на новую позицию.
mol[i].x:=mol[i].x+mol[i].Vx;
mol[i].y:=mol[i].y+mol[i].Vy;
// проверка на выход за границы области
if mol[i].x>PaintBox.Width-R then
begin
mol[i].x:=PaintBox.Width-R;
mol[i].Vx:=-mol[i].Vx;
end;
if mol[i].x<R then
begin
mol[i].x:=R;
mol[i].Vx:=-mol[i].Vx;
end;
if Mol[i].y>PaintBox.Height-R then
begin
mol[i].y:=PaintBox.Height-R;
mol[i].Vy:=-mol[i].Vy;
end;
if mol[i].y<R then
begin
mol[i].y:=R;
mol[i].Vy:=-Mol[i].Vy;
end;
// вывод на экран
PaintBox.Canvas.Brush.Color:=clBlue;
PaintBox.Canvas.Pen.Color:=clBlue;
PaintBox.Canvas.Ellipse(mol[i].x-R, mol[i].y-R, mol[i].x+R, mol[i].y+R);
Application.ProcessMessages;
end;
sleep(5);
Application.ProcessMessages;
if run=false then break;
until false;
end;
procedure TForm1.Button2Click(Sender: TObject);
begin
Run:=False;
end;
end.
{
// temp:=mol[i].Vx; mol[i].Vx:=mol[j].Vx; mol[j].Vx:=temp;
// temp:=mol[i].Vy; mol[i].Vy:=mol[j].Vy; mol[j].Vy:=temp;
// Random(360)*Pi/180;
mol[j].angle:=360*Pi-mol[j].angle;
// temp:=mol[i].angle; mol[i].angle:=mol[j].angle; mol[j].angle:=temp;
// cоставляющие движения частицы по осям
mol[j].Vx := Round(mol[j].speed * Sin(mol[j].angle));
mol[j].Vy := Round(mol[j].speed * Cos(mol[j].angle));
mol[i].angle:=360*Pi-mol[i].angle;
// cоставляющие движения частицы по осям
mol[i].Vx := Round(mol[i].speed * Sin(mol[i].angle));
mol[i].Vy := Round(mol[i].speed * Cos(mol[i].angle));
// сдвигаем на новую позицию.
mol[i].x:=mol[i].x+mol[i].Vx;
mol[i].y:=mol[i].y+mol[i].Vy;
//mol[j].Vx:=mol[j].Vx+mol[i].Vx;
// mol[j].Vy:=mol[j].Vy+mol[i].Vy;
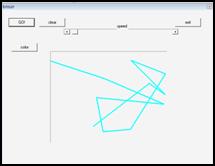
4.2 Код программы «Построение траектории броуновское движение»
unit Unit1;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, ExtCtrls, StdCtrls;
type
TForm1 = class(TForm)
Button1: TButton;
Timer1: TTimer;
ScrollBar1: TScrollBar;
StaticText1: TStaticText;
Button2: TButton;
Button3: TButton;
Bevel1: TBevel;
ColorDialog1: TColorDialog;
Button4: TButton;
procedure Button1Click(Sender: TObject);
procedure initz;
procedure paint;
procedure ScrollBar1Change(Sender: TObject);
procedure FormCreate(Sender: TObject);
procedure Button2Click(Sender: TObject);
procedure Button3Click(Sender: TObject);
procedure Timer1Timer(Sender: TObject);
procedure Button4Click(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;
var
Form1: TForm1;
x1,x2,y1,y2,time,tx,ty:integer;
implementation
{$R *.dfm}
procedure tform1.initz;
begin
tx:=136;
ty:=120;
x1:=tx;
y1:=ty;
canvas.MoveTo(x1,y1);
canvas.Pen.Color:=clblue;
canvas.Pen.Width:=3;
scrollbar1.SetParams(80,0,99);
time:=100-scrollbar1.Position;
timer1.Enabled:=false;
end;
procedure tform1.paint;
begin
x2:=random(bevel1.Width)+tx;
y2:=random(bevel1.Height)+ty;
canvas.LineTo(x2,y2);
canvas.Pen.color:=canvas.pen.color+1;
end;
procedure TForm1.Button1Click(Sender: TObject);
begin
if not timer1.Enabled then
begin
timer1.Enabled:=true;
timer1.Interval:=time;
button1.Caption:='STOP!';
end else
begin
timer1.enabled:=false;
button1.Caption:='GO!';
end;
end;
procedure TForm1.ScrollBar1Change(Sender: TObject);
begin
time:=100-scrollbar1.Position;
timer1.Interval:=time;
end;
procedure TForm1.FormCreate(Sender: TObject);
begin
initz;
end;
procedure TForm1.Button2Click(Sender: TObject);
begin
repaint;
end;
procedure TForm1.Button3Click(Sender: TObject);
begin
close;
end;
procedure TForm1.Timer1Timer(Sender: TObject);
begin
paint;
end;
procedure TForm1.Button4Click(Sender: TObject);
begin
if colordialog1.Execute then
canvas.Pen.color:=colordialog1.Color;
end;
end.
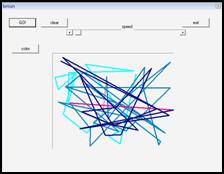
ЗАКЛЮЧЕНИЕ
В данной работе мною была освещена основная теория броуновского движения и история его открытия. Были рассмотрены вопросы моделирования броуновского движения на DELPFI, а также основная характеристика, преимущества и возможности данной среды программирования.
В итоге можно сказать, что изучение фракталов и хаоса, в нашем случае― это броуновское движение, открывает замечательные возможности, как в исследовании бесконечного числа приложений, так и в области чистой математики.
Архангельский А.Я. «Программирование в Delphi». Учебник по классическим версиям Delphi. – М.: ООО «Бином-Пресс», 2006
Барлет М.С. «Введение в теория случайных процессов»
Булинский А.В., Ширяев А.Н. «Теория случайных процессов». ―М.:
ФИЗМАТЛИТ, 2005 г
Кроновер Р.М. «Фракталы и хаос в динамических системах. Основы теории». Москва: Постмаркет, 2000 г.
Миллер Б.М., Панков А.Р. « Теория случайных процессов»
«Немного о фракталах» http://edu.ioffe.ru
© 2010 Интернет База Рефератов