
Рефераты по сексологии
Рефераты по информатике программированию
Рефераты по биологии
Рефераты по экономике
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Рефераты по авиации и космонавтике
Рефераты по административному праву
Рефераты по безопасности жизнедеятельности
Рефераты по арбитражному процессу
Рефераты по архитектуре
Рефераты по астрономии
Рефераты по банковскому делу
Рефераты по биржевому делу
Рефераты по ботанике и сельскому хозяйству
Рефераты по бухгалтерскому учету и аудиту
Рефераты по валютным отношениям
Рефераты по ветеринарии
Рефераты для военной кафедры
Рефераты по географии
Рефераты по геодезии
Рефераты по геологии
Рефераты по геополитике
Рефераты по государству и праву
Рефераты по гражданскому праву и процессу
Рефераты по делопроизводству
Рефераты по кредитованию
Рефераты по естествознанию
Рефераты по истории техники
Рефераты по журналистике
Рефераты по зоологии
Рефераты по инвестициям
Рефераты по информатике
Исторические личности
Рефераты по кибернетике
Рефераты по коммуникации и связи
Курсовая работа: Приближенное вычисление значений определенного интеграла
Курсовая работа: Приближенное вычисление значений определенного интеграла
Федеральное агентство по образованию РФ
Тульский государственный университет
Кафедра АОТ и ОС
КУРСОВАЯ РАБОТА
по курсу информатика
"ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ЗНАЧЕНИЙ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА"
Тула, 2007
Содержание
Введение
Метод средних прямоугольников
Метод трапеций
Метод Ньютона-Котеса
Метод Чебышева
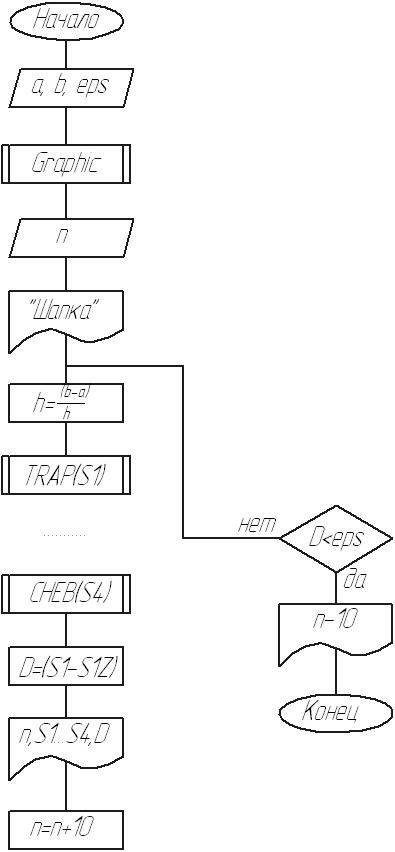
Блок-схема основной программы
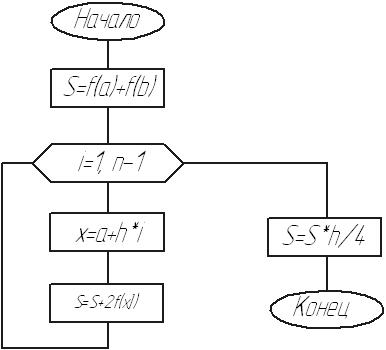
Блок-схема процедуры: метод трапеций
Блок-схема процедуры: метод Ньютона-Котеса
Блок-схема процедуры: метод Чебышева
Текст программы
Список используемой литературы
Введение
На практике редко удается вычислить точно определенный интеграл. Например, в элементарных функциях не вычисляется функция Лапласа
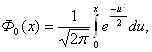
широко используемая в теории вероятностей для вычисления вероятностей, связанных с нормально распределенными случайными величинами.
Задача численного интегрирования состоит в нахождении приближенного значения интеграла:
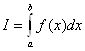 (1)
(1)
от
непрерывной на отрезке [a, b] функции ![]() .
.
Численные методы интегрирования применяются в случаях,
когда не удается найти аналитическое выражение первообразной для функции ![]() либо если функция
либо если функция ![]() задана таблично. Формулы
численного интегрирования называются квадратурными формулами.
задана таблично. Формулы
численного интегрирования называются квадратурными формулами.
Пример: Приближенное неравенство
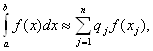 (2)
(2)
где qj – некоторые числа, xj – некоторые точки отрезка [a, b], называется квадратурной формулой, определяемой весами qj и узлами xj.
Говорят, что квадратурная формула точна для многочленов
степени m, если при замене ![]() на
произвольный алгебраический многочлен степени m приближенное равенство
(2) становится точным.
на
произвольный алгебраический многочлен степени m приближенное равенство
(2) становится точным.
Рассмотрим некоторые широко используемые примеры приближенного вычисления определенных интегралов, квадратурные формулы.
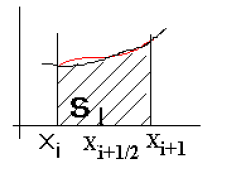
Метод средних прямоугольников
Вычисление
определенного интеграла геометрически означает вычисление площади фигуры,
ограниченной кривой ![]() , прямыми х=а и
х=b и осью абсцисс.
Приближенно эта площадь равна сумме площадей прямоугольников.
, прямыми х=а и
х=b и осью абсцисс.
Приближенно эта площадь равна сумме площадей прямоугольников.
Обозначим ![]()
![]() , где
, где
n – количество шагов.
Формула левых прямоугольников:
![]()
Формула правых прямоугольников:
![]()
Более точной является формула средних прямоугольников:
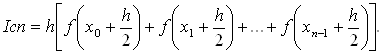
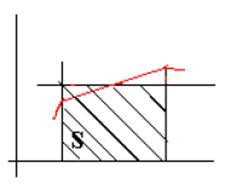
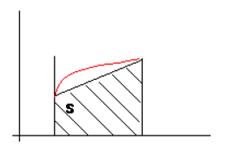
Метод трапеций
Площадь под кривой заменяется суммой площадей трапеций:
![]()
или ![]()
Нетрудно
убедиться, что ![]()
Поскольку точность вычислений по приведенным формулам зависит от числа разбиений n исходного отрезка [a; b], то вычислительный процесс целесообразно строить итерационным методом, увеличивая n до тех пор, пока не будет выполнено условие
![]() <
<![]()
где ![]() – значения интеграла на
– значения интеграла на ![]() шаге, а
шаге, а ![]() – точность вычислений.
– точность вычислений.
Метод Ньютона-Котеса
Заменим подынтегральную функцию f(x) интерполяционным многочленом Лагранжа:
![]()
![]() .
.
Тогда
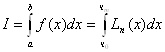 ;
;
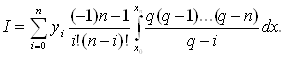 (1)
(1)
Так как dx=hdq, то
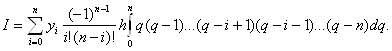
Так как ![]() , то
, то
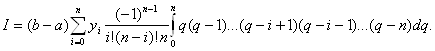
Окончательно получаем формулу Ньютона-Котеса:
![]()
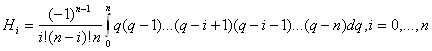 (2)
(2)
Величины Hi называют коэффициентами Ньютона-Котеса. Они не зависят от f(x). Их можно вычислить заранее для различного числа узлов n (таблица 1).
Формула Ньютона-Котеса с n узлами точна для полиномов степени не выше n. Для получения большей точности не рекомендуется использовать формулы с большим числом узлов, а лучше разбивать отрезок на подотрезки, к каждому из которых применяется формула с одним и тем же небольшим числом узлов.
Таблица 1. Значения коэффициентов Ньютона-Котеса
H |
N |
|||
|
1 |
2 |
3 |
4 |
|
H0 |
1/2 | 1/6 | 1/8 | 7/90 |
|
H1 |
1/2 | 2/3 | 3/8 | 16/45 |
|
H2 |
- | 1/6 | 3/8 | 2/15 |
|
H3 |
- | - | 1/8 | 16/45 |
|
H4 |
- | - | - | 7/90 |
Интересно отметить, что из формулы (2) следуют как частные случаи: формула трапеций при n=1
![]() ;
;
формула Симпсона при n=2
![]() ;
;
правило трех восьмых при n=3
![]() .
.
Формулу (2) при n>6 не применяют, так как коэффициенты Ньютона-Котеса становятся слишком большими и вычислительная погрешность резко возрастает.
Метод Чебышева
П.Л. Чебышев предложил формулу:
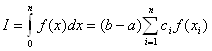 ,
,
в которой коэффициенты ci фиксированы, а хi подлежат определению.
Пользуясь алгебраическими свойствами симметричных многочленов, опустив преобразования, ограничимся готовыми результатами. В таблице 2 приведены значения узлов квадратурной формулы Чебышева для некоторых значений n.
Таблица 2. Значения узлов квадратурной формулы Чебышева
| Число интервалов n | Номер узла i |
Значение узла Xi |
| 1 |
1 2 |
0,211325 0,788675 |
| 2 |
1 2 3 |
0,146447 0,500000 0,853553 |
| 3 |
1 2 3 4 |
0,102673 0,406204 0,593796 0,897327 |
| 4 |
1 2 3 4 5 |
0,083751 0,312730 0,500000 0,687270 0,916249 |
| 5 |
1 2 3 4 5 6 |
0,066877 0,288740 0,366682 0,633318 0,712260 0,933123 |
Для любых пределов интегрирования имеем:
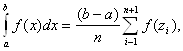 где
где ![]() ,
,
![]()
Значения xi берутся из таблицы при выбранном значении n. Для повышения точности можно не только увеличивать количество узлов, но и разбивать отрезок [a, b] на подотрезки, к каждому из которых применяется соответствующая формула. Не рекомендуется применять формулы с большим количеством узлов (n>=8).Доказано, что для n=8 построить квадратурную формулу Чебышева невозможно.
Блок-схема основной программы

![]()

![]()
![]()
Блок-схема процедуры: метод трапеций
Блок-схема процедуры: метод Ньютона-Котеса
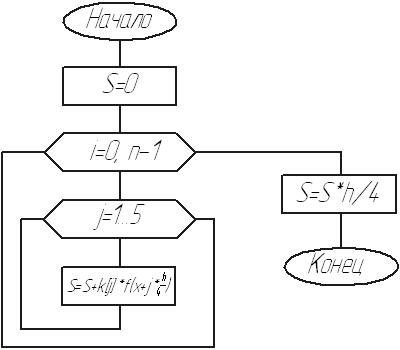
Блок-схема процедуры: метод Чебышева
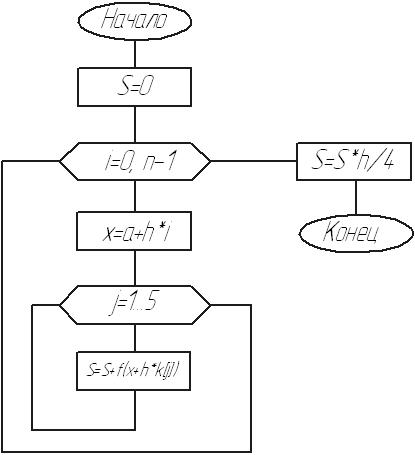
Текст программы
program Curs;
uses crt, graph;
var i, n:integer;
t:byte;
a, b, eps, h:real;
x, sum1, sum2, seps, m0, m1, m2, m3, m4:real;
lf:text;
st:string;
function f (x:real):real;
begin
f:=19.44*exp (0.224*x);
end;
procedure gr (xn, xk:real);
var x, y, mx, my, dx, dy,
ymin, ymax, xh:real;
xb, yb, xm, ym, xl, yv, xp, yn, bord1, bord2, bord3, bord4, xt, yt, xt1, yt1, dxp, dyp, nd, nr, i, kx, ky, k:integer;
st:string;
begin
k:=100;
xh:=(xk-xn)/100;
ymax:=f(xn);
dx:=(xk-xn)/100;
for i:=1 to 100 do
begin x:=xn+dx*i;
y:=f(x);
if y>ymax then ymax:=y;
end;
ymin:=0;
ymax:=round(ymax);
nd:=detect;
initgraph (nd, nr, 'c:\tp7\bgi');
bord1:=60; kx:=6;
bord2:=30; ky:=8;
bord3:=30;
bord4:=80;
xb:=0; yb:=0; xm:=getmaxx; ym:=getmaxy;
xl:=xb+bord1;
xp:=xm-bord2;
yv:=yb+bord3;
yn:=ym-bord4;
dxp:=(xp-xl) div kx;
dyp:=(yn-yv) div ky;
dx:=(xk-xn)/kx;
dy:=(ymax-ymin)/ky;
xl:=xp-dxp*kx;
yn:=yv+dyp*ky;
mx:=(xp-xl)/(xk-xn);
my:=(yn-yv)/(ymax-ymin);
setfillstyle (1,15);
bar (xb, yb, xm, ym);
setcolor(0);
setlinestyle (0,0,1);
bar (xl, yv, xp, yn);
rectangle (xl, yv, xp, yn);
settextjustify (0,2);
settextstyle (2,1,4);
setcolor(9);
for i:=0 to kx do begin
xt:=xl+dxp*i;
str (xn+dx*i:6:3, st);
line (xt, yn‑3, xt, yn+3);
outtextxy (xt+4, yn+8, st);
end;
settextstyle (0,0,1);
for i:=0 to ky do begin
yt:=yv+dyp*i;
str (ymax-dy*i:6:3, st);
line (xl‑3, yt, xl+3, yt);
outtextxy (xl‑56, yt‑4, st);
end;
outtextxy (xl+100, bord3 div 2,'y=19.44*exp (0.224*x)');
setcolor(12);
if xn*xk<0 then begin
xt:=xl-trunc (xn*mx);
line (xt, yv, xt, yn);
end;
if ymax*ymin<0 then begin
yt:=yv+trunc (ymax*my);
line (xl, yt, xp, yt);
end;
xh:=(xk-xn)/5;
for i:=0 to 5 do begin
setcolor(3);
x:=xn+xh*i;
y:=f(x);
xt:=xl+trunc((x-xn)*mx);
yt:=yv+trunc((ymax-y)*my);
circle (xt, yt, 3);
if i>0 then
line (xt, yt, xt1, yt1);
setcolor(5);
rectangle (xt1, yt1, xt, yn);
xt1:=xt;
yt1:=yt;
end;
repeat until keypressed;
closegraph;
end;
function pr:real;
var s, x:real;
begin
s:=0;
x:=a;
for i:=1 to n do
begin
s:=s+abs (f(x))*h;
x:=x+h;
end;
pr:=s;
end;
function tr:real;
var s, x:real;
begin
s:=0;
x:=a;
for i:=1 to n do
begin
s:=s+(f(x)+f (x+h))/2*h;
x:=x+h;
end;
tr:=s;
end;
function ch:real;
var s, dp, kf, a1, b1:real;
begin
s:=0;
kf:=sqrt (1/3);
for i:=2 to n+1 do
begin
a1:=a+h*(i‑2);
b1:=a1+h;
s:=s+((b1‑a1)/2)*(f((a1+b1)/2‑kf*((b1‑a1)/2))+f((a1+b1)/2+kf*((b1‑a1)/2)));
end;
ch:=s;
end;
function si:real;
var s, x, f1, f2:real;
begin
s:=0;
x:=a;
i:=1;
f1:=0;
repeat
f1:=f1+f (a+h*i);
i:=i+2;
until i>=n;
i:=2;
f2:=0;
repeat
f2:=f2+f (a+h*i);
i:=i+2;
until i>=n;
s:=h/3*(f(a)+f (b-h)+(4*f1)+(2*f2));
si:=s;
end;
begin
assign (lf, 'otchet.txt');
rewrite(lf);
clrscr;
write ('Введите значение левого предела интегрирования: '); readln(a);
write ('Введите значение правого предела интегрирования: '); readln(b);
write ('Введите значение погрешности: '); readln(eps);
write ('Введите начальное значение количества разбиений: '); readln(n);
writeln;
gr (a, b);
write ('Ждите, идет обработка данных ');
m0:=0;
writeln (lf, ' КУРСОВАЯ РАБОТА');
writeln (lf, ' ПО КУРСУ ИНФОРМАТИКА');
writeln (lf, ' «ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ЗНАЧЕНИЙ');
writeln (lf, ' ОПРЕДЕЛЕННОГО ИНТЕГРАЛА» ');
writeln (lf, ' Выполнил: студент гр. ');
writeln (lf, ' Вариант 22 y=19.44*exp (0.224*x)');
writeln (lf, ' Xn=', a:5:3,' Xk=', b:5:3,' Eps=', eps:5:3);
writeln(lf);
writeln (lf, ' РЕЗУЛЬТАТЫ ВЫЧИСЛЕНИЙ');
repeat
h:=abs (b-a)/n;
m1:=pr;
m2:=tr;
m3:=si;
m4:=ch;
seps:=abs (m1‑m0);
writeln (lf, ' │', n:7,' │', m1:11:8,'│', m2:11:8,'│', m3:11:8,'│', m4:11:8,'│', seps:11:8,'│');
m0:=m1;
n:=n+200;
until (seps<=eps);
clrscr;
reset(lf);
while not eof(lf) do
begin
readln (lf, st);
writeln(st);
end;
{write ('Нажмите <Enter> для выхода из программы');
repeat until keypressed;}
close(lf);
end.
Список используемой литературы
1. Бахвалов Н.С. «Численные методы». М.: Наука, 1987 – 598 с.
2. Калиткин Н.Н. «Численные методы». М.: Наука, 1988 – 512 с.
3. Крылов В.И. «Вычислительные методы». М.: Наука, 1977 – 408 с.
4. Нечаев В.И., Нечаева О.А., Почуева Л.Н. «Численные методы». Тула, 1999.
© 2010 Интернет База Рефератов