Рефераты по сексологии
Рефераты по информатике программированию
Рефераты по биологии
Рефераты по экономике
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Рефераты по авиации и космонавтике
Рефераты по административному праву
Рефераты по безопасности жизнедеятельности
Рефераты по арбитражному процессу
Рефераты по архитектуре
Рефераты по астрономии
Рефераты по банковскому делу
Рефераты по биржевому делу
Рефераты по ботанике и сельскому хозяйству
Рефераты по бухгалтерскому учету и аудиту
Рефераты по валютным отношениям
Рефераты по ветеринарии
Рефераты для военной кафедры
Рефераты по географии
Рефераты по геодезии
Рефераты по геологии
Рефераты по геополитике
Рефераты по государству и праву
Рефераты по гражданскому праву и процессу
Рефераты по делопроизводству
Рефераты по кредитованию
Рефераты по естествознанию
Рефераты по истории техники
Рефераты по журналистике
Рефераты по зоологии
Рефераты по инвестициям
Рефераты по информатике
Исторические личности
Рефераты по кибернетике
Рефераты по коммуникации и связи
Курсовая работа: Разработка програмного обеспечения для расчёта дисперсионной характеристики планарного волновода
Курсовая работа: Разработка програмного обеспечения для расчёта дисперсионной характеристики планарного волновода
Федеральное агентство образования и науки Российской Федерации
ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ
УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ
Кафедра сверхвысокочастотной и квантовой радиотехники
Применение методов вычислительной математики
Пояснительная записка к курсовой работе по информатике
Студент группы 164__________. «___»__________г. |
|
|
Руководитель Аспирант кафедры _________ «___»__________. |
РЕФЕРАТ.
Курсовая работа 26 с., 9 рис., 2 источника, 3 приложения.
МЕТОД ДИХОТОМИИ, ДИСПЕРСИОННАЯ ХАРАКТЕРИСТИКА, НАПРАВЛЯЮЩИЕ УГЛЫ, ПЛАНАРНЫЙ ВОЛНОВОД, ПРОФИЛИ ТЕ-МОД.
Объектом исследования является асимметричный планарный волновод, предназначенный для распространения в нём ТЕ-мод.
Цель работы – разработка програмного обеспечения для расчёта дисперсионной характеристики планарного волновода, нахождения направляющих углов для ТЕ-мод и построения соответствующих им профилей.
В процессе работы реализована программа для расчёта дисперсионной характеристики планарного волновода, отработана методика нахождения корней уравнений численными методами.
В результате исследования получены зависимости количества, направляющих углов и профилей ТЕ-мод от характеристик волновода и длины волны излучения.
Пояснительная записка к дипломной работе выполнена в текстовом редакторе Microsoft Word 2002.
"УТВЕРЖДАЮ"
Зав.каф.
________.
"___" г.
ЗАДАНИЕ № 9
на курсовую работу по дисциплине "ИНФОРМАТИКА"
студенту гр.
(фамилия, имя, отчество)
1. Тема работы: применение методов вычислительной математики
2. Срок сдачи работы на кафедру -
3. Содержание работы и сроки выполнения работы:
3.1. Изучение задания и рекомендованной литературы - 2я неделя.
3.2. Разработка алгоритма решения и составление схемы алгоритма - 4я неделя.
3.3. Составление программы для решения задачи в пакете MATHCAD - 7я неделя.
3.4. Написание программы и создание пользовательского интерфейса в среде программирования Borland Delphi”. - 10я неделя.
3.5. Отладка программы на ПК. - 12я неделя.
3.6. Выполнение вычислений на ПК. - 14я неделя.
3.7. Оформление пояснительной записки в соответствии с требованиями к оформлению курсовых работ. - 15я неделя.
4. Рекомендуемая литература:
4.1. Фигурнов В.Э. IBM PC для пользователя. - М.: Финансы и статистика, 1990г, - 240с.
4.2. Сергиевский М.В., Шалашов А.В., Турбо Паскаль 7.0., Язык, среда, программирования. - М.: Машиностроение. - 1994. - 254с.
4.3. Мудров А.Е., Численные методы для ПЭВМ на языках Бейсик, Фортран и Паскаль. - Томск : МП "РАСКО", 1991. - 272с.
4.4. Дьяконов В.П. Система MathCAD: Справочник, - М.: Радио и связь, 1993. - 128с.
4.5. Кудрявцев Е.М. Mathcad2000 Pro: - М.: ДМК Пресс, 2001. – 576 с.: ил.
5. Дополнительную литературу студент ищет самостоятельно в зависимости
от темы и сложности задания.
6. Исходные данные:
Определить профили мод ТЕ в планарном волноводе, если профиль компоненты Еу задан в трех слоях как:
![]() , x£0
, x£0
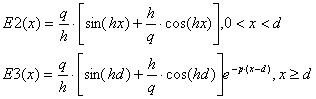 ,
,
где
![]()
![]()
![]() - поперечные волновые числа
1, 2 и 3-й сред соответственно.
- поперечные волновые числа
1, 2 и 3-й сред соответственно.
6.2.Дисперсионная характеристика для ТЕ-мод в планарном волноводе задается выражением:
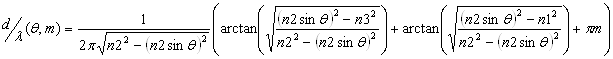 где n1, n2, n3 – показатели преломления трех сред;
где n1, n2, n3 – показатели преломления трех сред;
m – порядок моды;
θ угол падения луча на границу раздела сред;
d – толщина волноводного слоя;
l - длина волны света в вакууме.
- Построить семейство диспесионных характериситик для заданных значений n1, n2, n3, l;
- Для заданного значения d определить количесвто направляемых мод и соответствующие углы ввода для каждой из них;
- Построить профили ТЕ мод распрастроняющихся в волноводе с заданными конструктивными параметрами.
6.3. Пункт 6.1.-6.2. повторить на пакете MATHCAD.
- Точность вычислений обеспечить не хуже 10-3.
- Ввод исходных данных организовать с помощью меню.
7. Состав пояснительной записки:
7.1. Титульный лист.
7.2. Аннотация.
7.3. Лист задания с подписью преподавателя.
7.4. Содержание.
7.5. Введение. Постановка задачи.
7.6. Математическое описание используемого метода для решения задачи. Кратко, понятно, лаконично изложение теории.
7.7. Описание алгоритма решения задачи и схема алгоритма.
7.8. Описание программы. Результаты решения.
7.9. Интерпретация результатов и выводы по проделанной работе.
7.10. Список используемой литературы.
7.11. Распечатка программы с комментариями (в виде приложения).
8. Отчетность по работе:
8.1. В ходе выполнения работы - отчетность по фактическому материалу в рабочей тетради ( в соответствии со сроками выполнения основных этапов, указанных в п.3).
8.2. Пояснительная записка, в обязательном порядке со всеми разделами по п.7. без исключения.
8.3. На дискете - передается: файл программы, подробное описание программы.
8.4. После оформления пояснительной записки - защита на кафедре.
Дата выдачи задания .
Подпись руководителя _____________
Подпись студента _____________
Содержание:
1 |
Введение |
6 | |
| 2 | Математическое описание использованного для решения задачи метода | 7 | |
| 3 | Описание алгоритма решения задачи и схема алгоритма | 8 | |
| 4 | Описание программы | 15 | |
| 5 | Результаты решения, их интерпретация и выводы по проделанной работе | 10 | |
| 5.1 | Результаты работы программы | 10 | |
| 5.2 | Результаты проверки в пакете «MathCAD» | 12 | |
| 5.3 | Интерпретация результатов и выводы по проделанной работе | 13 | |
| 6 | Список использованной литературы | 14 | |
| 7 | Приложение А | 15 | |
| 8 | Приложение В | 18 | |
| 9 | Приложение С | 25 | |
1. Введение
В этой работе перед нами ставится цель научиться применять некоторые численные методы при решении метематических задач при помощи ПК. Математическое моделирование процессов и явлений в различных областях науки и техники является одним из основных способов получения новых знаний и технологических решений. Для решения поставленной в этом курсовом проекте задачи необходи иметь основные навыки программирования на языке «Pascal» и в объектно-ориентированной среде «Delphi». Эти знания могут пригодиться и в будущем, при написании каких-либо программ вычислительного характера.
В данной работе необходимо написать программу, которая бы рассчитала дисперсионную характеристику планарного волновода и построила профили направляемых в нём ТЕ-мод. Для нахождения направляющих углов был использован метод дихотомии (половинного деления). Он наиболее прост в реализации, имеет относительно быструю сходимость и позволяет легко контролировать погрешность вычислений.
2. Математическое описание использованного
для решения задачи МЕТОДА.
Нажождение корня уравнения методом дихотомии.
Считаем, что на отрезке [а, b] расположен один корень, который необходимо уточнить с погрешностью e.
Метод дихотомии, или половинного деления, заключается в следующем. Определяем середину отрезка [а, b]
Х= (а + b)/2
и вычисляем функцию f(Х). Далее делаем выбор, какую из двух частей отрезка взять для дальнейшего уточнения корня. Если левая часть уравнения f(x) есть непрерывная функция аргумента х, то корень будет находиться в той половине отрезка, на концах которой f(x) имеет разные знаки.Это будет отрезок [а, Х], т.е. для очередного шага уточнения точку b перемещаем в середину отрезка Х и продолжаем процесс деления как с первоначальным отрезком [а,b].
Итерационный (повторяющийся) процесс будем продолжать до тех пор, пока интервал [а,b] не станет меньше заданной погрешности e.
Следует учитывать, что функция f(x) вычисляется с некоторой абсолютной погрешностью e1. Вблизи корня значения функции f(x) малы по абсолютной величине и могут оказаться сравнимыми с погрешностью ее вычисления. Другими словами, при подходе к корню мы можем попасть в полосу шумов 2e1 и дальнейшее уточнение корня окажется невозможным. Поэтому надо задать ширину полосы шумов и прекратить итерационный процесс при попадании в нее. Также необходимо иметь в виду, что при уменьшении интервала [а,b] увеличивается погрешность вычисления его длины (b – а) за счет вычитания близких чисел.
Метод дихотомии позволяет значительно уменьшить объем вычислений по сравнению с графическим методом. Так как за каждую итерацию интервал, где расположен корень, уменьшается в два раза, то через n итераций интервал будет равен (b - а)/2n. За 10 итераций интервал уменьшится в 2 10 =1024 раз, за 20 итераций - в 220=1048576 раз.
3. Описание алгоритма решения задачи и схема алгоритма.
Основная задача, которая
решается в этой программе, это решение приведённого далее уравнения
относительно ![]() :
:
![]() , (3.1)
, (3.1)
| где |
|
|
|
|
|
|
|
|
|
|
|
|
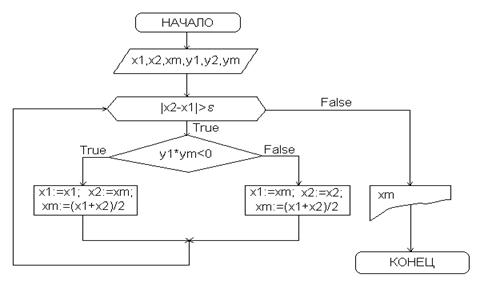
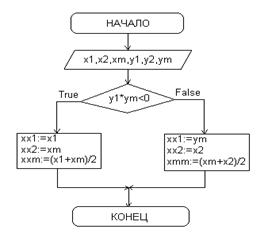
В программе решение данного уравнения реализавано методом дихотомии, схема которого приведена ниже.
|
Рисунок 3.1 блок-схема метода дихотомии. |
Далее, используя полученные значения направляющих углов, строится график, отображающий профили ТЕ-мод. График, отображающий правую часть уравнения (3.1), практической ценности для решения задачи не имеет и носит чисто иллюстративный характер.
4. ОПИСАНИЕ ПРОГРАММЫ.
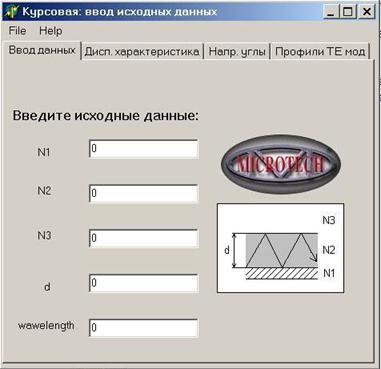
Вид программы представлен на рисунке 4.1. По своей внешней форме она представляет собой 4 закладки, расположенные на 1 форме. На первой закладке осуществляется ввод исходных данных, на второй строится график дисперсионной характеристики волновода, на третьей выводятся значения направляющих углов, а на чётвертой строятся профили ТЕ-мод.
|
Рисунок 4.1 - Основной вид программы, закладка для ввода исходных данных. |
Все вычисления и построения графиков производятся при смене закладки с первой на любую другую (событие объекта TPageControl «OnChange»). Перед сменой (событие «OnChanging») осуществляется проверка на полноту исходных данных: если хоть в одном из окон осталось стоящее по умолчанию число «0», то смены закладки не произойдёт, зато возникнет информационное окно, которое укажет пользователю на его ошибку. При повторном переходе с первой закладки на другую будет произведён перерасчёт.
Вычисление направляющих углов осуществляется с указанной в задании точностью – 0,001.
Полная схема и листинг программы находятся в приложении А и В соответственно.
5. Результаты решения, их интерпретация и выводы по проделанной работе.
5.1. результаты работы программы.
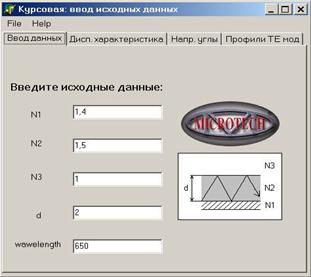
Расчёты проводились при следующих исходных данных:
|
Рисунок 5.1 ввод исходных данных в программу. |
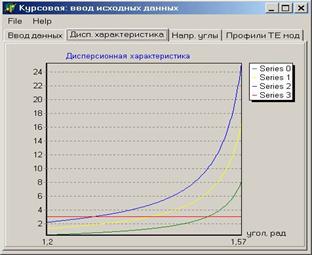
При таких введённых параметрах программа рассчитала следующую дисперсионную характеристику:
|
Рисунок 5.2 дисперсионная характеристика волновода. |
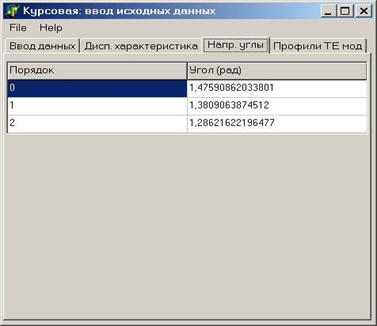
Подсчитанные направляющие углы составили:
|
Рисунок 5.3 направляющие углы ТЕ-мод. |
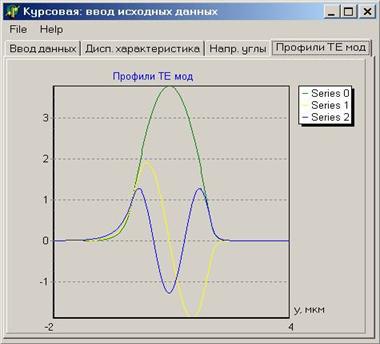
И при этих углах программа построила вот такие профили ТЕ-мод:
|
Рисунок 5.4 профили ТЕ-мод. |
5.2. Результаты проверки в пакете «MathCAD».
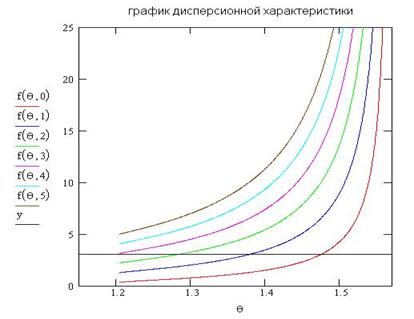
При аналогичных исходных данных «MathCAD» выдал следующие результаты:
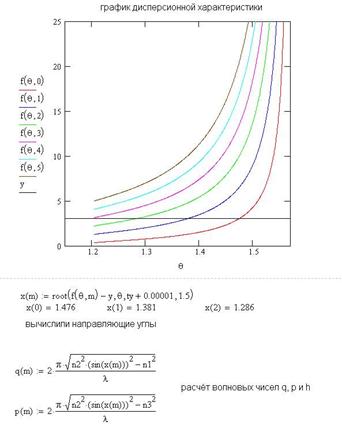
|
Рисунок 5.5 – график дисперсионной характеристики, полученный при помощи пакета «MathCAD». |
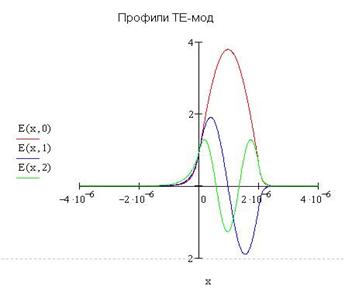
|
|
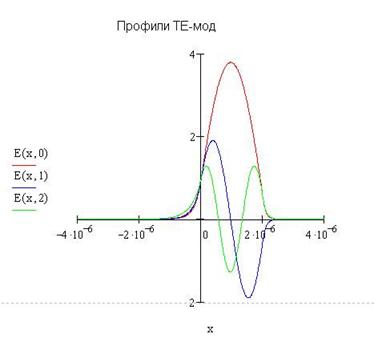
|
Рисунок 5.6 – график с профилями ТЕ-мод, полученный при помощи пакета «MathCAD» |
Полный листинг решения поставленной задачи в пакете «MathCAD» приведён в приложении С.
5.3. Интерпретация результатов и выводы по проделанной работе.
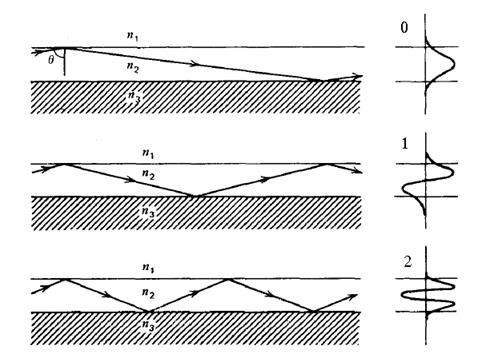
Проведя сравнительный анализ результатов, полученных при помощи написанной в «Delphi» программы и пакета «MathCAD», мы видим их полное совпадение в пределах заданной погрешности. Кроме того, конечные результаты, а именно профили ТЕ-мод, совпадают со справочными:
|
Рисунок 5.7 три низшие ТЕ-моды асимметричного планарного волновода и соответствующие им зигзагообразные лучи. |
Из этого можно сделать вывод, что поставленная задача была решена мною верно и в полном объёме. Я не только создал конечный програмный продукт, ограниченно пригодный для практического использования, но и получил практические навыки программирования в объектно ориентированной среде «Delphi».
6. Список используемой литературы:
1. «Численные методы для ПЭВМ на языках Бейсик, Фортран и Паскаль». А.Е.Мудров – МП «Раско», Томск, 1992г, 270с.
2. «Оптические волны в кристаллах». А. Ярив, П. Юх – издательство «Мир», Москва, 1987г, 616с.
Приложение А.
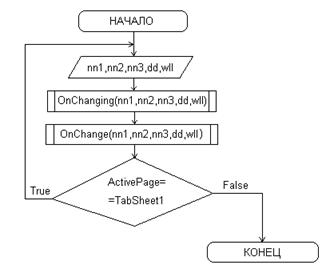
Блок-схема тела основной программы.
|
Рисунок А.1 блок-схема тела основной программы. |
nn1,nn2,nn3 – показатели преломления, исходные данные, вводимые пользователем;
dd – толщина волновода, вводится пользователем;
wll – длина волны используемого света, вводится пользователем.
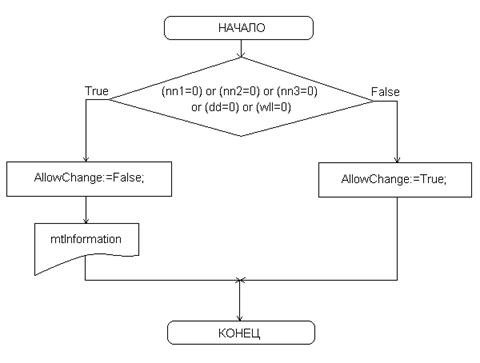
Блок-схема Процедуры «OnChanging».
|
Рисунок А.2 блок-схема процедуры «OnChanging». |
AllowChange – свойство объекта TPageControl, отвечающее за разрешение/неразрешение смены закладки;
mtInformation – информационное окно, уведомляющее пользователя о том, что он ввёл не все исходные данные.
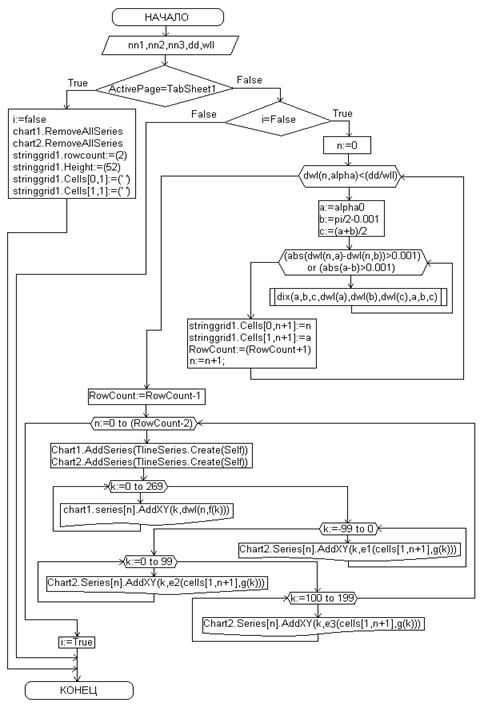
Блок-схема Процедуры «OnChange».
|
Рисунок А.3 блок-схема процедуры «OnChange». |
i – переменная типа boolean, которая отвечает за то, будет ли при смене закладки осуществлён пересчёт;
chart1 – график, отображающий дисперсионную характеристику волновода;
chart2 – график, отображающий профили ТЕ-мод;
stringgrid1 – таблица, которая по ходу выполнения программы заполняется значениями направляющих углов;
n – переменная типа byte, соответствующая порядку моды;
a, b – переменные, задающие диапазон, на котором производится уточнение направляющих углов;
dwl – функция, задающая дисперсионную характеристику волновода (численно равна правой части уравнения (3.1));
dix – процедура, осуществляющая одну итерацию метода дихотомии;
k – вспомогательная переменнная типа integer, используемая для построения графика;
f(k), g(k) – функции от k, выступающие в роли аргумента для других функций;
e1, e2, e3 – функции, определяющие профиль моды в различных средах.
Блок-схема процедуры «dix».
|
Рисунок А.4 блок схема процедуры «dix». |
х1, х2, хm крайние и среднее значения интервала, на котором производится уточнение корня;
y1, y2 ym значения уточняемой функции от x1, x2 и xm соответственно;
xx1, xx2 , xxm новые крайние и среднее значения интервала, полученные после его уменьшения вдвое.
Приложение В.
Модуль формы Form1.
unit Unit1;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, StdCtrls, ExtCtrls, jpeg, ComCtrls, TeEngine, Series, TeeProcs,
Chart,math, Grids, Menus;
type
TForm1 = class(TForm)
PageControl1: TPageControl;
TabSheet1: TTabSheet;
TabSheet2: TTabSheet;
Label1: TLabel;
Label2: TLabel;
Label3: TLabel;
Label4: TLabel;
Label5: TLabel;
Label6: TLabel;
Image1: TImage;
Image2: TImage;
Edit1: TEdit;
Edit2: TEdit;
Edit3: TEdit;
Edit4: TEdit;
Edit5: TEdit;
TabSheet3: TTabSheet;
Chart1: TChart;
TabSheet4: TTabSheet;
Chart2: TChart;
StringGrid1: TStringGrid;
MainMenu1: TMainMenu;
File1: TMenuItem;
Exit1: TMenuItem;
Help1: TMenuItem;
About1: TMenuItem;
Label7: TLabel;
Label8: TLabel;
Label9: TLabel;
Label10: TLabel;
Label11: TLabel;
Label12: TLabel;
procedure Edit1KeyPress(Sender: TObject; var Key: Char);
procedure Edit2KeyPress(Sender: TObject; var Key: Char);
procedure Edit3KeyPress(Sender: TObject; var Key: Char);
procedure Edit4KeyPress(Sender: TObject; var Key: Char);
procedure Edit5KeyPress(Sender: TObject; var Key: Char);
procedure PageControl1Changing(Sender: TObject;
var AllowChange: Boolean);
procedure PageControl1Change(Sender: TObject);
procedure FormActivate(Sender: TObject);
procedure Exit1Click(Sender: TObject);
procedure About1Click(Sender: TObject);
private
{ Private declarations }
public
i:boolean;
nn1,nn2,nn3,dd,wll:real;
{ Public declarations }
end;
var
Form1: TForm1;
implementation
uses Unit4;
{$R *.dfm}
procedure TForm1.Edit1KeyPress(Sender: TObject; var Key: Char);
begin
case key of
'0'..'9', chr(8): ;
'-': if length(edit1.text)<>0 then key:=chr(0) else key:=chr(45);
'.': if pos(',',edit1.text)<>0 then key:=chr(0) else key:=chr(44);
',': if pos(',',edit1.text)<>0 then key:=chr(0) else key:=chr(44);
else key:=chr(0);
end;
end;
procedure TForm1.Edit2KeyPress(Sender: TObject; var Key: Char);
begin
case key of
'0'..'9', chr(8): ;
'-': if length(edit2.text)<>0 then key:=chr(0) else key:=chr(45);
'.': if pos(',',edit2.text)<>0 then key:=chr(0) else key:=chr(44);
',': if pos(',',edit2.text)<>0 then key:=chr(0) else key:=chr(44);
else key:=chr(0);
end;
end;
procedure TForm1.Edit3KeyPress(Sender: TObject; var Key: Char);
begin
case key of
'0'..'9', chr(8): ;
'-': if length(edit3.text)<>0 then key:=chr(0) else key:=chr(45);
'.': if pos(',',edit3.text)<>0 then key:=chr(0) else key:=chr(44);
',': if pos(',',edit3.text)<>0 then key:=chr(0) else key:=chr(44);
else key:=chr(0);
end;
end;
procedure TForm1.Edit4KeyPress(Sender: TObject; var Key: Char);
begin
case key of
'0'..'9', chr(8): ;
'-': if length(edit4.text)<>0 then key:=chr(0) else key:=chr(45);
'.': if pos(',',edit4.text)<>0 then key:=chr(0) else key:=chr(44);
',': if pos(',',edit4.text)<>0 then key:=chr(0) else key:=chr(44);
else key:=chr(0);
end;
end;
procedure TForm1.Edit5KeyPress(Sender: TObject; var Key: Char);
begin
case key of
'0'..'9', chr(8): ;
'-': if length(edit5.text)<>0 then key:=chr(0) else key:=chr(45);
'.': if pos(',',edit5.text)<>0 then key:=chr(0) else key:=chr(44);
',': if pos(',',edit5.text)<>0 then key:=chr(0) else key:=chr(44);
else key:=chr(0);
end;
end;
procedure TForm1.PageControl1Changing(Sender: TObject;
var AllowChange: Boolean);
begin
allowchange:= tschng(strtofloat(edit1.text),strtofloat(edit2.text),strtofloat(edit3.text),strtofloat(edit4.text),strtofloat(edit5.text));
end;
procedure TForm1.PageControl1Change(Sender: TObject);
//основная процедура программы, привязанная к смене закладки
//по её ходу и осуществляются все вычисления и построение графиков
var
n:byte;
k:integer;
a,b,c,f:real;
begin
nn1:=strtofloat(edit1.text);
nn2:=strtofloat(edit2.text);
nn3:=strtofloat(edit3.text);
dd:=strtofloat(edit4.text)/1000000;
wll:=strtofloat(edit5.text)/1000000000;
if pagecontrol1.activepage=(tabsheet1) then
begin
i:=false;
chart1.RemoveAllSeries;
chart2.RemoveAllSeries;
stringgrid1.rowcount:=(2);
stringgrid1.Height:=(52);
stringgrid1.Cells[0,1]:=(' ');
stringgrid1.Cells[1,1]:=(' ');
end
else
begin
if i=false then
begin
n:=0;
while dwl(n,(arcsin(nn1/nn2)+0.00005),nn1,nn2,nn3)<(dd/wll) do
begin
a:=(arcsin(nn1/nn2)+0.001);
b:=(pi/2-0.001);
c:=(a+b)/2;
while (abs(dwl(n,a,nn1,nn2,nn3)-dwl(n,b,nn1,nn2,nn3))>0.001) or (abs(a-b)>0.001) do
begin
dix(a,b,c,(dwl(n,a,nn1,nn2,nn3)-(dd/wll)),(dwl(n,b,nn1,nn2,nn3)-(dd/wll)),(dwl(n,c,nn1,nn2,nn3)-(dd/wll)),a,b,c);
end;
stringgrid1.Cells[0,n+1]:=floattostr(n);
stringgrid1.Cells[1,n+1]:=floattostr(a);
stringgrid1.RowCount:=(stringgrid1.RowCount+1);
if n<14 then stringgrid1.Height:=(stringgrid1.Height+26);
n:=n+1;
end;
stringgrid1.RowCount:=(stringgrid1.RowCount-1);
stringgrid1.Height:=(stringgrid1.Height-26);
for n:=0 to (stringgrid1.RowCount-2) do
begin
Chart1.AddSeries( TlineSeries.Create( Self ) );
chart1.Serieslist[n].SeriesColor:=chart1.getfreeseriescolor(false);
for k:=0 to 269 do
begin
f:=(arcsin(nn1/nn2)+k*(((pi/2)-0.001-arcsin(nn1/nn2))/300));
chart1.Series[n].AddXY(k,dwl(n,f,nn1,nn2,nn3),'',clteecolor);
end;
end;
Chart1.AddSeries( TlineSeries.Create( Self ) );
for k:=1 to 269 do
begin
chart1.Series[chart1.SeriesCount-1].AddXY(k,(dd/wll),'',clteecolor);
end;
for n:=0 to (stringgrid1.RowCount-2) do
begin
Chart2.AddSeries( TlineSeries.Create( Self ) );
chart2.Serieslist[n].SeriesColor:=chart2.getfreeseriescolor(false);
for k:=(-99) to 0 do
begin
chart2.Series[n].AddXY(k,e1(wll,dd,nn1,nn2,nn3,strtofloat(stringgrid1.Cells[1,n+1]),(k*dd/100)),'',clteecolor);
end;
for k:=0 to 99 do
begin
chart2.Series[n].AddXY(k,e2(wll,dd,nn1,nn2,nn3,strtofloat(stringgrid1.cells[1,n+1]),(k*dd/100)),'',clteecolor);
end;
for k:=100 to 199 do
begin
chart2.Series[n].AddXY(k,e3(wll,dd,nn1,nn2,nn3,strtofloat(stringgrid1.Cells[1,n+1]),(k*dd/100)),'',clteecolor);
end;
end;
label7.Caption:=floattostrf(arcsin(nn1/nn2),ffgeneral,3,3);
label8.caption:=floattostrf((pi/2-0.001-(pi/2-arcsin(nn1/nn2))/300),ffgeneral,3,3);
label10.Caption:=floattostr(-dd*1000000);
label11.Caption:=floattostr(2*dd*1000000);
i:=true;
end;
end;
end;
procedure TForm1.FormActivate(Sender: TObject);
begin
i:=false;
stringgrid1.Cells[0,0]:=('Порядок');
stringgrid1.Cells[1,0]:=('Угол (рад)');
end;
procedure TForm1.Exit1Click(Sender: TObject);
begin
close;
end;
procedure TForm1.About1Click(Sender: TObject);
begin
messagedlg('Курсовая работа по информатике, ТУСУР,'
+#13+' 1 курс, специальность 210405.'
+#13+' Выполнил студент группы 164'
+#13+' Филатов Александр.', mtinformation, [mbOK],0);
end;
end.
Вспомогательный модуль, содержащий математические процедуры и функции.
unit Unit4;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, StdCtrls, ExtCtrls, jpeg, ComCtrls, TeEngine, Series, TeeProcs,
Chart,math;
function tschng(n1,n2,n3,d,wl:real):boolean;
function dwl(m:byte; tetta,n1,n2,n3:real):real;
function q(wl,tetta,n2,n1:real):real;
function h(wl,tetta,n2:real):real;
function p(wl,tetta,n2,n3:real):real;
function e1(wl1,d1,n11,n21,n31,tetta1,x1:real):real;
function e2(wl2,d2,n12,n22,n32,tetta2,x2:real):real;
function e3(wl3,d3,n13,n23,n33,tetta3,x3:real):real;
procedure dix(x1,x2,xm,y1,y2,ym:real; var xx1,xx2,xxm:real);
implementation
function tschng(n1,n2,n3,d,wl:real):boolean;
//осуществляет проверку исходных данных на полноту
begin
if (n1=0) or (n2=0) or (n3=0) or (d=0) or (wl=0) then
begin
messagedlg('Вы должны ввести значения всех параметров!', mtinformation, [mbOK],0);
tschng:=(False);
end
else
tschng:=(True);
end;
function dwl(m:byte; tetta,n1,n2,n3:real):real;
//функция дисперсионной характеристики волновода
var
aa,bb,cc,dd: real;
begin
aa:= sqrt(1-sqr(sin(tetta)));
aa:= 1/(2*pi*n2*aa);
bb:= sqrt(sqr(n2*sin(tetta))-sqr(n3));
cc:= sqrt(sqr(n2*sin(tetta))-sqr(n1));
dd:= n2*sqrt(1-sqr(sin(tetta)));
dwl:=aa*(arctan(bb/dd)+arctan(cc/dd)+pi*m);
end;
function q(wl,tetta,n2,n1:real):real;
//функция, вычисляющая волновое число q
begin
q:=(2*pi*sqrt(sqr(n2*sin(tetta))-n1*n1))/wl;
end;
function h(wl,tetta,n2:real):real;
//функция, вычисляющая волновое число h
begin
h:=(2*pi*cos(tetta)*n2)/wl;
end;
function p(wl,tetta,n2,n3:real):real;
//функция, вычисляющая волновое число p
begin
p:=(2*pi*sqrt(sqr(n2*sin(tetta))-n3*n3))/wl;
end;
function e1(wl1,d1,n11,n21,n31,tetta1,x1:real):real;
//функция, задающая профиль Еу ТЕ моды при условии х<=0
begin
e1:=exp(q(wl1,tetta1,n21,n11)*x1);
end;
function e2(wl2,d2,n12,n22,n32,tetta2,x2:real):real;
//функция, задающая профиль Еу ТЕ моды при условии 0<х<d
begin
e2:=(q(wl2,tetta2,n22,n12)/h(wl2,tetta2,n22))*(sin(x2*h(wl2,tetta2,n22))+(h(wl2,tetta2,n22)/q(wl2,tetta2,n22,n12))*cos(h(wl2,tetta2,n22)*x2));
end;
function e3(wl3,d3,n13,n23,n33,tetta3,x3:real):real;
//функция, задающая профиль Еу ТЕ моды при условии х>=d
begin
e3:=(q(wl3,tetta3,n23,n13)/h(wl3,tetta3,n23))*(sin(d3*h(wl3,tetta3,n23))+(h(wl3,tetta3,n23)/q(wl3,tetta3,n23,n13))*cos(h(wl3,tetta3,n23)*d3))*exp(-p(wl3,tetta3,n23,n33)*(x3-d3));
end;
procedure dix(x1,x2,xm,y1,y2,ym:real; var xx1,xx2,xxm:real);
//процедура, осуществляющая 1 итерацию метода дихотомии
begin
if (y1*ym)<0 then
begin
xx1:=x1;
xx2:=xm;
xxm:=(x1+xm)/2;
end;
if (ym*y2)<0 then
begin
xx1:=xm;
xx2:=x2;
xxm:=(xm+x2)/2;
end;
end;
end.
Приложение c.
|
|
|
|
|
|
|
|
© 2010 Интернет База Рефератов