Курсовая работа: Використання елементарних перетворень для знаходження оберненої матриці

Міністерство освіти і науки України

Факультет інформатики

Курсова робота

Тема:

“Використання елементарних перетворень

для знахожження оберненої матриці ”

Виконав студент ІІ-го курсу

Факультету нформатики

Заочної форми навчання

Науковий керівник:

Ужгород 2009

Зміст

Зміст. 2

Вступ. 3

1. Теория. 4

2. Опис програми. 8

3. Програма. 10

Висновок. 45

Список використаної літератри. 46

Квадратна матриця називається виродженою (для особливої), якщо її визначник дорівнює нулю, і невиродженою (чи неособливої) - у протилежному випадку. Відповідно лінійне перетворення невідомих називається виродженим чи невиродженим у залежності від того, чи буде дорівнює чи нулю відмінний від нуля визначник з коефіцієнтів цього приобразования. З теореми випливає наступне твердження:

Добуток матриць, хоча б одна з яких вироджена, буде вродженою матрицею.

Добуток будь-яких невироджених матриць саме буде невирожденою матрицею. Звідси випливає, через зв'язок, що існує між множенням матриць і послідовним виконанням лінійних перетворень, таке твердження: результат послідовного виконання декількох лінійних перетворень тоді і тільки тоді буде невиродженим перетворенням, якщо всі задан перетворення невироджені.

1. Теория

Добуток матриць, хоча б одна з яких вироджена, буде вродженою матрицею.

Роль одиниці у множенні матриць грає одинична матриця

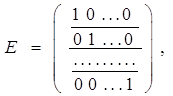причому вона перестановочна з будь-якою матрицею А даним порядком

АЕ=ЕА=А (1)

Доводяться ці чи рівності безпосереднім приминением правилаумножения матриць, чи ж на підставі зауваження, що еденичная матриця відповідає тотожному лінійний приобразованию невідомих

x1=y1

x2= y2

... ... ... .

xn= yn

Виконання якого до чи після будь-якого іншого лінійного переутворення, очевидно не змінює цього останнього.

Помітимо, що матриця Е є єдиною матрицею, що задовольняє умові (1) при будь-якій матриці А. Дійсно, якби існувала матриця Е' з цією же властивістю, то ми мали б

E’E=E’, E’E=E,

звідки E’=E.

Питання про існування для даної матирцы А зворотної матриці виявляється болеее складним. Через некомутативности множення матриць ми будемо говорити зараз про праву зворотну матрицю, тоесть про таку зворотну матрицю А-1

Що добуток матриці А праворуч на цю матрицю дає еденичную матрицю,

AA-1=E (2)

Якщо матриця А вырожденная, то, якби матриця А-1 існувала, добуток, що коштує в лівій частині рівності (2), було б, як ми знаємо, вырожденной матрицею, у той час як насправді матриця Е, що коштує в правій частині цієї рівності, є невырожденной, тому що його визначник дорівню еденице. Таким чином, вырожденная матриця не може мати правої зворотної матриці. Такого ж розуміння показують, сто вона не має і лівої зворотний і тому для вырожденной матриці обратеая матриця воопше не існує.

Переходячи до випадку невырожденной матриці, уведемо спочатку наступне допоміжне поняття. Нехай дана матриця n-го порядку

a11 a12... a1n

a21 a22... a2n

А=... ... ... ... ... ... ... ... .

an1 an1... ann

Матриця

a11 a12... a1n

A*= a21 a22... a2n

... ... ... ... ... ... ... ... .

an1 an1... ann

Складання з алгебраїчних доповнень до елементів матриці А, причому алгебраїчне доповнення до елементу aіj коштує на перетинанні j-й рядка й і-го стовпця, називається приєднаної (чи взаємної) до матриці А.

Знайдемо добуток АА* і А*А. Використовуючи відому формулу розкладання визначника по чи рядку стовпцю, а також теорему про суму добутків елементів будь-якого рядка (стовпця) визначника на алгебраїчн доповнення до відповідних елементів іншого рядка (стовпця), і позначаючи через d визначник матриці А,

d=|A|,

ми одержимо наступні рівності:

d 0...0

0 d...0

АА*=А*А=... ... ... . . (3)

0 0... d

Звідси випливає, що якщо матриця А невырожденная, те її присоедененная матриця А* також буде невырожденной, причому визначник d* матриці А* дорівнює (n-1) - й ступеня визначника d матриц А.

Справді, переходячи від рівностей (3) до рівності між визначниками, ми одержимо

dd*= dn,

звідки d≠0

d*= dn-1

Тепер можна довести існування зворотно матриці для всякої не виродженої матриці А и знайти її вид. Помітимо спочатку, що якщо ми розглянемо добуток двох матриць АВ і всі елементи одногоиз множників, наприклад У, розділимо на те саме число d, те всі елементи добутку АВ також розділяться на це ж число: для доказу потрібно лише згадати визначення множення матриць. Таки мобразом, якщо

d=|A|≠0

те з рівностей (3) випливає, що зворотною матрицею для А буде служити матриця, що виходить із присоедененной матриці А* розподілом усіх її елементів на d:

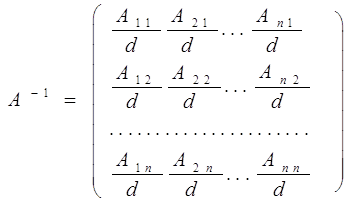
Дійсно, з (3) випливають рівності

(4)

Ще раз підкреслимо, що в і-й рядку матриці А-1 коштують алгебраическиедополнения до елементів і-го стовпця визначника |А|, ділені на d=|A|.

Легко довести що матриця А-1 є єдиною матрицею, що задовольняє умові (4) для даної невырожденной матриці А. Дійсно, якщо матриця З така, що

АС=СА=Е

то

САА-1=С(АА-1) =СЕ=С

САА-1=(СА) А-1=ЕА=А-1

Звідки С=А-1.

З (4) і теореми про множення визначників випливає, що визначник матриц А-1 дорівнює, так що ця матриця так само

буде невиродженою. Зворотної для неї служить матриця А.

Якщо тепер дані квадратні матриці n-го порядку А и В, з яких А-невырожденная, а В - довільна, то ми можемо виконати правий лівий розподіл У на А, тобто, вирішити матричні рівняння

AX=B, YA=B (5)

Для цього, через асоціативності множення матриць, досить покласти

X=A-1B, Y=BA-1,

причому ці рішення рівнянь (5) буду, через некоммутативности множення матриць, у загальному випадку різними.

2. Опис програми

Програма Matrtest. pas являється демо программою, котра показує роботу процедур з модуля Matr. pas.

Модуль програми Matr. pas – в ній розміщен процедури і функції, котрі роблять перетворення матриць.

У файлі – Time. dat записані коефіціенти матриці, розмірність матриці. Він мусить містити в собі початкову матрицю, розмірність, тому, що програма без цих даних працювати не буде.

Нижче приведений “скрин” програми, тобто вигляд програми в роботі.

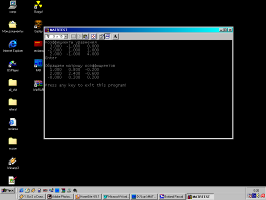
3. Програма

{============================Matrtest. pas=========================}

Uses matr;

Var A,C: MAtrix;

Begin

A. VMT; C. VMT;

Writeln(' Коэффициеты уравнения ');

A. ReadOfText('time',' Коэффициеты уравнения ');

A. WriteToText('con',7,3);

Write('Enter'); Readln;

Writeln('Обращаем матрицу коэффициентов');

C. RevWithGauss(A);

C. WriteToText('con',7,3);

Write('Enter'); Readln;

End.

{============================ Matr. pas ==========================}

{$A+,B-,D-,E-,F+,G+, I-,L-,N+,O-,P-,Q-,R-,S-,T+,V+,X+}

{$M 24000,32,655360}

Unit Matr;

Interface

Const

CTooManySize=1;

CBadPosition=2;

CFileNotFound=3;

CFileError=4;

CReadError=5; {A}

CWriteError=6; {A}

COutOfData=7;

CBadOperands=8;

CMulError=9; {A}

CSearchError=10;

CNotExist=11;

CMNotSquare=12;

CAddError=13; {A}

CReversError=14; {A}

CMDegenerate=15;

CUnkNownError=16;

CMDgError=17; {A}

CMSqrError=18; {A}

CDetError=19; {A}

CSortError=20; {A}

CDGaussError=21; {A}

CCuanZeeroError=22; {A}

CSwapError=23; {A}

CMulToNumError=24; {A}

CStopped=25;

CDegrError=26; {A}

CIgError=27; {A}

CZFE=28;

Type

TOE=Extended;

Ar=Array [1. . (Word(Pred(0)) +1) div SizeOf(TOE)] of TOE;

Ar31=Array [1. .31,1. .31] of TOE;

Ar63=Array [1. .63,1. .63] of TOE;

Tabl=Object

CBars,CLines: Byte;

M: Pointer; {**}

SizeInMemory: Word; {**}

Errors: Set of Byte;

Exist: Boolean;

Constructor VMT;

Procedure DataInit(L,B: Byte); Virtual;

Procedure SetE(I,J: Byte; E: TOE);

Function GetE(I,J: Byte): TOE;

Procedure Del;

Procedure ReadOfText(Name: String; Search: String);

Procedure WriteToText(Name: String; F1,F2: Byte);

Procedure AllClear; Virtual; {}

Procedure Let(Var A); Virtual;

Procedure ZeeroFill;

{ Errors }

Procedure TooManySize; Virtual;

Procedure BadPosition; Virtual;

Procedure FileNotFound; Virtual;

Procedure FileError; Virtual;

Procedure ReadError; Virtual;

Procedure WriteError; Virtual;

Procedure OutOfData; Virtual;

Procedure SearchError; Virtual;

Procedure NotExist; Virtual;

Procedure UnkNownError; Virtual;

Procedure AnyError; Virtual;

Procedure ZFE; Virtual;

End;

Line=Set of Byte;

Mem=Record

mPlus: Boolean;

mDirection: Boolean;

mSortLines: Boolean;

mBeginZeero: Boolean;

mSpecialSort: Boolean;

mGauss: Boolean;

mDetForRev: Boolean;

End;

Matrix=Object(Tabl)

Lin,Bar: Line;

Plus: Boolean;

Direction: Boolean;

SortLines: Boolean;

BeginZeero: Boolean;

SpecialSort: Boolean;

Chek: Integer;

Gauss: Boolean;

DetForRev: Boolean; {ўбҐ Ї а ¬Ґвал - гваҐЁҐ}

{Mem}

Procedure AllClear; virtual;

Function SIgn(C: Word): TOE;

Procedure Revers(Var A: Matrix); {®Ўа й Ґв бҐЎп ¬Ґ¤«Ґл¬ бЇ®б®Ў®¬}

Procedure RevWithGauss(Var A: Matrix); {®Ўа й Ґв бҐЎ ў®а®зҐл¬ бЇ®б®Ў®¬}

Procedure InnerRevers(Var A: Matrix); Virtual;

Procedure ZeeroSortBars;

Procedure ZeeroSortLines;

Procedure UniversalSort;

Function DetWithGauss: TOE; Virtual; {®Ўа й Ґв бҐЎп ў®а®зҐл¬ (Ўлбвал¬) бЇ®б®Ў®¬}

Function CuanZeeroInLine(L1: Integer): Integer;

Procedure SwapLines(L1,L2: Integer); Virtual;

Procedure SwapBars(B1,B2: Integer);

Function CuanZeeroInBar(B1: Integer): Integer;

Procedure SpecialSortLines;

Procedure SpecialSortBars;

Procedure SelfClear; Virtual;

Procedure StepRevers; Virtual;

Procedure RemSettings(Var FM: Mem); Virtual;

Procedure RestoreSettings(Var FM: Mem); Virtual;

Procedure MSqr(Var A: Matrix); {ў®§ў®¤Ёв ўб н«Ґ¬Ґвл ¬ ваЁжл ў Єў ¤а в}

Procedure MDg(Var A: Matrix);

{errors}

Procedure BadOperands; Virtual;

Procedure MulError; Virtual;

Procedure MNotSquare; Virtual;

Procedure AddError; Virtual;

Procedure ReversError; Virtual;

Procedure MDegenerate; Virtual;

Procedure MDgError; Virtual;

Procedure MSqrError; Virtual;

Procedure DetError; Virtual;

Procedure SortError; Virtual;

Procedure DGaussError; Virtual;

Procedure CuanZeeroError; Virtual;

Procedure SwapError; Virtual;

Procedure MulToNumError; Virtual;

Procedure Stopped; Virtual;

Procedure DegrError; Virtual;

Procedure IgError; Virtual;

End;

Matrix31=Object(Matrix)

Function DetWithGauss: TOE; Virtual;

Procedure SwapLines(L1,L2: Integer); Virtual;

End;

Matrix63=Object(Matrix)

Function DetWithGauss: TOE; Virtual;

Procedure SwapLines(L1,L2: Integer); Virtual;

End;

Implementation

{**************************************************************************}

Procedure TAbl. ZeeroFill;

Var i,j: Integer;

Begin

IF Not Exist Then Begin NotExist; ZFE; Exit; End;

IF (Errors<> [0]) Then Begin ZFE; Exit; End;

For i: =1 to CLines do

For j: =1 to CBars do

SetE(i,j,0);

End;

Procedure Tabl. Let(Var A);

Begin

End;

Procedure Tabl. AllClear;

Begin

CBars: =0;

CLines: =0;

SizeInMemory: =0;

Errors: = [0] ;

M: =Nil;

End;

Procedure Tabl. DataInit(L,B: Byte);

Begin

IF Exist Then Del;

AllClear;

IF 1.0*SizeOf(TOE) *L*B>(Word(Pred(0)) +1) *1.0 Then Begin TooManySize; Exit; End;

CBars: =B;

CLines: =L;

SizeInMemory: =SizeOf(TOE) *CBars*CLines;

If MaxAvail < SizeInMemory Then Begin TooManySize; Exit; End;

GetMem(M,SizeInMemory);

Exist: =True;

End;

Procedure Tabl. SetE(I,J: Byte; E: TOE);

Begin

IF Errors<> [0] Then Exit;

IF Not Exist Then Begin NotExist; Exit; End;

IF (I>CLines) or (J>CBars) or (I<1) or (J<1) Then Begin BadPosition; Exit; End;

Ar(M^) [((I-1) *CBars+J)]: =E;

End;

Function Tabl. GetE(I,J: Byte): TOE;

Begin

IF Errors<> [0] Then Exit;

IF Not Exist Then Begin NotExist; Exit; End;

IF (I>CLines) or (J>CBars) or (I<1) or (J<1)

Then

Begin

GetE: =0.0;

BadPosition;

End

Else

GetE: =Ar(M^) [((I-1) *CBars+J)] ;

End;

Procedure Tabl. Del;

Begin

IF Errors<> [0] Then Exit;

IF Not Exist Then Begin NotExist; Exit; End;

IF SizeInMemory<>0 Then FreeMem(M,SizeInMemory);

AllClear;

Exist: =False;

End;

Procedure Tabl. ReadOfText(Name: String; Search: String);

Var F: Text;

I,J: Byte;

Prom: TOE;

Help: Integer;

Function Searcher: Boolean;

Var Prom: String;

Begin

Repeat

Readln(F,Prom);

IF IOResult<>0 Then Begin ReadError; Close(F); Exit; End;

Until (EOF(F)) or (Pos(Search,Prom) <>0);

IF Pos(Search,Prom) =0

Then

Begin

SearchError;

Searcher: =False;

End

Else Searcher: =True;

End;

Begin

IF Exist Then Del;

Assign(F,Name);

{$I-}

Reset(F);

IF IOResult=2 Then Begin FileNotFound; ReadError; Exit; End;

IF IOResult<>0 Then Begin FileError; ReadError; Exit; End;

IF Not Searcher Then Exit;

Readln(F,CLines);

IF IOResult<>0 Then Begin AllClear; ReadError; Close(F); Exit; End;

Readln(F,CBars);

IF IOResult<>0 Then Begin AllClear; ReadError; Close(F); Exit; End;

DataInit(CLines,CBars);

IF Errors<> [0] Then Exit;

IF Not Exist Then Exit;

For I: =1 to CLines do

For J: =1 to CBars do

Begin

Read(F,Prom);

IF (EOF(F)) and (I<>CLines) And (I<>CBars) Then Begin Del; OutOfData; ReadError; Close(F); Exit; End;

IF IOResult<>0 Then Begin Del; ReadError; Close(F); Exit; End;

SetE(I,J,Prom);

End;

Close(F);

{$I+}

End;

Procedure Tabl. WriteToText(Name: String; F1,F2: Byte);

Var F: Text;

I,J: Byte;

Begin

IF Errors<> [0] Then Exit;

IF Not Exist Then Begin NotExist; WriteError; Exit; End;

Assign(F,Name);

{$I-}

ReWrite(F);

IF IOResult<>0 Then Begin FileError; WriteError; Exit; End;

For I: =1 to CLines do

Begin

For J: =1 to CBars do

Begin

Write(F,GetE(I,J): F1: F2,' ');

IF IOResult<>0 Then Begin Close(F); WriteError; Exit; End;

End;

Writeln(F)

End;

Close(F);

{$I+}

End;

Procedure Tabl. TooManySize;

Begin

Errors: =Errors+ [CTooManySize] ;

AnyError

End;

Procedure Tabl. BadPosition;

Begin

Errors: =Errors+ [CBadPosition] ;

AnyError

End;

Procedure Tabl. FileNotFound;

Begin

Errors: =Errors+ [CFileNotFound] ;

AnyError

End;

Procedure Tabl. FileError;

Begin

Errors: =Errors+ [CFileError] ;

AnyError

End;

Procedure Tabl. ReadError;

Begin

Errors: =Errors+ [CReadError] ;

AnyError

End;

Procedure Tabl. WriteError;

Begin

Errors: =Errors+ [CWriteError] ;

AnyError

End;

Procedure Tabl. OutOfData;

Begin

Errors: =Errors+ [COutOfData] ;

AnyError

End;

Procedure Tabl. SearchError;

Begin

Errors: =Errors+ [CSearchError] ;

AnyError

End;

Procedure Tabl. NotExist;

Begin

Errors: =Errors+ [CNotExist] ;

AnyError

End;

Procedure Tabl. ZFE;

Begin

Errors: =Errors+ [CZFE] ;

AnyError

End;

Procedure Tabl. UnkNownError;

Begin

Errors: =Errors+ [CUnkNownError] ;

AnyError

End;

Procedure Tabl. AnyError;

Begin

End;

Constructor TAbl. VMT;

Begin

Exist: =False;

End;

Procedure Matrix. MSqr;

Var i,j: Integer;

Begin

IF Not A. Exist Then Begin A. NotExist; BadOperands; MSqrError; Exit; End;

IF A. Errors<> [0] Then Begin MsqrError; Exit; End;

IF Self. Exist Then Del;

Self. DataInit(A. CLines,A. CBars);

For i: =1 to CLines do

For j: =1 to CBars do

SetE(i,j,Sqr(A. GetE(i,j)));

Self. SelfClear;

End;

Procedure Matrix. MDg;

Var i,j: Integer;

Begin

IF Not A. Exist Then Begin A. NotExist; BadOperands; MDgError; Exit; End;

IF A. Errors<> [0] Then Begin MDgError; Exit; End;

IF A. CLines<>A. CBars Then Begin MNotSquare; MDgError; Exit; End;

IF Exist Then Del;

DataInit(A. CLines,A. CBars);

For i: =1 to A. CLines do

For j: =1 to A. CBars do

IF i=j Then SetE(i,j,A. GetE(i,j))

Else SetE(i,j,0);

Self. SelfClear;

End;

Procedure Matrix. BadOperands;

Begin

Errors: =Errors+ [CBadOperands] ;

AnyError;

End;

Procedure Matrix. MulError;

Begin

Errors: =Errors+ [CMulError] ;

AnyError;

End;

Procedure Matrix. MDgError;

Begin

Errors: =Errors+ [CMDgError] ;

AnyError;

End;

Procedure Matrix. SortError;

Begin

Errors: =Errors+ [CSortError] ;

AnyError;

End;

Procedure Matrix. DetError;

Begin

Errors: =Errors+ [CDetError] ;

AnyError;

End;

Procedure Matrix. DGaussError;

Begin

Errors: =Errors+ [CDGaussError] ;

AnyError;

End;

Procedure Matrix. MSqrError;

Begin

Errors: =Errors+ [CMSqrError] ;

AnyError;

End;

Procedure MAtrix. CuanZeeroError;

Begin

Errors: =Errors+ [CCuanZeeroError] ;

AnyError;

End;

Procedure MAtrix. SwapError;

Begin

Errors: =Errors+ [CSwapError] ;

AnyError;

End;

Procedure Matrix. MulToNumError;

Begin

Errors: =Errors+ [CMulToNumError] ;

AnyError

End;

Procedure Matrix. DegrError;

Begin

Errors: =Errors+ [CDegrError] ;

AnyError

End;

Procedure Matrix. IgError;

Begin

Errors: =Errors+ [CIgError] ;

AnyError

End;

Procedure MAtrix. SelfClear;

Begin

Lin: = [0] ;

Bar: = [0] ;

Plus: =True;

Direction: =True;

SortLines: =True;

BeginZeero: =True;

SpecialSort: =False;

Chek: =0;

Gauss: =False;

DetForRev: =False;

End;

Procedure Matrix. AllClear;

Begin

inherited AllClear;

SelfClear;

End;

Procedure Matrix. Revers;

VAr FM: Mem;

Begin

Gauss: =False;

InnerRevers(A);

End;

Procedure Matrix. RevWithGauss;

Var FM: Mem;

Begin

Gauss: =True;

InnerRevers(A);

End;

Procedure Matrix. InnerRevers;

Var P,A1: Matrix;

D: TOE;

i,j: Integer;

Var Ver: TOE;

Var FM: Mem;

Begin

IF Not A. Exist Then Begin A. NotExist; BadOperands; ReversError; Exit; End;

IF (A. Errors<> [0]) Then Begin Exit; ReversError; End;

IF (A. CBars<>A. Clines) Then Begin BadOperands; ReversError; Exit; End;

P. VMT;

P. DataInit(A. CLines,A. CBars);

A1. VMT;

A1: =A;

IF A1. CLines=31 Then Begin Matrix31(A1). VMT; A1. Exist: =True; End;

IF A1. CLines=63 Then Begin Matrix63(A1). VMT; A1. Exist: =True; End;

IF Gauss Then D: =A1. DetWithGauss;

IF D=0 Then

Begin

MDegenerate;

ReversError;

Exit;

End;

DetForRev: =True;

For i: =1 to P. Clines do

Begin

A. StepRevers;

For j: =1 to P. CBars do

Begin

A1. Lin: =A1. Lin+ [i] ;

A1. Bar: =A1. Bar+ [j] ;

IF Gauss Then Ver: =A1. DetWithGauss;

IF (A1. Errors<> [0]) or (A. Errors<> [0]) Then Begin ReversError; Exit; End;

P. SetE(j, i,(Ver) *Sign(i+j) /D);

A1. Lin: =A1. Lin- [i] ;

A1. Bar: =A1. Bar- [j] ;

End;

IF Self. Exist Then Self. del;

Self: =P;

Self. SelfClear;

End;

Procedure Matrix. SwapBars(B1,B2: Integer);

Var Prom: TOE;

i: Integer;

Begin

IF Not Exist Then BEgin NotExist; SwapError; Exit; End;

IF (Errors<> [0]) Then Begin SwapError; Exit; End;

For i: =1 to CLines do

Begin

Prom: =GetE(i,B1);

SetE(i,B1,GetE(i,B2));

SetE(i,B2,Prom)

End;

Function Matrix. CuanZeeroInBar(B1: Integer): Integer;

Var i: Integer;

Sum: Integer;

Begin

IF Not Exist Then Begin NotExist; CuanZeeroError; Exit; End;

IF (Errors<> [0]) Then Begin CuanZeeroError; Exit; End;

Sum: =0;

IF Not SpecialSort

Then

For i: =1 to CLines do IF GetE(i,B1) =0 Then Inc(Sum) else

Else

IF BeginZeero

Then

Begin

Sum: =1;

While (GetE(Sum,B1) =0) and (Sum<=CLines) do inc(Sum);

Dec(Sum);

End

Else

Begin

Sum: =CLines;

While (GetE(Sum,B1) =0) and (Sum>0) do Dec(Sum);

Sum: =Clines-Sum;

End;

CuanZeeroinBar: =Sum;

End;

Procedure Matrix. ZeeroSortBars;

Var i,j: Integer;

Max,NMax,CZ: Integer;

FM: Mem;

Begin

IF Not Exist Then Begin NotExist; Exit; End;

IF (Errors<> [0]) Then Exit;

RemSettings(FM);

SortLines: =False;

SpecialSort: =False;

UniversalSort;

RestoreSettings(FM);

End;

Function Matrix. CuanZeeroinLine(L1: Integer): Integer;

Var i: Integer;

Sum: Integer;

Begin

IF Not Exist Then Begin NotExist; CuanZeeroError; Exit; End;

IF (Errors<> [0]) Then Begin CuanZeeroError; Exit; End;

Sum: =0;

IF Not SpecialSort

Then

For i: =1 to CBars do IF GetE(L1, i) =0 Then Inc(Sum) else

Else

IF BeginZeero

Then

Begin

Sum: =1;

While (GetE(L1,Sum) =0) and (Sum<=CBars) do inc(Sum);

Dec(Sum);

End

Else

Begin

Sum: =CBars;

While (GetE(L1,Sum) =0) and (Sum>0) do Dec(Sum);

Sum: =CBars-Sum;

End;

CuanZeeroinLine: =Sum;

End;

Procedure Matrix. SwapLines(L1,L2: Integer);

Var Prom: TOE;

i: Integer;

Begin

IF Not Exist Then Begin NotExist; SwapError; Exit; End;

IF (Errors<> [0]) Then Begin SwapError; Exit; End;

For i: =1 to CBars do

Begin

Prom: =GetE(L1, i);

SetE(L1, i,GetE(L2, i));

SetE(L2, i,Prom)

End;

Procedure Matrix. ZeeroSortLines;

VAr FM: Mem;

Begin

IF Not Exist Then Begin NotExist; Exit; End;

IF (Errors<> [0]) Then Exit;

RemSettings(FM);

SortLines: =True;

SpecialSort: =False;

UniversalSort;

RestoreSettings(FM);

End;

Procedure Matrix. UniversalSort;

Var i,j: Integer;

Max,NMax,CZ: Integer;

Cuan: Integer;

Begin

IF Not Exist Then Begin NotExist; SortError; Exit; End;

IF (Errors<> [0]) Then Begin SortError; Exit; End;

IF SortLines Then Cuan: =CLines

Else Cuan: =CBars;

For i: =1 to Cuan do

Begin

IF SortLines Then Max: =CuanZeeroInLine(i)

Else Max: =CuanZeeroInBar(i);

Nmax: =i;

For j: =i to Cuan do

Begin

IF SortLines Then CZ: =CuanZeeroInLine(j)

Else CZ: =CuanZeeroInBar(j);

IF (CZ<Max) xor Direction

Then

Begin

Max: =CZ;

NMax: =j;

End;

IF i<>NMax Then

Begin

IF SortLInes Then SwapLines(i,NMax)

Else SwapBars(i,NMax);

Inc(Chek);

End;

Function Matrix. DetWithGauss: TOE;

Var i,j: Integer;

K: TOE;

P: TOE;

S: Matrix;

Si,Sj: Integer;

Procedure SortLinesOfTheBar(B1: Integer);

Var i: Integer;

Max: TOE;

nMax: Integer;

Begin

Max: =S. GetE(1,B1);

nMax: =1;

For i: =2 to S. Clines do

IF Abs(Max) <Abs(S. GetE(i,B1))

Then

Begin

Max: =S. GetE(i,B1);

nMAx: =i;

End;

IF S. Clines<>nMAx Then

Begin

S. SwapLines(S. Clines,nMAx);

Inc(S. Chek);

End;

Procedure AddLines(l1,l2: Integer; K: TOE);

Var i: Integer;

Begin

For i: =1 to S. CBars do

S. SetE(l2, i,(S. GetE(l2, i) - S. GetE(l1, i) *K));

End;

Procedure InitObject;

Var i,j: Integer;

Ver: TOE;

Begin

Si: =0;

Sj: =0;

For i: =1 to CLines do IF not (i in Lin) Then Inc(Si);

For j: =1 to CBars do IF not (j in Bar) Then Inc(sj);

S. VMT;

S. DataInit(Si,Sj);

Si: =0;

For i: =1 to CLines do

IF not (i in Lin) Then

Begin

Inc(Si);

Sj: =0;

For j: =1 to CBars do

IF not (j in Bar) Then

Begin

Inc(sj);

Ver: =GetE(i,j);

S. SetE(Si,Sj,Ver);

End

End;

Begin

IF Not Exist Then Begin NotExist; DGaussError; Exit; End;

IF (Errors<> [0]) Then Begin DGaussError; Exit; End;

IF CBars<>CLines Then Begin MNotSquare; DGaussError; Exit; End;

InitObject;

IF S. CBars<>S. CLines Then Begin MNotSquare; DGaussError; Exit; End;

For i: =Si downto 2 do

Begin

S. Clines: =i;

SortLinesOfTheBar(i);

S. Clines: =Si;

IF S. GetE(i, i) =0 Then Begin DetWithGauss: =0; Exit; End;

For j: =i-1 downto 1 do

IF S. GetE(j, i) <>0 Then

Begin

K: =S. GetE(j, i) /S. GetE(i, i);

AddLines(i,j,K);

End;

P: =1;

S. Clines: =Si;

S. CBars: =Sj;

For i: =1 to S. Clines do

P: =P*S. GetE(i, i);

DetWithGauss: =P*S. Sign(S. Chek);

S. Del;

End;

Function Matrix. Sign;

Begin

IF (C div 2) *2=C Then Sign: =1.0 Else Sign: =-1.0;

End;

Procedure Matrix. SpecialSortLines;

VAr FM: Mem;

Begin

IF Not Exist Then Begin NotExist; Exit; End;

IF (Errors<> [0]) Then Exit;

RemSettings(FM);

SpecialSort: =True;

SortLines: =True;

UniversalSort;

RestoreSettings(FM);

End;

Procedure Matrix. SpecialSortBars;

VAr FM: Mem;

Begin

IF Not Exist Then Begin NotExist; Exit; End;

IF (Errors<> [0]) Then Exit;

RemSettings(FM);

SpecialSort: =True;

SortLines: =False;

UniversalSort;

RestoreSettings(FM);

End;

Procedure RemSettings;

Begin

End;

Procedure MAtrix. MNotSquare;

Begin

Errors: =Errors+ [CMNotSquare] ;

AnyError

End;

Procedure Matrix. AddError;

Begin

Errors: =Errors+ [CAddError] ;

AnyError

End;

Procedure Matrix. ReversError;

Begin

Errors: =Errors+ [CReversError] ;

AnyError

End;

Procedure Matrix. MDegenerate;

Begin

Errors: =Errors+ [CMDegenerate] ;

AnyError

End;

Procedure Matrix. Stopped;

Begin

Errors: =Errors+ [CStopped] ;

AnyError

End;

Procedure Matrix. StepRevers;

Begin

End;

Procedure Matrix. RemSettings;

Begin

With FM do

Begin

mPlus: = Plus;

mDirection: = Direction;

mSortLines: = SortLines;

mBeginZeero: = BeginZeero;

mSpecialSort: = SpecialSort;

mGauss: = Gauss;

mDetForRev: = DetForRev;

End

End;

Procedure Matrix. RestoreSettings;

Begin

With FM do

Begin

Plus: = mPlus;

Direction: = mDirection;

SortLines: = mSortLines;

BeginZeero: = mBeginZeero;

SpecialSort: = mSpecialSort;

Gauss: = mGauss;

DetForRev: = mDetForRev;

End;

{********************************Quick metods *****************************}

Function Matrix31. DetWithGauss;

Var i,j: Integer;

K: TOE;

P: TOE;

S: Matrix31;

si,sj: Integer;

Procedure SortLinesOfTheBar(B1: Integer);

Var i: Integer;

Max: TOE;

nMax: Integer;

Begin

Max: =Ar31(S. M^) [1,B1] ;

nMax: =1;

For i: =2 to S. Clines do

IF Abs(Max) <Abs(Ar31(S. M^) [i,B1])

Then

Begin

Max: =Ar31(S. M^) [i,B1] ;

nMAx: =i;

End;

IF S. Clines<>nMAx Then

Begin

S. SwapLines(S. Clines,nMAx);

Inc(S. Chek);

End;

Procedure AddLines(l1,l2: Integer; K: TOE);

Var i: Integer;

Begin

For i: =1 to S. CBars do

Begin

Ar31(S. M^) [l2, i]: =Ar31(S. M^) [l2, i] -Ar31(S. M^) [l1, i] *K;

End;

Procedure InitObject;

Var i,j: Integer;

Ver: TOE;

Begin

S. VMT;

S. DataInit(31,31);

Si: =0;

IF DetForRev

Then

Begin

si: =31;

sj: =31;

Ar31(S. M^): =Ar31(M^)

End

Else

For i: =1 to CLines do

IF not (i in Lin) Then

Begin

Inc(Si);

Sj: =0;

For j: =1 to CBars do

IF not (j in Bar) Then

Begin

Inc(sj);

Ar31(S. M^) [Si,Sj]: =Ar31(M^) [i,j] ;

End

End;

Begin

IF Not Exist Then Begin NotExist; DGaussError; Exit; End;

IF (Errors<> [0]) Then Begin DGaussError; Exit; End;

IF CBars<>CLines Then Begin MNotSquare; DGaussError; Exit; End;

InitObject;

S. Clines: =si;

S. CBars: =sj;

IF S. CBars<>S. CLines Then Begin MNotSquare; DGaussError; Exit; End;

For i: =si downto 2 do

Begin

S. Clines: =i;

SortLinesOfTheBar(i);

S. Clines: =si;

IF Ar31(S. M^) [i, i] =0 Then Begin DetWithGauss: =0; Exit; End;

For j: =i-1 downto 1 do

IF Ar31(S. M^) [j, i] <>0 Then

Begin

K: =Ar31(S. M^) [j, i] /Ar31(S. M^) [i, i] ;

AddLines(i,j,K);

End;

P: =1;

S. Clines: =si;

S. CBars: =sj;

For i: =1 to S. Clines do

P: =P*Ar31(S. M^) [i, i] ;

DetWithGauss: =P*S. Sign(S. Chek);

S. Del;

End;

Procedure Matrix31. SwapLines(L1,L2: Integer);

Var Prom: TOE;

i: Integer;

Begin

IF Not Exist Then BEgin NotExist; SwapError; Exit; End;

IF (Errors<> [0]) Then Begin SwapError; Exit; End;

For i: =1 to CBars do

Begin

Prom: =Ar31(M^) [L1, i] ;

Ar31(M^) [L1, i]: =Ar31(M^) [L2, i] ;

Ar31(M^) [L2, i]: =Prom

End;

{-------------------------------------------------------------------------}

Function Matrix63. DetWithGauss;

Var i,j: Integer;

K: TOE;

P: TOE;

S: Matrix63;

si,sj: Integer;

Procedure SortLinesOfTheBar(B1: Integer);

Var i: Integer;

Max: TOE;

nMax: Integer;

Begin

Max: =Ar63(S. M^) [1,B1] ;

nMax: =1;

For i: =2 to S. Clines do

IF Abs(Max) <Abs(Ar63(S. M^) [i,B1])

Then

Begin

Max: =Ar63(S. M^) [i,B1] ;

nMAx: =i;

End;

IF S. Clines<>nMAx Then

Begin

S. SwapLines(S. Clines,nMAx);

Inc(S. Chek);

End;

Procedure AddLines(l1,l2: Integer; K: TOE);

Var i: Integer;

Begin

For i: =1 to S. CBars do

Begin

Ar63(S. M^) [l2, i]: =Ar63(S. M^) [l2, i] -Ar63(S. M^) [l1, i] *K;

End;

Procedure InitObject;

Var i,j: Integer;

Ver: TOE;

Begin

S. VMT;

S. DataInit(63,63);

Si: =0;

IF DetForRev

Then

Begin

si: =63;

sj: =63;

Ar63(S. M^): =Ar63(M^)

End

Else

For i: =1 to CLines do

IF not (i in Lin) Then

Begin

Inc(Si);

Sj: =0;

For j: =1 to CBars do

IF not (j in Bar) Then

Begin

Inc(sj);

Ar63(S. M^) [Si,Sj]: =Ar63(M^) [i,j] ;

End

End;

Begin

IF Not Exist Then Begin NotExist; DGaussError; Exit; End;

IF (Errors<> [0]) Then Begin DGaussError; Exit; End;

IF CBars<>CLines Then Begin MNotSquare; DGaussError; Exit; End;

InitObject;

S. Clines: =si;

S. CBars: =sj;

IF S. CBars<>S. CLines Then Begin MNotSquare; DGaussError; Exit; End;

For i: =si downto 2 do

Begin

S. Clines: =i;

SortLinesOfTheBar(i);

S. Clines: =si;

IF Ar63(S. M^) [i, i] =0 Then Begin DetWithGauss: =0; Exit; End;

For j: =i-1 downto 1 do

IF Ar63(S. M^) [j, i] <>0 Then

Begin

K: =Ar63(S. M^) [j, i] /Ar63(S. M^) [i, i] ;

AddLines(i,j,K);

End;

P: =1;

S. Clines: =si;

S. CBars: =sj;

For i: =1 to S. Clines do

P: =P*Ar63(S. M^) [i, i] ;

DetWithGauss: =P*S. Sign(S. Chek);

S. Del;

End;

Procedure Matrix63. SwapLines(L1,L2: Integer);

Var Prom: TOE;

i: Integer;

Begin

For i: =1 to CBars do

Begin

Prom: =Ar63(M^) [L1, i] ;

Ar63(M^) [L1, i]: =Ar63(M^) [L2, i] ;

Ar63(M^) [L2, i]: =Prom

End;

END.

Контрольні приклади

Дана матриця:

3 - 1 0

А= - 2 1 1

2 - 1 4

Відповідь:

1 0,8 - 0,2

А-1 = 2 2,4 - 0,6

0 0,2 0,2

Висновок

Добуток матриць, хоча б одна з яких вироджена, буде вродженою матрицею.

Список використаної літератри

1. А.Г. Курош «курс высшей алгебры», «наука», Москва 1975

2.С.Т. Завало, В.М. Костарчук, Б.И. Хацет «алгебра и теория чисел», Том 1,«высшая школа», Киев 1974

3. С.Т. Завало, В.М. Костарчук, Б.И. Хацет «алгебра и теория чисел», Том 2, «высшая школа», Киев 1976