
Рефераты по сексологии
Рефераты по информатике программированию
Рефераты по биологии
Рефераты по экономике
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Рефераты по авиации и космонавтике
Рефераты по административному праву
Рефераты по безопасности жизнедеятельности
Рефераты по арбитражному процессу
Рефераты по архитектуре
Рефераты по астрономии
Рефераты по банковскому делу
Рефераты по биржевому делу
Рефераты по ботанике и сельскому хозяйству
Рефераты по бухгалтерскому учету и аудиту
Рефераты по валютным отношениям
Рефераты по ветеринарии
Рефераты для военной кафедры
Рефераты по географии
Рефераты по геодезии
Рефераты по геологии
Рефераты по геополитике
Рефераты по государству и праву
Рефераты по гражданскому праву и процессу
Рефераты по делопроизводству
Рефераты по кредитованию
Рефераты по естествознанию
Рефераты по истории техники
Рефераты по журналистике
Рефераты по зоологии
Рефераты по инвестициям
Рефераты по информатике
Исторические личности
Рефераты по кибернетике
Рефераты по коммуникации и связи
Курсовая работа: Выбор параметров контроля с использованием метода динамического программирования и метода ветвей и границ
Курсовая работа: Выбор параметров контроля с использованием метода динамического программирования и метода ветвей и границ
Московский Авиационный Институт
(Технический Университет)
Кафедра 308
Курсовая работа
Выбор параметров контроля с использованием метода динамического программирования и метода ветвей и границ
Вариант II(2)
Выполнила
студентка
группы КТ-515
Принял
Москва
2008г.
Содержание
Задание
1. Метод динамического программирования
1.1 Теоретическая часть
2.2 Практическая часть
- ручной счёт
- листинг программы
2. Метод ветвей и границ
2.1 Теоретическая часть
2.2 Практическая часть
- ручной счёт
- листинг программы
Вывод
Литература
Задание
Вариант II(2)
Выбор параметров контроля с использованием метода динамического программирования и метода ветвей и границ при непересекающихся элементах объекта контроля и ограничениях по затратам на контроль С≤16.
Исходные данные: вероятность отказов элементов и затраты на контроль параметров.
Выбрать такие параметры, чтобы С≤16 при Q=Qmax.
N |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Qi | 0.17 | 0.03 | 0.15 | 0.09 | 0.13 | 0.08 | 0.07 | 0.02 | 0.06 | 0.04 |
| с(xi) | 5 | 1 | 4 | 2 | 6 | 3 | 2 | 3 | 1 | 1 |
1. Метод динамического программирования
1.1 Теоретическая часть
Математически задачу выбора набора параметров из заданной их совокупности можно сформулировать следующим образом.
Пусть работоспособность объекта контроля характеризуется совокупностью n взаимосвязанных параметров, образующих множество S={x1, x2, …, xn}. Проверка всех параметров из S влечет контроль всех N элементов системы и дает однозначный ответ: объект исправен, если все N элементов исправны, или неисправен, если по крайней мере один из элементов отказал. Для " xi определено подмножество R(xi) элементов, проверяемых при контроле i-го параметра, причем предполагаем, что эти подмножества могут пересекаться, т.е. $ i, j: R(xi)ÇR(xj). Пусть W - некоторый набор параметров из множества S, т.е. WÍS. Тогда WÇW=Æ и WÈW=S. Значения xi из S можно представить булевым вектором, причем
xi = 1, если xiÎW,
0, если xiÎW.
Задача выбора параметров в этом случае формулируется двояко:
1) найти набор Ω, для которого
P(Ω)=max
при ∑xi·c(xi)≤C; iЄΩ
2) найти набор Ω, для которого
∑xi·c(xi)=min
при P(Ω)≥Pз,
где P(Ω) – апостериорная вероятность работоспособного состояния объекта контроля при положительном исходе контроля выбранных параметров WÍS; с(xi) – затраты на контроль i-го параметра; Рз требуемая достоверность контроля; С – ограничение на общую стоимость контроля.
Значение P(Ω) зависит от принятых допущений и может быть найдено по формуле Байеса. Так, если предполагать в изделии наличие лишь одного отказа, то
P(Ω)=Р0/1-∑Рi,
iЄR(Ω)
где Р0=∏(1-рi) – априорная вероятность безотказной работы объекта:
iЄR(S)
Р0=1-∑Рi;
iЄR(S)
Рi - нормированная вероятность отказа системы из-за отказа i-го элемента:
Рi=(pi/(1-pi))/(1+∑ pk/(1-pk);
kЄR(S)
pi – априорная вероятность отказа i-го элемента. Тогда вероятность того, что отказ будет обнаружен при проверке k-го параметра, можно вычислить по формуле:
Qk=∑Pk
kЄR(xk)
При возможности наличия в ОК произвольного числа отказов
P(Ω)=∏(1-pi)/∏(1-pi)
iЄR(S) iЄR(Ω)
Можно использовать простой перебор вариантов, однако возникающие при этом вычислительные трудности не позволяют сделать этого даже для простых систем (при n>10). В связи с этим комплектование набора будем трактовать как многошаговый процесс, состоящий из последовательного выбора отдельных параметров.
В соответствии с общим принципом оптимальности разобьем весь имеющийся ресурс стоимости С на С отрезков единичной длины. (В практических случаях заданные положительные величины с(xi) и С можно считать всегда целыми. Если это не так, то необходимо перейти к более мелким стоимостным единицам в зависимости от разрядности дробной части.). Рассмотрим наряду с интересующей нас исходной задачей множество аналогичных задач
f(Y)=max λ(x), Y Є [0,C],
xЄXY
где через XY обозначено множество неотрицательных целочисленных векторов Ω, отвечающих наборам, в которых общая стоимость проверки параметров не превосходит величины Υ.
Пусть Υ0=min c(xi).
i=1,…,n
Тогда при всех Υ Є [0,Υ0] соответствующие множества ΧΥ состоят, из одного нулевого элемента и f(Y)=0 для всех таких Υ. Для ресурса Υ Є [Υ0, С] согласно общей схеме динамического программирования справедливы следующие рекуррентные соотношения:
f(Yk)=max [Qi + f[Yk – c(xi)] – Gi (1)
iЄIY
где k=Y0, Y0+1, …, C; IY множество тех i, для которых с(xi)≤Yk, начиная с номера k=max c(xi) уравнение (1) решается для всех i= 1,…,n;
Gi = ∑Pi – сумма вероятностей элементов i-го параметра, которые пересекаются с
IЄR(xi)∩Ωl*
элементами подмножества Ωl*, образованного на шаге Yk – c(xi).
Если " i, j; R(xi)∩R(xj)= Æ, то Gi=0 и
f(Yk)=max {Qi + f[Yk – c(xi)]} (2)
iЄIY
![]() Для решения интересующей нас задачи
опишем простой численный метод, не требующий предварительного определения всех
допустимых наборов и основанный на рекуррентных соотношениях (1). Для всех
целых Υ = Υ0, С по формуле (1) вычисляются величины f(Yk) и при этом
фиксируются индексы iYk*, на которых достигаются максимумы в (1).
Искомый вектор Ω формируется последовательно включением в набор параметра iYk и подмножества Ωl*, зафиксированного
на шаге Yk – c(xi). При этом, если YkЄ Ωl*, то на данном
шаге этот параметр исключается из рассмотрения, так как каждый параметр может
включаться в набор не более одного раза. Если на некотором ν-м шаге
окажется, что f(Yν)< f(Yν-1), то в качестве Ων* принимается
подмножество Ων-1* и фиксируется
параметр iY ν-1, причем за f(Yν)< принимается
значение f(Yν-1). Заметим, что
если в задаче P(Ω)=max при
Для решения интересующей нас задачи
опишем простой численный метод, не требующий предварительного определения всех
допустимых наборов и основанный на рекуррентных соотношениях (1). Для всех
целых Υ = Υ0, С по формуле (1) вычисляются величины f(Yk) и при этом
фиксируются индексы iYk*, на которых достигаются максимумы в (1).
Искомый вектор Ω формируется последовательно включением в набор параметра iYk и подмножества Ωl*, зафиксированного
на шаге Yk – c(xi). При этом, если YkЄ Ωl*, то на данном
шаге этот параметр исключается из рассмотрения, так как каждый параметр может
включаться в набор не более одного раза. Если на некотором ν-м шаге
окажется, что f(Yν)< f(Yν-1), то в качестве Ων* принимается
подмножество Ων-1* и фиксируется
параметр iY ν-1, причем за f(Yν)< принимается
значение f(Yν-1). Заметим, что
если в задаче P(Ω)=max при
∑xi·c(xi)≤C
iЄΩ
принять более жесткое ограничение, а именно ∑c(xi)=C, то последнее не допустимо, iЄΩ так как в этом случае max f(Yk) может быть меньше max f(Yk-1) из-за того, что он достигается на другом подмножестве параметров.
Общая сложность метода, очевидно, φ(n) ≤ c(n+1), т.е. экспоненциальная функция при переборе заменена линейной функцией. При этом для запоминания промежуточных значений необходимо k≤2c ячеек памяти. Если в качестве максимизируемого критерия использовать P(Ω)=∏(1-pi)/∏(1-pi), то необходимо решить задачу динамического iЄR(S) iЄR(Ω) программирования с мультипликативным критерием. Для этого достаточно прологарифмировать это выражение и обозначить
V=lgP(Ω)=lgР0-∑lg(1-pi). (3)
iЄR(Ω)
Так как выражение, стоящее под знаком ∑ в (3), отрицательно, то, V= Vmax тогда, когда максимальна величина суммы, т.е. в этом случае получим новую целевую функцию
V=∑νi, где νi=lg (1-pi),
iЄR(Ω)
обладающую свойством аддитивности и обращающуюся в максимум одновременно с P(Ω).
1.2 Практическая часть
Ручной счёт
Данные для расчета:
С≤16
Таблица 1
N |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Qi | 0.17 | 0.03 | 0.15 | 0.09 | 0.13 | 0.08 | 0.07 | 0.02 | 0.06 | 0.04 |
| с(xi) | 5 | 1 | 4 | 2 | 6 | 3 | 2 | 3 | 1 | 1 |
Для удобства расчетов проранжируем таблицу1 следующим образом:
Таблица 2
N |
9 | 10 | 2 | 4 | 7 | 6 | 8 | 3 | 1 | 5 |
| Qi | 0.06 | 0.04 | 0.03 | 0.09 | 0.07 | 0.08 | 0.02 | 0.15 | 0.17 | 0.13 |
| с(xi) | 1 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 5 | 6 |
Вычисления сведем в таблицу 3:
Таблица 3
| Yk | f(Yk) | iYk | Ωl* |
| 1 | 0,06 | 9 | 9 |
| 2 | 0,1 | 10 | 9,10 |
| 3 | 0,15 | 4 | 4,9 |
| 4 | 0,19 | 4 | 4,10,9 |
| 5 | 0,22 | 7 | 7,4,9 |
| 6 | 0,26 | 7 | 7,4,10,9 |
| 7 | 0,3 | 3 | 3,4,9 |
| 8 | 0,34 | 3 | 3,4,10,9 |
| 9 | 0,37 | 3 | 3,7,4,9 |
| 10 | 0,41 | 7 | 7,3,4,10,9 |
| 11 | 0,44 | 2 | 2,7,3,4,10,9 |
| 12 | 0,47 | 1 | 1,3,4,9 |
| 13 | 0,51 | 1 | 1,3,4,10,9 |
| 14 | 0,54 | 2 | 2,1,3,4,10,9 |
| 15 | 0,58 | 7 | 7,1,3,4,10,9 |
| 16 | 0,61 | 1 | 1,2,7,3,4,10,9 |
Оптимальный набор включает параметры Ω*= {1,2,7,3,4,10,9} при этом
P(Ω) = 0,61+0,16 = 0,77 и С = 16.
Листинг программы
unit Unit1;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, ToolWin, ComCtrls, mdCONTROLS, Grids, StdCtrls, ExtCtrls, Unit2,
Buttons;
type
TForm1 = class(TForm)
sgH: TStringGrid;
sgP: TStringGrid;
sgC: TStringGrid;
sgQ: TStringGrid;
lbC: TLabeledEdit;
BitBtn1: TBitBtn;
Label1: TLabel;
sgW: TStringGrid;
Label2: TLabel;
procedure FormCreate(Sender: TObject);
procedure BitBtn1Click(Sender: TObject);
procedure sgExit(Sender: TObject);
private
{ Private declarations }
public
H: TH;
P: TP;
C: TC;
W: TW;
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
procedure TForm1.FormCreate(Sender: TObject);
var i,j: integer;
x: Byte;
f: TextFile;
begin
AssignFile(f, 'data.txt');
Reset(f);
sgW.Cells[0,0] := 'W';
// Ввод исходной матрицы
readln(f);
for j:=1 to 10 do
begin
sgH.Cells[0,j] := IntToStr(j);
sgW.Cells[0,j] := IntToStr(j);
for i:=1 to 10 do
begin
sgH.Cells[i,0] := IntToStr(i);
read(f, x);
sgH.Cells[i,j] := IntToStr(x);
if x = 1 then
H[i-1,j-1] := true
else
H[i-1,j-1] := false;
end;
readln(f);
end;
// Ввод вероятностей
readln(f);
readln(f);
sgP.Cells[0,0] := 'P';
for i:=1 to 10 do
begin
read(f, P[i-1]);
sgP.Cells[i,0] := FloatToStr(P[i-1]);
end;
readln(f);
// Ввод стоимостей
readln(f);
readln(f);
sgC.Cells[0,0] := 'C';
for j:=1 to 10 do
begin
read(f, C[j-1]);
sgC.Cells[0,j] := IntToStr(C[j-1]);
end;
CloseFile(f);
// Ввод вероятностей обнаружения отказа
sgQ.Cells[0,0] := 'Q';
for j:=1 to 10 do
sgQ.Cells[0,j] := FloatToStr(Q(j-1,H,P));
lbC.Text := '1';
end;
procedure TForm1.BitBtn1Click(Sender: TObject);
var i: integer;
begin
label1.Caption := FloatToStr(maxf(1, StrToInt(lbC.Text), H,P,C, W));
for i:=1 to 10 do
begin
sgW.Cells[2,i] := IntToStr(W[i-1].N);
if W[i-1].E then
sgW.Cells[1,i] := '1'
else
sgW.Cells[1,i] := '0';
end;
end;
procedure TForm1.sgExit(Sender: TObject);
var i,j: integer;
begin
for j:=1 to 10 do
for i:=1 to 10 do
if sgH.Cells[i,j] = '1' then
H[i-1,j-1] := true
else
H[i-1,j-1] := false;
for i:=1 to 10 do
P[i-1] := StrToFloat(sgP.Cells[i,0]);
for j:=1 to 10 do
C[j-1] := StrToInt(sgC.Cells[0,j]);
// Ввод вероятностей обнаружения отказа
for j:=1 to 10 do
sgQ.Cells[0,j] := FloatToStr(Q(j-1,H,P));
end;
end.
unit Unit2;
interface
type
TH = array [0..9, 0..9] of boolean;
TP = array [0..9] of extended;
TC = array [0..9] of integer;
TDateW = record
E: boolean;
N: integer;
end;
TW = array [0..9] of TDateW;
function Q(j: integer; H: TH; P: TP): extended;
function maxf(n, Yk: integer; H: TH; P: TP; C: TC; var W: TW): extended;
implementation
function Q(j: integer; H: TH; P: TP): extended;
var i: integer;
begin
Result := 0;
for i:=0 to 9 do
if H[i,j] then
Result := Result + P[i];
end;
function G(j: integer; H: TH; P: TP; W: TW): extended;
var i,k: integer;
begin
Result := 0;
for i:=0 to 9 do
if H[i,j] then
for k:=0 to 9 do
if W[k].E and H[i,k] then
begin
Result := Result + P[i];
Break;
end;
end;
function f(n, Yk, j: integer; H: TH; P: TP; C: TC; var W: TW): extended;
begin
Result := Q(j,H,P) + maxf(n+1, Yk - C[j], H,P,C, W) - G(j,H,P,W);
end;
function maxf(n, Yk: integer; H: TH; P: TP; C: TC; var W: TW): extended;
var j,i: integer;
ft: extended;
Wt: TW;
begin
Result := 0;
for i:=0 to 9 do
begin
W[i].E := false;
W[i].N := 0;
end;
for j:=0 to 9 do
if C[j] <= Yk then
begin
for i:=0 to 9 do
begin
Wt[i].E := false;
Wt[i].N := 0;
end;
ft := f(n, Yk, j, H,P,C, Wt);
if Result < ft then
begin
Result := ft;
W := Wt;
W[j].E := true;
W[j].N := n;
end;
end;
end;
end.
2. Метод ветвей и границ
2.1 Теоретическая часть
Рассмотрим следующую задачу целочисленного программирования. Требуется максимизировать выражение:
n
L=∑cj∙xj (4)
j=1
при ограничениях
n
∑аij∙xj≤bi, i=1, …,m (5)
j=1
xjЄ{0;1}, j=1, …,n
причем сj≥0, aij≥0.
Метод ветвей и границ использует последовательно-параллельную схему построения дерева возможных вариантов. Первоначально ищут допустимый план и для каждого возможного варианта определяют верхнюю границу целевой функции. Ветви дерева возможных вариантов, для которых верхняя граница ниже приближенного решения, из дальнейшего рассмотрения исключают.
Эффективность вычислительных алгоритмов зависит от точности и простоты способа определения верхней границы возможных решений и точности определения приближенного решения. Чем точнее способ определения верхней границы целевой функции, тем больше бесперспективных ветвей отсекается в процессе оптимизации. Однако увеличение точности расчета верхних границ связано с возрастанием объема вычислений. Например, если для оценки верхней границы использовать симплекс-метод, то результат будет достаточно точным, но потребует большого объема вычислительной работы.
Рассмотрим алгоритм решения задачи методом ветвей и границ с простым и эффективным способом оценки верхней границы целевой функции.
Обозначим: U – множество переменных xj; S – множество фиксированных переменных, вошедших в допустимое решение; Es – множество зависимых переменных, которые не могут быть включены в множество S, так как для них выполняется неравенство
аij> bi - ∑аij∙xj, i=1, …,m
xjЄS
GS – множество свободных переменных, из которых производится выбор для включения в S очередной переменной.
Рассмотрим первоначально одномерную задачу, когда m=1 и задача (4) имеет только одно ограничение вида (5).
Обозначим h1j = cj/a1j и допустим, что xjЄS (j=1, …,k<n) и выполняются условия
h1,k+1≥ h1,k+2≥ …≥ h1l, l≤n,
l
∑a1j>b1 - ∑ a1j∙xj,
j=k+1 xjЄS
l-1
∑a1j≤ b1 - ∑ a1j∙xj,
j=k+1 xjЄS
Условия означают, что во множество S без нарушения неравенства (5) можно дополнительно ввести элементы xk+1, xk+2, …, xl-1. При введении во множество S элементов xk+1, xk+2, …, xl неравенство (5) не выполняется.
Для определения верхней границы решения может быть использовано выражение
Hs =∑cj∙xj + Ls’,
xjЄS
где
l-1
Ls’ = ∑сj + h1l∆ b1 ,
j=k+1
l-1
∆ b1 = b1 - ∑ a1j∙xj - ∑a1j.
xjЄS j=k+1
Из условий следует, что Ls’ не меньше максимального значения величины
∑cj∙xj
xjЄGS
при ограничениях
∑ a1j ∙xj b1 - ∑ a1j∙xj = b1’,
xjЄGS xjЄS
xjЄ {0;1}, xjЄGS ,
Выбор очередной переменной для включения во множество S производится с помощью условия
h1r(xr) = max h1j(xj)
![]() xjЄGS
xjЄGS
Для выбранной переменной xr определяются величины Hs(xr) и Hs(xr), т.е. в S включаются xr = 1 или xr = 0.
Если в процессе решения окажется, что во множестве GS нет элементов, которые могут быть введены во множество S без нарушения ограничения (5), то полученное решение Ls =∑cj∙xj принимается в качестве первого приближенного xjЄS решения L0.
Все вершины дерева возможных вариантов, для которых выполняются условия
Hs≤ L0, из дальнейшего рассмотрения исключаются.
Из оставшихся ветвей выбирается ветвь с максимальным значением Hs, и процесс поиска оптимального варианта продолжается. Если в процессе решения будет найдено Ls = ∑cj∙xj > L0, то полученное решение принимается
xjЄS
в качестве нового приближенного результата. Вычислительная процедура заканчивается, если для оставшихся ветвей выполняется условие Hs≤ L0.
2.2 Практическая часть
Ручной счёт
Данные для расчета:
С≤16
Таблица 4
N |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Qi | 0.17 | 0.03 | 0.15 | 0.09 | 0.13 | 0.08 | 0.07 | 0.02 | 0.06 | 0.04 |
| с(xi) | 5 | 1 | 4 | 2 | 6 | 3 | 2 | 3 | 1 | 1 |
| hj | 0.034 | 0.03 | 0.0375 | 0.045 | 0.0217 | 0.0267 | 0.035 | 0.0067 | 0.06 | 0.04 |
Для удобства расчетов проранжируем таблицу 4 в порядке убывания hj и присвоим новые номера элементам, следующим образом:
Таблица 5
N |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
n |
9 | 4 | 10 | 3 | 7 | 1 | 2 | 6 | 5 | 8 |
| Qi | 0.06 | 0.09 | 0.04 | 0.15 | 0.07 | 0.17 | 0.03 | 0.08 | 0.13 | 0.02 |
| с(xi) | 1 | 2 | 1 | 4 | 2 | 5 | 1 | 3 | 6 | 3 |
| hj | 0.06 | 0.045 | 0.04 | 0.0375 | 0.035 | 0.034 | 0.03 | 0.0267 | 0.02167 | 0.0067 |
Для формирования таблицы 6 произведем расчеты:
1)
8
∑сj=19>b1 - ∑ cj∙xj=16-0=16;
j=1 xjЄS
7
∑сj=16£16;
j=1
7
∆ с = с - ∑ сj∙xj - ∑сj=16-0-16=0
xjЄS j=1
Hs(x1) = q1+q2+q3+q4+q5+q6+q7+h8∆ с = 0.61
8
∑сj=18>b1 - ∑ cj∙xj=16-0=16;
j=2 xjЄS
7
∑сj=15£16;
j=2
7
∆ с = с - ∑ сj∙xj - ∑сj=16-0-15=1
xjЄS j=2
Hs(x1) = q2+q3+q4+q5+q6+q7+h8∆ с = 0.5767
2)
8
∑сj=18>b1 - ∑ cj∙xj=16-1=15;
j=2 xjЄS
7
∑сj=15£15;
j=2
7
∆ с = с - ∑ сj∙xj - ∑сj=16-1-15=0
xjЄS j=2
Hs(x2) = q1+q2+q3+q4+q5+q6+q7+h8∆ с = 0.61
8
∑сj=16>b1 - ∑ cj∙xj=16-1=15;
j=3 xjЄS
7
∑сj=13£15;
j=3
7
∆ с = с - ∑ сj∙xj - ∑сj=16-1-13=2
xjЄS j=3
Hs(x2) = q1+q3+q4+q5+q6+q7+h8∆ с = 0.5734
3)
8
∑сj=16>b1 - ∑ cj∙xj=16-1-2=13;
j=3 xjЄS
7
∑сj=13£13;
j=3
7
∆ с = с - ∑ сj∙xj - ∑сj=16-1-2-13=0
xjЄS j=3
Hs(x3) = q1+q2+q3+q4+q5+q6+q7+h8∆ с = 0.61
8
∑сj=15>b1 - ∑ cj∙xj=16-1-2=13;
j=4 xjЄS
7
∑сj=12£13;
j=4
7
∆ с = с - ∑ сj∙xj - ∑сj=16-1-2-12=1
xjЄS j=4
Hs(x3) = q1+q2+q4+q5+q6+q7+h8∆ с = 0.5967
4)
8
∑сj=15>b1 - ∑ cj∙xj=16-1-2-1=12;
j=4 xjЄS
7
∑сj=12£12;
j=4
7
∆ с = с - ∑ сj∙xj - ∑сj=16-1-2-1-12=0
xjЄS j=4
Hs(x4) = q1+q2+q3+q4+q5+q6+q7+h8∆ с = 0.61
9
∑сj=17>b1 - ∑ cj∙xj=16-1-2-1=12;
j=5 xjЄS
8
∑сj=11£12;
j=5
8
∆ с = с - ∑ сj∙xj - ∑сj=16-1-2-1-11=1
xjЄS j=5
Hs(x4) = q1+q2+q3+q5+q6+q7+q8+h9∆ с = 0.56167
5)
8
∑сj=11>b1 - ∑ cj∙xj=16-1-2-1-4=8;
j=5 xjЄS
7
∑сj=8£8;
j=5
7
∆ с = с - ∑ сj∙xj - ∑сj=16-1-2-1-4-8=0
xjЄS j=5
Hs(x5) = q1+q2+q3+q4+q5+q6+q7+h8∆ с = 0.61
8
∑сj=9>b1 - ∑ cj∙xj=16-1-2-1-4=8;
j=6 xjЄS
7
∑сj=6£8;
j=6
7
∆ с = с - ∑ сj∙xj - ∑сj=16-1-2-1-4-6=2
xjЄS j=6
Hs(x5) = q1+q2+q3+q4+q6+q7+h8∆ с = 0.5934
6)
8
∑сj=9>b1 - ∑ cj∙xj=16-1-2-1-4-2=6;
j=6 xjЄS
7
∑сj=6£6;
j=6
7
∆ с = с - ∑ сj∙xj - ∑сj=16-1-2-1-4-2-6=0
xjЄS j=6
Hs(x6) = q1+q2+q3+q4+q5+q6+q7+h8∆ с = 0.61
9
∑сj=10>b1 - ∑ cj∙xj=16-1-2-1-4-2=6;
j=7 xjЄS
8
∑сj=4£6;
j=7
7
∆ с = с - ∑ сj∙xj - ∑сj=16-1-2-1-4-2-4=2
xjЄS j=6
Hs(x6) = q1+q2+q3+q4+q5+q7+q8+h9∆ с = 0.56334
7) Cs = ∑ cj∙xj, проверяем условие С-Сs. Если с (xj)> С-Сs, то эти
xjЄS
элементы вводятся в множество Es.
Es = {x8,x9,x10}
с7=1>b1 - ∑ cj∙xj=16-1-2-1-4-2-5=1;
xjЄS
с7=1£1;
Условие не выполняется.
8) Ls = q1+q2+q3+q4+q5+q6+q7 = 0.61
Ls принимается в качестве приближенного решения L0. Так как все вершины дерева, для которых выполняется условие Hs£ L0, из дальнейшего рассмотрения исключаются, то процесс расчета прекращается.
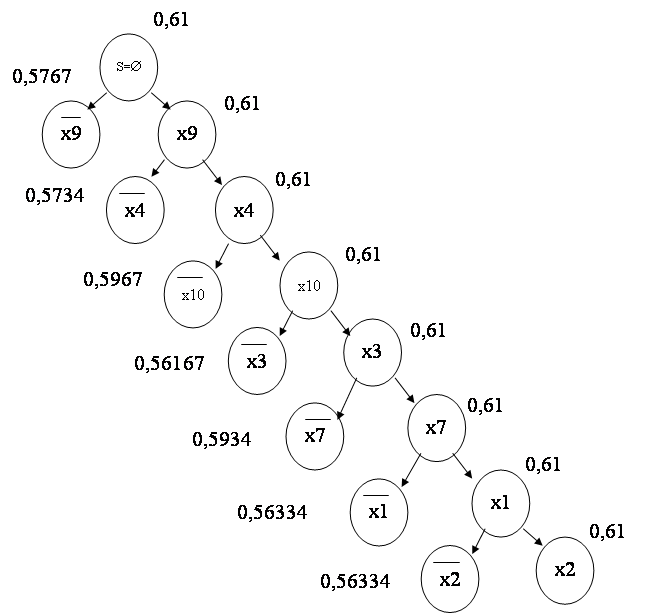
Таблица 6
|
|
S | Es | Gs | Hs | xr | Hs(xr) | Hs(xr) | L0 |
| 1 | Æ | Æ | 1…10 | 0.61 | x1 | 0.61 | 0.5767 | |
| 2 | x1 | Æ | 2…10 | 0.61 | x2 | 0.61 | 0.5734 | |
| 3 | x1,x2 | Æ | 3…10 | 0.61 | x3 | 0.61 | 0.5967 | |
| 4 | x1,x2,x3 | Æ | 4…10 | 0.61 | x4 | 0.61 | 0.56167 | |
| 5 | x1,x2,x3,x4 | Æ | 5…10 | 0.61 | x5 | 0.61 | 0.5934 | |
| 6 | x1,x2,x3,x4,x5 | Æ | 6…10 | 0.61 | x6 | 0.61 | 0.56334 | |
| 7 | x1,x2,x3,x4,x5,x6 | 8,9,10 | 7 | 0.61 | x7 | 0.61 | 0.56334 | |
| 8 | x1,x2,x3,x4,x5,x6,x7 | 8,9,10 | Æ | - | - | - | - | 0.61 |
Для контроля системы необходимо использовать следующие параметры контроля: x1,x2,x3,x4,x5,x6,x7.
Перейдем на старую нумерацию элементов и построим дерево возможных вариантов решения. Оно представлено на рис.1. Около каждой вершины указана верхняя граница решения. Так как все эти оценки не превышают величины 0,61, то, следовательно, полученное решение L0 = 0,61 является оптимальным. Таким образом необходимо использовать следующие параметры контроля: x9,x4,x10,x3,x7,x1,x2.
 |
|||
|
|||
Листинг программы
program vetvi;
const
maxmatrix=1000;
maxsize=200;
type linear=array[1..10000] of integer;
label skip;
var matrix:array[1..1000] of pointer;
n:integer;
sizeofm:word;
q,w,e,r:integer;
start_m:integer;
sm:^linear;
bestx,besty:integer;
bz:integer;
ochered:array[1..1000] of
record
id:integer;
ocenka:integer;
end;
nochered:integer;
workm,workc:integer;
leftm,rightm:integer;
first,last:integer;
best:integer;
bestmatr:array[1..maxsize] of integer;
bestmatr1:array[1..maxsize] of integer;
curr:integer;
procedure swapo(a,b:integer);
begin
ochered[1000]:=ochered[a];
ochered[a]:=ochered[b];
ochered[b]:=ochered[1000];
end;
procedure addochered(id,ocenka:integer);
var
curr:integer;
begin
inc(nochered);
ochered[nochered].id:=id;
ochered[nochered].ocenka:=ocenka;
{Uravnoveshivanie ocheredi}
curr:=nochered;
while true do
begin
if curr=1 then break;
if ochered[curr].ocenka< ochered[curr div 2].ocenka
then
begin
swapo(curr,curr div 2);
curr:=curr div 2;
end
else break;
end;
end;
procedure getochered(var id,ocenka:integer);
var
curr:integer;
begin
id:=ochered[1].id;
ocenka:=ochered[1].ocenka;
ochered[1]:=ochered[nochered];
dec(nochered);
curr:=1;
while true do
begin
if (curr*2+1> nochered) then break;
if (ochered[curr*2].ocenka< ochered[curr].ocenka) or
(ochered[curr*2+1].ocenka<ochered[curr].ocenka) then
begin
if ochered[curr*2].ocenka> ochered[curr*2+1].ocenka
then
begin
swapo(curr*2+1,curr);
curr:=curr*2+1;
end
else
begin
swapo(curr*2,curr);
curr:=curr*2;
end;
end else break;
end;
end;
function getid:integer;
var q:integer;
qw:^linear;
begin
if memavail<10000 then
begin
q:=ochered[nochered].id;
{ exit;}
end else
begin
for q:=1 to maxmatrix do
if matrix[q]=nil then break;
getmem(matrix[q],sizeofm);
end;
qw:=matrix[q];
fillchar(qw^,sizeofm,0);
getid:=q;
end;
procedure freeid(id:integer);
begin
freemem(matrix[id],sizeofm);
matrix[id]:=nil;
end;
function i(x,y:integer):integer;
begin
i:=(y-1)*n+x+1;
end;
function simplize(id:integer):integer;
var
q,w:integer;
t:^linear;
add:integer;
min:integer;
begin
t:=matrix[id];
add:=0;
for q:=1 to n do
begin
min:=maxint;
for w:=1 to n do
if t^[i(w,q)]< >-1 then
if min> t^[i(w,q)] then min:=t^[i(w,q)];
if min<>0 then
for w:=1 to n do
if t^[i(w,q)]< >-1 then
dec(t^[i(w,q)],min);
if min>32000 then min:=0;
inc(add,min);
end;
for q:=1 to n do
begin
min:=maxint;
for w:=1 to n do
if t^[i(q,w)]< >-1 then
if min> t^[i(q,w)] then min:=t^[i(q,w)];
if min<>0 then
for w:=1 to n do
if t^[i(q,w)]< >-1 then
dec(t^[i(q,w)],min);
if min>32000 then min:=0;
inc(add,min);
end;
simplize:=add;
end;
function bestziro(id:integer):integer;
var
t:^linear;
q,w,e,x,y:integer;
min1,min2:integer;
l1,l2:array[1..maxsize] of integer;
begin
t:=matrix[id];
fillchar(l1,sizeof(l1),0);
fillchar(l2,sizeof(l2),0);
for q:=1 to n do
begin
min1:=maxint;min2:=maxint;
for w:=1 to n do
if t^[i(w,q)]< >-1 then
begin
if min2> t^[i(w,q)] then min2:=t^[i(w,q)];
if min1> min2 then
begin
e:=min1;
min1:=min2;
min2:=e;
end;
end;
if min1<>0 then min2:=0;
if min2>32000 then min2:=0;
l2[q]:=min2;
end;
for q:=1 to n do
begin
min1:=maxint;min2:=maxint;
for w:=1 to n do
if t^[i(q,w)]< >-1 then
begin
if min2> t^[i(q,w)] then min2:=t^[i(q,w)];
if min1> min2 then
begin
e:=min1;
min1:=min2;
min2:=e;
end;
end;
if min1<>0 then min2:=0;
if min2>32000 then min2:=0;
l1[q]:=min2;
end;
bz:=-32000;
bestx:=0;besty:=0;
for y:=n downto 1 do
for x:=1 to n do
if (t^[i(x,y)]=0) then
if l1[x]+l2[y]> bz then
begin
bestx:=x;
besty:=y;
bz:=l1[x]+l2[y];
end;
bestziro:=bz;
end;
begin
assign(input,'input.txt');
assign(output,'vetvi.out');
reset(input);
rewrite(output);
nochered:=0;
read(n);
sizeofm:=n*(n+2)*2+2;
start_m:=getid;
sm:=matrix[start_m];
for q:=1 to n do
for w:=1 to n do
read(sm^[i(w,q)]);
addochered(start_m,0);
{ ;
bestziro(start_m);}
{Sobstvenno reshenie}
best:=maxint;
while true do
begin
if nochered=0 then break;
getochered(workm,workc);
{process MATRIX}
inc(workc,simplize(workm));
if workc> best then goto skip;
sm:=matrix[workm];
if sm^[1]=n-1 then
begin
best:=workc;
for q:=1 to n do
begin
bestmatr [q]:=sm^[i(q,n+2)];
bestmatr1[q]:=sm^[i(q,n+1)];
end;
goto skip;
end;
q:=bestziro(workm);
if q=-32000 then goto skip;
{Pravaia vetka}
if(bestx=0) or (besty=0) then goto skip;
rightm:=getid;
move(matrix[workm]^,matrix[rightm]^,sizeofm);
sm:=matrix[rightm];
sm^[i(bestx,besty)]:=-1;
addochered(rightm,workc+q);
{Levaia vetka}
leftm:=getid;
move(matrix[workm]^,matrix[leftm]^,sizeofm);
sm:=matrix[leftm];
{Dobavliaetsia rebro iz bestx v besty}
inc(sm^[1]);
sm^[i(bestx,n+2)]:=besty;
sm^[i(besty,n+1)]:=bestx;
first:=bestx;last:=besty;
if sm^[1]< >n-1 then
begin
while true do
begin
if sm^[i(last,n+2)]=0 then break;
last:=sm^[i(last,n+2)];
end;
while true do
begin
if sm^[i(first,n+1)]=0 then break;
first:=sm^[i(first,n+1)];
end;
sm^[i(last,first)]:=-1;
sm^[i(first,last)]:=-1;
sm^[i(besty,bestx)]:=-1;
end;
for w:=1 to n do
begin
sm^[i(w,besty)]:=-1;
sm^[i(bestx,w)]:=-1;
end;
addochered(leftm,workc);
skip:
{Free Matrix}
freeid(workm);
end;
{ freeid(start_m);}
if best=maxint then
begin
writeln('Путь не существует');
end else
begin
writeln('Длина пути:',best);
for q:=1 to n do
if bestmatr[q]=0 then break;
e:=q;
for curr:=1 to n do
if bestmatr[curr]=q then break;
while true do
begin
write(curr,' ');
curr:=bestmatr1[curr];
if curr=0 then
begin
writeln(e);
break;
end;
end;
end;
close(input);
close(output);
end.
Вывод
При решении поставленной задачи оба метода дали одинаковый результат, что показывает правильность понимания и выполнения курсовой работы. Таким образом, необходимо использовать следующие параметры контроля: x9,x4,x10,x3,x7,x1,x2.
Метод динамического программирования достаточно прост для выполнения, но имеет существенный недостаток: при его использовании для счёта вручную возникают вычислительные трудности даже для простых систем.
Метод ветвей и границ является более сложным для понимания, но он оказался проще при ручном счёте. Недостатком является большая сложность программирования метода.
Литература
1. Селезнев А.В., Добрица Б.Т., Убар Р.Р. «Проектирование автоматизированных систем контроля бортового оборудования летательных аппаратов» стр. 90-95
2. Алексеев О.Г. «Комплексное применение методов дискретной оптимизации» стр. 18-25
© 2010 Интернет База Рефератов