Реферат: Нелинейное программирование

Реферат: Нелинейное программирование

Южно-Уральский Государственный Университет

Кафедра АиУ

реферат на тему:

Нелинейное программирование

Выполнил: Пушников А. А., ПС-263.

Проверил: Разнополов О.А.

Челябинск – 2003.

Оглавление

1.         Постановка задачи нелинейного программирования

2.         Критерии оптимальности в задачах с ограничениями

2.1.     Задачи с ограничением в виде равенств

2.2.     Множители Лагранжа

3.         Условия Куна-Таккера

3.1.     Условия Куна-Таккера и задача Куна-Таккера

3.2.     Интерпретация условий Куна-Таккера

3.3.     Теоремы Куна-Таккера

4.         Функции нескольких переменных

4.1.     Методы прямого поиска

4.1.1. Метод поиска по симплексу (S2 - метод)

4.1.2. Метод поиска Хука-Дживса

1. Постановка задачи нелинейного программирования.

В задаче нелинейного программирования (НЛП) требуется найти значение многомерной переменной х=(), минимизирующее целевую функцию f(x) при условиях, когда на переменную х наложены ограничения типа неравенств

 ,   i=1,2,…,m                                 (1)

а переменные , т.е. компоненты вектора х, неотрицательны:

                                                          (2)

Иногда в формулировке задачи ограничения (1) имеют противоположные знаки неравенств. Учитывая, однако, что если  , то  , всегда можно свести задачу к неравенствам одного знака. Если некоторые ограничения входят в задачу со знаком равенства, например , то их можно представить в виде пары неравенств , , сохранив тем самым типовую формулировку задачи.

Ряд инженерных задач связан с оптимизацией при наличии некоторого количества ограничений на управляемые пере­менные. Такие ограничения существенно уменьшают размеры об­ласти, в которой проводится поиск оптимума. На первый взгляд может показаться, что уменьшение размеров допустимой области должно упростить процедуру поиска оптимума. Между тем, напро­тив, процесс оптимизации становится более сложным, поскольку установленные выше критерии оптимальности нельзя использовать при наличии ограничений. При этом может нарушаться даже ос­новное условие, в соответствии с которым оптимум должен достигаться в стационарной точке, характеризующейся нулевым гра­диентом. Например, безусловный минимум функции  имеет место в стационарной точке х=2. Но если задача минимиза­ции решается с учетом ограничения , то будет найден условный минимум, которому соответствует точка x=4. Эта точка не является стационарной точкой функции f, так как (4)=4. Далее исследуются необходимые и достаточные условия оптимальности решений задач с ограничениями. Изложение начинается с рассмот­рения задач оптимизации, которые содержат только ограничения в виде равенств.

2.1. Задачи с ограничениями в виде равенств

Рассмотрим общую задачу оптимизации, содержащую несколь­ко ограничений в виде равенств:

Минимизировать            

при ограничениях           ,  k=1,…,n

Эта задача в принципе может быть решена как задача безусловной оптимизации, полученная путем исключения из целевой функции k независимых переменных с помощью заданных равенств. Наличие ограничений в виде равенств фактически позволяет уменьшить размерность исходной задачи с n до n-k.. В качестве иллюстрации рассмотрим следующий пример.

Пример 1

Минимизировать         

при ограничении         

Исключив переменную , с помощью уравнения , получим

оптимизационную задачу с двумя  переменными без ограничений

min  

Метод исключения переменных применим лишь в тех случаях, когда уравнения, представляющие ограничения, можно разрешить относительно некоторого конкретного набора независимых пере­менных. При наличии большого числа ограничений в виде равенств, процесс исключения переменных становится весьма трудоемкой процедурой. Кроме того, возможны ситуации, когда уравнение не удается разрешить относительно переменной. В частности, если в примере 1 ограничение  задать в виде

то получить аналитическое выражение какой-либо из переменных через другие не представляется возможным. Таким образом, при решении задач, содержащих сложные ограничения в виде равенств, целесообразно использовать метод множителей Лагранжа, описа­ние которого дается в следующем разделе.

2.2. Множители Лагранжа

С помощью метода множителей Лагранжа по существу устанавливаются необходимые условия, позволяющие идентифицировать точки оптимума в задачах оптимизации с ограничениями в виде ра­венств. При этом задача с ограничениями преобразуется в эквива­лентную задачу безусловной оптимизации, в которой фигурируют некоторые неизвестные параметры, называемые множителями Ла­гранжа.

Рассмотрим задачу минимизации функции n переменных с уче­том одного ограничения в виде равенства:

Минимизировать                                                (3)

при ограничениях                                                        (4)

В соответствии с методом множителей Лагранжа эта задача преобразуется в следующую задачу безусловной оптимизации:

минимизировать  L(x,u)=f(x)-u*h(x)                                               (5)

Функция  L(х;u) называется функцией Лагранжа, u — неизвест­ная постоянная, которая носит название множителя Лагранжа. На знак u никаких требований не накладывается.

Пусть при заданном значении u=u0 безусловный минимум функ­ции L(x,u) по х достигается в точке  и  удовлетворяет урав­нению . Тогда, как нетрудно видеть, x0 минимизирует (1) с учетом (4), поскольку для всех значений х, удовлетворяющих (4),  и  L(x,u)=min f(x).

Разумеется, необходимо подобрать значение u=u° таким обра­зом, чтобы координата точки безусловного минимума х° удовлетво­ряла равенству (4). Это можно сделать, если, рассматривая u как переменную, найти безусловный минимум функции (5) в виде функции u, а затем выбрать значение u, при котором выполняется равенство (4). Проиллюстрируем это на конкретном примере.

Пример 2

Минимизировать   

при ограничении   =0

Соответствующая задача безусловной оптимизации записывается в следующем виде:

минимизировать        L(x,u)= -u

Решение. Приравняв две компоненты градиента L к нулю, получим

Для того чтобы проверить, соответствует ли стационарная точка х° минимуму, вычислим элементы матрицы Гессе функции L(х;u), рассматриваемой как функция х,

,

которая оказывается положительно определенной. Это означает, что L(х,,u) — выпуклая функция х. Следовательно, координаты   , определяют точку глобального минимума. Оптималь­ное значение u находится путем подстановки значений  и   в урав­нение =2, откуда 2u+u/2=2 или . Таким образом, условный минимум достигается при  и   и равен min f(x)=4/5.

При решении задачи из примера 2 мы рассматривали L(х;u) как функцию двух переменных  и  и, кроме того, предполагали, что значение параметра u выбрано так, чтобы выполнялось ограни­чение. Если же решение системы

,    j=1,2,3,…,n

в виде явных функций u получить нельзя, то значения х и u нахо­дятся путем решения следующей системы, состоящей из n+1 урав­нений с n+1 неизвестными:

 ,     j=1,2,3,…,n       

Для нахождения всех возможных решений данной системы можно использовать численные методы поиска (например, метод Ньютона). Для каждого из решений () сле­дует вычислить элементы матрицы Гессе функции L, рассматри­ваемой как функция х, и выяснить, является ли эта матрица поло­жительно определенной (локальный минимум) или отрицательно определенной (локальный максимум).

Метод множителей Лагранжа можно распространить на случай, когда задача имеет несколько ограничений в виде равенств. Рас­смотрим общую задачу, в которой требуется

Минимизировать  f(x)

при ограничениях =0, k=1, 2, ..., К.

Функция Лагранжа принимает следующий вид:

L(x,u)=f(x)-

Здесь —множители Лагранжа, т.е. неизвестные параметры, значения которых необходимо определить. Приравни­вая частные производные L по х к нулю, получаем следующую систему n уравнении с n неизвестными:

………..

Если найти решение приведенной выше системы в виде функций вектора u оказывается затруднительным, то можно расширить систему путем включения в нее ограничений в виде равенств

Решение расширенной системы, состоящей из n+К уравнений с n+К неизвестными, определяет стационарную точку функции L. Затем реализуется процедура проверки на минимум или максимум, которая проводится на основе вычисления элементов матрицы Гессе функции L, рассматриваемой как функция х, подобно тому, как это было проделано в случае задачи с одним ограничением. Для некоторых задач расширенная система n+К уравнений с n+K неизвестными может не иметь решений, и метод множителей Лагранжа оказывается неприменимым. Следует, однако, отметить, что такие задачи на практике встречаются достаточно редко.

В предыдущем разделе было установлено, что множители Лаг­ранжа можно использовать при построении критериев оптималь­ности для задач оптимизации с ограничениями в виде равенств. Кун и Таккер обобщили этот подход на случай общей задачи нели­нейного программирования с ограничениями, как в виде равенств, так и в виде неравенств.   

Рассмотрим следующую общую задачу не­линейного программирования:

минимизировать                                                   (0)

при ограничениях                            (1)

                                (2)

Определение:

Ограничение в виде неравенства  называется активным, или связывающим, в точке , если , и неактивным, или несвязывающим, если

Если существует возможность обнаружить ограничения, ко­торые неактивны в точке оптимума, до непосредственного решения задачи, то эти ограничения можно исключить из модели и тем самым уменьшить ее размеры. Основная трудность заключается при этом в идентификации неактивных ограничений, предшествующей ре­шению задачи.

Кун и Таккер построили необходимые и достаточные условия оптимальности для задач нелинейного программирования, исходя из предположения о дифференцируемости функций . Эти условия оптимальности, широко известные как условия Куна—Таккера, можно сформулировать в виде задачи нахождения решения некоторой системы нелинейных уравнений и неравенств, или, как иногда говорят, задачи Куна—Таккера.

3.1. Условия Куна—Таккера и задача Куна—Таккера

Найти векторы   ,удовлетворяющие следующим условиям

(3)

(4)

(5)

(6)

(7)

Прежде всего проиллюстрируем условия  Куна — Таккера на примере.

Пример 3

Минимизировать  

при ограничениях

Решение.

Записав данную задачу в виде задачи нелиней­ного  программирования (0)-(2), получим

Уравнение (3),  входящее в состав условий   Куна—Таккера, принимает следующий  вид:

откуда

Неравенства (4) и уравнения (5) задачи Куна — Таккера в данном случае записываются в виде

Уравнения (5.16), известные как условие дополняющей нежесткости, принимают вид

Заметим, что на переменные  и  накладывается требование не­отрицательности, тогда как ограничение на знак  отсутствует.

Таким образом, этой задачи условия  Куна—Танкера записываются в следующем виде:

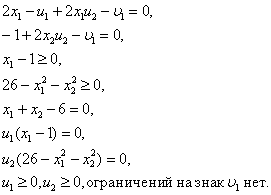
3.2. Интерпретация условий Куна — Таккера

Для того чтобы интерпретировать условия Куна — Таккера, рассмотрим задачу нелинейного программирования с ограничения­ми в виде равенств:

минимизировать

при ограничениях

Запишем условия Куна—Таккера

 (8)

  (9)

Далее рассмотрим функцию Лагранжа для задачи нелинейного программирования с ограничениями в виде равенств

Для этой функции условия оптимальности первого порядка запи­сываются в виде

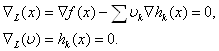
Нетрудно видеть, что условия Куна-Таккера (8) и (9) совпадают с условиями оптимальности первого порядка для задачи Лагранжа.

Рассмотрим задачу нелинейного программирования  с ограни­чениями  в виде неравенств:

минимизировать

при ограничениях 

Запишем  условия  Куна—Таккера

Соответствующая функция Лагранжа имеет вид

Условия оптимальности первого порядка записываются как

Заметим, что - множитель Лагранжа, соответствующий ограни­чению . Раньше было показано, что  представляет неявную цену, ассоциированную с ограничением ; другими словами, вели­чина  отражает изменение минимального значения целевой функ­ции , вызываемое единичным приращением правой части - го ог­раничения.

Если предположить, что - е ограничение является неактивным (т.е.  С другой стороны, если -е ограничение активное (т. е. ), то соответствующая неявная цена  не обязательно равна нулю, однако , так как . Таким образом, для всех значений .

Для того чтобы определить знак  (неявной цены, ассоциирован­ной с ограничением ), следует увеличить правую часть ограничения от 0 до 1. Ясно, что при этом область допустимых решений сужается, поскольку любое решение, удовлетворяющее ограничению , автоматически удовлетворяет неравенству . Следовательно, размеры допустимой области уменьша­ются, и минимальное значение  улучшить невозможно (так как вообще оно может только возрастать). Другими словами, неявная цена , ассоциированная с -м ограничением, должна быть неотри­цательной, что соответствует условиям Куна—Таккера.

3.3. Теоремы Куна—Таккера

В предыдущем разделе построены условия Куна—Таккера для задач условной оптимизации. С помощью метода множителей Лагранжа получено интуитивное представление о том, что условия Куна — Танкера тесно связаны с необходимыми условиями опти­мальности. В данном разделе рассматриваются строгие формули­ровки необходимых и достаточных условий оптимальности решения задачи нелинейного программирования.

Теорема 1. Необходимость условий Куна—Таккера

Рассмотрим задачу нелинейного программирования (0)-(2). Пусть -  дифференцируемые функции, а х* — допус­тимое решение данной задачи. Положим . Далее пусть  линейно неза­висимы. Если х* — оптимальное решение задачи нелинейного про­граммирования, то существует такая пара векторов , что  является решением задачи Куна—Таккера (3)—(7).

Условие, согласно которому должны быть линейно независимыми, известно как ус­ловие линейной независимости и по существу представляет собой некоторое условие регулярности допустимой области, которое поч­ти всегда выполняется для встречающихся на практике задач опти­мизации. Однако вообще проверка выполнения условия линейной независимости весьма затруднительна, так как требуется, чтобы оптимальное решение задачи было известно заранее. Вместе с тем условие линейной независимости всегда выполняется для задач нелинейного программирования, обладающих следующими свой­ствами.

1. Все ограничения в  виде равенств и  неравенств содержат линейные функции.

2. Все ограничения в виде неравенств содержат вогнутые функ­ции,  все ограничения-равенства — линейные функции, а также существует, по крайней мере, одна допустимая точка х, которая рас­положена во внутренней части области,  определяемой ограниче­ниями-неравенствами. Другими словами, существует такая точка х, что

Если условие линейной независимости в точке оптимума не вы­полняется, то задача Куна—Таккера может не иметь решения.

Пример 4

Минимизировать

при ограничениях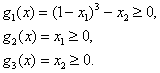

Решение.

На рис.1 изображена область допустимых ре­шений сформулированной выше нелинейной задачи. Ясно, что оптимальное решение этой задачи есть . Пока­жем, что условие линейной независимости не выполняется в точке оптимума.

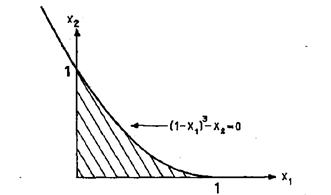
Рис.1 Допустимая область в задаче 4

Так как

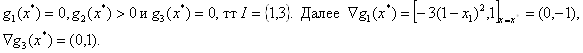Легко видеть, что векторы линейно зависимы, т. е. условие линейной независимости в точке не выпол­няется.

Запишем условия Куна—Таккера и проверим, выполняются ли они в точке (1, 0). Условия (3), (6) и (7) принимают сле­дующий вид;

 (11)

 (12)

(13)

 (14)

  (15)

(16)

При  из уравнения (11) следует, что , тогда как уравнение (14) дает , Следовательно, точка оптимума не является точкой Куна — Таккера.

Заметим, что нарушение условия линейной независимости не обязательно означает, что точка Куна—Таккера не существует. Для того чтобы подтвердить это, заменим целевую функцию из этого примера функцией. При этом оптимум по-прежнему достигается в точке (1,0), в которой условие линейной независимости не выполняется. Условия Куна—Так­кера (12) - (16) остаются неизменными, а уравнение (11) принимает вид

Нетрудно проверить, что точка  является точкой Куна—Таккера, т. е. удовлетворяет условиям Куна—Таккера.

Теорема о необходимости условий Куна—Таккера позволяет идентифицировать неоптимальные точки. Другими словами, тео­рему 1 можно использовать для доказательства того, что задан­ная допустимая точка, удовлетворяющая условию линейной неза­висимости, не является оптимальной, если она не удовлетворяет условиям Куна—Таккера. С другой стороны, если в этой точке условия Куна—Таккера выполняются, то нет гарантии, что най­дено оптимальное решение нелинейной задачи. В качестве примера рассмотрим следующую задачу нелинейного программирования.

Следующая теорема устанавливает условия, при выполнении которых точка Куна—Таккера автоматически соответствует оптимальному решению задачи нелинейного программирования.

Теорема.2 Достаточность условий Куна—Таккера

Рассмотрим задачу нелинейного программирования (0) — (2). Пусть целевая функция  выпуклая, все ограничения в виде неравенств содержат вогнутые функции , а ограничения в виде равенств содержат линейные функции . Тогда если существует решение , удовлет­воряющее условиям Куна—Таккера (3) — (7), то х* — оп­тимальное решение задачи нелинейного программирования.

Если условия теоремы 2 выполняются, то нахождение точки Куна—Таккера обеспечивает получение оптимального решения задачи нелинейного программирования.

Теорему 2 можно также использовать для доказательства оптимальности данного решения задачи нелинейного программирования. В качестве иллюстрации опять рассмотрим пример:

Минимизировать        

при ограничениях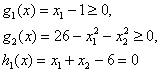

С помощью теоремы 2 докажем, что решение является оптимальным. Имеем

Так как матрица положительно полуопределена при всех х, функция  оказывается выпуклой. Первое ограничение в виде неравенства содержит линейную функцию , которая одновре­менно является как выпуклой, так и вогнутой. Для того

чтобы показать, что функция является вогнутой, вычислим

Поскольку матрица  отрицательно определена, функция является вогнутой. Функция  входит в линейное ограни­чение в вяде равенства. Следовательно, все условия теоремы 2 выполнены; если мы покажем, что  - точка Куна-Так­кера, то действительно установим оптимальность решения . Условия Куна-Таккера для примера 2 имеют вид

(22)

 (23)

  (24)

 (25)

,  (26)

, (27)

 (28)

(29)

Точка удовлетворяет ограничениям (24) — (26) и, следовательно, является допустимой. Уравнения (22) и (23) принимают следующий вид:

Положив  ,получим и. Таким образом, реше­ние х*=(1, 5),  удовлетворяет условиям Куна—Таккера. Поскольку условия теоремы 2 выполнены, то  оптимальное решение задачи из примера 3. Заметим, что существуют также и другие значения и , которые удов­летворяют системе (22) -(29).

Замечания

1.Для  встречающихся на практике задач условие линейной независимости,   как   правило,   выполняется.   Если   в  задаче   все функции  дифференцируемы,  то точку   Куна—Таккера  следует рассматривать как возможную точку оптимума. Таким образом, многие из методов нелинейного программирования сходятся к точке Куна—Таккера. (Здесь уместно провести аналогию со случаем безусловной оптимизации, когда соответствующие алгоритмы позволяют определить стационарную точку.)

2. Если условия теоремы 2 выполнены, точка Куна—Таккера в то же время оказывается точкой глобального минимума. К сожа­лению, проверка достаточных условий весьма затруднительна, и, кроме того, прикладные задачи  часто не обладают требуемыми свойствами. Следует отметить, что наличие хотя бы одного нелиней­ного ограничения в виде равенства приводит к нарушению предпо­ложений теоремы 2.

3.Достаточные условия, установленные теоремой 2, можно обобщить на случай задач с невыпуклыми функциями, входящими в ограничения в виде неравенств, невыпуклыми целевыми функ­циями и нелинейными ограничениями-равенствами. При этом ис­пользуются такие обобщения выпуклых функций, как квазивыпук­лые и псевдовыпуклые функции.

Ограниченные возможности симплексного метода, заключенные в задачах со сложными видами ограничений и произвольным видом целевой функции, привели к широкому использованию итеративных методов поиска оптимального решения. 

Сначала рассмотрим вопрос анализа «в статике» с использова­нием положений линейной алгебры и дифференциального исчисле­ния, а также условия, которые (в достаточно общих возможных ситуациях) позволяют идентифицировать точки опти­мума. Такие условия используются для проверки выбранных точек и дают возможность выяснить, являются ли эти точки точками ми­нимума или максимума. При этом задача вы­бора указанных точек остается вне рамок проводимого анализа; основное внимание уделяется решению вопроса о том, соответствуют ли исследуемые точки решениям многомерной задачи безусловной оптимизации, в которой требуется минимизировать f(x)     x   при отсутствии ограничений на x, где x — вектор управляемых переменных размерности n, f скалярная целевая функция. Обыч­но предполагается, что xi (для всех значений i=1, 2, …, n) могут принимать любые значения, хотя в ряде практических при­ложений область значений x выбирается в виде дискретного мно­жества. Кроме того, часто оказывается удобным предполагать, что функция f и ее производные существуют и непрерывны всюду, хотя известно, что оптимумы могут достигаться в точках разрыва f или ее градиента

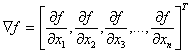
Градиентом функции  f(х) называют вектор, величина которого определяет скорость изменения функции f(x), а направление совпадает с направлением наибольшего возрастания этой функции.

Следует помнить, что функция f может принимать минимальное значение в точке x, в которой f или  претерпевают разрыв. Кроме того, в этой точке  может не существовать. Для того чтобы по­строить систему конструктивных критериев оптимальности, необ­ходимо (по крайней мере на первой стадии исследования) исключить из рассмотрения подобные ситуации, которые весьма усложня­ют анализ.

4.1. Методы прямого поиска

Ниже рассматривается вопрос анализа «в динамике» для функций нескольких переменных, т. е. исследуются методы и алгоритмы, позволяющие на итерацион­ной основе получать оценки х*— вектора управляемых переменных, которому соответствует минимальное значение функции f(x). Ука­занные методы применимы также к задачам максимизации, в кото­рых целевую функцию следует заменить на -f(х). Методы, ориен­тированные на решение задач безусловной оптимизации, можно разделить на три широких класса в соответствии с типом используе­мой при реализации того или иного метода информации.

1. Методы прямого поиска, основанные на вычислении только значений целевой функции.

2. Градиентные методы, в которых используются точные значе­ния  первых  производных f(x).

3. Методы второго порядка, в которых наряду с первыми про­изводными используются также вторые производные функции f(x).

Ниже рассматриваются методы, относящиеся к каждому из пере­численных классов, поскольку ни один метод или класс методов не отличается высокой эффективностью при решении оптимизационных задач различных типов. В частности, возможны случаи, когда про­исходит переполнение памяти ЭВМ; в других ситуациях вычисление значений целевой функции требует чрезмерных затрат времени; в некоторых задачах требуется получить решение с очень высокой степенью точности. В ряде приложений либо невозможно, либо весьма затруднительно найти аналитические выражения для произ­водных целевой функции. Поэтому если предполагается использо­вать градиентные методы, следует применить процедуру разностной аппроксимации производных. В свою очередь это приводит к необ­ходимости экспериментального определения длины шагов, позво­ляющего установить надлежащее соответствие между ошибкой округления и ошибкой аппроксимации. Таким образом, инженер вынужден приспосабливать применяемый метод к конкретным ха­рактеристикам решаемой задачи.

Методы решения задач безусловной оптимизации отличаются относительно высоким уровнем развития по сравнению с другими методами нелинейного программирования. Ниже речь идет о методах прямого поиска, для реализации которых требуются только значения целевой функции; в следующем разделе рассматриваются градиентные методы и методы второго порядка. Здесь предполагается, что f(x) непрерывна, а  может как существовать, так и не существовать, поскольку соответствующие числовые значения не используются. Однако следует отметить, что методы прямого поиска можно приме­нять для решения задач, в которых  существует, и они часто используются в тех случаях, когда  представляет собой сложную векторную функцию управляемых переменных. Наконец, в этом и последующих разделах предполагается, что функция f(х) унимо­дальна в рассматриваемой области. Если же изучаемые методы применяются для анализа мультимодальных функций, то приходит­ся ограничиваться идентификацией локальных минимумов.

Многомерные методы, реализующие процедуру поиска оптиму­ма на основе вычисления значений функции, с общих позиций можно разделить на эвристические и теоретические. Эвристические методы, как это следует из названия, реализуют процедуры поиска с помощью интуитивных геометрических представлений и обеспечи­вают получение частных эмпирических результатов. С другой сто­роны, теоретические методы основаны на фундаментальных математических теоремах и обладают такими операционными свойствами, как сходимость (по крайней мере при выполнении некоторых опре­деленных условий). Ниже подробно рассматриваются три метода прямого поиска:

1) поиск по симплексу, или S2-метод;

2) метод поиска Хука—Дживса;

3) метод сопряженных направлений Пауэлла.

Первые два из перечисленных методов относятся к категории эвристических и реализуют принципиально различающиеся стра­тегии поиска. В процессе поиска по S2-методу последовательно опе­рируют регулярными симплексами в пространстве управляемых переменных, тогда как при реализации метода Хука-Дживса используется фиксированное множество (координатных) направле­ний, выбираемых рекурсивным способом. Метод Пауэлла основан на теоретических результатах и ориентирован на решение задач с квадратичными целевыми функциями; для таких задач метод сходится за конечное число итераций. К числу общих особенностей всех трех методов следует отнести относительную простоту соответ­ствующих вычислительных процедур, которые легко реализуются и быстро корректируются. С другой стороны, реализация указанных  методов может требовать (и часто требует) более значительных затрат времени по сравнению с методами с использованием производных.

4.1.1. Метод поиска по симплексу(S2 -метод)

Первые попытки решения оптимизационных задач без ограниче­ний на основе прямого поиска связаны с использованием одномер­ных методов оптимизации. Как правило, при реализации таких методов допустимая область определения показателя качества функционирования системы (целевой функции) заменяется дискрет­ным множеством (решеткой) точек пространства управляемых пере­менных, а затем используются различные стратегии уменьшения области, которая содержит решение задачи. Часто эта процедура оказывается эквивалентной равномерному поиску в узлах решетки и, следовательно, непригодной для решения задач с числом пере­менных, превышающим 2. Более полезная идея заключается в выбо­ре базовой точки и оценивании значений целевой функции в точках, окружающих базовую точку. Например, при решении задачи с дву­мя переменными можно воспользоваться квадратным образцом, изображенным на рис.2

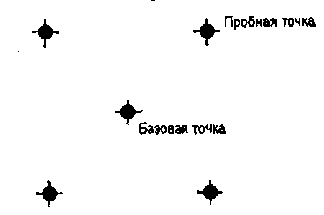
Рис 2. Квадратный образец (частный случай кубического образца)

За­тем «наилучшая» из пяти исследуемых точек выбирается в ка­честве следующей базовой точ­ки, вокруг которой строится аналогичный образец. Если ни одна из угловых точек не имеет преимущества перед базовой, размеры образца следует уменьшить, после чего продолжить поиск.

Этот тип эволюционной опти­мизации был использован Бок­сом  и другими исследователями для анализа функционирования промышленных предприятий, когда эффект варьирования значений переменных, описывающих производственные процессы, измеряется с ошибкой. В задачах большой размерности вычисление значений целевой функции проводится во всех вершинах, а также в центре тяжести гиперкуба (гиперкуб куб в n-мерном евклидовом пространстве, т.е. множество S=x=() , где а и b заданные числа ) , т. е. в точках так называемого кубического образца. Если количество переменных (размерность пространства, в котором ведется поиск) равно n, то поиск по кубическому образцу требует +1 вычислений значения функций для одного образца. При увеличении размерности задачи необходимое количество вы­числений значения целевой функции возрастает чрезвычайно быст­ро. Таким образом, несмотря на логическую простоту поиска по кубическому образцу, возникает необходимость использования более эффективных методов прямого поиска для решения возникаю­щих на практике задач оптимизации.

Одна из вызывающих особый интерес стратегий поиска положе­на в основу метода поиска по симплексу, предложенного Спендли, Хекстом и Химсвортом. Следует отметить, что указанный метод и другие подобные методы не имеют отношения к симплекс-методу линейного программирования, а сходство названий носит случай­ный характер. Процедура симплексного поиска Спендли, Хекста и Химсворта базируется на том, что экспериментальным образцом, содержащим наименьшее количество точек, является регулярный симплекс. Регулярный симплекс в n-мерном пространстве пред­ставляет собой многогранник, образованный n+1 равностоящими друг от друга точками-вершинами. Например, в случае двух пере­менных симплексом является равносторонний треугольник; в трех­мерном пространстве симплекс представляет собой тетраэдр. В алго­ритме симплексного поиска используется важное свойство симплек­сов, согласно которому новый симплекс можно построить на любой грани начального симплекса путем переноса выбранной вершины на надлежащее расстояние вдоль прямой, проведенной через центр тяжести остальных вершин начального симплекса. Полученная та­ким образом точка является вершиной нового симплекса, а выбран­ная при построении вершина начального симплекса исключается. Нетрудно видеть, что при переходе к новому симплексу требуется одно вычисление значения целевой функции. Рис 3 иллюстрирует процесс построения нового симплекса на плоскости.

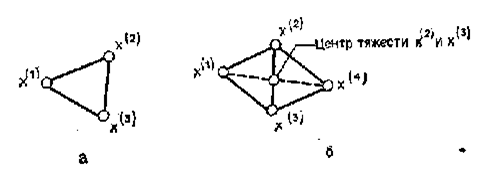
Рис.3.Построение нового симплекса.

а начальный симплекс

б новый симплекс 

Работа алгоритма симплексного поиска начинается с построения регулярного симплекса в пространстве независимых переменных и оценивания значений целевой функции в каждой из вершин симп­лекса. При этом определяется вершина, которой соответствует наибольшее значение целевой функции. Затем найденная вершина проецируется через центр тяжести остальных вершин симплекса в новую точку, которая используется в качестве вершины нового симплекса. Если функция убывает достаточно плавно, итерации продолжаются до тех пор, пока либо не будет накрыта точка мини­мума, либо не начнется циклическое движение по двум или более симплексам. В таких ситуациях можно воспользоваться следую­щими тремя правилами.

Правило 1. «Накрытие» точки минимума

Если вершина, которой соответствует наибольшее значение це­левой функции, построена на предыдущей итерации, то вместо нее берется вершина, которой соответствует следующее по величине значение целевой функции.

Правило 2. Циклическое движение

Если некоторая вершина симплекса не исключается на протя­жении более чем М итераций, то необходимо уменьшить размеры симплекса с помощью коэффициента редукции и построить новый симплекс, выбрав в качестве базовой точку, которой соответствует минимальное значение целевой функции. Спендли, Хекст и Химс-ворт предложили вычислять М по формуле

M=1,65n+0,05

где n — размерность задачи, а М округляется до ближайшего целого числа. Для применения данного правила требуется уста­новить величину коэффициента редукции.

Правило 3. Критерий окончания поиска

Поиск завершается, когда или размеры симплекса, или разности между значениями функции в вершинах становятся достаточно ма­лыми. Чтобы можно было применять эти правила, необходимо за­дать величину параметра окончания поиска.

Реализация изучаемого алгоритма основана на вычислениях двух типов: (1) построении регулярного симплекса при заданных базовой точке и масштабном множителе и (2) расчете координат отраженной точки. Построение симплекса является достаточно простой процедурой, так как из элементарной геометрии известно, что при заданных начальной (базовой) точке  и масштабном мно­жителе  координаты остальных n вершин симплекса в n-мерном пространстве вычисляются по формуле

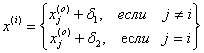                 (7)

для i  и j=1,2,3,…,n

Приращения  и , зависящие только от n и выбранного мас­штабного множителя, определяются по формулам

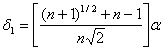                          (8)

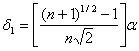                        (9)

Заметим, что величина масштабного множителя выбирается ис­следователем, исходя из характеристик решаемой задачи. При =1 ребра регулярного симплекса имеют единичную длину. Вычисления второго типа, связанные с отражением относи­тельно центра тяжести, также представляют несложную процедуру. Пусть — точка, подлежащая отражению. Центр тяжести осталь­ных n точек расположен в точке

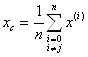                       (10)

Все точки прямой, проходящей через  и хс, задаются формулой

                (11)

При =0 получаем исходную точку , тогда как значение =1 соответствует центру тяжести хс. Для того чтобы построенный симп­лекс обладал свойством регулярности, отражение должно быть сим­метричным. Следовательно, новая вершина получается при =2. Таким образом,

                    (12)

Проиллюстрируем вычислительную схему метода следующим при­мером.

Пример 5. Вычисления в соответствии с методом поиска по симплексу

Минимизировать f(x)=

Решение.

Для построения исходного симплекса требуется задать начальную точку и масштабный множитель. Пусть x =и =2. Тогда

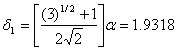
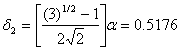
Используя эти два параметра, вычислим координаты двух остальных вершин симплекса:

которым соответствуют значения целевой функции, равные =0,2374 и 3,0658. Так как 5, необходимо отразить точку относительно центра тяжести двух остальных вершин симплекса

Используя формулу (12),  получаем

В полученной точке 2,3027, т. е. наблюдается уменьшение целевой функции. Новый симплекс образован точками и. В соответствии с алгоритмом следует отразить точку х(2), ко­торой соответствует наибольшее значение целевой функции, отно­сительно центра тяжести точек и х(3). Итерации продолжаются до тех пор, пока не потребуется применение правил 1, 2 и 3, которые были сформулированы выше.

Изложенный выше алгоритм - метода имеет несколько очевид­ных преимуществ.

1. Расчеты и логическая структура метода отличаются сравни­тельной простотой, и, следовательно, соответствующая программа для ЭВМ оказывается относительно короткой.

2. Уровень требований к объему памяти ЭВМ невысокий, мас­сив имеет размерность (n+1, n+2).

3. Используется сравнительно небольшое число заранее уста­новленных  параметров: масштабный множитель , коэффициент уменьшения множителя (если применяется правило 2) и параметры окончания поиска.

4. Алгоритм оказывается эффективным даже в тех случаях, когда ошибка вычисления значений целевой функции велика, по­скольку при его реализации оперируют наибольшими значениями функции в вершинах, а не наименьшими.

Перечисленные факторы характеризуют метод поиска по симплек­су как весьма полезный при проведении вычислений в реальном времени.

Алгоритм обладает также рядом существенных недостатков.

1. Не исключено возникновение трудностей, связанных с масштабированием, поскольку все координаты вершин симплекса за­висят от одного и того же масштабного множителя . Чтобы обойти трудности такого рода, в практических задачах следует промасштабировать все переменные с тем, чтобы их значения были сравнимыми по величине.

2. Алгоритм работает слишком медленно, так как полученная на предыдущих итерациях информация не используется для уско­рения поиска.

3. Не существует простого способа расширения симплекса, не требующего пересчета значений целевой функции во всех точках образца. Таким образом, если по какой-либо причине уменьшается (например, если встречается область с узким «оврагом» или «хреб­том»), то поиск должен  продолжаться с уменьшенной величиной шага.

4.1.2. Метод поиска Хука-Дживса.

Метод, разработанный Хуком и Дживсом, является одним из первых алгоритмов, в которых при определении нового направления поиска учитывается информация, полученная на предыдущих итерациях. По существу процедура Хука—Дживса представляет собой комбинацию «исследующего» поиска с циклическим изменением переменных и ускоряющегося поиска по образцу с использованием определенных эвристических правил. Исследующий поиск ориентирован на выявление характера локального поведения целевой функции и определение направлений вдоль «оврагов». Полученная в результате исследующего поиска информация затем используется в процессе поиска по образцу при движении по «оврагам».

Исследующий поиск.

Для проведения исследующего поиска необходимо задать величину шага, которая может быть раз­личной для разных координатных направлений и изменяться в про­цессе поиска. Исследующий поиск начинается в некоторой исходной точке. Если значение целевой функции в пробной точке не превы­шает значения функции в исходной точке, то шаг поиска рассматри­вается как успешный. В противном случае необходимо вернуться в предыдущую точку и сделать шаг в противоположном направлении с последующей проверкой значения целевой функции. После пере­бора всех N координат исследующий поиск завершается. Получен­ную в результате точку называют базовой точкой.

Поиск по образцу.

Поиск по образцу заключается в реализации единственного шага из полученной базовой точки вдоль-прямой, соединяющей эту точку с предыдущей базовой точкой. Новая точка образца определяется в соответствии с формулой

Как только движение по образцу не приводит к уменьшению целе­вой функция, точка  фиксируется в качестве временной базо­вой точки и вновь проводится исследующий поиск. Если в резуль­тате получается точка с меньшим значением целевой функции, чем в точке , то она рассматривается как новая базовая точка . С другой стороны, если исследующий поиск неудачен, необходимо вернуться в точку  и провести исследующий поиск с целью вы­явления нового направления минимизации. В конечном счете, воз­никает ситуация, когда такой поиск не приводит к успеху. В этом случае требуется уменьшить величину шага путем введения неко­торого множителя и возобновить исследующий поиск. Поиск завер­шается, когда величина шага становится достаточно малой. После­довательность точек, получаемую в процессе реализации метода, можно записать в следующем виде:

-   текущая базовая точка,

- предыдущая базовая точка,

-  точка, построенная при движении по образцу,

- следующая (новая) базовая точка.

Приведенная последовательность характеризует логическую струк­туру поиска по методу Хука Дживса.

Структура метода поиска Хука — Дживса

Шаг  1 . Определить:

начальную точку  ,

приращения

коэффициент уменьшения шага ,

параметр окончания поиска .

Ш а г 2.  ровести исследующий поиск.

Ш а г 3. Был ли исследующий поиск удачным (найдена ли точ­ка с меньшим значением  

целевой функции)?

Да: перейти к шагу 5.

Нет: продолжать.

Ш а г 4. Проверка на окончание поиска.

Выполняется ли неравенство ?

Да: прекратить поиск; текущая точка аппроксимирует точку оп­тимума.

Нет: уменьшить приращения по формуле

Перейти к шагу 2.

Ш а г 5. Провести поиск по образцу:

Шаг 6. Провести исследующий поиск, используя  в ка­честве базовой точки;

пусть  полученная в результате точка.

Ш а г 7. Выполняется  ли  неравенство ?

Да: положить  Перейти к шагу 5.

Нет: перейти к шагу 4.

Пример 6  Поиск по методу Хука — Дживса

Найти точку минимума функции   используя начальную точку .

Решение.

Для того чтобы применить метод прямого поиска .Хука — Дживса,  необходимо задать следующие величины:

 векторная величина приращения = ,

  коэффициент уменьшения шага = 2,

 параметр окончания поиска = 10-4.

Итерации начинаются с исследующего поиска вокруг точки , которой соответствует значение функции Фиксируя , дадим приращение переменной :

Успех.

Следовательно, необходимо зафиксировать  и дать прираще­ние переменной :

 Успех.

Таким образом, в результате исследующего поиска найдена точка

Поскольку исследующий поиск был удачным, переходим к поиску по образцу:

Далее проводится исследующий поиск вокруг точки , который оказывается удачным при использовании положительных прираще­ний переменных х1 и х2. В результате получаем точку

Поскольку , поиск по образцу следует считать успеш­ным, и  становится новой базовой точкой при следующем про­ведении поиска по образцу. Итерации продолжаются, пока умень­шение величины шага не укажет на окончание поиска в окрестности точки минимума. Последовательные шаги реализации метода показаны на рисунке.

   Из примера  следует, что метод Хука — Дживса характери­зуется несложной стратегией поиска, относительной простотой вычислений и невысоким уровнем требований к объему памяти ЭВМ, который оказывается даже ниже, чем в случае использования ме­тода поиска по симплексу.

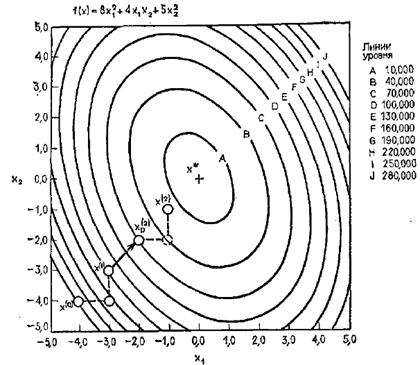
Итерации поиска по методу Хука-Дживса на примере