
Рефераты по сексологии
Рефераты по информатике программированию
Рефераты по биологии
Рефераты по экономике
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Рефераты по авиации и космонавтике
Рефераты по административному праву
Рефераты по безопасности жизнедеятельности
Рефераты по арбитражному процессу
Рефераты по архитектуре
Рефераты по астрономии
Рефераты по банковскому делу
Рефераты по биржевому делу
Рефераты по ботанике и сельскому хозяйству
Рефераты по бухгалтерскому учету и аудиту
Рефераты по валютным отношениям
Рефераты по ветеринарии
Рефераты для военной кафедры
Рефераты по географии
Рефераты по геодезии
Рефераты по геологии
Рефераты по геополитике
Рефераты по государству и праву
Рефераты по гражданскому праву и процессу
Рефераты по делопроизводству
Рефераты по кредитованию
Рефераты по естествознанию
Рефераты по истории техники
Рефераты по журналистике
Рефераты по зоологии
Рефераты по инвестициям
Рефераты по информатике
Исторические личности
Рефераты по кибернетике
Рефераты по коммуникации и связи
Реферат: Решение задачи линейного программирования симплекс-методом
Реферат: Решение задачи линейного программирования симплекс-методом
Государственное образовательное учреждение высшего
профессионального образования
"Московский государственный технический университет им. Н.Э. Баумана"
Калужский филиал
Реферат
"Решение задачи линейного программирования симплекс-методом"
2008
Цель работы: изучить и научиться применять на практике симплекс - метод для решения прямой и двойственной задачи линейного программирования
Теоретическая часть.
Математическая постановка задачи линейного программирования.
Из практики рассмотрения задач математического программирования следует, что в общем виде решить их практически невозможно. Целесообразно рассматривать отдельные классы (виды) задач. Для каждого такого класса удается сформулировать алгоритм решения, приемлемый только для данного класса задач. Наиболее разработанными в математическом программировании являются задачи линейного программирования (ЛП).
В задачах линейного программирования целевая функция линейна, а условия-ограничения содержат линейные равенства и линейные неравенства. Переменные могут быть подчинены или не подчинены требованию неотрицательности. Одна и та же задача линейного программирования может быть записана в различной форме. Если все ограничения имеют вид неравенств, то задача записана в стандартной форме. Если все ее ограничения, кроме
![]()
представляют собой равенства, то задача линейного программирования записана в канонической форме.
Общий вид задачи линейного программирования
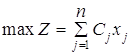
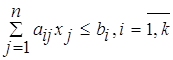
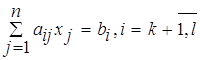
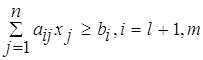
![]() ,
,![]()
Ограничения:
1. Правые части всех ограничений должны быть
неотрицательными ![]() . Если какой-нибудь из
коэффициентов
. Если какой-нибудь из
коэффициентов ![]() < 0, то необходимо коэффициенты
ограничения слева и справа домножить на "-1" и изменить знак данного
ограничения на противоположный;
< 0, то необходимо коэффициенты
ограничения слева и справа домножить на "-1" и изменить знак данного
ограничения на противоположный;
2. Все ограничения должны быть представлены в виде равенств, поэтому при переходе от неравенства к равенству используют аппарат дополнительных переменных.
Если исходные ограничения определяют расход некоторого
ресурса (знак "![]() "), то переменные
"), то переменные ![]() следует
интерпретировать как остаток, или неиспользованную часть ресурса. В этом случае
следует
интерпретировать как остаток, или неиспользованную часть ресурса. В этом случае
![]() остаточная переменная и вводится в уравнение со знаком "+".
остаточная переменная и вводится в уравнение со знаком "+".
Если исходные ограничения определяют избыток некоторого
ресурса (знак "![]() "), то вводится избыточная
переменная
"), то вводится избыточная
переменная ![]() знаком
"-".
знаком
"-".
Переменные:
Все переменные должны быть неотрицательными, т.е. ![]() .
.
Если переменная не имеет ограничения в знаке, то её нужно представить
как разность двух неотрицательных переменных: ![]() , где
, где ![]() . Такую подстановку следует
использовать во всех ограничениях, содержащих эту переменную, а также в выражении
для целевой функции.
. Такую подстановку следует
использовать во всех ограничениях, содержащих эту переменную, а также в выражении
для целевой функции.
Если такая переменная попадает в оптимальное решение, то
![]() .
.
Целевая функция:
Подлежит максимизации или минимизации. ![]()
Система ограничений в виде равенств и неравенств образует выпуклое множество - выпуклый многогранник. Это множество может быть ограниченным и неограниченным. Целевая функция задачи линейного программирования также является выпуклой функцией. Таким образом, задача линейного программирования является частным случаем задачи выпуклого программирования.
Рассмотрим систему ограничений задачи линейного программирования в виде равенств
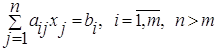 (1)
(1)
Система (1) линейных уравнений совместна, если она имеет, по крайней мере, одно решение. Система (1) называется избыточной, если одно из уравнений можно выразить в виде линейной комбинации остальных.
В системе (1) число переменных (неизвестных ![]() n
больше, чем число ограничений m. Будем считать, что
ранг этой системы равен m (система неизбыточна) и что
система (1) совместна. Тогда m переменных из общего их
числа образуют базисные переменные, а остальные
n
больше, чем число ограничений m. Будем считать, что
ранг этой системы равен m (система неизбыточна) и что
система (1) совместна. Тогда m переменных из общего их
числа образуют базисные переменные, а остальные ![]() переменных называют небазисными.
Если система уравнений имеет решение, то она имеет и базисное решение. Решение
системы уравнений (1) называют допустимым, если все его компоненты
неотрицательны. Если система линейных уравнений обладает допустимым решением,
то она имеет и базисное допустимое решение. Совокупность всех допустимых
решений системы (1) есть выпуклое множество, т.е. множество решений задачи
линейного программирования выпукло. Так как это множество образовано
плоскостями (гиперплоскостями), то оно имеет вид выпуклого многогранника. Базисное
допустимое решение соответствует крайней точке выпуклого многогранника (его
грани или вершине). Если существует оптимальное решение задачи линейного программирования,
то существует базисное оптимальное решение.
переменных называют небазисными.
Если система уравнений имеет решение, то она имеет и базисное решение. Решение
системы уравнений (1) называют допустимым, если все его компоненты
неотрицательны. Если система линейных уравнений обладает допустимым решением,
то она имеет и базисное допустимое решение. Совокупность всех допустимых
решений системы (1) есть выпуклое множество, т.е. множество решений задачи
линейного программирования выпукло. Так как это множество образовано
плоскостями (гиперплоскостями), то оно имеет вид выпуклого многогранника. Базисное
допустимое решение соответствует крайней точке выпуклого многогранника (его
грани или вершине). Если существует оптимальное решение задачи линейного программирования,
то существует базисное оптимальное решение.
Целевая функция задачи линейного программирования есть уравнение плоскости (или гиперплоскости для числа переменных больше трех). Максимальное или минимальное значение целевая функция задачи линейного программирования достигает либо в вершине выпуклого многогранника, либо на одной из его граней. Таким образом, решение (решения) задачи линейного программирования лежит в вершинах выпуклого многогранника и для его нахождения надо вычислить значения целевой функции в вершинах выпуклого многогранника, определяемого условиями-ограничениями задачи.
Решение задачи линейного программирования графическим методом.
Трудность построения математической модели заключается в идентификации переменных и последующем представлении цели и ограничений в виде математических функций этих переменных. Если модель содержит только две переменные, то задачу линейного программирования можно решить графически. В случае трёх переменных графическое решение становится менее наглядным, а при большем значении переменных – даже невозможным. Однако графическое решение позволяет сделать выводы, которые служат основой для разработки общего метода решения задачи линейного программирования.
Первый шаг при использовании графического метода заключается
в геометрическом представлении допустимых решений, т.е. построении области
допустимых решений (ОДР.), в которой одновременно удовлетворяются все
ограничения модели. При получении графического решения переменная ![]() откладывается
по горизонтальной оси, а
откладывается
по горизонтальной оси, а ![]() – по вертикальной. При
формировании ОДР необходимо предотвратить получение недопустимых решений,
которые связаны с необходимостью выполнения условия неотрицательности
переменных. Перед построением необходимо определить квадранты, в которых будет
располагаться ОДР. Квадранты определяются знаками переменных
– по вертикальной. При
формировании ОДР необходимо предотвратить получение недопустимых решений,
которые связаны с необходимостью выполнения условия неотрицательности
переменных. Перед построением необходимо определить квадранты, в которых будет
располагаться ОДР. Квадранты определяются знаками переменных ![]() и
и ![]() . Условия
неотрицательности переменных
. Условия
неотрицательности переменных ![]() и
и ![]() ограничивают область их
допустимых значений первым квадрантом. Если переменная
ограничивают область их
допустимых значений первым квадрантом. Если переменная ![]() не ограниченна в знаке, то
область ограничивается первым и вторым квадрантом, если
не ограниченна в знаке, то
область ограничивается первым и вторым квадрантом, если ![]() , то – первым и
четвёртым квадрантом. Другие границы пространства решений на плоскости
, то – первым и
четвёртым квадрантом. Другие границы пространства решений на плоскости ![]() ,
, ![]() изображены
прямыми линиями, построенными по уравнениям ограничений при условии замены
знака
изображены
прямыми линиями, построенными по уравнениям ограничений при условии замены
знака ![]() на
знак "=". При этом необходимо учитывать следующее: правые части всех
ограничений должны быть неотрицательными
на
знак "=". При этом необходимо учитывать следующее: правые части всех
ограничений должны быть неотрицательными ![]() . Если какое-нибудь ограничение
. Если какое-нибудь ограничение ![]() < 0, то
необходимо коэффициенты соответствующего ограничения слева и справа до-множить
на "-1" и изменить знак неравенства данного ограничения на
противоположный. Области, в которых выполняются соответствующие ограничения в
виде неравенств, указываются стрелками, направленными в сторону допустимых
значений переменных.
< 0, то
необходимо коэффициенты соответствующего ограничения слева и справа до-множить
на "-1" и изменить знак неравенства данного ограничения на
противоположный. Области, в которых выполняются соответствующие ограничения в
виде неравенств, указываются стрелками, направленными в сторону допустимых
значений переменных.
В результате построений получается многоугольник, который определяет пространство решений. Если одно из ограничений имеет знак "=", то ОДР вырождается в отрезок.
В каждой точке, принадлежащей области или границам
многоугольника решений, все ограничения выполняются, поэтому все решения,
соответствующие этим точкам, являются допустимыми. Пространство решений
содержит бесконечное число таких точек, несмотря на это, можно найти
оптимальное решение. Для этого необходимо построить в плоскости переменных ![]() ,
,![]() градиент целевой
функции. Определение оптимальной точки зависит от той задачи, которую
необходимо решить.
градиент целевой
функции. Определение оптимальной точки зависит от той задачи, которую
необходимо решить.
Если в целевой функции определена задача максимизации, то оптимальная точка будет располагаться в направлении увеличения градиента, если задача минимизации – то в направлении уменьшения градиента целевой функции. Для определения оптимальной точки будем перемещать целевую функцию в направлении увеличения (уменьшения) градиента до тех пор, пока она не сместиться в область недопустимых решений.
После нахождения оптимальной точки пространства решений
определяют её координаты ![]() ,
,![]() и значение целевой функции
и значение целевой функции ![]() в ней.
Правильность выбора оптимальной точки можно проверить расчётом целевой функции
в вершинах многогранника решений. В ЗЛП область допустимых решений всегда
является выпуклым множеством, т.е. таким множеством, что наряду с любыми двумя
точками, принадлежащими этому множеству, этому же множеству принадлежит и
отрезок, соединяющий эти две точки. Любая функция наискорейшим образом
увеличивается в направлении своего градиента.
в ней.
Правильность выбора оптимальной точки можно проверить расчётом целевой функции
в вершинах многогранника решений. В ЗЛП область допустимых решений всегда
является выпуклым множеством, т.е. таким множеством, что наряду с любыми двумя
точками, принадлежащими этому множеству, этому же множеству принадлежит и
отрезок, соединяющий эти две точки. Любая функция наискорейшим образом
увеличивается в направлении своего градиента.
Решение задачи линейного программирования симплекс-методом.
Прямая задача.
Рассмотрим задачу линейного программирования в канонической форме:
Найти максимум (минимум) функции 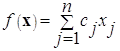 при условиях
при условиях
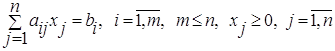
Предполагается, что решение этой задачи существует. Чтобы найти оптимальное решение, надо найти допустимые базисные решения, а из них выбрать оптимальное базисное решение.
Симплекс – метод – это алгебраический метод решения задач линейного программирования. В процессе вычислений производиться последовательный обход вершин многогранника решений (ОДР.) с проверкой в каждой вершине условий оптимальности. При этом каждый переход в смежную вершину сопровождается улучшением целевой функции.
Вычислительные процедуры симплекс - метода.
При графическом методе решения ЗЛП оптимальному решению соответствует всегда одна из угловых (экстремальных) точек пространства решений. Это результат положен в основу построения симплекс-метода. Симплекс-метод не обладает наглядностью геометрического представления пространства решений.
Симплекс-метод реализует упорядоченный процесс, при котором, начиная с некоторой исходной допустимой угловой точки, осуществляются последовательные переходы от одной допустимой экстремальной точки к другой, пока не будет найдена точка оптимального решения.
Обозначим: ![]() – общее количество переменных в
ЗЛП, представленной в канонической форме;
– общее количество переменных в
ЗЛП, представленной в канонической форме; ![]() - количество исходных переменных;
- количество исходных переменных;
![]() - количество ограничений,
- количество ограничений, ![]() - количество
дополнительных переменных, тогда
- количество
дополнительных переменных, тогда ![]() .
.
Каждая вершина многогранника решений имеет ![]() -
ненулевых переменных и (
-
ненулевых переменных и (![]() ) - нулевых переменных.
) - нулевых переменных.
Ненулевые переменные называются базисными, нулевые переменные – небазисными.
Дополним систему равенств равенством целевой функции, при
этом будем считать, что ![]() является
является ![]() базисной
переменной, которая всегда присутствует в базисе для любой вершины.
базисной
переменной, которая всегда присутствует в базисе для любой вершины.
Для получения решения составляется начальный допустимый базис, в котором базисные переменные должны быть представлены в виде единичных орт. Это означает, что уравнения, представляющие данную вершину должны включать каждую базисную переменную только в одной строке с коэффициентом, равным 1.
При выборе начального допустимого базиса для составления
симплекс-табли-цы на первом шаге СТ(0) исходные ![]() переменные приравниваются к нулю
и являются небазисными, среди введённых дополнительных переменных выбираются
переменные с коэффициентами равными единице. Переменные
переменные приравниваются к нулю
и являются небазисными, среди введённых дополнительных переменных выбираются
переменные с коэффициентами равными единице. Переменные ![]() в равенствах (2) - (4)
являются базисными и в
в равенствах (2) - (4)
являются базисными и в ![]() - строку входят с коэффициентами,
равными 0. Для заполнения симплекс-таблицы необходимо целевую функцию
преобразовать к виду
- строку входят с коэффициентами,
равными 0. Для заполнения симплекс-таблицы необходимо целевую функцию
преобразовать к виду 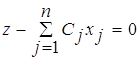 . Таким образом, окончательно
получаем:
. Таким образом, окончательно
получаем:
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
![]() (4)
(4)
При составлении симплекс-таблицы придерживаются следующих правил:
в крайнем левом столбце располагаются базисные переменные и ![]() ;
;
в крайнем правом столбце располагаются правые части ограничений;
в первой строке располагаются переменные в определённом порядке:
сначала ![]() , потом небазисные переменные,
базисные переменные располагаются в последних
, потом небазисные переменные,
базисные переменные располагаются в последних ![]() столбцах перед
правой частью (ПЧ). Запишем коэффициенты в СТ(0):
столбцах перед
правой частью (ПЧ). Запишем коэффициенты в СТ(0):
|
|
|
|
|
|
|
ПЧ | |
|
|
1 |
- |
- |
0 | 0 | 0 | 0 |
|
|
0 |
|
|
1 | 0 | 0 |
|
|
|
0 |
|
|
0 | 1 | 0 |
|
|
|
0 |
|
|
0 | 0 | 1 |
|
Оптимальность любой из вершин определяется коэффициентами
при небазисных переменных в ![]() – строке текущей симплекс-таблицы:
– строке текущей симплекс-таблицы:
Для задачи максимизации данная вершина является оптимальной,
если все коэффициенты при небазисных переменных в ![]() – строке являются
неотрицательными (>0);
– строке являются
неотрицательными (>0);
Для задачи минимизации данная вершина является оптимальной,
если все коэффициенты при небазисных переменных в ![]() – строке являются неположительными
(< 0).
– строке являются неположительными
(< 0).
Если в задаче максимизации (минимизации) у одной небазисной
переменной в ![]() – строке коэффициент
<0(>0), то текущая точка не является оптимальной и необходимо изменить
базис. Для этого выбирают небазисную переменную, имеющую максимально отрицательный
(положительный) коэффициент в
– строке коэффициент
<0(>0), то текущая точка не является оптимальной и необходимо изменить
базис. Для этого выбирают небазисную переменную, имеющую максимально отрицательный
(положительный) коэффициент в ![]() – строке. Выбранная небазисная
переменная будет включаться в новый базис, поэтому называется включаемой
переменной. Базисная переменная, которая будет выведена из базиса, называется
исключаемой переменной.
– строке. Выбранная небазисная
переменная будет включаться в новый базис, поэтому называется включаемой
переменной. Базисная переменная, которая будет выведена из базиса, называется
исключаемой переменной.
Исключаемой переменой будет та базисная переменная, которая первой обратится в "0" при переходе в смежную вершину после ввода включаемой переменной.
Столбец включаемой переменной будем называть разрешающим столцом.
Строку исключаемой переменной будем называть разрешающей строкой.
Пересечение разрешающего столбца и строки определяют разрешающий элемент (РЭ).
Чтобы определить исключаемую переменную необходимо:
разделить правые части всех базисных переменных (кроме ![]() - строки) на
соответствующие положительные коэффициенты разрешающего столбца;
- строки) на
соответствующие положительные коэффициенты разрешающего столбца;
выбрать из полученных отношений наименьшее.
Делить на "0" и отрицательную величину нельзя, т. к. это приводит к отсутствию пересекающейся вершины или к вершине вне ОДР.
Для перехода в смежную вершину необходимо сформировать матрицу перехода B(0), которая определит связь между СТ(0) и СТ(1): СТ(1) = В(0) СТ(0).
Для произвольной квадратной матрице размерности n, имеющей в качестве (n - 1) столбца единичные орты, расположенные в соответствии с единичными ортами единичной матрицы, и одного произвольного столбца с ненулевым элементом на главной диагонали, обратная матрица находится по следующему правилу:

Каждый элемент j – столбца делится на РЭ и меняет знак на противоположный, кроме разрешающего элемента.
Искусственный начальный базис. М – метод.
Если исходное ограничение записано в виде равенства
"=" или имеет знак "![]() ", то нельзя сразу получить
допустимое начальное базисное решение, т. к. при записи задачи в стандартной
форме, после введения дополнительных переменных может получиться вариант, когда
полученные уравнения не позволяют сформировать начальный допустимый базис в
виде единичных орт.
", то нельзя сразу получить
допустимое начальное базисное решение, т. к. при записи задачи в стандартной
форме, после введения дополнительных переменных может получиться вариант, когда
полученные уравнения не позволяют сформировать начальный допустимый базис в
виде единичных орт.
В этом случае для нахождения начального допустимого базиса
вводятся дополнительно искусственные переменные ![]() . Искусственные переменные не
имеют отношения к содержанию поставленной задачи, их введение допустимо только
в том случае, если соответствующая схема вычислений будет обеспечивать
получение оптимального решения, в котором все искусственные переменные окажутся
равными нулю.
. Искусственные переменные не
имеют отношения к содержанию поставленной задачи, их введение допустимо только
в том случае, если соответствующая схема вычислений будет обеспечивать
получение оптимального решения, в котором все искусственные переменные окажутся
равными нулю.
Переменные R определяют начальный допустимый базис с точки зрения возможного дальнейшего перехода в одну из вершин ОДР. За использование искусственных переменных в целевой функции вводится штраф М. В задаче максимизации М отрицательное (М<<0), в задаче минимизации М положительное (М>>0).
![]()
![]()
Свойство М: При сложении (вычитании) с любой конечной
величиной ![]() ,
определяющей любое значение, которое может принимать каждая из переменных
исходной ЗЛП, её значение (переменной М) не меняется, а именно,
,
определяющей любое значение, которое может принимать каждая из переменных
исходной ЗЛП, её значение (переменной М) не меняется, а именно,
![]()
![]()
При составлении начальной симплекс-таблицы все переменные начального допустимого базиса (дополнительные и искусственные) должны располагаться в последних m столбцах перед правой частью.
Алгоритм получения оптимального решения:
1. Переход от неравенств к равенствам с учётом правил перехода - введение остаточных, избыточных, искусственных переменных и коэффициентов штрафа;
2. Определение числа базисных и небазисных переменных;
3. Получение ![]() - строки для заполнения СТ(0. Для
этого необходимо целевую функцию преобразовать к виду
- строки для заполнения СТ(0. Для
этого необходимо целевую функцию преобразовать к виду  ; для чего из соответствующих
равенств ограничений выразить искусственные переменные
; для чего из соответствующих
равенств ограничений выразить искусственные переменные ![]() и подставить в
и подставить в ![]() строку и привести к
рациональному виду;
строку и привести к
рациональному виду;
4. Заполнение СТ(0). Перенесение коэффициентов ![]() - строки и
равенств ограничений в соответствующие строки и столбцы симплекс-таблицы;
- строки и
равенств ограничений в соответствующие строки и столбцы симплекс-таблицы;
5. Исследование ![]() функции на условие оптимальности:
функции на условие оптимальности:
определение разрешающего столбца (по знаку и величине
коэффициентов небазисных переменных ![]() - строки);
- строки);
определение включаемой переменной из небазисных переменных;
6. Определение разрешающей строки по условию допустимости:
определение минимального отношения при делении правых частей ограничений на положительные коэффициенты разрешающего столбца;
определение исключаемой переменной из начального базиса;
7. Определение разрешающего элемента РЭ;
8. Получение B (0). Замена в матрице начального базиса коэффициентов исключаемой переменной на коэффициенты включаемой переменной; вычисление B (0) по соответствующему правилу;
9. Определение элементов СТ(1) = В(0) СТ(0);
10. Исследование ![]() -строки СТ(1) на условие
оптимальности.
-строки СТ(1) на условие
оптимальности.
Если условие не выполнено, то вычисления продолжаются и необходимо повторить пункты 5-10.
Если условие оптимальности выполнено, то решение ЗЛП симплекс-методом закончено, необходимо выделить оптимальные значения переменных и оптимальное значение целевой функции.
Решение задачи линейного программирования симплекс-методом.
Двойственная задача.
Двойственная задача (ДЗ) – это вспомогательная задача
линейного программирования, формулируемая с помощью определённых правил
непосредственно из условий прямой задачи. Заинтересованность в определении
оптимального решения прямой задачи путём решения двойственной к ней задачи
обусловлена тем, что вычисления при решении ДЗ могут оказаться менее сложными,
чем при ПЗ. Трудоёмкость вычислений при решении ЗЛП в большей степени зависит
от числа ограничений, а не от количества переменных. Для перехода к ДЗ
необходимо, чтобы прямая задача была записана в стандартной канонической форме.
При представлении ПЗ в стандартной форме в состав переменных ![]() включаются
также избыточные и остаточные переменные.
включаются
также избыточные и остаточные переменные.
Двойственная задача имеет:
m переменных, соответствующих числу ограничений прямой задачи;
n ограничений, соответствующих числу переменных прямой задачи.
Двойственная задача получается путём симметричного структурного преобразования условий прямой задачи по следующим правилам:
Каждому ограничению ![]() ПЗ соответствует переменная
ПЗ соответствует переменная ![]() ДЗ;
ДЗ;
Каждой переменной ![]() ПЗ соответствует ограничение
ПЗ соответствует ограничение ![]() ДЗ;
ДЗ;
Коэффициенты при ![]() в ограничениях ПЗ становятся
коэффициентами левой части соответствующего ограничения ДЗ;
в ограничениях ПЗ становятся
коэффициентами левой части соответствующего ограничения ДЗ;
Коэффициенты ![]() при
при ![]() в целевой функции ПЗ становятся
постоянными правой части ограничения ДЗ;
в целевой функции ПЗ становятся
постоянными правой части ограничения ДЗ;
Постоянные ограничений ![]() ПЗ становятся коэффициентами
целевой функции ДЗ.
ПЗ становятся коэффициентами
целевой функции ДЗ.
Рассмотрим правила составления двойственной задачи:
Прямая задачаДвойственная задача
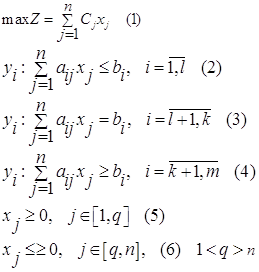
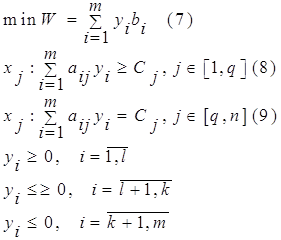
Остановимся более подробно на определении областей допустимых решений двойственных переменных при переходе от прямой задачи к двойственной.
Области допустимых решений для двойственных переменных
Вид ограничений прямой задачи, а также дополнительные и искусственные переменные, образующие начальный допустимый базис, определяют ОДР для соответствующих двойственных переменных.
1. Рассмотрим ограничение (2) прямой задачи:
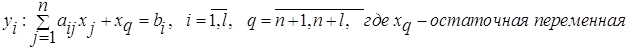 Область допустимых решений ДП (
Область допустимых решений ДП (![]() ) определяется
знаками ограничений (8) и (9) двойственной задачи и знаком ограничения (2)
прямой задачи. Для определения ОДР
) определяется
знаками ограничений (8) и (9) двойственной задачи и знаком ограничения (2)
прямой задачи. Для определения ОДР ![]() найдём ограничения ДЗ,
соответствующие остаточным переменным ПЗ. Коэффициенты целевой функции для
остаточных переменных равны нулю (
найдём ограничения ДЗ,
соответствующие остаточным переменным ПЗ. Коэффициенты целевой функции для
остаточных переменных равны нулю (![]() ).Т. о., при решении задачи максимизации
ограничениям прямой задачи, имеющим знак ограничения
).Т. о., при решении задачи максимизации
ограничениям прямой задачи, имеющим знак ограничения ![]() , соответствуют неотрицательные
двойственные переменные:
, соответствуют неотрицательные
двойственные переменные: ![]() .
.
2. Рассмотрим ограничение (3) прямой задачи:
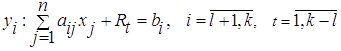 .
.
При введении искусственных переменных в целевую функцию вводятся коэффициенты штрафа М, поэтому для задачи максимизации получим:
![]() .
.
Т. о., при решении задачи максимизации ограничениям прямой
задачи, имеющим знак равенства, соответствуют двойственные переменные, не
ограниченные в знаке ![]() .
.
3. Рассмотрим ограничение (4) прямой задачи:
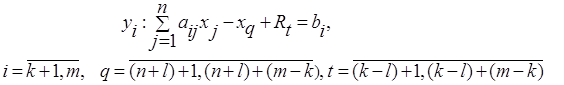
В целевой функции избыточные переменные имеют коэффициенты,
равные нулю (![]() ), а искусственные переменные
коэффициенты, равные величине штрафа со своим знаком, в результате для задачи
максимизации получим:
), а искусственные переменные
коэффициенты, равные величине штрафа со своим знаком, в результате для задачи
максимизации получим:
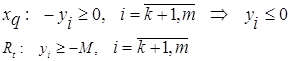
Т. о., при решении задачи максимизации ограничениям прямой
задачи, имеющим знак ![]() , соответствуют неположительные
двойственные переменные
, соответствуют неположительные
двойственные переменные ![]() .
.
4. Если в прямой задаче есть переменная, неограниченная в знаке, то в двойственной задаче получатся два ограничения, имеющие одинаковые коэффициенты при двойственных переменных, но разные знаки ограничений. Для удобства решения эти ограничения сворачивают в одно со знаком равенства (тем самым число ограничений двойственной задачи сводится к числу исходных переменных прямой задачи).
По аналогии можно записать условия двойственной задачи при решении задачи минимизации. Для удобства пользования некоторые соотношения при переходе от прямой задаче к двойственной приведены в таблице.
| Прямая задача | Двойственная задача | |||
| Целевая функция | Ограничения | Целевая функция | Ограничения | Переменные |
| Максимизация |
|
Минимизация |
|
|
| = |
|
|||
|
|
|
|||
| Минимизация |
|
Максимизация |
|
|
| = |
|
|||
|
|
|
|||
В двойственной задаче переменные могут быть неотрицательными
(![]() ), не ограниченными
в знаке (
), не ограниченными
в знаке (![]() ),
неположительными (
),
неположительными (![]() ). При решении ДЗ, как и ПЗ должны
выполняться условия неотрицательности ограничений и переменных. Для представления
двойственной задачи в стандартной форме используются следующие подстановки:
). При решении ДЗ, как и ПЗ должны
выполняться условия неотрицательности ограничений и переменных. Для представления
двойственной задачи в стандартной форме используются следующие подстановки:
если переменная ![]() не ограничена в знаке, то
не ограничена в знаке, то ![]() ;
;
если ![]() , то
, то ![]() .
.
Такие подстановки следует использовать во всех ограничениях, содержащих эти переменные, а также в выражении для целевой функции.
После приведения ДЗ к стандартному виду используется симплекс - метод. Алгоритм получения решения тот же, что и для прямой задачи.
II. Практическая часть
1. Решение задачи линейного программирования графическим методом.
Дана следующая задача линейного программирования (ЗЛП).
![]()
![]()
![]()
![]()
![]() ,
, ![]()
1.1. Все ограничения задачи ![]() .
.
1.2. Переменная ![]() ограниченна в знаке, поэтому
ограниченна в знаке, поэтому ![]() . Переменная
. Переменная ![]() не ограничена
в знаке, поэтому вводим замену
не ограничена
в знаке, поэтому вводим замену ![]() , где
, где ![]() .
.
Область допустимых решений будет ограничиваться I и IV квадрантом.
1.3. Построение ограничений и градиента целевой функции ![]() :
:
1.4. Область допустимых решений – отрезок AB.
1.5. Точка А – оптимальная. Координаты т. А:

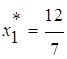 ;
; 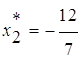 ;
; 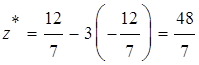 .
.
2. Решение задачи линейного программирования симплекс-методом.
Прямая задача.
Задачу линейного программирования для любой вершины в
компактной форме можно представить в виде: ![]()
![]()
![]()
Для получения используем алгоритм, приведённый в теоретической части.
1. Переход от неравенств к равенствам по правилам введения
дополнительных переменных. Исходную задачу необходимо привести к стандартной
форме: введем замену по переменной ![]() ,
,![]() и дополнительные переменные:
и дополнительные переменные: ![]()
![]()
![]()
![]()
![]() ,
, ![]()
Полученный вид ЗЛП не позволяет сформировать начальный
допустимый базис, т. к. нельзя выделить единичные орты во втором и третьем
равенствах. Для получения начального допустимого базиса введём искусственные
переменные. В результате получим: ![]()
![]()
![]()
![]()
![]() ,
, ![]()
2. Общее число переменных определим по формуле: ![]() =3+2+2=7, где
=3+2+2=7, где ![]() - число
искусственных переменных. Число базисных переменных определяется числом
ограничений, т. к.
- число
искусственных переменных. Число базисных переменных определяется числом
ограничений, т. к. ![]() , то система имеет три базисные
переменные
, то система имеет три базисные
переменные ![]() и
и
![]() небазисные
переменные
небазисные
переменные ![]() .
.
3. Получение![]() - строки для СТ (0). Приведём
целевую функцию к виду
- строки для СТ (0). Приведём
целевую функцию к виду
![]() .
.
Получим из (2): ![]() , из (3):
, из (3): ![]()
![]()
4. Формирование симплекс – таблицы на первом шаге:
![]()
![]() Начальный
базис
Начальный
базис
![]() СТ
(0) РС
СТ
(0) РС
|
|
|
|
|
|
|
|
|
ПЧ | |
|
|
1 | -1-4M | 3+3M | -3M-3 | M | 0 | 0 | 0 | -12M |
|
|
0 | 1 | 2 | -2 | 0 | 1 | 0 | 0 | 4 |
|
|
0 | 3 | -4 | 4 | 0 | 0 | 1 | 0 | 12 |
|
|
0 | 1 | 1 | -1 | -1 | 0 | 0 | 1 | 0 |
5. Определение разрешающего столбца.
При решении задачи максимизации выбираем в ![]() - строке максимально
отрицательный коэффициент:
- строке максимально
отрицательный коэффициент: ![]() - включаемая переменная.
- включаемая переменная.
6. Определение разрешающей строки: ![]() – исключаемая переменная.
– исключаемая переменная.
7. Разрешающий элемент РЭ = 1.
8. Получение матрицы перехода
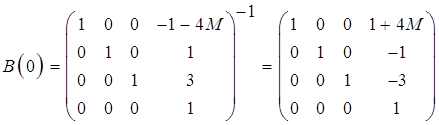 , где В(0) - матрица
перехода
, где В(0) - матрица
перехода
9. Определение элементов таблицы СТ(1) = В(0) СТ(0);
10. Исследование z-строки СТ(1) на условие оптимальности:
![]() СТ(1)
СТ(1)
| z |
|
|
|
|
|
|
|
ПЧ | |
| z | 1 | 0 | 4+7M | -7M-4 | -3M-1 | 0 | 0 | 1+4M | -12M |
|
|
0 | 0 | 1 | -1 | 1 | 1 | 0 | -1 | 4 |
|
|
0 | 0 | -7 | 7 | 3 | 0 | 1 | -3 | 12 |
|
|
0 | 1 | 1 | -1 | -1 | 0 | 0 | 1 | 0 |
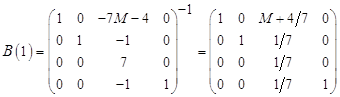
СТ(2)
| z |
|
|
|
|
|
|
|
ПЧ | |
| z | 1 | 0 | 0 | 0 | 5/7 | 0 | M+4/7 | M-5/7 | 48/7 |
|
|
0 | 0 | 0 | 0 | 10/7 | 1 | 1/7 | -10/7 | 40/7 |
|
|
0 | 0 | -1 | 1 | 3/7 | 0 | 1/7 | -3/7 | 12/7 |
|
|
0 | 1 | 0 | 0 | -4/7 | 0 | 1/7 | 4/7 | 12/7 |
![]()
![]()
СТ(2) – оптимальная, т. к. коэффициенты при НБП![]() .
.
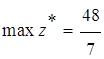 ,
, 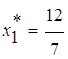 ,
, 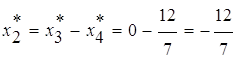 .
.
3. Решение задачи линейного программирования симплекс-методом.
Двойственная задача.
Составим двойственную задачу по условиям прямой задачи и определим области допустимых решений ДП:
Прямая задачаДвойственная задача
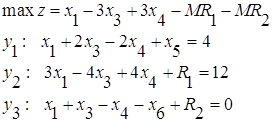
![]()
![]()
![]()
![]() (1)
(1)
![]() (2)
(2)
![]()
![]()
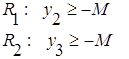
Итак, получено: ![]() ,
, ![]() ,
, ![]() .
.
2. Приведём запись двойственной задачи к канонической форме.
На основании полученных ОДР двойственных переменных введём необходимые
подстановки: ![]() .
.
Для удобства решения свернём ограничения (1) и (2) в одно со знаком равенства, а также введем в ограничения и целевую функцию избыточные, остаточные и искусственные переменные.
![]()
![]() (3)
(3)
![]() (4)
(4)
3. Решим ДЗ симплекс методом:
Из (3): выразим![]()
Из (4) выразим: ![]()
![]()
![]() СТ(0)
СТ(0)
| W |
|
|
|
|
|
|
|
ПЧ | |
| W | 1 | -4-M | 7M-12 | 12-7M | 0 | -M | 0 | 0 | 4M |
|
|
0 | 1 | 3 | -3 | -1 | -1 | 1 | 0 | 1 |
|
|
0 | -2 | 4 | -4 | 1 | 0 | 0 | 1 | 3 |
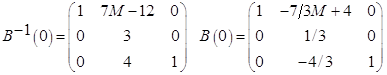
СТ(1)
| W |
|
|
|
|
|
|
|
ПЧ | |
| W | 1 | -10/3M | 0 | 0 | 7/3M-4 | 4/3M-4 | -7/3M+4 | 0 | 5/3M+4 |
|
|
0 | 1/3 | 1 | -1 | -1/3 | -1/3 | 1/3 | 0 | 1/3 |
|
|
0 | -10/3 | 0 | 0 | 7/3 | 4/3 | -4/3 | 1 | 5/3 |
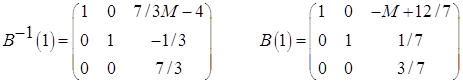
СТ(2)
| W |
|
|
|
|
|
|
|
ПЧ | |
| W | 1 | -40/7 | 0 | 0 | 0 | -12/7 | -7/3M+4 | -M+12/7 | 48/7 |
|
|
0 | -1/7 | 1 | -1 | 0 | -1/7 | 1/3 | 1/7 | 4/7 |
|
|
0 | -10/7 | 0 | 0 | 1 | 4/7 | -4/3 | -3/7 | 5/7 |
СТ(2) – оптимальная, т. к. коэффициенты при ![]()
![]() ,
, ![]() ,
,
![]()
Задание:
1. Изучить методы решения задачи линейного программирования (графический и симплекс-метод):
2. Для заданного варианта получить решение задачи линейного программирования:
- графическим методом;
- симплекс методом для прямой задачи;
- симплекс методом для двойственной задачи.
© 2010 Интернет База Рефератов