
Рефераты по сексологии
Рефераты по информатике программированию
Рефераты по биологии
Рефераты по экономике
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Рефераты по авиации и космонавтике
Рефераты по административному праву
Рефераты по безопасности жизнедеятельности
Рефераты по арбитражному процессу
Рефераты по архитектуре
Рефераты по астрономии
Рефераты по банковскому делу
Рефераты по биржевому делу
Рефераты по ботанике и сельскому хозяйству
Рефераты по бухгалтерскому учету и аудиту
Рефераты по валютным отношениям
Рефераты по ветеринарии
Рефераты для военной кафедры
Рефераты по географии
Рефераты по геодезии
Рефераты по геологии
Рефераты по геополитике
Рефераты по государству и праву
Рефераты по гражданскому праву и процессу
Рефераты по делопроизводству
Рефераты по кредитованию
Рефераты по естествознанию
Рефераты по истории техники
Рефераты по журналистике
Рефераты по зоологии
Рефераты по инвестициям
Рефераты по информатике
Исторические личности
Рефераты по кибернетике
Рефераты по коммуникации и связи
Учебное пособие: Решение дифференциальных уравнений в среде MathCAD
Учебное пособие: Решение дифференциальных уравнений в среде MathCAD
Лекция №1. Система Mathcad
Назначение и состав системы. Входной язык и язык реализации системы. Основные объекты входного языка системы Mathcad
В последнее время широкое распространение получили пакеты математических программ (или математические системы), которые можно использовать для различных вычислений и вычерчивания графиков (Mathematica, Derive, Statistica, MathCAD, MathLAB и др.). В этих системах процесс вычислений сильно автоматизирован, что позволяет экономить время и больше внимания уделять физическому смыслу получаемого результата. Выбор системы зависит от характера решаемых задач, от вкуса, от практики.
Система MathCAD -разработка фирмы MathSoft. Примерно каждый год появляется новая версия этой системы. В настоящий момент известна версия Mathcad 12.
Назначение системы: MathCAD - это интегрированная система программирования, ориентированная на проведение математических и инженерно-технических расчетов. MathCAD содержит текстовый редактор, вычислитель, символьный процессор и графический процессор.
Вид окна системы MathCAD аналогичен окнам приложений ОС семейства Windows (Word, Exel и др.).
1. Интерфейс пользователя в системе MathCAD. Интерфейс пользователя состоит из:
1. строки заголовка
2. строки главного меню
3. из строки состояния
которая включается командой View/Status Bar, и на которой отображается следующая информация (слева направо): контекстно-зависимая подсказка о готовящемся действии, режим вычислений (AUTO (автоматический) или Calc 9 (ручной)), режим Gaps Lock (CAP), режим Num Lock (NUM,), номер страницы, на которой находится курсор (Page 1);
4. из панелей Standard, Formatting, Math, Controls, Recources:
На каждой из панелей имеется характерная вешка перемещения в виде выпуклой вертикальной черты в начале каждой панели. С помощью нее можно переносить панели в любое место окна редактирования или "прилепить" ее к любой стороне окна.
Настройка состава панелей инструментов. Установить курсор над нужной панелью и правой кнопкой вызвать контекстное меню, из которого выбрать пункт Customize (Настроить), появится диалоговое окно. В левой панели этого окна расположены еще не добавленные пиктограммы, в правой – добавленные. По команде Add пиктограмма переходит в правое окно, а по команде Remove пиктограмма возвращается в левую панель.
Пиктограммы панели ![]() дублируют основные команды главного меню. На панели
дублируют основные команды главного меню. На панели ![]() собраны
команды, предназначенные для форматирования текста, такие как изменение стиля и
шрифта текста, выравнивание, создание списков.
собраны
команды, предназначенные для форматирования текста, такие как изменение стиля и
шрифта текста, выравнивание, создание списков.
Панель ![]() служит для вставки в
документ стандартных элементов управления интерфейса пользователя (флажков,
переключателей, полей ввода и т.п.).
служит для вставки в
документ стандартных элементов управления интерфейса пользователя (флажков,
переключателей, полей ввода и т.п.).
Панель ![]() служит для вызова
ресурсов MathCAD (примеров, учебников, но только на
английском языке).
служит для вызова
ресурсов MathCAD (примеров, учебников, но только на
английском языке).
Наибольший интерес для
нас в системе MathCAD представляет математическая панель
![]() . Она
содержит перемещаемые палитры математических знаков, которые служат для ввода
практически всех известных математических символов и шаблонов операторов и
функций
. Она
содержит перемещаемые палитры математических знаков, которые служат для ввода
практически всех известных математических символов и шаблонов операторов и
функций
1. ![]()
![]() – служит для ввода арифметических
операций и часто используемых простых функций. Эта палитра фактически дублирует
обычный калькулятор.
– служит для ввода арифметических
операций и часто используемых простых функций. Эта палитра фактически дублирует
обычный калькулятор.
2 ![]()
![]() – содержит команды для построения
семи типов графиков.
– содержит команды для построения
семи типов графиков.
3. ![]()
![]() - для создания векторов и матриц
и некоторые операции для работы с ними.
- для создания векторов и матриц
и некоторые операции для работы с ними.
4. ![]()
![]() - для вставки операторов
управления вычислениями и для ыставки пользовательских операторов..
- для вставки операторов
управления вычислениями и для ыставки пользовательских операторов..
5. ![]()
![]() - эта палитра содержит операции
высшей математики (производные, интегралы, пределы и др.),а также знак бесконечности
- эта палитра содержит операции
высшей математики (производные, интегралы, пределы и др.),а также знак бесконечности
![]() .
.
6. ![]()
![]() - для вставки операций сравнения
и логических операций Not
- для вставки операций сравнения
и логических операций Not![]() , And
, And![]() , Or
, Or![]()
7. ![]()
![]() - инструменты программирования
системы MathCAD.
- инструменты программирования
системы MathCAD.
8. ![]()
![]() - палитра для набора греческих
символов.
- палитра для набора греческих
символов.
9. ![]()
![]() - содержит ключевые слова,
управляющие символьными вычислениями.
- содержит ключевые слова,
управляющие символьными вычислениями.
10 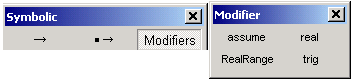 эта панель вместе с
панелью
эта панель вместе с
панелью ![]() содержит
ключевые слова, используемые при символьных вычислениях. Здесь расположены
команды, задающие тип символьной переменной.
содержит
ключевые слова, используемые при символьных вычислениях. Здесь расположены
команды, задающие тип символьной переменной.
2. Документ в
системе MathCAD.
Состоит из блоков, т.е. отдельных частей. В документе блоки имеют точку
привязки, расположенную слева ![]()
Блоки м.б. трех типов - текстовые, вычислительные, графические. Текстовые блоки играют роль неисполняемых комментариев. Они служат лишь для повышения наглядности документа. Вычислительные блоки состоят из исполняемых математических выражений, например, формул, уравнений, равенств неравенств и т.д. Графические блоки также являются исполняемыми.
Блоки можно перемещать по документу и располагать в удобной для пользователя форме, но для правильного функционирования системы имеет большое значение правильный порядок расположения блоков. Например, если в некотором блоке содержатся операции, требующие данных из другого блока, то этот другой блок обязательно должен выполняться первым и располагаться перед использующим его блоком. Иная ситуация приведет к появлению ошибки. Сигнал ошибки имеет вид надписи, от которой отходит черта, указывающая место ошибки:
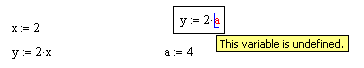 .
.
При манипуляциях с блоками на экране могут оставаться нежелательные искажения. Для их устранения следует использовать команду Refresch (обновить) меню View.
В документе MathCad эффективно решена проблема сквозной передачи данных от одного блока к другому, например, от одного математического выражения к другому, от него к таблицам, от таблиц к графикам и т.д. Поэтому изменение в любой формуле или в задании входных данных тут же ведет к пересчету задачи по всей цепи взаимодействия блоков (это не относится, однако к символьным операциям, реализуемым с помощью команд меню).
Размеры блоков
устанавливаются автоматически в зависимости от числа входящих в них знаков, либо от заданных
размеров графиков. Обычно границы блоков не видны, но можно установить подсвеченный
режим показа блоков (команда View Regions)![]() Блоки не должны налагаться друг
на друга
Блоки не должны налагаться друг
на друга ![]() .
Если такое произошло, то надо воспользоваться командой разделения
перекрывающихся областей в документе (Formatt/Separate Regions), предварительно выделив эти
перекрывающиеся области.
.
Если такое произошло, то надо воспользоваться командой разделения
перекрывающихся областей в документе (Formatt/Separate Regions), предварительно выделив эти
перекрывающиеся области.
Сразу после запуска
система готова к созданию документа с необходимыми пользователю вычислениями.
Соответствующее новому документу окно редактирования получает название Untitled: N , где N – порядковый номер документа. ![]() При сохранении на диск документ
системы MathCad записывается в файл с расширением
.mcd.
При сохранении на диск документ
системы MathCad записывается в файл с расширением
.mcd.
Окно редактирования
содержит (даже когда очищено) два важных объекта – курсор ввода в виде красного крестика и вертикальную линию, отделяющую
текущую страницу от соседней (справа) ![]() . Если документ большой, то в
некотором месте будет наблюдаться и прерывистая горизонтальная линия раздела
страниц
. Если документ большой, то в
некотором месте будет наблюдаться и прерывистая горизонтальная линия раздела
страниц ![]() .
Эти линии раздела показывают, каким образом будет осуществляться разбиение на
страницы при распечатке документа на принтере. Изменить параметры страницы
можно с помощью команды File/Page Setup. В
окне редактирования документа можно включить линейку с помощью команды View/Ruler
.
Эти линии раздела показывают, каким образом будет осуществляться разбиение на
страницы при распечатке документа на принтере. Изменить параметры страницы
можно с помощью команды File/Page Setup. В
окне редактирования документа можно включить линейку с помощью команды View/Ruler ![]() . Масштаб документа можно
изменить по команде View/Zoom.
. Масштаб документа можно
изменить по команде View/Zoom.
3. Основные объекты входного языка системы MathCAD.
Фактически документы MathCad представляют собой программу, написанную на визуально-ориентированном языке программирования. Визуально- ориентированные языки программирования задают программу не в виде малопонятных кодов, а в виде визуально понятных объектов. Язык программирования MathCad ориентирован на математические вычисления и потому практически не отличается от обычного языка математических статей, отчетов и книг.
Входной язык MathCad относится к интерпретируемому типу. Это значит, что, когда система опознает какой-либо объект, она немедленно исполняет указанные в блоке операции.
Визуально-ориентированный язык общения системы MathCad надо отличать от языка реализации системы, т.е. обычного языка программирования высокого уровня, на котором написана система. Языком реализации системы MathCad является один из самых мощных языков высокого уровня – С++.
По существу входной язык системы – промежуточное звено между скрытым от пользователя языком документа и языком реализации системы. По мере того как пользователь создает (средствами текстового, формульного, символьного и графического редакторов) в окне редактирования объекты (тексты, формулы, таблицы и графики), система сама составляет программу на некотором промежуточном языке связи. Эта программа хранится в оперативной памяти до тех пор, пока не будет записана на диск в виде файла с расширением .mcd. Однако от пользователя не требуется знание языков программирования (реализации и связи), достаточно освоить приближенный к естественному математическому языку входной язык системы.
К основным объектам входного языка системы MathCAD можно отнести: алфавит, константы, переменные, операторы, функции.
Алфавит – строчные и прописные латинские буквы, цифры от 0 до 9, греческие буквы. Следует отметить, что MathCAD различает строчные и прописные буквы (X и x – разные переменные) и различает шрифт (X и X – тоже разные переменные). Также в алфавит входят символ бесконечности ¥, штрих ¢(набирается с помощью клавиш ctrl/F7), символ подчеркивания _, символ процента, нижний индекс (набирается с помощью клавиши «.», индекс в определении имени переменных и функций, например К2 , не надо путать с числовым индексом векторной переменной). Имя переменной или функции в системе MathCAD может быть любой длины, но:
- имена не должны начинаться с цифры, символа подчеркивания, штриха или процента;
- символ бесконечности может быть только первым в имени;
- все буквы в имени должны иметь один стиль и шрифт;
- имена не могут совпадать с именами встроенных функций, констант и размерностей, например, sin или TOL. Тем не менее, допускается их переопределение, но тогда одноименная встроенная функция не будет использоваться по первоначальному назначению;
- MathCAD не различает имен переменных и функций: если сначала определить функцию f(x), а потом переменную f, то в оставшейся части документа будет утерян доступ к функции f(x);
-
в некоторых
случаях желательно использовать имена переменных и функций, содержащие символы
операторов MathCAD или другие символы, которые нельзя
вставлять в имена непосредственно, для этого надо набрать комбинацию клавиш Ctrl/Shift/J,
которая позволит вставить пару квадратных скобок с местозаполнителем внутри ![]() . Имя, составленное из любых
символов и заключенное в эти квадратные скобки, MathCAD будет воспринимать корректно
. Имя, составленное из любых
символов и заключенное в эти квадратные скобки, MathCAD будет воспринимать корректно ![]() .
.
Константы – это числа и предварительно определенные системные константы:
![]()
![]()
![]() .
.
Эти значения системных констант устанавливаются после загрузки системы.
![]() - погрешность для
условий ограничения при решении оптимизационных задач с применением функций Find, Minerr, Maximize, Minimize;
- погрешность для
условий ограничения при решении оптимизационных задач с применением функций Find, Minerr, Maximize, Minimize;
![]() - ширина столбца,
используемая при записи файлов функцией WRITEPRN;
- ширина столбца,
используемая при записи файлов функцией WRITEPRN;
![]() - число значащих цифр
при записи файлов функцией WRITEPRN.
- число значащих цифр
при записи файлов функцией WRITEPRN.
Формат вывода системных
констант ![]() можно
изменить. Для этого достаточно дважды щелкнуть по числу в блоке вывода
результата, при этом появится диалоговое окно, в котором надо будет установить
число знаков после запятой. Таким же образом можно изменить формат вывода любых
других результатов вычислений. По умолчанию формат вывода имеет три
знака после запятой.
можно
изменить. Для этого достаточно дважды щелкнуть по числу в блоке вывода
результата, при этом появится диалоговое окно, в котором надо будет установить
число знаков после запятой. Таким же образом можно изменить формат вывода любых
других результатов вычислений. По умолчанию формат вывода имеет три
знака после запятой.
Значения некоторых
системных констант можно изменить с помощью команды ![]() /
/![]() в диалоговом окне, либо эти
значения можно переопределить через оператор присваивания
в диалоговом окне, либо эти
значения можно переопределить через оператор присваивания ![]() .
.
Переменные – это объект, числовое значение которого может
меняться по ходу выполнения документа. Для присваивания переменной числа
или результата выражения используется знак локального присваивания ![]() , который можно
набрать с клавиатуры (клавиша «двоеточие» на латинском шрифте), с палитры
, который можно
набрать с клавиатуры (клавиша «двоеточие» на латинском шрифте), с палитры ![]()
![]() и с палитры
и с палитры ![]()
![]() . Знак присваивания
. Знак присваивания ![]() в системе MathCAD означает, что действие происходит
справа налево (а не слева направо). Если при оформлении документа необходимо,
чтобы присваивание выглядело на экране как знак равенства без двоеточия, то
правой кнопкой надо вызвать контекстное меню и в диалоговом окне вместо пункта
Default” выбрать пункт “Equal”.
в системе MathCAD означает, что действие происходит
справа налево (а не слева направо). Если при оформлении документа необходимо,
чтобы присваивание выглядело на экране как знак равенства без двоеточия, то
правой кнопкой надо вызвать контекстное меню и в диалоговом окне вместо пункта
Default” выбрать пункт “Equal”.
Знак обычного
равенства ![]() (который применяется в системе MathCAD в основном для вывода результата) можно
использовать только для первого присваивания.
(который применяется в системе MathCAD в основном для вывода результата) можно
использовать только для первого присваивания.
При локальном
присваивании надо обязательно соблюдать правильное расположение блоков.
Но иногда в документах возникает необходимость использовать значение некоторой
переменной выше на листе, чем расположен оператор присваивания ![]() . В таких случаях вместо
локального присваивания используется знак глобального присваивания
. В таких случаях вместо
локального присваивания используется знак глобального присваивания ![]() , который можно
набрать либо с клавиатуры (клавиша «волнистая черта»), либо с палитры
, который можно
набрать либо с клавиатуры (клавиша «волнистая черта»), либо с палитры ![]()
![]() . Если в документе используется
глобальное присваивание, то MathCAD проводит вычисления в следующей последовательности: вычисляются
сверху вниз все блоки с оператором глобального присваивания, а затем снова с
самого начала документа вычисляются сверху вниз все оставшиеся блоки. Это
означает, что в блоках с оператором глобального присваивания нельзя использовать
результат вычислений из обычного блока.
. Если в документе используется
глобальное присваивание, то MathCAD проводит вычисления в следующей последовательности: вычисляются
сверху вниз все блоки с оператором глобального присваивания, а затем снова с
самого начала документа вычисляются сверху вниз все оставшиеся блоки. Это
означает, что в блоках с оператором глобального присваивания нельзя использовать
результат вычислений из обычного блока.
В отличие от языков
программирования система MathCAD не требует точного задания типов переменных: целочисленные,
вещественные, комплексные, текстовые, логические. Тип переменной автоматически
определяется присвоенным ей значением: 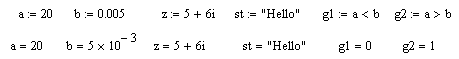 . В нижней строке показан
результат вывода соответствующей переменной. Целые переменные пояснений
не требуют.
. В нижней строке показан
результат вывода соответствующей переменной. Целые переменные пояснений
не требуют.
Вещественная переменная может быть набрана и
как десятичное число с любым количеством десятичных цифр после точки ![]() , и в
экспоненциальной форме, для чего после ввода числа надо напечатать символ умножения
и ввести 10 в нужной степени
, и в
экспоненциальной форме, для чего после ввода числа надо напечатать символ умножения
и ввести 10 в нужной степени ![]() .
.
При вводе комплексных
переменных мнимая единица набирается с палитры![]()
![]() , либо с клавиатуры как
, либо с клавиатуры как![]() . Если просто
набрать как
. Если просто
набрать как ![]() ,
то она будет восприниматься как простая переменная. Форму представления мнимой
единицы можно изменить
,
то она будет восприниматься как простая переменная. Форму представления мнимой
единицы можно изменить ![]() . Для этого дважды щелкнуть в окне
вывода с мнимой единицей и в диалоговом окне сделать соответствующий выбор
. Для этого дважды щелкнуть в окне
вывода с мнимой единицей и в диалоговом окне сделать соответствующий выбор
Текстовая переменная заключается в кавычки. Значением логической переменной может быть 0 (что соответствует «лжи») или 1 (что соответствует «истине»).
В MathCAD есть и специальный тип переменных, именуемых ранжированными или циклическими переменными, которые задаются следующим образом:
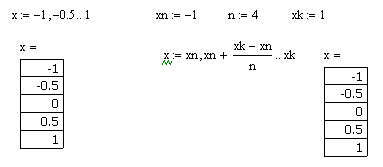
Ранжированная переменная, так же как и массив, хранит целый набор значений, но, в отличие от массивов, невозможно получить доступ к отдельному элементу этой переменной. С помощью ранжированных переменных можно задать значения всех элементов матрицы или вывести график по точкам
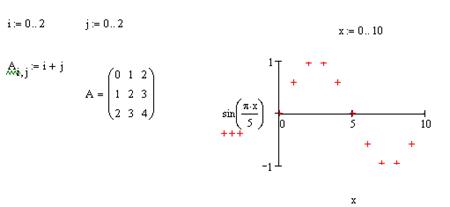 .
.
Верхняя граница ранжированной переменной необязательно должна быть элементом последовательности, это число просто ограничивает последовательность сверху (или снизу для убывающей последовательности).
Массивы. Большим преимуществом системы MathCAD является возможность оперировать
не только скалярными величинами, но и с массивами. MathCAD поддерживает два вида массивов – одномерные
(векторы) и двумерные (матрицы). Элементы массивов характеризуются числовыми
индексами, которые вставляется с помощью клавиши “[”, либо командой ![]() с панели
с панели ![]() . Обычно
нумерация идет с нуля. Нумерация задается значением системной переменной ORIGIN, которая по умолчанию равна нулю. V0- первый элемент вектора, M 0, 0- первый элемент матрицы. Можно
обратиться не только к элементу массива, но и к его колонке, например, M<0>- первая колонка матрицы. Элементами
массива могут быть числа, константы, переменные, математические выражения и
даже другие массивы. Соответственно массивы могут быть численными и
символьными. Основные операции для работы с векторами и матрицами собраны
на панели
. Обычно
нумерация идет с нуля. Нумерация задается значением системной переменной ORIGIN, которая по умолчанию равна нулю. V0- первый элемент вектора, M 0, 0- первый элемент матрицы. Можно
обратиться не только к элементу массива, но и к его колонке, например, M<0>- первая колонка матрицы. Элементами
массива могут быть числа, константы, переменные, математические выражения и
даже другие массивы. Соответственно массивы могут быть численными и
символьными. Основные операции для работы с векторами и матрицами собраны
на панели ![]() .
.
Существует несколько способов создания массивов. Самый простой и наглядный способ создания матрицы с помощью команды Insert/Matrix . При вызове этой команды появляется диалоговое окно, в котором надо задать число строк и число колонок матрицы (вектор - это матрица с одной колонкой). Появится шаблон матрицы, в черные квадратики которого надо ввести значения элементов матрицы.
Добавление в уже созданную матрицу строк или столбцов производится точно так же. Для этого надо выделить элемент матрицы, правее и ниже которого будет осуществлена вставка столбцов и (или) строк
Для того, чтобы удалить строки и столбцы из матрицы, надо установить курсор на элемент матрицы, который находится в самом левом столбце из тех, которые нужно удалить и в самой верхней строке из тех, которые нужно удалить
Также матрицу можно создать через определение его элементов
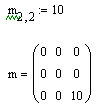
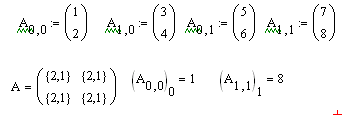
Развернуть вложенные
массивы можно, установив, флажок ![]() (Разворачивать вложенные массивы)
в окне
(Разворачивать вложенные массивы)
в окне
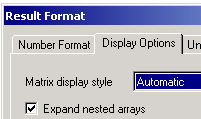
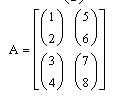
Есть и другие способы создания матриц – создание матрицы с помощью таблицы ввода, создание матрицы путем импорта данных.
Функции. В системе MatCAD различают встроенные функции (функции, заранее введенные разработчиком системы) и пользовательские функции (созданные пользователем).
Встроенные функции. Вставляются с помощью команды Insert/Function ![]() или набором с
или набором с
клавиатуры. При этом следует помнить, что имена встроенных функций чувствительны к регистру, их следует вводить в точности, как они приведены в системе. Параметры встроенных функций заключаются в скобки. В качестве параметра м.б. константа, переменная или математическое выражение, при этом константа, переменная, выражение должны быть определены ранее
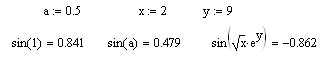
Функции пользователя. В MathCAD, как и в языках программирования, есть возможность задания функций пользователя. Имена функций пользователя подчиняются тем же правилам, что и имена переменных. Для задания функции пользователя нужно ввести имя, а затем в круглых скобках через запятую ввести все аргументы. Для аргументов можно использовать любые имена, подчиняющиеся тем же правилам, что и имена переменных. Далее, как обычно, надо ввести оператор присваивания и после него выражение, зависящее от введенных аргументов. Все переменные, присутствующие справа в выражении определения функции, либо должны входить в список аргументов функции, либо должны быть определены ранее. В противном случае будет выведено сообщение об ошибке, причем имя неопределенной переменной будет выделено красным цветом

Операторы. Каждый оператор в MathCAD обозначает некоторое
математическое действие в виде символа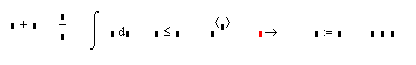 . Каждый оператор действует на
одно или два числа (переменную или функцию), которые называются операндами.
Если в момент вставки оператора одного или обоих операндов не хватает, то
недостающие операнды будут отображены в виде местозаполнителей. Математические
палитры содержат сгруппированные по смыслу математические операторы:
. Каждый оператор действует на
одно или два числа (переменную или функцию), которые называются операндами.
Если в момент вставки оператора одного или обоих операндов не хватает, то
недостающие операнды будут отображены в виде местозаполнителей. Математические
палитры содержат сгруппированные по смыслу математические операторы:
1.
Операторы,
обозначающие арифметические действия, называются арифметическими и вводятся с
палитры ![]() .
.
2.
Операторы,
которые вставляются с палитры ![]() (Вычисления), называются
вычислительными операторами (дифференцирование, интегрирование, суммирование,
вычисление произведения, пределы).
(Вычисления), называются
вычислительными операторами (дифференцирование, интегрирование, суммирование,
вычисление произведения, пределы).
3.
Логические
операторы – вводятся с палитры ![]() .
.
4.
Матричные
операторы – предназначены для совершения различных действий над векторами и
матрицами, вводятся с палитры ![]() .
.
5.
Операторы
выражения – сгруппированы на панели ![]() (Evaluation – Выражения) (оператор численного
вывода
(Evaluation – Выражения) (оператор численного
вывода ![]() ,
оператор локального присваивания
,
оператор локального присваивания ![]() , оператор глобального
присваивания
, оператор глобального
присваивания ![]() , оператор символьного вывода).
, оператор символьного вывода).
6.
Операторы
пользователя. Запросы взыскательного пользователя могут не исчерпываться
набором встроенных операторов MathCAD. Для вставки в документы заранее созданных операторов пользователя
применяется панель![]()
![]()
![]() . Оператор пользователя может
иметь абсолютно любое имя. Присваивать оператору некоторое действие следует
точно так же, как функции пользователя. Создание бинарного оператора выглядит
след. образом:
. Оператор пользователя может
иметь абсолютно любое имя. Присваивать оператору некоторое действие следует
точно так же, как функции пользователя. Создание бинарного оператора выглядит
след. образом:
 .
.
Унарный оператор пользователя создается аналогично

Вывод результатов вычислений и значений переменных осуществляется с помощью
знака обычного
равенства ![]() .
В различных задачах выводить результаты вычислений требуется в различном виде:
как десятичную или простую дробь, десятичную дробь в обычной или экспоненциальной
форме. Формат вывода задается командой Forma/Result. После вызова этой команды (двойной
щелчок на нужном блоке) появляется диалоговое окно Result Format:
.
В различных задачах выводить результаты вычислений требуется в различном виде:
как десятичную или простую дробь, десятичную дробь в обычной или экспоненциальной
форме. Формат вывода задается командой Forma/Result. После вызова этой команды (двойной
щелчок на нужном блоке) появляется диалоговое окно Result Format:
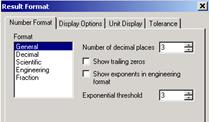
В списке Format слева можно выбрать один из пяти различных форматов отображения числа, а с помощью полей и флажков справа можно настроить выбранный формат.
General – это используемый по умолчанию
формат результатов вычислений. Число представляется в виде десятичной дроби. Количество
знаков после запятой задается в поле ![]() . Если установлен флажок
. Если установлен флажок ![]() , то дробь
будет при необходимости дополнена нулями до количества знаков, указанных выше
, то дробь
будет при необходимости дополнена нулями до количества знаков, указанных выше ![]() . Поле
. Поле ![]() задает
границу перехода ET (Exponential threshold) к экспоненциальной форме (такую
форму числа приобретают, если их значение больше 10ET и меньше 10-ET). При установленном флажке
задает
границу перехода ET (Exponential threshold) к экспоненциальной форме (такую
форму числа приобретают, если их значение больше 10ET и меньше 10-ET). При установленном флажке ![]() в
экспоненциальной форме записи используются только порядки, кратные трем
в
экспоненциальной форме записи используются только порядки, кратные трем ![]() . Это является
стандартной инженерной формой записи, поскольку для физических величин в
системе CИ со степенями, кратными трем,
связаны различные стандартные приставки: кило-, мега-, милли- и др.
. Это является
стандартной инженерной формой записи, поскольку для физических величин в
системе CИ со степенями, кратными трем,
связаны различные стандартные приставки: кило-, мега-, милли- и др.
Decimal – формат вывода результата в виде десятичной дроби без экспоненты.
Scientific – в этом формате результат всегда выводится в экспоненциальной форме.
Engineering – также используется только экспоненциальная форма записи дробей, но при этом используются только порядки, кратные трем.
Fraction – в этом формате результат выводится в виде простой дроби
В диалоговом окне Result Format также можно изменять представление машинного нуля для комплексных чисел CT (Complex threshold) (если Re(Z)/Im(Z) > 10CT, то Z выводится
как реальное, если наоборот, то как мнимое) и значение машинного нуля ZT (Zero threshold)
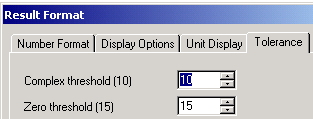 .
.
Формат вывода может быть глобальным и локальным. Чтобы установить локальный формат, можно сделать двойной щелчок по блоку, при этом появится диалоговое окно Result Format. Данный блок будет иметь локальный формат, а все остальные - глобальный.
Управление процессом вычислений. После запуска MathCAD находится в режиме автоматических вычислений. Это означает, что при внесении каких-либо изменений в документ, все видимые в данный момент формульные блоки и графики пересчитываются и строятся заново. В некоторых случаях такой режим работы может быть нежелательным, например, если в документе есть сложные вычисления, требуется обработка больших объемов данных или выполняются операции, занимающие много времени. В таких случаях работать с документом оказывается очень неудобно, и возникает необходимость запретить автоматическое вычисление либо всего документа, либо для блоков, содержащих наиболее сложные вычисления.
Для того чтобы
отключить/включить режим автоматического вычисления для всего документа, надо
выбрать команду меню ![]() /
/![]() /
/![]() . При отключенном режиме
автоматического вычисления, для того чтобы пересчитать все блоки в документе
можно выбрать команду меню
. При отключенном режиме
автоматического вычисления, для того чтобы пересчитать все блоки в документе
можно выбрать команду меню ![]() /
/![]() /
/![]() . Для того чтобы пересчитать не
весь документ, а лишь тот блок, в котором находится курсор, следует выбрать
команду меню
. Для того чтобы пересчитать не
весь документ, а лишь тот блок, в котором находится курсор, следует выбрать
команду меню ![]() /
/![]() /
/![]() (если курсор находится в
свободном месте рабочей области документа, то пересчитаны будут все блоки,
которые в данный момент видны на экране).
(если курсор находится в
свободном месте рабочей области документа, то пересчитаны будут все блоки,
которые в данный момент видны на экране).
Для того чтобы временно
отключить вычисление одного блока, можно воспользоваться командой контекстного
меню ![]() . После выбора этой команды MathCAD при просчете документа вообще не
будет «обращать внимания» на данный блок и производить вычисления так, как
будто его удалили. Для того чтобы возобновить вычисление «отключенного» блока,
нужно выбрать команду контекстного меню
. После выбора этой команды MathCAD при просчете документа вообще не
будет «обращать внимания» на данный блок и производить вычисления так, как
будто его удалили. Для того чтобы возобновить вычисление «отключенного» блока,
нужно выбрать команду контекстного меню ![]() .
.
Прервать вычисление можно клавишей <Esc>. При этом оставшаяся часть формул будет подсвечена красным цветом.
Единицы измерения физических величин. При проведении физико-технических
расчетов почти всегда имеют дело не просто с абстрактными числами, а с
некоторыми физическими величинами. Для того чтобы число в выражении
рассматривалось как некоторая физическая величина, нужно ввести единицы
измерения следующим образом: после введенного числа ввести знак умножения,
выбрать команду ![]() /
/![]() , в диалоговом окне
, в диалоговом окне ![]() в списках
в списках ![]() и
и ![]() выбрать
нужную единицу измерения
выбрать
нужную единицу измерения ![]() . Над размерными переменными можно
производить любые корректные с физической точки зрения расчеты
. Над размерными переменными можно
производить любые корректные с физической точки зрения расчеты ![]() . Нельзя
складывать переменные разной размерности, будет получено сообщение об ошибке
. Нельзя
складывать переменные разной размерности, будет получено сообщение об ошибке 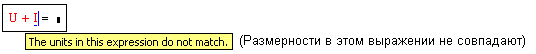 . Но позволяется
складывать, например, амперы с кило амперами
. Но позволяется
складывать, например, амперы с кило амперами ![]() .
.
Для любого результата
вычислений есть возможность изменить его единицы измерения. Если
щелкнуть на формульном блоке, содержащем результаты вычислений, то справа от единиц
измерения результата появится черный квадратик – поле ввода единиц измерения, к
которым необходимо привести результат. Если введенные здесь единицы измерения
не будут соответствовать единицам результата, то MathCAD автоматически допишет нужный коэффициент
![]() . В MathCAD по умолчанию все результаты
вычислений представлены в системе СИ. Однако систему измерений можно изменить с
помощью команды
. В MathCAD по умолчанию все результаты
вычислений представлены в системе СИ. Однако систему измерений можно изменить с
помощью команды ![]() /
/![]() и диалогового окна
и диалогового окна ![]() .
.
4. Текстовый редактор служит для ввода и редактирования текстов. Именно тексты делают документы MathCad документами в общепринятом смысле этого слова.
В простейшем случае для
ввода текста достаточно ввести символ " на английском регистре. Нередко
пользователь начинает набор текстов, забыв установить кавычки. MathCad воспринимает такой набор как ввод
математического выражения. Однако, нажав клавишу Пробел, можно тут же превратить
набранный фрагмент в текстовый. Признаком текстового блока являются черные
квадратики на правой и нижней границах блока, а курсор в текстовом блоке приобретает вид красной
вертикальной черты ![]() .
.
Текст может состоять из слов, математических выражений и формул, спец. знаков. Русский текст вводится с помощью любого кириллического шрифта Courier, Times New Roman Cyr, Arial Cyr). Также для работы с текстом предусмотрены команды меню Format/Text и Format/Paragraph. Можно создать текстовую область (текст начинается на позиции курсора), создать текстовый параграф (текст начинается первой строкой на позиции курсора), форматировать текст (панель форматирования), внедрять в текст математические формулы (команда Insert/Math Region , при этом надо находится в текстовом блоке), проверять орфографию (Check Spelling) для англоязычных текстов, изменять размер шрифта, начертание, цвет текста и т.д. Т.е. для текстовых блоков используются типовые средства редактирования (как в любых текстовых редакторах).
5. Графический процессор служит для создания графиков. Это очень удобно для вывода результатов математических расчетов в графической форме. Графики могут размещаться в любом логически дозволенном месте документа, т.е. после тех вычислительных блоков системы, которые готовят исходные данные для построения графиков.
После включения графического процессора для двухмерного графика на экране появляется шаблон будущего графика в виде прямоугольной рамки с маленькими прямоугольниками, расположенными вдоль осей x и y .
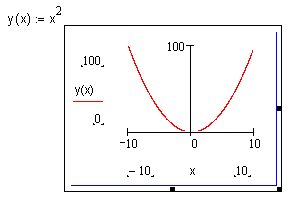
Крайние задают пределы изменения переменных (пределы проставляются системой автоматически, но можно их изменять - для этого в диалоговом окне Formatting флажок "autoscale" надо отключить), а в средние надо ввести имена аргумента и функции. После нажатия Enter график будет построен. Для форматирования графика достаточно сделать двойной щелчок по полю графика, при этом появится диалоговое окно Formatting.
Если строятся графики нескольких функций в одном шаблоне, то имена функций следует разделять запятыми.
6. Вычислитель(формульный редактор) обладает поистине уникальными возможностями. Он обеспечивает вычисления по сложным математическим формулам, имеет большой набор встроенных математических формул, позволяет вычислять ряды, суммы и произведения, интегралы и производные, работать с комплексными числами, производить символьные преобразования, решать линейные и нелинейные уравнения, проводить минимизацию функций, выполнять векторные и матричные операции. В вычислитель входят и такие мощные средства, как линейная и сплайн-интерполяция, прямое и обратное быстрое преобразование Фурье.
Для запуска формульного
редактора достаточно установить указатель мыши в любом свободном месте окна
документа, щелкнуть левой кнопкой и начинать ввод. Поместить формулу в документ
можно, просто начиная вводить символы![]() , числа
, числа ![]() или операторы
или операторы ![]() . Во всех этих случаях
на месте курсора ввода создается математическая область (регион) с формулой,
содержащей и линии ввода. В области формульного блока курсор ввода превращается
в синий уголок, указывающий направление и место ввода
. Во всех этих случаях
на месте курсора ввода создается математическая область (регион) с формулой,
содержащей и линии ввода. В области формульного блока курсор ввода превращается
в синий уголок, указывающий направление и место ввода![]() . Клавиша Insert меняет направление охвата курсором
. Клавиша Insert меняет направление охвата курсором ![]() объекта. Для
расширения охваченной уголком области (вплоть до полного охвата выражения)
нужно пользоваться клавишей Пробел
объекта. Для
расширения охваченной уголком области (вплоть до полного охвата выражения)
нужно пользоваться клавишей Пробел ![]() .
.
Перемещать линии ввода внутри формульного блока можно также с помощью клавиш со стрелками или щелкая в нужном месте мышью.
Большинство операций
редактирования формул реализованы естественным образом, однако некоторые из них
несколько отличаются от общепринятых, что связано с особенностью MathCAD как вычислительной системы, например,
вставка операторов. Операторы могут быть унарными (действующими на один
операнд)![]()
![]() и бинарными
(действующими на два операнда)
и бинарными
(действующими на два операнда) ![]() . При вставке нового оператора в
документ MathCAD определяет, сколько операндов ему требуется. Если в точке вставки
оператора один или оба операнда отсутствуют, MathCAD автоматически помещает рядом с
оператором один или два местозаполнителя. То выражение в формуле,
которое выделено линиями ввода в момент вставки оператора, становится
его первым операндом
. При вставке нового оператора в
документ MathCAD определяет, сколько операндов ему требуется. Если в точке вставки
оператора один или оба операнда отсутствуют, MathCAD автоматически помещает рядом с
оператором один или два местозаполнителя. То выражение в формуле,
которое выделено линиями ввода в момент вставки оператора, становится
его первым операндом
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Как видно, MathCAD сам расставляет, если необходимо,
скобки, чтобы часть формулы, отмеченная линиями ввода, стала первым операндом. Местозаполнители
(черный квадратик – для символа и прямоугольная рамка – для оператора)
появляются внутри незавершенных формул ![]() . Символ в черный квадратик
вводится обычным образом, а чтобы в прямоугольную рамку ввести оператор,
например +, необходимо курсор расположить перед этой прямоугольной рамкой
. Символ в черный квадратик
вводится обычным образом, а чтобы в прямоугольную рамку ввести оператор,
например +, необходимо курсор расположить перед этой прямоугольной рамкой ![]()
![]() .
.
Вопросы
1. Назначение системы MathCAD. Какие еще пакеты математических программ вы знаете?
2. Интерфейс пользователя в системе MathCAD.
3. Документ в системе MathCAD(заголовок, расширение при сохранении на диск, типы и расположение блоков, точка привязки блока, размеры блоков, сквозная передача данных в документе).
4. Объясните, что такое входной язык системы MathCAD и язык реализации системы MathCAD?
5. Перечислите основные объекты входного языка системы MathCAD. Расскажите об алфавите языка и о встроенных и пользовательских функциях системы MathCAD. Что такое определение функции и обращение к функции?
6. Константы и переменные в системе MathCAD? Как задаются типы данных в MathCAD? Что такое глобальное и локальное присваивание переменных в документе MathCAD? Как вставляется мнимая единица для комплексных чисел? Что такое ранжированная переменная и как она задается?
7. Как задаются массивы в MathCADе? Как можно добавлять строки и столбцы в готовые матрицы? Как удаляются строки и столбцы из матриц?
8. Перечислите операторы входного языка системы MathCAD?
9. Как осуществляется вывод результатов в системе MathCAD? Как можно настроить формат вывода результатов? Как осуществляется управление процессом вычислений в системе MathCAD?
10. Как работать с единицами измерений физических величин в системе MathCAD?
11. Подробно охарактеризуйте текстовые, графические и математические блоки.
Лекция №2. Задачи линейной алгебры и решение дифференциальных уравнений в среде MathCAD
В задачах линейной алгебры практически всегда возникает необходимость выполнять различные операции с матрицами. Панель операторов с матрицами находится на панели Math.
![]()

Операторы ![]() ,
, ![]() вам уже знакомы. Напомним только,
что оператор
вам уже знакомы. Напомним только,
что оператор ![]() вычисляет только детерминант
матрицы, а модуль вектора, который равен квадратному корню из суммы квадратов
его элементов, вычисляется с помощью оператора
вычисляет только детерминант
матрицы, а модуль вектора, который равен квадратному корню из суммы квадратов
его элементов, вычисляется с помощью оператора ![]() , который расположен на панели Calculator. К сожалению, по внешнему виду они не отличаются.
, который расположен на панели Calculator. К сожалению, по внешнему виду они не отличаются.
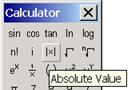
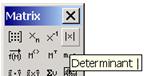
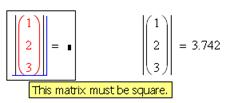
При попытке вычислить модуль вектора с панели Matrix будет ошибочное состояние. Точно также будет ошибочное состояние при попытке вычислить детерминант матрицы с панели Calculator.
Рассмотрим неизвестные вам до сих пор операторы панели Matrix.
![]()
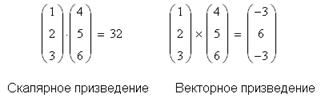
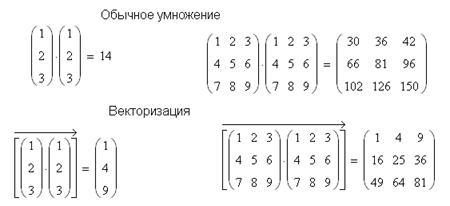
Скалярное произведение векторов определяется как скаляр,
равный сумме попарных произведений соответствующих элементов (идентичен
обычному оператору умножения). Векторы должны иметь одинаковый размер. Для
обозначения скалярного произведения используется символ «точка». Векторное произведение
двух векторов u и v с углом q
между ними равно вектору с модулем ![]() , направленным перпендикулярно
плоскости векторов u и v. Векторное произведение векторов применимо только
для трехкомпонентных векторов. Обозначают векторное произведение символом х,
который можно ввести нажатием кнопки на панели Matrix/
, направленным перпендикулярно
плоскости векторов u и v. Векторное произведение векторов применимо только
для трехкомпонентных векторов. Обозначают векторное произведение символом х,
который можно ввести нажатием кнопки на панели Matrix/
![]() - сумма элементов
вектора.
- сумма элементов
вектора.
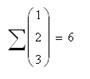
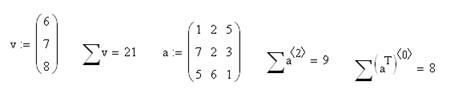
![]() - оператор векторизации. Он
позволяет провести однотипную операцию над всеми элементами массива
(т.е. матрицы или вектора), упрощая тем самым программирование циклов.
Например, иногда требуется умножить каждый элемент одного вектора на соответствующий
элемент другого вектора. Непосредственно такой операции в MathCAD нет, но ее легко осуществить с помощью векторизации. Оператор
векторизации можно использовать только с векторами и матрицами одинакового
размера.
- оператор векторизации. Он
позволяет провести однотипную операцию над всеми элементами массива
(т.е. матрицы или вектора), упрощая тем самым программирование циклов.
Например, иногда требуется умножить каждый элемент одного вектора на соответствующий
элемент другого вектора. Непосредственно такой операции в MathCAD нет, но ее легко осуществить с помощью векторизации. Оператор
векторизации можно использовать только с векторами и матрицами одинакового
размера.
Для решения задач линейной алгебры в MathCAD встроены матричные функции. Их можно разделить на три основные группы:
- функции определения (генерации) матриц и операции с блоками матриц;
- функции вычисления различных числовых характеристик матриц;
- функции, реализующие численные алгоритмы решения задач линейной алгебры.
Из каждой группы приведем по несколько, наиболее часто используемых функций.
Первая группа:
1. matrix(m, n, f) – создает и заполняет матрицу размерности m x n, элемент которой, расположенный в i-ой строке и j-ом столбце равен значению f(i, j) функции f(x, y);
2. diag(v) – создает диагональную матрицу, элементы главной диагонали которой хранятся в векторе v;
3. identity(n) – создает единичную матрицу порядка n;
4. augment(A, B) –объединяет матрицы A и B; матрица B располагается справа от матрицы A, при этом матрицы должны иметь одинаковое число строк;
5. stack(A, B) – объединяет матрицы A и B, матрица В располагается внизу под матрицей А, при этом матрицы должны иметь одинаковое число столбцов;
6. submatrix(A, ir, jr, ic, jc) – формирует матрицу, которая является блоком матрицы А, расположенным в строках с ir по jr и в столбцах с ic по jc, причем ir £ jr, ic £ jc.

Вторая группа:
1. last(v) – вычисляет номер последнего элемента вектора V;
2. length(v) – вычисляет количество элементов вектора V;
3. min(v), max(v) – вычисляет минимальное и максимальное значения вектора V;
4. Re(v) – создает вектор из реальных частей комплексных элементов вектора V;
5. Im(v) - создает вектор из мнимых частей комплексных элементов вектора V;
6. sort(V) – сортировка элементов вектора V по возрастанию;
7. reverse (sort(v)) – сортировка элементов вектора V по убыванию;
8. csort (A,n) – сортировка элементов n – го столбца матрицы А по возрастанию (перестановкой строк);
9. rsort (A,n) – сортировка элементов n – ой строки матрица А по возрастанию (перестановкой столбцов);
10. rows(A) – вычисляет число строк в матрице А;
11. cols(A) – вычисляет число столбцов в матрице А;
12. max(A), min(A) – определяет максимальное и минимальное значения матрицы А;
13. tr(A) – вычисляет след квадратной матрицы А (след матрицы равен сумме ее диагональных элементов по главной диагонали);
14. mean(A) – среднее значение элементов матрица А.
Действие функций второй группы ясно из их названия, поэтому примеры для них приводить не будем.
Третья группа:
1. rref(A) – приведение матрицы к ступенчатому виду с единичным базисным минором (выполняются элементарные операции со строками матрицы: перестановка строк, умножение строки на число, сложение строк);
2. rank(A) – вычисляет ранг матрицы А (количество линейно-независимых строк или это число ненулевых строк ступенчатой матрицы rref(A));
3. eigenvals(A) – вычисление собственных значений квадратной матрицы А;
4. eigenvecs (A) – вычисление собственных векторов квадратной матрицы А, значением функции является матрица, столбцы которой есть собственные векторы матрицы А, причем порядок следования векторов отвечает порядку следования собственных значений, вычисленных с помощью функции eigenvals(A);
5. eigenvec(A,e) – вычисление собственного вектора матрицы А, отвечающего собственному значению e;
6. normi(A) – max – норма, или ¥ - норма (infinity norm). в линейной алгебре используются различные матричные нормы, которые ставят в соответствие матрице некоторую скалярную числовую характеристику;
7.
lsolve (A,b) – решение системы линейных алгебраических
уравнений вида ![]() .
.
Функции третьей группы реализуют, как правило, довольно сложные вычислительные алгоритмы. Приведем примеры на использование функций rref и функций для вычисления собственных значений и собственных векторов матрицы. Задача поиска собственных значений и собственных векторов матрицы очень часто встречается в вычислительной практике.

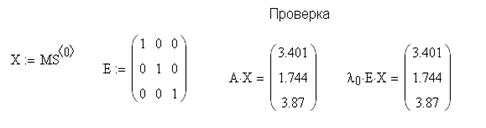
В самом простом виде задача на
собственные значения матрицы формулируется следующим образом: требуется найти
такие значения l, чтобы матричное
уравнение ![]() имело
решение. В таком случае число l называют
собственным числом матрицы А, а n- компонентный вектор Х,
приводящий уравнение с заданным l
в тождество – собственным вектором. В вышеприведенном примере собственные
вектора матрицы А получены в матрице MS. Проверка проведена для
первого столбца матрицы MS и соответствующего ему собственного числа l0=5.439.
имело
решение. В таком случае число l называют
собственным числом матрицы А, а n- компонентный вектор Х,
приводящий уравнение с заданным l
в тождество – собственным вектором. В вышеприведенном примере собственные
вектора матрицы А получены в матрице MS. Проверка проведена для
первого столбца матрицы MS и соответствующего ему собственного числа l0=5.439.
Решение систем линейных алгебраических уравнений. Этот вопрос является центральным в вычислительной линейной алгебре.
В математике рассматриваются системы линейных уравнений двух видов - однородные и неоднородные.
Неоднородная система уравнений в матричном виде записывается
следующим образом: ![]() . Здесь А – матрица коэффициентов
системы, В – вектор свободных членов, Х – вектор неизвестных системы.
. Здесь А – матрица коэффициентов
системы, В – вектор свободных членов, Х – вектор неизвестных системы.
Неоднородная система имеет одно единственное решение, если определитель матрицы отличен от нуля. Для нахождения точного решения неоднородных систем линейных уравнений в линейной алгебре используются три основных метода:
- метод обратной матрицы, он вам уже известен;
- метод исключений Гаусса;

- метод Крамера.

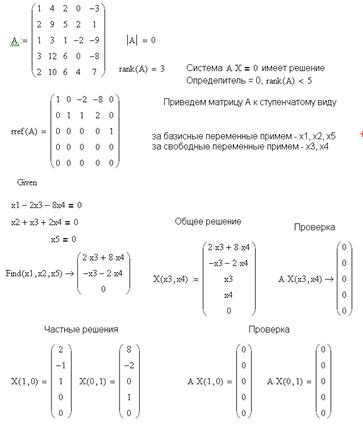
Неоднородная система линейных уравнений в случае равенства ее определителя нулю имеет множество решений, если ранг матрицы системы равен рангу расширенной матрицы системы, либо не имеет решения, если это условие не выполняется. Решить такие системы в MatCADe можно методом Гаусса.

В выше приведенном примере получили систему из трех уравнений с пятью неизвестными, поэтому решение системы будет иметь два свободных параметра (x4, x5).
Однородная система линейных алгебраических уравнений может
быть представлена в виде ![]() , т.е. правая часть уравнения
представляет вектор из нулевых элементов. Как известно, для того чтобы
однородная система линейных уравнений имела решение, определитель
соответствующей матрицы должен равняться нулю. Это означает, что
количество независимых уравнений в системе (т.е. ранг матрицы) меньше, чем
количество неизвестных (т.е. порядок матрицы): rank(A)
< n. Но вначале нужно выделить в системе эти самые
независимые уравнения. Это делается с помощью функции rref, которая с помощью метода исключений Гаусса приводит матрицу к
ступенчатому виду.
, т.е. правая часть уравнения
представляет вектор из нулевых элементов. Как известно, для того чтобы
однородная система линейных уравнений имела решение, определитель
соответствующей матрицы должен равняться нулю. Это означает, что
количество независимых уравнений в системе (т.е. ранг матрицы) меньше, чем
количество неизвестных (т.е. порядок матрицы): rank(A)
< n. Но вначале нужно выделить в системе эти самые
независимые уравнения. Это делается с помощью функции rref, которая с помощью метода исключений Гаусса приводит матрицу к
ступенчатому виду.
Дифференциальные уравнения являются основой огромного количества расчетных задач из самых различных областей науки и техники.
В MathCAD нет средств символьного (точного) решения дифференциальных уравнений, но достаточно хорошо представлены численные методы их решения. Дифференциальные уравнения это уравнения, в которых неизвестные являются не переменные (т.е. числа), а функции одной или нескольких переменных. Эти уравнения (или системы) включают соотношения между искомыми функциями и их производными. Если в уравнения входят производные только по одной переменной, то они называются обыкновенными дифференциальными уравнениями (ОДУ). В противном случае говорят об уравнениях в частных производных. Таким образом, решить (иногда говорят проинтегрировать) дифференциальное уравнение – значит, определить неизвестную функцию на определенном интервале изменения ее переменных.
Как известно, одно обыкновенное дифференциальное уравнение или система ОДУ имеет единственное решение, если помимо уравнения определенным образом заданы начальные или граничные условия. Имеется два типа задач, для которых возможно численное решение ОДУ с помощью MathCAD:
- задачи Коши, для которых определены начальные условия на искомые функции, т.е. заданы значения этих функций в начальной точке интервала интегрирования уравнения;
- краевые задачи, для которых заданы определенные соотношения сразу на обеих границах интервала. Из дифференциальных уравнений в частных производных есть возможность решать только уравнения с двумя независимыми переменными: одномерные параболические и гиперболические уравнения, такие как уравнения теплопроводности, диффузии, волновые уравнения, а также двухмерные эллиптические уравнения (уравнения Пуассона и Лапласа).
В MathCAD нет универсальной функции для решения дифференциальных уравнений, а есть около двадцати функций для различных видов уравнений, дополнительных условий и методов решения. Эти функции можно найти в библиотеке Insert/Function, категория “Differential Equation Solving (решение дифференциальных уравнений).
Решение Обыкновенных Дифференциальных Уравнений (ОДУ)
ОДУ первого порядка называется уравнение
F(x,y,y’)=0
F – известная функция трех переменных;
x – независимая переменная на интервале интегрирования[a,b];
y – неизвестная функция;
y’ – ее производная.
Функция y(x) является решением дифференциального уравнения, если она при всех xÎ[a,b] удовлетворяет уравнению
F(x,y(x),y’(x))=0
График решения y(x) называется интегральной кривой дифференциального уравнения. Если не заданы начальные условия, таких решений y(x) будет множество. При известных начальных условиях y(x0)= y0 решение y(x) будет единственным. Вычислительный процессор MathCAD может работать только с нормальной формой ОДУ. Нормальная форма ОДУ – это ОДУ, разрешенное относительно производной y’=f(x,y)
ОДУ высших порядков
Обыкновенным дифференциальным уравнением n-го порядка называется уравнение вида
F(x,y,y’,y’’, ,y(n))=0
F – известная функция n+2 переменных;
x – независимая переменная на интервале интегрирования[a,b];
y – неизвестная функция;
n – порядок уравнения.
Функция y(x) является решением дифференциального уравнения, если она при всех xÎ[a,b] удовлетворяет уравнению
F(x, y(x), y’(x), y’’(x),…, y(n)(x))=0
Нормальная форма ОДУ высшего порядка имеет вид
Y(n) =f(x, y, y’, …, y(n-1))
Если не заданы начальные условия, то дифференциальное уравнение n – го порядка имеет бесконечное множество решений, при задании начальных условий y(x0)= y0, y’(x0)= y0,1, y’’(x0)= y0,2, …, y(n-1)(x0)= y0,n-1 решение становится единственным (задача Коши).
Задача Коши для дифференциального уравнения n – го порядка может быть сведена к задаче Коши для нормальной системы n дифференциальных уравнений 1 го порядка, которая в векторной форме имеет вид
Y’ = F(x, Y), Y(x0) = Y0
Y(x0) = Y0 – вектор начальных условий;
|
|
F(x, Y) = (y2, y3, …, yn, f(x,y1, … , yn) – вектор правых частей;
Y = (y2, y3, …, yn) – вектор искомого решения.
Эта система получается в результате следующей замены:
|
|
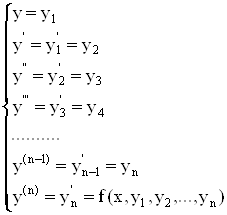 ,где
,где


Для численного интегрирования ОДУ в MathCAD имеется выбор – либо использовать вычислительный блок Given/Odesolve, либо встроенные функции. Оба способа обладают одинаковыми возможностями, но при использовании блока решения запись уравнений более привычна и наглядна, однако отдельная функция может быть использована в составе других функций и программ. Рассмотрим оба варианта решения.
Вычислительный блок Given/Odesolve
Ниже приведены два примера для решения дифференциальных уравнений первого и второго порядка с использованием вычислительного блока решения Given/Odesolve.
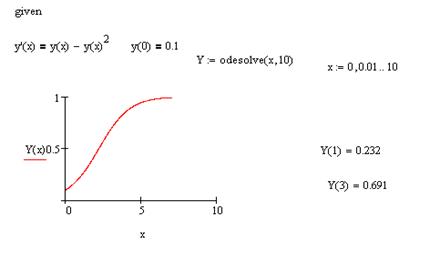
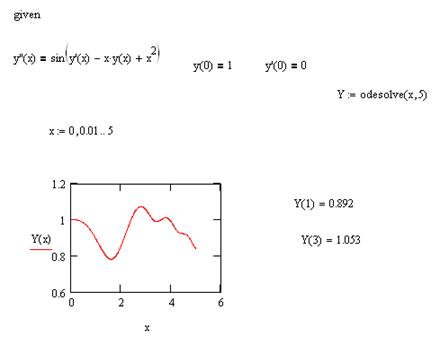
Вычислительный блок для решения одного ОДУ состоит из трех частей:
- ключевое слово given;
- ОДУ и начальные условия, записанные с помощью логического равенства;
- встроенная функция Odesolve(x, b) относительно независимой переменной x на интервале [a, b]; b – верхняя граница отрезка интегрирования. Допустимо и даже предпочтительнее задание функции Odesolve(a, b, step) с тремя параметрами, где step внутренний параметр численного метода, определяющий количество шагов; чем больше step, тем с лучшей точностью будет получен результат, но тем больше времени будет затрачено на его поиск.
Функция Odesolve возвращает решение задачи в виде функции. Эта функция не имеет символьного представления и может только вернуть численное значение решения уравнения в любой точке интервала интегрирования.
Функция Odesolve использует для решения дифференциальных уравнений наиболее популярный алгоритм Рунге-Кутта четвертого порядка, описанный в большинстве книг по методам вычислений. Он обеспечивает малую погрешность для широкого класса систем ОДУ за исключением жестких систем. Если щелчком правой кнопки мыши на блоке формул с функцией Odesolve вызвать контекстное меню, то можно изменить метод вычисления решения, выбрав один из трех вариантов: Fixed метод Рунге-Кутта с фиксированным шагом интегрирования (этот метод используется по умолчанию), Adaptive – также метод Рунге-Кутта, но с переменным шагом, изменяемым в зависимости от скорости изменения функции решения, Stiff – метод, адаптированный для решения жестких уравнений и систем (используется так называемый метод PADAUS).
Альтернативный метод решения ОДУ заключается в использовании одной из встроенных функций: rkfixed, Rkadapt, или Bulstoer. Все они решают задачу Коши для системы дифференциальных уравнений первого порядка, но каждая из них использует для этого свой метод. Для простых систем не играет большой роли, какой метод использовать – все равно получите решение достаточно быстро и с высокой точностью. Но для сложных или специфических систем бывает, что некоторые методы вообще не могут дать удовлетворительного решения за приемлемое время. Именно для таких сложных, но не редких случаев в MathCAD и введено несколько различных методов решения систем ДУ.
- rkfixed – метод Рунге-Кутта с фиксированным шагом интегрирования. Самый простой и быстрый метод, но далеко не всегда самый точный. Полностью аналогичен использованию функции Odesolve с выбранным в контекстном меню методом Fixed.
- Rkadapt – метод Рунге-Кутта с переменным шагом интегрирования. Величина шага адаптируется к скорости изменения функции решения. Данный метод позволяет эффективно находить решения уравнений, в случае если оно содержит как плавные, так и быстро меняющиеся участки. Там, где решение меняется слабо, шаги выбираются более редкими, а в областях его сильных изменений – частыми. В результате для достижения одинаковой точности требуется меньшее число шагов, чем для rkfixed. Полностью аналогичен использованию функции Odesolve с выбранным в контекстном меню методом Adaptive.
- Bulstoer – метод Булирша – Штера. Этот метод более эффективен, чем метод Рунге-Кутта, в случае если решение является плавной функцией.
Имена функций Rkadapt и Bulstoer начинаются с прописной буквы. В MathCAD для некоторых имен функций неважно, с какой буквы они записаны, но для перечисленных функций это принципиально, т.к. в MathCAD также существуют функции с такими же именами, только записанные с маленькой буквы – rkadap, bulstoer. Эти функции используются в тех случаях, когда важным является решение задачи в конечной точке интервала интегрирования.
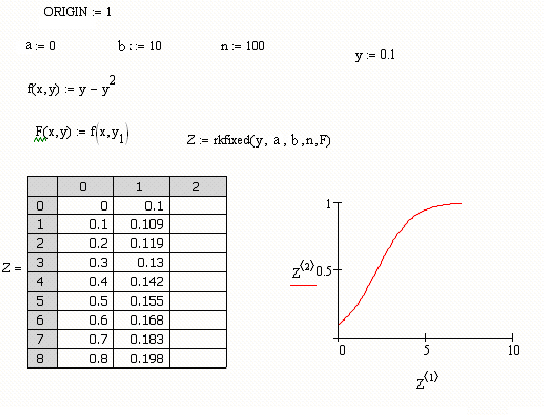
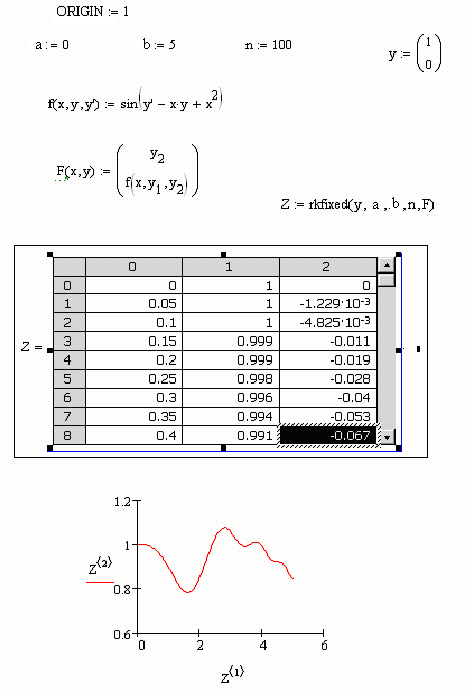
Выше приведены примеры решения тех же дифференциальных уравнений первого и второго порядка, которые были решены с использованием вычислительного блока Given/Odesolve.
Применение встроенных функций в документах MathCAD выглядит сходным образом, т.е. функции Rkadapt и Bulstoer имеют тот же синтаксис, что и выше приведенная функция rkfixed. Назначение аргументов в этих встроенных функциях следующее:
- y – вектор начальных значений неизвестных функций, входящих в систему. В случае одного уравнения и одной неизвестной функции – это просто число.
- а – начало отрезка, на котором ищется решение системы (отрезка интегрирования). Именно в этой точке значения неизвестных функций принимаются равными элементам вектора y.
- b – конец отрезка интегрирования.
- n – количество частей, на которые разбивается отрезок [a, b] при решении системы. Чем больше это число, тем точнее получается решение, но расчет занимает больше времени.
- F(x,y) – векторная функция, элементы которой содержат правые части уравнений системы в нормальной форме (когда левые части первые производные от соответствующих функций, а в правых частях производные отсутствуют). Аргументами этой функции являются вектор y, элементы которого соответствуют различным неизвестным функциям системы, и скалярный аргумент x , соответствующий независимой переменной в системе. В случае одного уравнения функция F может быть скалярной функцией, зависящей от двух скалярных переменных x и y.
Возвращаемым значением всех вышеперечисленных встроенных функций является матрица. Первый столбец этой матрицы – это точки, на которые разбивается отрезок [a, b], а остальные столбцы – это значения функций системы в этих точках. Если в аргументе функции rkfixed было указано количество частей n = 100, то матрица будет содержать 101 строку вместе с начальной.
Решение систем обыкновенных дифференциальных уравнений.
Для численного интегрирования систем ОДУ в MathCAD также имеется выбор – либо использовать вычислительный блок Given/Odesolve, либо встроенные функции rkfixed, Rkadapt и Bulstoer.
При решении систем ОДУ MathCAD требует, чтобы система ОДУ была представлена в нормальной форме (когда левые части – первые производные от соответствующих функций, а в правых частях производные отсутствуют):
![]()
где Y и Y’ – соответствующие неизвестные векторные функции переменной t, а F – вектор правых частей системы уравнений первого порядка. Именно векторное представление используется для ввода системы ОДУ в среде MathCAD.
Если в систему ОДУ входят и уравнения высших порядков, то оно тоже сводится к системе уравнений первого порядка, как было показано выше. При этом количество нулевых условий для вычислительного блока Given/Odesolve, а также размер вектора начальных условий y и размер вектора правых частей F(x,y) для встроенных функций rkfixed, Rkadapt и Bulstoer должны быть равны сумме порядков всех уравнений.
Вначале покажем решение систем ОДУ первого порядка с использованием вычислительного блока Given/Odesolve
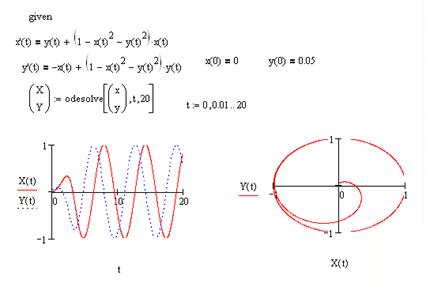
Функция Odesolve для системы ОДУ имеет несколько иной, по сравнению с одним уравнением, синтаксис. Теперь она возвращает вектор функций, составляющих решение системы. Поэтому в качестве первого аргумента функции нужно ввести вектор, состоящий из имен функций, использованных при вводе системы. Второй и третий аргументы то же самое, что и в задаче с одним ОДУ.
Решение системы ОДУ показано на графике слева. Как известно, решения ОДУ часто удобнее изображать не в таком виде, а в фазовом пространстве, по каждой из осей которого откладываются значения каждой из найденных функций (как показано на рисунке справа). При этом аргумент входит в них лишь параметрически. В рассматриваемом случае двух ОДУ такой график – фазовый портрет системы – является кривой на фазовой плоскости. В общем случае, если система состоит из N ОДУ, то фазовое пространство является N мерным. При N > 3 наглядность теряется, и для визуализации фазового портрета приходится строить его различные проекции.
Рассмотрим решение этой же системы ОДУ первого порядка с использованием встроенной функции rkfixed.
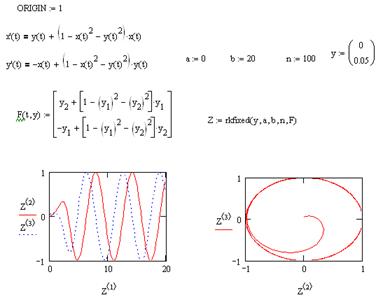
Полученное решение полностью соответствует вышеприведенному решению с использованием вычислительного блока Given/Odesolve. Следует отметить, что начальные условия здесь задаются в виде вектора y, а функциям x(t) и y(t) соответствуют элементы этого вектора y1 и y2. Вектор начальных условий y и вектор правых частей F имеют размер равный двум, т.к. система состоит из двух уравнений первого порядка. Для системы ОДУ, состоящей из двух уравнений второго порядка, размер этих векторов будет равен четырем

Вопросы
1. Поясните работу команд панели Matrix – скалярное и векторное произведение, детерминант матрицы, сумма элементов вектора, операция векторизации.
2. Перечислите три основные группы матричных функций. Расскажите о матричных функциях, возвращающих числовые характеристики. Приведите примеры.
3. Матричные функции, реализующие генерацию матриц и операции работы с блоками матриц.
4. Перечислите матричные функции, реализующие численные алгоритмы решения задач линейной алгебры. Объясните, как работают функции rref и rank.
5. Какие функции вычисляют собственные вектора и собственные числа квадратной матрицы?
6. Решение в системе MathCAD неоднородных систем линейных уравнений, когда определитель матрицы не равен нулю. Три способа.
7. Как осуществляется в системе MathCAD решение неоднородных систем линейных уравнений, когда определитель равен нулю и при условии, что ранг матрицы системы равен рангу расширенной матрицы системы?
8. Как осуществляется в системе MathCAD решение однородных систем линейных уравнений, когда определитель матрицы равен нулю (т.е. ранг матрицы должен быть меньше порядка матрицы)?
9. Какие дифференциальные уравнения называются ОДУ первого порядка? Высшего порядка? Что такое нормальная форма ОДУ первого и высшего порядка? К чему сводятся ОДУ высшего порядка при решении?
10. Можно ли решить дифференциальные уравнения в MathCADе символьно?
11. Как решаются ОДУ с помощью вычислительного блока Given/Odesolve? Какой метод решения реализует функция Odesolve? Как можно изменить метод решения для этой функции?
12. Как решаются ОДУ с помощью встроенной функции rkfixed? Чем функция rkfixed отличается от функции Rkadapt?
13. Как осуществляется решение системы ОДУ с помощью вычислительного блока Given/Odesolve? Приведите примеры.
14. Как осуществляется решение системы ОДУ с помощью функции rkfixed? Приведите примеры.
© 2010 Интернет База Рефератов