
Рефераты по сексологии
Рефераты по информатике программированию
Рефераты по биологии
Рефераты по экономике
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Рефераты по авиации и космонавтике
Рефераты по административному праву
Рефераты по безопасности жизнедеятельности
Рефераты по арбитражному процессу
Рефераты по архитектуре
Рефераты по астрономии
Рефераты по банковскому делу
Рефераты по биржевому делу
Рефераты по ботанике и сельскому хозяйству
Рефераты по бухгалтерскому учету и аудиту
Рефераты по валютным отношениям
Рефераты по ветеринарии
Рефераты для военной кафедры
Рефераты по географии
Рефераты по геодезии
Рефераты по геологии
Рефераты по геополитике
Рефераты по государству и праву
Рефераты по гражданскому праву и процессу
Рефераты по делопроизводству
Рефераты по кредитованию
Рефераты по естествознанию
Рефераты по истории техники
Рефераты по журналистике
Рефераты по зоологии
Рефераты по инвестициям
Рефераты по информатике
Исторические личности
Рефераты по кибернетике
Рефераты по коммуникации и связи
Реферат: Анализ качества дискретных систем управления
Реферат: Анализ качества дискретных систем управления
Реферат
Предмет: Теория автоматического управления
Тема: Анализ качества дискретных систем управления
Методы определения качества дискретных систем автоматического управления аналогичны методам определения качества непрерывных систем с учетом некоторых особенностей.
1. Оценка качества дискретной системы по переходной функции
Порядок использования этого метода рассмотрим на примере.
Пример 1. Рассчитать переходный процесс в заданной дискретной системе (рис. 1), и определить качество переходного процесса при различных значениях T и kv .
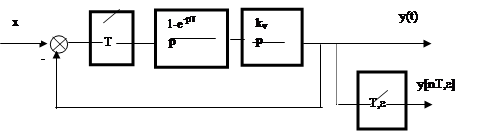
Рис. 1
Решение: Выходной дискретный сигнал равен
![]()
Если x(t) = 1(t),
то 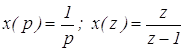 .
.
Определим передаточную функцию разомкнутой непрерывной части
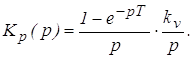
Выполним дискретное преобразование
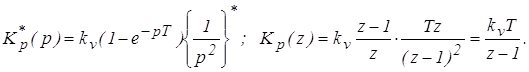
Передаточная функция замкнутой дискретной системы
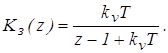
Подставим x(z) и Kз(z,e) в выражение для выходного дискретного сигнала
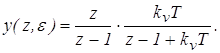
При этом
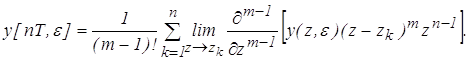 .
.
Определим значения полюсов - zk их число -n и кратность -m.
z1 = 1, z2 = 1 - kvT = A, n = 2, m = 1.
Выражение для переходной функции имеет вид:
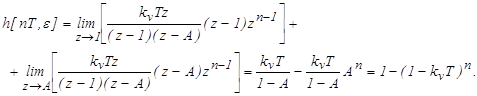
Определим установившееся значение переходной функции:
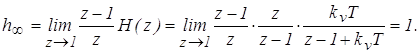
Рассчитаем переходную функцию для различных значений параметров системы
1. Пусть kvT = 1.
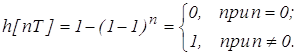
Переходный процесс приведен на рис. 2а. При этом система имеет следующие показатели качества: время регулирования tp = T; относительное перерегулирование s% = 0; число переколебаний N = 0; период собственных колебаний T0 = T.
2. Пусть kvT = 2.
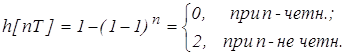
Переходный процесс приведен на рис. 2б. При этом система находится на границе устойчивости.
3. Пусть kvT = 1,5.
![]()
Результаты расчета приведены в таблице 1.
Таблица 1
| n | 0 | 1 | 2 | 3 | 4 | 5 |
|
(-0,5)n |
1 | -0,5 | 0,25 | -0,125 | 0,0625 | -0,03125 |
| h[nT] | 0 | 1,5 | 0,75 | 1,125 | 0,9375 | 1,03125 |
Переходный процесс приведен на рис. 2в.
При этом система имеет следующие показатели качества:
tp = (4¸5)T; s% = 50; N = 4; T0 = 2T.
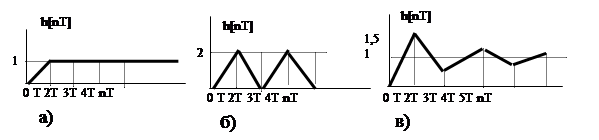
Рис. 2
2. Корневые методы анализа качества
Корневые методы позволяют оценить качество с помощью косвенных показателей качества, при этом анализируется расположение корней характеристического уравнения ki = ±si ±jwi в комплексной плоскости в пределах основной полосы.
При этом используются следующие косвенные показатели качества:
1.
Степень
устойчивости ![]() .
.
2. Колебательность m = w0/s0.
Демпфирование c = s0/w0.
3. Интегральные методы анализа качества
Линейная интегральная оценка
Площадь регулирования может быть определена с помощью суммы ряда
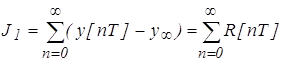 . (1)
. (1)
По аналогии с непрерывными системами сумму ряда (1) можно вычислить по формуле
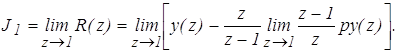 (2)
(2)
Пример 2. Вычислить величину J1 для заданной системы (рис. 3).
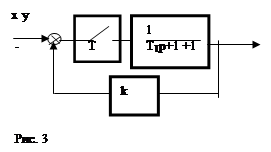
Решение: Определим y(z)
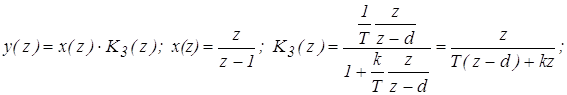
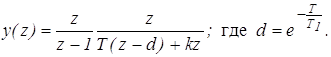
Определим y¥
![]()
![]()
Определим величину интеграла J1
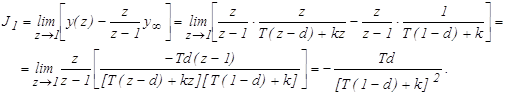
Интегральная квадратичная оценка
Интегральная квадратичная оценка пригодна для любых переходных процессов, и вычисляется по формуле
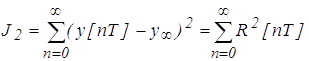 . (3)
. (3)
В соответствии с дуальной теоремой для дискретных оригиналов, можно записать следующую формулу для расчета квадратичной интегральной оценки
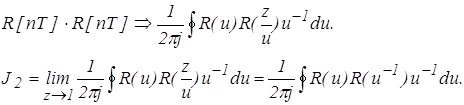 (4)
(4)
Этот интеграл можно вычислить либо с помощью вычетов по полюсам подынтегральной функции, либо с использованием табулированных значений интеграла (см. табл. 2) для функции
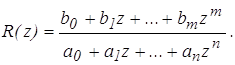
Таблица 2
| n | R(z) |
J2 |
| 1 |
|
|
| 2 |
|
|
Пример 7. Вычислить величину J2 для заданной системы (рис. 4).
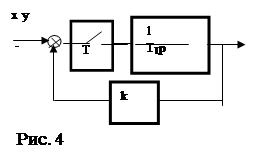
Решение:
1. Определим значение выходной величины y(z)
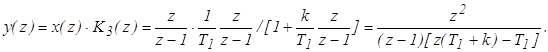
2. Определим установившееся значение выходной величины y¥
![]()
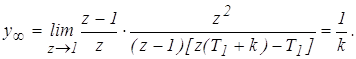
3. Определим R(z)
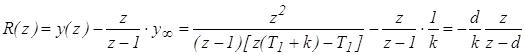 ,
,
где d=T1 /(T1 +k).
4. Определим величину интеграла J2 с помощью вычетов z1 = d
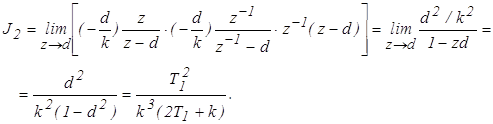
![]()
5. Определим величину интеграла J2 с помощью таблиц
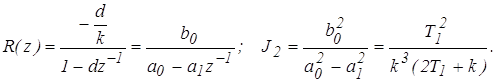
4. Точность дискретных систем управления
Точность дискретных САУ оценивается аналогично, как и непрерывных, с учетом некоторых особенностей.
Изображение ошибки для дискретной системы равно
![]() (5)
(5)
Установившееся значение ошибки определяется с помощью теоремы о конечном значении дискретной функции
![]() (6)
(6)
При определении ошибок используют типовые воздействия, дискретные преобразования Лапласа для типовых воздействий имеют вид:
-для воздействия с постоянной амплитудой
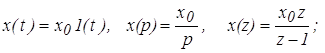 (7)
(7)
-для воздействия с постоянной скоростью
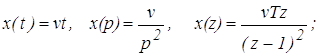 (8)
(8)
-для воздействия с постоянным ускорением
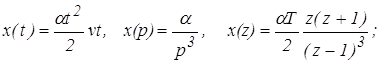 (9)
(9)
Рассмотрим ошибки в дискретных системах. Ошибки в системах управления можно классифицировать как статические, кинетические и инерционные.
Статическая ошибка – это ошибка, возникающая в системе при отработке единичного воздействия.
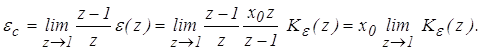 (10)
(10)
Кинетическая ошибка – это ошибка, возникающая в системе при отработке линейно – возрастающего воздействия.
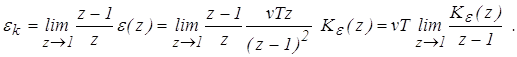 (11)
(11)
Инерционная ошибка – это ошибка, возникающая в системе при отработке квадратичного воздействия.
![]()
Рассмотрим примеры расчета установившихся ошибок в дискретных системах.
Пример 1. Для заданной системы (рис. 5) определить установившиеся ошибки.
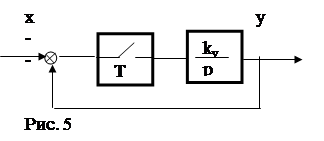
Решение: Определим выражения для установившихся ошибок.
1. Статическая ошибка
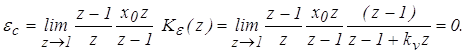
2. Кинетическая ошибка
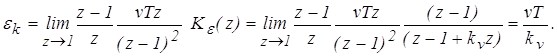
3. Инерционная ошибка
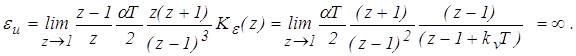
Пример 2. Для заданной системы (рис. 6) определить установившиеся ошибки.
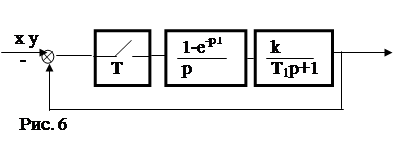
Решение:
1. Определим передаточную функцию разомкнутой системы
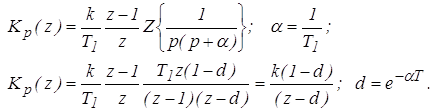
2. Определим передаточную функцию системы по ошибке
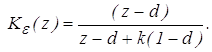
3. Определим статическую ошибку
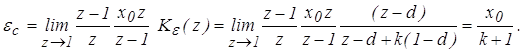
4. Определим кинетическую ошибку
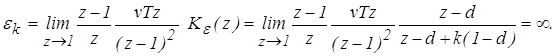
Пример 3. Для заданной системы (рис. 7) рассчитать установившиеся ошибки, если алгоритм функционирования цифровой части описывается уравнением:
 x y
x y
Рис. 7
Решение: Исходную схему можно представить в виде (рис. 8).
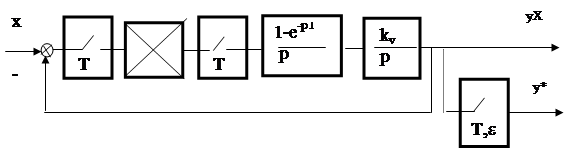
Рис. 8
1. Определим передаточную функцию разомкнутой непрерывной части
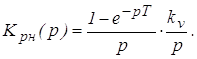
Выполним дискретное преобразование
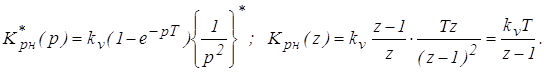
2. Определим передаточную функцию цифрового автомата в соответствии с алгоритмом его функционирования
![]()
3. Определим передаточную функцию разомкнутой дискретной системы
![]()
4. Определим передаточную функцию системы по ошибке
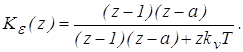
5. Определим статическую ошибку
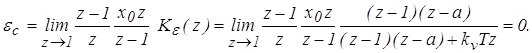
6. Определим кинетическую ошибку
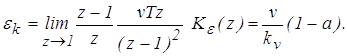
Литература
1. Теория автоматического управления: Учебник для вузов. Ч1/Под ред. А.А. Воронова- М.: Высш. Шк.,1986.-367 с.
2. Теория автоматического управления: Учебник для вузов. Ч2/Под ред. А.А. Воронова- М.: Высш. Шк.,1986. -504 с.
3. Вероятностные методы в вычислительной технике. Под ред. А.Н. Лебедева и Е.А. Чернявского - М.: Высш. Шк.,1986. -312 с.
4. Справочник по теории автоматического управления. /Под ред. А.А. Красовского- М.: Наука, 1987. -712 с.
5. Васильев В.Г. Теорія сигналів і систем: Навч. посібник. – К.: ІСДО, 1995. –68 с.
6. Бойко Н.П., Стеклов В.К. Системы автоматического управления на базе микро-ЭВМ.- К.: Тэхника,1989. –182 с.
7. Автоматизированное проектирование систем автоматического управления./Под ред. В.В. Солодовникова. М.: Машиностроение, 1990. -332 с.
© 2010 Интернет База Рефератов