
Рефераты по сексологии
Рефераты по информатике программированию
Рефераты по биологии
Рефераты по экономике
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Рефераты по авиации и космонавтике
Рефераты по административному праву
Рефераты по безопасности жизнедеятельности
Рефераты по арбитражному процессу
Рефераты по архитектуре
Рефераты по астрономии
Рефераты по банковскому делу
Рефераты по биржевому делу
Рефераты по ботанике и сельскому хозяйству
Рефераты по бухгалтерскому учету и аудиту
Рефераты по валютным отношениям
Рефераты по ветеринарии
Рефераты для военной кафедры
Рефераты по географии
Рефераты по геодезии
Рефераты по геологии
Рефераты по геополитике
Рефераты по государству и праву
Рефераты по гражданскому праву и процессу
Рефераты по делопроизводству
Рефераты по кредитованию
Рефераты по естествознанию
Рефераты по истории техники
Рефераты по журналистике
Рефераты по зоологии
Рефераты по инвестициям
Рефераты по информатике
Исторические личности
Рефераты по кибернетике
Рефераты по коммуникации и связи
Курсовая работа: Анализ цепи во временной области различными методами
Курсовая работа: Анализ цепи во временной области различными методами
Содержание
1. Введение
2. Постановка
3. Анализ цепи во временной области методом переменных состояния при постоянных воздействиях
3.1 Составление уравнений состояния цепи.
3.2 Определение точных решений уравнений. Решение уравнений состояния численным методом
4. Анализ цепи операторным методом при апериодическом воздействии.
4.1 Определение функции передачи, е нулей и полюсов
4.2 Определение переходной и импульсной функции
4.3 Определение напряжения через нагрузку
5. Анализ цепи частотным методом при апериодическом воздействии.
5.1 Определение амплитудно-фазовой (АФХ), амплитудно-частотной (АЧХ) и фазо-частотной (ФЧХ) характеристик функции передачи
5.2 Определение амплитудного и фазового спектра входного сигнала
5.3 Определение амплитудного и фазового спектра выходного сигнала
5.4 Определение выходного сигнала по вещественной характеристике при помощи приближенного метода Гиллемина
6. Анализ цепи частотным методом при периодическом воздействии
6.1 Разложение в ряд Фурье периодической функции и определение её амплитудного и фазового спектров
6.2 Определение напряжения через нагрузку
7. Заключение.
8. Список используемой литературы.
Введение
Практическое применение расчета электрических цепей очень важно. В курсовой работе требуется провести анализ линейной разветвленной электрической цепи различными методами.
Целью курсовой работы является овладение некоторыми современными методами анализа линейной электрической цепи при различных воздействиях в переходном и установившемся режимах с применением вычислительной техники.
В курсовой работе использован следующий материал курса теоретических основ электротехники: методы расчёта сложных цепей, анализ цепей во временной области, операторный метод анализа цепей, частотный метод анализа цепей.
При выполнении курсовой работы применялась программа MathCAD Profession, что позволило значительно упростить вычисления и расчёты в ряде случаев.
2. Постановка задачи
На рисунке 1
представлена анализируемая цепь. Параметры элементов цепи следующие: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Здесь
. Здесь ![]() - единичная ступенчатая
функция (функция включения). Параметры одиночного и последовательности
импульсов:
- единичная ступенчатая
функция (функция включения). Параметры одиночного и последовательности
импульсов: ![]() ,
, ![]() ,
, ![]() .
График одиночного импульса приведён на рисунке 1.1.
.
График одиночного импульса приведён на рисунке 1.1.
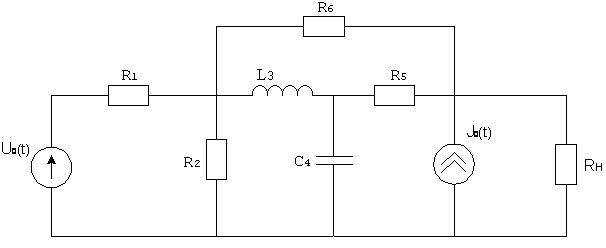 |
Рисунок 1. Схема анализируемой цепи.
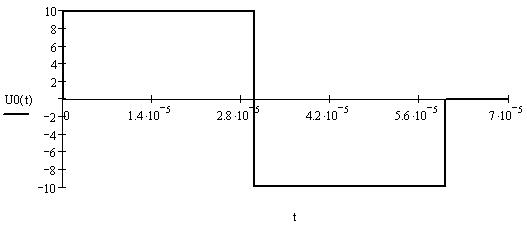
Рисунок 1.1. Входной импульс.
3. Анализ цепи во временной области методом переменных состояния при постоянных воздействиях
3.1 Составление уравнений состояния цепи
Уравнения электромагнитного состояния – это система уравнений, определяющих режим работы (состояние) электрической цепи.
Метод переменных состояния основывается на упорядоченном составлении и решении системы дифференциальных уравнений первого порядка, которые разрешены относительно производных, т.е. записаны в виде, наиболее удобном для применения численных методов интегрирования, реализуемых средствами вычислительной техники. Количество переменных состояния, следовательно, число уравнений состояния равно числу независимых накопителей энергии.
В данной задаче переменными состояния являются напряжения на ёмкостях и
ток в индуктивности: ![]() и
и ![]() . При этом
переменные состояния
образуют систему из наименьшего числа переменных, полностью определяющих
реакции всех ветвей цепи при заданных начальных условиях и приложенных при
. При этом
переменные состояния
образуют систему из наименьшего числа переменных, полностью определяющих
реакции всех ветвей цепи при заданных начальных условиях и приложенных при ![]() внешних воздействиях.
внешних воздействиях.
Требуемая система уравнений может быть получена из системы уравнений, составленной по законам Кирхгофа. При этом целесообразно записывать напряжения и токи на емкости и индуктивности через переменные состояния.
Выберем направления токов (рисунок 2).
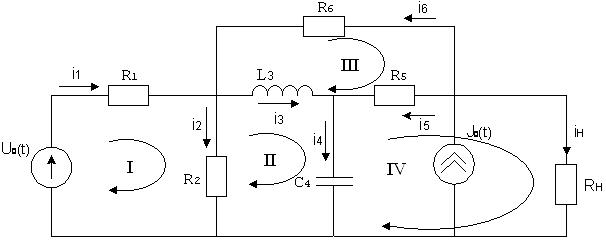 |
Рисунок 2. Выбор направлений токов в ветвях и контуров.
Составим уравнения по законам Кирхгофа:
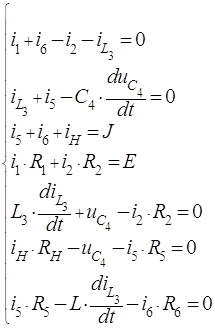
Исключив из уравнений токи и напряжения, не связанные с переменными состояния, получим систему уравнений по методу переменных состояния, разрешенную относительно первых производных (форма Коши):
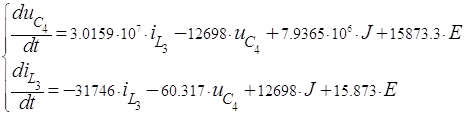 (1)
(1)
В матричной форме записи эта система имеет вид:
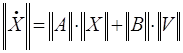 ,
(2)
,
(2)
где ![]() матрица коэффициентов при переменных
состояния, называемая
матрицей Якоби;
матрица коэффициентов при переменных
состояния, называемая
матрицей Якоби; ![]() - вектор - столбец переменных
состояния;
- вектор - столбец переменных
состояния; ![]() - матрица коэффициентов источников тока и
э.д.с.;
- матрица коэффициентов источников тока и
э.д.с.; ![]() - вектор - столбец параметров источников.
- вектор - столбец параметров источников.
В нашем случае это:
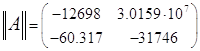
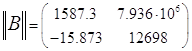
![]()
![]()
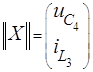
3.2 Определение точных решений уравнений состояния
Решение системы (1) определяется выражением:
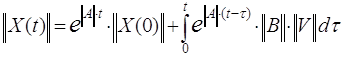
Так как в цепи действуют источники постоянной ЭДС Е и постоянного тока J, то решение может быть представлено в более простом виде:
![]() ,
(3)
,
(3)
Здесь ![]() - матричная экспоненциальная функция;
- матричная экспоненциальная функция; ![]() - вектор-столбец начальных значений
переменных состояния;
- вектор-столбец начальных значений
переменных состояния; ![]() - единичная матрица.
- единичная матрица.
Начальные значения переменных состояния могут быть определены из анализа схемы до коммутации. Предполагается, что в схеме до коммутации существовал установившийся режим постоянного тока, что позволяет представить схему в виде:
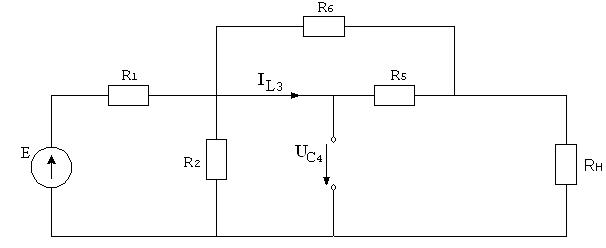
Рисунок 2.1. Схема определения независимых начальных условий.
Анализ схемы рис. 2.1 позволяет определить независимые начальные условия:
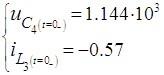 (4)
(4)
Для определения матричной экспоненциальной функции ![]() используем разложение в ряд Тейлора:
используем разложение в ряд Тейлора:
![]() ,
(5)
,
(5)
Число членов разложения
должно быть равно числу переменных состояния. ![]() и
и ![]() являются некоторыми функциями времени,
которые в свою очередь находятся из системы:
являются некоторыми функциями времени,
которые в свою очередь находятся из системы:
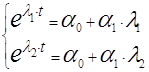 (6)
(6)
Найдя собственные
значения матрицы ![]() :
:
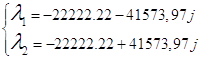
подставляем их в (6) и
находим ![]() и
и ![]() :
:
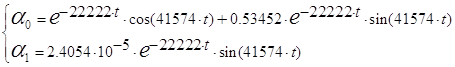
3.3 Решение уравнений состояния численным методом
Решение системы уравнений (1) может быть найдено с помощью какого-либо численного метода интегрирования дифференциальных уравнений. В этих методах интересующий промежуток разбивается на равные малые интервалы h. Приближённые дискретные значения переменных состояния определяются последовательно, на каждом шаге, начиная от времени t = 0.
Решение системы (1) с использованием явного метода Эйлера (или алгоритма Рунге-Кутта первого порядка) имеет вид:
![]()
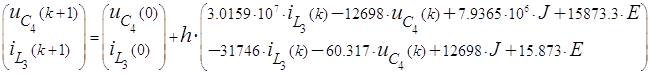 Начальным значениям переменных
состояния соответствует k = 0. Оценить
временной интервал Dtрасч
расчета можно на основе известных собственных значений матрицы
Начальным значениям переменных
состояния соответствует k = 0. Оценить
временной интервал Dtрасч
расчета можно на основе известных собственных значений матрицы ![]() как Dtрасч = 4/ |lmin|. Здесь |lmin| - минимальное собственное значение,
если собственные значения являются вещественными, отрицательными и различными,
или вещественная часть комплексного собственного значения, если собственные
значения являются комплексно сопряженными. Тогда шаг расчета может быть найден
исходя из выражения: h = Dtрасч/N. N - число шагов, на которые разбит интервал Dtрасч. Положим
N=80, тогда h = 2,25*10-6. Погрешность
расчёта пропорциональна h2 .
как Dtрасч = 4/ |lmin|. Здесь |lmin| - минимальное собственное значение,
если собственные значения являются вещественными, отрицательными и различными,
или вещественная часть комплексного собственного значения, если собственные
значения являются комплексно сопряженными. Тогда шаг расчета может быть найден
исходя из выражения: h = Dtрасч/N. N - число шагов, на которые разбит интервал Dtрасч. Положим
N=80, тогда h = 2,25*10-6. Погрешность
расчёта пропорциональна h2 .
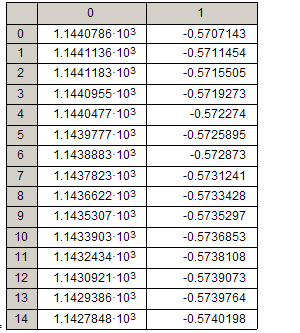
Таблица значений переменных состояния на каждом шаге.
Таблица 1.
|
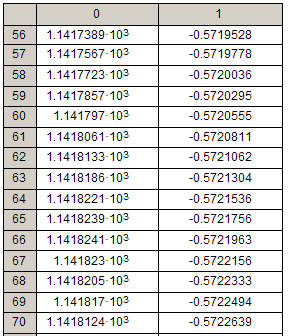
|
|
 U,B I, A
U,B I, A
![]()
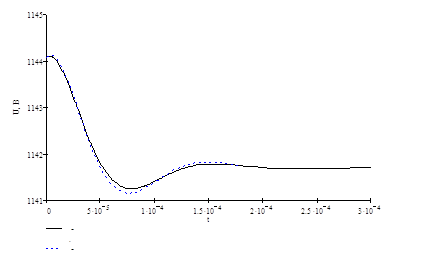
![]() - аналитическое решение
- аналитическое решение
![]() - численное решение
- численное решение
Рисунок 2.2 Изменение напряжения на конденсаторе С4
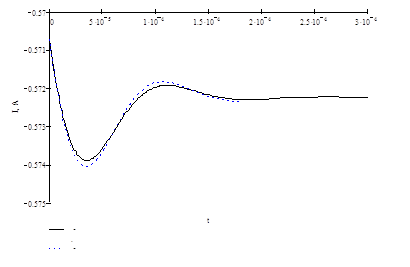
![]() - аналитическое решение
- аналитическое решение
![]() - численное решение
- численное решение
Рисунок 2.3 Изменение тока в катушке индуктивности L3
4. Анализ цепи операторным методом при
апериодическом воздействии
4.1 Определение функции передачи, её нулей и полюсов
Анализу подлежит схема представленная на рис. 3. Начальные условия в цепи нулевые, в момент t = 0 на вход цепи источником напряжения подан импульс (рисунок 1) с амплитудой 10 В и длительностью 60 мкс., j(t) = 0.
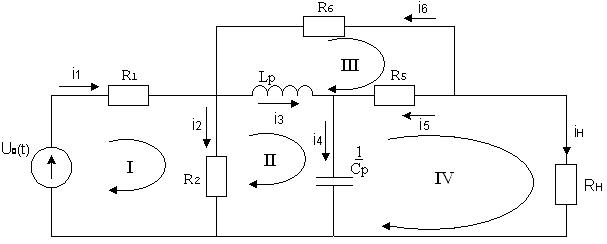
Рисунок 3.Операторная схема замещения.
Составим уравнения в
операторной форме по законам Кирхгофа, найдём отношение 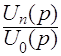 .
Это отношение является функцией передачи
.
Это отношение является функцией передачи ![]() .
.
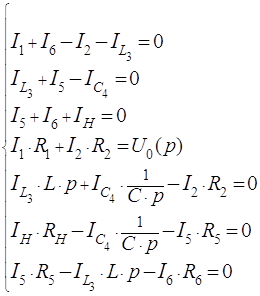
Таким образом, функция передачи будет иметь вид:
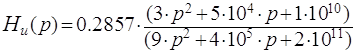 (7)
(7)
Полюсы функции передачи могут быть найдены путём нахождения корней полинома второй степени, находящегося в знаменателе самой функции:
![]()
Таким образом:
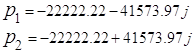
Совпадение полюсов
функции передачи ![]() и
и ![]() с собственными
значениями матрицы
с собственными
значениями матрицы ![]() -
- ![]() и
и ![]() даёт дополнительную информацию о
правильности нахождения передаточной функции.
даёт дополнительную информацию о
правильности нахождения передаточной функции.
Аналогично из числителя функции передачи находятся нули функции:
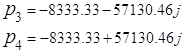
Наиболее наглядным способом охарактеризовать передаточную функцию является графическое расположение ее полюсов и нулей на комплексной плоскости, называемой диаграммой полюсов-нулей (рис.3.1).
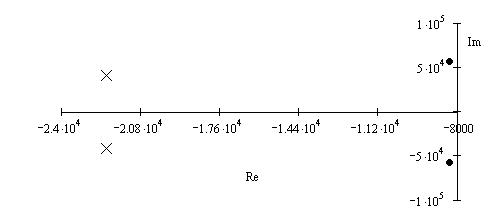
Рисунок 3.1. Диаграмма полюсов-нулей.
Так как полюсы передаточной функции лежат в левой полуплоскости, в линейной пассивной цепи имеются резистивные элементы, в результате чего будет происходить затухание свободной составляющей напряжения. Передаточные функции, полюса которых не лежат в правой полуплоскости комплексной плоскости, называются устойчивыми.
Нули передаточной функции при учете потерь могут располагаться в любой части комплексной плоскости.
4.2 Определение переходной и импульсной характеристик
Переходная характеристика
цепи представляет собой реакцию цепи на воздействие единичной ступенчатой
функции (функции Хэвисайда 1(t)) и может быть найдена как
обратное преобразование Лапласа от ![]() , либо с помощью формулы разложения:
, либо с помощью формулы разложения:
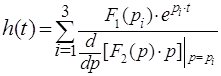 , (8) где
, (8) где ![]() и
и ![]() числитель
и знаменатель передаточной функции
числитель
и знаменатель передаточной функции ![]() соответственно, а
соответственно, а ![]() - корни выражения
- корни выражения ![]() :
:
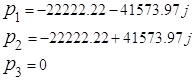
Таким образом, подставляя
корни ![]() и, применяя преобразование Эйлера, получим:
и, применяя преобразование Эйлера, получим:
![]()
Импульсная характеристика
цепи ![]() представляет собой реакцию цепи на воздействие единичной
импульсной функции
представляет собой реакцию цепи на воздействие единичной
импульсной функции ![]() и может быть найдена как обратное преобразование Лапласа от
передаточной функции, либо с помощью формулы разложения:
и может быть найдена как обратное преобразование Лапласа от
передаточной функции, либо с помощью формулы разложения:
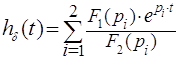 , (9) где
, (9) где ![]() и
и ![]() числитель
и знаменатель передаточной функции
числитель
и знаменатель передаточной функции ![]() соответственно, а
соответственно, а ![]() - полюсы
- полюсы ![]() :
:
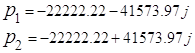
Таким образом:
![]()
Первое слагаемое
определяется действием на входе цепи d - импульса тока и существует только для t=0. В
дальнейшем переходной процесс протекает за счет энергии, накопленной в
электрическом поле конденсатора и магнитном поле индуктивности в результате
действия d - импульса
тока. Из приведенного выражения видно, что, как и в первом случае, переходной
процесс носит затухающий колебательный характер с частотой, равной собственной
частоте рассматриваемой цепи: wсв = 41574 рад/сек. Подобного вида решения (с d -функцией) возникают всякий раз,
когда степени полиномов числителя и знаменателя передаточной функции оказываются
равными. Коэффициент при ![]() соответствует части входного импульса поступающей в нагрузку.
соответствует части входного импульса поступающей в нагрузку.
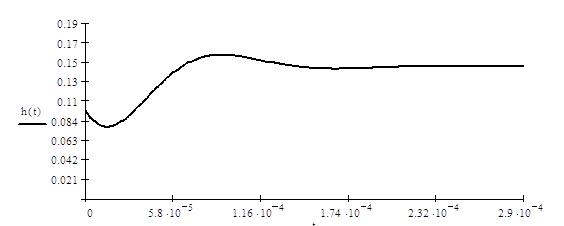 |
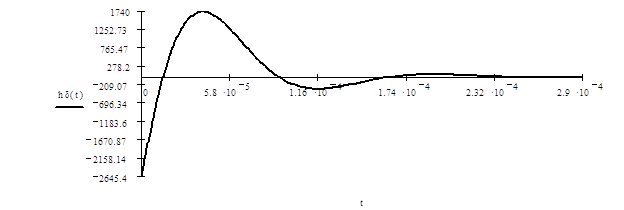
Рисунок 3.2. Импульсная и передаточная характеристики
4.3 Определение напряжения на нагрузке
Входной импульс в данном задании представляет собой знакопеременное прямоугольное напряжение. Его можно представить как сумму следующих функций:
![]()
Применяя теорему Запаздывания, найдём операторное изображение для одиночного импульса напряжения:
![]() (10)
(10)
Так как ![]() , выразим
, выразим ![]() :
:
![]() (11)
(11)
Подставив в (11) выражения (10) и (7), получим:
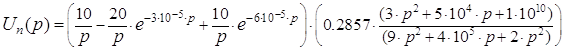
Для того чтобы найти оригинал этой функции, воспользуемся таблицами для преобразований Лапласа:
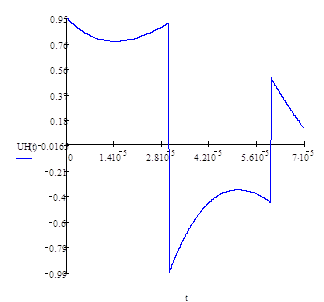
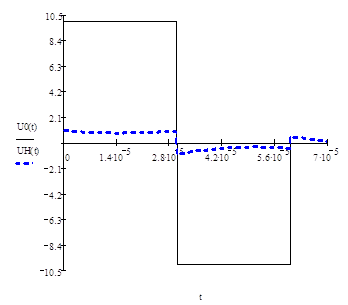
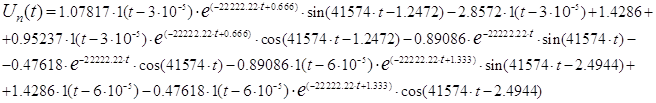
Рисунок 3.3 Графики входного и Рисунок 3.4 График выходного
выходного сигналов сигнала
5. Анализ цепи частотным методом при апериодическом воздействии
5.1 Определение амплитудно-фазовой (АФХ), амплитудно-частотной (АЧХ)и фазо-частотной (ФЧХ) характеристик функции передачи
Амплитудно-частотная
характеристика – это зависимость от частоты модуля входной, выходной или
передаточной функции цепи, выраженных в комплексной форме (ГОСТ 19880-74).
Амплитудно-частотная характеристика (АЧХ) является одной из самых важных
характеристик любой цепи и позволяет исследовать искажения вносимые цепью в
спектр входного сигнала. Наличие частотно - зависимых элементов (L и C)
в исследуемой цепи приводит к неравномерному изменению составляющих спектра
входного сигнала. Наиболее простой способ получения АЧХ цепи - это замена в
выражении для ![]() операторной переменной p
на мнимую частоту jw и нахождение модуля полученной комплексной функции
частоты:
операторной переменной p
на мнимую частоту jw и нахождение модуля полученной комплексной функции
частоты:
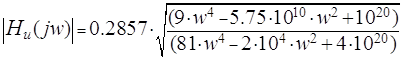
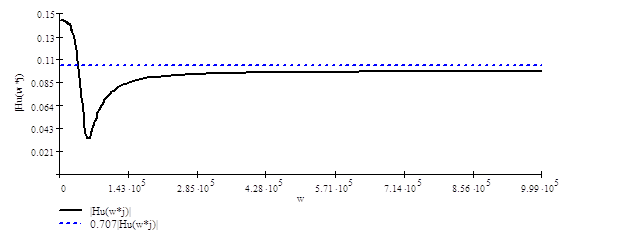 Рисунок 4.1 АЧХ функции передачи по
напряжению
Рисунок 4.1 АЧХ функции передачи по
напряжению
Характеристика имеет вид,
качественно сходный с подобной характеристикой параллельного колебательного
контура. По построенной характеристике может быть определена полоса
пропускания. Полоса пропускания – полоса частот, в пределах которой затухание
остаётся ниже определённого значения (СТ МЭК 50(151)-78). Т. е.
коэффициент передачи для этой полосы не более чем в ![]() отличается
от его максимального значения. Для рассматриваемой цепи максимальное значение
передаточной функции достигается на нулевой частоте (для постоянного
напряжения) и составляет
отличается
от его максимального значения. Для рассматриваемой цепи максимальное значение
передаточной функции достигается на нулевой частоте (для постоянного
напряжения) и составляет ![]() . Границе полосы
пропускания соответствует значение передаточной функции
. Границе полосы
пропускания соответствует значение передаточной функции ![]() .
Это значение достигается на частоте
.
Это значение достигается на частоте ![]() . Таким образом, полоса
пропускания равна:
. Таким образом, полоса
пропускания равна: ![]() .
.
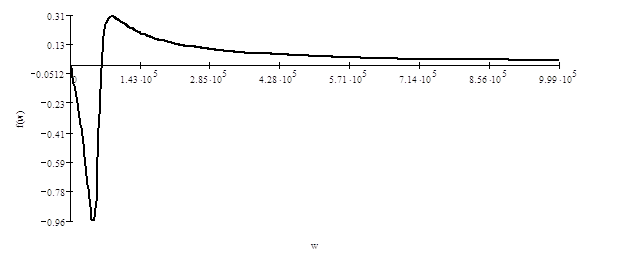 |
Фазо-частотная характеристика зависимость от частоты аргумента входной, выходной или передаточной функций цепи, выраженных в комплексной форме (ГОСТ 19880-74). Таким образом, для данной цепи ФЧХ будет иметь вид:
Рисунок 4.2 ФЧХ функции передачи по напряжении
Амплитуднофазочастотная
характеристика цепи (годограф) связывает воедино изменение коэффициента
передачи (в нашем случае, по напряжению - ![]() ) и
фазового сдвига между выходным и входным напряжением
) и
фазового сдвига между выходным и входным напряжением ![]() во всем диапазоне частот. Годограф
включает сведения, которые содержатся как в АЧХ, так и в ФЧХ.
во всем диапазоне частот. Годограф
включает сведения, которые содержатся как в АЧХ, так и в ФЧХ.
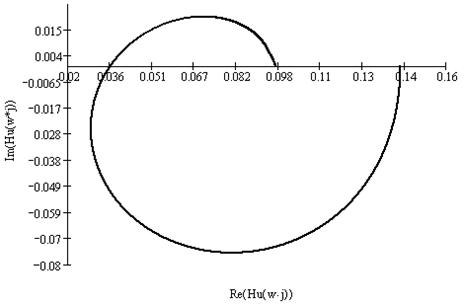
Рисунок 4.3 Годограф анализируемой цепи
Годограф является
параметрической кривой, параметром которой является частота w. Длина вектора, проведенного из
начала координат к какой-либо точке годографа, соответствует абсолютному
значению передаточной функции на этой частоте ![]() , а угол
между ним и положительным направлением вещественной оси - аргументу
передаточной функции
, а угол
между ним и положительным направлением вещественной оси - аргументу
передаточной функции ![]() . Нулевой частоте (постоянному
напряжению) соответствует точка с координатой 0.1428 на вещественной
оси, очень большой (в пределе бесконечной) частоте соответствует точка с
координатой 0.09524 на вещественной оси. На этих граничных частотах
влияние реактивных элементов на фазовый сдвиг отсутствует.
. Нулевой частоте (постоянному
напряжению) соответствует точка с координатой 0.1428 на вещественной
оси, очень большой (в пределе бесконечной) частоте соответствует точка с
координатой 0.09524 на вещественной оси. На этих граничных частотах
влияние реактивных элементов на фазовый сдвиг отсутствует.
5.2 Определение амплитудного и фазового спектра входного сигнала
Для нахождения
спектральной характеристики входного сигнала ![]() можно
воспользоваться непосредственно прямым преобразованием Фурье. Второй путь
решения этой задачи основан на аналогии между преобразованиями Лапласа и Фурье
и состоит в замене в операторном изображении входного сигнала (10) операторной
переменной p на мнимую частоту jw. В итоге после простых
преобразований получим:
можно
воспользоваться непосредственно прямым преобразованием Фурье. Второй путь
решения этой задачи основан на аналогии между преобразованиями Лапласа и Фурье
и состоит в замене в операторном изображении входного сигнала (10) операторной
переменной p на мнимую частоту jw. В итоге после простых
преобразований получим:
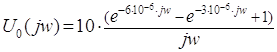
Амплитудный спектр
входного сигнала ![]() может быть найден как модуль
спектральной характеристики сигнала:
может быть найден как модуль
спектральной характеристики сигнала:
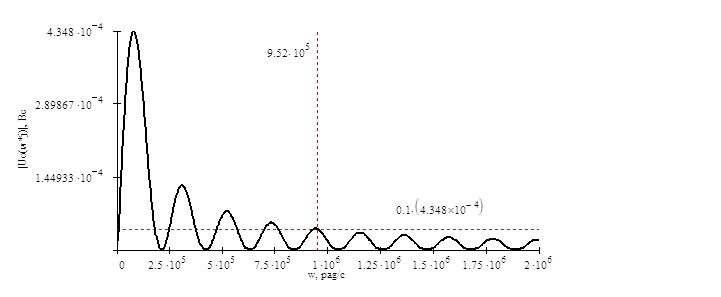
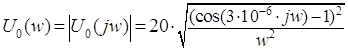
Рисунок 4.4 АЧХ входного
сигнала ![]()
Максимальное значение
спектральной характеристики достигается при ![]() и
составляет
и
составляет ![]() . Определенная по уровню
. Определенная по уровню ![]() ширина спектра сигнала составляет
ширина спектра сигнала составляет ![]() . Между шириной спектра сигнала и его
длительностью существует следующее соотношение:
. Между шириной спектра сигнала и его
длительностью существует следующее соотношение: ![]() . Для
данного вида сигнала получаем:
. Для
данного вида сигнала получаем: ![]() . Эта константа называется
базой сигнала. Уменьшение длительности импульса в 100 раз приводит к такому же
(в 100 раз) увеличению ширины его спектра. Наличие широкого спектра у коротких
импульсов дает возможность использования таких импульсов для исследования
частотных свойств различных цепей. В математическом смысле спектр
несинусоидального сигнала неограничен.
. Эта константа называется
базой сигнала. Уменьшение длительности импульса в 100 раз приводит к такому же
(в 100 раз) увеличению ширины его спектра. Наличие широкого спектра у коротких
импульсов дает возможность использования таких импульсов для исследования
частотных свойств различных цепей. В математическом смысле спектр
несинусоидального сигнала неограничен.
Фазовый спектр входного
сигнала определяется как аргумент от входной спектральной характеристики: ![]() .
.
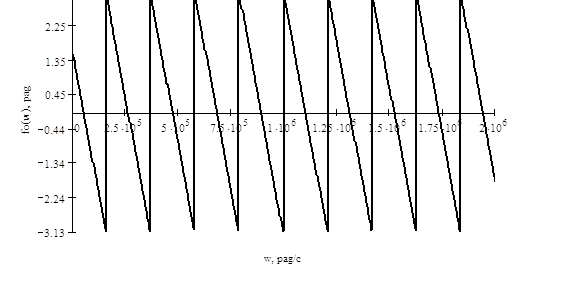
Рисунок 4.5 Фазовый спектр входного сигнала
5.3 Определение амплитудного и фазового спектра выходного сигнала
Амплитудно-частотная
характеристика выходного сигнала может быть получена перемножением амплитудно-частотных
характеристик входного сигнала ![]() и цепи
и цепи ![]() :
: ![]()
![]() .
.
График АЧХ выходного сигнала приведён на рис. 4.6.
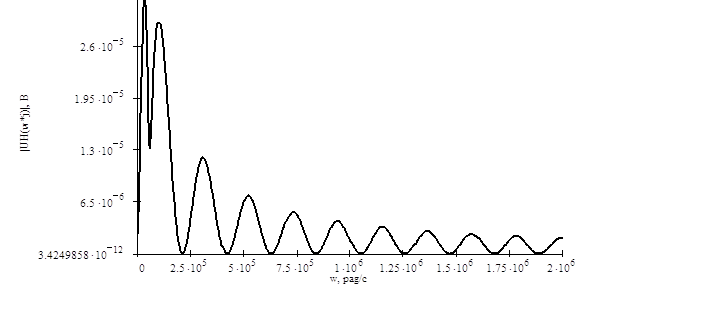
Рисунок 4.6 Амплитудно-частотная характеристика
входного сигнала ![]()
Сравнение АЧХ ![]() с соответствующей характеристикой
с соответствующей характеристикой ![]() позволяет предположить значительное
искажение формы выходного сигнала. Искажения связаны с различием величины передаточной
функции для различных составляющих спектра входного сигнала. Для резистивной
цепи выходной сигнал был бы подобен входному и имел бы ту же длительность. В
данном случае цепи содержащей частотнозависимые элементы значительные изменения
будут иметь место и для фазового спектра входного сигнала. Это приведет к
нарушению фазовых соотношений между составляющими сигнала и станет другой
причиной искажения формы выходного сигнала. Искажение на рис. 4.6 и рис. 4.7
ярко выражено на частоте
позволяет предположить значительное
искажение формы выходного сигнала. Искажения связаны с различием величины передаточной
функции для различных составляющих спектра входного сигнала. Для резистивной
цепи выходной сигнал был бы подобен входному и имел бы ту же длительность. В
данном случае цепи содержащей частотнозависимые элементы значительные изменения
будут иметь место и для фазового спектра входного сигнала. Это приведет к
нарушению фазовых соотношений между составляющими сигнала и станет другой
причиной искажения формы выходного сигнала. Искажение на рис. 4.6 и рис. 4.7
ярко выражено на частоте ![]() , т. е. той же частоте,
что имела место в АЧХ функции передачи по напряжению(рис. 4.1), определяющей
характеристику данной цепи как параллельного колебательного контура. Анализ
преобразования импульсного сигнала основывается на представлении о том, что
искажение фронта выходного импульса по сравнению с формой входного импульса
зависит от свойств цепи на высоких частотах (теоретически на бесконечно высоких
частотах). Искажение формы вершины импульса определяется свойствами цепи на
низких частотах. Используя подобный подход, например, для анализа искажений
фронта входного импульса «закорачивают» конденсаторы, находящиеся на пути
следования сигнала в нагрузку и заменяют разрывом индуктивные элементы,
включенные параллельно резистивным элементам схемы.
, т. е. той же частоте,
что имела место в АЧХ функции передачи по напряжению(рис. 4.1), определяющей
характеристику данной цепи как параллельного колебательного контура. Анализ
преобразования импульсного сигнала основывается на представлении о том, что
искажение фронта выходного импульса по сравнению с формой входного импульса
зависит от свойств цепи на высоких частотах (теоретически на бесконечно высоких
частотах). Искажение формы вершины импульса определяется свойствами цепи на
низких частотах. Используя подобный подход, например, для анализа искажений
фронта входного импульса «закорачивают» конденсаторы, находящиеся на пути
следования сигнала в нагрузку и заменяют разрывом индуктивные элементы,
включенные параллельно резистивным элементам схемы.
Фазовый спектр выходного сигнала может быть получен суммированием аргумента спектральной характеристики и ФЧХ цепи:
![]()
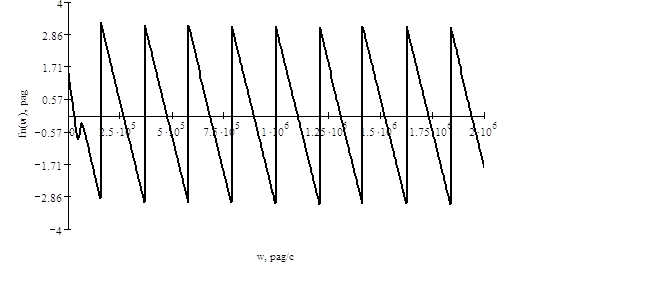
Рисунок 4.7 Фазовый спектр выходного сигнала
5.4 Определение выходного сигнала по вещественной характеристике при помощи приближенного метода Гиллемина
Метод Гиллемина является одним из методов позволяющих восстановить функцию времени (какой - либо сигнал) по известной вещественной (или мнимой) частотной характеристике. Метод основан на такой аппроксимации, когда аппроксимирующая частотную характеристику функция либо ее производные состоят из последовательности бесконечно коротких импульсов. Последовательность бесконечно коротких импульсов представляет собой заданную функцию в так называемой квантованной форме. Погрешность метода преимущественно связана со ступенчатым характером аппроксимирующей функции. Уменьшение этой погрешности требует увеличения общего числа членов в аппроксимации. Исходная частотная характеристика аппроксимируется кусочнолинейным образом, после чего два последовательных дифференцирования позволяют свести аппроксимирующую функцию к последовательности бесконечно коротких импульсов. Окончательное выражение для искомой функции времени f(t) полученной по вещественной частотной характеристике имеет вид:
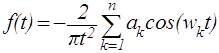 (12)
(12)
 Здесь ak -
величины бесконечно коротких импульсов, wk - координаты импульсов на частотной
оси. Вещественная частотная характеристика
Здесь ak -
величины бесконечно коротких импульсов, wk - координаты импульсов на частотной
оси. Вещественная частотная характеристика ![]() может быть
определена из соотношений:
может быть
определена из соотношений: ![]() ;
; ![]() ;
;
![]() , где
, где ![]() - фазо-частотная характеристика цепи,
- фазо-частотная характеристика цепи, ![]() - фазо-частотная характеристика
входного сигнала.
- фазо-частотная характеристика
входного сигнала.
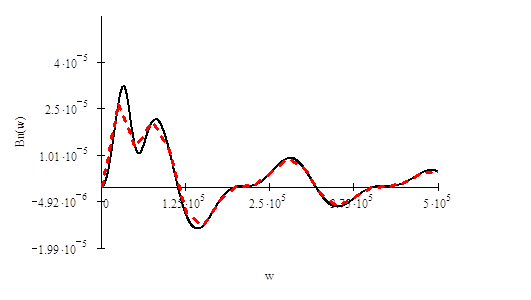
Рисунок 4.8 Аппроксимация
вещественной частотной характеристики ![]()
Аппроксимация позволяет
найти точки ![]() , необходимые для записи и построения первой
производной вещественной частотной характеристики
, необходимые для записи и построения первой
производной вещественной частотной характеристики ![]() :
:

Рисунок 4.9 Первая
производная - ![]()
На этом шаге уже можно
восстановить функцию времени (![]() ). Для этого воспользуемся
выражением вида:
). Для этого воспользуемся
выражением вида:
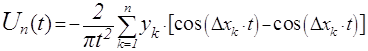
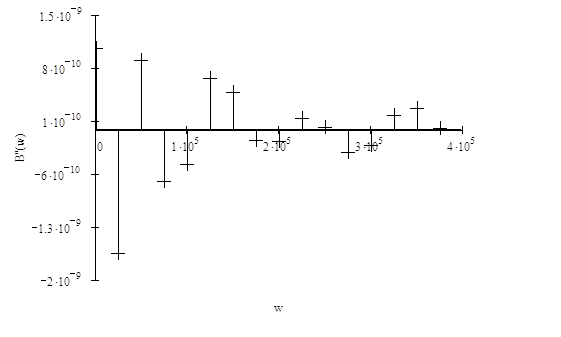 Аналогично вычисляется вторая производная вещественной частотной
характеристики
Аналогично вычисляется вторая производная вещественной частотной
характеристики ![]() :
:
Рисунок 4.11 Вторая
производная - ![]()
 Применяя выражение (12), можно восстановить выходной сигнал
Применяя выражение (12), можно восстановить выходной сигнал ![]() :
:
Рисунок 4.12
Аппроксимированный выходной сигнал по ![]()
6. Анализ цепи частотным методом при периодическом воздействии
6.1 Разложение в ряд Фурье заданной периодической функции, определение амплитудного и фазового спектров
Разложение периодической
последовательности импульсов может быть осуществлено с учетом очевидной связи
комплексной амплитуды гармоники ряда Фурье и спектральной плотности одиночного
импульса той же формы ![]() . Коэффициенты ряда Фурье могут
быть найдены по формуле:
. Коэффициенты ряда Фурье могут
быть найдены по формуле:
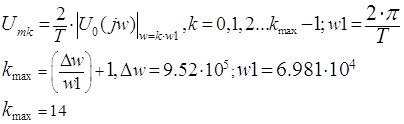
Фазовые коэффициенты ![]() определяются как аргумент комплексного числа
определяются как аргумент комплексного числа
![]() :
:
![]()
Результаты вычислений:
Таблица 2.
|
k, номер гармоники |
Амплитуда k - той гармоники Uок, B |
Начальная фаза k - той гармоники ak, рад |
| 1 | 9.549 | -0.524 |
| 2 | 4.775 | -2.618 |
| 3 | 0 | - |
| 4 | 2.387 | -0.524 |
| 5 | 1.91 | -2.618 |
| 6 | 0 | - |
| 7 | 1.364 | -0.524 |
| 8 | 1.194 | -2.618 |
| 9 | 0 | - |
| 10 | 0.955 | -0.524 |
| 11 | 0.868 | -2.618 |
| 12 | 0 | - |
| 13 | 0.735 | -0.524 |
| 14 | 0.682 | -2.618 |
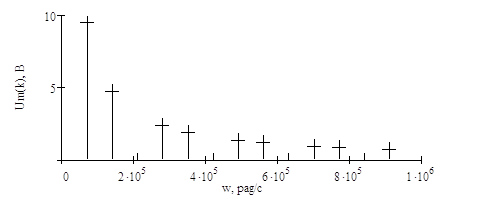
Рисунок 5.1 Амплитудный спектр входного сигнала
На рис. 5.1 представлен
амплитудный спектр входного сигнала. Огибающая дискретного спектра
периодического сигнала совпадает с амплитудно-частотной характеристикой одиночного
импульса. При всех частотах ![]() амплитуды спектра
периодической функции отличаются от значений спектральной плотности
непериодической только постоянным множителем
амплитуды спектра
периодической функции отличаются от значений спектральной плотности
непериодической только постоянным множителем ![]() .
Увеличение периода следования импульсов ведет к уменьшению расстояния между соседними
гармониками амплитудного спектра. При увеличении периода до бесконечности
дискретный амплитудный спектр периодической последовательности переходит в
непрерывный спектр одиночного импульса. Вид этого спектра наглядно позволяет судить
о свойствах периодических функций времени, например, по скорости уменьшения амплитудного
спектра можно судить о степени гладкости периодической функции, а по наличию
или отсутствию гармоник на высоких частотах – есть ли участки с быстрыми
изменениями. Амплитудный спектр является четной функцией частоты, а фазовый
нечетной функцией.
.
Увеличение периода следования импульсов ведет к уменьшению расстояния между соседними
гармониками амплитудного спектра. При увеличении периода до бесконечности
дискретный амплитудный спектр периодической последовательности переходит в
непрерывный спектр одиночного импульса. Вид этого спектра наглядно позволяет судить
о свойствах периодических функций времени, например, по скорости уменьшения амплитудного
спектра можно судить о степени гладкости периодической функции, а по наличию
или отсутствию гармоник на высоких частотах – есть ли участки с быстрыми
изменениями. Амплитудный спектр является четной функцией частоты, а фазовый
нечетной функцией.
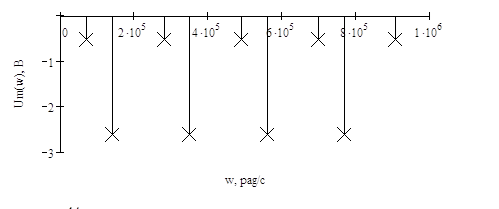
Рисунок 5.2 Фазовый спектр входного сигнала
Таким образом, входной сигнал можно представить как
6.2 Определение напряжения на нагрузке
Для определения коэффициентов ряда Фурье выходного тока вычислим значения АЧХ и ФЧХ функции передачи, полученной нами в пункте 4.1, для значений (k×w1), k=0,1,2,3...14. Тогда:
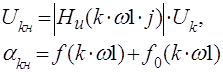
Результаты вычислений:
Таблица 3.
|
k, номер гармоники |
Амплитуда k - той гармоники Uкн, B |
Начальная фаза k - той гармоники kн, рад |
| 1 | 0.43 | -0.307 |
| 2 | 0.405 | -2.416 |
| 3 | 0 | - |
| 4 | 0.222 | -0.423 |
| 5 | 0.179 | -2.538 |
| 6 | 0 | - |
| 7 | 0.129 | -0.467 |
| 8 | 0.113 | -2.568 |
| 9 | 0 | - |
| 10 | 0.091 | -0.484 |
| 11 | 0.082 | -2.582 |
| 12 | 0 | - |
| 13 | 0.07 | -0.493 |
| 14 | 0.065 | -2.59 |
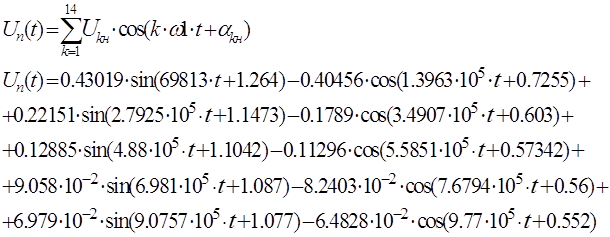
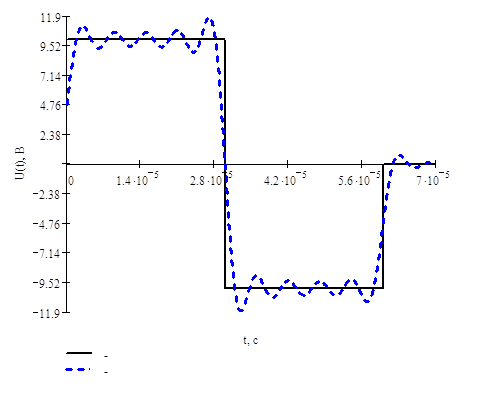
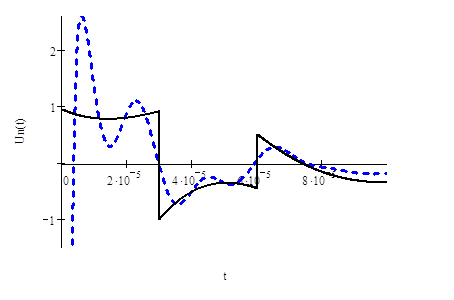
Заданная периодическая
последовательность импульсов ![]()
Аппроксимация отрезком ряда Фурье
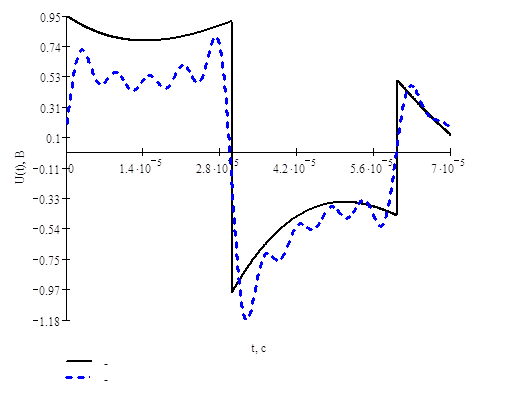
Напряжение на выходе цепи ![]()
Аппроксимация отрезком ряда Фурье
7. Заключение
В данной курсовой работе были применены различные современные методы для анализа разветвлённой линейной электрической цепи при различных воздействиях в переходном и установившемся режимах с применением вычислительной техники.
Вычисления, проводимые с помощью математического пакета MathCAD Profession, в большинстве случаев были проверены встроенными функциями, согласующимися с поставленной задачей в данной курсовой работе.
Анализ графиков показывает, что характер их изменения весьма соответствует характеру физической реализации цепи с данным включением L и С элементов.
Применяемые аппроксимации в качестве дополнительной информации о правильности, в результате подтвердили выполненные расчёты.
8. Список используемой литературы
1. Бессонов Л.А. Теоретические основы электротехники. - М.: Высшая школа, 1996.
2. Матханов П.Н. Основы анализа электрических цепей. Линейные цепи. - М.: Высшая школа, 1990.
3. Зевеке Г.В. и др. Основы анализа цепей. - М.: Энергоатомиздат, 1989. 5-е изд. - 528.
4. Лосев А.К. Теория линейных электрических цепей. – М: Высшая школа, 1987.
5. Шебес М.Р. Каблукова М.В. Задачник по теории линейных электрических цепей. –М: Высшая школа, 1990.
6. Зевеке Г.В. и др. Основы анализа цепей. - М.: Энергоатомиздат, 1975. 4-е изд. - 752
© 2010 Интернет База Рефератов