Курсовая работа: Беспроводные телекоммуникационные системы

Курсовая работа: Беспроводные телекоммуникационные системы

Содержание:

1. Принципы построения беспроводных телекоммуникационных систем

1.1 Архитектура сотовых систем связи.

1.2 Обслуживание абонента сетью.

1.3 Методы разделения абонентов в сотовой связи

1.4 Стандарт DECT для связи.

1.5 Стандарты Bluetooth, Wi-Fi (802.11, 802.16).

2. Системы сложных сигналов для телекоммуникационных систем.

2.1 Спектры сигналов

2.2 Корреляционные свойства сигналов

2.3 Типы сложных сигналов

2.4 Производные системы сигналов

3. Модуляция сложных сигналов

3.1 Геометрическое представление сигналов

3.2 Методы фазовой манипуляции сигналов (ФМ2, ФМ4, ОФМ).

3.3 Модуляция с минимальным частотным сдвигом.

3.4 Квадратурная модуляция и ее характеристики (QPSK, QAM).

3.5 Реализация квадратурных модемов.

4. Характеристики приема сигналов в телекоммуникационных системах.

4.1 Вероятность ошибок различения М известных сигналов

4.2 Вероятность ошибок различения М флуктуирующих сигналов.

4.3 Расчет ошибок различения М сигналов с неизвестными

неэнергетическими параметрами.

4.4 Сравнение синхронных и асинхронных систем связи.

5. Заключение.

6. Список литературы

1. Принципы построения беспроводных телекоммуникационных систем

1.1 Архитектура сотовых систем связи

Система сотовой связи - это сложная и гибкая техническая система, допускающая большое разнообразие, как по вариантам конфигураций, так и по набору выполняемых функций. Примером сложности и гибкости системы является то, что она может обеспечивать передачу, как речи, так и других видов информации, в частности текстовых сообщений и компьютерных данных. В части передачи речи, в свою очередь, может быть реализована обычная двусторонняя телефонная связь, многосторонняя телефонная связь (так называемая конференцсвязь – с участием в разговоре более двух абонентов одновременно), голосовая почта. При организации обычного двустороннего телефонного разговора, начинающегося с вызова, возможны режимы автодозвона, ожидания вызова, переадресации вызова.

Система сотовой связи строится в виде совокупности ячеек, или сот, покрывающих обслуживаемую территорию, например, территорию города  с пригородами. Ячейки обычно схематически изображают в виде правильных равновеликих шестиугольников (рис. 1.1.), что по сходству с пчелиными сотами  и послужило поводом назвать систему сотовой. Ячеечная, или сотовая, структура системы непосредственно связана с принципом повторного использования частот – основным принципом сотовой системы, определяющим эффективное использование выделенного частотного диапазона и высокую емкость системы.

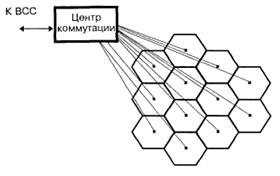
Рис. 1.1. Ячейки (соты) системы, покрывающие всю обслуживаемую территорию.

В центре каждой ячейки находится базовая станция, обслуживающая все подвижные станции (абонентские радиотелефонные аппараты) в пределах своей ячейки (рис. 1.2.). При перемещении абонента из одной ячейки в другую происходит передача его обслуживания от одной базовой станции к другой. Все базовые станции системы, в свою очередь, замыкаются на центр коммутации, с которого имеется выход во Взаимоувязанную сеть связи (ВСС) России, в частности, если дело происходит в городе, - выход в обычную городскую сеть проводной телефонной связи.

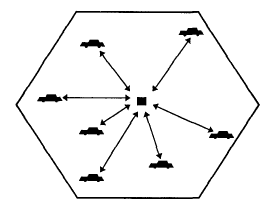
Рис. 1.2. Одна ячейка с базовой станцией в центре, обслуживающей все подвижные станции в ячейке.

На рис. 1.3. приведена функциональная схема, соответствующая описанной структуре.

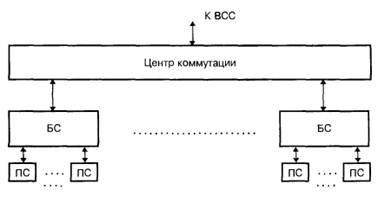
Рис. 1.3. Упрощенная функциональная схема системы сотовой связи: БС – базовая станция; ПС подвижная станция (абонентский радиотелефонный аппарат).

В действительности ячейки никогда не бывают строгой геометрической формы. Реальные границы ячеек имеют вид неправильных кривых, зависящих от условий распространения и затухания радиоволн, т.е. от рельефа местности, характера и плотности растительности и застройки и тому подобных факторов. Более того, границы ячеек вообще не являются четко определенными, так как рубеж передачи обслуживания подвижной станции из одной ячейки в другую может в некоторых пределах смещаться с изменением условий распространения радиоволн и в зависимости от направления движения подвижной станции. Точно так же и положение базовой станции лишь приближенно совпадает с центром ячейки, который к тому же не так просто определить однозначно, если ячейка имеет неправильную форму. Если же на базовых станциях используются направленные (не изотропные в горизонтальной плоскости) антенны, то базовые станции фактически оказываются на границах ячеек. Далее, система сотовой связи может включать более одного центра коммутации, что может быть обусловлено эволюцией развития системы или ограниченностью емкости коммутатора. Возможна, например, структура системы типа показанной на рис. 1.4. – с несколькими центрами коммутации, один из которых условно можно назвать «головным» или «ведущим».

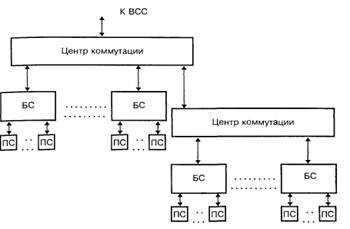
Рис. 1.4. Система сотовой связи с двумя центрами коммутации.

Рассмотрим подвижную станцию – наиболее простой по функциональному назначению и устройству элемент системы сотовой связи, к тому же это единственный элемент системы, который реально доступен пользователю.

Блок-схема подвижной станции приведена на рис. 1.5. В ее состав входят:

- блок управления;

- приемопередающий блок;

- антенный блок.

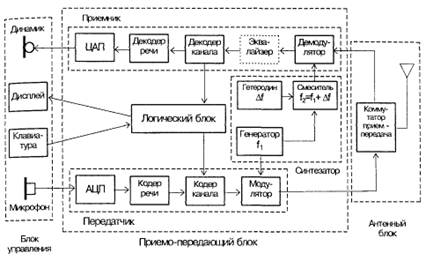
Рис. 1.5. Блок-схема подвижной станции (абонентского радиотелефонного аппарата).

Приемопередающий блок, в свою очередь, включает передатчик, приемник, синтезатор частот и логический блок.

Наиболее прост по составу антенный блок: он включает собственно антенну и коммутатор прием-передача. Последний для цифровой станции может представлять собой электронный коммутатор, подключающий антенну либо на выход передатчика, либо на вход приемника, поскольку подвижная станция цифровой системы никогда не работает на прием и передачу одновременно.

Блок управления включает микротелефонную трубку – микрофон и динамик, клавиатуру и дисплей. Клавиатура (наборное поле с цифровыми и функциональными клавишами) служит для набора номера телефона вызываемого абонента, а также команд, определяющих режим работы подвижной станции. Дисплей служит для отображения различной информации, предусматриваемой устройством и режимом работы станции.

Приемопередающий блок значительно сложнее.

В состав передатчика входят:

- аналого-цифровой преобразователь (АЦП) – преобразует в цифровую форму сигнал с выхода микрофона, и вся последующая обработка и передача сигнала речи производятся в цифровой форме, вплоть до обратного цифро-аналогового преобразования;

- кодер речи осуществляет кодирование сигнала речи – преобразование сигнала, имеющего цифровую форму, по определенным законам с целью сокращения его избыточности, т.е. с целью сокращения объема информации, передаваемой по каналу связи;

- кодер канала добавляет в цифровой сигнал, получаемый с выхода кодера речи, дополнительную (избыточную) информацию, предназначенную для защиты от ошибок при передаче сигнала по линии связи; с той же целью информация подвергается определенной переупаковке (перемножению); кроме того, кодер канала вводит в состав передаваемого сигнала информацию управления, поступающую от логического блока;

- модулятор осуществляет перенос информации кодированного видеосигнала на несущую частоту.

Приемник по составу в основном соответствует передатчику, но с обратными функциями входящих в него блоков:

- демодулятор выделяет из модулированного радиосигнала кодированный видеосигнал, несущий информацию;

- декодер канала выделяет из входного потока управляющую информацию и направляет ее на логический блок; принятая информация проверяется на наличие ошибок, и выделенные ошибки по возможности исправляются; до последующей обработки принятая информация подвергается обратной (по отношению к кодеру) переупаковке;

- декодер речи восстанавливает поступающий на него с декодера канала сигнал речи, переводя его в естественную форму, со свойственной ему избыточностью, но в цифровом виде;

- цифро-аналоговый преобразователь (ЦАП) преобразует принятый сигнал речи в аналоговую форму и подает его на выход динамика;

- эквалайзер служит для частичной  компенсации искажений сигнала  вследствие многолучевого распространения; по существу, он является адаптивным фильтром, настраиваемым по обучающей последовательности символов, входящей в состав передаваемой информации; блок эквалайзера не является, вообще говоря, функционально необходимым и в некоторых случаях может отсутствовать.

Для сочетания кодера и декодера иногда употребляют наименование кодек.

Помимо передатчика и приемника, в приемопередающий блок  входят логический блок и синтезатор частот. Логический блок – это, по сути, микрокомпьютер со своей оперативной и постоянной памятью, осуществляющий управление работой подвижной станции. Синтезатор является источником колебаний несущей частоты, используемой для передачи информации по радиоканалу. Наличие гетеродина и преобразователя частоты обусловлено  тем, что для передачи и приема используются различные участки спектра.

Блок- схема  базовой станции приведена на рис. 1.6.

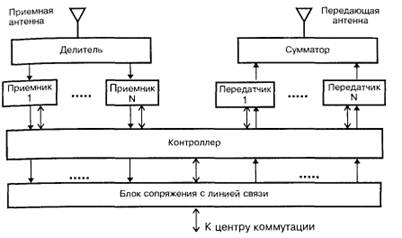
Рис. 1.6. Блок-схема базовой станции.

Наличие нескольких приемников и такого же числа передатчиков позволяет вести одновременную работу на нескольких каналах с различными частотами.

Одноименные приемники и передатчики имеют общие перестраиваемые опорные генераторы, обеспечивающие их согласованную перестройку при переходе с одного канала на другой. Для обеспечения одновременной работы N приемников на одну приемную и N передатчиков на одну передающую антенну между приемной антенной и приемниками устанавливается делитель мощности  на N выходов, а между передатчиками и передающей антенной – сумматор мощности на N входов.

Приемник и передатчик имеют ту же структуру, что и в подвижной станции, за исключением того, что здесь в них отсутствуют ЦАП и АЦП, поскольку и входной сигнал передатчика, и выходной сигнал приемника имеют цифровую форму.

Блок сопряжения с линией связи осуществляет упаковку информации, передаваемой по линии связи на центр коммутации, и распаковку принимаемой от него информации.

Контроллер базовой станции, представляющий собой достаточно мощный и совершенный компьютер, обеспечивает управление работой станции, а также контроль работоспособности всех входящих в нее блоков и узлов.

Центр коммутации является мозговым центром и одновременно диспетчерским пунктом системы сотовой связи, на который замыкаются потоки информации со всех базовых станций и через который осуществляется выход на другие сети связи – стационарную телефонную сеть, сети междугородной связи, спутниковой связи, другие сотовые сети.

Блок-схема центра коммутации представлена на рис. 1.7. Коммутатор осуществляет переключение потоков информации между соответствующими линиями связи. Он может, в частности, направить поток информации от одной базовой станции к другой, или от базовой станции к стационарной сети связи, или наоборот.

Коммутатор подключается к линиям связи через соответствующие контроллеры связи, осуществляющие промежуточную обработку (упаковку/распаковку, буферное хранение) потоков информации. Общее управление работой центра коммутации и системы в целом производится от центрального контроллера, который имеет мощное математическое обеспечение. Работа центра коммутации предполагает активное участие операторов, поэтому в состав центра входят соответствующие терминалы, а также средства отображения и регистрации (документирования) информации. Оператором вводятся данные об абонентах и условиях их обслуживания, исходные данные по режимам работы системы.

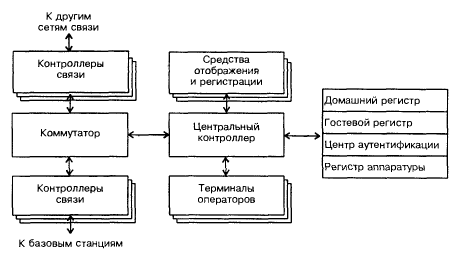
Рис. 1.7. Блок-схема центра коммутации.

Важными элементами системы являются базы данных – домашний регистр, гостевой регистр, центр аутентификации, регистр аппаратуры. Домашний регистр содержит сведения обо всех абонентах, зарегистрированных в данной системе, и о видах услуг, которые могут быть им оказаны. Здесь же фиксируется местоположение абонента для организации его вызова, и регистрируются фактически оказанные услуги. Гостевой регистр содержит примерно такие же сведения об абонентах – гостях (роумерах), т.е. об абонентах, зарегистрированных в другой системе, но пользующихся в настоящее время услугами сотовый связи в данной системе. Центр аутентификации обеспечивает процедуры аутентификации абонентов и шифрования сообщений. Регистр аппаратуры, если он существует, содержит сведения об эксплуатируемых подвижных станциях на предмет их исправности и санкционированного использования. [1]

1.2 Обслуживание абонента сетью

Интерфейс – система сигналов, посредством которых устройства системы сотовой связи соединяются друг с другом. В каждом стандарте сотовой связи используется несколько интерфейсов (различных в разных стандартах).

Из всех интерфейсов, используемых в сотовой связи, один занимает особое место – это интерфейс обмена между подвижной и базовой станциями. Он носит название эфирного интерфейса. Эфирный интерфейс обязательно используется в любой системе сотовой связи, при любой ее конфигурации и в единственном возможном для своего стандарта сотовой связи варианте.

Эфирный интерфейс системы D-AMPS стандарта IS-54 отличается сравнительной простотой (рис. 1.8.).

Канал трафика – это канал передачи речи или данных. Передача информации в канале трафика организуется следующими один за другим кадрами длительностью 40 мс. Каждый кадр состоит из шести временных интервалов – слотов; длительность слота (6.67 мс) соответствует 324 битам. При полноскоростном кодировании на один речевой канал в каждом кадре отводится два слота, т.е. 20-миллисекундный сегмент речи упаковывается в один слот, длительность которого втрое меньше. При полускоростном кодировании на один речевой канал отводится один слот в кадре, т.е. упаковка сигнала речи оказывается вдвое более плотной, чем при полноскоростном кодировании.

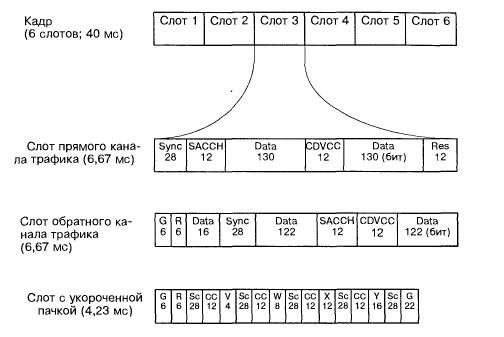
Рис.1.8. Структура кадра и слота системы D-AMPS (канал трафика; стандарт IS-54): Data – информация речи; Sync(Sc) синхронизирующая (обучающая) последовательность; SACCH – информация медленного совмещения канала управления; CDVCC(CC) – кодированный цифровой код подтверждения цвета; G – защитный бланк; R – интервал фронта импульса передатчика; V,W,X,Y – шестнадцатеричные нули; Res – резерв.

Слот имеет несколько различную структуру в прямом канале трафика – от базовой станции к подвижной и в обратном канале трафика – от подвижной станции к базовой. В обоих случаях на передачу речи отводится 260 бит. Еще 52 бита занимает управляющая и вспомогательная информация. Она включает: 28-битовую обучающую последовательность, используемую для идентификации слота в пределах кадра, синхронизации слота во времени и настройки эквалайзера; 12-битовое сообщение сигнализации (контроля и управления) канала SACCH; 12-битовое поле кодированного цифрового кода окраски (CDVCC), служащего для идентификации подвижной станции при приеме ее сигнала базовой станцией (код назначается базовой станцией индивидуально для каждого канала, т.е. для каждой подвижной станции и ретранслируется последней обратно на базовую).

Оставшиеся 12 бит в прямом канале не используются (резерв), а в обратном канале выполняют функцию защитного интервала, в течение которого не передается никакой полезной информации.

На начальном этапе установления связи используется укороченный слот, в котором многократно повторяются синхронизирующая последовательность и код CDVCC, разделяемые нулевыми числами различной длинны. В конце укороченного слота имеется дополнительный защитный бланк. Подвижная станция передает укороченные слоты до тех пор, пока базовая станция не выберет необходимую временную задержку, определяемую удалением подвижной станции от базовой.

Существуют несколько каналов связи: частотные, физические и логические.

Частотный канал – это полоса частот, отводимая для передачи информации одного канала связи. В одном частотном канале могут размещаться несколько физических, например, в методе TDMA.

Физический канал в системе с множественным доступом на основе временного разделения (TDMA) – это временной слот с определенным номером в последовательности кадров эфирного интерфейса.

Логические каналы разделяют по виду информации, передаваемой в физическом канале на канал трафика и канал управления. По каналу управления передается сигнальная информация, включающая информацию управления и информацию контроля состояния аппаратуры, а по каналу трафика передаются речь и данные.

(Трафик – это совокупность сообщений, передаваемых по линии связи).

Рассмотрим работу подвижной станции в пределах одной ячейки своей («домашней») системы, без передачи обслуживания. В этом случае в работе подвижной станции можно выделить четыре этапа, которым соответствуют четыре режима работы:

-включение и инициализация;

-режим ожидания;

-режим установления связи (вызова);

-режим ведения связи (телефонного разговора).

После включения подвижной станции производится инициализация – начальный запуск. В течение этого этапа происходит настройка подвижной станции на работу в составе системы – по сигналам, регулярно передаваемым базовыми станциями по соответствующим каналам управления, после чего подвижная станция переходит в режим ожидания.

Находясь в режиме ожидания, подвижная станция отслеживает:

-изменения информации системы – эти изменения могут быть связаны как с изменениями режима работы системы, так и с перемещениями самой подвижной станции;

-команды системы например, команду подтвердить свою работоспособность;

-получение вызова со стороны системы;

-инициализацию вызова со стороны собственного абонента.

Кроме того, подвижная станция может периодически, например раз в 10…15 минут, подтверждать свою работоспособность, передавая соответствующие сигналы на базовую станцию. В центре коммутации для каждой из включенных подвижных станций фиксируется ячейка, в которой она «зарегистрирована», что облегчает организацию процедуры вызова подвижного абонента.

Если со стороны системы поступает вызов номера подвижного абонента, центр коммутации направляет этот вызов на базовую станцию той ячейки, в которой «зарегистрирована» подвижная станция, или на несколько базовых станций в окрестности этой ячейки – с учетом возможного перемещения абонента за время, прошедшее с момента последней «регистрации», а базовые станции передают его по соответствующим каналам вызова. Подвижная станция, находящаяся в режиме ожидания, получает вызов и отвечает на него через свою базовую станцию, передавая одновременно данные, необходимые для проведения процедуры аутентификации. При положительном результате аутентификации назначается  канал трафика, и подвижной станции сообщается номер соответствующего частотного канала. Подвижная станция настраивается на выделенный канал и совместно с базовой станцией выполняет необходимые шаги по подготовке сеанса связи. На этом этапе подвижная станция настраивается на заданный номер слота в кадре, уточняет задержку во времени, подстраивает уровень излучаемой мощности и т.п. Выбор временной задержки производится с целью временного согласования слотов в кадре при организации связи с подвижными станциями, находящимися на разных дальностях от базовой. При этом временная задержка передаваемой подвижной станцией пачки регулируется по командам базовой станции.

Затем базовая станция выдает сообщение о подаче сигнала вызова (звонка), которое подтверждается подвижной станцией, и вызывающий абонент получает возможность услышать сигнал вызова. Когда вызываемый абонент отвечает на вызов, подвижная станция выдает запрос на завершение соединения. С завершением соединения начинается сеанс связи.

В процессе разговора подвижная станция производит обработку передаваемых и принимаемых сигналов речи, а также передаваемых одновременно с речью сигналов управления. По окончании разговора происходит обмен служебными сообщениями между подвижной и базовой станцией, после чего передатчик подвижной станции выключается и станция переходит в режим ожидания.

Если вызов инициируется со стороны подвижной станции, т.е. абонент набирает номер вызываемого абонента и нажимает кнопку «вызов» на панели управления, то подвижная станция передает через свою базовую станцию сообщение с указанием вызываемого номера и данными для аутентификации подвижного абонента. После аутентификации базовая станция назначает канал трафика, и последующие шаги по подготовке сеанса связи такие же, как и при поступлении вызова со стороны системы.

Затем базовая станция сообщает на центр коммутации о готовности подвижной станции, центр коммутации передает вызов в сеть, а абонент подвижной станции получает возможность слышать сигналы «вызов» или «занято». Соединение завершается на стороне сети.

При каждом установлении связи выполняются процедуры аутентификации и идентификации.

Аутентификация процедура подтверждения подлинности (действительности, законности, наличия прав на пользование услугами сотовой связи) абонента системы подвижной связи. Необходимость введения этой процедуры вызвана неизбежным соблазном получения несанкционированного доступа к услугам сотовой связи.

Идентификация – процедура установления принадлежности подвижной станции к одной из групп, обладающих определенными свойствами или признаками. Эта процедура используется для выявления утерянных, украденных или неисправных аппаратов.

Идея процедуры аутентификации в цифровой системе  сотовой связи заключается в шифровании некоторых паролей-идентификаторов с использованием квазислучайных чисел, периодически передаваемых на подвижную станцию с центра коммутации, и индивидуального для каждой подвижной станции алгоритма шифрования. Такое шифрование, с использованием одних и тех же исходных данных и алгоритмов, производится как на подвижной станции, так и в центре коммутации, и аутентификация считается закончившейся успешно, если оба результата совпадают.

Процедура идентификации заключается в сравнении идентификатора абонентского аппарата с номерами, содержащимися в соответствующих «черных списках» регистра аппаратуры, с целью изъятия из обращения украденных и технически неисправных аппаратов. Идентификатор аппарата делается таким, чтобы его изменение или подделка были трудными и экономически невыгодными.

При перемещении подвижной станции из одной ячейки в другую ее обслуживание передается от базовой станции первой ячейки к базовой станции второй (рис. 1.9.). Этот процесс называется передачей обслуживания. Он имеет место только тогда, когда подвижная станция пересекает границу ячеек во время сеанса связи и связь при этом не прерывается. Если же подвижная станция находится в режиме ожидания, она просто отслеживает эти перемещения по информации системы, передаваемой по каналу  управления, и в нужный момент перестраивается на более сильный сигнал другой базовой станции.

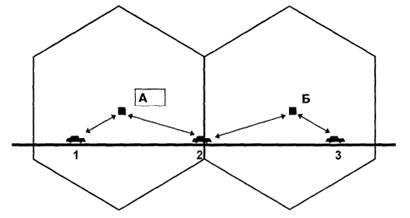
Рис. 1.9. Передача обслуживания из ячейки А в ячейку Б при пересечении подвижной станцией границы ячеей.

Необходимость в передаче обслуживания возникает, когда качество канала связи, оцениваемое по уровню сигнала и/или частоте битовой ошибки, падает ниже допустимого предела. В стандарте D-AMPS подвижная станция измеряет эти характеристики только для рабочей ячейки, но при ухудшении качества связи она сообщает об этом через базовую станцию на центр коммутации, и по команде последнего аналогичные измерения выполняются подвижными станциями в соседних ячейках. По результатам этих измерений центр коммутации выбирает ячейку, в которую должно быть передано обслуживание.

Обслуживание передается из ячейки с худшим качеством канала связи в ячейку с лучшим качеством, причем указанное различие должно быть не менее некоторой заданной величины. Если не требовать выполнения этого условия, то, например, при перемещении подвижной станции примерно вдоль границы ячеек, возможна многократная передача обслуживания из первой ячейки во вторую и обратно, приводящая к загрузке системы бессмысленной работой и к снижению качества связи.

Приняв решение о передаче обслуживания, и выбрав новую ячейку, центр коммутации сообщает об этом базовой станции новой ячейки, а подвижной станции через базовую станцию старой ячейки выдает необходимые команды с указанием нового частотного канала, номера рабочего слота и т.п. Подвижная станция перестраивается на новый канал и настраивается на совместную работу с новой базовой станцией, выполняя примерно те же шаги, что и при подготовке сеанса связи, после чего связь продолжается через базовую станцию новой ячейки. При этом перерыв в телефонном разговоре не превышает долей секунды и остается незаметным для абонента.

Система сотовой связи может оказывать функцию роуминга – это процедура предоставления услуг сотовой связи абоненту одного оператора в системе другого оператора.

Идеализированная и упрощенная схема организации роуминга такова: абонент сотовой связи, оказавшийся на территории «чужой» системы, допускающей реализацию роуминга, инициирует вызов так, как если бы он находился на территории «своей» системы. Центр коммутации, убедившись, что в его домашнем регистре этот абонент не значится, воспринимает его как роумера и заносит в гостевой регистр. Одновременно он запрашивает в домашнем регистре «родной» системы роумера относящиеся к нему сведения, необходимые для организации обслуживания, и сообщает, в какой системе роумер находится в настоящее время; последняя информация фиксируется в домашнем регистре «родной» системы роумера. После этого роумер пользуется сотовой связью как дома. [1]

1.3 Методы разделения абонентов в сотовой связи

Ресурс связи представляет время и ширину полосы, доступные для передачи сигнала в определенной системе. Для создания эффективной системы связи необходимо спланировать распределение ресурса между пользователями системы, чтобы время/частота использовались максимально эффективно. Результатом такого планирования должен быть равноправный доступ пользователей к ресурсу. Существует три основных метода разделения абонентов в системе связи.

1. Частотное разделение. Распределяются определенные поддиапазоны используемой полосы частоты.

2. Временное разделение. Абонентам выделяются периодические временные интервалы. В некоторых системах пользователям предоставляется ограниченное время для связи. В  других случаях время доступа пользователей к ресурсу определяется динамически.

3. Кодовое разделение. Выделяются определенные элементы набора ортогонально (либо почти ортогонально) распределенных спектральных кодов, каждый из которых использует весь диапазон частот.

При частотном разделении (FDMA) ресурс связи распределяется согласно рис. 1.10. Здесь распределение сигналов или пользователей по диапазону частот является долгосрочным или постоянным. Ресурс связи может одновременно содержать несколько сигналов, разнесенных в спектре.

Первичный частотный диапазон содержит сигналы, которые используют промежуток частот между f0 и f1, второй – между f2 и f3 и т.д. Области спектра, находящиеся между используемыми диапазонами, называются защитными полосами частот. Защитные полосы выполняют роль буфера, что позволяет снизить интерференцию между соседними (по частоте) каналами.

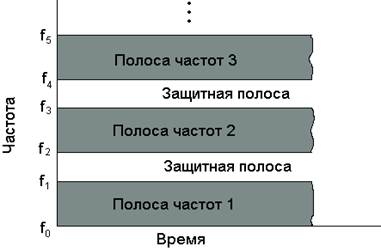
Рис. 1.10. Уплотнение с частотным разделением.

Чтобы немодулированный сигнал использовал более высокий диапазон частот, его преобразуют при помощи наложения или смешивания (модуляции) этого сигнала и синусоидального сигнала фиксированной частоты.

При временном разделении (TDMA) ресурс связи распределен путем предоставления каждому из M сигналов (пользователей) всего спектра в течение небольшого отрезка времени, называемого временным интервалом  (рис. 1.11.). Промежутки времени, разделяющие используемые интервалы, называются защитными интервалами.

Защитный интервал создает некоторую временную неопределенность между соседними сигналами и выступает в роли буфера, снижая тем самым интерференцию. Обычно время разбито на интервалы, называемые кадрами. Каждый кадр делится на временные интервалы, которые могут быть распределены между пользователями. Общая структура кадров периодически повторяется, так что передача данных по схеме TDMA это один или более временных интервалов, которые периодически повторяются на протяжении каждого кадра.

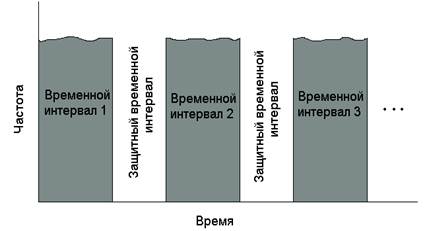
Рис. 1.11. Уплотнение с временным разделением.

Множественный доступ с кодовым разделением (CDMA) является практическим приложением методов расширения спектра, которые можно разделить на две основные категории: расширение спектра методом прямой последовательности и расширение спектра методом скачкообразной перестройки частоты.

Рассмотрим расширение спектра методом прямой последовательности. Метод расширения спектра получил свое название благодаря тому, что полоса, используемая для передачи сигнала, намного шире минимальной, необходимой для передачи данных. Итак, N пользователей получают индивидуальный код gi(t), где i = 1,2,…,N. Коды являются приблизительно ортогональными.

Блок-схема стандартной системы CDMA приведена на рис. 1.12.

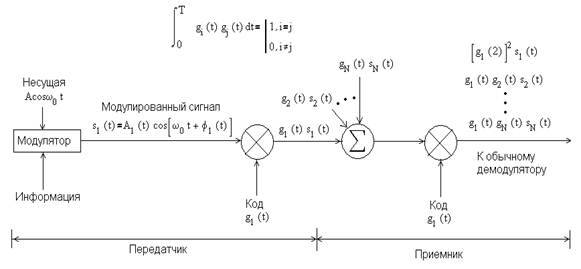
Рис. 1.12. Множественный доступ с кодовым разделением.

Первый блок схемы соответствует модуляции данными несущей волны Acosω0t. Выход модулятора, принадлежащего пользователю из группы 1, можно записать в следующем виде: s1(t)=A1(t)cos(ω0t+φ1(t)).

Вид полученного сигнала может быть произвольным. Модулированный сигнал умножается на расширяющий сигнал g1(t), закрепленный за группой 1; результат g1(t)s1(t) передается по каналу. Аналогичным образом для пользователей групп от 2 до N берется произведение кодовой функции и сигнала. Довольно часто доступ к коду ограничен четко определенной группой пользователей. Результирующий сигнал в канале является линейной комбинацией всех передаваемых сигналов. Пренебрегая задержками в передаче сигналов, указанную линейную комбинацию можно записать следующим образом: g1(t)s1(t)+ g2(t)s2(t)+…+ gN(t)sN(t).

Умножение s1(t) и g1(t) дает в результате функцию, спектр которой является сверткой спектров s1(t) и g1(t). Поскольку сигнал s1(t) можно считать узкополосным (по сравнению с g1(t)), полосы g1(t)s1(t) и g1(t) можно считать приблизительно равными. Рассмотрим приемник, настроенный на получение сообщений от группы пользователей 1. Предположим, что полученный сигнал и код g1(t), сгенерированный приемником, полностью синхронизированы между собой. Первым шагом приемника будет умножение полученного сигнала на g1(t). В результате будет получена функция g12(t)s1(t) и набор побочных сигналов g1(t)g2(t)s2(t)+ g1(t)g3(t)s3(t)+…+ g1(t)gN(t)sN(t). Если кодовые функции gi(t) взаимно ортогональны, полученный сигнал может быть идеально извлечен при отсутствии шумов, т.к.

.

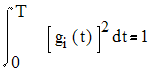Побочные сигналы легко отсеиваются системой, так как

.

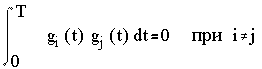Основными преимуществами CDMA являются конфиденциальность и помехоустойчивость.

1. Конфиденциальность. Если код группы пользователей известен лишь разрешенным членам этой группы, CDMA обеспечивает конфиденциальность связи, поскольку несанкционированные лица, не имеющие кода, не могут получить доступ к передаваемой информации. [2]

2. Помехоустойчивость. Модуляция сигнала последовательностью при передаче требует его повторной модуляции той же последовательностью при приеме (что эквивалентно демодуляции сигнала), в результате чего восстанавливается исходный узкополосный сигнал. Если помеха узкополосная, то демодулирующая прямая последовательность при приеме воздействует на нее как модулирующая, т.е. «размазывает» ее спектр по широкой полосе Wss, в результате чего в узкую полосу сигнала Ws попадает лишь 1/G часть мощности помехи, так что узкополосная помеха будет ослаблена в G раз, где G=Wss/Ws (Wss – полоса расширенного спектра, Ws – исходный спектр). Если же помеха широкополосная – с полосой порядка Wss или шире, то демодуляция не изменит ширины ее спектра, и в полосу сигнала помеха попадет ослабленной во столько раз, во сколько ее полоса шире полосы Ws  исходного сигнала. [1]

1.4 Стандарт DECT для связи

Системы и устройства DECT распространены более чем в 30 странах на всех континентах планеты. Фактически DECT – это набор спецификаций, определяющих радиоинтерфейсы для различных видов сетей связи и оборудования. DECT объединяет требования, протоколы и сообщения, обеспечивающие взаимодействие сетей связи и оконечного оборудования. Организация самих сетей и устройство оборудования в стандарт не входят. Важнейшая задача DECT – обеспечить совместимость оборудования различных изготовителей.

Изначально DECT был ориентирован на телефонию радиоудлинители, беспроводные учрежденческие АТС, предоставление радиодоступа к телефонным сетям общего пользования. Но стандарт оказался столь удачным, что его стали использовать в системах передачи данных, беспроводного абонентского доступа к сетям связи общего пользования. DECT нашел применение в приложениях мультимедиа и домашних радиосетях, для доступа в Интернет и факсимильной связи.

Что же представляет собой радиоинтерфейс DECT? В диапазоне шириной 20 МГц (1880 – 1900 МГц) выделено 10 несущих частот с интервалом 1,728 МГц. В DECT применяется технология доступа с временным разделением каналов – TDMA. Временной спектр разделен на отдельные кадры по 10мс (рис. 1.13.). Каждый кадр разбит на 24 временных слота: 12 слотов для приема (с точки зрения носимого терминала) и 12 – для передачи. Таким образом, на каждой из 10 несущих частот формируется 12 дуплексных каналов – всего 120. Дуплекс обеспечивается временным разделением (с интервалом 5 мс) приема/передачи. Для синхронизации применяется 32-битная последовательность «101010…». В DECT предусмотрено сжатие речи в соответствии с технологией адаптивной дифференциальной импульсно-кодовой модуляции со скоростью 32 Кбит/с. Поэтому информационная часть каждого слота – 320 бит. При передаче данных возможно объединение временных слотов. В радиотракте использована гауссова частотная модуляция.

Базовые станции (БС) и абонентские терминалы (АТ) DECT постоянно сканируют все доступные каналы (до 120). При этом измеряется мощность сигнала на каждом из каналов, которая заносится в список RSSI. Если канал занят или сильно зашумлен, показатель RSSI для него высокий. БС выбирает канал с самым низким значением RSSI для постоянной передачи служебной информации о вызовах абонентов, идентификаторе станции, возможностях системы и т.д. Эта информация играет роль опорных сигналов для АТ – по ним абонентские устройства определяют, есть ли право доступа к той или иной БС, предоставляет ли она требуемые абоненту услуги, есть ли в системе свободная емкость и выбирают БС с наиболее качественным сигналом.

В DECT канал связи всегда определяет АТ. При запросе соединения от БС (входящее соединение) АТ получает уведомление и выбирает радиоканал. Служебная информация передается базовой станцией и анализируется абонентским терминалом постоянно, следовательно, АТ всегда синхронизируется с самой близкой из доступных БС. При установлении нового соединения АТ выбирает канал с самым низким значением RSSI – это гарантирует, что новое соединение происходит на самом «чистом» канале из доступных. Данная процедура динамического распределения каналов позволяет избавиться от частотного планирования важнейшее свойство DECT.

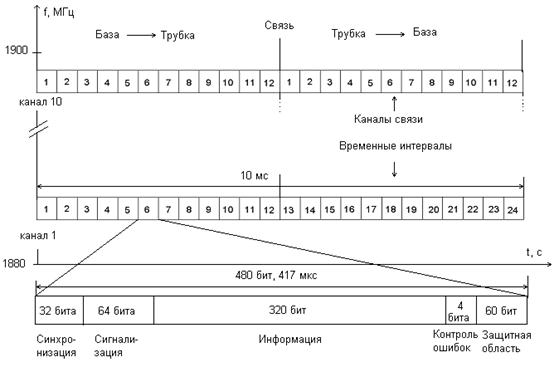
Рис. 1.13. Спектр DECT.

Поскольку АТ постоянно, даже при установленном соединении, анализирует доступные каналы, может происходить их динамическое переключение во время сеанса связи. Такое переключение возможно как на другой канал той же БС, так и на другую БС. Эта процедура называется «хэндовер». При хэндовере АТ устанавливает новое соединение, и какое-то время связь поддерживается по обоим каналам. Затем выбирается лучший. Автоматическое переключение между каналами разных БС происходит практически незаметно для пользователя и полностью инициируется АТ.

Существенно, что в радиотракте аппаратуры DECT мощность сигнала весьма мала – от 10 до 250 мВт. Причем 10 мВт – практически номинальная мощность для микросотовых систем с радиусом соты 30 – 50 м внутри здания и до 300 – 400 м на открытом пространстве. Передатчики мощностью до 250 мВт используются для радиопокрытия больших территорий (до 5 км).

При мощности 10 мВт возможно располагать базовые станции на расстоянии 25 м. В результате достигается рекордная плотность одновременных соединений (около 100 тыс. абонентов) при условии расположения БС по схеме шестиугольника в одной плоскости (на одном этаже).

Для защиты от несанкционированного доступа в системах DECT используется процедура аутентификации БС и АТ. АТ регистрируется в системе или на отдельных базовых станциях, к которым имеет допуск. При каждом соединении происходит аутентификация: БС посылает АТ «запрос» - случайное число (64 бит). АТ и БС на основании этого числа и ключа аутентификации по заданному алгоритму вычисляют аутентификационный ответ (32 бит), который АТ передает на БС. БС сравнивает вычисленный ответ с принятым и при их совпадении разрешает подключение АТ. В DECT существует стандартный аутентификационный алгоритм DSAA.

Как правило, ключ аутентификации вычисляется на основании абонентского аутентификационного ключа UAK длиной 128 бит либо аутентификационного кода AC (16 32 бит). UAK хранится в ПЗУ АТ либо в карточке DAM – аналоге SIM-карты. AC можно и вручную записать в ПЗУ АТ либо вводить при аутентификации. Совместно с UAK применяют и персональный идентификатор пользователя UPI длиной 16- 32 бита, вводимый только вручную. Кроме того, несанкционированный съем информации в системах с TDMA крайне сложен и доступен только специалистам. [3]

1.5 Стандарты Bluetooth, Wi-Fi (802.11, 802.16)

Спецификация Bluetooth описывает пакетный способ передачи информации с временным мультиплексированием. Радиообмен происходит в полосе частот 2400-2483,5 МГц. В радиотракте применен метод расширения спектра посредством частотных скачков и двухуровневая гауссова частотная модуляция.

Метод частотных скачков подразумевает, что вся отведенная для передачи полоса частот подразделяется на определенное количество подканалов шириной 1МГц каждый. Канал представляет собой псевдослучайную последовательность скачков по 79 или 23 радиочастотным подканалам. Каждый канал делится на временные сегменты продолжительностью 625 мкс, причем каждому сегменту соответствует определенный подканал. Передатчик в каждый момент времени использует только один подканал. Скачки происходят синхронно в передатчике и приемнике в заранее зафиксированной псевдослучайной последовательности. За секунду может происходить до 1600 частотных скачков. Такой метод обеспечивает конфиденциальность и некоторую помехозащищенность передач. Помехозащищенность обеспечивается тем, что если на каком-либо подканале передаваемый пакет не смог быть принят, то приемник сообщает об этом и передача пакета повторяется на одном из следующих подканалов, уже на другой частоте.

Протокол Bluetooth поддерживает как соединения типа точка-точка, так и точка-многоточка. Два или более использующих один и тот же канал устройства образуют пикосеть. Одно из устройств работает как основное, а остальные – как подчиненные. В одной пикосети может быть до семи активных подчиненных устройств, при этом остальные подчиненные устройства находятся в состоянии «парковки», оставаясь синхронизированными с основным устройством. Взаимодействующие пикосети образуют «распределенную сеть».

В каждой пикосети действует только одно основное устройство, однако подчиненные устройства могут входить в различные пикосети. Кроме того, основное устройство одной пикосети может являться подчиненным в другой (рис.1.14.). Пикосети не синхронизированы друг с другом по времени и частоте – каждая из них использует свою  последовательность частотных скачков. В одной же пикосети все устройства синхронизированы по времени и частотам. Последовательность скачков является уникальной для каждой пикосети и определяется адресом ее основного устройства. Длина цикла псевдослучайной последовательности – 227 элементов.

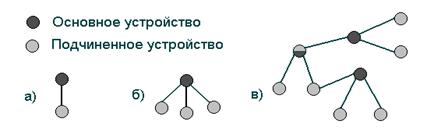
Рис. 1. 14. Пикосеть с одним подчиненным устройством а), несколькими б) и распределенная сеть в).

В стандарте Bluetooth предусмотрена дуплексная передача на основе разделения времени. Основное устройство передает пакеты в нечетные временные сегменты, а подчиненное устройство – в четные (рис. 1.15.). Пакеты в зависимости от длины могут занимать до пяти временных сегментов. При этом частота канала не меняется до окончания передачи пакета (рис. 1.16.).

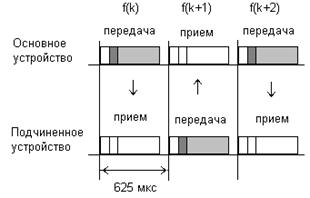
Рис. 1. 15. Временная диаграмма работы канала.

Протокол Bluetooth может поддерживать асинхронный канал данных, до трех синхронных (с постоянной скоростью) голосовых каналов или канал с одновременной асинхронной передачей данных и синхронной передачей голоса.

При синхронном соединении основное устройство резервирует временные сегменты, следующие через так называемые синхронные интервалы. Даже если пакет принят с ошибкой, повторно при синхронном соединении он не передается. При асинхронной связи используются временные сегменты, не зарезервированные для синхронного соединения. Если в адресном поле асинхронного пакета адрес не указан, пакет считается «широковещательным» – его  могут читать все устройства. Асинхронное соединение позволяет повторно передавать пакеты, принятые с ошибками.

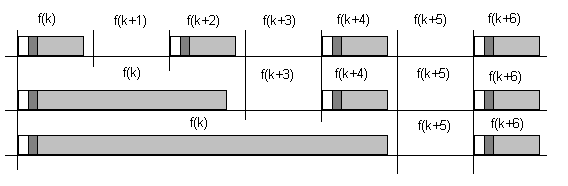
Рис. 1. 16. Передача пакетов различной длины.

Стандартный пакет Bluetooth содержит код доступа длиной 72 бита, 54-битный заголовок и информационное поле длиной не более 2745 бит. Код доступа идентифицирует пакеты, принадлежащие одной пикосети, а также используется для синхронизации и процедуры запросов. Он включает преамбулу (4 бита), слово синхронизации (64 бита) и трейлер – 4 бита контрольной суммы.

Заголовок содержит информацию для управления связью и состоит из шести полей: AM_ADDR – 3-битный адрес активного элемента; TYPE – 4-битный код типа данных; FLOW – 1 бит управления потоком данных, показывающий готовность устройства к приему; ARQN 1 бит подтверждения правильного приема; SEQN – 1 бит, служащий для определения последовательности пакетов; HEC – 8-битная контрольная сумма.

Информационное поле, в зависимости от типа пакетов, может содержать либо поля голоса, либо поля данных, либо оба типа полей одновременно.

Рассмотрим стандарт IEEE 802.11, используемый в локальных сетях передачи данных – т.е. в Ethernet-подобных беспроводных сетях, принципиально асинхронных по своей природе.

IEEE 802.11 рассматривает два нижних уровня модели взаимодействия открытых систем – физический (определяются способ работы со средой передачи, скорость и методы модуляции) и уровень звена данных, причем на последнем уровне рассматривается нижний подуровень – MAC, т.е. управление доступом к каналу (среде передачи). IEEE 802.11 использует диапазон 2,400 – 2,4835 ГГц с шириной полосы 83,5 МГц и предусматривает пакетную передачу с 48-битовыми адресными пакетами.

Стандарт предусматривает два основных способа организации локальной сети – по принципу «каждый с каждым» (связь устанавливается непосредственно между двумя станциями, все устройства должны находится в зоне радиовидимости, никакого администрирования не происходит) и в виде структурированной сети (появляется дополнительное устройство – точка доступа, как правило, стационарная и действующая на фиксированном канале; связь между устройствами происходит только через точки доступа, через них же возможен выход во внешние проводные сети).

Как правило, функции управления распределены между всеми устройствами сети IEEE 802.11 – режим DCF. Однако для структурированных сетей возможен режим PCF, когда управление передано одной определенной точке доступа. Необходимость в режиме PCF возникает при передаче чувствительной к задержкам информации. Ведь сети IEEE 802.11 действуют по принципу конкурентного доступа к каналу – приоритетов нет. Чтобы их при необходимости задавать, и введен режим PCF. Однако работа в данном режиме может происходить только в определенные периодически повторяющиеся интервалы.

Для безопасности передачи данных на MAC-уровне предусмотрены аутентификация станций и шифрование передаваемых данных.

IEEE 802.11 осуществляет множественный доступ к каналу связи с контролем несущей и обнаружением конфликтов. Станция может начать передачу, только если канал свободен. Если станции обнаруживают, что на одном канале пытаются работать несколько станций, все они прекращают передачу и пытаются возобновить ее через случайный промежуток времени. Таким образом, даже при передаче устройство должно контролировать канал, т.е. работать на прием.

Перед первой попыткой получить доступ к каналу устройство загружает длительность случайного интервала ожидания в специальный счетчик. Его значение декрементируется с заданной частотой, пока канал свободен. Как только счетчик обнулится, устройство может занимать канал. Если до обнуления счетчика канал занимает другое устройство, счет останавливается, сохраняя достигнутое значение. При следующей попытке отсчет начинается с сохраненной величины. В результате не успевший в прошлый раз получает больше шансов занять канал в следующий раз. В проводных сетях Ethernet подобного нет.

Пакеты, посредством которых происходит передача, фактически формируются на MAC-уровне, на физическом уровне к ним добавляется заголовок физического уровня (PLCP), состоящий из преамбулы и собственно PLCP-заголовка. Пакеты MAC-уровня могут быть трех типов – пакеты данных, контрольные и пакеты управления. Их структура одинакова. Каждый пакет включает MAC-заголовок, информационное поле и контрольную сумму. [3]

В широкополосных городских беспроводных сетях передачи данных с фиксированным доступом используется стандарт IEEE 802.16.

Стандарт IEEE 802.16 описывает работу в диапазоне 10 – 66 ГГц систем с архитектурой «точка-многоточка» (из центра - многим). Это двунаправленная система, т.е. предусмотрены нисходящий (от базовой станции к абонентам) и восходящий (к базовой станции) потоки. При этом каналы подразумеваются широкополосные (порядка 25 МГц), а скорости передачи – высокие (например, 120 Мбит/с).

Стандарт IEEE 802.16 предусматривает схему с модуляцией одной несущей (в каждом частотном канале) и допускает три типа квадратурной амплитудной модуляции: четырехпозиционную QPSK и 16-позиционную 16-QAM(обязательны для всех устройств), а также 64-QAM(опционально).

Данные на физическом уровне передаются в виде непрерывной последовательности кадров. Каждый кадр имеет фиксированную длительность – 0,5; 1 и 2 мс. Кадр состоит из преамбулы (синхропоследовательности  длиной 32 QPSK-символа), управляющей секции, последовательности пакетов с данными. Поскольку определяемая стандартом IEEE 802.16 система двунаправленная, необходим дуплексный механизм. Он предусматривает как частотное, так и временное разделение восходящего и нисходящего каналов. При временном дуплексировании каналов кадр делится на нисходящий и восходящий субкадры, разделенные специальным интервалом. При частотном дуплексировании восходящий и нисходящий каналы транслируются каждый на своей несущей.

MAC-уровень IEEE 802.16 подразделяется на три подуровня – подуровень преобразования сервиса (сервисы это различные приложения), основной подуровень и подуровень защиты. На подуровне защиты реализуются механизмы аутентификации и шифрование данных. На подуровне преобразования сервиса происходит трансформация потоков данных протоколов верхних уровней для передачи данных через сети IEEE 802.16. Для каждого типа приложений верхних уровней стандарт предусматривает свой механизм преобразования. На основном подуровне MAC формируются пакеты данных, которые затем передаются на физический уровень и транслируются через канал связи. Пакет MAC включает заголовок и поле данных, за которым может следовать контрольная сумма.

Ключевой момент в стандарте IEEE 802.16 – это понятие сервисного потока и связанные с ним понятия «соединение» и «идентификатор соединения» (CID). Сервисным потоком в стандарте IEEE 802.16 называется поток данных, связанный с определенным приложением. В этом контексте соединение – это установление логической связи на MAC-уровнях на передающей и приемной стороне для передачи сервисного потока. Каждому соединению присваивается 16-разрядный идентификатор CID, с которым однозначно связаны тип и характеристики соединения. Сервисный поток характеризуется набором требований к каналу передачи информации (к времени задержки символов, уровню флуктуаций задержек и гарантированной пропускной способности). Каждому сервисному потоку присваивается идентификатор SFID, основываясь на котором БС определяют необходимые параметры связанного с данным сервисным потоком конкретного соединения.

Основной принцип предоставления доступа к каналу в стандарте IEEE 802.16 – это доступ по запросу. Ни одна АС (абонентская станция) не может ничего передавать, кроме запросов на регистрацию и предоставление канала, пока БС не разрешит ей этого, т.е. отведет временной интервал в восходящем канале и укажет его расположение. АС может, как запрашивать определенный размер полосы в канале, так и просить об изменении уже предоставленного ей канального ресурса. Стандарт IEEE 802.16 предусматривает два режима предоставления доступа – для каждого отдельного соединения и для всех соединений определенной АС. Очевидно, что первый механизм обеспечивает большую гибкость, однако второй существенно сокращает объем служебных сообщений и требует меньшей производительности от аппаратуры. [7]

2. Системы сложных сигналов для телекоммуникационных систем

2.1 Спектры сигналов

Спектр сигнала s(t) определяется преобразованием Фурье

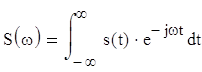
В общем случае спектр является комплексной функцией частоты ω. Спектр может быть представлен в виде

,

где |S(ω)| – амплитудный, а φ(ω) – фазовый спектр сигнала s(t).

Спектр сигнала обладает следующими свойствами:

1. Линейность: если имеется совокупность сигналов s1(t), s2(t), …, причем s1(t)S1(ω), s2(t)S2(ω), …, то сумма сигналов преобразуется по Фурье следующим образом:

,

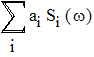где ai – произвольные числовые коэффициенты.

2. Если сигналу s(t) соответствует спектр S(ω), то такому же сигналу, смещенному на t0, соответствует спектр S(ω) умноженный на e-jωt0 s(t-t0)S(ω)e-jωt0.

3. Если s(t)S(ω), то

4. Если s(t)S(ω) и f(t)=ds/dt, то f(t)F(ω)=jωS(ω).

5. Если s(t)S(ω) и g(t)=∫s(t)dt, то g(t)G(ω)=S(ω)/jω.

6. Если u(t)U(ω), v(t)V(ω) и s(t)=u(t)v(t), то

.

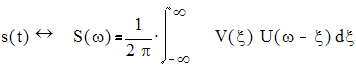Сигнал находится по спектру с помощью обратного преобразования Фурье

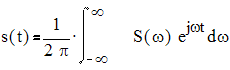.[4]

Рассмотрим спектры некоторых сигналов.

1. Прямоугольный импульс.

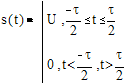
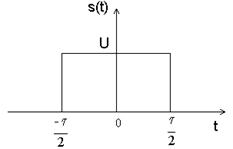
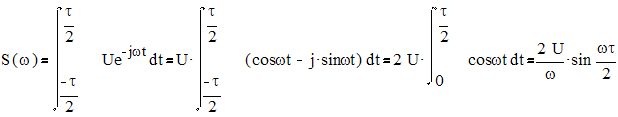
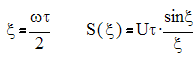
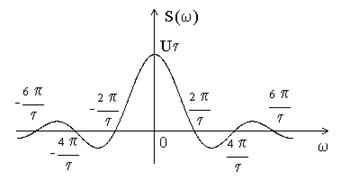
Рис.2.1. Спектр прямоугольного импульса.

2. Гауссовский импульс.

s(t)=Uexp(-βt2)

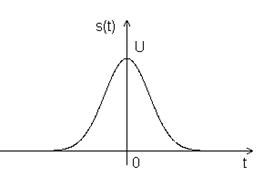
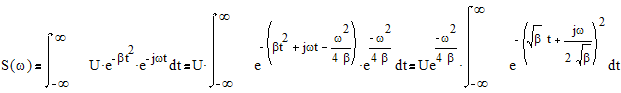
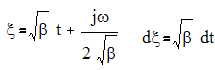
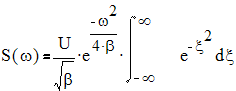
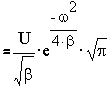
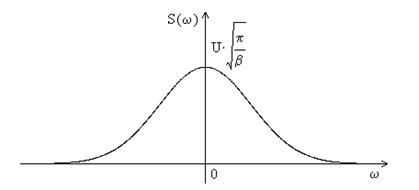
Рис.2.2. Спектр гауссовского импульса.

3. Сглаженный импульс

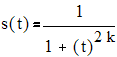
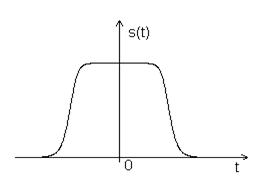
С помощью численного интегрирования находим спектр S(ω).

S(0)=2.052                  S(6)=-0.056

S(1)=1.66                    S(7)=0.057

S(2)=0.803                  S(8)=0.072

S(3)= 0.06                   S(9)=0.033

S(4)=-0.259                S(10)=-0.0072

S(5)=-0.221                S(ω)=S(-ω)

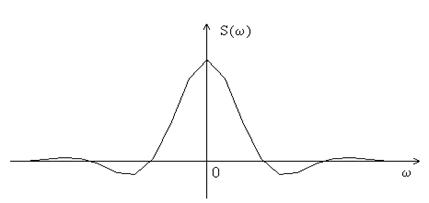
Рис. 2.3. Спектр сглаженного импульса.

2.2 Корреляционные свойства сигналов

Для сравнения сигналов, сдвинутых во времени, вводят автокорреляционную функцию (АКФ) сигнала. Она количественно определяет степень отличия сигнала u(t) и его смещенной во времени копии u(t - τ) и равна скалярному произведению сигнала и копии:

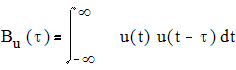
Непосредственно видно, что при τ=0 автокорреляционная функция становится равной энергии сигнала: Bu(0)=Eu.

Автокорреляционная функция четна: Bu(τ)=Bu(-τ).

При любом значении временного сдвига τ модуль АКФ не превосходит энергии сигнала |Вu(τ)|≤Bu(0)=Eu.

АКФ связана со спектром сигнала следующим соотношением:

.

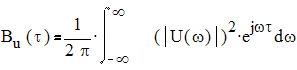Верно и обратное:

.

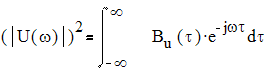Для дискретного сигнала АКФ определяется в следующем виде:

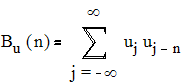
и обладает следующими свойствами.

Дискретная АКФ четна: Bu(n)=Bu(-n).

При нулевом сдвиге АКФ определяет энергию дискретного сигнала:

.

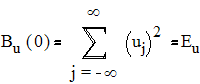Иногда вводят взаимнокорреляционную функцию (ВКФ) сигналов, которая описывает не только сдвиг сигналов друг относительно друга по времени, но и различие в форме сигналов.

ВКФ определяется следующим образом

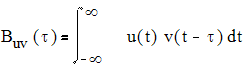
для непрерывных сигналов и

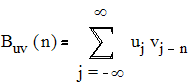
для дискретных сигналов. [4]

Рассмотрим АКФ некоторых сигналов.

1. Последовательность прямоугольных импульсов

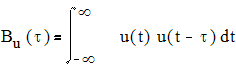
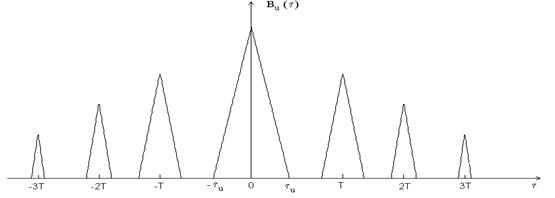
Рис. 2.4. АКФ последовательности прямоугольных импульсов.

2. 7-позиционный сигнал Баркера

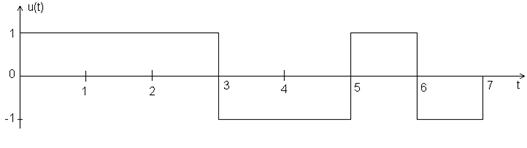
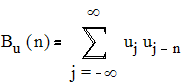
Bu(0)=7, Bu(1)= Bu(-1)=0, Bu(2)= Bu(-2)=-1, Bu(3)= Bu(-3)=0, Bu(4)= Bu(-4)=-1, Bu(5)= Bu(-5)=0, Bu(6)= Bu(-6)=-1, Bu(7)= Bu(-7)=0.

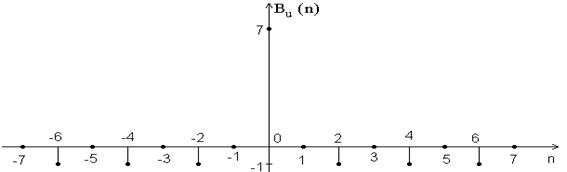
Рис. 2.5. АКФ 7-позиционного сигнала Баркера.

3. 8-позиционные функции Уолша

Функция Уолша 2-го порядка

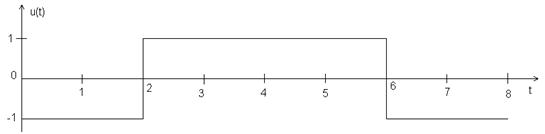
Bu(0)=8, Bu(1)= Bu(-1)=3, Bu(2)= Bu(-2)=-2, Bu(3)= Bu(-3)=-3, Bu(4)= Bu(-4)=-4, Bu(5)= Bu(-5)=-1, Bu(6)= Bu(-6)=2, Bu(7)= Bu(-7)=1, Bu(8)= Bu(-8)=0.

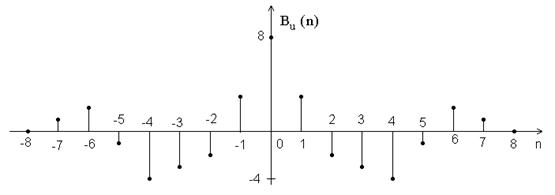
Рис. 2.6. АКФ функции Уолша 2-го порядка.

Функция Уолша 7-го порядка

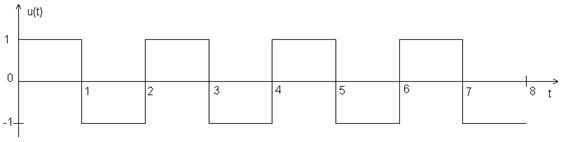
Bu(0)=8, Bu(1)= Bu(-1)=-7, Bu(2)= Bu(-2)=6, Bu(3)= Bu(-3)=-5, Bu(4)= Bu(-4)=4, Bu(5)= Bu(-5)=-3, Bu(6)= Bu(-6)=2, Bu(7)= Bu(-7)=-1, Bu(8)= Bu(-8)=0.

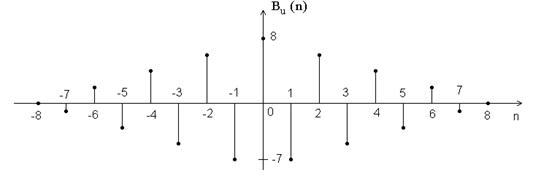
Рис. 2.7. АКФ функции Уолша 7-го порядка.

2.3 Типы сложных сигналов

Сигнал – это физический процесс, который может нести полезную информацию и распространяться по линии связи. Под сигналом s(t) будем понимать функцию времени, отображающую физический процесс, имеющий конечную длительность Т.

Сигналы, у которых база В, равная произведению длительности сигнала Т на ширину его спектра, близка к единице, называются «простыми» или «обыкновенными». Различение таких сигналов может быть осуществлено по частоте, времени (задержке) и фазе.

Сложные, многомерные, шумоподобные сигналы формируются по сложному закону. За время длительности сигнала Т он подвергается дополнительной манипуляции (или модуляции) по частоте или фазе. Дополнительная модуляция по амплитуде используется редко. За счет дополнительной модуляции спектр сигнала Δf (при сохранении его длительности Т) расширяется. Следовательно, для такого сигнала B=T Δf>>1.

При некоторых законах формирования сложного сигнала его спектр оказывается сплошным и практически равномерным, т.е. близким к спектру шума с ограниченной шириной полосы. При этом функция автокорреляции сигнала имеет один основной выброс, ширина которого определяется не длительностью сигнала, а шириной его спектра, т.е. имеет вид, аналогичный функции автокорреляции шума с ограниченной полосой частот. В связи с этим такие сложные сигналы называют шумоподобными. [5]

Шумоподобные сигналы получили применение в широкополосных системах связи, так как: обеспечивают высокую помехозащищенность систем связи; позволяют организовать одновременную работу многих абонентов в общей полосе частот; позволяют успешно бороться с многолучевым распространением радиоволн путем разделения лучей; обеспечивают лучшее использование спектра частот на ограниченной территории по сравнению с узкополосными системами связи.

Известно большое число различных шумоподобных сигналов (ШПС). Тем не менее, выделяют следующие основные ШПС: частотно-модулированные сигналы; многочастотные сигналы; фазоманипулированные сигналы; дискретные частотные сигналы; дискретные составные частотные сигналы.

Частотно-модулированные сигналы (ЧМ) являются непрерывными сигналами, частота которых меняется по заданному закону (рис. 2.8.).

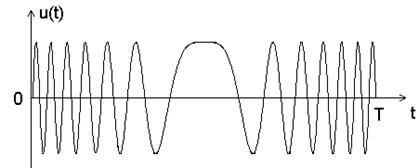
Рис. 2.8. ЧМ сигнал.

В системах связи необходимо иметь множество сигналов. При этом необходимость быстрой смены сигналов и переключения аппаратуры формирования и обработки приводят к тому, что закон изменения частоты становится дискретным. При этом от ЧМ сигналов переходят к ДЧ сигналам.

Многочастотные (МЧ) сигналы являются суммой N гармоник u1(t)…uN(t), амплитуды и фазы которых определяются в соответствии с законами формирования сигналов (рис. 2.9.).

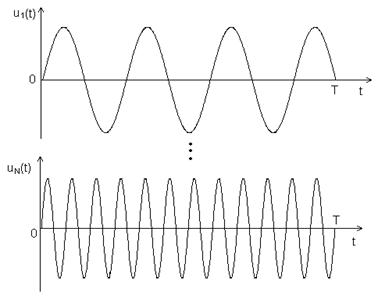
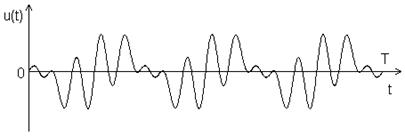
Рис. 2.9. МЧ сигнал.

МЧ сигналы являются непрерывными и для их формирования и обработки трудно приспособить методы цифровой техники.

Фазоманипулированные (ФМ) сигналы представляют последовательность радиоимпульсов, фазы которых изменяются по заданному закону (рис. 2.10., а). Обычно фаза принимает два значения (0 или π). При этом радиочастотному ФМ сигналу соответствует видео-ФМ сигнал (рис. 2.10., б).

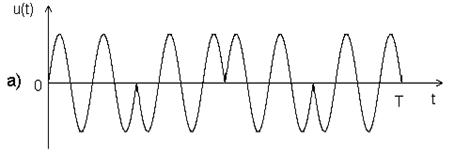
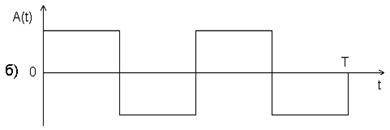
Рис. 2.10. ФМ сигнал.

ФМ сигналы весьма распространены, т.к. они позволяют широко использовать цифровые методы при формировании и обработке, и можно реализовать такие сигналы с относительно большими базами.

Дискретные частотные (ДЧ) сигналы представляют последовательность радиоимпульсов (рис. 2.11.), несущие частоты которых изменяются по заданному закону.

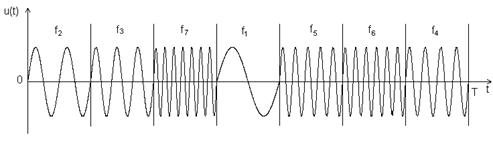
Рис. 2.11. ДЧ сигнал.

Дискретные составные частотные (ДСЧ) сигналы являются ДЧ сигналами, у которых каждый импульс заменен шумоподобным  сигналом.

На рис. 2.12. изображен видеочастотный ФМ сигнал, отдельные части которого передаются на различных несущих частотах. [6]

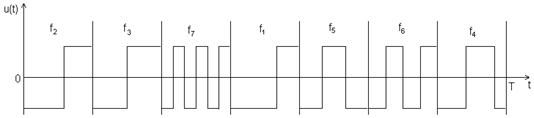
Рис. 2.12. ДСЧ сигнал.

2.4 Производные системы сигналов

Производным сигналом называется сигнал, который получается в результате перемножения двух сигналов. В случае ФМ сигналов перемножение должно осуществляться поэлементно или, как чаще называют, посимвольно. Система, составленная из производных сигналов, называется производной. Среди производных систем особое значение имеют системы, построенные следующим образом. В качестве основы используется некоторая система сигналов, корреляционные свойства которой не вполне удовлетворяют требованиям к КФ, но которая обладает определенными преимуществами с точки зрения простоты формирования и обработки. Такая система называется исходной. Затем выбирается сигнал, который обладает определенными свойствами. Такой сигнал называется производящим. Умножая производящий сигнал на каждый сигнал исходной системы, получаем производную систему. Производящий  сигнал следует выбирать так, чтобы производная система была действительно лучше исходной, т.е. чтобы она обладала хорошими корреляционными свойствами. Комплексная огибающая производного сигнала Sμm(t) равна произведению комплексных огибающих исходных сигналов Um(t)  и производящего сигнала Vμ(t), т.е. Sμm(t)= Um(t)Vμ(t). Если индексы изменяются в пределах m=1..M, μ=1..H, то объем производной системы сигналов L=MH.

Выбор производящих сигналов определяется рядом факторов, в том числе и исходной системой. Если сигналы исходной системы широкополосные, то производящий сигнал может быть широкополосным и иметь малые уровни боковых пиков функции неопределенности, близкие к среднеквадратическому значению. Если же сигналы исходной системы узкополосные, то достаточно выполнения неравенства FV>>FU (FV – ширина спектра производящих сигналов, FU – ширина спектра исходных сигналов) и требования малости боковых пиков АКФ.

Возьмем в качестве исходной – систему Уолша. В этом случае производящие сигналы должны быть широкополосными и иметь хорошие АКФ. Кроме того, производящий сигнал должен иметь столько же элементов, что и исходные сигналы, т.е. N=2k элементов, где k – целое число. Этим условиям в целом удовлетворяют нелинейные последовательности. Поскольку основным является требование малости боковых пиков АКФ, то в классе нелинейных последовательностей были отобраны наилучшие сигналы с числом элементов N=16, 32, 64. Эти сигналы показаны на рис. 2.13. На рис. 2.13. указаны также значения числа блоков μ для каждого производящего сигнала. Они близки к оптимальному значению μ0=(N+1)/2. Это и является необходимым условием получения хорошей АКФ с малыми боковыми пиками.

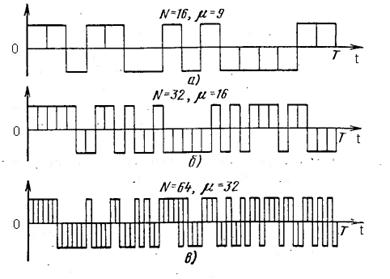
Рис. 2.13. Производящие ФМ сигналы.

Объем производной системы равен объему системы Уолша N. Производные системы обладают лучшими корреляционными свойствами, чем системы Уолша. [6]

3. Модуляция сложных сигналов

3.1 Геометрическое представление сигналов

Рассмотрим геометрическое или векторное представление сигналов. Определим  N-мерное ортогональное пространство как пространство, определяемое набором N линейно независимых функций {ψj(t)}, именуемых базисными. Любая функция этого пространства может выражаться через линейную комбинацию базисных функций, которые должны удовлетворять условию

,

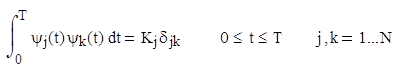где оператор   называется символом Кронекера. При ненулевых константах Kj пространство именуется ортогональным. Если базисные функции нормированы так, что все Kj=1, пространство называется ортонормированным. Основное условие ортогональности можно сформулировать следующим образом: каждая функция ψj(t) набора базисных функций должна быть независимой от остальных функций набора. Каждая функция ψj(t) не должна интерферировать с другими функциями в процессе обнаружения. С геометрической точки зрения все функции ψj(t) взаимно перпендикулярны.

В ортогональном сигнальном пространстве проще всего определяется Евклидова мера расстояния, используемая в процессе обнаружения. Если волны, переносящие сигналы, не формируют подобного пространства, они могут преобразовываться в линейную комбинацию ортогональных сигналов. Можно показать, что произвольный конечный набор сигналов {si(t)} (i=1…M), где каждый элемент множества физически реализуем и имеет длительность T, можно выразить как линейную комбинацию N ортогональных сигналов ψ1(t), ψ2(t), …, ψN(t), где N M, так что

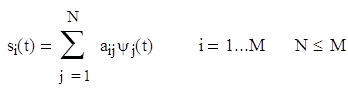где

.

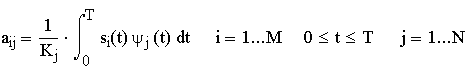Вид базиса {ψj(t)} не задается; эти сигналы выбираются с точки зрения удобства и зависят от формы волн передачи сигналов. Набор таких волн {si(t)} можно рассматривать как набор векторов {si}={ai1, ai2, ,aiN}. Взаимная ориентация векторов сигналов описывает связь между сигналами (относительно их фаз или частот), а амплитуда каждого вектора набора {si} является мерой энергии сигнала, перенесенной в течение времени передачи символа. Вообще, после выбора набора из N ортогональных функций, каждый из переданных сигналов si(t) полностью определяется вектором его коэффициентов si=(ai1, ai2, ,aiN) i=1…M. [2]

3.2 Методы фазовой манипуляции сигналов (ФМ2, ФМ4, ОФМ)

Фазовая манипуляция (PSK) была разработана в начале развития программы исследования дальнего космоса; сейчас схема PSK широко используется в коммерческих и военных системах связи. Сигнал в модуляции PSK имеет следующий вид:

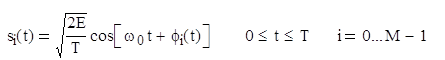
Здесь фаза φi(t) может принимать M дискретных значений, обычно определяемых следующим образом:

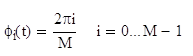
Самым простым примером фазовой манипуляции является двоичная фазовая манипуляция (ФМ2). Параметр E – это энергия символа, T – время передачи символа. Работа схемы модуляции заключается в смещении фазы модулируемого сигнала si(t) на одно из двух значений, нуль или π (1800). Типичный вид сигнала ФМ2 приведен на рис. 3.1.a), где явно видны характерные резкие изменения фазы при переходе между символами; если модулируемый поток данных состоит из чередующихся нулей и единиц, такие резкие изменения будут происходить при каждом переходе. Модулированный сигнал можно представить как вектор на графике в полярной системе координат; длина вектора соответствует амплитуде сигнала, а его ориентация в общем M-арном случае – фазе сигнала относительно других M – 1 сигналов набора. При модуляции ФМ2 (рис. 3.1.б)) векторное представление дает два противофазных (1800) вектора. Наборы сигналов, которые могут быть представлены подобными противофазными векторами, называются антиподными. [2]

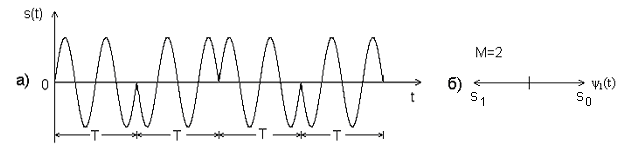
Рис. 3.1. Двоичная фазовая манипуляция.

Еще одним примером фазовой манипуляции является модуляция ФМ4 (М=4). При модуляции ФМ4 параметр E – это энергия двух символов, время T –  время передачи двух символов. Фаза модулированного сигнала принимает одно из четырех возможных значений: 0, π/2, π, 3π/2. В векторном представлении сигнал ФМ4 имеет вид, показанный на рис. 3.2.

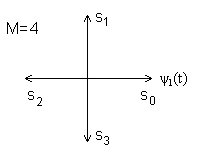
Рис. 3.2. Сигнал ФМ4 в векторном представлении.

Рассмотрим еще один вид фазовой манипуляции – относительную фазовую манипуляцию (ОФМ) или дифференциальную фазовую манипуляцию (DPSK). Название дифференциальная фазовая манипуляция требует некоторого пояснения, поскольку со словом «дифференциальный» связано два различных аспекта процесса модуляции/демодуляции: процедура кодирования и процедура обнаружения. Термин «дифференциальное кодирование» употребляется тогда, когда кодировка двоичных символов определяется не их значением (т.е. нуль или единица), а тем, совпадает ли символ с предыдущим или отличается от него. Термин «дифференциальное когерентное обнаружение» сигналов в дифференциальной модуляции PSK  (именно в этом значении обычно используется название DPSK) связан со схемой обнаружения, которая зачастую относится к некогерентным схемам, поскольку не требует согласования по фазе с принятой несущей.

В некогерентных системах не предпринимаются попытки определить действительное значение фазы поступающего сигнала. Следовательно, если переданный сигнал имеет вид

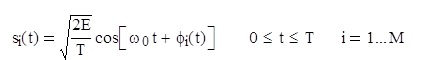
то принятый сигнал можно описать следующим образом.

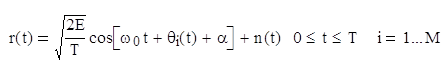
Здесь α произвольная константа, обычно предполагаемая случайной переменной, равномерно распределенной между нулем и 2π, а n(t) – шум.

Для когерентного обнаружения используются согласованные фильтры; для некогерентного обнаружения подобное невозможно, поскольку в этом случае выход согласованного фильтра будет зависеть от неизвестного угла α. Но если предположить, что α меняется медленно относительно интервала в два периода (2Т), то разность фаз между двумя последовательными сигналами не будет зависеть от α.

Основа дифференциального когерентного обнаружения сигналов в модуляции DPSK состоит в следующем. В процессе демодуляции в качестве опорной фазы может применяться фаза несущей предыдущего интервала передачи символа. Ее использование требует дифференциального кодирования последовательности сообщений в передатчике, поскольку информация кодируется разностью фаз между двумя последовательными импульсами. Для передачи i-го сообщения (i=1,2,…,M) фаза текущего сигнала должна быть смещена на φi=2πi/M радиан относительно фазы предыдущего сигнала. Вообще, детектор вычисляет координаты поступающего сигнала путем определения его корреляции с локально генерируемыми сигналами cosω0t и  sinω0t. Затем, как показано на рис. 3.3., детектор измеряет угол между вектором текущего принятого сигнала и вектором предыдущего сигнала.

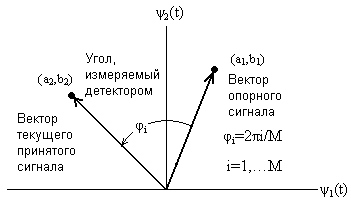
Рис. 3.3. Сигнальное пространство для схемы DPSK.

Схема DPSK менее эффективна, чем PSK, поскольку в первом случае, вследствие корреляции между сигналами, ошибки имеют тенденцию к распространению (на соседние времена передачи символов). Стоит помнить, что схемы PSK и DPSK отличаются тем, что в первом случае сравнивается принятый сигнал с идеальным опорным, а во втором – два зашумленных сигнала. Отметим, что модуляция DPSK дает вдвое больший шум, чем модуляция PSK. Следовательно, при использовании DPSK следует ожидать вдвое большей вероятности ошибки, чем в случае PSK. Преимуществом схемы DPSK можно назвать меньшую сложность системы. [2]

3.3 Модуляция с минимальным частотным сдвигом.

Одной из схем модуляции без разрыва фазы является манипуляция с минимальным частотным сдвигом (MSK). MSK можно рассматривать как частный случай частотной манипуляции без разрыва фазы. Сигнал MSK можно представить следующим образом.

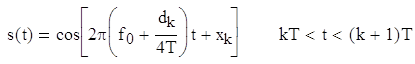
Здесь f0 – несущая частота, dk=±1 представляет биполярные данные, которые передаются со скоростью R=1/T, а xk – это фазовая постоянная для k-го интервала передачи двоичных данных. Отметим, что при dk=1 передаваемая частота – это f0+1/4T, а при dk=-1 – это f0-1/4T. В течение каждого Т-секундного интервала передачи данных значение xk постоянно, т.е. xk=0 или π, что диктуется требованием непрерывности фазы сигнала в моменты t=kT. Это требование накладывает ограничение на фазу, которое можно представить следующим рекурсивным соотношением для xk.

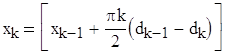
Уравнение для s(t) можно переписать в квадратурном представлении.

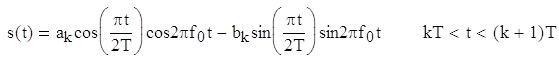
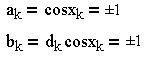
Синфазный компонент обозначается как akcos(πt/2T)cos2πf0t, где cos2πf0t – несущая, cos(πt/2T) – синусоидальное взвешивание символов, ak – информационно-зависимый член. Подобным образом квадратурный компонент – это  bksin(πt/2T)sin2πf0t, где sin2πf0t – квадратурное слагаемое несущей, sin(πt/2T) – такое же синусоидальное взвешивание символов, bk – информационно-зависимый член. Может показаться, что величины ak и bk могут изменять свое значение каждые T секунд. Однако из-за требования непрерывности фазы величина ak может измениться лишь при переходе функции cos(πt/2T) через нуль, а bk – только при переходе через нуль sin(πt/2T). Следовательно, взвешивание символов в синфазном или квадратурном канале – это синусоидальный импульс с периодом 2T и переменным знаком. Синфазный и квадратурный компоненты сдвинуты относительно друг друга на T секунд.

Выражение для s(t) можно переписать в иной форме.

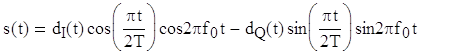
Здесь dI(t) и dQ(t) имеют такой же смысл синфазного и квадратурного потоков данных. Схема MSK, записанная в таком виде, иногда называется MSK с предварительным кодированием. Графическое представление s(t) дано на рис. 3.4. На рис. 3.4. а) и в) показано синусоидальное взвешивание импульсов синфазного и квадратурного каналов, здесь умножение на синусоиду дает более плавные переходы фазы, чем в исходном представлении данных. На рис. 3.4. б) и г) показана модуляция ортогональных компонентов cos2πf0t и sin2πf0t синусоидальными потоками данных. На рис. 3.4. д) представлено суммирование ортогональных компонентов, изображенных на рис. 3.4. б) и г). Из выражения для s(t) и рис.3.4. можно заключить следующее: 1) сигнал s(t) имеет постоянную огибающую; 2) фаза радиочастотной несущей непрерывна при битовых переходах; 3) сигнал s(t) можно рассматривать как сигнал, модулированный FSK, с частотами передачи f0+1/4T и f0-1/4T. Таким образом, минимальное разнесение тонов, требуемое при модуляции MSK, можно записать следующим образом:

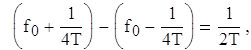
что равно половине скорости передачи битов. Отметим, что разнесение тонов, требуемое для MSK, – это  половина (1/T) разнесения, необходимого при некогерентном обнаружении сигналов, модулированных FSK. Это объясняется тем, что фаза несущей известна и непрерывна, что позволяет осуществить когерентную демодуляцию сигнала. [2]

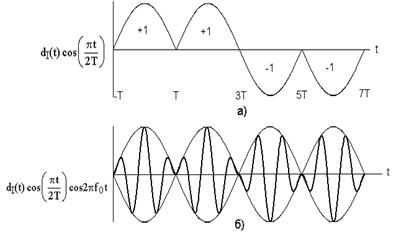
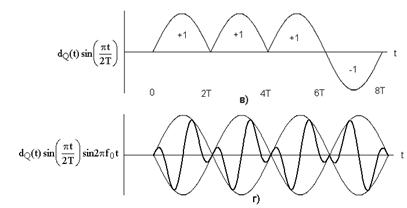
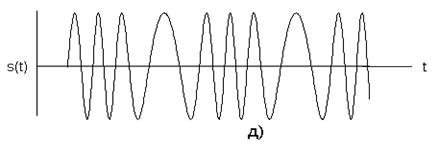
Рис. 3.4. Манипуляция с минимальным сдвигом: а) модифицированный  синфазный поток битов; б) произведение синфазного потока битов и несущей; в) модифицированный квадратурный поток битов; г) произведение квадратурного потока битов и несущей; д) сигнал MSK.

3.4 Квадратурная модуляция и ее характеристики (QPSK, QAM)

Рассмотрим квадратурную фазовую манипуляцию (QPSK). Исходный поток данных dk(t)=d0, d1, d2,… состоит из биполярных импульсов, т.е. dk принимают значения +1 или -1 (рис. 3.5.а)), представляющие двоичную единицу и двоичный нуль. Этот поток импульсов разделяется на синфазный поток dI(t) и квадратурный - dQ(t), как показано на рис. 3.5.б).

dI(t)=d0, d2, d4,… (четные биты)

dQ(t)=d1, d3, d5,… (нечетные биты)

Удобную ортогональную реализацию сигнала QPSK можно получить, используя амплитудную модуляцию синфазного и квадратурного потоков на синусной и косинусной функциях несущей.

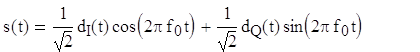
С помощью тригонометрических тождеств s(t) можно представить в следующем виде: s(t)=cos(2πf0t+θ(t)). Модулятор QPSK, показанный на рис. 3.5.в), использует сумму синусоидального и косинусоидального слагаемых. Поток импульсов dI(t) используется для амплитудной модуляции (с амплитудой +1 или -1) косинусоиды. Это равноценно сдвигу фазы косинусоиды на 0 или π; следовательно, в результате получаем сигнал BPSK. Аналогично поток импульсов dQ(t) модулирует синусоиду, что дает сигнал BPSK, ортогональный предыдущему. При суммировании этих двух ортогональных компонентов несущей получается сигнал QPSK. Величина θ(t) будет соответствовать одному из четырех возможных сочетаний dI(t) и dQ(t) в выражении для s(t): θ(t)=00, ±900 или 1800; результирующие векторы сигналов показаны в сигнальном пространстве на рис. 3.6. Так как cos(2πf0t) и sin(2πf0t) ортогональны, два сигнала BPSK можно обнаруживать раздельно. QPSK обладает рядом преимуществ перед BPSK: т.к. при модуляции QPSK один импульс передает два бита, то в два раза повышается скорость передачи данных или при той же скорости передачи данных, что и в схеме BPSK, используется в два раза меньшая полоса частот; а так же повышается помехоустойчивость, т.к. импульсы в два раза длиннее, а следовательно и больше по мощности, чем импульсы BPSK. [2]

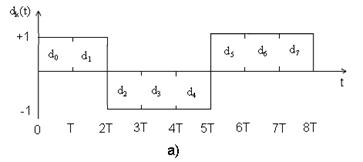
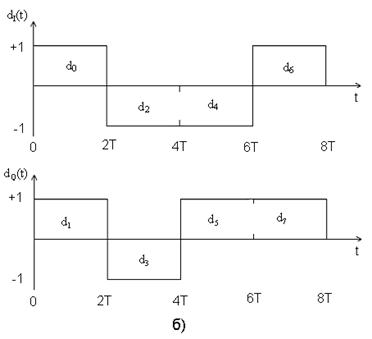
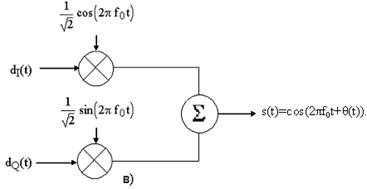
Рис. 3.5. Модуляция QPSK.

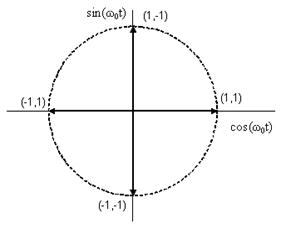
Рис. 3.6. Сигнальное пространство для схемы QPSK.

Квадратурную амплитудную модуляцию (KAM, QAM) можно считать логическим продолжением QPSK, поскольку сигнал QAM также состоит из двух независимых амплитудно-модулированных несущих.

При квадратурной амплитудной модуляции изменяется как фаза, так и амплитуда сигнала, что позволяет увеличить количество кодируемых бит и при этом существенно повысить помехоустойчивость. Квадратурное представление сигналов является удобным и достаточно универсальным средством их описания. Квадратурное представление заключается в выражении колебания линейной комбинацией двух ортогональных составляющих – синусоидальной и косинусоидальной (синфазной и квадратурной):

s(t)=A(t)cos(ωt + φ(t))=x(t)sinωt + y(t)cosωt, где

x(t)=A(t)(-sinφ(t)),y(t)=A(t)cosφ(t)

Такая дискретная модуляция (манипуляция) осуществляется по двум каналам, на несущих, сдвинутых на 900 друг относительно друга, т.е. находящихся в квадратуре (отсюда и название).

Поясним работу квадратурной схемы на примере формирования сигналов четырехфазной ФМ (ФМ-4) (рис. 3.7).

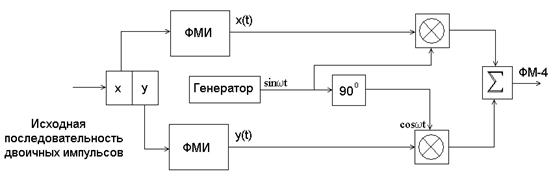
Рис. 3.7. Схема квадратурного модулятора.

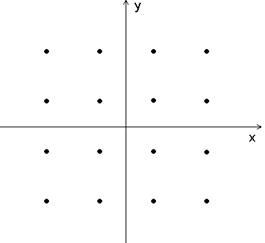
Рис. 3.8. 16-ричное пространство сигналов (QAM-16).

Исходная последовательность двоичных символов длительностью Т при помощи регистра сдвига разделяется на нечетные импульсы y, которые подаются в квадратурный канал (cosωt), и четные – x, поступающие в синфазный канал (sinωt). Обе последовательности импульсов поступают на входы соответствующих формирователей манипулированных импульсов, на выходах которых образуются последовательности биполярных импульсов x(t) и y(t) с амплитудой ±Um и длительностью 2T. Импульсы x(t) и y(t) поступают на входы канальных перемножителей, на выходах которых формируются двухфазные (0, π) ФМ колебания. После суммирования они образуют сигнал ФМ-4.

На рис. 3.8. показано двухмерное пространство сигналов и набор векторов сигналов, модулированных 16-ричной QAM и изображенных точками, которые расположены в виде прямоугольной совокупности.

Из рис. 3.8. видно, что расстояние между векторами сигналов в сигнальном пространстве при QAM больше, чем при QPSK, следовательно, QAM является более помехоустойчивой по сравнению с QPSK,

3.5 Реализация квадратурных модемов

Модем предназначен для передачи/приема информации по обычным телефонным проводам. В этом смысле модем осуществляет роль интерфейса между компьютером и телефонной сетью. Его основная задача заключается в преобразовании передаваемой информации к виду, приемлемому для передачи по телефонным каналам связи, и в преобразовании принимаемой информации к виду, приемлемому для компьютера. Как известно, компьютер способен обрабатывать и передавать информацию в двоичном коде, то есть в виде последовательности логических нулей и единиц, называемых битами. Логической единице можно поставить в соответствие высокий уровень напряжения, а логическому нулю — низкий. При передаче информации по телефонным проводам необходимо, чтобы характеристики передаваемых электрических сигналов (мощность, спектральный состав и т.д.) соответствовали требованиям приемной аппаратуры АТС. Одно из основных требований заключается в том, чтобы спектр сигнала лежал в диапазоне от 300 до 3400 Гц, то есть имел ширину не более 3100 Гц. Для того чтобы удовлетворить этому и многим другим требованиям, данные подвергаются соответствующему кодированию, которым, собственно, и занимается модем. Существует несколько способов возможной кодировки, при которых данные можно передавать по абонентским коммутируемым каналам. Эти способы отличаются друг от друга, как скоростью передачи, так и помехоустойчивостью. В то же время, независимо от способа кодировки, данные передаются по абонентским каналам только в аналоговом виде. Это означает, что для передачи информации используется синусоидальный несущий сигнал, который подвергается аналоговой модуляции. Применение аналоговой модуляции приводит к спектру гораздо меньшей ширины при неизменной скорости передачи информации. Аналоговая модуляция — это такой способ физического кодирования, при котором информация кодируется изменением амплитуды, частоты и фазы синусоидального сигнала несущей частоты. Существует несколько базовых способов аналоговой модуляции: амплитудная, частотная и относительная фазовая. В модемах используются перечисленные способы модуляции, но не по отдельности, а все вместе. К примеру, амплитудная модуляция может использоваться совместно с фазовой модуляцией (амплитудно-фазовая модуляция). Главная проблема, возникающая при передаче информации по абонентским каналам, — это повышение скорости. Скорость ограничивается шириной спектральной полосы пропускания канала связи. Однако имеется способ, позволяющий значительно повысить скорость передачи информации без увеличения ширины спектра сигнала. Основная идея такого способа заключается в использовании многопозиционного кодирования. Последовательность бит данных разбивается на группы (символы), каждой из которых ставится в соответствие некоторое дискретное состояние сигнала. Например, используя 16 различных состояний сигнала (они могут отличаться друг от друга, как по амплитуде, так и по фазе), можно закодировать все возможные комбинации для последовательностей из 4 бит. Соответственно 32 дискретных состояния позволят закодировать в одном состоянии группу из пяти бит. На практике для повышения скорости передачи информации используется в основном многопозиционная амплитудно-фазовая модуляция с несколькими возможными значениями уровней амплитуды и сдвига фазы сигнала. Такой тип модуляции получил название квадратурной амплитудной модуляции (КАМ). В случае КАМ состояния сигнала удобно изображать на сигнальной плоскости. Каждая точка сигнальной плоскости имеет две координаты: амплитуду и фазу сигнала и представляет собой закодированную комбинацию последовательности бит. Для повышения помехоустойчивости квадратурной амплитудной модуляции может использоваться так называемая треллис-модуляция (Trellis Code Modulation, ТСМ) или, иначе, решетчатое кодирование. При треллис-модуляции к каждой группе бит, передаваемых за одно дискретное состояние сигнала, добавляется еще один избыточный треллис-бит. Если, к примеру, информационные биты разбиты на группы по 4 бита (всего возможно 16 различных комбинаций), то в сигнальной плоскости размещается 16 сигнальных точек. Добавление пятого треллис-бита приведет к тому, что возможных комбинаций окажется 32, то есть количество сигнальных точек увеличится вдвое. Однако не все комбинации бит являются разрешенными, то есть имеющими смысл. В этом и заключается идея треллис-кодирования. Значение добавляемого треллис-бита определяется по особому алгоритму. Расчетом добавляемого треллис-бита занимается специальный кодер. На принимающем модеме для анализа поступающих последовательностей битов предназначен специальный декодер — так называемый декодер Витерби. Если принимаемые последовательности являются разрешенными, то считается, что передача происходит без ошибок и треллис-бит просто удаляется. Если же среди принимаемых последовательностей встречаются запрещенные последовательности, то при помощи особого алгоритма декодер Витерби находит наиболее подходящую разрешенную последовательность, исправляя, таким образом, ошибки передачи. Итак, смысл решетчатого кодирования — ценой сравнительно небольшой избыточности повысить помехоустойчивость передачи. Использование треллис-кодирования позволяет главным образом, защитить от перепутывания именно соседние в сигнальном пространстве точки, которые как раз более всего подвержены возможности «перепутаться» под действием помех.

4. Характеристики приема сигналов в телекоммуникационных системах

4.1 Вероятности ошибок различения M известных сигналов

Под обнаружением сигнала в радиоэлектронике понимают анализ принятого колебания y(t), завершающийся вынесением решения о наличии или отсутствии в нем некоторой полезной составляющей, которую и называют сигналом. Различение М сигналов определяют как анализ принятого колебания y(t), заканчивающийся принятием решения о том, какой именно из М сигналов, принадлежащих указанному заранее множеству S{s0(t), s1(t), …, sM-1(t)} присутствует в y(t). Обнаружение сигнала есть частный случай различения двух сигналов, один из которых равен нулю на всем интервале наблюдения.

Пусть наблюдаемое колебание y(t) является реализацией случайного процесса, который имеет распределение Wy, т.е. n-мерную плотность вероятности (ПВ) W(y) [либо функционал ПВ W(y(t))], принадлежащее одному из М непересекающихся классов Wi (Wi∩Wk=Ø, i≠k, i, k=0, 1, …, M-1). Необходимо, пронаблюдав реализацию y(t), решить, какому из классов принадлежит Wy. Предположение о том, что WyWi, называют гипотезой Hi: WyWi. Решения, являющиеся результатом проверки гипотез, будем обозначать , где i{0, 1, …, M-1} – номер гипотезы, истинность которой декларируется принятым решением. Анализируемое колебание y(t) является результатом взаимодействия присутствующего в нем сигнала si(t) с мешающим случайным процессом (помехой, шумом) x(t): y(t)=F[si(t), x(t)]. От того, какой из М возможных сигналов присутствует в y(t), зависит ПВ ансамбля, которому принадлежит y(t), так что каждому si(t) соответствует некоторый класс Wi распределений ансамбля, представляемого y(t). Таким образом, гипотезы Hi трактуются как предположения о наличии i-го (и только i-го) сигнала в y(t). При этом решения , одно из которых служит итогом процедуры различения, есть утверждения о том, что в принятом колебании содержится именно i-й сигнал. Гипотезам Hi соответствуют классы Wi. Гипотезу Hi называют простой, если класс Wi содержит одно и только одно распределение. Любую другую гипотезу называют сложной. М сложных гипотез называют параметрическими, если соответствующие им классы отличаются друг от друга только значениями конечного числа параметров одного и того же распределения, описываемого известным законом. В противном случае гипотезы именуют параметрическими.

Рассмотрим различение М детерминированных ненулевых сигналов одинаковой энергии. При этом за основу будет принято правило максимального правдоподобия (МП)

оптимальное в том случае, когда критерием качества служит сумма условных вероятностей ошибок, либо полная вероятность ошибки при равных апостериорных вероятностях всех сигналов pi=1/M.

При произвольном М различитель, придерживающийся правила МП, считает присутствующим в y(t) сигнал, наименее удаленный от y(t) в смысле евклидова расстояния  или, что при одинаковых энергиях сигналов равносильно, имеющий с y(t) максимальную корреляцию 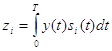. Если рассматривать сигналы  s0(t), s1(t), …, sM-1(t) как пучок векторов, расположенный в М-мерном пространстве, то для того чтобы по возможности уменьшить вероятность перепутывания i-го сигнала с k-м, следует максимально «раздвинуть» i-й и k-й векторы. Таким образом, оптимальный выбор М детерминированных сигналов сводится к поиску такой конфигурации пучка М векторов, в которой минимальное евклидово расстояние между парой векторов было бы максимальным: min dik=max (i≠k). Так как при равенстве энергий, т.е. длин векторов

,

где ρik – коэффициент корреляции i-го и k-го сигналов, Е – энергия сигнала, то требование максимума минимального расстояния тождественно условию минимума максимального коэффициента корреляции в множестве сигналов S{s0(t), s1(t), …, sM-1(t)}. Предельно достижимый минимум максимального коэффициента корреляции устанавливается довольно легко. Просуммировав ρik по всем i и k, получим

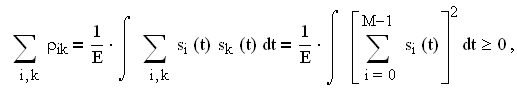
где неравенство следует из неотрицательности квадрата под интегралом. Кроме того, в сумме слева М слагаемых при i=k равны единице, а остальные М(М-1) не больше ρмакс=max ρik (i≠k). Поэтому М+М(М-1)ρмакс≥0 и ρмакс≥-1/(М-1).

Конфигурацию из М векторов, в которой косинус угла между любой парой векторов равен -1/(М-1), называют правильным симплексом. Если эти векторы взять в качестве М сигналов, то полученный детерминированный ансамбль при равновероятности всех si(t) обеспечит минимум полной вероятности ошибки Pош, что и решает вопрос об оптимальном выборе М сигналов. При М>>1 выполняется соотношение -1/(М-1)≈0, и поэтому при большом числе различаемых сигналов ортогональный ансамбль практически не проигрывает симплексному в значении Pош.

Последовательность вывода точного выражения для вероятности ошибки различения М сигналов с произвольными ρik такова. Плотность вероятности (ПВ) системы случайных величин z0, z1, …, zM-1 есть М-мерный нормальный закон, для задания которого достаточно знать средние всех zi и их корреляционную матрицу. Для средних при истинности гипотезы Hl имеем . Корреляционный же момент i-й и k-й корреляций равен N0Eρik/2. После того как М-мерная ПВ найдена, ее М-кратный интеграл по области zl≥zi, i=0, 1, …, M-1, позволяет получить вероятность правильного решения при условии истинности Hl. Сумма таких вероятностей, деленная на М (с учетом равновероятности сигналов), будет полной вероятностью правильного решения Pпр, связанной с Pош очевидным равенством Pош=1-Pпр. Получаемый таким образом М-кратный интеграл в ряде важных случаев удается свести к однократному. Так, для любых равнокоррелированных (равноудаленных) сигналов (ρik=ρ, i≠k)

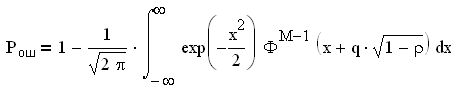
В практических расчетах это выражение используют редко из-за необходимости численного интегрирования. Полезна его оценка сверху, для вывода которой будем считать, что истинна гипотеза Hl. При этом ошибка происходит всегда, когда истинно хотя бы одно из событий zi>zl, i≠l. Вероятность ее Pошl, равная вероятности объединения  событий zi>zl, i≠l, по теореме сложения вероятностей,

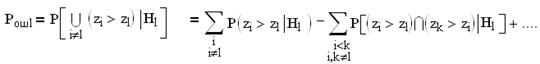
и в силу неравенства Буля не больше первой суммы справа. Так как каждое слагаемое этой суммы есть вероятность перепутывания двух сигналов [sl(t) с si(t)], то для равноудаленных сигналов

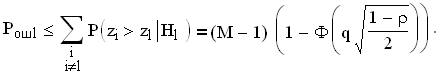
Здесь  - отношение сигнал/шум на выходе фильтра, согласованного с si(t) при гипотезе Hi,  - вероятность перепутывания двух сигналов. При равновероятных сигналах (pi=1/M) приходим к так называемой аддитивной границе полной вероятности ошибки

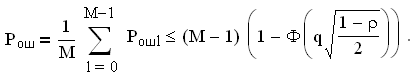
Использование этого выражения оправдывается, с одной стороны, асимптотическим сближением его правой части и Pош по мере роста требований к качеству различения (Pош→0), а с другой – тем, что, выбирая необходимую энергию сигналов (минимальное значение q) исходя из правой части выражения, разработчик всегда действует с известной перестраховкой, гарантируя удержание фактической вероятности ошибки ниже цифры, принятой им при расчете. [9]

4.2 Вероятности ошибок различения M флуктуирующих сигналов

Далеко не всегда наблюдатель подробно априори осведомлен о различаемых сигналах. Чаще ему заранее не известны не только номер присутствующего в анализируемой реализации сигнала, но и значения каких-либо параметров (амплитуды, частоты, фазы и пр.) каждого из М возможных сигналов. Сами сигналы при этом уже не являются детерминированными, поскольку параметры их не заданы; соответствующую задачу различения называют различением сигналов с неизвестными параметрами.

Рассмотрим решение этой задачи на примере различения сигналов со случайными начальными фазами. Такие сигналы описываются моделью

si(t; φ)=Re{i(t)exp[j(2πf0t+φ)]},

где f0 – известная центральная частота; φ – случайная начальная фаза с априорной ПВ W0(φ); (t) =S(t)ejγ(t) – комплексная огибающая сигнала s(t), являющегося реализацией s(t; φ) при φ=0: s(t)=s(t; 0); S(t) и γ(t) – известные законы амплитудной и угловой модуляции. Применению правила МП должно предшествовать вычисление  функции (функционала) правдоподобия (ФП) W(y(t)|Hi), т.е. усреднение ФП W(y(t)|Hi, φ), построенной для детерминированных сигналов с фиксированной фазой φ по всем ее возможным значениям с учетом априорной ПВ W0(φ). При равномерной ПВ фазы W0(φ)=1/(2π), |φ|≤π, с учетом равенства энергий всех различаемых сигналов W(y(t)|Hi) представляет собой модифицированную функцию Бесселя нулевого порядка:

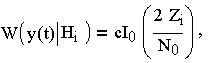
где c – коэффициент, содержащий сомножители, не зависящие от i, а 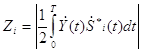 - модуль корреляции комплексных огибающих принятого колебания y(t) и i-го сигнала. Монотонность функции I0(·) на положительной полуоси позволяет перейти к достаточной статистике Zi и записать правило МП в виде

Таким образом, оптимальный различитель М сигналов равной энергии со случайными начальными фазами должен вычислить все М величин Zi и, если максимальной из них является Zk, принять решение о присутствии в y(t) k-го сигнала. Это означает, что содержащимся в наблюдаемом колебании y(t) считается тот сигнал, комплексная огибающая которого имеет наибольшую по модулю корреляцию с комплексной огибающей y(t).

Точные формулы для вероятностей ошибок различения М произвольных сигналов достаточно громоздки даже при  М=2, однако в приложениях чаще других встречаются ансамбли сигналов, ортогональных в усиленном смысле. Последнее означает, что любые два несовпадающих сигнала si(t; φi), sk(t; φk) ортогональны при любых значениях начальных фаз:

∫si(t; φi)sk(t; φk)dt=0 при любых φi, φk и i≠k,

или, что эквивалентно, ортогональны детерминированные комплексные огибающие этих сигналов:

 .

Условие ортогональности в усиленном смысле жестче обычного требования ортогональности, фигурировавшего ранее в применении к детерминированным сигналам. Так, два отрезка косинусоиды, сдвинутые на угол ±π/2, являясь ортогональными в обычном смысле, не ортогональны при изменении сдвига фаз, т.е. в усиленном смысле. В то же время сигналы, не перекрывающиеся по времени или по спектру, ортогональны и в усиленном смысле.

Если обратиться сначала к различению двух сигналов, нетрудно понять, что противоположная пара, минимизирующая Pош в классе детерминированных сигналов, в задачах, где начальные фазы сигналов случайны, неприемлема. Действительно, единственным признаком, по которому различаются противоположные сигналы, является знак, т.е. присутствие или отсутствие в начальной фазе слагаемого π. Однако, когда перед поступлением на различитель каждый из сигналов приобретает случайный фазовый сдвиг, попытки использовать начальную фазу, в качестве характерного признака сигнала, бессмысленны, и в различителе от неинформативной величины φ приходится избавляться. Таким образом, можно прийти к выводу, что в классе М≥2 сигналов со случайными фазами симплексные ансамбли оптимальными свойствами не обладают. Оптимальными же оказываются именно ансамбли сигналов, ортогональных в усиленном смысле: каждый из таких сигналов вызывает отклик на выходе только одного из фильтров приемной схемы, и поэтому перепутывание i-го сигнала с k-м произойдет лишь в том случае, когда огибающая шума на выходе k-го согласованного фильтра (СФ) будет иметь значение, превосходящее значение огибающей суммы сигнала с шумом на выходе i-го СФ. Нарушение условия ортогональности в усиленном смысле  приведет к появлению реакции на i-й сигнал на выходе не только i-го, но и других СФ, например k-го, в результате чего выброс огибающей на выходе k-го СФ, больший значения Zi, станет более вероятным.

Чтобы найти вероятность перепутывания p01 s0(t; φ) с s1(t; φ) при различении двух сигналов, необходимо проинтегрировать совместную ПВ Z0, Z1 при гипотезе H0 W(Z0, Z1|H0) по области Z1>Z0. Для ортогональных в усиленном смысле сигналов величины Z0 и Z1 независимы, поэтому W(Z0, Z1|H0)=W(Z0|H0)W(Z1|H0). Одномерные же ПВ Z0 и Z1 известны: при истинности H0 Z0 как огибающая суммы сигнала с шумом имеет обобщенную рэлеевскую ПВ; Z1 как огибающая только шума является рэлеевской случайной величиной. Перемножив эти ПВ, после интегрирования полученной ПВ W(Z0, Z1|H0) и с учетом очевидного равенства p01=p10 для полной вероятности ошибки различения двух равновероятных ортогональных в усиленном смысле сигналов со случайными фазами получим

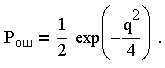
Повторение рассуждений пункта 4.2. (для детерминированных сигналов) приводит к аддитивной границе

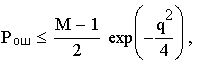
которой, как правило, и пользуются для оценки вероятности ошибки, если число равновероятных ортогональных в усиленном смысле сигналов М≥2. [9]

4.3 Расчет ошибок различения M сигналов с неизвестными неэнергетическими параметрами

Рассмотрим задачу различения «М» ортогональных сигналов с неизвестным временным положением в асинхронных системах связи с кодовым разделением каналов. Решение о наличии сигнала в канале выносится по методу максимального правдоподобия. Найдем вероятность ошибки различения с учетом выбросов шума на интервале возможных временных задержек сигналов.

Предположим, что имеется «М» абонентов системы связи, каждый из которых использует свой сигнал. Наибольшую помехоустойчивость при передаче информации в таких условиях обеспечивают симплексные сигналы. При М>>1 помехоустойчивость такой системы сигналов практически совпадает с помехоустойчивостью системы ортогональных сигналов, для которых

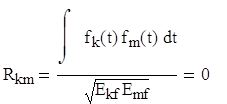
Здесь Ekf – энергия сигнала fk. Условие ортогональности, которое можно назвать «ортогональностью в точке», на практике требует системы единого времени для организации синхронной связи. В асинхронных системах используются ортогональные в усиленном смысле сигналы, для которых  при всех значениях τk и τm

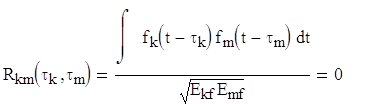
Если Rkm(τk, τm)<0.25 – 0.3, то можно считать ансамбль сигналов практически удовлетворяющим условию ортогональности.

Будем рассматривать систему сложных сигналов {fk(t)}, k=1…M ортогональную при произвольном сдвиге. Среди сложных сигналов весьма широкое применение получили фазоманипулированные (ФМ) сигналы с комплексной огибающей вида

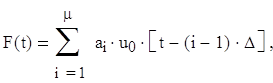
где ai – код последовательности, u0(t) форма огибающей элементарной посылки, Δ – ее длительность. В случае прямоугольной формы огибающей элементарной посылки автокорреляционная функция (АКФ) имеет вид:

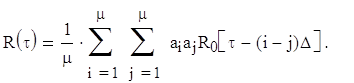
Здесь R0(τ)=(1-|τ|/Δ). В окрестности максимума АКФ R(τ)= R0(τ)=(1-|τ|/Δ). На входе приемника после прохождения многолучевого канала полезный сигнал может быть записан как

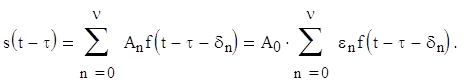
δn – относительная задержка сигнала по лучу с номером n, τ неизвестное время прихода, которое находится внутри интервала [T1,T2]. εn=An/A0 – относительная амплитуда «n»-го луча, параметр ν имеет смысл числа дополнительных лучей распространения. Относительные задержки δn>Δ, т.е. лучи разделяются при обработке сложного сигнала. При ν=0 сигнал имеет вид s(t)=A0f(t-τ0).

Рассмотрим алгоритм обработки. На вход приемника поступает смесь

x(t)=sk(t-τ0k)+η(t),            (t[0,TН]),

где sk(t) – один из возможных сигналов, k=1…M, τ0k временная задержка сигнала, η(t) – белый гауссовский шум с нулевым средним значением и спектральной плотностью мощности N0/2. Необходимо вынести решение, какой из M возможных сигналов присутствует на входе приемника. Рассмотрим приемник без компенсации многолучевости. Линейная часть такого приемника содержит М каналов, в которых формируются статистики вида

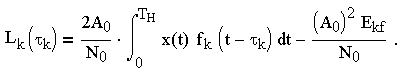
Выражение для Lk(τk) можно переписать в боле удобном для анализа виде

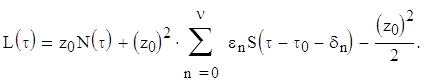
Здесь и в последующих формулах индекс k для краткости опускается, если исследуются характеристики одного канала, z02=2A02Ef/N0 – энергетическое отношение сигнал/шум, S(τ-τ0)=∫f(t-τ) f(t-τ0)dt/Ef – нормированная сигнальная функция, N(τ)=∫n(t)f(t-τ)dt – нормированная шумовая функция с нулевым средним значением, единичной дисперсией и корреляционной функцией <N(τ')N(τ'')>=S(τ'-τ''). Огибающая сигнальной функции S(τ-τ0) есть АКФ.

Согласно алгоритму максимального правдоподобия решение в пользу сигнала с номером m выносится, если sup Lm(τm)≥sup Lk(τk). Для нахождения вероятностей правильных и неправильных решений по этому правилу необходимо вычислить распределение абсолютных максимумов процессов L(τ) на интервале [Т1,Т2].

Рассмотрим методику расчета вероятности ошибки различения M сигналов с неизвестными параметрами при однолучевом распространении сигналов (или в схеме оптимального сложения сигналов). Обозначим через Hk=sup Lk(τk) – величину абсолютного максимума статистики на выходе k-го канала приемника. Совместное распределение случайных величин {H1,H2,..HM} запишем как w(u1,u2,..uM). Условие ортогональности для сигналов fk(t) в статистическом смысле означает независимость случайных величин Hk, k=1..M. Тогда вероятность правильного решения по алгоритму максимального правдоподобия можно записать

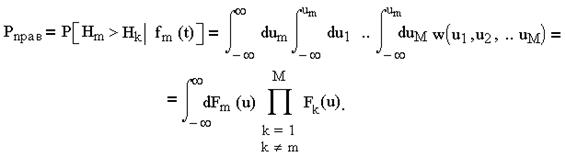
Если учесть условие ортогональности системы сигналов {sk(t)}, то

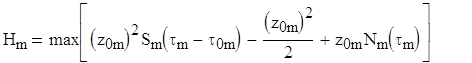
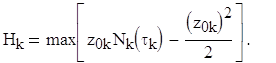
Предположим, что система сигналов {sk(t)} имеет одинаковую энергию, то есть z0m=z0k=z0. Тогда формулы для Hm и Hk можно переписать в виде

Функция распределения абсолютного максимума hk реализации гауссовского процесса с корреляционной функцией R(τ) может быть аппроксимирована формулой

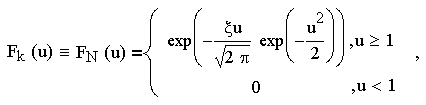
ξ=(T2-T1)/Δ – приведенная длина априорного интервала [Т1,Т2], имеющая смысл числа разрешения ФМ сигналов на этом интервале. Аппроксимация асимптотически точна при ξ→∞, u→∞. При конечных значениях ξ и u можно использовать более точную аппроксимацию

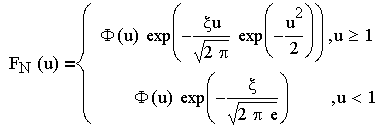
Здесь

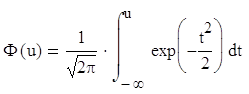
- интеграл вероятности. При ξ>>1 и z0>>1 функция распределения абсолютного максимума hm может быть записана как Fm(u)=Fs(u)FN(u)≈Φ(u-z0)FN(u). Подставляя выражения FN(u) и Fm(u) в соотношение для Pправ, получаем после соответствующих преобразований

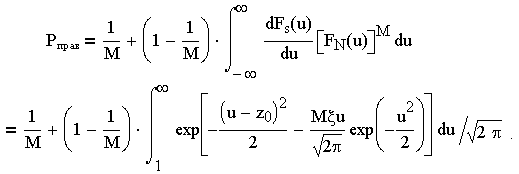
Первое слагаемое соответствует априорной вероятности правильного решения для M равновозможных событий. Второе слагаемое определяет изменения вероятности за счет принятия решения. При z0→∞ интеграл в выражении для Pправ стремится к 1 и, соответственно, Pправ→1.

Полная вероятность ошибки различения М сигналов с неизвестными параметрами равна

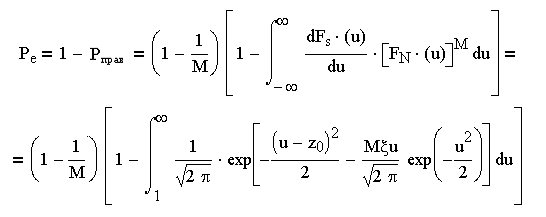
Из формул видно, что с увеличением числа различаемых сигналов вероятность ошибки принятия решения Pe(z0) увеличивается. С увеличением априорного интервала временных задержек сигналов ξ вероятность ошибки различения Pe(z0) значительно возрастает. [8]

4.4 Сравнение синхронных и асинхронных систем связи

Как правило, при рассмотрении производительности приемника или демодулятора предполагается наличие некоторого уровня синхронизации сигнала. Например, при когерентной фазовой демодуляции (схема PSK) предполагается, что приемник может генерировать опорные сигналы, фаза которых идентична (возможно, с точностью до постоянного смещения) фазе элементов сигнального алфавита передатчика. Затем в процессе принятия решения относительно значения принятого символа (по принципу максимального правдоподобия) опорные сигналы сравниваются с поступающими.

При генерации подобных опорных сигналов приемник должен быть синхронизирован с принимаемой несущей. Это означает, что фаза поступающей несущей и ее копии в приемнике должны согласовываться. Другими словами, если в поступающей несущей не закодирована информация, поступающая несущая и ее копия в приемнике будут проходить через нуль одновременно. Этот процесс называется фазовой автоподстройкой частоты (это условие, которое следует удовлетворить максимально близко, если в приемнике мы хотим точно демодулировать когерентно модулированные сигналы). В результате фазовой автоподстройки частоты местный гетеродин приемника синхронизируется по частоте и фазе с принятым сигналом. Если сигнал-носитель информации модулирует непосредственно не несущую, а поднесущую, требуется определить как фазу несущей, так и фазу поднесущей. Если передатчик не выполняет фазовой синхронизации несущей и поднесущей (обычно так и бывает), от приемника потребуется генерация копии поднесущей, причем управление фазой копии поднесущей производится отдельно от управления фазой копии несущей. Это позволяет приемнику получать фазовую синхронизацию как по несущей, так и по поднесущей.

Кроме того, предполагается, что приемник точно знает, где начинается поступающий символ и где он заканчивается. Эта информация необходима, чтобы знать соответствующий промежуток интегрирования символа – интервал интегрирования энергии перед принятием решения относительно значения символа. Очевидно, если приемник интегрирует по интервалу несоответствующей длины или по интервалу, захватывающему два символа, способность к принятию точного решения будет снижаться.

Можно видеть, что символьную и фазовую синхронизации объединяет то, что обе включают создание в приемнике копии части преданного сигнала. Для фазовой синхронизации это будет точная копия несущей. Для символьной – это меандр с переходом через нуль одновременно с переходом поступающего сигнала между символами. Говорят, что приемник, способный сделать это, имеет символьную синхронизацию. Поскольку на один период передачи символа обычно приходится очень большое число периодов несущей, этот второй уровень синхронизации значительно грубее фазовой синхронизации и обычно выполняется с помощью другой схемы, отличной от используемой при фазовой синхронизации.

Во многих системах связи требуется еще более высокий уровень синхронизации, который обычно называется кадровой синхронизацией. Кадровая синхронизация требуется, когда информация поставляется блоками, или сообщениями, содержащими фиксированное число символов. Это происходит, например, при использовании блочного кода для реализации схемы прямой защиты от ошибок или если канал связи имеет временное разделение и используется несколькими пользователями (технология TDMA). При блочном кодировании декодер должен знать расположение границ между кодовыми словами, что необходимо для верного декодирования сообщения. При использовании канала с временным разделением нужно знать расположение границ между пользователями канала, что необходимо для верного направления информации. Подобно символьной синхронизации, кадровая равнозначна возможности генерации меандра на скорости передачи кадров с нулевыми переходами, совпадающими с переходами от одного кадра к другому.

Большинство систем цифровой связи, использующих когерентную модуляцию, требуют всех трех уровней синхронизации: фазовой, символьной и кадровой. Системы с некогерентной модуляцией обычно требуют только символьной и кадровой синхронизации; поскольку модуляция является некогерентной, точной синхронизации фазы не требуется. Кроме того, некогерентным системам необходима частотная синхронизация. Частотная синхронизация отличается от фазовой тем, что копия несущей, генерируемая приемником, может иметь произвольные сдвиги фазы от принятой несущей. Структуру приемника можно упростить, если не предъявлять требование относительно определения точного значения фазы поступающей несущей. К сожалению, это упрощение влечет за собой ухудшение зависимости достоверности передачи от отношения сигнал/шум.

До настоящего момента в центре обсуждения находилась принимающая часть канала связи. Однако иногда передатчик играет более активную роль в синхронизации – он изменяет отчет времени и частоту своих передач, чтобы соответствовать ожиданиям приемника. Примером того является спутниковая сеть связи, где множество наземных терминалов направляют сигналы на единственный спутниковый приемник. В большинстве подобных случаев передатчик для определения точности синхронизации использует обратный канал связи от приемника. Следовательно, для успеха синхронизации передатчика часто требуется двусторонняя связь или сеть. По этой причине синхронизация передатчика часто называется сетевой.

Необходимость синхронизации приемника связана с определенными затратами. Каждый дополнительный уровень синхронизации подразумевает большую стоимость системы. Наиболее очевидное вложение денег – необходимость в дополнительном программном или аппаратном обеспечении для приемника, обеспечивающего получение и поддержание синхронизации. Кроме того, что менее очевидно, иногда мы платим временем, затраченным на синхронизацию до начала связи, или энергией, необходимой для передачи сигналов, которые будут использоваться в приемнике для получения и поддержания синхронизации. В данном случае может возникнуть вопрос, почему разработчик системы связи вообще должен рассматривать проект системы, требующий высокой степени синхронизации. Ответ: улучшенная производительность и универсальность.

Рассмотрим обычное коммерческое аналоговое АМ-радио, которое может быть важной частью системы широковещательной связи, включающей центральный передатчик и множество приемников. Данная система связи не синхронизирована. В то же время полоса пропускания приемника должна быть достаточно широкой, чтобы включать не только информационный сигнал, но и любые флуктуации несущей, возникающие вследствие эффекта Доплера или дрейфа опорной частоты передатчика. Это требование к полосе пропускания передатчика означает, что на детектор поступает дополнительная энергия шума, превышающая энергию, которая теоретически требуется для передачи информации. Несколько более сложные приемники, содержащие систему слежения за частотой несущей, могут включать узкий полосовой фильтр, центрированный на несущей, что позволит значительно снизить шумовую энергию и увеличить принятое отношение сигнал/шум. Следовательно, хотя обычные радиоприемники вполне подходят для приема сигналов от больших передатчиков на расстоянии несколько десятков километров, они могут оказаться недееспособными при менее качественных условиях.

Для цифровой связи компромиссы между производительностью и сложностью приемника часто рассматриваются при выборе модуляции. В число простейших цифровых приемников входят приемники, разработанные для использования с бинарной схемой FSK с некогерентным обнаружением. Единственное требование – битовая синхронизация и сопровождение частоты. Впрочем, если в качестве модуляции выбрать когерентную схему BPSK, то можно получить ту же вероятность битовой ошибки, но при меньшем отношении сигнал/шум (приблизительно на 4 дБ). Недостатком модуляции BPSK является то, что приемник требует точного отслеживания фазы, что может представлять сложную конструктивную проблему, если сигналы обладают высокими доплеровскими скоростями или для них характерно замирание.

Еще один компромисс между ценой и производительностью затрагивает кодирование с коррекцией ошибок. При использовании подходящих методов защиты от ошибок возможно значительное улучшение производительности. В то же время цена, выраженная в сложности приемника, может быть высока. Для надлежащей работы блочного декодера требуется, чтобы приемник достигал блочной синхронизации, кадровой или синхронизации сообщений. Эта процедура является дополнением к обычной процедуре декодирования, хотя существуют определенные коды коррекции ошибок, имеющие встроенную блочную синхронизацию. Сверточные коды также требуют некоторой дополнительной синхронизации для получения оптимальной производительности. Хотя при анализе производительности сверточных кодов часто делается предположение о бесконечной длине входной последовательности, на практике это не так. Поэтому для обеспечения минимальной вероятности ошибки декодер должен знать начальное состояние (обычно все нули), с которого начинается информационная последовательность, конечное состояние и время достижения конечного состояния. Знание момента окончания начального состояния и достижения конечного состояния эквивалентно наличию кадровой синхронизации. Кроме того, декодер должен знать, как сгруппировать символы канала для принятия решения при разветвлении. Это требование также относится к синхронизации.

Приведенное выше обсуждение компромиссов велось с точки зрения соотношения между производительностью и сложностью отдельных каналов и приемников. Стоит отметить, что способность синхронизировать также имеет значительные потенциальные последствия, связанные с эффективностью и универсальностью системы. Кадровая синхронизация позволяет использовать передовые, универсальные методы множественного доступа, подобные схемам множественного доступа с предоставлением каналов по требованию (DAMA). Кроме того, использование методов расширения спектра – как схем множественного доступа, так и схем подавления интерференции требует высокого уровня синхронизации системы. Эти технологии предлагают возможность создания весьма разносторонних систем, что является очень важным свойством при изменении системы или при воздействии преднамеренных или непреднамеренных помех от различных внешних источников. [2]  

Заключение

В первом разделе моей работы описаны принципы построения беспроводных телекоммуникационных систем связи: приведена схема построения системы сотовой связи, указаны методы разделения абонентов в сотовой связи и отмечены преимущества (конфиденциальность и помехоустойчивость) кодового разделения по сравнению с временным и частотным, а также рассмотрены распространенные стандарты беспроводной связи DECT, Bluetooth и Wi-Fi (802.11, 802.16).

Далее рассмотрены корреляционные и спектральные свойства сигналов и, для примера, приведены расчеты спектров некоторых сигналов (прямоугольного импульса, гауссовского колокола, сглаженного импульса) и автокорреляционных функций распространенных в цифровой связи сигналов Баркера и функций Уолша, а также указаны типы сложных сигналов для телекоммуникационных систем.

В третьей главе приведены методы модуляции сложных сигналов: методы фазовой манипуляции, модуляция с минимальным частотным сдвигом (один из методов модуляции с непрерывной фазой), квадратурная амплитудная модуляция; и указаны  их преимущества и недостатки.

Последняя часть работы содержит рассмотрение вероятностей ошибок различения М известных и М флуктуирующих сигналов на фоне помех, а также алгоритм расчета ошибок различения М ортогональных сигналов с неизвестным временным положением в асинхронных системах связи с кодовым разделением.

Список литературы:

1. Ратынский М.В. Основы сотовой связи / Под ред. Д. Б. Зимина – М.: Радио и связь, 1998. – 248 с.

2. Скляр Б. Цифровая связь. Теоретические основы и практическое применение, 2-е издание.: Пер. с англ. М.: Издательский дом “Вильямс”, 2003. – 1104 с.

3. Шахнович И. Современные технологии беспроводной связи. Москва: Техносфера, 2004. – 168 с.

4. Баскаков С.И. Радиотехнические цепи и сигналы: Учеб. для вузов по спец. «Радиотехника». – 3-е изд., перераб. и доп. – М.: Высш. шк., 2000. – 462 с.

5. Шумоподобные сигналы в системах передачи информации. Под ред. проф. В.Б. Пестрякова. М., «Сов. радио», 1973. 424 с.

6. Варакин Л.Е. Системы связи с шумоподобными сигналами. – М.: Радио и связь, 1985. – 384 с.

7. Вишневский В.М., Ляхов А.И., Портной С.Л., Шахнович И.В. Широкополосные беспроводные сети передачи информации. Москва: Техносфера, 2005. – 592 с.

8. Радченко Ю.С., Радченко Т.А. Эффективность кодового разделения сигналов с неизвестным временем прихода. Труды 5 междунар. конф. «Радиолокация, навигация, связь» - RLNC-99, Воронеж, 1999, т.1, с. 507-514.

9. Радиотехнические системы: Учеб. для вузов по спец. «Радиотехника» / Ю.П. Гришин, В.П. Ипатов, Ю.М. Казаринов и др.; Под ред. Ю.М. Казаринова. – М.: Высш. шк., 1990. – 469 с.