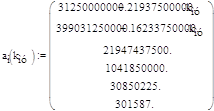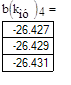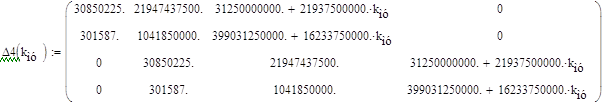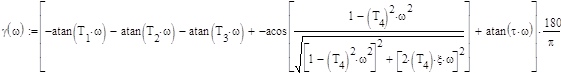Лабораторная работа: Анализ устойчивости электротехнической системы

Лабораторная работа: Анализ устойчивости электротехнической системы

Министерство Топлива и Энергетики Украины

СЕВАСТОПОЛЬСКИЙ НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ

ЯДЕРНОЙ ЭНЕРГИИ И ПРОМЫШЛЕННОСТИ

Практическое занятие

по дисциплине

«Использование ЭВМ в инженерных расчетах электротехнических систем»

Тема: АНАЛИЗ УСТОЙЧИВОСТИ ЭЛЕКТРОТЕХНИЧЕСКОЙ СИСТЕМЫ

Выполнил: студент группы ЭСЭ 22-В

Левицкий П.В.

Проверил:_______________________

Севастополь 2008

ПЛАН

1. Введение

2. Анализ САУ на устойчивость

2.1 Анализ устойчивости системы с помощью корней характеристического уравнения передаточной функции замкнутой системы

2.2 Анализ влияния параметров элементов системы на ее устойчивость с помощью расположения корней характеристического уравнения передаточной функции замкнутой системы на комплексной плоскости

2.3 Использование алгебраического критерия Рауса - Гурвица для анализа устойчивости системы

2.4 Построение годографов Найквиста по передаточной функции разомкнутой системы заданной в виде полинома

2.5 Использование ЛАХЧ и фазовых частотных характеристик для анализа устойчивости системы

Выводы

1. Введение

Целью данной работы является изучить возможности математического пакета MathCad в среде Windows для анализа устойчивости электротехнической системы, изучить различные методы определения устойчивости электротехнической системы, достоинства и недостатки методов и критериев, используемых при анализе устойчивости.

Для того чтобы электротехническая система выполняла свое назначение, она должна быть, прежде всего, устойчива.

Электротехническая система считается устойчивой, если она, будучи выведена из состояния равновесия внешним возмущающим воздействием, приходит с течением времени в состояние равновесия. Если же электротехническая система после снятия возмущающего воздействия не приходит в состояние равновесия, а совершает колебания с нарастающей или постоянной амплитудой, она является неустойчивой или находящейся на грани устойчивости.

Для анализа устойчивости электротехническая система, используют следующие методы и критерии:

а) анализ устойчивости с помощью корней характеристического уравнения замкнутой системы. Анализ влияния параметров элементов системы на ее устойчивость с помощью изменения расположения корней характеристического уравнения замкнутой системы на комплексной плоскости;

б) использование алгебраического критерия Рауса - Гурвица для анализа устойчивости системы и определения критического коэффициента передачи системы;

в) частотный критерий Найквиста и устойчивость системы с определением запасов устойчивости;

г) использование логарифмических амплитудных (л.а.ч.х.) и фазовых частотных характеристик (ф.ч.х.) для анализа устойчивости системы и определения запасов устойчивости;

д) метод D - разбиения для определения области устойчивости и выявления параметров элементов системы, влияющих на ее устойчивость.

В работе будут рассмотрены алгебраические и графические критерии устойчивости. Построены частотные характеристики и проведён анализ влияния коэффициента усиления системы на устойчивость.

2. Анализ САУ на устойчивость

2.1 Анализ устойчивости системы с помощью корней характеристического уравнения передаточной функции замкнутой системы

Для анализа устойчивости системы с помощью корней можно воспользоваться характеристическим полиномом передаточной функции замкнутой системы полученной в Практическом занятии №5.

Переходной процесс будет устойчив, если все действительные корни и вещественные части комплексно-сопряженных корней будут отрицательны, следовательно, будет устойчива и электротехническая система. Если же хотя бы один действительный корень или вещественная часть комплексно-сопряженного корня будет положительна, то переходной процесс будет расходящимся и электротехническая система будет не устойчива. Если же хотя бы одна пара комплексно-сопряженных корней будет иметь только мнимую часть, то переходной процесс будет иметь незатухающий колебательный процесс, а электротехническая система будет на грани устойчивости.

По виду корней характеристического полинома передаточной функции замкнутой системы можно сделать заключение, что для заданных выше параметров элементов системы она устойчива, так как действительный корень и вещественные части комплексно сопряженных корней отрицательны.

2.2 Анализ влияния параметров элементов системы на ее устойчивость с помощью расположения корней характеристического уравнения передаточной функции замкнутой системы на комплексной плоскости

На практике важно уметь определять влияние параметров элементов электротехнической системы на ее устойчивость. Можно изменить общий коэффициент усиления системы и она из неустойчивой станет устойчивой. Например, определим влияние коэффициента усиления электромашинного усилителя на устойчивость системы. Для этого передаточную функцию замкнутой системы и ее характеристический полином запишем запищим в символьно-цифровом виде относительно параметра kму.

Данный характеристический полином позволяет выявить влияние kму на устойчивость системы. В частности, можно определить чувствительность изменения устойчивости системы от его величины и определить его критическое значение, т.е. построить область устойчивости системы при изменении этого коэффициента в заданной области. Для этого выделим вещественную и мнимые части вектора polyroots (ai(kэму) корней характеристического уравнения, т.е. представим их в виде: si = ai + j·βi

И построим график , откладывая по оси х действительные, а по оси y мнимые части

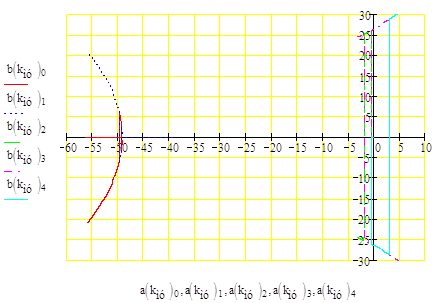
Рис.1 Расположения корней характеристического уравнения замкнутой системы на комплексной плоскости.

Из рис.1 видно, что пара комплексно-сопряженных корней s3 = a3 + j·β3 и s4 = a4 - j·β4 при изменении kму в заданной области переходят из левой полуплоскости в правую полуплоскость. Следовательно, по изменению этой пары корней можно определить критический коэффициент усиления магнитного усилителя. Графический способ определения критического коэффициента магнитного усилителя, показан на рис. 2.

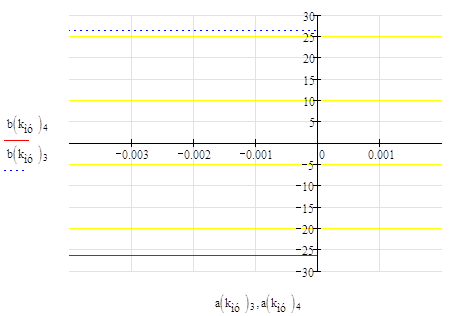
Рис.2. Графический способ определения критического коэффициента передачи магнитного усилителя.

Табличный метод определения критического коэффициента передачи магнитного усилителя.

Kму=11,18

2.3. Использование алгебраического критерия Рауса - Гурвица для анализа устойчивости системы

Для анализа устойчивости и определения критического коэффициента передачи прямого канала усиления системы в функции kму рассматриваемой системы с помощью алгебраического критерия устойчивости Рауса-Гурвица воспользуемся детерминантами D4 и D2, рекомендуемые Льенара – Шипара, так как характеристическое уравнение имеет пятый порядок.

а) детерминант D2:

б) детерминант D4.

Как видим, детерминант ∆2 > 0, а ∆4 при коэффициенте передачи магнитного усилителя kму = 11,186980560011235894 равен нулю, т.е. система находится на грани устойчивости. Следовательно, критический коэффициент передачи магнитного усилителя равен kмукр =11,186980560011235894

Для того, чтобы убедиться что это действительно критическое значение коэффициента магнитного усилителя, определим корни характеристического уравнения для найденного коэффициента магнитного усилителя.

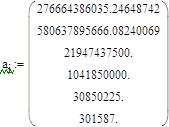
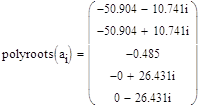
Как видим, характеристический полином имеет пару чисто мнимых корней, следовательно, система находится на грани устойчивости.

2.4 Построение годографов Найквиста по передаточной функции разомкнутой системы заданной в виде полинома

Частотный критерий Найквиста при исследовании устойчивости автоматических систем базируется на амплитудно-фазовой частотной характеристики разомкнутой системы и может быть сформулирован следующим образом:

если характеристическое уравнение разомкнутой системы n -го порядка имеет k корней с положительной вещественной частью (k = 0, 1, ….. n ) и n-k корней с отрицательной вещественной частью, то для устойчивости замкнутой системы необходимо и достаточно, чтобы годограф амплитудно-фазовой частотной характеристики разомкнутой системы (годограф Найквиста) охватывал точку (-1, j0) комплексной плоскости на угол k π , или что тоже самое, охватывал точку (-1, j0) в положительном направлении, т.е. против часовой стрелки, k раз.

Для частного случая, когда характеристическое уравнение разомкнутой системы не имеет корней с положительной вещественной частью (k = 0), т.е. , когда она устойчива в разомкнутом состоянии, критерий Найквиста формулируется следующим образом:

система автоматического регулирования устойчива в замкнутом состоянии, если амплитудно-фазовая частотная характеристика разомкнутой системы при изменении частоты от 0 до ∞ не охватывает точку комплексной плоскости с координатами (-1, j0).

Критерий устойчивости Найквиста удобно применять для систем с обратной связью, особенно систем высокого порядка.

Для построения годографа Найквиста воспользуемся передаточной функцией разомкнутой системы в символьном виде из Практического занятия №5

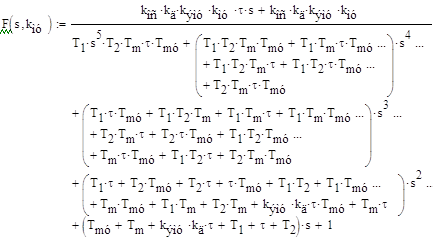
Запишем ее в символьно-цифровом виде для заданных параметров всех элементов системы, кроме коэффициента передачи магнитного усилителя:

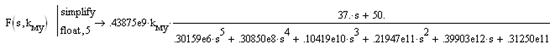
Запишем уравнение амплитудно-фазовой частотной характеристики,, выделим вещественную и мнимые частотные характеристики и построим семейство годографов Найквиста в функции частоты и коэффициента передачи магнитного усилителя.

Построения графика амплитудно-фазовой частотной характеристики в MathСad

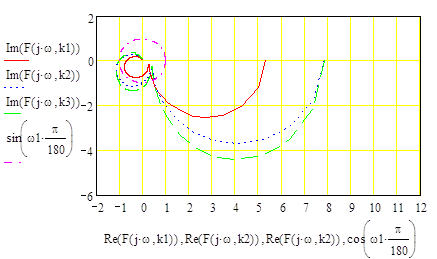
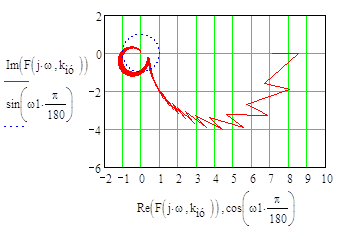
Рис.3. Семейство кривых годографа Найквиста, построенный для передаточной функции разомкнутой системы в функции от kму.

Из рис.3 видно, что один из годографов Найквиста проходит через точку с координатами (j0, -1). Следовательно, в заданной области изменения коэффициента передачи магнитного усилителя есть и его критическое значение. Для его определения воспользуемся следующими соотношениями:

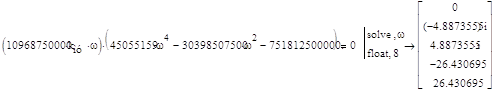
Следовательно, критический коэффициент передачи магнитного усилителя есть:

kмукр =11.186981170416560078

Убедимся, что это действительно так. Для этого построим кривые годографа Найквиста для трех значений коэффициента передачи магнитного усилителя: kму = 0.6 kмукр; kму = kмукр; kму =1.2 kмукр

Рис.4. Кривые годографа Найквиста, построенные для

kму = 0.6 kмукр; kму = kмукр; kму =1.2 kмукр

Кривые рис.4 подтверждают, что критический коэффициент передачи магнитного усилителя найден верно.

2.5 Использование л.а.ч.х. и фазовых частотных характеристик для анализа устойчивости системы

Критерий устойчивости системы по логарифмической амплитудной частотной характеристике (л.а.ч..х ) и фазовой частотной характеристике можно сформулировать следующим образом:

Система автоматического регулирования, неустойчивая в разомкнутом состоянии, устойчива в замкнутом состоянии, если разность между числами положительных переходов (переход фазовой частотной характеристики снизу вверх через линию φ(ω) = -180° ) и числами отрицательных переходов (переход фазовой частотной характеристики сверху в низ через линию φ(ω) = -180° ) фазовой частотной характеристики φ(ω) через линию φ(ω) = -180° равно нулю в диапазоне частот, на которых л.а.ч..х (L(ω)> 0) .

Для построения фазовой частотной характеристики, желательно представить передаточную функцию в виде типовых динамических звеньев.

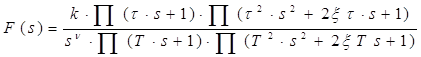
и строить фазовую характеристику, используя выражение:

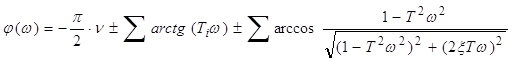
где:

«+» – соответствует типовым динамическим звеньям числителя передаточной функции;

«-« - соответствует типовым динамическим звеньям знаменателя передаточной функции.

Для построения асимптотической л.а.ч.х. используем передаточную функцию разомкнутой системы, представленной в виде типовых динамических звеньев:

Для этого используем передаточную функцию вида:

Представим эту передаточную функцию в виде типовых динамических звеньев:

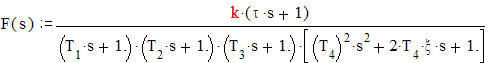
Параметры типовых динамических звеньев определяются, как показано ниже:

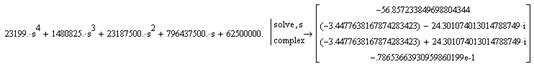
Уравнение фазовой характеристики будет иметь вид:

Определим частоту, при которой фазовая частотная характеристика пересекает ось φ(ω) = -180°

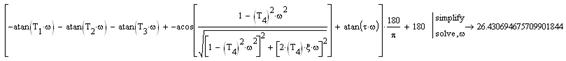
Для построения л.а.ч.х. воспользуемся выражением:

На рис.5 представлены графики л.а.ч.х для двух значений коэффициента передачи магнитного усилителя kму = 10 и kму = 80.

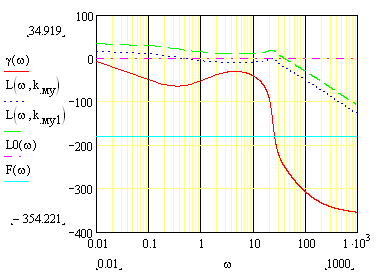
Рис.5. Графики л.а.ч.х. и фазовой частотной характеристик.

Анализ л.а.ч.х. и фазовой частотной характеристики показывают, что при увеличении коэффициента передачи магнитного усилителя от 8 до 80 система из устойчивой становится неустойчивой. Определим критический коэффициент передачи магнитного усилителя.

Если нет дополнительных требований по запасам устойчивости к системе, то рекомендуется принимать их равными:

ΔL(ω) = -12db Δφ(ω) = 35˚÷ 45˚

Определим, при каком коэффициенте передачи магнитного усилителя это условие выполняется.

Это же подтверждается графиками, приведёнными на рисунке 6.

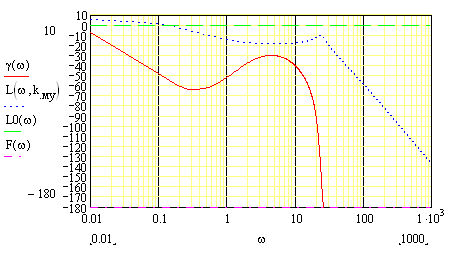
Рис.6. Графики л.а.ч.х. и ф.ч.х., построенные для рекомендуемых запасов устойчивости.

Выводы

В данной практической работе мы ознакомились с возможностями математического пакета MathCad в среде Windows для анализа устойчивости электротехнической системы. Основными методами определения устойчивости являются: определение устойчивости с помощью корней характеристического уравнения. Достаточно к уравнению применить solve,s и получим корни уравнения , даже если оно 8-ой или более высокой степени. Отрицательные действительные корни или части комплексных корней являются критерием устойчивости. Критерии Рауса предполагают построение таблиц(матриц) и расчёт определителей . В MathCad задача определителей решается с помощью значка на панели матричных вычислений. Частотный критерий Найквиста самый наглядный из всех рассмотренных в данной работе. Если на графике кроме годографа Найквиста построить единичную окружность, то легко можно увидеть, при каких коэффициентах усиления система неустойчива, находится на грани устойчивости и устойчива. Если линия графика не охватывает точку (-1;j0), то замкнутая система устойчива. На основе использования критерия Найквиста можно определять запасы устойчивости по фазе и по амплитуде т.е. оценить степень устойчивости системы. Также в работе была исследована устойчивость при помощи логарифмических частотных характеристик. Зависимость отношения амплитуд выходного и входного сигнала от частоты называют амплитудно-частотной характеристикой (АЧХ). Зависимость фазового сдвига между входным и выходным сигналом от частоты- фазочастотной характеристикой (ФЧХ). Для построения логарифмической АЧХ и ФЧХ их графики строят в системе координат (20lgА(w)- lg(w) и φ(w)- lg(w)) то есть в логарифмической неравномерной шкале по оси частот. Были построены графики ЛАЧХ и ФЧХ для рекомендуемых запасов устойчивости. Кроме того в работе мы оценили влияние коэффициента усиления системы на устойчивость системы и нашли критический коэффициент усиления системы. Опыт показывает, что обычно с увеличением коэффициента усиления система стремится к неустойчивой.