
Рефераты по сексологии
Рефераты по информатике программированию
Рефераты по биологии
Рефераты по экономике
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Рефераты по авиации и космонавтике
Рефераты по административному праву
Рефераты по безопасности жизнедеятельности
Рефераты по арбитражному процессу
Рефераты по архитектуре
Рефераты по астрономии
Рефераты по банковскому делу
Рефераты по биржевому делу
Рефераты по ботанике и сельскому хозяйству
Рефераты по бухгалтерскому учету и аудиту
Рефераты по валютным отношениям
Рефераты по ветеринарии
Рефераты для военной кафедры
Рефераты по географии
Рефераты по геодезии
Рефераты по геологии
Рефераты по геополитике
Рефераты по государству и праву
Рефераты по гражданскому праву и процессу
Рефераты по делопроизводству
Рефераты по кредитованию
Рефераты по естествознанию
Рефераты по истории техники
Рефераты по журналистике
Рефераты по зоологии
Рефераты по инвестициям
Рефераты по информатике
Исторические личности
Рефераты по кибернетике
Рефераты по коммуникации и связи
Контрольная работа: Исследование операций и теория систем
Контрольная работа: Исследование операций и теория систем
Министерство Образования Российской Федерации
Южно-Уральский Государственный Университет
Кафедра Системы Управления
КУРСОВАЯ РАБОТА
по дисциплине: Исследование операций
Вариант 8
Руководитель:
Плотникова Н.В.
«___»__________2004 г.
Автор проекта:
студентка группы
ПС – 317
Куликова Мария
«___»__________2004 г.
Проект защищен
с оценкой
«___»__________2004 г.
Челябинск
2004 г.
Содержание.
Задача 1………………………………………………………………….3
Задача 2………………………………………………………………….8
Задача 3…………………………………………………………………10
Задача 4…………………………………………………………………13
Задача 1 (№8)
Условие:
На производстве четырёх видов кабеля выполняется пять групп технологических операций. Нормы затрат на 1 км. кабеля данного вида на каждой из групп операций, прибыль от реализации 1 км. каждого вида кабеля, а также общий фонд рабочего времени, в течение которого могут выполняться эти операции, указаны в таблице.
Определить такой план выпуска кабеля, при котором общая прибыль от реализации изготовляемой продукции является максимальной.
| Технологическая операция | Нормы затрат времени на обработку 1 км кабеля вида | Общий фонд рабочего времени (ч) | |||
| 1 | 2 | 3 | 4 | ||
| Волочение | а11 | а12 | а13 | а14 | А1 |
| Наложение изоляций | а21 | а22 | а23 | а24 | А2 |
| Скручивание элементов в кабель | а31 | а32 | а33 | а34 | А3 |
| Освинцовывание | а41 | а42 | а43 | а44 | А4 |
| Испытание и контроль | а51 | а52 | а53 | а54 | А5 |
| Прибыль от реализации 1 км кабеля | В1 | В2 | В3 | В4 | |
| №вар. | а11 | а12 | а13 | а14 | а21 | а22 | а23 | а24 | а31 | а32 | а33 | а34 | а41 |
| 1 | 1,5 | 1 | 2 | 1 | 1 | 2 | 0 | 2 | 4 | 5 | 5 | 4 | 2 |
| № вар. | а42 | а43 | а44 | а51 | а52 | а53 | а54 | А1 | А2 | А3 | А4 | 5 |
| 1 | 1 | 4 | 0 | 1 | 2 | 1,5 | 4 | 6500 | 4000 | 11000 | 4500 | 4500 |
| В1 | В2 | В3 | В4 |
| 1 | 2 | 1,5 | 1 |
Решение:
Составляем математическую модель задачи:
пусть x1 –длина 1-ого кабеля (км);
x2 – длина 2-ого кабеля (км);
x3 – длина 3-ого кабеля (км);
x4 – длина 4-ого кабеля (км)
тогда целевая функция L - общая прибыль от реализации изготовляемой продукции, будет иметь следующий вид
L= В1x1 + В2x2 + В3x3 + В4x4 = x1+ 2x2 + 1,5x3 + x4 → max
Получим систему ограничений:
1,5x1 + x2 + 2x3+ x4 £ 6500;
x1 + 2x2 + 0x3+2x4 £ 4000;
4x1 + 5x2 + 5x3+4x4 £11000;
2x1 + x2 +1,5x3+0x4 £ 4500;
x1 + 2x2 +1,5x3+4x4 £ 4500.
Приведём полученную математическую модель к виду ОЗЛП с помощью добавочных неотрицательных переменных, число которых равно числу неравенств:
1,5x1 + x2 + 2x3+ x4 + x5 = 6500;
x1 + 2x2 + 0x3+2x4 + x6= 4000;
4x1 + 5x2 + 5x3+4x4 + x7=11000;
2x1 + x2 +1,5x3+0x4 + x8 =4500;
x1 + 2x2 +1,5x3+4x4 + x9 =4500.
Итак, выберем x1, x2, x3, x4 - свободными переменными, а x5, x6, x7, x8, x9 - базисными переменными (каждая из них встречаются в системе лишь в одном уравнении с коэффициентом 1, а в остальных с нулевыми коэффициентами). Приведём систему к стандартному виду, выразив для этого все базисные переменные через свободные:
x5 = 6500 – (1,5x1 + x2 + 2x3+ x4 );
x6 = 4000 – ( x1 + 2x2 + 0x3+2x4);
x7 =11000 - ( 4x1 + 5x2 + 5x3+4x4);
x8 =4500 – ( 2x1 + x2 +1,5x3+0x4);
x9 =4500 – ( x1 + 2x2 +1,5x3+4x4)
L=0 –(- x1- 2x2 - 1,5x3 - x4)
Решим методом симплекс-таблиц:
Это решение опорное, т.к. все свободные члены положительны.
Выберем столбец в таблице, который будет разрешающим, пусть это будет x1, выберем в качестве разрешающего элемента тот, для которого отношение к нему свободного члена будет минимально (это x8).
|
A |
|
|
|
|
|
| L |
0 2250 |
-1 0,5 |
-2 0,5 |
-1,5 2 |
-1 0 |
|
|
6500 -3375 |
1,5 -0,75 |
1 -0,75 |
2 -3 |
1 0 |
|
|
4000 -2250 |
1 -0,5 |
2 -0,5 |
0 -2 |
3 0 |
|
|
11000 -9000 |
4 -2 |
5 -2 |
5 -8 |
4 0 |
| x8 |
4500 2250 |
2 0,5 |
1 0,5 |
4 2 |
0 0 |
| x9 |
4500 -2250 |
1 -0,5 |
2 -0,5 |
1,5 -2 |
4 0 |
Меняем ![]() и
и ![]()
|
A |
x8 |
|
|
|
|
| L |
2250 1000 |
0,5 -1 |
-1,5 0,5 |
0,5 -1,5 |
-1 2 |
|
|
3125 -500/3 |
-0,75 1/6 |
0,25 -1/12 |
-1 0,25 |
1 -1/3 |
|
|
1750 -1000 |
-0,5 1 |
1,5 -0,5 |
-2 1,5 |
3 -2 |
|
|
2000 2000/3 |
-2 -2/3 |
3 1/3 |
-3 -1 |
4 4/3 |
|
|
2250 -1000/3 |
0,5 1/3 |
0,5 -1/6 |
2 0,5 |
0 -2/3 |
| x9 |
2250 -1000 |
-0,5 1 |
1,5 -0,5 |
-0,5 1,5 |
4 -2 |
Меняем ![]() и x9
и x9
|
A |
x8 |
|
|
|
|
| L |
3250 250 |
-0,5 0,5 |
0,5 -0,5 |
-1 1 |
1 2 |
|
|
8875/3 187,5 |
-7/12 0,375 |
-1/12 -0,375 |
-0,75 0,75 |
2/3 1,5 |
|
|
750 125 |
0,5 0,25 |
-0,5 -0,25 |
-0,5 0,5 |
1 1 |
|
|
2000/3 250 |
-2/3 0,5 |
1/3 -0,5 |
-1 1 |
4/3 2 |
|
|
5750/3 -625 |
5/6 -1,25 |
-1/6 1,25 |
2,5 -2,5 |
-2/3 -5 |
| x9 |
250 250 |
0,5 0,5 |
-0,5 -0,5 |
1 1 |
2 2 |
|
A |
x8 |
|
x9 |
|
|
| L | 3500 | 0 | 0 | 1 | 3 |
|
|
18875/6 | -5/24 | -11/24 | 0,75 | 13/6 |
|
|
875 | 0,75 | -0,75 | 0,5 | 2 |
|
|
2750/3 | -1/6 | -1/6 | 1 | 10/3 |
|
|
3875/3 | -5/12 | 13/12 | -2,5 | -17/3 |
|
|
250 | 0,5 | -0,5 | 1 | 2 |
Видим, что коэффициенты при переменных в целевой функции положительны, значит, найденное решение будет оптимальным.
Итак, ![]() =0,
=0, ![]() =3875/3,
=3875/3, ![]() =2750/3,
=2750/3, ![]() =250, L=3500.
=250, L=3500.
Ответ: если предприятие будет изготавливать только три вида проволоки 1,2,3 причем 3875/3 км, 2750/3 км, 250 км соответственно, то общая прибыль от реализации изготовляемой продукции будет максимальной и равной 3500(ед).
Задача 2 (№28)
Условие:
С помощью симплекс–таблиц найти решение задачи линейного программирования: определить экстремальное значение целевой функции Q=CTx при условии Ax ³ £B,
где CT = [ c1 c2 . . . c6 ]T , ВT = [ b1 b2 . . . b6 ]T ,
XT = [ x1 x2 . . . x6]T , А= [aij] (i=1,6; j=1,3).
| № вар. | с1 | с2 | с3 | с4 | с5 | с6 | b1 | b2 | b3 | Знаки ограничений | a11 | a12 | a13 | a14 | |||
| 1 | 2 | 3 | |||||||||||||||
| 28 | -6 | 0 | 1 | -1 | -1 | 0 | 8 | 2 | 3 | = | = | = | 4 | 1 | 1 | 2 | |
| № вар. | a15 | a16 | a21 | a22 | a23 | a24 | a25 | a26 | a31 | a32 | a33 | a34 | a35 | a36 | Тип экстрем. |
| 1. 34 | 1 | 0 | 2 | -1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | max |
Решение:
Получим систему:
4 x1 + x2 + x3+2x4 + x5 =8;
2x1 - x2 +x4=2;
x1 + x2+x5=3
L= -6x1+ x3 -x4 -x5 → max
Пусть x2, x4 – свободные переменные, а x1, x3, x5 - базисные переменные. Приведем систему и целевую функцию к стандартному виду, для построения симплекс-таблицы:
x5 =2-(1,5x2 -0,5 x4);
x3 =6-(1,5x2 +0,5 x4);
x1=1-(-0,5x2+0,5x4)
L=-2-(3x2- x4) → max
Составим симплекс-таблицу:
Выберем разрешающим столбцом x4,т.к. только перед этой переменной в целевой функции отрицательное число, выберем в качестве разрешающего элемента тот, для которого отношение к нему свободного члена будет минимально (это x1). Меняем x4 и x1
|
b |
x2 | x4 | ||
| L |
-2 2 |
3 -1 |
-1 2 |
|
| x1 |
1 2 |
-0,5 -1 |
0,5 2 |
1/0,5=2 |
|
|
6 -1 |
1,5 0,5 |
0,5 -1 |
6/0,5=12 |
|
|
2 1 |
1,5 -0,5 |
-0,5 1 |
|
b |
x2 | x1 | |
| L | 0 | 2 | 2 |
| x4 | 2 | -1 | 2 |
|
|
5 | 2 | -1 |
|
|
3 | 1 | 1 |
Получили оптимальное решение, т.к. все коэффициенты положительны.
Итак, x1= x2=0, x3 =5, x4=2, x5 =3, L=0.
Ответ: x1= x2=0, x3 =5, x4=2, x5 =3, L=0.
Задача 3 (№8)
Условие:
Решение транспортной задачи:
1. Записать условия задачи в матричной форме.
2. Определить опорный план задачи.
3. Определить оптимальный план задачи.
4. Проверить решение задачи методом потенциалов.
| №вар. | а1 | а2 | а3 | b1 | b2 | b3 | b4 | b5 | с11 | с12 | с13 |
| 8 | 200 | 200 | 600 | 200 | 300 | 200 | 100 | 200 | 25 | 21 | 20 |
| с14 | с15 | с21 | с22 | с23 | с24 | с25 | с31 | с32 | с33 | с34 | с35 |
| 50 | 18 | 15 | 30 | 32 | 25 | 40 | 23 | 40 | 10 | 12 | 21 |
Решение:
Составим таблицу транспортной задачи. Заполним таблицу методом северо-западного угла:
| B1 | B2 | B3 | B4 | B5 | ai | |
| A1 |
25 200 |
21 | 20 | 50 | 18 | 200 |
| A2 | 15 |
30 200 |
32 | 25 | 40 | 200 |
| A3 | 23 |
40 100 |
10 200 |
12 100 |
21 200 |
600 |
| bj | 200 | 300 | 200 | 100 | 200 | 1000 |
Количество заполненных ячеек r=m+n-1=6.
Проверим сумму по столбцам, сумму по строкам и количество базисных (заполненных) клеток:
r =6, å ai=å bj=1000, всё выполняется, значит, найденный план является опорным.
L=25*200+30*200+40*100+10*200+12*100+21*200=22400
Постараемся улучшить план перевозок.
1) Рассмотрим цикл (1;1)-(1;2)-(2;2)-(2;1)
Подсчитаем цену цикла: j=15-30+21-25=-19<0
| B1 | B2 | B3 | B4 | B5 | ai | |
| A1 | 25 |
21 200 |
20 | 50 | 18 | 200 |
| A2 |
15 200 |
30 | 32 | 25 | 40 | 200 |
| A3 | 23 |
40 100 |
10 200 |
12 100 |
21 200 |
600 |
| bj | 200 | 300 | 200 | 100 | 200 | 1000 |
L=21*200+15*200+40*100+10*200+12*100+21*200=18600
2) Рассмотрим цикл (2;1)-(2;2)-(3;2)-(3;1)
j=-15+30+23-40=-2<0
| B1 | B2 | B3 | B4 | B5 | ai | |
| A1 | 25 |
21 200 |
20 | 50 | 18 | 200 |
| A2 |
15 100 |
30 100 |
32 | 25 | 40 | 200 |
| A3 |
23 100 |
40 |
10 200 |
12 100 |
21 200 |
600 |
| bj | 200 | 300 | 200 | 100 | 200 | 1000 |
L=21*200+15*100+30*100+23*100+10*200+12*100+21*200=18400
Проверим методом потенциалов:
Примем α1=0, тогда βj = cij – αi (для заполненных клеток).
Если решение верное, то во всех пустых клетках таблицы Δij = cij – (αi+ βj) ≥ 0
Очевидно, что Δij =0 для заполненных клеток.
В результате получим следующую таблицу:
| B1=6 | B2=21 | B3=-7 | B4=-5 | B5=4 | ai | |
| A1=0 | 25-6>0 |
21-21=0 200 |
20+7>0 | 50+5>0 | 18-4>0 | 200 |
| A2=9 |
15-9-6=0 100 |
30-21-9=0 100 |
32-9+7>0 | 25+5-9>0 | 40-4-9>0 | 200 |
| A3=17 |
23-17-6=0 100 |
40-21-17>0 |
10+7-17=0 200 |
12+5-17=0 100 |
21-4-17=0 200 |
600 |
| bj | 200 | 300 | 200 | 100 | 200 | 1000 |
Таким образом, решение верное, т.к. Δij > 0 для всех пустых клеток и Δij =0 для всех заполненных.
Тогда сумма всех перевозок:
L=18400
Ответ:
| B1 | B2 | B3 | B4 | B5 | ai | |
| A1 | 25 |
21 200 |
20 | 50 | 18 | 200 |
| A2 |
15 100 |
30 100 |
32 | 25 | 40 | 200 |
| A3 |
23 100 |
40 |
10 200 |
12 100 |
21 200 |
600 |
| bj | 200 | 300 | 200 | 100 | 200 | 1000 |
Задача 4 (№53)
Условие:
Определить экстремум целевой функции вида
F = c11x12+c22x22+c12x1x2+b1x1+b2x2
при условиях:
a11x1+a12x2<=>p1
a21x1+a22x2<=>p2.
1. Найти стационарную точку целевой функции и исследовать ее (функцию) на выпуклость (вогнутость) в окрестностях стационарной точки.
2. Составить функцию Лагранжа.
3. Получить систему неравенств в соответствии с теоремой Куна-Таккера.
4. Используя метод искусственных переменных составить симплекс-таблицу и найти решение полученной задачи линейного программирования.
5. Дать ответ с учетом условий дополняющей нежесткости.
| № | b1 | b2 | c11 | c12 | c22 | extr | a11 | a12 | a21 | a22 | p1 | p2 |
Знаки огр. 1 2 |
|
| 53 | 6 | 1,5 | -2 | -4 | –1 | max | 2,5 | -1 | 3 | 2,5 | 7 | 13 | ³ | ³ |
Решение:
Целевая функция:
F= -2x12-x22-4x1x2+6x1+1,5x2→max
Ограничения g1(x) и g2(x): 2,5x1-x2³7 2,5x1-x2–7³0
3x1+2,5x2³13 3x1+2,5x2-13³0
1) определим относительный максимум функции, для этого определим стационарную точку (х10, х20):
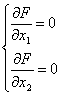 →
→
2) Исследуем стационарную точку на максимум, для чего определяем выпуклость или вогнутость функции
F11 (х10, х20) = -4 < 0
F12 (х10, х20)=-4
F21 (х10, х20)=-4
F22 (х10, х20)=-2
F11 F12 -4 -4
F21 F22 -4 -2
Т.к. условие выполняется, то целевая функция является строго выпуклой в окрестности стационарной точки
3) Составляем функцию Лагранжа:
L(x,u)=F(x)+u1g1(x)+u2g2(x)=-2x12-x22-4x1x2+6x1+1,5x2+u1 (2,5x1-x2–7)+ u2 (3x1+2,5x2-13).
Получим уравнения седловой точки, применяя теорему Куна-Таккера:
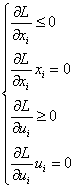 i=1;2
i=1;2
Объединим неравенства в систему А, а равенства в систему В:
Система А:
Система В:
Перепишем систему А:
6-4x1-4x2+2,5u1+3u2 <0
1,5-4x1-2x2-u1+2,5u2 <0
2,5x1-x2–7³0
3x1+2,5x2–13³0
4)Введем новые переменные
V={v1,v2}≥0; W={w1,w2}≥0
в систему А для того, чтобы неравенства превратить в равенства:
6-4x1-4x2+2,5u1+3u2 + v1=0
1,5-4x1-2x2-u1+2,5u2 + v2=0
2,5x1-x2–7- w1=0
3x1+2,5x2–13- w2=0
Тогда
- v1=6-4x1-4x2+2,5u1+3u2
- v2=1,5-4x1-2x2-u1+2,5u2
w1=2,5x1-x2–7
w2=3x1+2,5x2–13
Следовательно, система В примет вид:
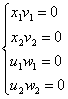 - это условия дополняющей
нежесткости.
- это условия дополняющей
нежесткости.
5) Решим систему А с помощью метода искусственных переменных.
Введем переменные Y={y1; y2} в 1 и 2 уравнения системы
6-4x1-4x2+2,5u1+3u2 + v1 -y1=0
1,5-4x1-2x2-u1+2,5u2 + v2 -y2=0
2,5x1-x2–7- w1=0
3x1+2,5x2–13- w2=0
и создадим псевдоцелевую функцию Y=My1+My2→min
Y’=-Y= -My1-My2→max.
В качестве свободных выберем х1, х2, v1, v2, u1, u2;
а в качестве базисных y1, y2, w1, w2.
Приведем систему и целевую функцию к стандартному виду, для построения симплекс-таблицы:
y1=6-(4x1+4x2-2,5u1-3u2 - v1)
y2=1,5-(4x1+2x2+u1-2,5u2 -v2)
w1=-7-(-2,5x1+x2)
w2=-13-(-3x1-2,5x2)
Y’=-Y=-My1-My2=-7,5M-(-8x1-6x2+1,5u1+5,5u2+ v1+v2) M
Решим с помощью симплекс-таблицы. Найдем опорное решение:
|
|
|
|
|
|
|
|
|
|
|
-7,5M 4,5M |
-8M 12M |
-6M 3M |
1,5M 3M |
5,5M -7,5M |
M 0 |
M -3M |
|
|
6 -3 |
4 -8 |
4 -2 |
-2,5 -2 |
-3 5 |
-1 0 |
0 2 |
|
|
1,5 3/4 |
4 2 |
2 0,5 |
1 0,5 |
-2,5 -5/4 |
0 0 |
-1 -0,5 |
|
|
-7 -3/4 |
-2,5 -2 |
1 -0,5 |
0 -0,5 |
0 5/4 |
0 0 |
0 0,5 |
|
|
-13 15/8 |
-3 5 |
-2,5 5/4 |
0 5/4 |
0 -25/16 |
0 0 |
0 -5/4 |
Меняем![]() и
и ![]()
|
|
|
|
|
|
|
|
|
|
|
-3M 3M |
4M -4M |
3M -2M |
4,5M -4,5M |
-2M M |
M -M |
-2M 2M |
|
|
3 3/2 |
-4 -2 |
-2 -1 |
-4,5 -9/4 |
2 0,5 |
-1 -0,5 |
2 1 |
|
|
3/4 15/8 |
2 -2,5 |
0,5 -5/4 |
0,5 -45/16 |
-5/4 5/8 |
0 -5/8 |
-0,5 5/4 |
|
|
-31/4 -15/8 |
-4,5 2,5 |
-0,5 5/4 |
-0,5 45/16 |
5/4 -5/8 |
0 5/8 |
0,5 -5/4 |
|
|
-89/8 75/32 |
2 -25/8 |
5/4 -25/16 |
5/4 -225/64 |
-25/16 25/32 |
0 -25/32 |
-5/4 25/16 |
Меняем ![]() и
и ![]()
|
|
|
|
|
|
|
|
|
|
|
0 0 |
0 0 |
M 0 |
0 0 |
M 0 |
0 0 |
0 0 |
|
|
3/2 77/8 |
-2 -1 |
-1 -3/4 |
-9/4 -37/16 |
0,5 5/8 |
-0,5 -5/8 |
1 3/4 |
|
|
21/8 77/32 |
-0,5 -1/4 |
-3/4 -3/16 |
-37/16 -37/64 |
5/8 5/32 |
-5/8 -5/32 |
3/4 -3/16 |
|
|
-77/8 77/16 |
-2 -0,5 |
3/4 -3/8 |
37/16 -37/32 |
-5/8 5/16 |
5/8 -5/16 |
-3/4 3/8 |
|
|
-281/32 693/128 |
-9/8 -9/16 |
-5/16 -27/64 |
-145/64 -333/256 |
25/32 45/128 |
-25/32 -45/128 |
5/16 27/64 |
Меняем ![]() и
и ![]()
|
|
|
|
|
|
|
|
|
|
|
0 0 |
0 0 |
M 0 |
0 0 |
M 0 |
0 0 |
0 0 |
|
|
89/8 431/18 |
-1 -16/9 |
-7/4 | -73/16 | 9/8 | -9/8 | 7/4 |
|
|
161/32 431/72 |
-1/4 -4/9 |
-15/16 | -185/64 | 25/32 | -25/32 | 9/16 |
|
|
77/16 431/36 |
-0,5 -8/9 |
-3/8 | -37/32 | 5/16 | -5/16 | 3/8 |
|
|
-431/32 431/18 |
-9/16 -16/9 |
-47/64 | -913/256 | 145/128 | -145/128 | 47/64 |
Меняем ![]() и
и ![]()
|
|
|
|
|
|
|
|
|
|
|
0 | 0 | M | 0 | M | 0 | 0 |
|
|
2525/72 | ||||||
|
|
3173/288 | ||||||
|
|
2417/144 | ||||||
|
|
431/18 |
Итак, ![]() =
=![]() =
=![]() =
=![]() =
=![]() =
=![]() ,
, ![]() =16,785,
=16,785, ![]() =11,017,
=11,017, ![]() =23,944,
=23,944, ![]() =35,07
=35,07
6) Условия дополняющей
нежесткости выполняются 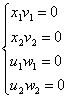 ,значит, решения исходной задачи
квадратичного программирования существует.
,значит, решения исходной задачи
квадратичного программирования существует.
Ответ: существует.
Литература.
1) Курс лекций Плотникова Н.В.
2) Пантелеев А.В., Летова Т.А. «Методы оптимизации в примерах и задачах».
© 2010 Интернет База Рефератов