Контрольная работа: Модификация модели М. Калецкого

Содержание

Введение……………………………………………………….............…………..2

1. Модификация модели М. Калецкого, описывающей динамику капитала....5

2. Пример 1………………………………………………………………….........10

3. Пример 2………………………………………………………………….........12

Выводы……………………………………………………………………...........15

Перечень ссылок………………………………………………………................16

Введение

В работе приведена модель динамики капитала, предложенная выдающимся польским ученым Михаилом Калецким. Эта модель модифицирована с учетом распределенных опозданий во время реализации инвестиций. Получено интегро-дифференциальное уравнение для описания динамики капитала, выполнен экономико - математичний анализ выявленных циклических изменений в нагромождении капитала и инвестиций.

Мировой финансово-экономический кризис вызвал необходимость в разработке новых экономических концепций и развитии уже признанных трактовок особенностей современного капитализма. Отечественная наука призвана активно включиться в эту работу также ввиду низкой эффективности рыночных преобразований, реализованных на основе монетаризма, в абсолютной уверенности, что англосакский путь экономической эволюции есть неоспоримый эталон. Как известно, выполняя рекомендации западных институтов, наши реформаторы существенно ослабили роль государства в экономике. Предполагалось, что стремительно появившийся вследствие всеобъемлющей приватизации класс предпринимателей немедленно возьмет на себя заботу о народном благе и осуществит долгожданное "национальное экономическое чудо". Как известно, ожидания не оправдались. Вполне очевидны различия в практических установках "новых украинцев" и западных предпринимателей: ведь мировоззрение последних сформировалось на базе прочных либеральных демократических традиций и глубокого понимания социальной ответственности бизнеса перед обществом. Сегодня как никогда остро Украина нуждается в эффективной государственной политике, ориентированной на устойчивый экономический рост, который обеспечит достижение европейских стандартов качества жизни граждан. В этом убеждают как рецессионные явления в хозяйстве, так и возможные новые угрозы во многих сферах хозяйствования. Такая политика должна опираться на точный прогноз направлений поступательного развития, исходящий из научных исследований динамики капитала.

Тезис о неразрывной связи политики и экономики не нуждается в доказательствах. Для принятия обоснованных долгосрочных политических решений по управлению государством следует использовать уже апробированные инвестиционные теории. В этой связи, по нашему мнению, заслуживают самого пристального внимания теоретические идеи и экономико-математические модели выдающегося польского ученого Михаила Калецкого (1899—1970). Если принять во внимание, что Дж Кейнс и М. Калецкий, оттолкнувшись от диаметрально противоположных точек зрения, в анализе реальных экономических процессов пришли к весьма близким выводам, то есть основания говорить о приложимости этих концепций, соответствующим образом модифицированных, к отечественным условиям. Попутно заметим, что, по мнению Дж Робинсон, М. Калецкий даже лучше, чем Дж Кейнс, изучил такие аспекты, как несовершенная конкуренция и эффективный спрос.

Идеи М. Калецкого можно с успехом использовать для разработки стратегии развития государства, направленной на достижение максимальной занятости трудоспособного населения путем выбора самого рационального варианта инвестиционных программ и планов, нацеленных на сбалансированный рост валового продукта и благосостояния.

Многие специалисты вполне заслуженно считают М. Калецкого одним из главных создателей теории, которая получила имя Дж Кейнса. В традициях классиков политэкономии польский ученый развил марксистские начала в экономических реалиях середины XX ст. и фактически предвосхитил главные идеи кейнсианства. В академических кругах Запада, особенно в Англии, его наследие получило широкое признание. В Советском Союзе труды М. Калецкого были известны меньше (правда, в год смерти ученого вышла его книга о теории роста социалистической экономики). В современных российских и украинских учебниках по экономической теории его имя упоминается крайне редко. Исключением являются уже названное учебное пособие и две статьи, где содержится полное жизнеописание М. Калецкого и дана надлежащая оценка его научным достижениям, а между тем библиография ученого насчитывает свыше 550 публикаций.

Цель настоящей работы - раскрыть определяющую роль инвестиций в накоплении капитала. Для этого подробно рассмотрен первоначальный вариант разработанной М. Калецким динамической модели, представленный в книге Р. Аллена.

1. Модификация модели М. Калецкого, описывающей динамику капитала

Следуя Р. Аллену и сохраняя его терминологию, мы приняли допущение о том, что условием действия модели служит известное разложение величины объема выпуска продукции через "доход" Y на потребление С, накопление I и независимые расходы G.

Y=C + I + G, (1)

где С=cY(c — предельная склонность к потреблению) и G - заданные величины. Доход определяется взаимодействием капиталовложений и статистического мультипликатора без запаздываний, то есть планируемые затраты полностью совпадают во времени с реальными инвестициями:

(2)

Величина I(t) есть не что иное, как фактические чистые затраты на капиталовложения; как правило, она имеет денежное выражение.

Ключевой переменной с позиции капиталовложений является величина B(t), определяющая программу инвестирования в момент времени t. М. Калецкий высказывает предположение, что в соответствии с решениями об инвестировании (по существу, с формированием портфеля заказов на капитальное оборудование) через планируемый интервал времени Q реализуются поставки и производятся финансовые расчеты в течение периода производства и ввода в эксплуатацию необходимого оборудования.

Обозначим через K(t) величину основного капитала в момент времени t и допустим, что скорость поставок нового оборудования является производной по времени величины капитала, то есть составит dK/dt. Тезис о том, что капиталовложения запаздывают, приводит к следующим уравнениям связи:

I(t) = (3)

(4)

Уравнения (3) и (4) отражают важную идею М. Калецкого о существенных различиях между плановыми инвестиционными проектами B(t) и фактически реализованными инвестициями I(t). Заметим, что в уравнениях (3) и (4) присутствует величина единственного фиксированного значения временного запаздывания Q, и это, на наш взгляд, весьма упрощает механизмы планирования и реализации инвестиционных программ.

Мы предлагаем, в отличие от М. Калецкого, рассмотреть взаимосвязи между капиталом K, решениями об инвестициях В и фактическими капиталовложениями I с использованием распределенных запаздываний. Формулы (3) и (4) получат следующий вид:

I(t) = (5)

K(t) = K0+ (6)

где К0- значение величины капитала в момент времени t=0; φ(t, τ) - ядро интегрального преобразования (5), имеющее смысл "экономической памяти" о всех прошлых значениях планируемых инвестиций на интервале времени τ [1, t]; ψ(t,τ) - ядро интегрального преобразования (6), интерпретируемое как реакция капитала на мгновенный скачок реальных инвестиций.

Часто в экономической теории, пренебрегая амортизацией капитала, полагают ψ(t, τ)=1. В таком случае уравнение (6) равносильно с начальным условием K(t = 0) = К0 дифференциальному уравнению

(7)

Далее рассматриваются предпосылки, на основании которых формируется структура плановых инвестиций B(t). Здесь мы солидарны с М. Калецким и Р. Алленом и утверждаем, что

B=aS-βK+ε, (8)

где S=(1—c)Y— сбережения, влияющие на В в прямом направлении; α, β— положительные константы; ε— слагаемое, отражающее автономную тенденцию планирования инвестиций.

Не нарушая единства, положим ε=const. Кроме того, отметим, что положительность коэффициента β характеризует в формуле (8) отрицательную корреляцию между величинами В и К. При этом β имеет размерность, обратную единице времени, а является безразмерной величиной.

Используя формулу (2), исключим из (8) зависимость от уровня дохода Y:

В=а1-βк+ε. (9)

Таким образом, уравнения (5), (7), (9) определяют функциональную взаимосвязь между переменными K(t), B(t), I(t). В данном случае наиболее просто вывести интегро-дифференциальное уравнение для динамики капитала:

(10)

Интегро-дифференциальное уравнение (10) вместе с начальным условием К(t=0)=К0 целиком описывает эволюцию капитала в данной экономической системе. Сложность исследования поведенческих свойств уравнения (10) во многом определяется явным видом ядра — функции φ (t, τ).

Рассмотрим случай, когда оно является вырожденным, то есть

φ (t, τ) = ξ(t)η(τ).

При такой структуре функции φ (t, τ) базовое интегро-дифференциальное уравнение (10) путем дифференцирования по времени с помощью несложных преобразований получает вид обыкновенного дифференциального уравнения второго порядка. Для простоты примем, что G — постоянное число, тогда величина А= также является постоянной.

Целесообразно ввести в рассмотрение переменную x(t) = K(t) — А, имеющую смысл отклонения величины капитала от некоего характерного постоянного значения А. В такой ситуации уравнение (10) примет следующую форму:

=dτ (11)

Отдифференцировав (11) по независимой переменной t и выполнив необходимые тождественные преобразования, получим искомое обыкновенное дифференциальное уравнение второго порядка по переменной X(t):

(12)

где

ρ(t) =

q(t)=βξ(t)η(t)

с ненулевыми начальными условиями;

X(0)=K0 – A, (13)

Дифференциальное уравнение (12) занимает особое место в общей теории обыкновенных дифференциальных уравнений, и совершенно невозможно дать исчерпывающий обзор свойств решения этого уравнения.

По поводу дифференциального уравнения (12) известный американский математик Р. Беллман утверждал, что значение уравнений указанного вида в физике трудно переоценить. Существует много исследований, связанных с данным уравнением. С математической точки зрения оно представляет собой постоянный вызов искусству аналитика: надо получать всевозможные свойства решений этого уравнения, не пользуясь такой роскошью, как явное представление последних через коэффициенты р и q.

Из-за многообразия возможных случаев и вытекающей отсюда трудности объединения их в общей теории мы ограничимся рассмотрением некоторых частных примеров, которые, кроме того что представляют экономико-математический интерес, иллюстрируют применение разработанных основных методов к исследованию задач экономической динамики.

2. Пример 1

При реализации планируемых инвестиционных проектов (формула (5)) с учетом распределенных запаздываний (взаимосвязь капитала, решений об инвестициях и фактических капиталовложений) используется функция φ1(t,τ)=be(τ-t), где b>0 есть некоторая постоянная времени. С экономической точки зрения такой выбор ядра интегрального преобразования (5) означает, что весовой коэффициент решения об инвестировании в момент времени τ(0<τ<t) возрастает с приближением к моменту времени t (когда инвестиции реализуются) и убывает, когда величина τ находится ближе к нулю.

Данный подход отражает реальное поведение инвесторов, когда принимаются решения об инвестировании.

Поскольку

φ1(t,τ)= ξ1(t)η1(τ),

то для определенности выберем

ξ1(t)= е-ы

η1(τ)= bеы.

Далее, после элементарных преобразований выражение (12) трансформируется к виду дифференциального уравнения второго порядка с постоянными коэффициентами:

(14)

Коэффициенты уравнения (14) есть строго положительные числа, так как 0 < α < 1, следовательно, решения X(t) будут устойчивыми.

Структура решений (14) имеет следующий вид:

X(t) = (15)

где

λ1,2=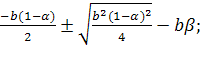

R1, R2 — произвольные постоянные, зависящие от начальных условий.

Таким образом, все решения X(t) дифференциального уравнения (14) экспоненциально стремятся от заданного начального условия Х0 к равновесному значению Х=0 (К=А). При этом характер движения X(t) к равновесию при условии b = является монотонным, а при противоположном знаке неравенства - колебательным гармоническим с частотой

ω = .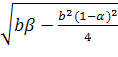

Здесь уместно напомнить, что разностное ядро φ1(t,τ)=beb(τ-t) так называемая "память о принятых инвестиционных решениях", по сути, является динамическим регулятором инвестиционного процесса, и вполне правомерна постановка задачи о выборе оптимального значения параметра b в соответствии с требованиями к качеству переходного процесса накопления капитала.

Установленная зависимость реализованных инвестиционных (в динамике) решений играет существенную роль для моделирования последствий поведения инвестора, что не всегда учитывается в инвестиционном процессе на макроуровне.

Пример 2

Рассмотрим ситуацию, когда реализуются инвестиционные проекты с учетом равной значимости на временном интервале τ [0, t] всех инвестиционных решений, что наиболее часто моделируется в ходе принятия стратегических решений. В таком случае ядро примет вид

φ2(t,τ)= 1/t,

то есть

ξ2(t,r) = 1/t,η2(τ)=1.

После необходимых преобразований дифференциальное уравнение (12) примет форму обыкновенного дифференциального уравнения второго порядка с переменными параметрами

(16)

Поведенческие свойства дифференциального уравнения (16) принципиально отличаются от свойств (14), так как имеют переменные коэффициенты, обращающиеся в бесконечность в нуле. Для уравнений типа (16) используются асимптотические методы, описывающие решения, когда параметры, от которых они зависят, стремятся к бесконечности.

В данном случае для уравнения (16) имеется решение:

X(t)= (17)

Здесь цилиндрическая функция (t) есть линейная комбинация специальных функций Бесселя первого Ja(t) и второго Ya(t) родов; С1, С2 — произвольные постоянные, зависящие от начальных условий. Для функций Бесселя существуют асимптотические представления при больших значениях аргумента t »1. Тогда решение (17) можно приближенно выразить через элементарные функции:

X(t)≈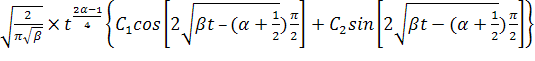 (18)

Вполне очевидно, что в выражении (18) имеют место колебания с переменной амплитудой и частотой. Представляет интерес частный случай решения (18) при α =1/2:

X(t)=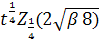=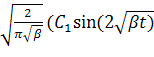+ (19)

Как видим, решение Х(t) в (19) является ограниченным, но колеблющимся с неограниченно возрастающим периодом, что само по себе есть факт, далекий от тривиальности при исследовании в динамике капитала низкочастотных (медленных) колебаний с позиций теорий экономических циклов.

Проанализировав два примера из первоначального варианта модели, предложенного М. Калецким еще в докейнсианский период, здесь мы не намерены рассматривать ее более поздние версии ввиду общности полученных ранее результатов. Кроме того, приведенные примеры наглядно демонстрируют принципиальное отличие динамических режимов накопления капитала при разных способах учета предварительных инвестиционных решений в момент их реализации. Данный модельный ряд динамики капитала инициирует соответствующие экономические интерпретации, адаптированные к реальным инвестиционным проектам, что существенно при решении задач макроэкономического анализа и формирования экономических систем кластерного типа.

Главной является мысль М. Калецкого о том, что макроэкономические процессы, описываемые с помощью мультипликатора-акселератора, имеют еще одну степень свободы, основанную на различии между инвестиционными решениями и фактическими капиталовложениями.

Выводы

На предложенных вариантах модификации модели было показано, что способ реализации инвестиционных проектов может как оказывать стабилизирующее влияние в целом на динамику капитала, так и вызывать негативные эффекты, нарушающие устойчивое функционирование экономической системы и провоцирующие нежелательные колебательные процессы.

Для улучшения инвестиционного климата в стране требуются научно обоснованные стратегии роста капиталовооруженности украинских предприятий, чтобы для самих инвесторов их инициативная деятельность в дальнейшем не принимала мистический характер "ритуальных жертвоприношений". Вот почему крайне важно в настоящее время для стимулирования экономического прогресса и повышения занятости расширять совокупный спрос путем инвестиций. При этом следует учитывать объективные требования к стабильности динамики капитала и осуществлять структурную оптимизацию всех составляющих эффективного спроса, обеспечивающих требуемую устойчивость инвестиционного процесса.

Перечень ссылок

1. Литвицький В. Найгірше позаду. "Урядовий кур'єр" № 132,2009, с. 7.

2. Габбард Р. Г. Гроші, фінансова система та економіка: Підручник. К., КНЕУ, 2004, с. 734.

3. Теория капитала и экономического роста. Под ред. С. С. Дзарасова. М., изд-во МГУ, 2004, с. 39.

4. Robinson J. Michal Kalecki on the Economic of Capitalism. "Oxford Bulletin of Economics and Statistics" № 39 (1), 1977, February, p. 7-17.

5. Kalecki M.,Kowalik T. Osservazionisulla"riformacruciale". "PoliticaedEconomia" №2-3,1971

6. Kalecki M. Dzieia. T. 2, Warszawa, 1980;Florek H.,Szefler S.Dywersjaw ekonomice. Yаrszawa, 1970.

7. Калецкий M. Очерк теории роста социалистической экономики. М., "Прогресс", 1970.

8. Дзарасов С. С. Михаил Калецкий: жизненный путь и научный вклад. "Экономическая наука современной России" № 2, 1999, с. 116—139

9. Мullег A. Michai Kalecki — wspornnienia і refleksje. "Gazeta SGH", 1.09.1999 r.

10. Аллeh P. Математическая экономия. M., Изд-во иностр. лит-ры, 1963, 668 с.

11. Чернышев С. И., Воронин А. В., Разумовский С. А. Проблема моделирования экономической динамики, http://chvr-article.narod.ru.

12. Беллман Р. Теория устойчивости решений дифференциальных уравнений. М., Изд-во иностр. лит-ры, 1954, 216 с.

13. Трикоми Ф. Дифференциальные уравнения. М., Изд-во иностр. лит-ры, 1962, 352 с.

14. Камке Э. Справочник по обыкновенным дифференциальным уравнениям. М., "Наука", 1971, с. 401 (уравнение 2.162).

15. Янке Е., Эмде Ф., Леш Ф. Специальные функции.- М., "Наука", 1977, 344 с.

16. Воронин А. В. Циклы в задачах нелинейной макроэкономики. - X., "ИНЖЭК", 2006, 136 с.