
Рефераты по сексологии
Рефераты по информатике программированию
Рефераты по биологии
Рефераты по экономике
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Рефераты по авиации и космонавтике
Рефераты по административному праву
Рефераты по безопасности жизнедеятельности
Рефераты по арбитражному процессу
Рефераты по архитектуре
Рефераты по астрономии
Рефераты по банковскому делу
Рефераты по биржевому делу
Рефераты по ботанике и сельскому хозяйству
Рефераты по бухгалтерскому учету и аудиту
Рефераты по валютным отношениям
Рефераты по ветеринарии
Рефераты для военной кафедры
Рефераты по географии
Рефераты по геодезии
Рефераты по геологии
Рефераты по геополитике
Рефераты по государству и праву
Рефераты по гражданскому праву и процессу
Рефераты по делопроизводству
Рефераты по кредитованию
Рефераты по естествознанию
Рефераты по истории техники
Рефераты по журналистике
Рефераты по зоологии
Рефераты по инвестициям
Рефераты по информатике
Исторические личности
Рефераты по кибернетике
Рефераты по коммуникации и связи
Контрольная работа: Основы научного исследования и планирование экспериментов на транспорте
Контрольная работа: Основы научного исследования и планирование экспериментов на транспорте
ОГЛАВЛЕНИЕВВЕДЕНИЕ
ЗАДАНИЕ
ПОДГОТОВКА ПЛАНА ПРОВЕДЕНИЯ ОДНОФАКТОРНОГО ЭКСПЕРИМЕНТА
ПЛАН ЭКСПЕРИМЕНТА И РЕЗУЛЬТАТЫ ОПЫТОВ
УРАВНЕНИЕ РЕГРЕССИИ
РЕЗУЛЬТАТЫ ОПЫТОВ В ГРАФИЧЕСКОМ ВИДЕ
ПРОВЕРКА АДЕКВАТНОСТИ И РАБОТОСПОСОБНОСТИ МОДЕЛИ
ВЫВОД
ЛИТЕРАТУРА
ВВЕДЕНИЕ
Современный этап научных исследований характеризуется тем, что наряду с классическим натурным экспериментом все шире применяется вычислительный эксперимент, проводимый на математической модели с помощью ЭВМ. Проведение вычислительного эксперимента значительно дешевле и мобильнее, чем проведение аналогичного натурного, и в ряде случаев вычислительный эксперимент является единственным возможным инструментом исследователя.
Математический аппарат теории планирования и обработки результатов экспериментов в полной мере может быть применен как к натурным, так и к вычислительным экспериментам. В данной контрольно-курсовой работе под проводимым экспериментом будем понимать эксперимент на математической модели, выполненный при помощи ЭВМ.
Основная задача теории планирования и обработки результатов экспериментов – это построение статистической модели изучаемого процесса в виде Y = f(X1, X2,…Xk), где X – факторы, Y – функция отклика. Полученную функцию отклика можно использовать для оптимизации изучаемых процессов, то есть определять значения факторов, при которых явление или процесс будет протекать наиболее эффективно.
Объект исследования – одноцилиндровый четырехтактный дизельный двигатель ТМЗ-450Д.
Предмет исследования – процесс функционирования двигателя.
Цель исследования анализ влияния одного из параметров двигателя на показатели его работы и получение соответствующей функциональной зависимости
ЗАДАНИЕ
Область планирования фактора X: Xmin = 0,012 м, Xmax = 0,055 м.
План проведения эксперимента:
| № опыта |
xj |
| 1 | -1 |
| 2 | -0,8 |
| 3 | -0,6 |
| 4 | -0,4 |
| 5 | -0,2 |
| 6 | 0 |
| 7 | 0,2 |
| 8 | 0,4 |
| 9 | 0,6 |
| 10 | 0,8 |
| 11 | 1 |
Используя приведенные исходные данные и программу расчета функционирования двигателя, проанализировать влияние радиуса кривошипа (X) на величину максимальной температуры (Y) рабочего тела в цилиндре двигателя. Получить функциональные зависимости между указанными величинами.
ПОДГОТОВКА ПЛАНА ПРОВЕДЕНИЯ ОДНОФАКТОРНОГО ЭКСПЕРИМЕНТАИспользуя указанный в задании план проведения эксперимента в кодовом виде, а также область планирования фактора Х (Хmin, Хmax), подготовим план проведения данного однофакторного эксперимента.
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() .
.
где ![]() - интервал (шаг)
варьирования фактора;
- интервал (шаг)
варьирования фактора;
![]() - натуральное значение основного уровня фактора;
- натуральное значение основного уровня фактора;
![]() - кодированное значение
фактора x;
- кодированное значение
фактора x;
![]() - натуральное значение
фактора в j-ом опыте, где j =
1, 2,…, N; N – число опытов.
- натуральное значение
фактора в j-ом опыте, где j =
1, 2,…, N; N – число опытов.
В дальнейших расчетах будем использовать только натуральные значения факторов и функции отклика.
ПЛАН ЭКСПЕРИМЕНТА И РЕЗУЛЬТАТЫ ОПЫТОВИспользуя выданную преподавателем программу расчета (математическую модель) проведем на ЭВМ необходимое количество опытов N. Полученные результаты представим в виде таблицы 1.
Табл. 1
| № опыта |
Xj |
Yj |
| 1 | 0,012 | 3601,8348 |
| 2 | 0,0163 | 2712,4310 |
| 3 | 0,0206 | 2195,4343 |
| 4 | 0,0249 | 1855,3637 |
| 5 | 0,0292 | 1626,8644 |
| 6 | 0,0335 | 1461,2450 |
| 7 | 0,0378 | 1339,577 |
| 8 | 0,0421 | 1250,5135 |
| 9 | 0,0464 | 1173,9877 |
| 10 | 0,0507 | 1126,4606 |
| 11 | 0,055 | 1092,5573 |
Получим функциональную зависимость Y = f(X) (уравнение регрессии) с помощью метода наименьших квадратов (МНК). В качестве аппроксимирующих функций использовать линейную (Y = a0 + a1X) и квадратичную зависимости (Y = a0 + a1X + a2X2). Посредством МНК значения a0, a1 и a2 найдем из условия минимизации суммы квадратов отклонений измеренных значений отклика Yj от получаемых с помощью регрессионной модели, т. е. путем минимизации суммы:
![]() .
.
Проведем минимизацию суммы квадратов с помощью дифференциального исчисления, путем приравнивания к 0 первых частных производных по a0, a1 и a2.
Рассмотрим реализацию метода наименьших квадратов применительно к уравнению вида Y = a0 + a1X. Получим:
![]() ;
;
![]() .
.
Выполнив ряд преобразований, получим систему нормальных уравнений метода наименьших квадратов:
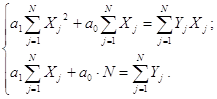
Решая эту систему, найдем коэффициенты a1 и a0:
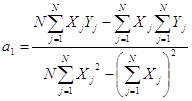 ;
; 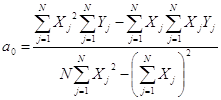 .
.
Для квадратичной зависимости Y = a0 + a1X + a2X2 система нормальных уравнений имеет вид:
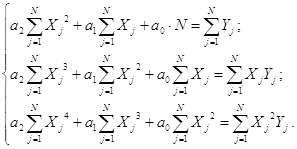
Вычислим из N опытов необходимые суммы и данные представим в виде таблицы 2.
Табл. 2
| № опыта |
Xj |
Yj |
Xj2 |
Xj Yj |
Xj2Yj |
Xj3 |
Xj4 |
| 1 | 0,012 | 3601,8348 | 0,000144 | 43,222017 | 0,5186642 | 0,0000017 | 0,000000020736 |
| 2 | 0,0163 | 2712,4310 | 0,0002656 | 44,212625 | 0,7204216 | 0,0000043 | 0,0000000705433 |
| 3 | 0,0206 | 2195,4343 | 0,0004243 | 45,225946 | 0,9315227 | 0,0000087 | 0,0000001800304 |
| 4 | 0,0249 | 1855,3637 | 0,00062 | 46,198556 | 1,1503254 | 0,0000154 | 0,0000003844 |
| 5 | 0,0292 | 1626,8644 | 0,0008526 | 47,50444 | 1,3870645 | 0,0000248 | 0,0000007269267 |
| 6 | 0,0335 | 1461,2450 | 0,0011222 | 48,951707 | 1,6398091 | 0,0000375 | 0,0000012593328 |
| 7 | 0,0378 | 1339,577 | 0,0014288 | 50,63601 | 1,9139876 | 0,000054 | 0,0000020414694 |
| 8 | 0,0421 | 1250,5135 | 0,0017724 | 52,646618 | 2,2164101 | 0,0000746 | 0,0000031414017 |
| 9 | 0,0464 | 1173,9877 | 0,0021529 | 54,473029 | 2,52747781 | 0,0000998 | 0,0000046349784 |
| 10 | 0,0507 | 1126,4606 | 0,0025704 | 57,111552 | 2,8954543 | 0,0001303 | 0,0000066069561 |
| 11 | 0,055 | 1092,5573 | 0,003025 | 60,090651 | 3,3049858 | 0,0001663 | 0,000009150625 |
| Σ | 0,3685 | 19436,266 | 0,0143782 | 550,27311 | 19,206122 | 0,0006174 | 0,0000282173998 |
Для уравнения регрессии вида Y = a0 + a1X найдем коэффициенты a1 и a0:
![]() .
.
![]() .
.
Для уравнения регрессии вида Y = a0 + a1X + a2X2 найдем коэффициенты a1 , a2 и a0:
Решим систему нормальных уравнений способом Крамера:
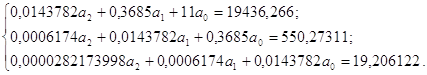
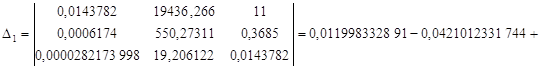
![]() .
.
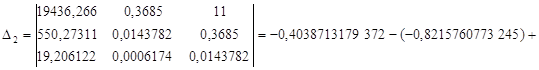
![]() .
.
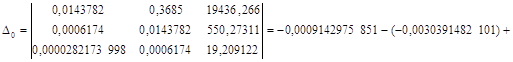
![]() .
.
Найдем определитель (det) матрицы:
![]() .
.
![]() ;
; ![]() ;
; ![]() .
.
![]() ;
; ![]() ;
; ![]() .
.
Построим графики функций Y = a0 + a1X ; Y = a0 + a1X + a2X2 :
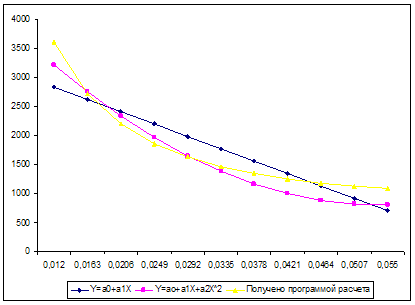
| X | 0,012 | 0,0163 | 0,0206 | 0,0249 | 0,0292 | 0,0335 | 0,0378 | 0,0421 | 0,0464 | 0,0507 | 0,055 |
|
Y=ao+a1X |
2619,9 | 2406,658 | 2193,415 | 1980,172 | 1766,929 | 1553,686 | 1340,443 | 1127,2 | 913,9573 | 700,7144 | |
|
Y=a0+a1X+a2 X2 |
3215,923 | 2748,207 | 2330,714 | 1963,444 | 1646,397 | 1379,574 | 1162,973 | 996,5962 | 880,4424 | 814,5117 | 798,8043 |
Для проверки
адекватности модели определим абсолютные DYj и
относительные погрешности ![]() в
каждом из опытов.
в
каждом из опытов.
DYj
= ![]() - Yj;
- Yj;
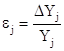 ,
,
где ![]() – расчетное значение
функции (отклика) в j-ой точке.
– расчетное значение
функции (отклика) в j-ой точке.
Данные представим в виде таблицы 3.
Табл. 3
| j |
Y = a0 + a1X |
Y = a0 + a1X + a2X2 |
||
|
DYj |
|
DYj |
|
|
| 1 | -768,6918 | -0,21342 | -385,9118 | -0,10714 |
| 2 | -92,531 | -0,03411 | 35,776 | 0,01319 |
| 3 | 211,2237 | 0,09621 | 135,2797 | 0,06162 |
| 4 | 338,0513 | 0,1822 | 108,0803 | 0,05825 |
| 5 | 353,3076 | 0,21717 | 19,5326 | 0,012 |
| 6 | 305,684 | 0,20919 | -81,671 | -0,05589 |
| 7 | 214,109 | 0,15983 | -176,604 | -0,13183 |
| 8 | 89,9295 | 0,07191 | -253,9173 | -0,20305 |
| 9 | -46,7877 | -0,0398 | -293,5453 | -0,25004 |
| 10 | -212,5033 | -0,1886 | -311,9489 | -0,27693 |
| 11 | -391,8429 | -0,35865 | -293,753 | -0,26887 |
Просматривая значения этих погрешностей, исследователь может легко понять, какова погрешность предсказания в точках, где проводились опыты, устраивают его или нет подобные ошибки. Таким образом, путем сопоставления фактических значений отклика с предсказанными по уравнению регрессии можно получить достаточно надежное свидетельство о точностных характеристиках модели.
С помощью анализа работоспособности регрессионной модели выясним практическую возможность ее использования для решения какой-либо задачи. Это анализ будем проводить, вычисляя коэффициент детерминации (квадрат корреляционного отношения). Коэффициент детерминации R2 вычисляется по формуле:
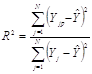
где 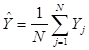 – общее среднее значение
функции отклика.
– общее среднее значение
функции отклика.
![]() .
.
Вычислим из N опытов необходимые суммы и данные представим в виде таблицы 4.
Табл. 4
|
Y = a0 + a1X |
Y = a0 + a1X + a2X2 |
||
| j |
|
|
|
| 1 | 3366863,62479 | 1136803,18835 | 1952571,23764 |
| 2 | 893965,95743 | 727552,24249 | 853898,13319 |
| 3 | 183613,13271 | 409247,73017 | 312848,71152 |
| 4 | 7819,94095 | 181886,66602 | 37616,467 |
| 5 | 19619,28834 | 45470,75597 | 14328,99238 |
| 6 | 93445,31841 | 0,00002 | 147047,20405 |
| 7 | 182633,3815 | 45474,39816 | 359786,00774 |
| 8 | 266689,37885 | 181893,9504 | 589419,20142 |
| 9 | 351584,44898 | 409258,65674 | 602866,06259 |
| 10 | 410205,24101 | 727568,0054 | 801506,847 |
| 11 | 454782,94891 | 1136822,67874 | 759273,70255 |
| Σ | 6231222,66188 | 5001978,27246 | 5732724,84892 |
Для уравнения регрессии Y = a0 + a1X:
![]()
Для уравнения регрессии Y = a0 + a1X + a2X2:
![]()
Т.к. в
уравнениях регрессии ![]() оба уравнения
принято считать работоспособными. В уравнении регрессии вида Y
= a0 + a1X + a2X2
оба уравнения
принято считать работоспособными. В уравнении регрессии вида Y
= a0 + a1X + a2X2
![]() , а в уравнении регрессии
вида Y = a0 + a1X
, а в уравнении регрессии
вида Y = a0 + a1X ![]() . Из этого следует, что в уравнении
вида Y = a0 + a1X + a2X2 найденное значение регрессии лучше объясняет
вариацию в значениях Y (N
>> (d+1)), чем в уравнении вида Y
= a0 + a1X.
. Из этого следует, что в уравнении
вида Y = a0 + a1X + a2X2 найденное значение регрессии лучше объясняет
вариацию в значениях Y (N
>> (d+1)), чем в уравнении вида Y
= a0 + a1X.
В процессе выполнения контрольно-курсовой работы мы научились:
- разрабатывать план проведения вычислительного эксперимента;
- проводить вычислительный эксперимент на ЭВМ и накапливать статистическую информацию;
- обрабатывать полученные статистические данные с помощью регрессионного анализа и получать формульные зависимости, связывающие значение выходной переменной (отклика) объекта с входными переменными (факторами);
- графически представлять и анализировать полученные результаты (проверять адекватность и работоспособность регрессионной модели);
- вычислять коэффициент детерминации (квадрат корреляционного отношения) и анализировать полученные результаты.
ЛИТЕРАТУРА
1. Гурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 1972.
2.Красовский Г.И., Филаретов Г.Ф. Планирование эксперимента. Минск, 1982.
3.Румшинский Л.З. Математическая обработка результатов эксперимента. Справочное руководство. – М.: Наука, 1971.
© 2010 Интернет База Рефератов