Контрольная работа: Схема Бернуллі

Міністерство освіти і науки України

Приватний вищий навчальний заклад

Європейський університет

Запорізька філія

Контрольна робота

з дисципліни: Теорія ймовірності і математична статистика

Варіант 5 - Схема Бернуллі

Виконав

Перевірив:

Запоріжжя,

2007р.

СХЕМА БЕРНУЛЛІ

У багатьох задачах теорії ймовірностей, статистики та повсякденної практики треба досліджувати послідовність (серію) п випробувань. Наприклад, випробування "кинуто 1000 однакових монет" можна розглядати як послідовність 1000 більш простих випробувань - "кинута одна монета". При киданні 1000 монет імовірність появи герба або надпису на одній монеті не залежить від того, що з'явиться на інших монетах. Тому можна казати, що у цьому випадку випробування повторюються 1000 разів незалежним чином.

Означення 1. Якщо усі п випробувань проводити в однакових умовах і імовірність появи події А в усіх випробуваннях однакова та не залежить від появи або непояви А в інших випробуваннях, то таку послідовність незалежних випробувань називають схемою Бернуллі.

Нехай випадкова подія А може з'явитись у кожному випробуванні з імовірністю Р(А) = р або не з'явитись з імовірністю q = Р{А) = 1 - р.

Поставимо задачу: знайти імовірність того, що при п випробуваннях подія А з'явиться т разів і не з'явиться п - т разів. Шукану імовірність позначимо Рп(т).

Спочатку розглянемо появу події А три рази в чотирьох випробуваннях. Можливі так події

тобто їх

Якщо подія А з'явилася 2 рази в 4 випробуваннях, то можливі такі події

У загальному випадку, коли подія А з'являється т разів у п випробуваннях, таких складних подій буде

Обчислимо імовірність однієї складної події, наприклад,

Імовірність сумісної появи п незалежних подій дорівнює добутку ймовірностей цих подій згідно з теоремою множення ймовірностей, тобто

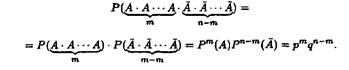
Кількість таких складних подійі вони несумісні. Тому, згідно з теоремою додавання ймовірностей несумісних подій, маємо

Формулу (1) називають формулою Бернуллі. Вона дозволяє знаходити імовірність появи події А т разів при п випробуваннях, які утворюють схему Бернуллі.

Зауваження 1. Імовірність появи події Арп випробуваннях схеми Бернуллі менш т разів знаходять за формулою

Імовірність появи події А не менше т разів можна знайти за формулою

або за формулою

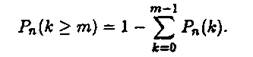
Імовірність появи події А хоча б один раз у п випробуваннях доцільно знаходити за формулою

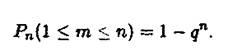
Зауваження 2. У багатьох випадках треба знаходити найбільш імовірне значення то числа т появ події А. Це значення т визначається співвідношеннями

Число то повинно бути цілим. Якщо (п + 1)р - ціле число, тоді найбільше значення імовірність має при двох числах

Зауваження 3. Якщо імовірність появи події А в кожному випробуванні дорівнює р, то кількість п випробувань, які необхідно здійснити, щоб з імовірністю Р можна було стверджувати, що подія А з'явиться хоча б один раз, знаходять за формулою,

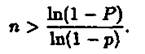
Приклад 1. Прилад складено з 10 блоків, надійність кожного з них 0.8. Блоки можуть виходити з ладу незалежно один від одного. Знайти імовірність того, що

а) відмовлять два блоки;

б) відмовить хоча б один блок;

в) відмовлять не менше двох блоків.

Розв'язання. Позначимо за подію А відмову блока. Тоді імовірність події А за умовою прикладу буде

Р(А) =р = 1-0.8 = 0.2, тому д = 1-р = 1-0.2=0.8.

Згідно з умовою задачі п = 10. Використовуючи формулу Бернуллі та Зауваження 1, одержимо

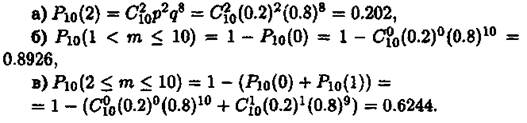
Приклад 2. За одну годину автомат виготовляє 20 деталей. За скільки годин імовірність виготовлення хоча б одн бракованої деталі буде не менше 0.952, якщо імовірність браку будь-якої детал дорівнює 0.01?

Розв'язання. Застосовуючи формулу (2), знайдемо спочатку таку кількість виготовлених деталей, щоб з імовірністю р = 0.952 можна було стверджувати про наявність хоча б однієї бракованої деталі, якщо імовірність браку за умовою р = 0.01

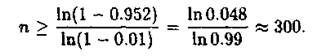
Отже, за час(годин) автомат з імовірністю 0.952 виготовить хоча б одну браковану деталь.

Приклад 3. При новому технологічному процесі 80 % усієї виготовленої продукції має найвищу якість. Знайти найбільш мовірне число виготовлених виробів найвищої якості серед 250 виготовлених виробів.

Розв'язання. Позначимо шукане число то-Згідно Зауваження

За умовою прикладу п = 250, р = 0.8, q — 0.2, тому

Але то повинно бути цілим числом, тому то = 200.

СПИСОК ВИКОРИСТАНОІ ЛІТЕРАТУРИ

1. Барковський В.В., Барковська Н.В., Лопатін О.К. теорія ймовірностей та математична статистика. К.: ЦУЛ, 2002. – 448с.

2. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 1980.

3. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. М.: Высшая школа, 1975.

4. Гнеденко Б.В. Курс теории вероятностей. – М.: наука, 1988.

5. Леоненко М.М., Мішура Ю.С. та ін. Теоретико-ймовірностні та статистичні методи в економетриц та фінансовій математиці. – К.: Інформтехніка, 1995.