Курсовая работа: Иррациональные уравнения

Курсовая работа: Иррациональные уравнения

Курсовая работа

Иррациональные уравнения

Содержание:

Введение

1. Основные определения и теоремы

2. Стандартные иррациональные уравнения и методы их решения

2.1 Уравнения вида

2.2. Уравнения вида

2.3 Иррациональные уравнения, которые решаются введением новой переменной

2.4 Уравнения вида , ,

3. Нестандартные методы решения иррациональных уравнений

3.1 Применение основных свойств функции

3.1.1 Использование области определения уравнения

3.1.2 Использование области значений функции

3.1.3 Использование монотонности функции

3.1.4 Использование ограниченности функции

3.2 Применение производной

3.2.1 Использование монотонности функции

3.2.2 Использование наибольшего и наименьшего значений функций

4. Смешанные иррациональные уравнения и методы их решения

4.1 Иррациональные уравнения, содержащие двойную иррациональность

4.2 Иррациональные показательные уравнения

4.3 Иррациональные логарифмические уравнения

Заключение

Литература

Введение

Тема моей курсовой работы − «иррациональные уравнения». Я выбрала её потому, что в учебном курсе, этому материалу посвящено мало часов, а в задачниках большое количество примеров посвящено именно этой теме.

Поэтому в изучении «иррациональных уравнений» я преследую цель - дать основные определение иррациональным уравнениям и теоремам. Определить какие бывают виды уравнений. Рассмотреть правила решения иррациональных уравнений.

Задачи моей работы изучить научную и методическую литературу, подобрать и рассмотреть задачи для данной темы, включая олимпиадные.

В моей курсовой работе показаны решения иррациональных уравнений как стандартного метода, так и не стандартного метода решения. Я старалась как можно доступнее охватить проблемы этой темы. Конечно, всё нельзя учесть в курсовой работе, но я постараюсь ниже изложить основные моменты. Я хотела бы сделать данную работу вспомогательным пособием при изучении темы «Иррациональные уравнения».

1. Основные определения и теоремы

Определение 1. Уравнение это два выражения, соединенные знаком равенства; в эти выражения входит одна или несколько переменных, называемых неизвестными.

Пример 1. - является уравнением с одной неизвестной.

Пример 2.  - является уравнением с двумя неизвестными.

Определение 2. Равенство вида  называется уравнением с одной переменной .

Пример 1.  - является уравнением с одной переменной х.

Далее рассматриваем уравнения с одной переменной.

Определение 3. Всякое значение переменной, при котором выражения  и  принимают равные числовые значения, называется корнем уравнения или его решением.

Пример 1. Уравнение  имеет два корня: -1 и 1.

Определение 4. Решить уравнение – значит, найти множество всех его решений или доказать, что их нет.

Пример 1. Уравнение  имеет единственный корень 4, так как при этом и только при этом значении переменной  обращается в верное равенство, таким образом, ответ записывается в следующем виде:

О т в е т: {4}.

Пример 2. Уравнение  не имеет действительных корней.

О т в е т:.

Пример 3. Уравнение  имеет бесконечное множество решений, так как после тождественных преобразований получили равенство . Т.е данное уравнение  есть тождественное равенство, верное для любого действительного значения .

О т в е т: .

Определение 5. Тождество (тождественное равенство) - это равенство двух выражений с переменными, верное при всех допустимых значениях входящих в него переменных. Тождествами считаются и верные числовые равенства, а также равенства, превращающиеся в верное числовое равенство для всех числовых значений букв, для которых эти выражения определены.

Пример 1. Равенство , справедливо для всех числовых значений и в, является тождественным.

Пример 2. Равенство 2=2 тождество.

Определение 6. Тождественное преобразование выражения – это замена выражения на тождественно равное ему выражение, т. е. равное для всех числовых значений входящих в него переменных.

К тождественным преобразованиям относятся, например, приведение подобных слагаемых; разложение на множители; приведение алгебраических дробей к общему знаменателю; разложение их на элементарные дроби и другие.

Определение 7. Иррациональным называют уравнение, в котором переменная содержится под знаком радикала или под знаком возведения в дробную степень.

Пример 1.  - иррациональное уравнение (переменная содержится под знаком радикала).

Пример 2.  иррациональное уравнение (переменная содержится под знаком возведения в дробную степень).

Определение 8. Областью определения уравнения (или областью допустимых значений переменной - ОДЗ) называют множество всех тех значений переменной , при которых и выражение , и имеют смысл.

Пример 1.  Выражение ( и  определены при всех . Значит, ОДЗ: .

Пример 2. . Выражение  не определено при , а выражение  не определено при .

Значит, ОДЗ: .

Пример 3. . Корень четной степени имеет смысл лишь при неотрицательных значениях подкоренного выражения. Значит, одновременно должны выполняться условия:  т.е. ОДЗ:

Определение 9. Пусть даны уравнения:  (1),  (2).

Если каждый корень уравнения (1) является одновременно корнем уравнения (2), то уравнение (2) называется следствием уравнения (1). Следствие обозначается следующим образом:  

Пример 1.

В процессе решения уравнения часто приходится применять такие преобразования, которые приводят к уравнению, являющемуся следствием исходного. Уравнению-следствию удовлетворяют все корни исходного уравнения, но, кроме них, уравнение-следствие может иметь и такие решение, которые не являются корнями исходного уравнения, так называемые, «посторонние» корни. Чтобы выявить и отсеять «посторонние» корни, обычно поступают так: все найденные корни уравнения-следствия проверяют подстановкой в исходное уравнение.

Рассмотрим примеры преобразований, которые могут привести к расширению ОДЗ, т.е. к появлению «посторонних» корней.

1.         Замена уравнения  уравнением

Если при некотором значении , равном , верно равенство , то верным является также равенство . Значит, уравнение  является следствием исходного уравнения. При этом может существовать такое значение , равное , при котором  и . Тогда число , являющееся корнем уравнения , не является корнем исходного уравнения, т.к. при  исходное уравнение не имеет смысла.

Пример 1. Решить уравнение .

Решение. . Тогда .

Проверка.

При  знаменатель уравнения не обращается в ноль, а при  - обращается. Следовательно, исходное уравнение имеет единственный корень: -10.

О т в е т: .

2. Возведение обеих частей уравнения в квадрат.

Пусть даны два уравнения  (1) и . Если - корень первого уравнения, то верно равенство . Из равенства двух чисел вытекает равенство их квадратов, т.е. , а это означает, что - корень уравнения (2). Значит из уравнения (1) следует уравнение (2).

В то же время из равенства квадратов чисел не следует равенство этих чисел (числа могут быть противоположенными). Поэтому из уравнения (2) не следует уравнение (1). Отсюда вытекает, что если при решении уравнения использовалось возведение обеих частей уравнения в квадрат, то нужно повести дополнительное исследование, позволяющее исключить «посторонние» корни, если они появились.

Пример 1. Решить уравнение .

Решение. Возведем обе части этого уравнения в квадрат.

; .Тогда , .

Проверка.

Если , то , равенство не верно, следовательно, -1- не является корнем исходного уравнения.

Если , то 4=4, равенство верно.

Следовательно, уравнение имеет единственный корень: 4.

О т в е т: {4}.

3. Выполнение в одной части (или в обеих частях) уравнения тождественных преобразований, приводящих к расширению области определения равнения.

Если некоторое тождественное преобразование привело к расширению области определения уравнения, то получаем уравнения - следствие. При этом могут существовать такие значения переменной, которые являются корнями исходного уравнения.

Пример 1. Решить уравнение .

Решение. Выполнив приведение подобных слагаемых, получим: . Тогда , .

Проверка.

Если , то выражение  не имеет смысла.

Если , то , равенство верно.

Следовательно, уравнение имеет единственный корень:5.

О т в е т: {5}.

Пример 2. Решить уравнение .

Решение.  или . Тогда , .

Проверка.

Если , то выражение  не имеет смысла.

Если , то , равенство верно.

Следовательно, уравнение имеет единственный корень:-2.

О т в е т: {-2}.

Если при решении уравнения мы заменили его уравнением - следствием, то указанная выше проверка является неотъемлемой частью решения уравнения. Поэтому важно знать, при каких преобразованиях данное уравнение переходит в следствие.

Рассмотрим уравнение  (3) и умножим обе части его на одно и тоже выражение , имеющее смысл при всех значениях . Получим уравнение:  (4), корнями которого служат как корни уравнения (3), так и корни уравнения .

Значит, уравнение (4) есть следствие уравнения (3). Ясно, что уравнения (3) и (4) равносильны, если «постороннее» уравнение  не имеет корней. Таким образом, справедлива следующая теорема.

Теорема 1. Если обе части уравнения умножить на , то получится уравнение, являющееся следствием исходного. Если уравнение  не имеет корней, то полученное уравнение равносильно исходному (если область допустимых значений не уже области допустимых значений переменной данного уравнения).

Пример 1.  .

Заметим, что подобное преобразование, т.е. переход от уравнения (4) к уравнению (3) делением обеих частей уравнения (4) на выражение , как правило, недопустимо, поскольку можно привести к потери корней, в этом случае могут «потеряться» корни уравнения .

Пример 2. Уравнение  имеет два корня: 3 и 4.

Деление обеих частей уравнения на  приводит к уравнению , имеющий только один корень 4, т.е. произошла потеря корня.

Снова возьмем уравнение (3) и возведем обе его части в квадрат. Получим уравнение:  (5), корнями которого служат как корни уравнения (3), так и корни «постороннего» уравнения . Ясно, что уравнения (3) и (5) равносильны, если у «постороннего» уравнения нет корней.

Пример 3. Уравнение  имеет корень 4. Если обе части этого уравнения возвести в квадрат, то получится уравнение , имеющие два корня: -2 и 4. Значит, уравнение - следствие уравнения . При переходе от уравнения к уравнению  появился «посторонний» корень: -2.

Теорема 2. При возведении обеих частей уравнения в квадрат (и вообще в любую четную степень) получается уравнение, являющееся следствием исходного.

Пример 1. .

При решении иррационального уравнения чаще всего стараются заменить его более простым, но равносильным исходному. Поэтому важно знать равносильные преобразования.

Определение 10. Уравнение, имеющее одни и те же корни, называют равносильными уравнениями. Уравнения, не имеющие корней, также считают равносильными. Другими словами два уравнения называют равносильными, если множества их решений совпадают. Равносильность обозначается следующим образом: .

Пример 1. Уравнения  и  равносильны, т.к. каждое из них имеет единственный корень – число 3. .

Пример 2. Уравнения  и  не равносильны, т.к. первое имеет только один корень: 6, а второе имеет два корня: 6 и -6.

Пример 3. Уравнения  и  равносильны, т.к. множества их решений пусты. .

Определение 11. Пусть даны уравнения  и  и некоторое множество М. Если любой корень первого уравнения, принадлежащий множеству М, удовлетворяют второму уравнению, а любой корень второго уравнения, принадлежащий множеству М, удовлетворяет первому уравнению, то эти уравнения называются равносильными на множестве М.

Пример 1.  и  не являются равносильными на множестве всех действительных чисел, т.к. первое уравнение имеет единственный корень 1, а второе имеет два корня: -1 и 1. Но эти уравнения равносильны на множестве всех неотрицательных чисел, т.к. каждое из них имеет на этом множестве единственный корень: 1.

Отметим, что часто множество М совпадает либо с ОДЗ уравнения , либо множеством всех действительных чисел.

Имеется ряд теорем о равносильности уравнений.

Теорема 3. При возведении обеих частей уравнения в одну и ту же нечетную степень получается уравнение, равносильное исходному.

Пример 1. .

Теорема 4. Если в уравнении какое-нибудь слагаемое перенести из одной части в другую, изменив его знак, то получится уравнение, равносильное исходному.

Пример 1. .

Теорема 5. Если обе части уравнения умножить или разделить на одно и тоже отличное от ноля число, то получится уравнение, равносильное исходному.

Пример 1.  (обе части первого уравнения разделили на 2).

Теорема 6. Если в какой либо части уравнения выполнить тождественные преобразования, не меняющие области определения уравнения, то получится уравнение, равносильное исходному.

В школьной практике при решении иррациональных уравнений чаще всего используются два основных метода:

1) обеих частей уравнения в одну и ту же степень;

2) введение новых (вспомогательных) переменных.

Эти методы будем считать стандартными. В обязательном школьном курсе обычно этими методами и ограничиваются. Однако иногда приходится применять нестандартные методы и искусственные приемы решения иррациональных уравнений.

Типичная ошибка при решении иррациональных уравнений состоит в том, что школьники без дополнительных пояснений используют преобразования, нарушающие равносильность, что приводит к потере корней и появлению «посторонних» корней.

При возведении обеих частей иррационального уравнения в одну и ту же степень надо иметь в виду, что если степень - не четное число, то получим равносильное уравнение, если же степень - четное число, то получим уравнение - следствие. Поэтому при решении иррациональных уравнений в большинстве случаев необходима проверка найденных решений.

Проверки можно избежать, если решать иррациональные уравнения с помощью равносильных замен. Для этого полезно знать следующие теоремы.

Теорема 7. Уравнение вида  равносильно смешанной системе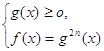

Уравнение вида

Теорема 8. Уравнение вида  или .

Уравнение вида .

Далее рассмотрим более подробно типы иррациональных уравнений и методы их решения.

2. Стандартные иррациональные уравнения

Как правило, в школьном курсе рассмотрение иррациональных уравнений сводится к разбору нескольких несложных примеров. Они в большинстве случаев решаются возведением в квадрат левой и правой частей уравнения. После решения обязательно выполняется проверка. Не обращается внимание на то, что иррациональные уравнения могут решаться и с использованием понятия равносильности. В данном параграфе представлены различные виды иррациональных уравнений, которые можно отнести к стандартным и решать одним из следующих методов, а именно:

1) метод перехода к уравнению - следствию с последующей проверкой полученных корней;

2) метод равносильного перехода к уравнению или к смешанной системе;

3) метод введения новой переменной.

2.1 Уравнения вида

Пример 1. Решить уравнение .

Решение. Возведем обе части исходного уравнения в квадрат..

О т в е т: {6}.

Пример 2. Решить уравнение .

Решение. В левой части исходного уравнения стоит арифметический квадратный корень – он по определению неотрицателен, а в правой части – отрицательное число.

Следовательно, уравнение не имеет корней.

О т в е т:.

Запишем равносильность, с помощью которой решаются уравнения данного вида.

 , если  и не имеет решения, если .

Пример 3. Решить уравнение .

Решение. Возведем обе части исходного уравнения в куб.

; .

О т в е т: {-5}.

Запишем равносильность, с помощью которой решаются уравнения данного вида: .

2.2 Уравнения вида

Довольно часто при решении уравнений данного вида учащиеся используют следующую формулировку свойства произведения «Произведение двух сомножителей равно нулю, когда хотя бы один из них равен нулю». Заметим, что формулировку свойства произведения должна выглядеть следующим образом: « произведение двух сомножителей равно нулю, когда хотя бы один из них равен нулю, а другой при этом имеет смысл».

Запишем равносильность, с помощью которой решаются уравнения данного вида:

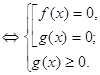
Пример 1. Решить уравнение .

Решение. 

.

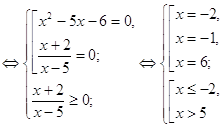О т в е т: {-2;6}.

Пример 2. Решить уравнение .

Решение. В данном случае уравнение не имеет вида, указанного в заголовке. Следовательно, его необходимо преобразовать. Но сначала найдем ОДЗ переменной .

ОДЗ: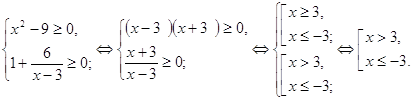

Преобразуем уравнение к виду

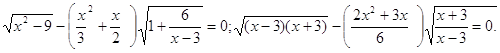
При решении уравнения учащиеся часто необоснованно делят обе части уравнения на выражение, содержащее неизвестное (в данном случае, на ), что приводит к потере корня и приобретению «постороннего». Подобные уравнения, содержащие в обеих частях общий множитель, следует решать переносом всех членов в одну часть и разложением полученного выражения на множители. 

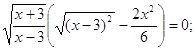
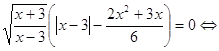
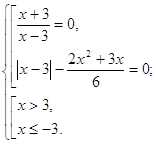
Решим каждое уравнение из совокупности.

; .

                                                  (1).

Учитывая, что ОДЗ:  получаем, что уравнение (1) равносильно совокупности: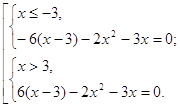

. Тогда ,  не удовлетворяет условию

, данное уравнение не имеет корней.

Следовательно, совокупность примет следующий вид:

Вернемся к системе: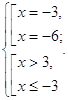

О т в е т: {-3;6}.

2.3 Иррациональные уравнения, которые решаются введением новой переменной

При решении различных видов уравнений: рациональных, тригонометрических, показательных часто используется метод введения новой переменной. Новая переменная в уравнениях иногда действительно очевидна, но иногда ее трудно увидеть, а можно выявить только лишь в процессе каких либо преобразований. Бывает полезно ввести не одну, а две переменные. Видим типичные случаи введения новых переменных в иррациональных уравнениях.

Пример 1. Решить уравнение

Решение. Введем новую переменную. Пусть , , где . Получаем, что  .Тогда - не удовлетворяет условию

Выполним обратную замену.

О т в е т:{34}.

Пример 2. Решить уравнение

Решение. Уединение радикала и возведение в степень обеих частей уравнения привело бы к громоздкому уравнению. В то же время, если проявить некоторую наблюдательность, то можно заметить, что данное уравнение сводиться к квадратному. Действительно, умножим обе части заданного уравнения на 2, получим, что    

Введем новую переменную. Пусть  Получаем, что . Тогда  - не удовлетворяет условию ,

Выполним обратную замену.   Тогда ,

Т.к. исходное уравнение равносильно уравнению  то проверка полученных корней не нужна.

О т в е т: {-2;3,5}.

Пример 3. Решить уравнение

Решение. Преобразуем данное уравнение.

Введем новую переменную. Пусть,  а  Получаем, что . Тогда - не удовлетворяет условию .

Выполним обратную замену. .

О т в е т:{1}.

2.4 Уравнения вида , ,

Данные уравнения можно решить при помощи основного метода решения иррациональных уравнений (возведение в квадрат обеих частей уравнения), но иногда их можно решить и другими методами.

Рассмотрим уравнение  (1). Пусть  - корень уравнения (1). Тогда справедливо числовое равенство . Найдем разность чисел  и , обозначив ее , и запишем данное равенство в виде  (2).

Используя, что , запишем равенство (2) в виде . Данное равенство означает, что число  есть корень уравнения  (3).

Таким образом, уравнение (3) является следствием уравнения (1). Складывая эти два уравнения и умножая полученное уравнение на а, получим уравнение (4), также являющееся следствием уравнения (1). Возведя уравнение (4) в квадрат и решив полученное уравнение, надо выполнить проверку найденных корней, т.е. проверить, являются ли его корни корнями уравнения (1).

Замечание. Отметим, что точно также доказывается, что уравнение (4) есть следствие уравнения .

Пример 1. Решить уравнение  (5).

Решение. Разность подкоренных выражений  и  есть

. ,

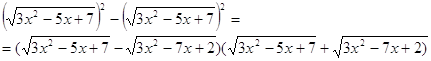то уравнение (6) является следствием исходного уравнения. Тогда, складывая уравнения (5) и (6), получим уравнение  (7), также являющееся следствием исходного уравнения (5). Возведем обе части уравнения (6) в квадрат, получим уравнение  (8), также являющееся следствием исходного уравнения. Решая уравнение (8), получаем, что ,

Проверкой убеждаемся, что оба этих числа являются корнями исходного уравнения.

О т в е т:.

Замечание. Уравнение вида  можно решать умножением обеих частей уравнения на некоторое выражение, не принимающее значение ноль (на сопряженное левой части уравнения т.е.

Пример 2. Решить уравнение  (8).

Решение. Т.к. , то умножим обе части уравнения на выражение , являющееся сопряженным левой части уравнения (8).  . После приведения подобных слагаемых получаем уравнение  (9), равносильное исходному, т.к. уравнение действительных корней не имеет. Складывая уравнения (8) и (9) получаем, что . Тогда

О т в е т:.

Замечание. Также уравнения вида  можно решать с помощью ОДЗ уравнения и равносильных переходов от одних уравнений к другим.

Пример 3. Решить уравнение

Решение. Найдем ОДЗ переменной х.

ОДЗ:Следовательно,

На ОДЗ обе части уравнения положительны, поэтому после возведения в квадрат получим уравнение: , равносильное для  уравнению

Иногда решения уравнения можно найти, решая его на разных числовых промежутках.

Для любого имеем , а . Следовательно, среди нет решений уравнения .

Для  имеем . Следовательно,  для . . Тогда . Т.к. , то  является корнем уравнения , равносильному уравнению  для этих х.

О т в е т: .

Пример 4. Решить уравнение

Решение. Преобразуем исходное уравнение.

Возведем обе части данного уравнения в квадрат.

Проверка показывает, что 5 является корнем исходного уравнения.

Замечание. Иногда значительно проще можно решать уравнения вида , если воспользоваться свойствами монотонности функций, а именно тем, что сумма двух возрастающих функций является возрастающей функцией, и всякая монотонная функция каждое свое значение принимает, лишь при одном значении аргумента. Действительно, функции  и - возрастающие. Следовательно, их сумма - возрастающая функция.

Значит, исходное уравнение, если имеет корень, то только один. В этом случае, учитывая, что , подбором легко найти, что 5 является корнем исходного уравнения.

О т в е т:{5}.

Пример 5. Решить уравнение

Решение. Если обе части исходного уравнения возвести в квадрат, то получится довольно сложное уравнение. Поступим по-другому: преобразуем уравнение к виду:

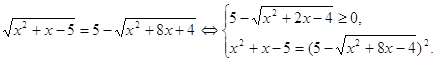
Решим неравенство системы.

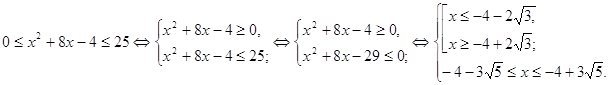
Решением системы является множество:

.

Решим уравнение системы.

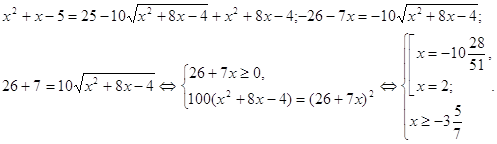
Убеждаемся, что 2 принадлежит множеству решений неравенства (рис.1).

Замечание. Если решать данное уравнение возведением обеих частей в квадрат, то необходимо выполнить проверку. 2 - целое число, поэтому при выполнении проверки трудностей не возникает. А что касается значения , то подстановка его в исходное уравнение приводит к весьма сложным вычислениям. Однако такой подстановки можно избежать, если заметить, что при этом значении правая часть уравнения  принимает отрицательное значение: . Тогда как левая часть уравнения отрицательной быть не может. Таким образом, не является корнем уравнения - следствия данного уравнения. Тем более, это значение не может быть корнем исходного уравнения. Итак, корень уравнения - число 2.

О т в е т:{2}.

Пример 6. Решить уравнение

Решение. Найдем ОДЗ переменной х.

ОДЗ: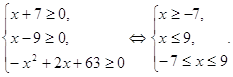  

Следовательно,

Для любых значений  из ОДЗ, удовлетворяющих условию , т.е. для  из промежутка  левая часть уравнения отрицательна, а первая – неотрицательна, значит, ни одно из этих  решением уравнения быть не может.

Пусть . Для таких  обе части уравнения неотрицательны, и поэтому оно равносильно на этом множестве уравнению: .

Введем новую переменную. . Получаем, что . Тогда  - не удовлетворяет условию , .

Выполним обратную замену.

; ;

.

Тогда - не удовлетворяет условию ,

О т в е т: .

Пример 7. Решить уравнение

Решение. Найдем ОДЗ переменной х.

ОДЗ: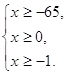  

Следовательно, что

Легко видеть, что , т.к. .

Разделим обе части уравнения на . Получаем, что

Преобразуем . Введем новую переменную. Пусть , а . Тогда уравнение примет вид: ; ; : . Тогда - не удовлетворяет условию , . Выполним обратную замену.

О т в е т: .

Пример 8. Решить уравнение

Решение. Преобразуем исходное уравнение. 

Возведем обе части полученного уравнения в квадрат.

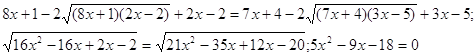
Тогда

Итак, проверка показывает, что -1,2 - не является корнем исходного уравнения, а 3 - является.

Замечание. Данное уравнение можно решать и с помощью равносильных переходов, но тогда его решении будет намного сложнее, чем приведенное выше.

О т в е т: {3}.

Пример 9. Решить уравнение

Решение. Заметим, что все квадратные трехчлены положительны относительно  . Перепишем уравнение в виде:

Обозначим для краткости подкоренные выражения через  соответственно. Умножим и разделим левую и правую часть уравнения на сопряженные сомножители. Получаем, что

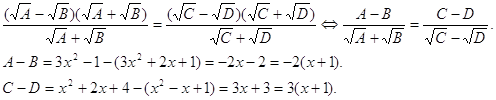
Вернемся к уравнению.

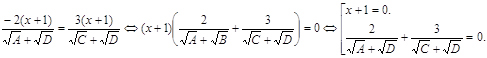
Второе уравнение совокупности решений не имеет, поскольку оба знаменателя положительны. Следовательно,

Замечание. Также решение данного уравнения можно найти, исследуя его на разных числовых промежутках.

Сначала выделим  и  соответственно в каждом из подкоренных выражений в правой части уравнения.

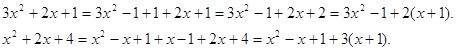
Следовательно, исходное уравнение имеет вид:

Обозначим для краткости подкоренные выражения через , ,  и  соответственно. Т.к. выражение  обращается в ноль при , то рассмотрим решение данного уравнения при ,  и .

Если , то >, >+>+.

Следовательно, при  исходное уравнение не имеет корней.

Если , то <, <+<+.

Следовательно, при  исходное уравнение не имеет корней.

Если , то =, =+=+.

Следовательно, -1 является единственным корнем исходного уравнения.

О т в е т:{-1}.

Замечание. Следовательно, при решении уравнений с радикалами надо уметь пользоваться любым из этих методов и выбирать в каждом случае оптимальный.

3. Не стандартные методы решения иррациональных уравнений

Существуют иррациональные уравнения, которые считаются для школьников обычных образовательных школ задачами повышенной трудности. Для решения таких уравнений лучше применять не традиционные методы, а приемы, которые не совсем привычны для учащихся. В этой главе приводятся решения уравнений основанных на графических соображений, свойствах функции (таких, как монотонность, ограниченность, четность), применении производной и т.д.

3.1 Применение основных свойств функции

3.1.1 Использование области определения уравнения

Иногда знание области определения уравнения позволяет доказать, что уравнение не имеет решений, а иногда позволяет найти решения уравнения непосредственной подстановкой чисел из нее.

Пример 1. Решить уравнение .

Решение. Найдем область определения уравнения.

ОДЗ: .

Следовательно, данная система решений не имеет.

Т.к. система решений не имеет, то и данное уравнение не имеет корней.

О т в е т: .

Пример 2. Решить уравнение

Решение. Найдем ОДЗ переменной х.

ОДЗ: .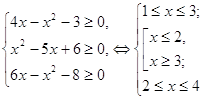

Следовательно,  или .

Таким образом, решения данного уравнения могут находиться среди найденных двух чисел.

Проверкой убеждаемся, что только 2 является корнем исходного уравнения.

О т в е т: {2}.

3.1.2 Использование области значений уравнений

Пример 1. Решить уравнение

Решение. Т.к. , следовательно, , но  (правая часть уравнения отрицательна, а левая положительна), значит данное уравнение не имеет решений.

О т в е т:

Пример 2. Решить уравнение .

Решение. Т.к. , то

; ; ; ; ; ; .

Следовательно, левая часть уравнения принимает неотрицательное значение только при . А это значит, что его корнем может быть только значение 5, а может случиться, что уравнение вообще не будет иметь корней. Для решения этого вопроса выполним проверку.

Проверка показывает, что 5 является корнем исходного уравнения.

О т в е т: {5}.

3.1.3 Использование монотонности функции

Решение уравнений и неравенств с использованием свойств монотонности основывается на следующих утверждениях.

1. Пусть f(x) - непрерывная и строго монотонная функция на промежутке Q, тогда уравнение f(x)=c, где c - данная константа может иметь не более одного решения на промежутке Q.

2. Пусть f(x) и g(x) - непрерывные на промежутке Q функции, f(x) - строго возрастает, а g(x)- строго убывает на этом промежутке, тогда уравнение f(x)= g(x) может иметь не более одного решения на промежутке Q.

Отметим, что в каждом из случаев промежутки Q могут иметь один из видов:

Пример 1. Решим уравнение

Решение. Найдем ОДЗ переменной х.

ОДЗ: .

Следовательно, .

На ОДЗ функции  и  непрерывны и строго убывают, следовательно, непрерывна и убывает функция . Поэтому каждое свое значение функция h(x) принимает только в одной точке. Т.к. h(2)=2 , то 2 является единственным корнем исходного уравнения.

О т в е т: {2}.

3.1.4 Использование ограниченности функции

Если при решении уравнения  удается показать, что для всех  из некоторого множества М справедливы неравенства  и , то на множестве М уравнение  равносильно системе уравнений: .

Пример 1. Решить уравнение .

Решение. Функции, стоящие в разных частях уравнения, определены на . Для любого  . Следовательно, данное уравнение равносильно системе уравнений

.

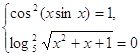Решим второе уравнение системы:

;  ;  

Тогда  

Проверка показывает, что 0 является корнем данного уравнения, а -1-не является.

О т в е т:{0}.

Пример 2. Решить уравнение

Решение. Оценим подкоренные выражения.

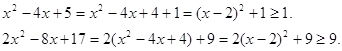
Следовательно, ,

Т.к. первое слагаемое левой части исходного уравнения ограничено снизу единицей, а второе слагаемое-3, то их сумма ограничена снизу 4. Тогда левая часть уравнения становится равной правой части уравнения при .

О т в е т:{2}.

3.2 Применение производной

В вышеприведенных уравнениях были рассмотрены применения некоторых свойств функции, входящих в уравнение. Например, свойства монотонности, ограниченности, существования наибольшего и наименьшего значений и т.д. Иногда вопрос о монотонности, об ограниченности и, в особенности, о нахождении наибольшего и наименьшего значений функции элементарными методами требует трудоемких и тонких исследований, однако он существенно упрощается при применении производной. (Например, не всегда можно догадаться, как и какое неравенство применить из «классических»).

Рассмотрим применение производной при решении уравнений.

3.2.1 Использование монотонности функции

В дальнейшем мы будем пользоваться следующими утверждениями:

1) если функция f(x) имеет положительную производную на промежутке М,  то эта функция возрастает на этом промежутке;

2) если функция  непрерывна на промежутке   и имеет внутри промежутка положительную (отрицательную) производную, то эта функции возрастает ( убывает) на промежутке;

3) если функция  имеет на интервале (а;b) тождественно равную нулю производную, то эта функция  есть постоянная на этом интервале.

Пример 1. Решить уравнение

Решение. Рассмотрим функцию

.

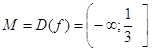На этом промежутке  непрерывна, внутри его имеет производную:

Эта производная положительна внутри промежутка . Поэтому функция  возрастает на промежутке М. Следовательно, она принимает каждое свое значение в одной точке. А это означает, что данное уравнение имеет не более одного корня. Легко видеть, что -1 является корнем данного уравнения и по сказанному выше других корней не имеет.

О т в е т:

3.2.2 Использование наибольшего и наименьшего значений функции

Справедливы следующие утверждения:

1)         наибольшее (наименьшее) значение непрерывной функции, принимаемое на интервале  может достигаться в тех точках интервала , в которых ее производная равна нулю или не существует (каждая такая точка называется критической точкой);

2)         чтобы найти наибольшее и наименьшее значение непрерывной на отрезке функции, имеющей на интервале (а;b) конечное число критических точек, достаточно вычислить значения функции во всех критических точках, принадлежащих интервалу (а;b), а также в концах отрезка и из полученных чисел выбрать наибольшее и наименьшее;

3)         если в критической точке  функция непрерывна, а ее производная, проходя через эту точку, меняет знак с «минуса» на «плюс», то точка - точка минимума, а если ее производная меняет знак с «плюса» на «минус», то - точка максимума.

Пример 1. Решить уравнение .

Решение. Найдем ОДЗ переменной x.

ОДЗ: .

Рассмотрим непрерывную функцию  на отрезке [2;4], где D(f)=[2;4].

Функция f(x) на интервале (2;4) имеет производную:, обращаются в ноль только при х=3.

Т.к. функция f(x)непрерывна на отрезке [2;4], то ее наибольшее и наименьшее значения находятся среди чисел f(3);f(2);f(4). Т.к. f(3)=2;f(2)=f(4)=, , то наибольшее значение f(x) есть f(3)=2.

Следовательно, данное уравнение имеет единственный корень: 3.

О т в е т:{3}.

4. Смешанные иррациональные уравнения и методы их решения

4.1 Иррациональные уравнения, содержащие двойную иррациональность

Пример 1. Решить уравнение

Решение. Возведем обе части уравнения в куб.

 Возведем обе части полученного уравнения в квадрат.

Введем новую переменную. Пусть , тогда . Получаем, что . Тогда .

Выполним обратную замену.  Или .

Тогда  или

Проверка показывает, что  не является корнем данного уравнения, а 1- является.

О т в е т: {1}.

Пример 2. Решить уравнение

Решение.

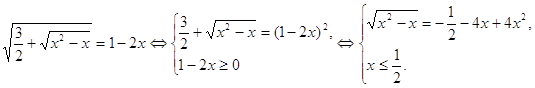
Введем новую переменную. Пусть . Тогда

Тогда система примет следующий вид:

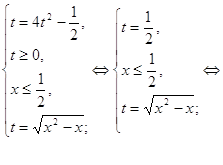
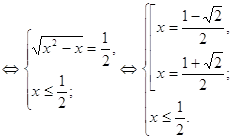
О т в е т: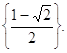

Пример 3. Решить уравнение

Решение. Введем новую переменную. Пусть . Тогда . Получаем, что

.

Т.к. , то данное уравнение равносильно следующему:

Получаем, что . Учитывая, что , то решения: . Следовательно, .

Выполним обратную замену. . Тогда

О т в е т: [-4;0].

Пример 4. Решить уравнение

Решение. Преобразуем подкоренные выражения.

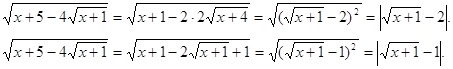
Вернемся к исходному уравнению.

Последнее уравнение решим методом интервалов.

1.         Пусть . Получаем, что

.

Т.к. , то на данном промежутке уравнение не имеет корней.

2.         Пусть . Получаем, что Равенство верно. Найдем все значения  из данного промежутка.. Следовательно,

3.         Пусть . Получаем, что . Т.к. , то на данном промежутке уравнение не имеет корней.

Замечание. Данное уравнение можно решать, выполнив замену переменной . После решения исходного уравнения относительно переменной , выполнив обратную замену, найдем корень уравнения.

О т в е т: [0;3].

Замечание. Выражение вида  обычно называют двойным радикалом или сложным радикалом.

Если подкоренное выражение представляет собой полный квадрат, то можно в двойном радикале освободиться от внешнего радикала, воспользовавшись равенством .

Преобразование двойных радикалов.

Упражнение 1. Освободиться от внешнего радикала в выражении .

Решение. Слагаемое  можно рассматривать как удвоенное произведение чисел  и  или чисел  и . Число 7 должно быть равно сумме квадратов этих чисел. Подбором находим, что это условие выполняется для чисел  и , т.е. .

Получаем, что

О т в е т:.

 4.2. Иррациональные показательные уравнения

Пример 1. Решить уравнение .

Решение. ;  - решений нет.

О т в е т:

Пример 2. Решить уравнение

Решение.

- Решений нет, т.к.

О т в е т:

Пример 3. Решить уравнение

Решение.

;

О т в е т: .

Приме 4. Решить уравнение

Решение.

;

Введем новую переменную. Пусть . Получаем, что . Тогда

Выполним обратную замену.  Или

; 

- решений нет.

;.

О т в е т:{3}.

Пример 5. Решить уравнение

Решение. Множество М общая часть (пересечение) областей существования функций - есть все

На множестве М функции  и  положительны. Поэтому, логарифмируя обе части уравнения, получим уравнение, равносильное исходному на М.

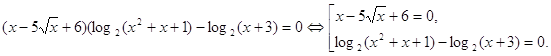
Решим уравнения совокупности.

. Введем новую переменную. Пусть . Получаем, что . Тогда . Выполним обратную замену.  или . Тогда  или .

Получаем, что исходное уравнение равносильно системе:

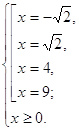
О т в е т: .

Замечание. В задачах повышенной сложности встречаются уравнения вида , где - некоторые положительные числа. Такие уравнения не являются иррациональными уравнениями, т.к. не содержат переменной под знаком радикала, но все, же разберем их решение в данном пункте.

Пример 6. Решить уравнение

Решение. Преобразуем выражение

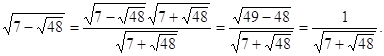
Тогда исходное уравнение примет вид: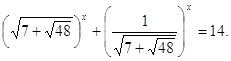

Замечание. Можно заметить, что , следовательно,  и - взаимно обратные числа. Тогда . Введем новую переменную. Пусть , а Получаем, что исходное уравнение равносильно следующему . Тогда

Выполним обратную замену.

 или

; ;

Тогда .

;

Тогда

О т в е т :{-2;2}.

4.3 Иррациональные логарифмические уравнения

Пример 1. Решить уравнения

Решение. ;

Учитывая, что , данное уравнение равносильно системе:

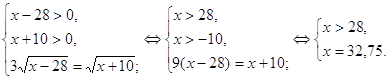
О т в е т:{32,75}.

Пример 2. Решить уравнения

Решение. . Преобразуем правую часть уравнения.

Вернемся к исходному уравнению.

;

Введем новую переменную. Пусть . Получаем, что

.

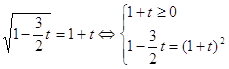Решим уравнение системы.

; .

Тогда

Вернемся к системе: 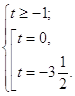Следовательно,

Выполним обратную замену:

Проверка показывает, что 1 является корнем исходного уравнения.

О т в е т: {1}.

Пример 3. решить уравнение

Решение. Найдем ОДЗ переменной х.

ОДЗ:

.

На ОДЗ исходное уравнение равносильно уравнению

; ;

Введем новую переменную. Пусть  или

;

;

О т в е т: {3;81}.

Заключение

Данная курсовая работа помогла мне научиться решать иррациональные уравнения следующих типов: стандартные, нестандартные, показательные, логарифмические, повышенного уровня. Применять основные свойства функции, область определения, область значения функции. Использовать наибольшее и наименьшее значения функции. Применение производной. Я считаю, что цели которые поставлены перед выполнением курсовой работы выполнены.

Литература

О.В. Харькова «Иррациональные уравнения».

А.Н. Колмогоров «Алгебра и начала анализа».

Е.Д. Куланин, В.П. Норин «3000 конкурсных задач по математике».

В.А. Гусев, А.Г. Мордкович «Справочные материалы по математике».

М.И. Сканави «Сборник задач по математике».