
Рефераты по сексологии
Рефераты по информатике программированию
Рефераты по биологии
Рефераты по экономике
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Рефераты по авиации и космонавтике
Рефераты по административному праву
Рефераты по безопасности жизнедеятельности
Рефераты по арбитражному процессу
Рефераты по архитектуре
Рефераты по астрономии
Рефераты по банковскому делу
Рефераты по биржевому делу
Рефераты по ботанике и сельскому хозяйству
Рефераты по бухгалтерскому учету и аудиту
Рефераты по валютным отношениям
Рефераты по ветеринарии
Рефераты для военной кафедры
Рефераты по географии
Рефераты по геодезии
Рефераты по геологии
Рефераты по геополитике
Рефераты по государству и праву
Рефераты по гражданскому праву и процессу
Рефераты по делопроизводству
Рефераты по кредитованию
Рефераты по естествознанию
Рефераты по истории техники
Рефераты по журналистике
Рефераты по зоологии
Рефераты по инвестициям
Рефераты по информатике
Исторические личности
Рефераты по кибернетике
Рефераты по коммуникации и связи
Курсовая работа: Исследование операций
Курсовая работа: Исследование операций
Министерство общего и профессионального образования РФ
Кафедра «Системы управления»
КУРСОВАЯ РАБОТА
ПО ИССЛЕДОВАНИЮ ОПЕРАЦИЙ
Вариант 14
Челябинск, 2004
Содержание
1. Задача 1
2. Задача 2
3. Задача 3
4. Задача 4
Приложение
1. Задача 1
Условие:
Нефтеперерабатывающий завод получает 4 полуфабриката: x1 тыс. л. алкилата, x2 тыс. л. крекинг-бензина, x3 тыс. л. бензина прямой перегонки и x4 тыс. л. изопентана. В результате смешивания этих четырех компонентов в разных пропорциях образуется три сорта авиационного бензина: бензин А (а1:а2:а3:а4), бензин В (b1:b2:b3:b4) и бензин С (с1:с2:с3:с4).
Стоимость 1 тыс. л. бензина каждого сорта равна y1 руб., y2 руб. и y3 руб.
Определить соотношение компонентов, при котором будет достигнута максимальная стоимость всей продукции.
| № вар. | x1 | x2 | x3 | x4 | y1 | y2 | y3 | а1 | а2 | а3 | а4 | b1 | b2 |
| 1 | 400 | 250 | 350 | 100 | 120 | 100 | 150 | 2 | 3 | 5 | 2 | 3 | 1 |
| № вар. | b1 | b2 | c1 | c2 | c3 | c4 |
| 1 | 2 | 1 | 2 | 2 | 1 | 3 |
Решение:
Составим математическую модель задачи.
Обозначим через t1 количество бензина А;
через t2 количество бензина В;
через t3 количество бензина С.
Тогда, целевая функция будет
L=y1t1+ y2t2+ y3t3=120t1+100t2+150t3 →max
Система ограничений:
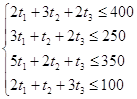
Приведем систему ограничений к виду основной задачи линейного программирования (введем новые переменные t4 , t5 ,t6 ,t7, которые входят в целевую функцию с нулевыми коэффициентами):
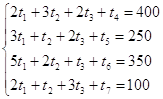
Выберем t1 , t2 ,t3 свободными переменными, а t4 , t5 ,t6 ,t7 – базисными и приведем к стандартному виду для решения с помощью симплекс-таблицы:
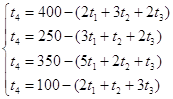
L=0-(-120t1-100t2-150t3)
Составим симплекс-таблицу.
Это решение опорное, т.к. все свободные члены положительны.
Т. к. все коэффициенты в целевой функции отрицательные, то можно взять любой столбец разрешающим (пусть t1). Выберем в качестве разрешающего элемента тот, для которого отношение к нему свободного члена будет минимально (это t7)
| b | t1 | t2 | t3 | ||||||
| L | 0 | -120 | -100 | -150 | |||||
| 6000 | 60 | 60 | 180 | ||||||
| t4 | 400 | 2 | 3 | 2 | 400/2=200 | ||||
| -100 | -1 | -1 | -3 | ||||||
| t5 | 250 | 3 | 1 | 2 | 250/3=83,3 | ||||
| -150 | -1,5 | -1,5 | -4,5 | ||||||
| t6 | 350 | 5 | 2 | 1 | 350/5=70 | ||||
| -250 | -2,5 | -2,5 | -7,5 | ||||||
| t7 | 100 | 2 | 1 | 3 | 100/2=50 | ||||
| 50 | 0,5 | 0,5 | 1,5 | ||||||
Далее меняем t2 и t1 .
| b | t7 | t2 | t3 | ||||||
| L | 6000 | 60 | -40 | 30 | |||||
| 4000 | 40 | 80 | 120 | ||||||
| t4 | 300 | -1 | 2 | -1 | 300/2=150 | ||||
| -200 | -2 | -4 | -6 | ||||||
| t5 | 100 | -1,5 | -0,5 | -2,5 | |||||
| 50 | 0,5 | 1 | -4,5 | ||||||
| t6 | 50 | -2,5 | -0,5 | -6,5 | |||||
| 50 | 0,5 | 1 | -7,5 | ||||||
| t1 | 50 | 0,5 | 0,5 | 1,5 | 50/0,5=100 | ||||
| 100 | 1 | 2 | 1,5 | ||||||
| b | t7 | t1 | t3 | |||||
| L | 10000 | 100 | 80 | 150 | ||||
| t4 | 100 | -3 | -4 | -7 | ||||
| t5 | 150 | -1 | 1 | -1 | ||||
| t6 | 100 | -2 | 1 | -5 | ||||
| t2 | 100 | 1 | 2 | 3 | ||||
Т.к. коэффициенты при переменных в целевой функции положительны, следовательно, это оптимальное решение.
Таким образом, t1 = t3 =0; t2=100; L=10000.
Т.е. для получения максимальной прибыли следует производить только бензин В (100 тыс. л.), при этом выручка составит 10000 руб.
ОТВЕТ: для получения максимальной прибыли следует производить только бензин В (100 тыс. л.), при этом выручка составит 10000 руб.
2. Задача 2
Условие:
С помощью симплекс–таблиц найти решение задачи линейного программирования: определить экстремальное значение целевой функции Q=CTx при условии Ax ³ £B,
где CT = [ c1 c2 . . . c6 ]T , ВT = [ b1 b2 . . . b6 ]T ,
XT = [ x1 x2 . . . x6]T , А= [aij] (i=1,6; j=1,3).
| № вар. | с1 | с2 | с3 | с4 | с5 | с6 | b1 | b2 | b3 | Знаки ограничений | a11 | a12 | a13 | a14 | ||||||||||||||||||
| 1 | 2 | 3 | ||||||||||||||||||||||||||||||
| 34 | 3 | 3 | 1 | 1 | 0 | 0 | 4 | 4 | 15 | = | = | = | 2 | 0 | 3 | 1 | ||||||||||||||||
| № вар. | a15 | a16 | a21 | a22 | a23 | a24 | a25 | a26 | a31 | a32 | a33 | a34 | a35 | a36 | Тип экстрем. |
|
||||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|
|||||||||||||||||
| 1. 34 | 0 | 0 | 1 | 0 | –1 | 2 | 3 | 0 | 3 | 3 | 6 | 3 | 6 | 0 | max |
|
||||||||||||||||
Решение:
Исходная система:
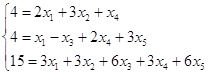
Целевая функция Q= x1+3x2+x3+3x5.
Пусть х3, х4 свободные переменные, х1, х2, х5 – базисные.
Приведем систему и целевую функцию к стандартному виду, для построения симплекс-таблицы:
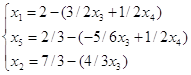
Q=9 - (9/2x3-1/2x4)
Составим симплекс-таблицу:
| b | x3 | x4 | |||||
| Q | 9 | 9/2 | -1/2 | ||||
| 2/3 | -5/6 | 1 | |||||
| x1 | 2 | 3/2 | 1/2 | 2/0,5=4 | |||
| -2/3 | 5/6 | -1 | |||||
| x2 | 7/3 | 4/3 | 0 | ||||
| 0 | 0 | 0 | |||||
| x5 | 2/3 | -5/6 |
1/2 |
2/3 : 1/2=4/3 | |||
| 4/3 | -5/3 | 2 | |||||
Это опорное решение, т.к. свободные члены положительны.
Т.к. коэффициент при х4 отрицательный, то это и будет разрешающий столбец. В качестве разрешающего элемента тот, для которого отношение к нему свободного члена будет минимально (это х5).
| b | x3 | x5 | ||||
| Q | 29/3 | 11/3 | 1 | |||
| x1 | 4/3 | 2/3 | -1 | |||
| x2 | 7/3 | 4/3 | 0 | |||
| x4 | 4/3 | -5/3 | 2 | |||
Т.к. коэффициенты при переменных в целевой функции положительны, следовательно, это оптимальное решение.
Т. о. Q=29/3
x3=x5=0; x1=4/3; x2=7/3; x4=4/3.
ОТВЕТ: Q=29/3ж
x3=x5=0; x1=4/3; x2=7/3; x4=4/3.
3. Задача 3
Условие:
Решение транспортной задачи:
1. Записать условия задачи в матричной форме.
2. Определить опорный план задачи.
3. Определить оптимальный план задачи.
4. Проверить решение задачи методом потенциалов.
| №вар. | а1 | а2 | а3 | b1 | b2 | b3 | b4 | b5 | с11 | с12 | с13 |
| 14 | 90 | 50 | 30 | 15 | 45 | 45 | 50 | 15 | 45 | 60 | 40 |
| с14 | с15 | с21 | с22 | с23 | с24 | с25 | с31 | с32 | с33 | с34 | с35 |
| 60 | 95 | 35 | 30 | 55 | 30 | 40 | 50 | 40 | 35 | 30 | 100 |
Решение:
Составим таблицу транспортной задачи и заполним ее методом северо-западного угла:
| B1 | B2 | B3 | B4 | B5 | a | ||||||
| A1 | 45 | 60 | 40 | 60 | 95 | 90 | |||||
| 15 | 45 | 30 | |||||||||
| A2 | 35 | 30 | 55 | 30 | 40 | 50 | |||||
| 15 | 35 | ||||||||||
| A3 | 50 | 40 | 35 | 30 | 100 | 30 | |||||
| 15 | 15 | ||||||||||
| b | 15 | 45 | 45 | 50 | 15 | 170 | |||||
Это будет опорный план.
Количество заполненных ячеек r=m+n-1=6.
1) Рассмотрим цикл (1,2)-(1,3)-(2,3)-(3,2):
с1,2+с2,3>c1.3+c3.2 (60+55>30+40)
Количество единиц товара, перемещаемых по циклу: min (с1,2 ; с2,3)=15
2) Рассмотрим цикл (2,4)-(2,5)-(3,5)-(3,4):
c2,4+с3,5>c2.5+c3.4 (30+40>30+100)
Количество единиц товара, перемещаемых по циклу: min (с2,4 ; с3,5)=15
В результате получится следующий план:
| B1 | B2 | B3 | B4 | B5 | a | ||||||
| A1 | 45 | 60 | 40 | 60 | 95 | 90 | |||||
| 15 | 30 | 45 | |||||||||
| A2 | 35 | 30 | 55 | 30 | 40 | 50 | |||||
| 15 | 20 | 15 | |||||||||
| A3 | 50 | 40 | 35 | 30 | 100 | 30 | |||||
| 30 | |||||||||||
| b | 15 | 45 | 45 | 50 | 15 | 170 | |||||
Больше циклов с «отрицательной ценой» нет, значит, это оптимальное решение.
Проверим методом потенциалов:
Примем α1=0, тогда βj = cij – αi (для заполненных клеток).
Если решение верное, то во всех пустых клетках таблицы Δij = cij – (αi+ βj) ≥ 0
Очевидно, что Δij =0 для заполненных клеток.
В результате получим следующую таблицу:
| β1=45 | β2=60 | β3=40 | β4=60 | β5=70 | |||||||
| α1=0 | 45 | 60 | 40 | 60 | 95 | 90 | |||||
| 15 | 30 | 45 | 0 | + | |||||||
| α2= -30 | 35 | 30 | 55 | 30 | 40 | 50 | |||||
| + | 15 | + | 20 | 15 | |||||||
| α3= -30 | 50 | 40 | 35 | 30 | 100 | 30 | |||||
| + | + | + | 30 | + | |||||||
| 15 | 45 | 45 | 50 | 15 | 170 | ||||||
Δ1,4=0 показывает, что существует еще один цикл с такой же ценой (1,2)-(1,4)-(2,4)-(2,2). Но так как при этом общая стоимость не изменится, то нет смысла менять перевозки.
Таким образом, решение верное, т.к. Δij ≥0.
ОТВЕТ:
| B1 | B2 | B3 | B4 | B5 | a | ||||||
| A1 | 45 | 60 | 40 | 60 | 95 | 90 | |||||
| 15 | 30 | 45 | |||||||||
| A2 | 35 | 30 | 55 | 30 | 40 | 50 | |||||
| 15 | 20 | 15 | |||||||||
| A3 | 50 | 40 | 35 | 30 | 100 | 30 | |||||
| 30 | |||||||||||
| b | 15 | 45 | 45 | 50 | 15 | 170 | |||||
4. Задача 4
Условие:
Определить экстремум целевой функции вида
F = c11x12+c22x22+c12x1x2+b1x1+b2x2
при условиях
a11x1+a12x2<=>p1
a21x1+a22x2<=>p2 .
1. Найти стационарную точку целевой функции и исследовать ее (функцию) на выпуклость (вогнутость) в окрестностях стационарной точки.
2. Составить функцию Лагранжа.
3. Получить систему неравенств в соответствии с теоремой Куна-Таккера.
4. Используя метод искусственных переменных составить симплекс-таблицу и найти решение полученной задачи линейного программирования.
5. Дать ответ с учетом условий дополняющей нежесткости.
| № | b1 | b2 | c11 | c12 | c22 | extr | a11 | a12 | a21 | a22 | p1 | p2 | Знаки огр.1 2 | |
| 59 | 4.5 | 1.5 | –5 | –2 | –1 | max | 2 | –3 | 5 | 4 | 9 | 13 | ³ | ³ |
Решение:
Целевая функция: F=-5x12-x22-2x1x2+4.5x1+1.5x2
Ограничения g1(x) и g2(x): 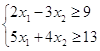 →
→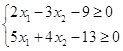
1) определим относительный максимум функции, для этого определим стационарную точку (х10, х20):
2)
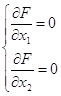 →
→ 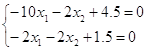 →
→ 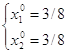
3) Исследуем стационарную точку на максимум, для чего определяем выпуклость или вогнутость функции
F11 (х10, х20) = -10 < 0
F12 (х10, х20) = -2
F21 (х10, х20) = -2
F22 (х10, х20) = -2
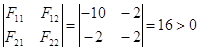
Т.к. условие выполняется, то целевая функция является строго вогнутой в окрестности стационарной точки
3) Составляем функцию Лагранжа:
L(x,u)=F(x)+u1g1(x)+u2g2(x)=
=-5x12-x22-2x1x2+4.5x1+1.5x2+u1(2x1-3x2-9)+u2(5x1+4x2-13)
Получим уравнения седловой точки, применяя теорему Куна-Таккера:
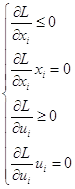 i=1;2
i=1;2
Объединим неравенства в систему А, а равенства в систему В:
Система А:
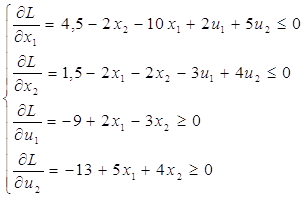
Система В:
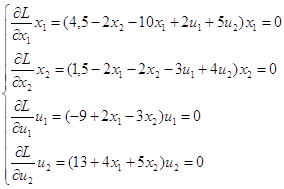
Перепишем систему А:
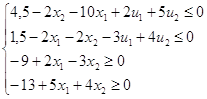
4)Введем новые переменные
V={v1,v2}≥0; W={w1,w2}≥0
в систему А для того, чтобы неравенства превратить в равенства:
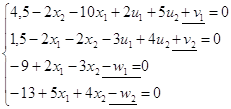
Тогда
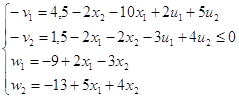 .
.
Следовательно, система В примет вид:
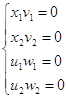 - это условия
дополняющей нежесткости.
- это условия
дополняющей нежесткости.
5) Решим систему А с помощью метода искусственных переменных.
Введем переменные Y={y1; y2} в 1 и 2 уравнения системы
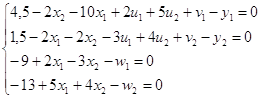
и создадим псевдоцелевую функцию Y=My1+My2→min
Y’=-Y= -My1-My2→max.
В качестве свободных выберем х1, х2, v1, v2, u1, u2; а в качестве базисных y1, y2, w1, w2.
Приведем систему и целевую функцию к стандартному виду, для построения симплекс-таблицы:
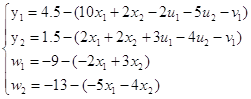
![]()
Решим с помощью симплекс-таблицы. Найдем опорное решение:
Примечание: вычисления производились программно, см Приложение
| b | x1 | x2 | u1 | u2 | v1 | v2 | ||||||||
| Y' | -6M | -12M | -4M | -M | 9M | M | M | |||||||
| y1 | 4,5 | 10 | 2 | -2 | -5 | -1 | 0 | |||||||
| y2 | 1,5 | 2 | 2 | 3 | -4 | 0 | -1 | |||||||
| w1 | -9 |
-2 |
3 | 0 | 0 | 0 | 0 | |||||||
| w2 | -13 | -5 | 4 | 0 | 0 | 0 | 0 | |||||||
| b | w1 | x2 | u1 | u2 | v1 | v2 | ||||||||
| Y' | 48M | -6M | -22M | -1M | 9M | 1M | 1M | |||||||
| y1 | -40,5 | 5 | 17 | -2 | -5 | -1 | 0 | |||||||
| y2 | -7,5 | 1 | 5 | 3 |
-4 |
0 | -1 | |||||||
| x1 | 4,5 | -0,5 | -1,5 | 0 | 0 | 0 | 0 | |||||||
| w2 | 9,5 | -2,5 | -3,5 | 0 | 0 | 0 | 0 | |||||||
| b | w1 | x2 | y1 | u2 | v1 | v2 | ||||||||
| Y' | 68,25M | -8,5M | -30,5M | -0,5M | 11,5M | 1,5M | 1M | |||||||
| u1 | 20,25 | -2,5 | -8,5 | -0,5 | 2,5 | 0,5 | 0 | |||||||
| y2 | -68,25 | 8,5 | 30,5 | 1,5 |
-11,5 |
-1,5 | -1 | |||||||
| x1 | 4,5 | -0,5 | -1,5 | 0 | 0 | 0 | 0 | |||||||
| w2 | 9,58 | -2,5 | -3,5 | 0 | 0 | 0 | 0 | |||||||
| b | w1 | x2 | y1 | y2 | v1 | v2 | ||||||||
| Y' | 0 | 0 | 0 | M | M | 0 | 0 | |||||||
| u1 | 5,413043 | |||||||||||||
| u2 | 5,934783 | |||||||||||||
| x1 | 4,5 | |||||||||||||
| w2 | 9,5 | |||||||||||||
Т. о, w1=x2=y1=y2=v1=v2=0; u1=5,413043; u2=5,934783; x1=4.5; w2=9.5.
б) Условия дополняющей нежесткости не выполняются (u2w2≠0), значит, решения исходной задачи квадратичного программирования не существует.
ОТВЕТ: не существует.
Приложение
#include <math.h>
#include <stdio.h>
main()
{
int i,j,k,m;
double h,n,a[5][7],b[5][7];
clrscr();
printf ("Введите числа матрицы А ");
for (i=0; i<5; i++){for(j=0; j<7; j++) {scanf ("%lf",&n); a[i][j]=n;}}
printf ("Введите координаты разрешающего элемента\n");
scanf("%d",&k) ;
scanf ("%d",&m);
printf (" матрицa A \n");
for (i=0; i<5; i++)
{for(j=0; j<7; j++) printf (" %lf",a[i][j]);printf ("\n");}
printf (" координаты \n ");
printf("%d %d",k,m) ;
h=1/a[k][m];
b[k][m]=h;
printf ("\n h=%lf",h);
for (i=0; i<7; i++)
{ if (i!=m) b[k][i]=a[k][i]*b[k][m]; }
for (i=0;i<5; i++)
{ if (i!=k) b[i][m]=-a[i][m]*b[k][m];}
for (i=0;i<5;i++)
{
for (j=0;j<7;j++)
if ((i!=k)&&(j!=m)) b[i][j]=a[i][j]+a[k][j]*b[i][m];
}
printf ("\n результат ");
printf (" матрицa B \n");
for (i=0; i<5; i++)
{for(j=0; j<7; j++) printf (" %lf",b[i][j]);printf ("\n");}
getch();
}
© 2010 Интернет База Рефератов