
Рефераты по сексологии
Рефераты по информатике программированию
Рефераты по биологии
Рефераты по экономике
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Рефераты по авиации и космонавтике
Рефераты по административному праву
Рефераты по безопасности жизнедеятельности
Рефераты по арбитражному процессу
Рефераты по архитектуре
Рефераты по астрономии
Рефераты по банковскому делу
Рефераты по биржевому делу
Рефераты по ботанике и сельскому хозяйству
Рефераты по бухгалтерскому учету и аудиту
Рефераты по валютным отношениям
Рефераты по ветеринарии
Рефераты для военной кафедры
Рефераты по географии
Рефераты по геодезии
Рефераты по геологии
Рефераты по геополитике
Рефераты по государству и праву
Рефераты по гражданскому праву и процессу
Рефераты по делопроизводству
Рефераты по кредитованию
Рефераты по естествознанию
Рефераты по истории техники
Рефераты по журналистике
Рефераты по зоологии
Рефераты по инвестициям
Рефераты по информатике
Исторические личности
Рефераты по кибернетике
Рефераты по коммуникации и связи
Курсовая работа: Итерационные методы решения систем нелинейных уравнений
Курсовая работа: Итерационные методы решения систем нелинейных уравнений
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
СУМСКИЙ ГОСУДАСТВЕННЫЙ УНИВЕРСИТЕТ
кафедра информатики
КУРСОВАЯ РАБОТА
ПО КУРСУ:
Численные методы
на тему:
«Итерационные методы решения систем нелинейных уравнений»
Сумы, 2006
Содержание
1. Методы решения систем нелинейных уравнений. Общая информация
2. Итерационные методы решения систем нелинейных уравнений
2.1 Метод простых итераций
2.2 Преобразование Эйткена
2.3 Метод Ньютона
2.3.1 Модификации метода Ньютона
2.3.2 Квазиньютоновские методы
2.4 Другие итерационные методы решения систем нелинейных уравнений
2.4.1 Метод Пикара
2.4.2 Метод градиентного спуска
2.4.3 Метод релаксаций
3. Реализация итерационных методов программно и с помощью математического пакета Maple
3.1 Метод простых итераций
3.2 Метод градиентного спуска
3.3 Метод Ньютона
3.4 Модифицированный метод Ньютона
Выводы
Список использованной литературы
1. Методы решения нелинейных уравнений. Общая информация.
Пусть нам дана система
уравнений, где ![]() - некоторые
нелинейные операторы:
- некоторые
нелинейные операторы:
![]()
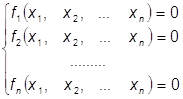 (1.1)
(1.1)
Она может быть также представлена в матричном виде:
![]() (1.1)
(1.1)
Где 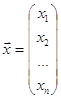
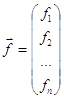
Её решением называется такое значение ![]() , для котрого
, для котрого ![]()
Очень распространенной является вычислительная задача нахождения некоторых или всех решений системы (1.1) из n нелинейных алгебраических или трансцендентных уравнений с n неизвестными.
Обозначим через Х вектор-столбец (х1, х2,..., хn)T и запишем систему уравнений в виде формулы (1.2): F(Х) = 0, где F = (f1, f2,..., fn)T.
Подобные системы уравнений могут возникать непосредственно, например, при конструировании физических систем, или опосредованно. Так, к примеру, при решении задачи минимизации некоторой функции G(х) часто необходимо определить те точки, в которых градиент этой функции равен нулю. Полагая F = grad G, получаем нелинейную систему.
В отличие от систем линейных алгебраических уравнений, для решения
которых могут применяться как прямые (или точные), так и итерационные
(или приближенные) методы, решение систем нелинейных уравнений можно
получить только приближенными, итерационными методами. Они позволяют получать
последовательность приближений ![]()
![]() . Если итерационный процесс сходится, то
граничное значение
. Если итерационный процесс сходится, то
граничное значение ![]() является
решением данной системы уравнений.
является
решением данной системы уравнений.
Для полноты представления о методах нахождения решения системы необходимо разъяснить такое понятие, как "скорость сходимости". Если для последовательности xn, сходящейся к пределу х*, верна формула
![]()
(k - положительное действительное число), то k называется скоростью сходимости данной последовательности.
2. Итерационные методы решения систем нелинейных уравнений
2.1 Метод простых итераций
Метод простых итераций (последовательных приближений) является одним из основных в вычислительной математике и применяется для решения широкого класса уравнений. Приведём описание и обоснование этого метода для систем нелинейных уравнений вида
fi(x1,x2,...xn) = 0, i=1,2,..n;
Приведём систему уравнений к специальному виду:
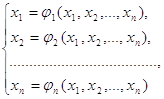 (2.1)
(2.1)
Или в векторном виде ![]() . (2.2)
. (2.2)
Причем переход к этой системе должен быть только при условии, что
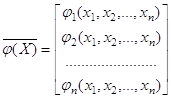 является
сжимающим отображением.
является
сжимающим отображением.
Используя некоторое начальное приближение X(0)= (x1(0),x2(0),...xn(0))
построим итерационный процесс X(k+1) =
(X(k)). Расчёты продолжаются до выполнения условия ![]() . Тогда решением системы уравнений
является неподвижная точка отображения
. Тогда решением системы уравнений
является неподвижная точка отображения ![]() .
.
Проведём обоснование метода в некоторой норме ![]() пространства
пространства ![]() .
.
Приведём теорему о сходимости, выполнение условий которой приводит к нахождению решения системы.
Теорема (о сходимости). Пусть
1). Вектор-функция Ф(х) определена в области
![]() ;
;
2). Для ![]() выполняется условие
выполняется условие
![]()
3). Справедливо неравенство
![]()
Тогда в итерационном процессе:
1. ![]()
2. ![]() ,
,
где ![]() – решение системы уравнений;
– решение системы уравнений;
3. ![]() ,
, ![]()
Замечание. Неравенство условия 2) есть условие Липшица
для вектор -функции Ф(х) в области S с константой ![]() (условие сжатия). Оно показывает, что Ф
является оператором сжатия в области S, т. е. для уравнения (2.2)
действует принцип сжатых отображений. Утверждения теоремы означают, что
уравнение (2.2) имеет решение
(условие сжатия). Оно показывает, что Ф
является оператором сжатия в области S, т. е. для уравнения (2.2)
действует принцип сжатых отображений. Утверждения теоремы означают, что
уравнение (2.2) имеет решение ![]() в
области S, и последовательные приближения
в
области S, и последовательные приближения ![]() сходятся к этому решению со скоростью
геометрической последовательности со знаменателем q.
сходятся к этому решению со скоростью
геометрической последовательности со знаменателем q.
Доказательство. Поскольку ![]() , то для приближения
, то для приближения ![]() в силу предположения 3) имеем
в силу предположения 3) имеем ![]() . Это значит, что
. Это значит, что ![]() . Покажем, что
. Покажем, что ![]() , k=2,3,… причём для соседних приближений
выполняется неравенство
, k=2,3,… причём для соседних приближений
выполняется неравенство
![]() (2.3)
(2.3)
Будем рассуждать по индукции. При ![]() утверждение справедливо, т.к.
утверждение справедливо, т.к. ![]() и
и ![]() . Допустим, что приближения
. Допустим, что приближения ![]() принадлежат S, и неравенство (2.3) выполнено для
принадлежат S, и неравенство (2.3) выполнено для ![]() . Поскольку
. Поскольку ![]() , то для
, то для ![]() с учётом условия 2) теоремы имеем
с учётом условия 2) теоремы имеем
![]() .
.
По индуктивному предположению
![]() .
.
Следовательно,
![]() ,
,
т.е. неравенство (2.3) справедливо для ![]() . Покажем, что
. Покажем, что ![]() . Учитывая свойство (2.3) при
. Учитывая свойство (2.3) при ![]() , получаем
, получаем
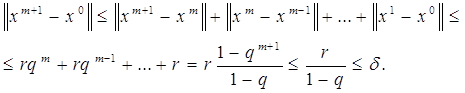
Итак, ![]() , и
первое утверждение теоремы доказано.
, и
первое утверждение теоремы доказано.
Покажем, что последовательность ![]() является сходящейся. С этой целью проверим признак
сходимости Коши (покажем, что последовательность
является сходящейся. С этой целью проверим признак
сходимости Коши (покажем, что последовательность ![]() является фундаментальной).
является фундаментальной).
По аналогии с предыдущим для любых р=1,2,… имеем
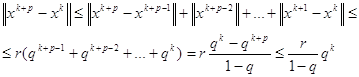
Поскольку ![]() , то
, то ![]() , поэтому для
, поэтому для ![]() найдётся такой номер
найдётся такой номер ![]() , что для
, что для ![]() будет
будет
![]()
Это означает выполнение признака Коши, что гарантирует сходимость
последовательности ![]() .
Обозначим
.
Обозначим ![]() . Утверждение 2)
теоремы доказано.
. Утверждение 2)
теоремы доказано.
Для доказательства последнего утверждения воспользуемся полученным выше неравенством
![]()
Перейдём здесь к пределу при ![]() . Учитывая непрерывность функции
. Учитывая непрерывность функции ![]() и тот факт, что
и тот факт, что ![]() , получаем требуемый результат – утверждение 3).
, получаем требуемый результат – утверждение 3).
Замечание 2. В условиях теоремы решение ![]() уравнения (2.2) в области S является единственным.
уравнения (2.2) в области S является единственным.
Действительно, пусть имеются два решения ![]() , причём
, причём ![]() . Тогда
. Тогда
![]() ,
,
Получили противоречие, что и требовалось доказать.
Обсудим условие 2) доказанной теоремы. Рассмотрим уравнение (2.2) в покомпонентной записи
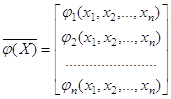
и предположим, что функции ![]() непрерывно-дифференцируемы в области S (т.е.
существуют и непрерывны в S частные производные
непрерывно-дифференцируемы в области S (т.е.
существуют и непрерывны в S частные производные
![]() ).
).
Теперь выясним достаточное условие выполнения неравенства 2) в этом случае.
Образуем матрицу Якоби системы функций ![]()
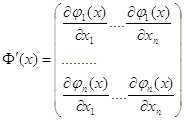 .
.
Далее, будем использовать обобщенную теорему о среднем (обобщение на случай вектор- функции формулы конечных приращений Лагранжа)
![]()
Здесь матричная норма согласована с векторной, ![]() ,
, ![]() – точка отрезка, соединяющего х, у.
– точка отрезка, соединяющего х, у.
Поскольку S – выпуклое множество, то ![]() . Предположим, что имеет место оценка
. Предположим, что имеет место оценка
![]() , причём
, причём ![]() . (2.4)
. (2.4)
Тогда согласно предыдущему выполняется условие 2) теоремы
![]() .
.
Таким образом, в случае дифференцируемости условие (2.4) на
матрицу Якоби ![]() гарантирует
условие сжатия для вектор- функции
гарантирует
условие сжатия для вектор- функции ![]()
2.2 Преобразование Эйткена
Поскольку сходимость метода простых итераций линейная, то она довольно медленна. Поэтому полезно уточнять результат процессом Эйткена по трём последним итерациям, чтобы увеличить точность найденного решения и ускорить процесс его нахождения.
Идею преобразования Эйткена поясним на простом примере.
![]()
Погрешность найденных значений на каждой итерации
равна,. если ![]()
найдем предел x через три значения последних приближений xk.
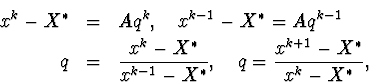 .
.
т. е.
![]()
Построим теперь процесс: ![]()
![]() , тогда
, тогда
![]() э
э
то итерационный процесс для уравнения:
![]() (А)
(А)
Рассмотрим порядок сходимости этого процесса

Теперь из (А).
![]()
Мы рассматривали процесс простых итераций процесс первого порядка,
![]()
![]() а получили процесс 2 –го порядка.
а получили процесс 2 –го порядка.
![]()
Легко показать, что если процесс имеет порядок, то схема Эйткена имеет порядок (2r-1). Более того, если процесс. не сходится, то итерационный процесс при выборе начального приближения так, чтобы,. будет сходиться.
2.3 Метод Ньютона
Основная идея метода Ньютона состоит в выделении из уравнений линейных частей, которые являются главными при малых приращениях аргументов. Это позволяет свести исходную задачу к решению последовательности линейных систем.
Рассмотрим систему уравнений
![]()
в предположении, что ![]() – непрерывно-дифференцируемые функции.
– непрерывно-дифференцируемые функции.
Полагая
![]() ,
,
прейдём к векторной записи
![]() (3.1)
(3.1)
Опишем общий шаг метода. Пусть уже получено
приближение ![]() проведём
линеаризацию вектор-функции
проведём
линеаризацию вектор-функции ![]() в
окрестности точки
в
окрестности точки ![]() -
разложим функцию
-
разложим функцию ![]() в ряд
Тейлора, оставив только два первых члена в силу малости отклонения приближения
в ряд
Тейлора, оставив только два первых члена в силу малости отклонения приближения ![]() от корня:
от корня:
![]() .
.
Здесь 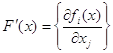 – матрица Якоби для вектор-функции
– матрица Якоби для вектор-функции ![]() .
.
Очередное приближение ![]() определяется как решение линейной системы
определяется как решение линейной системы ![]() , т.е.
, т.е.
![]()
Если матрица Якоби ![]() не вырожденна, то решение системы линейной системы
можно записать в явном виде, что приводит к стандартной формуле метода Ньютона
не вырожденна, то решение системы линейной системы
можно записать в явном виде, что приводит к стандартной формуле метода Ньютона
![]() (3.2)
(3.2)
Таким образом, в основе метода Ньютона лежит идея
линеаризации вектор-функции ![]() в
окрестности каждого приближения (на каждой итерации), что позволяет свести
решение системы (3.1) к последовательному решению линейных систем.
в
окрестности каждого приближения (на каждой итерации), что позволяет свести
решение системы (3.1) к последовательному решению линейных систем.
Через уже известное приближение ![]() к корню
к корню ![]() можно записать, что
можно записать, что ![]() , где
, где ![]() . Тогда после линеаризации получим систему
уравнений, линейную относительно
. Тогда после линеаризации получим систему
уравнений, линейную относительно ![]() . Таким образом, на каждом шаге мы будем находить
приращения
. Таким образом, на каждом шаге мы будем находить
приращения ![]() , и новое
приближение к решению по формулам:
, и новое
приближение к решению по формулам:
![]() – система линейных уравнений
– система линейных уравнений
![]()
Рассмотрим вопрос о сходимости метода Ньютона. Точное условие сходимости метода Ньютона для решения систем нелинейных уравнений имеет довольно сложный вид. можно отметить очевидный результат: в достаточно малой окрестности корня итерации сходятся, если матрица Якоби невырожденная, причём сходимость квадратичная.
Приведём ряд теорем, выполнение условий которых должно обеспечивать сходимость метода Ньютона.
Пусть в пространстве ![]() выбрана некоторая векторная норма
выбрана некоторая векторная норма ![]() и согласованная с ней матричная норма
и согласованная с ней матричная норма ![]() .
.
Теорема (о сходимости). Пусть
1)
вектор-функция
![]() определена и
непрерывно-дифференцируема в области
определена и
непрерывно-дифференцируема в области
![]()
где ![]() – решение уравнения (3.1),
– решение уравнения (3.1),
2) для всех ![]() существует обратная матрица
существует обратная матрица ![]() , причём
, причём
![]()
3)для всех ![]()
![]()
4) ![]()
Тогда метод Ньютона (3.2)
1) ![]()
2) ![]()
3) ![]()
Доказательство. Докажем первое утверждение
теоремы с помощью индукции. По условию ![]() . Допустим, что
. Допустим, что ![]() . Поскольку
. Поскольку ![]() , то
, то ![]() . Рассмотрим условие 3) теоремы для
. Рассмотрим условие 3) теоремы для ![]()
![]() .
.
Согласно формуле (3.2)
![]() ,
,
Кроме того ![]() . Тогда предыдущее неравенство принимает вид
. Тогда предыдущее неравенство принимает вид
![]()
Следовательно,
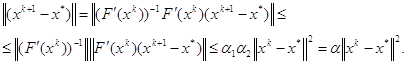
Таким образом, имеет место неравенство
![]() (3.3)
(3.3)
По предположению индукции ![]() . Поскольку в силу условия 4)
. Поскольку в силу условия 4)
![]() ,
то
,
то ![]()
Это значит, что для ![]() , и шаг индукции реализован. Превое утверждение
теоремы доказано.
, и шаг индукции реализован. Превое утверждение
теоремы доказано.
Продолжим доказательство. Положим ![]() перепишем оценку (3.3) после умножения на
перепишем оценку (3.3) после умножения на ![]() в виде
в виде ![]() . Покажем, что
. Покажем, что
![]() (3.4)
(3.4)
Будем рассуждать по индукции. При ![]() неравенство (3.4.) очевидно. Допустим,
что оно справедливо для некоторого
неравенство (3.4.) очевидно. Допустим,
что оно справедливо для некоторого ![]() . Тогда
. Тогда
![]()
Переход ![]() завершен, т.е. неравенство (3.4) справедливо для
всех
завершен, т.е. неравенство (3.4) справедливо для
всех ![]() . Перепишем его в
исходных обозначениях
. Перепишем его в
исходных обозначениях
![]()
Получили утверждение 3). При этом
![]() , т.е.
, т.е. ![]() .
.
Это значит, что имеет место сходимость: ![]()
Замечание 1. Неравенство (3.3) при условии ![]() означает, что последовательность
означает, что последовательность
![]() сходится к решению
сходится к решению ![]() с квадратичной скоростью.
с квадратичной скоростью.
Замечание 2. Поскольку ![]() , то из утверждения 3) следует оценка погрешности
метода Ньютона
, то из утверждения 3) следует оценка погрешности
метода Ньютона
![]()
Теорема. Если fi(x) непрерывны,
вместе с первыми производными в выпуклой области G, содержащей решение
системы ![]() и при
и при
![]() матрица Fx
не вырождена, то существует такая окрестность что при любом метод Ньютона
сходится к
матрица Fx
не вырождена, то существует такая окрестность что при любом метод Ньютона
сходится к ![]() .
.![]()
![]()
![]()
Доказательство. Рассмотрим
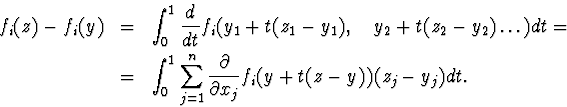
Введем и матрицу и матрицу. Очевидно, что F(x,x)= F(x), то есть имеем
![]() (12)
(12)
Есть тождества

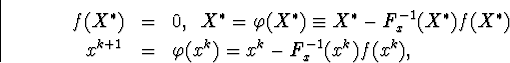
Тогда.
![]()
Вблизи окрестности ![]() для любого найдется такое x0,
что если,. то
для любого найдется такое x0,
что если,. то
Тогда
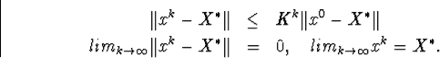
На начальное приближение x0 наложено труднопроверяемое условие.
![]() Теорема Канторовича. Если функции fi(x)
непрерывны вместе со своими 1 -ми и 2 -ми производными в некоторой выпуклой
области G, содержащей точку x0 вместе с ее
окрестностью и выполнены следующие условия:
Теорема Канторовича. Если функции fi(x)
непрерывны вместе со своими 1 -ми и 2 -ми производными в некоторой выпуклой
области G, содержащей точку x0 вместе с ее
окрестностью и выполнены следующие условия:
в точке x0 существует матрица F-1 такая
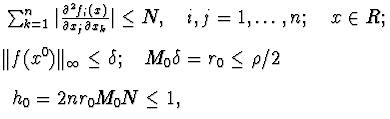
![]()
то последовательность xk+1=xk-f-1x(xk)F(xk)
сходится к ![]() .
.![]() является
единственным решением системы f(x)=0 в области и имеет место
оценка
является
единственным решением системы f(x)=0 в области и имеет место
оценка
![]()
![]()
Докажем 3 неравенства
а) ![]()
б)![]()
в) ![]()
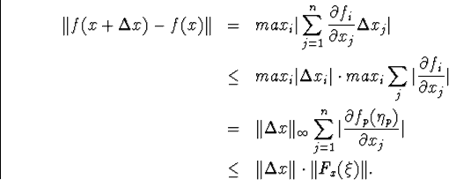
б)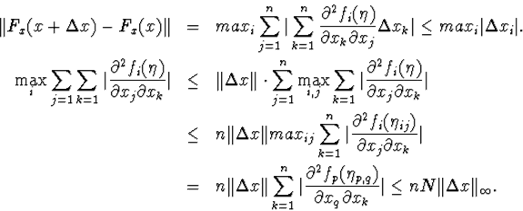
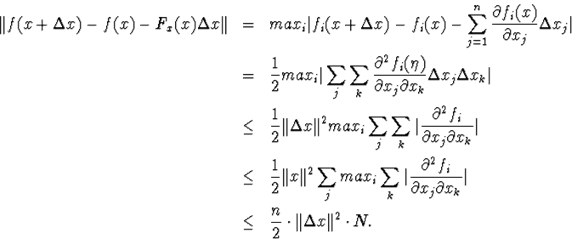
в)
![]()
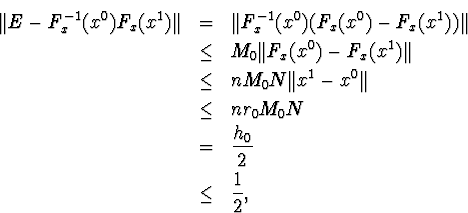
т.е. матрица F-1x(x0)Fx(x1) невырождена, и
![]()
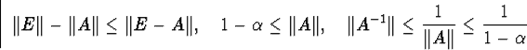
![]() и
и
![]()
Fx(x0)(x1-x0)+f(x0)=0
![]()
![]()
Покажем, что при всех k имеют место неравенства:
![]() (А)
(А)
![]()
![]()
Пусть имеет место m=k-1
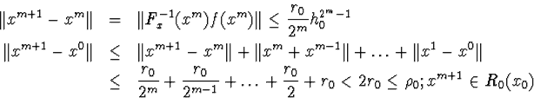
Повторим неравенства
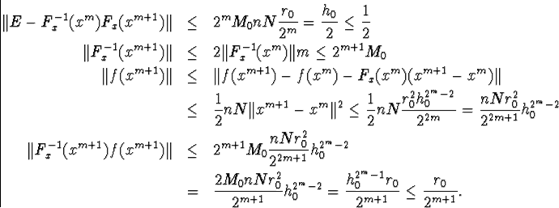
Неравенство (А) показывает, что в круге R последовательность xk является фундаментальной, т.е. имеется предел.
 Оценим сходимость
Оценим сходимость
![\begin{eqnarray*}\Vert x^{k+p}-x^k\Vert&\leq&\Vert x^{k+p}-x^{k+p-1}\Vert+\ldot... ...\ldots+\frac{1}{2^{p-1}}\big]\leq\frac{r_0}{2^{k-1}}h^{2^k-1}_0,\end{eqnarray*}](/image/8884_190_1.png) т.е.,
т.е.,
устремляя правая часть не меняется,, т.е. при очень хорошая сходимость.
2.3.1 Модификации метода ньютона
1. Вычисления в методе Ньютона гораздо сложнее, чем при простых итерациях, т.к. на каждой итерации требуется находить матрицу производных и решать систему линейных уравнений. Поэтому рекомендуется такой приём: матрица Якоби вычисляется только на начальном приближении. Однако сходимость при этом видоизменении становится линейной, причём обычно не с малой константой, ибо матрица производных на начальной итерации может заметно отличаться от окончательной. Поэтому скорость сходимости заметно уменьшается и требуемое сисло итераций возрастает.
![]()
2. В ещё одной модификации итерационную формулу
метода Ньютона вводится параметр ![]() следующим образом
следующим образом
![]()
![]()
На каждой итерации ![]() находится так, чтобы уменьшить невязку уравнения
(3.1), т.е. выполнить неравенство
находится так, чтобы уменьшить невязку уравнения
(3.1), т.е. выполнить неравенство
![]() (3.5)
(3.5)
Проведём обоснование такой процедуры в евклидовой норме.
Ведём в рассмотрение функцию-невязку для уравнения (3.1)
![]()
Найдём градиент ![]() , используя представление
, используя представление
![]()
С этой целью выделим главный член приращения
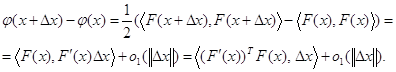
Следовательно, по определению ![]()
Обозначим ![]() и найдём производную функции
и найдём производную функции ![]() в точке
в точке ![]() по направлению
по направлению ![]() :
:
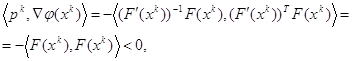
если ![]() .
.
Таким образом, ![]() – есть направление спуска для функции
– есть направление спуска для функции ![]() в точке
в точке ![]() для малых
для малых ![]() . Это значит, что выбор шага
. Это значит, что выбор шага ![]() согласно условию (3.5) возможен.
согласно условию (3.5) возможен.
2.3.2 Квазиньютоновкие методы
Одним из недостатков метода Ньютона является необходимость
вычислять матрицу Якоби и решать систему линейных алгебраических уравнений. Это
требует значительных расходов машинных действий, объём которых резко возрастает
с увеличением размерности системы. Поэтому были разработаны модификации метода
Ньютона, в которых на протяжении итерационного процесса вместо построения самой
матрицы Якоби или её обратной строится их аппроксимация. Это позволяет
существенно сократить количество арифметических действий на итерации. Такие
методы решения систем нелинейных уравнений получили название квазиньютоновских.
Большинство известных квазиньютоновских методов сходится локально с
надлинейной скоростью сходимости при тех самых предположениях о свойствах
функции ![]() , которые были
сделаны при использовании метода Ньютона, который имеет квадратичную скорость
сходимости. Квазиньютоновские методы можно разделить на два тесно связанных
между собой класса методов в зависимости от того, что аппроксимируется -
матрица Якоби или ей обратные.
, которые были
сделаны при использовании метода Ньютона, который имеет квадратичную скорость
сходимости. Квазиньютоновские методы можно разделить на два тесно связанных
между собой класса методов в зависимости от того, что аппроксимируется -
матрица Якоби или ей обратные.
Рассмотрим первый из классов, где матрица Вк с размерами п
х п аппроксимирует матрицу ![]() . Перед началом итераций задают начальную
точку
. Перед началом итераций задают начальную
точку ![]() а матрицу Во
обычно получают, или допуская, что она является единичной, или аппроксимируя
а матрицу Во
обычно получают, или допуская, что она является единичной, или аппроксимируя
![]() конечно-разностными формулами.
Потом для k = 0, 1.... вычисляют
конечно-разностными формулами.
Потом для k = 0, 1.... вычисляют

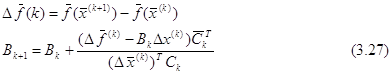
Где ![]() — n-
мерный вектор, который является параметром рассматриваемого класса методовв.
Если
— n-
мерный вектор, который является параметром рассматриваемого класса методовв.
Если ![]() взять таким, что
равняется
взять таким, что
равняется ![]() ,то будем иметь
первый метод Бройдена. Выбор
,то будем иметь
первый метод Бройдена. Выбор ![]() соответствует
методу Пирсона, а
соответствует
методу Пирсона, а ![]() симметрическому методу первого ранга.
симметрическому методу первого ранга.
Во втором из рассматриваемых здесь классов квазиньютоновских
методов матрица ![]() с размерами п
х п аппроксимирует матрицу
с размерами п
х п аппроксимирует матрицу ![]() . Перед началом итерации задают начальную
точку х{0) и матрицу
. Перед началом итерации задают начальную
точку х{0) и матрицу ![]() , которая обычно или равна единичной, или является
обратной к конечно-разностной аппроксимации
, которая обычно или равна единичной, или является
обратной к конечно-разностной аппроксимации ![]() . Потом вычисляют
. Потом вычисляют
![]()
![]()
где ![]() — n-мерный
вектор, который является параметром рассматриваемого класса методов. Конкретный
вид вектора
— n-мерный
вектор, который является параметром рассматриваемого класса методов. Конкретный
вид вектора ![]() отвечает
соответствующему методу: например,
отвечает
соответствующему методу: например, ![]() — второму методу Бройдена,
— второму методу Бройдена, ![]() — методу Мак-Кормика.
— методу Мак-Кормика.
Заметим, что если задать ![]() то можно вести перерасчет не Вк,
а матриц
то можно вести перерасчет не Вк,
а матриц ![]() по формуле
по формуле
![]() (3.30)
(3.30)
эквивалентной (3.27). Это требует порядка 0(п2) арифметических
действий вместо 0(п3), необходимых для решения системы
линейных уравнений ![]() .
.
Как видно из (3.30), между формулами (3.27) и (3.29) имеет место
определенная связь. Так.если ![]() ,
то
,
то ![]() при
при ![]() . Таким образом, один и тот же
метод может реализоваться двумя разными формулами (3.27) и (3.29), которые
эквивалентные теоретически, но их численная реализация может отличаться по
эффективности.
. Таким образом, один и тот же
метод может реализоваться двумя разными формулами (3.27) и (3.29), которые
эквивалентные теоретически, но их численная реализация может отличаться по
эффективности.
Рассмотрим, например, первый метод Бройдена. Его можно реализовать
по формуле (3.27) так, что это потребует в общем 0(n3)
арифметических действий. Это оказывается возможным, если подать матрицу Вк
в виде произведения ![]() ,
где
,
где ![]() — ортогональная, а
— ортогональная, а ![]() — верхняя треугольная матрица.
Действительно, в этом случае решение системы нуждается в только 0(n3)
арифметических действий. Имея
— верхняя треугольная матрица.
Действительно, в этом случае решение системы нуждается в только 0(n3)
арифметических действий. Имея![]() ,
на представление матрицы Вк+1, которая удовлетворяет
(3.27) в виде
,
на представление матрицы Вк+1, которая удовлетворяет
(3.27) в виде ![]() , необходимо
0(п2) арифметических действий. Важное преимущество формулы
(3.27) перед (3.39) заключается в том, что в (3.27) нет необходимости умножения
матрицы на вектор, поскольку
, необходимо
0(п2) арифметических действий. Важное преимущество формулы
(3.27) перед (3.39) заключается в том, что в (3.27) нет необходимости умножения
матрицы на вектор, поскольку
![]()
Существуют квазиньютоновские методы, которые учитывают
симметричность матрицы Якоби и вырабатывают последовательность симметричных
матриц Вк, (или![]() ). Эти методы также можно разделить на два
класса. В первом из них матрица Вк аппроксимирует F(х). В
отличие от описанного выше класса, который задается формулами (3.26) и (3.27),
здесь нужна симметричность матрицы Во, и вместо (3.27) используется
формула
). Эти методы также можно разделить на два
класса. В первом из них матрица Вк аппроксимирует F(х). В
отличие от описанного выше класса, который задается формулами (3.26) и (3.27),
здесь нужна симметричность матрицы Во, и вместо (3.27) используется
формула
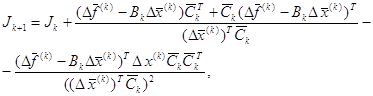
где значение параметра ![]() отвечает симметричному варианту Пауелла методу
Бройдена, а
отвечает симметричному варианту Пауелла методу
Бройдена, а ![]() — методу Давидона
- Флечера - Пауелла.
— методу Давидона
- Флечера - Пауелла.
Во втором из рассматриваемых классов квазиньютоновских методов
матрица Нк аппроксимирует матрицу ![]() . Здесь матрица Но должна быть
симметричной, а вместо (3.29) используется формула
. Здесь матрица Но должна быть
симметричной, а вместо (3.29) используется формула
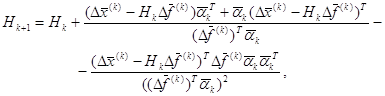
Где ![]() соответствует
методу Бройдена-Флечера-Голвдфарба-Шенно, что является одним из наилучших (с
вычислительной точки зрения), который учитывает симметричность матрицы Якоби.
соответствует
методу Бройдена-Флечера-Голвдфарба-Шенно, что является одним из наилучших (с
вычислительной точки зрения), который учитывает симметричность матрицы Якоби.
Описанные выше квазиньютоновские методы сходятся лишь при достаточно хорошом начальном приближении х(0). Для расширения области их сходимости можно использовать прием, который имеет название одномерного поиска.
Пусть имеем квазиньютоновское направление ![]() (или
(или ![]() ). Используем длину шага
). Используем длину шага ![]() = 1 и проверим неравенство
= 1 и проверим неравенство
![]() (3.34)
(3.34)
где ![]() -
евклидовая норма. Если оно выполняется, то заканчиваем одномерный поиск и
считаем
-
евклидовая норма. Если оно выполняется, то заканчиваем одномерный поиск и
считаем
![]() (3.35)
(3.35)
т.е.
уменьшаем длину шага (устанавливая, например, ![]() ), пока не выполнится (3.34). На этом заканчиваем
одномерный поиск и переходим к формуле (3.35).
), пока не выполнится (3.34). На этом заканчиваем
одномерный поиск и переходим к формуле (3.35).
Как видим, одномерный поиск (в случае успеха) обеспечивает
монотонное уменьшение нормы отклонения ![]() с ростом к. Если квазиньютоновское
направление
с ростом к. Если квазиньютоновское
направление ![]() сильно
отличается от ньютоновского, то одномерный поиск может оказаться неудачным, и
тогда необходимо возобновить матрицу Вк, (или
сильно
отличается от ньютоновского, то одномерный поиск может оказаться неудачным, и
тогда необходимо возобновить матрицу Вк, (или![]() )., приравняв ее, например, конечно-разносной
аппроксимации матрицы Якоби
)., приравняв ее, например, конечно-разносной
аппроксимации матрицы Якоби ![]() (или
(или
![]() ). Критерием окончания
итераций для квазиньютоновских методов есть неровность
). Критерием окончания
итераций для квазиньютоновских методов есть неровность ![]()
3. Другие итерационные методы решения систем нелинейных уравнений
3.1 Метод Пикара
Существуют также итерационные методы решения систем нелинейных уравнений, которые учитывают вид конкретной системы.
Так, если в уравнениях системы можно выделить линейную l(X) и нелинейную g(X)части функций fi(X) = li(X) + gi(x), то удобней применить к ней метод Пикара.
В таком случае систему уравнений можно записать в виде
li(X) = - gi(X), i=1,2,3...n;
или в векторной форме A X= - G(X);
где A- матрица коэффициентов линейных частей уравнений;
G(X) - вектор-функция нелинейных частей уравнений.
Выберем некоторый начальный вектор X(0) и построим итерационный процесс в виде
A X(k+1)=-G(X(k)).
Для выполнения одной итерации таким методом необходимо решать систему линейных уравнений, у которой вектором свободных членов будут нелинейные части функций fi(X). Причем поскольку матрица A остается неизменной при всех итерациях, то для решения СЛАУ можно использовать специальные алгоритмы, предусматривающие возможность преобразования только столбца свободных членов.
3.2 Метод релаксаций
Перепишем систему в виде
X=X+ F(X),
где - некоторая константа, и построим итерационный процесс по схеме
X(k+1) = X(k) + F(X(k)).
Параметр должен быть таким, чтобы в окрестности решения выполнялось достаточное условие сходимости
||Е+ W|| < 1,
где E- единичная матрица.
На практике выполнение этого условия достаточно сложно проверить, поэтому значение параметра выбирают пробным путем, проверяя выполнение необходимого условия сходимости после выполнения каждой итерации
||X(k)-X(k-1)||<||X(k-1)-X(k-2)||.
Если окажется, что на какой-либо итерации это условие не выполняется, то необходимо изменить значение параметра .
3.3 Метод градиентного спуска
Пусть имеем систему уравнений ![]() (А)
(А)
Предположим, что функции ![]() действительные и непрерывно дифференцированные в их
общей области определения. Рассмотрим функцию
действительные и непрерывно дифференцированные в их
общей области определения. Рассмотрим функцию
![]() (В)
(В)
Очевидно, что каждое решение системы (А) превращает в ноль функцию
U(x); наоборот, числа ![]() ,
для которых функция U(x) равняется нулю, является корнем системы (А).
,
для которых функция U(x) равняется нулю, является корнем системы (А).
Предположим, что система имеет лишь изолированное решение, которое
представляет собой точку строго минимума функции U(x) в n-мерном
пространстве ![]() .
.
Пусть x - вектор системы (А) и x0 - его нулевое приближение. Через точку x0 проведем поверхность уровня функции U(x). Если точка x0 довольно близка к корню x, то при наших предположениях поверхность уровня
U(x)= U(x0)
будет похожа на эллипсоид.
Из точки x0 движемся по нормали к поверхности U(x)= U(x0) до тех пор, пока эта нормаль не затронет в некоторой точке x1 какой-то другой поверхности уровня U(x)= U(x1).
Потом, отправляясь от точки x1, снова движемся по нормали к поверхности уровня U(x)= U(x1) до тех пор, пока эта нормаль не затронет в некоторой точке x2 новой поверхности уровня U(x)= U(x2), и т.д.
Поскольку U(x0)>U(x1)>U(x2)>..., то, двигаясь таким путем, мы быстро приближаемся к точке с наименьшим значением U ("дно ямы"), что отвечает искомому решению исходной системы. Обозначим через
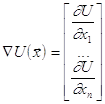
градиент функции U(x).
Находить нужное решение будем по формуле:
![]()
Остается определить множители ![]() . Для этого рассмотрим скалярную функцию
. Для этого рассмотрим скалярную функцию
![]()
![]()
Функция F(l) дает изменение уровня
функции U вдоль соответствующей нормали к поверхности уровня в точке xp.
Множитель ![]() надо выбрать
таким образом, чтобы F(l) имела минимум. Беря
производную по l и приравнивая ее нулю, получаем уравнение
надо выбрать
таким образом, чтобы F(l) имела минимум. Беря
производную по l и приравнивая ее нулю, получаем уравнение
![]() .
.
Наименьший положительный корень этого уравнения и даст нам
значение ![]() .
.
Будем считать, что l - малая величина, квадратом и высшими степенями которой можно пренебрегать. Имеем:
![]()
Раскладывая функции ![]() за степенями l с точностью до линейных
членов, получим:
за степенями l с точностью до линейных
членов, получим:
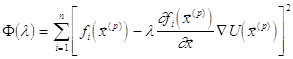 ,
,
где 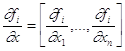 .
.
Отсюда
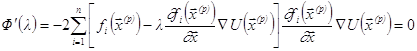
Итак,
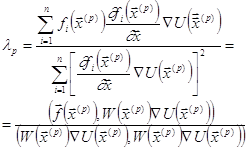 , где
, где 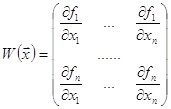
- матрица Якоби вектор- функции f.
Дальше, имеем:
![]() .
.
Отсюда
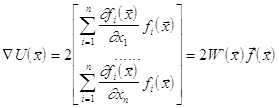 ,
,
где W'(x) - транспонированная матрица Якоби.
Поэтому окончательно
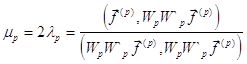 ,
,
причем
![]() .
.
3. Программная реализация итерационных методов
Реализация алгоритмов итерационных методов решения систем нелинейных уравнений будет показана на примере системы:
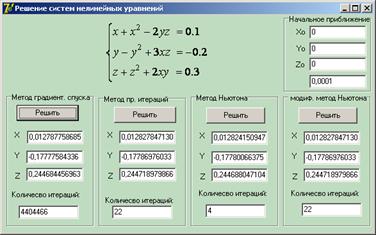
3.1 Метод простых итераций
Приведём систему к виду:
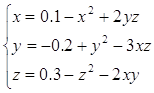
Проверим условие сходимости метода простых итераций.
Для этого построим матрицу Якоби
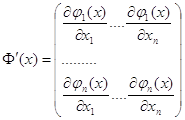
> f1:=0.1-x0^2+2*y0*z0;
![]()
f2:=-0.2+y0^2-3*x0*z0; ![]()
f3:=0.3-z0^2-2*x0*y0; ![]()
> f1x:=diff(f1,x0):
> f1y:=diff(f1,y0):
> f1z:=diff(f1,z0):
> f2x:=diff(f2,x0):
> f2y:=diff(f2,y0):
> f2z:=diff(f2,z0):
> f3x:=diff(f3,x0):
> f3y:=diff(f3,y0):
> f3z:=diff(f3,z0):
> A:=<<f1x|f1y|f1z>,<f2x|f2y|f2z>,<f3x|f3y|f3z>>;
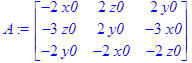
И найдём ей обратную, норму обратной матрицы сначала в общем виде:
> A1:=MatrixInverse(A);
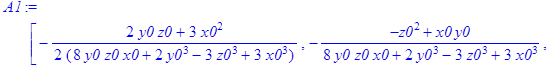
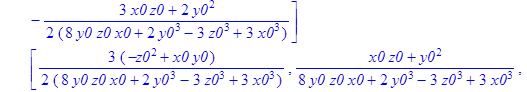
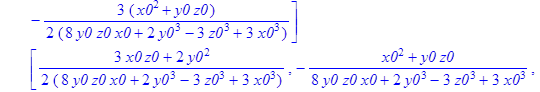
![]()
> norma:=MatrixNorm(A1,1);
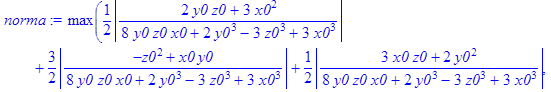
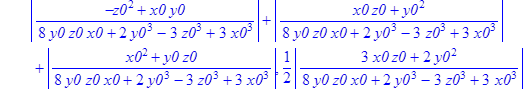
![]()
Найдём значения ![]() при которых норма обратной матрицы Якоби меньше
единицы.
при которых норма обратной матрицы Якоби меньше
единицы.
> x0:=1; y0:=1; z0:=1;
![]()
![]()
![]()
> norma;
![]()
Это означает, что по формулам
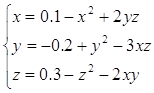
последовательность итераций будет сходиться к решению системы уравнений.
Построим итерационную последовательность
> restart;
> with(LinearAlgebra):
> x0:=0:
y0:=0:
z0:=0:
> x:=0.1-x0^2+2*y0*z0;
y:=-0.2+y0^2-3*x0*z0;
z:=0.3-z0^2-2*x0*y0;
i:=1;
![]()
![]()
![]()
> while (abs(x-x0)>0.0001)and(abs(y-y0)>0.0001)and(abs(z-z0)>0.0001) do
x0:=x:
y0:=y:
z0:=z:
x:=0.1-x0^2+2*y0*z0;
y:=-0.2+y0^2-3*x0*z0;
z:=0.3-z0^2-2*x0*y0;
i:=i+1;
end do:
Получили ответ:
![]()
![]()
![]()
Количество итераций:
![]()
Погрешность решения:
![]()
Отсюда можно получить коэффициент сжатия последовательности:
При ![]()
> P:= 0.3*q^22/(1-q)-0.0001;
![]()
> q:= fsolve(P);
![]()
Таким образом можно сказать, что было построено сжимающее отображение, для которого выполняется условие Липшица
![]()
Текст программы:
procedure TForm1.Button3Click(Sender: TObject);
var i:integer;
x0,y0,z0,x,y,z,eps: real;
begin
x0:=StrToFloat(Edit1.Text);
y0:=StrToFloat(Edit2.text);
z0:=StrToFloat(Edit3.Text);
eps:=StrToFloat(Edit20.Text);
i:=1;
x:=0.1-x0*x0+2*y0*z0;
y:=-0.2+y0*y0-3*x0*z0;
z:=0.3-z0*z0-2*x0*y0;
repeat
i:=i+1;
x0:=x;
y0:=y;
z0:=z;
x:=0.1-x0*x0+2*y*z;
y:=-0.2+y0*y0-3*x0*z0;
z:=0.3-z0*z0-2*x0*y0;
until ((abs(x-x0)<eps)and(abs(y-y0)<eps)and(abs(z-z0)<eps));
Edit8.Text:=FloatToStr(x);
Edit9.Text:=FloatToStr(y);
Edit10.Text:=FloatToStr(z);
Edit11.Text:=IntToStr(i);
end;
Преобразование Эйткена на примере метода простых итереций:
> restart;
> x0:=0:
y0:=0:
z0:=0:
> f1:=0.1-x0^2+2*y0*z0;
f2:=-0.2+y0^2-3*x0*z0;
f3:=0.3-z0^2-2*x0*y0;
ff1:=0.1-f1^2+2*f2*f3;
ff2:=-0.2+f2^2-3*f1*f3;
ff3:=0.3-f3^2-2*f1*f2;
x:=(x0*ff1-f1^2)/(ff1-2*f1+x0);
y:=(y0*ff2-f2^2)/(ff2-2*f2+y0);
z:=(z0*ff3-f3^2)/(ff3-2*f3+z0);
i:=1;
![]()
![]()
![]()
while (abs(x-x0)>0.0001)do
x0:=x:
y0:=y:
z0:=z:
f1:=0.1-x0^2+2*y0*z0;
f2:=-0.2+y0^2-3*x0*z0;
f3:=0.3-z0^2-2*x0*y0;
ff1:=0.1-f1^2+2*f2*f3;
ff2:=-0.2+f2^2-3*f1*f3;
ff3:=0.3-f3^2-2*f1*f2;
x:=(x0*ff1-f1^2)/(ff1-2*f1+x0);
y:=(y0*ff2-f2^2)/(ff2-2*f2+y0);
z:=(z0*ff3-f3^2)/(ff3-2*f3+z0):
i:=i+1;
end do:
Получили ответ:
![]()
![]()
![]()
Количество итераций:
![]()
3.2 Метод градиентного спуска
Построим функцию:
> U:=(0.1-x^2+2*y*z-x)^2+(-0.2+y^2-3*x*z-y)^2+(0.3-z^2-2*x*y-z)^2;
![]()
Найдём градиент функции:
![]()
> Ux:= diff(U,x);
Uy:= diff(U,y);
Uz:= diff(U,z);
![]()
![]()
![]()
Выберем начальное приближение и построим итерационную последовательность:
> x:=0;
y:=0;
z:=0;
> N1:=2*(.1-x^2+2*y*z-x)*(-2*x-1)-6*(-.2+y^2-3*x*z-y)*z-4*(.3-z^2-2*x*y-z)*y;
> N2:=4*(.1-x^2+2*y*z-x)*z+2*(-.2+y^2-3*x*z-y)*(2*y-1)-4*(.3-z^2-2*x*y-z)*x;
> N3:=4*(.1-x^2+2*y*z-x)*y-6*(-.2+y^2-3*x*z-y)*x+2*(.3-z^2-2*x*y-z)*(-2*z-1);
> x:=x-lambda*N1;
y:=y-lambda*N2;
z:=z-lambda*N3;
i:=1;
![]()
![]()
![]()
> N1:=2*(.1-x^2+2*y*z-x)*(-2*x-1)-6*(-.2+y^2-3*x*z-y)*z-4*(.3-z^2-2*x*y-z)*y;
N2:=4*(.1-x^2+2*y*z-x)*z+2*(-.2+y^2-3*x*z-y)*(2*y-1)-4*(.3-z^2-2*x*y-z)*x;
N3:=4*(.1-x^2+2*y*z-x)*y-6*(-.2+y^2-3*x*z-y)*x+2*(.3-z^2-2*x*y-z)*(-2*z-1);
x:=x-lambda*N1;
y:=y-lambda*N2;
z:=z-lambda*N3;
![]()
![]()
![]()
> while (abs(N3)>0.0001) do
N1:=2*(.1-x^2+2*y*z-x)*(-2*x-1)-6*(-.2+y^2-3*x*z-y)*z-4*(.3-z^2-2*x*y-z)*y:
N2:=4*(.1-x^2+2*y*z-x)*z+2*(-.2+y^2-3*x*z-y)*(2*y-1)-4*(.3-z^2-2*x*y-z)*x:
N3:=4*(.1-x^2+2*y*z-x)*y-6*(-.2+y^2-3*x*z-y)*x+2*(.3-z^2-2*x*y-z)*(-2*z-1):
x:=x-lambda*N1:
y:=y-lambda*N2:
z:=z-lambda*N3:
i:=i+1:
end do:
Получили ответ:
![]()
![]()
![]()
Количество итераций и данным шагом ![]() :
:
![]()
Текст программы:
procedure TForm1.Button1Click(Sender: TObject);
const
lambda=-0.0001;
n=3;
type mas=array[1..n]of real;
var //x,y,z:real;
Xp,nab,v:mas;
i:integer;
eps:real;
function max(x:mas):real;
var s:real;
i:integer;
begin s:=abs(x[1]);
for i:=2 to 4 do if abs(x[i])>s then s:=abs(x[i]);
max:=s;
end;
Procedure add(var a,b:mas);
var
i:integer;
begin
for i:=1 to n do
begin
a[i]:=a[i]+b[i];
end;
end;
Procedure mult(a:mas;c:real;var v:mas);
var
i:integer;
begin
for i:=1 to n do
begin
v[i]:=a[i]*c;
end;
end;
procedure nabla(Xp:mas; var nab:mas);
begin
nab[1]:=2*(0.1-xp[1]*xp[1]+2*xp[2]*xp[3]-xp[1])*(-2*xp[1]-1)-6*(-0.2+xp[2]*xp[2]-3*xp[1]*xp[3]-xp[2])*xp[3]-4*(0.3-xp[3]*xp[3]-2*xp[1]*xp[2]-xp[3])*xp[2];
nab[2]:=4*(0.1-xp[1]*xp[1]+2*xp[2]*xp[3]-xp[1])*xp[3]+2*(-0.2+xp[2]*xp[2]-3*xp[1]*xp[3]-xp[2])*(2*xp[2]-1)-4*(0.3-xp[3]*xp[3]-2*xp[1]*xp[2]-xp[3])*xp[1];
nab[3]:=4*(0.1-xp[1]*xp[1]+2*xp[2]*xp[3]-xp[1])*xp[2]-6*(-0.2+xp[2]*xp[2]-3*xp[1]*xp[3]-xp[2])*xp[1]+2*(0.3-xp[3]*xp[3]-2*xp[1]*xp[2]-xp[3])*(-2*xp[3]-1);
end;
begin
Xp[1]:=StrToFloat(Edit1.Text);
Xp[2]:=StrToFloat(Edit2.Text);
Xp[3]:=StrToFloat(Edit3.Text);
eps:=StrToFloat(Edit20.Text);
repeat
nabla(Xp,nab);
mult(nab,lambda,v);
add(Xp,v);
i:=i+1;
until max(nab)<eps;
Edit4.Text:=FloatToStr(Xp[1]);
Edit5.Text:=FloatToStr(Xp[2]);
Edit6.Text:=FloatToStr(Xp[3]);
Edit7.Text:=IntToStr(i);
//Edit21.Text:=IntToStr(kk);
end;
procedure TForm1.Button3Click(Sender: TObject);
var i:integer;
x0,y0,z0,x,y,z,eps: real;
begin
x0:=StrToFloat(Edit1.Text);
y0:=StrToFloat(Edit2.text);
z0:=StrToFloat(Edit3.Text);
eps:=StrToFloat(Edit20.Text);
i:=1;
x:=0.1-x0*x0+2*y0*z0;
y:=-0.2+y0*y0-3*x0*z0;
z:=0.3-z0*z0-2*x0*y0;
repeat
i:=i+1;
x0:=x;
y0:=y;
z0:=z;
x:=0.1-x0*x0+2*y*z;
y:=-0.2+y0*y0-3*x0*z0;
z:=0.3-z0*z0-2*x0*y0;
until ((abs(x-x0)<eps)and(abs(y-y0)<eps)and(abs(z-z0)<eps));
Edit8.Text:=FloatToStr(x);
Edit9.Text:=FloatToStr(y);
Edit10.Text:=FloatToStr(z);
Edit11.Text:=IntToStr(i);
end;
3.3 Метод Ньютона
Строим матрицу Якоби:
> restart;
> with(LinearAlgebra):
> f1:=0.1-x0^2+2*y0*z0-x0;
![]()
> f2:=-0.2+y0^2-3*x0*z0-y0;
![]()
> f3:=0.3-z0^2-2*x0*y0-z0;
![]()
> f1x:=diff(f1,x0);
> f1y:=diff(f1,y0);
> f1z:=diff(f1,z0);
> f2x:=diff(f2,x0);
> f2y:=diff(f2,y0);
> f2z:=diff(f2,z0);
> f3x:=diff(f3,x0);
> f3y:=diff(f3,y0);
> f3z:=diff(f3,z0);
> A:=<<f1x|f1y|f1z>,<f2x|f2y|f2z>,<f3x|f3y|f3z>>;
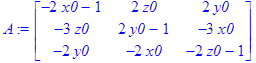
Выбираем начальное приближение, близкое к уже известному нам корню и строим последовательность:
> x0:=0;y0:=0;z0:=0;
![]()
![]()
![]()
> A:=A;
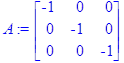
> A1:=A^(-1);
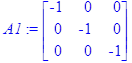
> f:=<f1,f2,f3>;
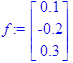
> X0:=<x0,y0,z0>:
> X:=Add(X0,(Multiply(A1,f)),1,-1);

> X0:=X;
> x0:=X[1];y0:=X[2];z0:=X[3];
> A:=<<f1x|f1y|f1z>,<f2x|f2y|f2z>,<f3x|f3y|f3z>>;
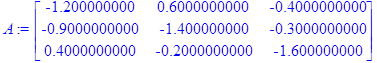
> A1:=A^(-1);
> f:=<f1,f2,f3>;
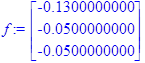
> X:=Add(X0,(Multiply(A1,f)),1,-1);
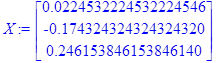
> i:=2:
> while (Norm(f))>0.0001 do
X0:=X;
x0:=X[1];y0:=X[2];z0:=X[3];
A:=<<f1x|f1y|f1z>,<f2x|f2y|f2z>,<f3x|f3y|f3z>>;
A1:=A^(-1);
f:=<f1,f2,f3>;
X:=Add(X0,(Multiply(A1,f)),1,-1);
i:=i+1;
end do:
> X:=X;
Получили ответ:

Количество итераций:
![]()
Текст программы
procedure TForm1.Button4Click(Sender: TObject);
type mas=array[1..3]of real;
matr=array[1..3,1..3]of real;
var a,a1:matr;
i,j:integer;
x,y,z,eps:real;
f,xk,xkk,temp:mas;
procedure jacobi(x,y,z:real; var a:matr);
begin
a[1,1]:=-2*x-1;
a[1,2]:=2*z;
a[1,3]:=2*y;
a[2,1]:=-3*z;
a[2,2]:=2*y-1;
a[2,3]:=-3*x;
a[3,1]:=-2*y;
a[3,2]:=-2*x;
a[3,3]:=-2*z-1;
end;
procedure inverse(a:matr;var a1:matr);
var i,j:integer;
det:real;
s:matr;
begin
det:=a[1,1]*a[2,2]*a[3,3]+a[2,1]*a[3,2]*a[1,3]+a[1,2]*a[2,3]*a[3,1]-a[3,1]*a[2,2]*a[1,3]-a[3,2]*a[2,3]*a[1,1]-a[2,1]*a[1,2]*a[3,3];
s[1,1]:=a[2,2]*a[3,3]-a[2,3]*a[3,2];
s[1,2]:=-a[1,2]*a[3,3]+a[1,3]*a[3,2];
s[1,3]:=a[1,2]*a[2,3]-a[1,3]*a[2,2];
s[2,1]:=-a[2,1]*a[3,3]+a[2,3]*a[3,1];
s[2,2]:=a[1,1]*a[3,3]-a[1,3]*a[3,1];
s[2,3]:=-a[1,1]*a[2,3]+a[1,3]*a[2,1];
s[3,1]:=a[2,1]*a[3,2]-a[2,2]*a[3,1];
s[3,2]:=-a[1,1]*a[3,2]+a[1,2]*a[3,1];
s[3,3]:=a[1,1]*a[2,2]-a[1,2]*a[2,1];
for i:=1 to 3 do
for j:=1 to 3 do
a1[i,j]:=(1/det)*s[i,j];
end;
procedure fx(x,y,z:real; var f:mas);
begin
f[1]:=-x-x*x+2*y*z+0.1;
f[2]:=-y+y*y-3*x*z-0.2;
f[3]:=-z-z*z-2*x*y+0.3;
end;
procedure minus(x,y:mas; var z:mas);
var i:integer;
begin
for i:=1 to 3 do
z[i]:=x[i]-y[i];
end;
function max(f:mas):real;
var p:real;
i:integer;
begin
p:=0;
for i:=1 to 3 do
if abs(f[i])>p then p:=abs(f[i]);
max:=p;
end;
procedure mult(a:matr;b:mas;var c:mas);
begin
c[1]:=a[1,1]*b[1]+a[1,2]*b[2]+a[1,3]*b[3];
c[2]:=a[2,1]*b[1]+a[2,2]*b[2]+a[2,3]*b[3];
c[3]:=a[3,1]*b[1]+a[3,2]*b[2]+a[3,3]*b[3];
end;
begin
xk[1]:=StrToFloat(Edit1.Text);
xk[2]:=StrToFloat(Edit2.Text);
xk[3]:=StrToFloat(Edit3.Text);
eps:=StrToFloat(Edit20.Text);
i:=0;
repeat
fx(xk[1],xk[2],xk[3],f);
jacobi(xk[1],xk[2],xk[3],a);
inverse(a,a1);
mult(a1,f,temp);
minus(xk,temp,xk);
i:=i+1;
until max(f)<eps;
Edit12.Text:=FloatToStr(xk[1]);
Edit13.Text:=FloatToStr(xk[2]);
Edit14.Text:=FloatToStr(xk[3]);
Edit15.Text:=IntToStr(i);
end;
3.4 Модифицированный метод Ньютона
Аналогично методу Ньютона построим матрицу Якоби для данной системы уравнений, выберем начальное приближение заведомо близко к решению, построим последовательность:
> with(LinearAlgebra):
![]()
![]()
![]()
> f1x:=diff(f1,x0);
> f1y:=diff(f1,y0);
> f1z:=diff(f1,z0);
> f2x:=diff(f2,x0);
> f2y:=diff(f2,y0);
> f2z:=diff(f2,z0);
> f3x:=diff(f3,x0);
> f3y:=diff(f3,y0);
> f3z:=diff(f3,z0);
> A:=<<f1x|f1y|f1z>,<f2x|f2y|f2z>,<f3x|f3y|f3z>>;
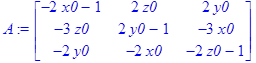
> x0:=0;y0:=0;z0:=0;
> A:=A;
> A1:=A^(-1);
> f:=<f1,f2,f3>;
> X0:=<x0,y0,z0>;
> X:=Add(X0,(Multiply(A1,f)),1,-1);
> X0:=X;
> x0:=X[1];y0:=X[2];z0:=X[3];
> f:=<f1,f2,f3>;
> i:=1;
> while (Norm(f))>0.0001 do
X0:=X;
x0:=X[1];y0:=X[2];z0:=X[3];
f:=<f1,f2,f3>;
X:=Add(X0,(Multiply(A1,f)),1,-1);
i:=i+1;
end do;
Получили ответ:

Количество итераций:
![]()
Текст программы
procedure TForm1.Button2Click(Sender: TObject);
type mas=array[1..3]of real;
matr=array[1..3,1..3]of real;
var x,y,z,ex,ey,ez,eps,b,c,d:real;
r,xk,f,temp:mas;
a,h,w,a1:matr;
i,kk: integer;
procedure jacobi(x,y,z:real; var a:matr);
procedure inverse(a:matr;var a1:matr);
procedure fx(x,y,z:real; var f:mas);
procedure minus(x,y:mas; var z:mas);
function max(f:mas):real;
procedure mult(a:matr;b:mas;var c:mas);
// все процедуры полностью совпадают с описанными выше реализации метода Ньютона
begin
xk[1]:=StrToFloat(Edit1.Text);
xk[2]:=StrToFloat(Edit2.Text);
xk[3]:=StrToFloat(Edit3.Text);
eps:=StrToFloat(Edit20.Text);
i:=0;
jacobi(xk[1],xk[2],xk[3],a);
inverse(a,a1);
repeat
fx(xk[1],xk[2],xk[3],f);
mult(a1,f,temp);
minus(xk,temp,xk);
i:=i+1;
until max(f)<eps;
Edit16.Text:=FloatToStr(xk[1]);
Edit17.Text:=FloatToStr(xk[2]);
Edit18.Text:=FloatToStr(xk[3]);
Edit19.Text:=IntToStr(i);
Выводы
Численное решение нелинейных алгебраических уравнений является сложной и не до конца разрешимой задачей вычислительной математики.
При решении систем нелинейных уравнений иногда поступают следующим образом. Строится функционал, минимум которого достигается в решении системы. Затем, задавши начальное приближение к точке минимума, проводят итерации каким-либо из методов спуска. И таким путём получают удовлетворительное приближение к решению системы. Исходя из этого приближения, проводят уточнения при помощи какого-либо итерационного метода, например метода Ньютона или Пикара.
Поясним причины, вызывающие такое комбинированное применение методов. Область сходимости метода – множество начальных условий, при которых итерации по данному методу сходятся к решению задачи. Применение методов спуска на первоначальном этапе вызвано тем, что они имеют более широкую область сходимости, чем методы специфические для задачи решения системы уравнений.
На нашем примере можно в этом убедиться.
Метод градиентного спуска при начальном приближении даже равном ![]() сходится к решению
сходится к решению ![]()
![]() . При более отдалённом начальном приближении, например,
. При более отдалённом начальном приближении, например,
![]() приводит к другому решению
(
приводит к другому решению
(![]()
![]() ) из множества решений системы. Как видим,
полученные ответы значительно отличаются от первоначального приближения, что
свидетельствует о широкой области сходимости метода градиентного спуска. Также
заметим, что при разных удачно выбранных начальных приближениях этот метод
может привести нас к любому решению системы уравнений. То есть, в построении
метода нет привязки только к конкретному решению, он универсален. Однако
скорость сходимости линейная, довольно медленная при выборе маленького шага.
Поэтому и применяют этот метод первоначально, с относительно большим шагом и
низкой точностью конечного решения для сокращения количества итераций при
поиске приближения к корню, которое используют далее в других методах.
) из множества решений системы. Как видим,
полученные ответы значительно отличаются от первоначального приближения, что
свидетельствует о широкой области сходимости метода градиентного спуска. Также
заметим, что при разных удачно выбранных начальных приближениях этот метод
может привести нас к любому решению системы уравнений. То есть, в построении
метода нет привязки только к конкретному решению, он универсален. Однако
скорость сходимости линейная, довольно медленная при выборе маленького шага.
Поэтому и применяют этот метод первоначально, с относительно большим шагом и
низкой точностью конечного решения для сокращения количества итераций при
поиске приближения к корню, которое используют далее в других методах.
Метод Ньютона имеет высокую скорость сходимости, поэтому его удобнее применять, когда требуемая точность велика и известно приближённое значение решения. Однако область сходимости значительно уже.
Для метода простых итераций в нашем примере построено такое
отображение, которое только при удачно выбранном начальном приближении к корню ![]() . При начальном приближении
. При начальном приближении ![]() итерационная последовательность
ещё сходится к решению, если взять начальные условия дальше от корня – метод не
сходится ни к указанному выше, какому другому решению системы. Исходя из
имеющихся данных про точное решение системы нелинейных уравнений, мы строим
последовательность. Эта последовательность сходится только с начальным
приближением лежащим в окрестности выбранного корня, и только к нему. Несмотря
на возможную близость начального приближения к какому-то другому решению, она к
нему не сойдётся, в отличие от других итерационных методов. Это говорит о том,
что для каждого из множества решений системы нужно строить своё отображение,
удовлетворяющее условиям сходимости. В этом проявляется недостаток метода
простых итераций. Но если сжимающее отображение построено правильно, то
преимущество метода состоит в простоте вычислений.
итерационная последовательность
ещё сходится к решению, если взять начальные условия дальше от корня – метод не
сходится ни к указанному выше, какому другому решению системы. Исходя из
имеющихся данных про точное решение системы нелинейных уравнений, мы строим
последовательность. Эта последовательность сходится только с начальным
приближением лежащим в окрестности выбранного корня, и только к нему. Несмотря
на возможную близость начального приближения к какому-то другому решению, она к
нему не сойдётся, в отличие от других итерационных методов. Это говорит о том,
что для каждого из множества решений системы нужно строить своё отображение,
удовлетворяющее условиям сходимости. В этом проявляется недостаток метода
простых итераций. Но если сжимающее отображение построено правильно, то
преимущество метода состоит в простоте вычислений.
При модификации метода путём расчёта обратной матрицы Якоби только в начальной точке ведёт также к сужению области сходимости и к значительному увеличению количества итераций по мере выбора начального приближения дальше от точного решения.
Для решения систем нелинейных уравнений можно использовать метод Ньютона, метод простых итераций и др. Методы градиентного спуска и простой итерации имеют линейную сходимость, метод Ньютона - квадратичную, а квазиньютоновские надлинейную скорость сходимости. Несмотря на то, что квазиньютоновские методы имеют худшую сравнительно с методом Ньютона теоретическую сходимость, они требуют при своей реализации меньшее количество машинных действий. Однако эти самые методы имеют локальную сходимости, то есть сходимость при хорошем начальном приближении. Для получения этого приближения во время решения систем нелинейных уравнений используют методы спуска и комбинируют их с методами, которые имеют большую скорость сходимости.
При применении того или иного метода к системе нелинейных уравнений нужно учитывать особенности постановки задачи и наличие начальных условий.
Список использованной литературы
1. Бахвалов Н.С., Лапин А.В., Чижонков Е.В. “Численные методы в задачах и упражнениях”. М.: Высшая школа, 2000.
2. Мышенков В.И., Мышенков Е.В., «Численные методы», учебное пособие,М., – 2001.
3. Амосов А.А., Дубинский Ю.А., Копченова Н.В. “Вычислительные методы для инженеров”. М.: Высшая школа, 1994.
4. Самарский А.А., Гулин А.В. «Численные методы».М.: Наука, 1989.
5. Назаренко Л.Д., «Численные методы», методическое пособие.
© 2010 Интернет База Рефератов