
Рефераты по сексологии
Рефераты по информатике программированию
Рефераты по биологии
Рефераты по экономике
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Рефераты по авиации и космонавтике
Рефераты по административному праву
Рефераты по безопасности жизнедеятельности
Рефераты по арбитражному процессу
Рефераты по архитектуре
Рефераты по астрономии
Рефераты по банковскому делу
Рефераты по биржевому делу
Рефераты по ботанике и сельскому хозяйству
Рефераты по бухгалтерскому учету и аудиту
Рефераты по валютным отношениям
Рефераты по ветеринарии
Рефераты для военной кафедры
Рефераты по географии
Рефераты по геодезии
Рефераты по геологии
Рефераты по геополитике
Рефераты по государству и праву
Рефераты по гражданскому праву и процессу
Рефераты по делопроизводству
Рефераты по кредитованию
Рефераты по естествознанию
Рефераты по истории техники
Рефераты по журналистике
Рефераты по зоологии
Рефераты по инвестициям
Рефераты по информатике
Исторические личности
Рефераты по кибернетике
Рефераты по коммуникации и связи
Курсовая работа: Комплексные числа: их прошлое и настоящее
Курсовая работа: Комплексные числа: их прошлое и настоящее
Комплексные числа, их прошлое и настоящее.
Содержание.
I. Введение.
II. Об истории возникновения комплексных чисел и их роли в процессе развития математики.
III. Алгебраические действия над комплексными числами и их геометрический смысл.
1. Основные понятия и арифметические действия над комплексными числами.
2. Геометрическое изображение комплексных чисел. Тригонометрическая и показательная формы.
3. Операция сопряжения и ее свойства.
4. Извлечение корней.
5. Геометрический смысл алгебраических операций.
IV. Применение комплексных чисел к решению алгебраических уравнений 3-ей и 4-ой степеней.
1. Формула Кердано.
2. Метод Феррари для уравнения 4-ой степени.
V. Дополнительные задачи и упражнения, связанные с использованием комплексных чисел.
VI. Заключение.
VII. Литература.
I. Введение.
Алгебраические уравнения с одним неизвестным и связанные с ними вопросы в нахождении решений относятся к числу наиболее важных в школьной программе. В общем виде в средней школе изучаются лишь уравнения 1-ой степени (линейные) и уравнения 2-ой степени (квадратные), поскольку для таких уравнений существуют простые формулы, выражающие корни уравнения через его коэффициенты с помощью арифметических операций и извлечения корней.
Именно, если дано:
(α) Линейное уравнение ax+b=0, где а≠0, то x=-b/a единственный корень;
(β) Квадратное уравнение ax+bx+c=0, где a,b,c действительные числа, a≠0, то x=-b±√b∙b-4ac/2a; при этом число корней зависит от величины D = b2 4ac, называемой дискриминантом квадратного уравнения, а именно:
При D>0 два действительных корня, D=0 один двукратный корень (или, что то же, два совпадающих корня), D<0 нет действительных корней.
Из уравнений более высоких степеней в школьном курсе алгебры рассматриваются лишь некоторые частные их типы – трехчленные (например, биквадратные), симметрические, … Однако никаких методов для решения произвольных уравнений 3-ей и 4-ой степени (хотя соответствующие формулы известны), в школьной алгебре не дается, т.к. эти методы существенно опираются на теорию комплексных чисел.
Цель данного реферата состоит в том, чтобы ознакомить учащихся средних школ с важнейшим и новым для них математическим понятием понятием комплексного числа, а также показать, насколько эффективно его применение при решении некоторых задач, в том числе и в первую очередь, при решении кубичных уравнений.
II. Об истории возникновения комплексных чисел и их роли в процессе развития математики.
Комплексные числа возникли в математике в начале XVI века в связи с решением алгебраических уравнений 3-ей степени, а позднее, и уравнений 2-ой степени. Некоторые итальянские математики того времени (- Сципион дель Ферро, Николо Тарталья, Джироломо Кардано, Рафаэль Бомбелли) ввели в рассмотрение символ √-1 как формальное решение уравнения х2+1=0, а также выражение более общего вида (а+b∙√-1) для записи решения уравнения (х-а)2+b2=0. Впоследствии выражения вида (а+b∙√-1) стали называть «мнимыми», а затем «комплексными» числами и записывать их в виде (а+bi) (символ i для обозначения √-1 ввел Леонард Эйлер в XVIII в.). Этих чисел, чисел новой природы оказалось достаточно для решения любого квадратного уравнения (включая случай D < 0), а также уравнения 3-ей и 4-ой степени.
МатематикиXVI в. и следующих поколений вплоть до начала XIXвека относились к комплексным числам с явным недоверием и предубеждением. Они считали эти числа «мнимыми» (Декарт), «несуществующими», «вымышленными», «возникшими от избыточного мудрствования» (Кардано)… Лейбниц называл эти числа «изящным и чудесным убежищем божественного духа», а √-1 считал символом потустороннего мира (и даже завещал начертать его на своей могиле).
Однако использование аппарата комплексных чисел (несмотря на подозрительное к ним отношение), позволило решить многие трудные задачи. Поэтому со временем комплексные числа занимали все более важное положение в математике и ее приложениях. В первую очередь они глубоко проникали в теорию алгебраических уравнений, существенно упростив их изучение. Например, один из трудных вопросов для математиков XVII-XVIII веков состоял в определении числа корней алгебраического уравнения n-ой степени, т.е. уравнения вида a0∙xn+a1∙xn-1+…+an-1∙x+an=0. Ответ на этот вопрос, как оказалось, зависит от того, среди каких чисел действительных или комплексных – следует искать корни этого уравнения. Если ограничиться действительными корнями, то можно лишь утверждать, что их не больше, чем n. А если считать допустимым наличие и комплексных решений, то ответ на поставленный вопрос получается исчерпывающий: любое алгебраическое уравнение степени n (n≥1) имеет ровно n корней (действительных или комплексных), если каждый корень считать столько раз, какова его кратность (а это – число совпадающих с ним корней). При n≥5 общее алгебраическое уравнение степени n неразрешимо в радикалах, т.е. не существует формулы, выражающей его корни через коэффициенты с помощью арифметических операций и извлечения корней натуральной степени.
После того как в XIX в появилось наглядное геометрическое изображение комплексных чисел с помощью точек плоскости и векторов на плоскости (Гаусс в 1831 г, Вессель в 1799 г, Арган в 1806 г), стало возможным сводить к комплексным числам и уравнениям для них многие задачи естествознания, особенно гидро- и аэродинамики, электротехники, теории упругости и прочности, а также геодезии и картографии. С этого времени существование «мнимых», или комплексных чисел стало общепризнанным фактом и они получили такое же реальное содержание, как и числа действительные. К настоящему времени изучение комплексных чисел развилось в важнейший раздел современной математики – теорию функций комплексного переменного (ТФКП).
III/ Алгебраические действия над комплексными числами и их геометрический смысл.
1. Основные понятия и арифметические действия над комплексными числами.
Логически строгую теорию комплексных чисел построил в XIX в (1835 г) ирландский математик Вильям Роумен Гамильтон. По Гамильтону комплексные числа – это упорядоченные пары z=(x,y) действительных чисел, для которых следующим образом определены операции сложения и умножения:
(x1,y1)+(x2,y2)=(x1+x2, y1+y2); (1)
(x1,y1)∙(x2,y2)=(x1∙x2 yiy2, xiy2 + x2y1). (2)
Действительные числа x и y называются при этом действительной и мнимой частями комплексного числа z=(x,y) и обозначаются символами Rez и Imz соответственно (real действительный, imanginerum мнимый).
Два комплексных числа z1=(x1,y1) и z2=(x2,y2) называются равными только в том случае, когда x1=x2 и y1=y2. Из определения следует, что всякое комплексное число (x,y) может быть представлено в следующем виде: (x,y)=(x,0)+(0,1)(y,0). (3)
Числа вида (х,0) отождествляются с действительными числами х, т.е. (х,0)=х, число (0,1), называемое мнимой единицей, обозначается символом i, т.е. (0,1)=i, причем i2=-1, равенство (3) принимает вид z=x+iy и называется алгебраической формой записи комплексного числа z=(x,y).
Операции сложения и умножения комплексных чисел имеют следующие свойства:
а) z1+z2=z2+z1 (переместительный закон или коммутативность сложения и умножения)
б) z1z2=z2z1
в) z1+(z2+z3)=(z1+z2)+z3 (сочетательный закон или ассоциативность)
г) z1(z2z3)=(z1z2)z3
д) (z1+z2)z3=z1z3+z2z3 (распределительный закон или дистрибутивность)
Вычитание и деление комплексных чисел z1=x1+iy1 и z2=x2+iy2 определяют, причем однозначно, их разность z1-z2 и частное z1/z2 как решения соответствующих уравнений z+z2=z1 и zz2=z1 (при z2≠0). Отсюда следует, что разность и частное от деления z1 на z2 вычисляются по формулам:
z1-z2=(x1-x2)+i(y1-y2), (4)
z1/z2=(x1x2+y1y2)/(x22+y22) + i((y1x2-x1y2)/(x22+y22)) (5)
Данное определение можно выразить в других терминах, а именно, вычитание – как действие, обратное сложению: z=z1+(-z2), где число (-z2) называется противоположным z2; деление – как действие, обратное умножению: z=z1(z2-1), где z2-1 число, обратное для z2 (z2≠0). Таким образом, анализ определений и свойств арифметических операций над комплексными числами приводит к следующим выводам:
- множество комплексных чисел (С) является
расширением множества R
действительных чисел, т.е. действительные числа содержатся как частный случай,
среди комплексных (точно так же как, например, целые числа содержатся среди
действительных);
- комплексные числа можно складывать, вычитать, умножать и делить по правилам,
которым подчиняются действительные числа, заменяя в итоге (или в процессе
вычислений) i2=-1.
2. Геометрическое изображение комплексных чисел. Тригонометрическая и показательная формы.
Замечание. Понятия «больше» или «меньше» для комплексных чисел лишено смысла (не принято никакого соглашения).
Если на плоскости введена декартова система координат 0xy, то всякому комплексному числу z=x+iy может быть поставлена в соответствие некоторая точка М(х,у) с абсциссой «х» и ординатой «у», а также радиус – вектор 0М. При этом говорят, что точка М(х,у) (или радиус – вектор 0М) изображает комплексное число z=x+iy.
Плоскость, на которой изображаются комплексные числа называется комплексной плоскостью, ось 0у – мнимой осью.
Число r=√x2+y2, равное длине вектора, изображающего комплексное число, т.е. расстоянию от начала координат до изображающей это число точки, называется модулем комплексного числа z=x+iy и обозначается символом |z|.
Угол φ=(0М,ˆ0х) между положительным направлением оси 0х и вектором 0М, изображающим комплексное число z=x+iy ≠0, называется его аргументом.
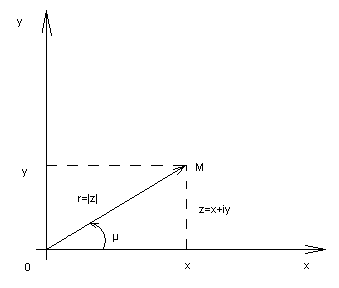
Из определения видно, что каждое комплексное число (≠0), имеет бесконечное множество аргументов. Все они отличаются друг от друга на целые кратные 2π и обозначаются единым символом Argz (для числа z=0 аргумент не определяется, не имеет смысла).
Каждое значение аргумента совпадает с величиной φ некоторого угла, на который следует повернуть действительную ось (ось 0ч) до совпадения ее направления с направлением радиус-вектора точки М, изображающей число z (при этом φ > 0, если поворот совершается против часовой стрелки и φ <0 в противном случае). Таким образом, аргумент комплексного числа z=x+iy ≠0 есть всякое решение φ системы уравнений cosφ=x/√x2+y2; sinφ=y/√x2+y2.
Значение Argz при условии 0≤Argz<2π называется главным значением аргумента и обозначается символом argz. В некоторых случаях главным значением аргумента считают наименьшее по абсолютной величине его значения, т.е. значение, выделяемое неравенством -π<φ≤π.
Между алгебраическими х, у и геометрическими r, φ характеристиками комплексного числа существует связь, выражаемая формулами x=rcosφ, y=rsinφ, следовательно, z=x+iy=r(cosφ+isinφ). Последнее выражение, т.е. z= r(cosφ+isinφ) (6) называется тригонометрической формой комплексного числа. Любое число z≠0 может быть представлено в тригонометрической форме.
Для практики число вида (cosφ+isinφ) удобнее записывать короче, с помощью символа eiφ=cosφ+isinφ (7). Доказанное для любых чисел φ (действительных или комплексных) это равенство называется формулой Эйлера. С ее помощью всякое комплексное число может быть записано в показательной форме z=reiφ (8)
3. Операция сопряжения и ее свойства.
Для данного комплексного числа z=x+iy число x-iy (отличающееся от z лишь знаком при мнимой части) называется сопряженным и обозначается символом z. Переход от числа z к числу z называется сопряжением, а сами эти числа сопряженными (друг к другу), т.к. (z)=z. Из определения следует, что только действительное число сопряжено самому себе. Геометрически сопряженные числа изображаются точками, симметричными относительно действительной оси (рис.2).
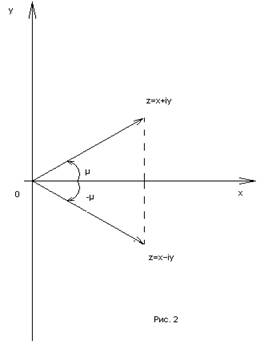
Отсюда следует, что |z|=|z|, argz=-argz. Кроме того,
![]() z+z=2x=2Rez;
z+z=2x=2Rez;
z-z=2iy=2iImz;
zz=x2+y2=|z|2,
а также: z1+z2=z1+z2; z1z2=z1z2; (z1/z2)=z1/z2; P(z)=P(z), где Р (z) – любой многочлен с действительными коэффициентами; (P(z)/Q(z))=(P(z)/Q(z)), где P и Q – многочлены с действительными коэффициентами.
4. Извлечение корней.
Извлечение корня из комплексного числа есть действие, обратное возведению в степень. С его помощью по данной степени (подкоренное число) и данному показателю степени (показатель корня) находят основание (корень). Иначе говоря, это действие равносильно решению уравнения zn=a для нахождения z. В множестве комплексных чисел действие извлечения корня всегда выполнимо, хотя причем и неоднозначно: в результате получается столько значений, каков показатель корня. В частности, квадратный корень имеет ровно два значения, которые можно найти по формуле:
√a=√α+iβ=±((√|a|+α)/2 ± i(√|a|-α)/2)), где знак «+» в скобках берется при β>0, «-» - при β<0.
5. Геометрический смысл алгебраических операций.
Пусть даны два комплексных числа z1 и z2. В результате сложения этих чисел получается число z3, изображаемое вектором 0С диагонали параллелограмма 0АСВ (по правилу параллелограмма сложения векторов): z1+z2=0A+0B=0C=z3.
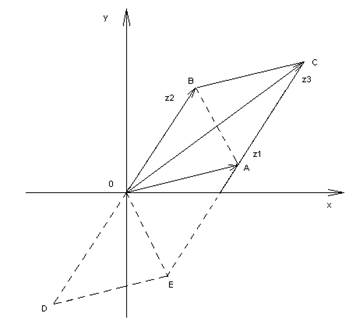 Рис.3
Рис.3
Разность (z1-z2) данных чисел, соответствующая их вычитанию, можно рассматривать как сумму вектора 0А, изображающего число z1 и вектора 0D=--0В, противоположного вектору 0В (симметричного ему относительно начала координат): z1-z2=z1+(-z2)=0A+0D=0E=BA. Таким образом, разности (z1-z2) данных чисел соответствует вектор ВА другой диагонали параллелограмма 0АСВ.
Для иллюстрации остальных алгебраических действий над комплексными числами более удобна тригонометрическая форма.
Умножение. Пусть даны два комплексных числа z1=r1(cosφ1+isinφ1) и z2=r2(cosφ2+isinφ2). Перемножая их получим z1z2=r1r2(cos(φ1+φ2)+isin(φ1+φ2)). Следовательно, при умножении комплексных чисел их модули перемножаются, а аргументы складываются. Это правило верно и для любого числа сомножителей.
Деление. Если требуется разделить z1 на z2, то выполняем следующие преобразования: z1/z2=(z1z2)/(z2z2)=(r1(cosφ1+isinφ1)r2(cosφ2-isinφ2))/ (r2(cosφ2+isinφ2)r2(cosφ2-isinφ2))=(r1/r2)(cos(φ1-φ2)+isin(φ1-φ2)), т.е. при делении двух комплексных чисел их модули делятся, а аргументы вычитаются.
Возведение в степень. Умножая число z=r(cosφ+isinφ) само на себя «n» раз, получаем согласно правилу умножения zn=rn(cosφ+isinφ)n=rn(cosnφ+isinnφ). Таким образом, при возведении комплексного числа в степень «n» в ту же степень возводимся его модуль, а аргумент умножается на «n» (на показатель степени). В частном случае, если r=1, то предыдущее равенство принимаем вид (cosφ+isinφ)n= cosnφ+isinnφ (9). Полученная формула называется формулой Муавра (1667-1754).
Извлечение корня. Пусть а=reiφ, z=ρeiσ. Решаем уравнение zn=a для вычисления n√a: ρneinσ=reiφ. Отсюда с учетом того, что аргументы чисел отличаются на целое кратное числу 2π, получаем: ρn=r, nσ-φ=2πK, или ρ=n√r; σK+1=(φ+2πK)/n (причем К=0,1,2…n-1). Таким образом, zk=n√r(cosφ+isinφ)=n√r((cosφ+2Kπ)/n+isin(φ+2Kπ)/n)) (10), где n√r , - арифметический корень, а К=0,1,2,…,n-1; т.е. корень степени n в множестве комплексных чисел имеет “n различных значений zk (исключение представляет z=0. В этом случае все значения корня равны между собой и равны нулю).
Заметим также, что разность между аргументами соседних чисел zk+1 и zk постоянна и равна 2π/n: σk+1-σk=(φ+2π(K+1))/n-(φ+2πK)/n=2π/n. Отсюда следует, что все значения n√a располагаются на комплексной плоскости в вершинах некоторого правильного n-угольника с центром в начале координат.
IV. Применение комплексных чисел к решению алгебраических уравнений 3-ей и 4-ой степеней.
1. Формула Кардано.
Рассмотрим приведенное алгебраическое уравнение 3-ей степени: x3+ax2+bx+c=0 (11).
(общее уравнение 3-ей степени сводится к приведенному делением на коэффициент при старшей степени). С помощью замены x=y-a/3 это уравнение примет вид y3+py+q=0 (11’), где p и q новые коэффициенты, зависящие от a,b,c. Пусть у0 – какой либо корень уравнения (11’). Представим его в виде у0=α+β, где α и β – неизвестные пока числа, и подставим в уравнение. Получим α3+β3+( α+β)(3αβ+p)+q=0 (12). Выберем теперь α и β так, чтобы 3αβ+р=0. Такой выбор чисел α и β возможен, т.к. они (вообще говоря комплексные) удовлетворяют системе уравнений
![]() α+β=у0;
α+β=у0;
αβ=-р/3, а значит, существуют.
При этих условиях уравнение (12) примет вид α3+β3+q=0, а т.к. еще α3β3=-р3/27, то получаем систему
![]() α3+β3=-q;
α3+β3=-q;
α3β3=-р3/27,
из которой по теореме Виета следует, что α3 и β3 являются корнями уравнения t2+qt-p3/27=0. Отсюда находим: α3=-q/2+√q2/4+p3/27; β3=-q/2-√q2/4+p3/27, где √q2/4+p3/27 означает одно из возможных значений квадратного корня. Отсюда следует, что корни уравнения (11’) выражаются формулой D=(q/2)2+(p/3)3.
y1.2.3=n√-q/2+√q2/4+p3/27+3√-q/2-√q2/4+p3/27, причем для каждого из трех значение первого корня 3√α соответствующие значения второго корня 3√β нужно брать так, чтобы было выполнено условие αβ=-р/3. Полученная формула называется формулой Кардано (ее можно записать в более компактном виде у=3√α+3√β, где α=-q/2+√q2/4+p3/27; β=-q/2-√q2/4+p3/27. Подставив в нее вместо р и q их выражения через a,b,c и вычитая а/3, получим формулу для уравнения (11).
2. Метод Феррари для уравнения 4-ой степени.
Рассмотрим приведенное уравнение 4-ой степени x4+ax3+bx2+cx+d=0 (13). Сделав замену переменной х=у-а/4, получим уравнение у4+ру2+qy+r=0 (14) c коэффициентами p,q,r, зависящими от a,b,c,d. Преобразуем это уравнение к виду (y2+p/2)2+qy+(r-p2/4)=0, а затем, введя произвольное пока число α, представим его левую часть в равносильной форме (y2+p/2+α)2-[2α(y2+p/2)+α2-qy+p2/4-r]=0 (15)
Выберем теперь число α так, чтобы выражение в квадратных скобках 2αy2-qy+(αp+α2+p2/4-r) стало полным (точным) квадратом относительно у. Для этого нужно, чтобы его дискриминант был равен нулю, т.е. чтобы q2-8α(αp+α2+p2/4-r)=0, или 8α3+8pα2+8α(p2/4-r)-q2=0. Таким образом, для нахождения α получается уравнение 3-ей степени, и задача сводится к предыдущей. Если в качестве «α» взять один из корней этого уравнения, то левая часть уравнения (15) будет разностью квадратов и поэтому может быть разложена в произведение двух многочленов 2-ой степени относительно «у».
V. Дополнительные задачи и упражнения, связанные с использованием комплексных чисел.
1. Вычислить: ii2i3…i10=?
Решение: ii2i3…i10=i1+2+…+10=i11∙10/2=i55=ii54=i(i2)27=i(-1)27=-i.
2. Каков геометрический смысл выражений: а) |z|, б)Argz; в) |z1-z2|, г) Arg(z1/z2)?
Ответ: а) расстояние от начала координат до точки, изображающей комплексное число z;
б) угол, на который нужно повернуть действительную ось до совпадения с направлением вектора 0М, изображающего комплексное число z;
в) |z1-z2|- расстояние между точками z1 и z2, изображающими комплексные числа z1 и z2;
г) Arg(z1/z2) угол между изображающими векторами 0z1 и 0z2.
3. Доказать, что cos3φ=cos3φ-3sin2φcosφ; sin3φ=3cos2φsinφ-sin3φ.
![]() Доказательство:
по формуле Муавра имеем: cos3φ+isin3φ=(cosφ+isinφ)3=(cos3φ-3cosφsin2φ)+(3cos2φsinφ-sin3φ)
, приравнивая действительные и мнимые части комплексных чисел, что cos3φ=cos3φ-3sin2φcosφ,
sin3φ=3cos2φsinφ-
sin3φ.
Доказательство:
по формуле Муавра имеем: cos3φ+isin3φ=(cosφ+isinφ)3=(cos3φ-3cosφsin2φ)+(3cos2φsinφ-sin3φ)
, приравнивая действительные и мнимые части комплексных чисел, что cos3φ=cos3φ-3sin2φcosφ,
sin3φ=3cos2φsinφ-
sin3φ.
4. Найти действительные решения уравнения (3+i)x+(-5+2i)y=4+16i.
![]() Решение:
(3x-5y)+i(x+2y)=4+16i
Решение:
(3x-5y)+i(x+2y)=4+16i
![]()
![]() 3x-5y=4
3x-5y=4
x+2y=16 x=8; y=4.
Ответ: z=8+4i.
5. Доказать тождество |z1+z2|2+|z1-z2|2=2(|z1|2+|z2|2) и вычислить его геометрический смысл.
Доказательство: |z1+z2|2+|z1-z2|2= (z1+z2)( z1+z2)+( z1-z2)( z1-z2)= (z1+z2)( z1+z2)+ +( z1-z2)( z1-z2)=2 z1 z1+2 z2 z2=2(|z1|2+|z2|2).
Геометрический смысл: сумма квадратов длин диагоналей равна сумме квадратов всех сторон параллелограмма.
6. Найти геометрическое место точек:
а) |z-z0|=R; б) z=z0+Reit (0≤t<2π)
Ответ: Окружность радиуса R с центром в z0.
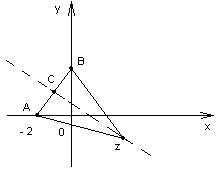 в) |z-3i|=|z+2|;
в) |z-3i|=|z+2|;
г) |z+i|=|z-3|=|z-1-i|;
![]() д)
|z|≤R
д)
|z|≤R
π/4≤argz≤5π/4
Решение:
в) точка z должна быть удалена на такое же расстояние от точки z1=-2, как и от точки z2=3i, т.е. должна находиться на серединном перпендикуляре, проведенном к отрезку АВ. Следовательно, искомое геометрическое место точек – это прямая, проходящая через точку С (хс;ус), где хс=(-2+0)/2=-1; ус=(3+0)/2=3/2, перпендикулярная отрезку АВ.
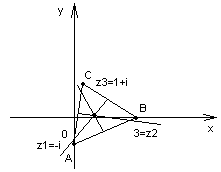 г) Рассматривая попарно
направленные равенства |z+i|=|z-3|
и |z-3|=|z-1-i|,
приходим к заключению, что искомое множество точек – это множество точек
пересечения серединных перпендикуляров, проведенных к отрезкам АВ и ВС (а также
и к АС).
г) Рассматривая попарно
направленные равенства |z+i|=|z-3|
и |z-3|=|z-1-i|,
приходим к заключению, что искомое множество точек – это множество точек
пересечения серединных перпендикуляров, проведенных к отрезкам АВ и ВС (а также
и к АС).
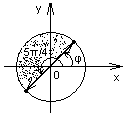 д) Верхний полукруг,
ограниченный лучами argz=π/4 и argz=5π/4
и окружностью |z|=R, не содержащий (∙)
z=0.
д) Верхний полукруг,
ограниченный лучами argz=π/4 и argz=5π/4
и окружностью |z|=R, не содержащий (∙)
z=0.
7. Доказать тождество:
(2x-z)2+(2x-z)2=2Re(z2).
Доказательство:
1) (2x-z)2+(2x-z)2= 4x2-4xz+z2+4x2-4xz+z2=8x2-4x(z+z)+z2+z2=8x2-4x2x+(z+z)2-
-2zz=(2x)2-2|z|2=4x2-2(x2+y2)=2(x2+y2)=2Re(z2).
2) 2Re(z2)=2Re(x+iy)2=2Re(x2-y2+2ixy)=2(x2-y2).
8. Решить систему уравнений
![]() (3-i)z1-(4+2i)z2=1+3i;
(3-i)z1-(4+2i)z2=1+3i;
(4+2i)z1+(2+3i)z2=7.
Решение: Применим правило Крамера:
![]()
![]() ∆= (3-i)-(4+2i) =(2+3i)(3-i)+(4+2i)2
=21+23i
∆= (3-i)-(4+2i) =(2+3i)(3-i)+(4+2i)2
=21+23i
(4+2i)+(2+3i)
![]()
![]() ∆z1=
(1+3i)-(4+2i) =(2+6i+3i-9)+28+14i =21+23i
∆z1=
(1+3i)-(4+2i) =(2+6i+3i-9)+28+14i =21+23i
7 (2+3i)
![]()
![]() ∆z2=
(3-i) (1+3i) =21-7i-4-2i-12i+6 =23-21i
∆z2=
(3-i) (1+3i) =21-7i-4-2i-12i+6 =23-21i
(4+2i) 7
![]()
![]()
![]() Z1=
21+23i =1; z2= 23-21i =-i(21+23i) =-i
Z1=
21+23i =1; z2= 23-21i =-i(21+23i) =-i
21+23i 21+23i 21+23i
Ответ: z1=1; z2=-i.
9. Доказать, что (а2+1)(b2+1)(c2+1) можно представить в виде суммы квадратов целых чисел (a,b,c целые числа).
Доказательство: заметим, что а2+1=|a+i|2, тогда имеем: (а2+1)(b2+1)(c2+1)=(a+i)(a-i)(b+i)(b-i)(c+i)(c-i)=(a+i)(b+i)(c+i)(a+i)(b+i)(c+i)= =((ab-1)+i(a+b))(c+i)((ab-1)+i(a+b))(c+i)=(((ab-1)c-a-b)+i((a+b)c+ab-1))((ab-1)c-a-b+i((a+b)c+ab-1)=(abc-(a+b+c))2+(ab+bc+ca-1)2.
10. Найти суммы:
С=cosφ+cos2φ+…+cosnφ; S=sinφ+sin2φ+…+sinnφ.
Решение: найдем сумму σ=с+iS=(eiφ+e2iφ+…+einφ) и выделим действительную и мнимую ее части, т.е. С=Reσ; S=Imσ. Последовательно имеем: eiφ+e2iφ+…+einφ= eiφ((1- einφ)/(1- eiφ))= (eiφ(1- einφ) (1- e-iφ))/( (1- eiφ) (1- e-iφ))= =(eiφ-1- eiφ(n+1)+ einφ)/|1- eiφ|2.
Поскольку |1- eiφ|2=|(1-cosφ)-isinφ|2=(1-cosφ)2+sin2φ=4sin2(φ/2);
Re(eiφ-1- eiφ(n+1)+ einφ)= cosφ-1-cos(n+1)φ+cosnφ= =- 2sin2(φ/2)+2sin(φ/2)sin(nφ+φ/2)= 2sin(φ/2)2sin(nφ/2)cos((n+1)φ)/2 и Im(eiφ-1- eiφ(n+1)+ einφ)=sinφ-sin(n+1)φ+sinnφ=2sin(φ/2)(cos(φ/2)-cos(nφ+φ/2))= =2sin(φ/2)2sin(nφ/2)sin(((n+1)φ)/2), то С=(4sin(φ/2)sin(nφ/2)cos(((n+1)φ)/2))/(4sin2(φ/2)) = =[sin(nφ/2) cos(((n+1)φ)/2))]/ sin(φ/2);
S=(4sin(φ/2)sin(nφ/2)cos(((n+1)φ)/2))/(4sin2(φ/2)) = =[sin(nφ/2) cos(((n+1)φ)/2))]/ sin(φ/2)
11. Найти сумму 1+eπcosπ+e2πcos2π+…+enπcosnπ.
Решение: Рассмотрим функцию
S(x)=1+excosx+e2xcos2x+…+enxcosnx и найдем ее значение при х=π.
В свою очередь, при нахождении суммы S(x) перейдем к комплексным числам:
σ(z)=1+ex+ix+e2x+i2x+…+enx+inx= 1+ex(1+i)+e2x(1+i)+…+enx(1+i)=(1-( ex(1+i))n+1)/(1- ex(1+i))= =1-ex(n+1)(1+i)/(1-ex(1+i))=((1-ex(n+1)(1+i))(1-ex(1-i))/((1-ex(1+i))(1-ex(1-i))) =(1- ex(n+1)(1+i)- ex(1-i)+ex(n+2+ni))/|1- ex(1+i)|2=
=(1-e(n+1)xei(n+1)x-exe-ix+e(n+2)xexni)/(1-2excosx+e2x)
т.к. S(x)=Reσ(z), то получаем формулу:
S(x)=1+excosx+e2xcos2x+…+enxcosnx=(1-e(n+1)xcos(n+1)x+e(n+2)xcosnx-excosx)/(1-2excosx+e2x)
Отсюда следует, что искомая сумма равна:
S(π)=1+eπcosπ+e2πcos2π+…+enπcosnπ= (1+eπ+eπ(n+2)(-1)n-e(n+1)(-1)n+1)/(1+2eπ+e2π)= =((1+eπ)+(-1)neπ(n+1)(eπ+1))/(eπ+1)2=(1+(-1)neπ(n+1))/(1+eπ)
![]() 12.
Доказать, что Re(z-1)/(z+1)=0
|z|=1.
12.
Доказать, что Re(z-1)/(z+1)=0
|z|=1.
Доказательство:
![]() Т.к.
(z-1)/(z+1)=((z-1)(z+1))/((z+1)(z+1))=(zz+z-z-1)/|z+1|2=((|z|2-1)+2iy)/|z+1|2;
то Re(z-1)(z+1)=0,
если только |z|2-1=0
|z|=1.
Т.к.
(z-1)/(z+1)=((z-1)(z+1))/((z+1)(z+1))=(zz+z-z-1)/|z+1|2=((|z|2-1)+2iy)/|z+1|2;
то Re(z-1)(z+1)=0,
если только |z|2-1=0
|z|=1.
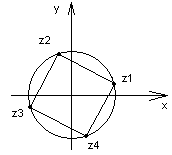 13. Найти все значения
корня 4√1+i√3.
Дать геометрическую иллюстрацию.
13. Найти все значения
корня 4√1+i√3.
Дать геометрическую иллюстрацию.
Решение:
z=4√1+i√3=4√a, где a=1+i√3.
Т.к. а=r(cosφ+isinφ)=2(cosπ/3+isinπ/3), то zk=4√2(cos(π/3+2Kπ)/4+isin(π/3+2Kπ), где К=0,1,2,3.
Получаем:
Z0= 4√2(cosπ/12+isinπ/12); z1=4√2(cos7π/12+isin7π/12);
Z2=4√2(cos13π/12+isin13π/12); z4=4√2(cos19π/12+isin19π/12).
14. Представить в алгебраической форме комплексное число 1/(1+i√3)6-1/(√3-i)6 =z
Решение: преобразуем данное число:
Z=((1-i√3)/((1+i√3)(1-i√3)))6-((√3+i)/((√3-i)(√3+i)))6= =(1-i√3)6/|1+i√3|12-(√3+i)6/|√3+i|12=z1-z2=(т.к. |z1|=|z2|=2; φ1=-π/3; φ2=π/6, то)=1/26∙26(cos(-π/3)+isin(-π/3))6-1/26∙26(cosπ/6+isinπ/6))6= =cos(-2π)+isin(-2π)-cosπ-isinπ=1-(-1)=2.
VII. Литература.
VIII.
1. Кураш А.Г. «Алгебраические уравнения произвольных степеней». М., «Наука», 1983.
2. Маркушевич А.И. «Комплексные числа и конформные отображения». М., «Физматгиз», 1960.
3. Стройк Д.Я. «Краткий очерк истории математики». М., «Наука», 1969.
4. Яглом И.И. « Комплексные числа и их применение в геометрии». М., Физматгиз, 1963.
5. Справочник по элементарной математике (для поступающих в ВУЗы) под редакцией Фильчакова П.Ф. «Наукова Думка», Киев – 1972.
© 2010 Интернет База Рефератов