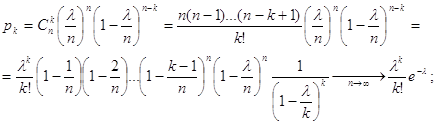Рефераты по сексологии
Рефераты по информатике программированию
Рефераты по биологии
Рефераты по экономике
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Рефераты по авиации и космонавтике
Рефераты по административному праву
Рефераты по безопасности жизнедеятельности
Рефераты по арбитражному процессу
Рефераты по архитектуре
Рефераты по астрономии
Рефераты по банковскому делу
Рефераты по биржевому делу
Рефераты по ботанике и сельскому хозяйству
Рефераты по бухгалтерскому учету и аудиту
Рефераты по валютным отношениям
Рефераты по ветеринарии
Рефераты для военной кафедры
Рефераты по географии
Рефераты по геодезии
Рефераты по геологии
Рефераты по геополитике
Рефераты по государству и праву
Рефераты по гражданскому праву и процессу
Рефераты по делопроизводству
Рефераты по кредитованию
Рефераты по естествознанию
Рефераты по истории техники
Рефераты по журналистике
Рефераты по зоологии
Рефераты по инвестициям
Рефераты по информатике
Исторические личности
Рефераты по кибернетике
Рефераты по коммуникации и связи
Курсовая работа: Распределение Пуассона. Аксиомы простейшего потока событий
Курсовая работа: Распределение Пуассона. Аксиомы простейшего потока событий
Министерство образования и науки Украины
Харьковский национальный университет радиоэлектроники
Факультет ПММ
Кафедра ПМ
КУРСОВАЯ РАБОТА
Тема: Распределение Пуассона. Аксиомы простейшего потока событий.
Дисциплина: Теория вероятностей и математическая статистика
Выполнил: Проверил:
ст. группы ******** проф. **********
*****************
Харьков 2007
РЕФЕРАТ
В данном курсовом проекте представлено описание понятий корреляционного момента и его свойств, коэффициента корреляции, случайных событий и их основных числовых характеристик, применения на практике корреляции, а также приведено решение практических задач.
Пояснительная записка состоит из вступления, основной части, выводов, списка литературы.
Записка 28с.
Ключевые слова и выражения:
СЛУЧАЙНАЯ ВЕЛИЧИНА, МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ, ДИСПЕРСИЯ, НАЧАЛЬНЫЙ МОМЕНТ, ЦЕНТРАЛЬНЫЙ МОМЕНТ, КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ, КОРРЕЛЯЦИОННЫЙ МОМЕНТ, ЗАКОН РАСПРЕДЕЛЕНИЯ, СРЕДНЕЕ КВАДРАТИЧНОЕ ОТКЛОНЕНИЕ, ПЛОТНОСТЬ РАСПРЕДЕЛЕНИЯ, ЗАВИСИМОСТЬ.
СОДЕРЖАНИЕ
Введение………………………………………………………………………..….4
1 Теоретическая часть……….……………………………………………………5
1.1 Доверительные оценки…………………………………………..……….….5
1.2 Метод наибольшего правдоподобия………………………………….…...10
1.3 Точечные оценки…………………………………………………………..13
1.4 Критерий согласия…………………………………………………….……18
1.5 Теорема Чебышева…………………………………………...……….……19
1.6 Понятие доверительного интервала………………...……………….….…23
1.7 Сравнение средних………………………………………………………....25
1.8 Метод минимума X2 ……………………………………………………..…26
1.9 Распределение Пуассона. Аксиомы простейшего потока событий…..…28
2 Практическая часть……………………………………………………………30
Выводы…………………………………………………………………………...37
Список литературы……………………………………………………………...38
ВВЕДЕНИЕ
Теория вероятности математическая наука, изучающая закономерности в случайных явлениях. При научном исследовании физических и технических задач, часто приходится встречаться с явлениями особого типа, которые принято называть случайными. Случайное явление – это такое явление, которое при неоднократном воспроизведении одного и того же опыта протекает несколько по-иному.
Очевидно, что в природе нет ни одного физического явления, в котором не присутствовали бы в той или иной мере элементы случайности. Как бы точно и подробно ни были фиксированы условия опыта, невозможно достигнуть того, чтобы при повторении опыта результаты полностью и в точности совпадали.
Случайности неизбежно сопутствуют любому закономерному явлению. Тем не менее, в ряде практических задач этими случайными элементами можно пренебречь, рассматривая вместо реального явления его упрощенную схему, т.е. модель, и предполагая, что в данных условиях опыта явление протекает вполне определенным образом. При этом из бесчисленного множества факторов, влияющих на данное явление, выделяют самые главные, решающие. Влиянием остальных, второстепенных факторов просто пренебрегают. Изучая закономерности в рамках некоторой теории, основные факторы, влияющие на то или иное явление, входят в понятия или определения, которыми оперирует рассматриваемая теория.
Как и всякая наука, развивающая общую теорию какого-либо круга явлений, теория вероятностей также содержит ряд основных понятий, на которых она базируется. Естественно, что не все основные понятия могут быть строго определены, так как определить понятие это значит свести его к другим, более известным. Этот процесс должен быть конечным и заканчиваться на первичных понятиях, которые только объясняются.
1 ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
1.1 Доверительные оценки
Выборочная оценка,
являясь точечной, дает оценочные значения соответствующего параметра из данной
выборки, но ничего не дает для точности и достоверности оценки. Такие данные
поставляют доверительные оценки. Пусть ![]() случайная выборка из генеральной
совокупности со случайной величиной
случайная выборка из генеральной
совокупности со случайной величиной ![]() , распределение которой зависит от
параметра
, распределение которой зависит от
параметра ![]() .
Пусть
.
Пусть ![]() такие функции выборок, что при произвольном
такие функции выборок, что при произвольном ![]() выполняется равенство
выполняется равенство
![]() . (1.1.1)
. (1.1.1)
Тогда случайный интервал ![]() называется
доверительной оценкой параметра
называется
доверительной оценкой параметра ![]() с мерой надежности
с мерой надежности ![]() (с уровнем значимости
(с уровнем значимости ![]() ).
).
Если имеется реализация ![]() выборки
выборки ![]() , то реализация доверительной
оценки дает доверительный интервал
, то реализация доверительной
оценки дает доверительный интервал ![]() и в большом ряду выборок истинное
значение лежит примерно в
и в большом ряду выборок истинное
значение лежит примерно в ![]() случаев внутри вычисленных
доверительных границ
случаев внутри вычисленных
доверительных границ ![]() и
и ![]() . Равенство (1.1.1) можно интерпретировать
и так: случайный интервал
. Равенство (1.1.1) можно интерпретировать
и так: случайный интервал ![]() “покрывает” истинный параметр с
доверительной вероятностью
“покрывает” истинный параметр с
доверительной вероятностью ![]() .
.
В математической статистике
часто используют понятие квантилей, процентных точек (односторонних критических
границ и двухсторонних критических границ). Квантилью уровня p или p–квантилью
![]() случайной
величины
случайной
величины ![]() с
функцией распределения
с
функцией распределения ![]() называется решение уравнения
называется решение уравнения ![]() .
.
Односторонней критической границей, отвечающей уровню значимости ![]() (процентной точкой
уровня
(процентной точкой
уровня ![]() ),
непрерывной случайной величины
),
непрерывной случайной величины ![]() с функцией распределения
с функцией распределения ![]() называется
значение случайной величины
называется
значение случайной величины ![]() , для которой
, для которой ![]() , или
, или ![]() . Нижней и верхней
критическими границами, отвечающими уровню значимости
. Нижней и верхней
критическими границами, отвечающими уровню значимости ![]() непрерывной случайной величины
непрерывной случайной величины ![]() с функцией
распределения
с функцией
распределения ![]() называются значения случайной
величины
называются значения случайной
величины ![]() и
и
![]() , для
которых
, для
которых ![]() ;
;
![]() ;
;
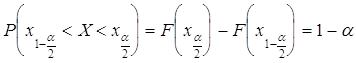 .
.
Для симметричных
случайных величин, у которых плотности
распределения симметричны относительно некоторой точки![]() , нижние и верхние критические
границы удовлетворяют условию
, нижние и верхние критические
границы удовлетворяют условию ![]() , что дает возможность приводить
таблицы лишь для процентных точек или квантилей, больших
, что дает возможность приводить
таблицы лишь для процентных точек или квантилей, больших ![]() . Так, для стандартной
нормальной случайной величины с уровнем значимости
. Так, для стандартной
нормальной случайной величины с уровнем значимости ![]()
![]() .
.
Квантиль, односторонние и двухсторонние критические границы изображены на рис.1.
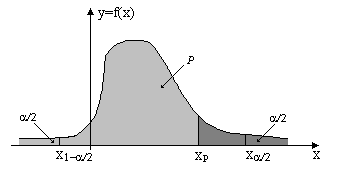
Рис.1. р-квантиль и
критические точки для закона распределения ![]() .
.
1.1.1 Доверительная оценка при неизвестной вероятности по большим выборкам
Частота ![]() является
точечной оценкой
является
точечной оценкой ![]() , она асимптотически нормально
распределена с
, она асимптотически нормально
распределена с ![]() и
и 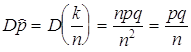 .
.
Если ![]() ,то
,то ![]() . Зададим
. Зададим ![]() . Величина
. Величина ![]() такая, что
такая, что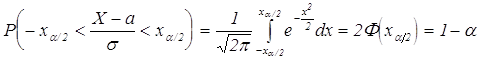 может быть
найдена из уравнения
может быть
найдена из уравнения ![]() при помощи таблиц для функций
Лапласа. Эти же рассуждения применим к
при помощи таблиц для функций
Лапласа. Эти же рассуждения применим к ![]() . По заданному
. По заданному ![]() можно найти
можно найти ![]() так, чтобы
так, чтобы 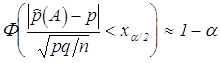 . Из
неравенства
. Из
неравенства 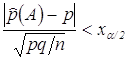 следует, что
следует, что 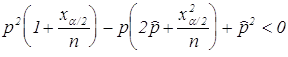 , откуда можно вычислить
оба значения
, откуда можно вычислить
оба значения ![]() и
и ![]() , которые представляют
доверительные оценки для
, которые представляют
доверительные оценки для ![]() . Если
. Если ![]() выбрано достаточно малым, то
случайный интервал
выбрано достаточно малым, то
случайный интервал ![]() “покрывает”
“покрывает” ![]() почти наверное.
почти наверное.
1.1.2 Доверительные оценки для параметров нормального закона
1.1.2.1 Доверительная
оценка ![]() при
известном
при
известном ![]()
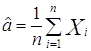 ,
,![]() , тогда
, тогда 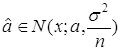 .
.
Соответственно,
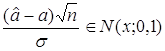 .
.
Для стандартной
нормальной случайной величины с уровнем значимости ![]() нижняя и верхняя критические
границы соответственно равны
нижняя и верхняя критические
границы соответственно равны ![]() и
и ![]() .
.
Имеем
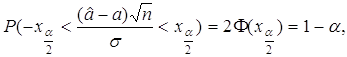 или
или
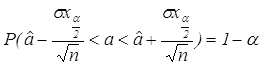 .
.
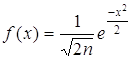 .
.
Таким образом, 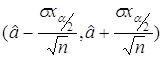 -
доверительная оценка для параметра a с мерой надежности
-
доверительная оценка для параметра a с мерой надежности ![]() .
.
1.1.2.2 Доверительная
оценка ![]() при
неизвестном
при
неизвестном ![]()
Оценка основана на том
факте, что при высказанных предположениях величина ![]() удовлетворяет t- распределению с
n-1 степенями свободы.
удовлетворяет t- распределению с
n-1 степенями свободы.
Определяя одностороннюю
критическую точку ![]() из условия
из условия 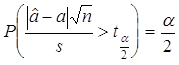 ,получим доверительную
оценку для а в виде
,получим доверительную
оценку для а в виде
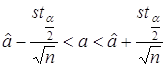 .
.
Для конкретной выборки ![]() объема n
доверительная оценки для а становится ее доверительным интервалом.
объема n
доверительная оценки для а становится ее доверительным интервалом.
1.1.2.3 Доверительная оценка![]() при
неизвестном
при
неизвестном ![]()
Отправной точкой является
тот факт, что при заданных предпосылках величина ![]() удовлетворяет
удовлетворяет ![]() - распределению с n-1
степенями свободы. По заданному уровню значимости
- распределению с n-1
степенями свободы. По заданному уровню значимости ![]() и
и ![]() степенями свободы находим
критические точки
степенями свободы находим
критические точки ![]() и
и ![]() распределения
распределения ![]() такие, что
такие, что
![]() ,
, ![]()
![]() , или
, или 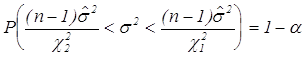 .
.
Таким образом , 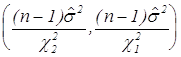 есть
доверительная оценка
есть
доверительная оценка ![]() с мерой надежности
с мерой надежности ![]() .
.
1.2 Метод наибольшего правдоподобия
Пусть дана
выборка ![]() объема
n из генеральной совокупности с непрерывно распределенной случайной величиной
X. Пусть плотность вероятности X содержит неизвестный параметр
объема
n из генеральной совокупности с непрерывно распределенной случайной величиной
X. Пусть плотность вероятности X содержит неизвестный параметр![]() , который следует
оценить по выборке, и имеет вид
, который следует
оценить по выборке, и имеет вид ![]() .
.
Функцией правдоподобия
называют функцию параметра ![]() , определяемую соотношением
, определяемую соотношением
![]() . (1.2.1)
. (1.2.1)
Рассмотрим случай
дискретной случайной величины X с возможными значениями ![]() и вероятностями
и вероятностями ![]() . Обозначим
через
. Обозначим
через ![]() наибольшее
из возможных значений, которое встречается в выборке, а через
наибольшее
из возможных значений, которое встречается в выборке, а через ![]() — абсолютные частоты,
с которыми появляются значения
— абсолютные частоты,
с которыми появляются значения ![]() в выборке
в выборке 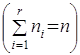 . В этом случае функцией
правдоподобия называют функцию параметра
. В этом случае функцией
правдоподобия называют функцию параметра ![]() , определяемую соотношением
, определяемую соотношением
![]() .
(1.2.2)
.
(1.2.2)
Метод наибольшего правдоподобия состоит в том, что в качестве оценки параметра берется значение, при котором функция правдоподобия достигает своего максимума.
Параметр ![]() находят, решая
относительно
находят, решая
относительно ![]() уравнение
уравнение
![]() .
(1.2.3)
.
(1.2.3)
Часто вместо (1.2.3) используют уравнение
![]() ,
, ![]() (1.2.4)
(1.2.4)
Если плотность ![]() или
вероятности
или
вероятности ![]() зависят от
зависят от ![]() параметров, то наиболее
правдоподобную оценку системы параметров
параметров, то наиболее
правдоподобную оценку системы параметров ![]() получают решением системы
уравнений
получают решением системы
уравнений
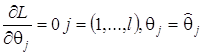 (1.2.5)
(1.2.5)
или
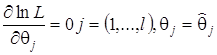 .
(1.2.6)
.
(1.2.6)
Наиболее правдоподобные оценки имеют некоторые замечательные свойства. При достаточно общих условиях они являются состоятельными и асимптотически нормально распределенными (однако не всегда несмещенными), имеют среди всех асимптотически нормально распределенных оценок наибольшую эффективность. Справедливо следующее положение: если вообще имеется эффективная оценка, то она получается методом наибольшего правдоподобия.
Пример 1.2.1
Оценить вероятность ![]() некоторого события
некоторого события ![]() . Пусть
. Пусть
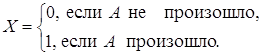
Решение. ![]() ;
; ![]() . Пусть в
. Пусть в ![]() независимых наблюдениях
событие
независимых наблюдениях
событие ![]() произошло
произошло
![]() раз, т.е.
раз, т.е.
![]() . Таким
образом, имеем
. Таким
образом, имеем ![]() ,
, 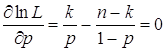 . Отсюда следует, что
. Отсюда следует, что ![]() .
Следовательно,
.
Следовательно, ![]() есть наиболее правдоподобная
оценка параметра
есть наиболее правдоподобная
оценка параметра ![]() . Случайная величина k биномиально
распределена,
. Случайная величина k биномиально
распределена, ![]() ;
; ![]() Следовательно,
Следовательно, ![]() — несмещенная оценка
вероятности, асимптотически состоятельная и асимптотически нормальная.
— несмещенная оценка
вероятности, асимптотически состоятельная и асимптотически нормальная.
Пример 1.2.2.
Пусть случайная величина ![]() распределена по закону Пуассона с
неизвестным параметром
распределена по закону Пуассона с
неизвестным параметром ![]() . Проведем выборку и получим
значения
. Проведем выборку и получим
значения ![]() (
(
![]() – целые
числа). Пусть
– целые
числа). Пусть ![]() – набольшее из наблюдаемых в
выборке чисел,
– набольшее из наблюдаемых в
выборке чисел, ![]() – абсолютные частоты, с которыми
числа
– абсолютные частоты, с которыми
числа ![]() появляются
в выборке ;
появляются
в выборке ; 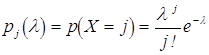 . Тогда согласно формуле (3.2)
. Тогда согласно формуле (3.2) 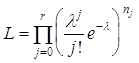 . Из
соотношения получаем
. Из
соотношения получаем 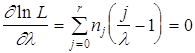 , откуда
, откуда 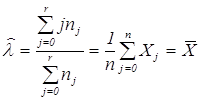 .
.
Величина ![]() есть, таким образом,
правдоподобная оценка для
есть, таким образом,
правдоподобная оценка для ![]() и вместе с тем состоятельная,
асимптотически нормально распределенная.
и вместе с тем состоятельная,
асимптотически нормально распределенная.
Пример 1.2.3.
Пусть случайная величина ![]() распределена нормально с параметрами
распределена нормально с параметрами
![]() и
и ![]() . Их следует
оценить исходя их выборки
. Их следует
оценить исходя их выборки ![]() объема
объема ![]() .
.
Решение. Функция правдоподобия
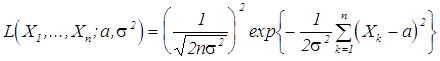 ,
,
следовательно
![]() .
.
Согласно (2.5), получаем
следующие уравнения для определения ![]() и
и ![]() :
: ![]() ;
; ![]() , откуда
, откуда ![]() и
и ![]() . Следовательно,
. Следовательно, ![]() есть наиболее
правдоподобная оценка параметров
есть наиболее
правдоподобная оценка параметров ![]() . Мы уже знаем, что
. Мы уже знаем, что ![]() не является несмещенной
оценкой, а только асимптотически не смещена.
не является несмещенной
оценкой, а только асимптотически не смещена.
1.3 Точечные оценки
Одной из задач математической статистики является оценка неизвестных параметров выбранной параметрической модели.
Очень часто в приложениях рассматривают параметрическую модель. В этом случае предполагают, что закон распределения генеральной совокупности принадлежит множеству
![]() , где вид функции распределения
задан, а вектор параметров
, где вид функции распределения
задан, а вектор параметров![]() неизвестен. Требуется найти
оценку для
неизвестен. Требуется найти
оценку для![]() или
некоторой функции от него (например, математического ожидания, дисперсии)
по случайной выборке
или
некоторой функции от него (например, математического ожидания, дисперсии)
по случайной выборке ![]() из генеральной совокупности X.
из генеральной совокупности X.
Например, предположим,
что масса X детали имеет нормальный закон
распределения, но его параметры![]() неизвестны. Нужно найти
приближенное значение параметров по результатам наблюдений х, …, хп,
полученным в эксперименте (по реализации случайной выборки).
неизвестны. Нужно найти
приближенное значение параметров по результатам наблюдений х, …, хп,
полученным в эксперименте (по реализации случайной выборки).
Как уже отмечалось , в математической статистике существуют два вида оценок: точечные и интервальные. В этой главе будут рассмотрены точечные оценки, а интервальным оценкам посвящена следующая глава.
1.3.1. Состоятельные, несмещенные и эффективные оценки
Пусть![]() — случайная выборка из генеральной
совокупности X, функция распределения
— случайная выборка из генеральной
совокупности X, функция распределения![]() которой известна, а
которой известна, а![]() — неизвестный параметр,
т.е. рассматривается параметрическая модель
— неизвестный параметр,
т.е. рассматривается параметрическая модель![]() (для простоты изложения будем
считать пока, что
(для простоты изложения будем
считать пока, что![]() — скаляр).
— скаляр).
Требуется построить статистику![]() , которую можно
было бы принять в качестве точечной оценки параметра
, которую можно
было бы принять в качестве точечной оценки параметра![]() .
.
Интуитивно ясно, что в
качестве оценки параметра![]() можно использовать различные
статистики. Например, в качестве точечной оценки для
можно использовать различные
статистики. Например, в качестве точечной оценки для![]() можно предложить такие статистики:
можно предложить такие статистики:
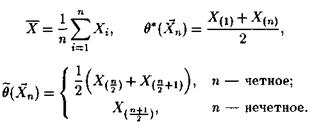
Какую же из этих
статистик предпочесть? В общем случае нужно дать ответ на вопрос: какими
свойствами должна обладать статистика![]() , чтобы она была в некотором
смысле наилучшей оценкой параметра в? Рассмотрению требований к оценкам и
методам их нахождения посвящена настоящая глава.
, чтобы она была в некотором
смысле наилучшей оценкой параметра в? Рассмотрению требований к оценкам и
методам их нахождения посвящена настоящая глава.
Заметим, что в
дальнейшем, как правило, будем говорить об оценке параметра![]() параметрической модели,
хотя все сказанное можно перенести и на функцию от в.
параметрической модели,
хотя все сказанное можно перенести и на функцию от в.
Определение 1.3.1.1 Статистику![]() называют состоятельной оценкой параметра
называют состоятельной оценкой параметра![]() , если с ростом
объема выборки п она сходится по вероятности к оцениваемому параметру
, если с ростом
объема выборки п она сходится по вероятности к оцениваемому параметру ![]() , т.е.
, т.е.![]()
Иными словами, для
состоятельной оценки![]() отклонение ее от
отклонение ее от![]() на величину е и более
становится маловероятным при большом объеме выборки. Это свойство оценки
является очень важным, ибо несостоятельная оценка практически бесполезна.
Однако следует отметить, что на практике приходится оценивать неизвестные
параметры и при малых объемах выборки.
на величину е и более
становится маловероятным при большом объеме выборки. Это свойство оценки
является очень важным, ибо несостоятельная оценка практически бесполезна.
Однако следует отметить, что на практике приходится оценивать неизвестные
параметры и при малых объемах выборки.
Естественным является то
требование, при выполнении которого оценка не дает систематической погрешности
в сторону завышения (или занижения) истинного значения параметра![]() .
.
Определение 1.3.1.2. Статистику![]() называют несмещенной оценкой параметра
называют несмещенной оценкой параметра![]() , если ее
математическое ожидание совпадает с
, если ее
математическое ожидание совпадает с![]() , т.е.
, т.е.![]() для любого фиксирован_испер.
для любого фиксирован_испер.
Если оценка является смещенной
(т.е. последнее равенство не имеет места), то величина смещения![]() Как мы увидим далее,
смещение оценки часто можно устранить, введя соответствующую поправку.
Как мы увидим далее,
смещение оценки часто можно устранить, введя соответствующую поправку.
Говорят также, что оценка![]() является асимптотически
несмещенной, если при
является асимптотически
несмещенной, если при![]() она сходится по вероятности к
своему математическому ожиданию, т.е. для любого
она сходится по вероятности к
своему математическому ожиданию, т.е. для любого
![]()
![]()
![]() Предположим, что имеются две
несмещенные оценки
Предположим, что имеются две
несмещенные оценки![]() и
и ![]() для параметра
для параметра![]() . Если дисперсии
. Если дисперсии![]() удовлетворяют
условию
удовлетворяют
условию
![]() (1.3.1)
(1.3.1)
для любого фиксированного
пи![]() , то
следует предпочесть оценку
, то
следует предпочесть оценку![]() , поскольку разброс статистики
, поскольку разброс статистики![]() относительно
параметра
относительно
параметра![]() меньше,
чем разброс статистики
меньше,
чем разброс статистики![]()
![]()
Определение 1.3.1.3. Если в некотором классе
несмещенных оценок параметра![]() , имеющих конечную дисперсию,
существует такая оценка
, имеющих конечную дисперсию,
существует такая оценка![]() , что неравенство (2.1)
выполняется для всех оценок
, что неравенство (2.1)
выполняется для всех оценок![]() из этого класса, то говорят, что
оценка
из этого класса, то говорят, что
оценка ![]() является
эффективной в данном классе оценок.
является
эффективной в данном классе оценок.
оценивать неизвестные параметры и при малых объемах выборки.
Естественным является то
требование, при выполнении которого оценка не дает систематической погрешности
в сторону завышения (или занижения) истинного значения параметра![]() .
.
Определение 1.3.1.4. Статистику![]() называют несмещенной оценкой параметра
называют несмещенной оценкой параметра![]() , если ее
математическое ожидание совпадает с
, если ее
математическое ожидание совпадает с![]() , т.е.
, т.е.![]() для любого фиксированн_испер
для любого фиксированн_испер
Если оценка является смещенной
(т.е. последнее равенство не имеет места), то величина смещения![]() Как мы увидим далее,
смещение оценки часто можно устранить, введя соответствующую поправку.
Как мы увидим далее,
смещение оценки часто можно устранить, введя соответствующую поправку.
Говорят также, что оценка![]() является асимптотически
несмещенной, если при
является асимптотически
несмещенной, если при![]() она сходится по вероятности к
своему математическому ожиданию, т.е. для любого
она сходится по вероятности к
своему математическому ожиданию, т.е. для любого
![]()
![]()
![]() Предположим, что
имеются две несмещенные оценки
Предположим, что
имеются две несмещенные оценки![]() и
и ![]() для параметра
для параметра![]() . Если ди_исперсии
. Если ди_исперсии
удовлетворяют условию
![]() (1.3.2)
(1.3.2)
для любого фиксированного
пи![]() , то
следует предпочесть оценку
, то
следует предпочесть оценку![]() , поскольку разброс статистики
, поскольку разброс статистики![]() относительно
параметра
относительно
параметра![]() меньше,
чем разброс статистики
меньше,
чем разброс статистики![]()
![]()
Определение. Если в некотором классе несмещенных
оценок параметра![]() , имеющих конечную дисперсию,
существует такая оценка
, имеющих конечную дисперсию,
существует такая оценка![]() , что неравенство (3.2)
выполняется для всех оценок
, что неравенство (3.2)
выполняется для всех оценок![]() из этого класса, то говорят, что
оценка
из этого класса, то говорят, что
оценка ![]() является
эффективной в данном классе оценок.
является
эффективной в данном классе оценок.
Иными словами, дисперсия эффективной оценки параметра в некотором классе является минимальной среди дисперсий всех оценок из рассматриваемого класса несмещенных оценок.
Замечание 1.3.1.1. Эффективную оценку в классе всех несмещенных оценок будем называть эффективной оценкой, не добавляя слов „в классе несмещенных оценок".
Замечание 1.3.1.2. В литературе по математической статистике при рассмотрении параметрических моделей вместо термина «эффективная оценка» классе всех несмещенных оценок используют и другие: «несмещенная оценка с минимальной дисперсией», «оптимальная оценка». Теорема 1.3.1. Оценка
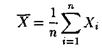
(выборочное среднее) математического ожидания
![]()
генеральной совокупности X с конечной дисперсией является несмещенной, состоятельной и эффективной в классе всех линейных оценок, т.е. оценок вида
где ![]() , для произвольной
, для произвольной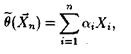 параметрической
модели.
параметрической
модели.
Напомним, что элементы ![]() случайной
выборки
случайной
выборки
![]() являются независимыми
случайными величинами и распределенными так же, как и сама генеральная
совокупность X. Следовательно,
являются независимыми
случайными величинами и распределенными так же, как и сама генеральная
совокупность X. Следовательно,![]()
1.4 Критерии согласия
Пусть (X1,..,Xn) - выборка с неизвестным законом распределения F(X). Рассмотрим гипотезы Н0: F(x)=F0(x) при конкурирующей Н1: F(x)¹F0(x). F0(x)- некоторая заданная функция распределения.
Задача проверки гипотез относительно законов распределения называется задачей проверки согласия, а критерий для этой задачи - –ритерием согласия.
Рассмотрим критерий согласия c2, или критерий Пирсона.
Разобьем ось х на т
интервалов ![]() Если
истинная функция распределения F(x) совпадает с F0(x), то при больших n
Если
истинная функция распределения F(x) совпадает с F0(x), то при больших n
![]()
Рассмотрим случайную величину (ni - –лучайное)
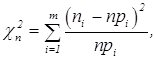
при ![]() она стремится к c2 - –аспределению случайной величины
с т-е-1 степенями свободы (е- число статистических параметров).
она стремится к c2 - –аспределению случайной величины
с т-е-1 степенями свободы (е- число статистических параметров).
Решающее правило для уровня значимости a:
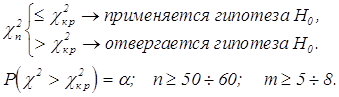
При построении c2n должно выполняться условие ni³10, в противном случае объединяют интервалы.
В случае применения гипотезы Н0 говорят, что различие между F(x) и F0(x) является случайным с доверительной вероятностью 1-a и обусловлено конечностью выборки.
1.5 Теорема Чебышева
Неравенство Чебышева. Для любой случайной величины Х, имеющей математическое ожидание МХ и дисперсию DX, справедливо неравенство
![]()
где a — любое положительное число.
Доказательство. Доказательство проведём сначала для непрерывной случайной величины Х с плотностью распределения f(x).
Обозначим через А событие, состоящее в том, что случайная точка Х попадает за пределы участка (MX-a; MX+a), то есть
А:
a a
MX -a MX MX+a
Вероятность попадания Х в этот участок равна
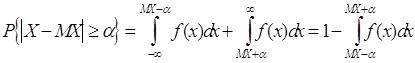
Найдём дисперсию случайной величины Х
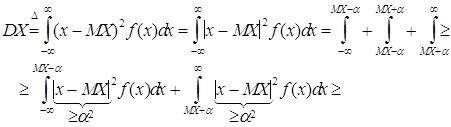
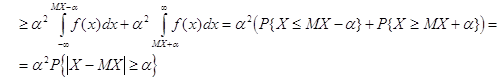
![]()
Совершенно аналогично доказывается неравенство Чебышева и для дискретной случайной величины, имеющей значения x1, x2, ... с вероятностями p1, p2, ... Тогда вместо интеграла во всех формулах ставится знак суммы, где суммирование ведётся по тем xi , для которых
|xi-MX|³a,
что и требовалось доказать.
Определение. Пусть имеется последовательность чисел
x1, x2, ... , xn , ...
Говорят, что эта последовательность сходится по вероятности к неслучайной величине а, если при неограниченном увеличении п вероятность события
Хп-а,
(где e>0 - произвольное малое фиксированное число) стремится к единице, то есть
![]()
Иными словами, каковы бы ни были произвольно малые наперёд заданные числа e>0 и d>0 всегда существует N, такое, что при n>N
PXn-a>1-d
Первая теорема Чебышева (Закон больших чисел). Пусть имеется случайная величина Х с медианой МХ и дисперсией DX. Над этой случайной величиной Х производится п независимых опытов, в результате которых она принимает значения Х1, Х2, ... , Хп (п экземпляров” случайной величины Х). Пусть
![]()
Тогда последовательность ![]() сходится по
вероятности к MX:
сходится по
вероятности к MX: ![]()
Доказательство. Найдём MYn и DYn :
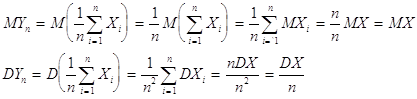
Применим к случайной величине Yn неравенство Чебышева, в котором положим a равным e, где e>0 — сколь угодно малое, наперёд заданное число.
![]()
Как бы ни было мало e, всегда можно выбрать n таким большим, чтобы правая часть последнего неравенства стала меньше сколь угодно малого положительного числа d; следовательно, при достаточно большом п
P<d
ÞP<e>1-d,
а это равносильно сходимости по вероятности Yn к MX
![]()
Замечание 1.5.1. Первую теорему Чебышева можно записать и иначе, если положить Zn:=Yn-MX
![]()
Замечание 1.5.2. Первая теорема Чебышева относится к случаю, когда случайные величины Х1, Х2, ... , Хп независимы и имеют одно и то же распределение, а значит одно и то же MX и DX.
Рассмотрим случай, когда условия производимых опытов меняются.
Вторая теорема Чебышева. Пусть имеется случайная величина Х. Над ней производятся независимые опыты, в результате чего мы получаем последовательность
Х1, Х2, ..., Хn, ...
с различными, в общем
случае, MХi и DXi (i=![]() ). Пусть
). Пусть
![]()
Если DXi£D i=1, 2, ... , где D - некоторое положительное число, то
![]()
Доказательство.
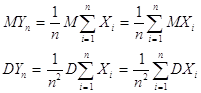 (1.5.1)
(1.5.1)
Согласно неравенства Чебышева
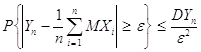
или, учитывая (1.5.1), имеем
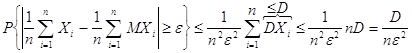
Как бы ни было мало произвольное наперёд заданное e, всегда можно выбрать n таким большим, чтобы правая часть последнего неравенства стала меньше произвольно малого d. Следовательно
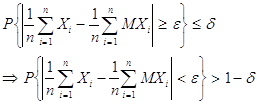 ,
,
что и требовалось доказать.
Замечание 1.5.3. При формулировке второй теоремы Чебышева нельзя говорить, что
![]()
так как ![]() зависят от n, а понятие
сходимость по вероятности” определено нами только для постоянной а, не
зависящей от n.
зависят от n, а понятие
сходимость по вероятности” определено нами только для постоянной а, не
зависящей от n.
1.6 Понятие доверительного интервала
Будем считать, что
независимая выборка ![]() взята из распределения, зависящего
от скалярного параметра
взята из распределения, зависящего
от скалярного параметра ![]() . Будем обозначать через
. Будем обозначать через ![]() распределение
вероятностей, соответствующее значению
распределение
вероятностей, соответствующее значению ![]() неизвестного параметра.
неизвестного параметра.
Определение 1.6.1
![]() -доверительным интервалом
называется интервал вида
-доверительным интервалом
называется интервал вида ![]() где
где ![]() такой, что
такой, что
![]()
Число ![]() называют доверительной
вероятностью.
называют доверительной
вероятностью.
Другими словами,
доверительный интервал обладает тем свойством, что, во-первых, его границы
вычисляются исключительно по выборке (и, следовательно, не зависят от
неизвестного параметра), и, во-вторых, он накрывает неизвестный параметр с
вероятностью ![]() .
.
Значение доверительной
вероятности ![]() выбирается
заранее, этот выбор определяется конкретными практическими приложениями.
выбирается
заранее, этот выбор определяется конкретными практическими приложениями.
Смысл величины ![]() -- вероятность допустимой ошибки.
Часто берут значения
-- вероятность допустимой ошибки.
Часто берут значения ![]() и т.п.
и т.п.
Ниже мы приводим один из методов построения доверительных интервалов. Он состоит из трех этапов.
1.
Выбираем функцию ![]() , зависящую от
выборки и от неизвестного параметра, такую, что ее функция распределения
, зависящую от
выборки и от неизвестного параметра, такую, что ее функция распределения
![]()
не зависит от неизвестного параметра ![]() .
.
2.
Выбираем два
числа ![]() и
и ![]() таким образом,
чтобы
таким образом,
чтобы ![]() .
Подбираем
.
Подбираем ![]() и
и
![]() ,
удовлетворяющие условиям
,
удовлетворяющие условиям
| (6.1) |
3. Таким образом,
| (6.2) |
причем ![]() и
и ![]() не зависят от
не зависят от ![]() .
.
4.
Решим двойное
неравенство ![]() относительно
относительно ![]() . В том случае, когда
его решением является интервал, обозначим его левый и правый концы через
. В том случае, когда
его решением является интервал, обозначим его левый и правый концы через ![]() и
и ![]() соответственно.
Естественно, они зависят от выборки:
соответственно.
Естественно, они зависят от выборки: ![]() ,
, ![]() . В силу (6.2)
. В силу (6.2)
![]()
Следовательно, ![]() -- искомый
-- искомый ![]() -доверительный
интервал.
-доверительный
интервал.
Замечание 1.6.1
Описанная процедура,
разумеется, не является универсальной. Во-первых, вопрос о выборе функции ![]() решается в
каждом конкретном случае и по этому поводу нет общих рекомендаций. Во-вторых,
совершенно не гарантировано, что решением неравенства в п. 3 будет
интервал конечной длины. Вместе с тем, во многих важных случаях изложенный выше
метод приводит к хорошим доверительным интервалам. Например, оправдано
применение такого метода в случае, когда при каждой фиксированной выборке
решается в
каждом конкретном случае и по этому поводу нет общих рекомендаций. Во-вторых,
совершенно не гарантировано, что решением неравенства в п. 3 будет
интервал конечной длины. Вместе с тем, во многих важных случаях изложенный выше
метод приводит к хорошим доверительным интервалам. Например, оправдано
применение такого метода в случае, когда при каждой фиксированной выборке ![]() функция
функция ![]() является
строго монотонной и непрерывной по переменной
является
строго монотонной и непрерывной по переменной ![]() .
.
Замечание 1.6.2
В силу неоднозначности
выбора функции ![]() и чисел
и чисел ![]() и
и ![]() , можно заключить, что
, можно заключить, что ![]() -доверительный
интервал неединственен.
-доверительный
интервал неединственен.
1.7 Сравнение средних
Теперь рассмотрим случай, когда обе совокупности подчиняются нормальному распределению, но проверка гипотез о равенстве двух генеральных дисперсий закончилась отвержением гипотезы равенства. Такую задачу сравнения двух генеральных средних при неравных генеральных дисперсиях принято называть проблемой Беренса-Фишера (по имени учёного У. Беренса опубликовавшего первую работу на эту тему в 1929 г.). В этом случае вместо одной общей генеральной дисперсии мы имеем дело с двумя неравными генеральными дисперсиями: σ12 ≠ σ22. Соответственно имеем и две выборочные дисперсии s12 и s22. Тогда искомая t-статистика будет вычисляться по следующему выражению [1.7.1]:
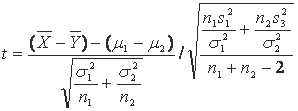 (1.7.1)
(1.7.1)
Введём обозначения: θ= σ12 / σ22 , u = s12 / s22 и N= n1/ n2 . В этом случае выражение (1.7.1) можно переписать в следующем виде [(1.7.1)]:
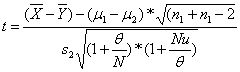 (1.7.2).
(1.7.2).
Основная сложность этого случая заключается в том, что подкоренное выражение в знаменателе не имеет Хи-квадрат распределение, и потому статистика t не имеет распределения Стьюдента. В 40-60-е годы 20 века Бокс, Уэлч, Саттерзвайт, Кохрэн, Боно, Шеффе и многие другие статистики провели детальный анализ этой проблемы. Так в 1938 г. Уэлч исследовал приближённое распределение статистики (1.7.1) и показал, что при равных объёмах выборок n1 = n2 незнание величины θ= σ12 / σ22 не очень сильно влияет на итоговый результат. Однако для случая неравных объёмов выборок ошибки становятся весьма значительными. Другие подходы позволяли аппроксимировать статистику (1.7.2) распределение Стьюдента с дробными степенями свободы.
1.8 Метод минимума X2.
Метод минимума X2 применим лишь и случае группированного непрерывною распределения или дискретного распределения. Оценки, получаемые этим методом, при больших п асимптотически эквивалентны оценкам, полученным с помощью более простого видоизмененного метода минимума X2, выражаемого уравнениями
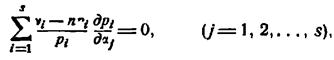 (1.8.1)
(1.8.1)
или
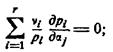 (1.8.2)
(1.8.2)
в рассматриваемых случаях последний метод совладает с методом максимума правдоподобия.
Основная теорема о предельном распределении X2 для случая, когда некоторые параметры оцениваются по выборке что оценки находятся с помощью видоизмененного метода минимума X2. Однако там же было указано, что имеется целый класс методов нахождения оценок, приводящих к тому же самому предельному распределению для X2. Теперь мы докажем это утверждение.
Асимптотические выражения для оценок, получаемых с помощью видоизмененного метода минимума X2 были приведены в явной форме
![]() (1.8.3)
(1.8.3)
для общего случая у неизвестных параметров а1,...,аг. Предположим, что выполнены условия 1)—3) предыдущего параграфа или аналогичные условия для дискретного распределения. Тогда из предыдущего параграфа следует, что оценки (1.8.3)асимптотически нормальны (это уже было показано в параграфе 30.3) и асимптотически эффективны.
Во всех множествах
асимптотически нормальных и асимптотически эффективных оценок для параметров
имеются члены порядка n-1/2
такие же, как и в
(1.8.3). Однако из вывода предельного распределения для у2 следует,
что это предельное распределение полностью определяется членами порядка n-1/2 в (1.8.3). Действительно, по формулам ![]() и
и
![]()
получаем ![]() и показывает,что
предельное распределение для .у = (
и показывает,что
предельное распределение для .у = (![]() , ....
, .... ![]() ) определяется именно указанными
членами.
) определяется именно указанными
членами.
Таким образом, теорема о предельном распределении величины X2 справедлива для любого множества асимптотически нормальных и асимптотически-эффективных оценок параметров.
1.9 Распределение Пуассона. Аксиомы простейшего потока событий
Говорят, что случайная величина Х имеет распределение Пуассона, если её возможные значения 0, 1, 2, ... , т, ... (бесконечное, но чёткое множество значений), а соответствующие вероятности выражаются формулой:
![]()
| x | 0 | 1 | … | k | … |
P |
e-l |
le-l |
… |
|
… |
Число l называется параметром распределения.
Простейший поток событий такая последовательность событий, происходящих в случайный момент времени.
Поток событий называется пуассоновским, если он удовлетворяет аксиомам простейшего потока событий:
При таких допущениях с большой степенью точности выполняются следующие условия:
1. Отсутствие последействия: вероятность того, что на произвольном временном промежутке (с точки зрения длины и расположения на временной оси) не зависит от того, что происходило в момент времени, предшествующему этому моменту.
2. Однородность потока: Вероятность того, что на некотором временном промежутке произойдет 0,1,2,…,n событий зависит только от его длины и не зависит от положення этого отрезка на временной оси.
3. Пусть Dt - длина временного промежутка, тогда: ![]() (Dt)=l Dt+o(Dt), Dt®0.
(Dt)=l Dt+o(Dt), Dt®0.
4. ![]() (Dt)=1-l Dt+o(Dt), Dt®0.
(Dt)=1-l Dt+o(Dt), Dt®0.
Математическое ожидание распределения Пуассона равно:
M![]() =
=![]()
Вариант 23
Задача 1
На отрезок единичной длины ![]() наугад
ставится точка. Вычислить вероятность того, что расстояние от точки до концов
отрезка превышает величину
наугад
ставится точка. Вычислить вероятность того, что расстояние от точки до концов
отрезка превышает величину ![]() .
.
Решить задачу при ![]() ,
, ![]() .
.
Решение:
Пусть дан отрезок ![]() длины
длины ![]() (Рис. 2.1).
Расстояние от точки
(Рис. 2.1).
Расстояние от точки ![]() до концов отрезка превышает
величину
до концов отрезка превышает
величину ![]() в
том случае, если
в
том случае, если ![]() , где
, где ![]() ,
, ![]() .
.
![]()
Рис. 2.1
Пусть А – событие, когда
![]() . Тогда
искомая вероятность
. Тогда
искомая вероятность 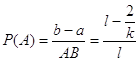 .
.
Для заданных значений ![]() и
и ![]()
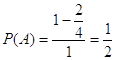 .
.
Задача 2
В круг радиуса R наудачу ставится точка. Найти
вероятность того, что она попадет в одну из двух непересекающихся фигур,
которые имеют площади ![]() и
и ![]() .
.
Решить задачу при ![]() ,
, ![]() ,
, ![]() .
.
Решение:
Поскольку фигуры не
пересекаются, то площадь, в которую должна попасть точка, равна ![]() . Общая площадь, в
которую может попасть точка, равна
. Общая площадь, в
которую может попасть точка, равна ![]() . Таким образом искомая
вероятность
. Таким образом искомая
вероятность ![]() .
Для заданных значений
.
Для заданных значений ![]() ,
, ![]() и
и ![]()
![]() .
.
Задача 3
Среди ![]() лотерейных билетов
лотерейных билетов ![]() выигрышных.
Наудачу взяли
выигрышных.
Наудачу взяли ![]() билетов. Определить вероятность
того, что среди них не менее L выиграшных.
билетов. Определить вероятность
того, что среди них не менее L выиграшных.
Решить задачу при ![]() ,
, ![]() ,
, ![]() ,
,![]() .
.
Решение:
Число способов купить ![]() билетов, среди
которых L выигрышных составляет
билетов, среди
которых L выигрышных составляет ![]() .
.
Число способов купить ![]() билетов, среди
которых L+1 выигрышных составляет
билетов, среди
которых L+1 выигрышных составляет ![]() , и так далее.
, и так далее.
Число способов купить ![]() билетов, среди
которых
билетов, среди
которых ![]() выигрышных
составляет
выигрышных
составляет ![]() .
.
Таким образом, число
способов купить ![]() билетов, среди которых не менее
половины выигрышных составляет
билетов, среди которых не менее
половины выигрышных составляет
![]() +
+![]() +…+
+…+![]() .
.
Общее число способов
купить ![]() билетов
из
билетов
из ![]() составляет
составляет
![]() .
.
Искомая вероятность ![]() .
.
Для заданных значений ![]() ,
, ![]() и
и ![]() .
.
![]()
Задача 4
В лифт ![]() -этажного дома сели
-этажного дома сели ![]() пассажиров (
пассажиров (![]() ). Каждый
независимо от других с одинаковой вероятностью может выйти на любом (начиная со
второго) этажа. Определить вероятность того, что хотя бы двое вышли на одном этаже.
). Каждый
независимо от других с одинаковой вероятностью может выйти на любом (начиная со
второго) этажа. Определить вероятность того, что хотя бы двое вышли на одном этаже.
Решить задачу при ![]() ,
, ![]() .
.
Решение:
Пусть ![]() – событие, когда все
пассажиры вышли на разных этажах. Тогда вероятность искомого события
– событие, когда все
пассажиры вышли на разных этажах. Тогда вероятность искомого события ![]() .
.
Найдем ![]() . Количество способов
всем пассажирам выйти на разных этажах составляет
. Количество способов
всем пассажирам выйти на разных этажах составляет ![]() . Общее число способов выхода
. Общее число способов выхода ![]() пассажиров на
одном из
пассажиров на
одном из ![]() -го
этажа составляет
-го
этажа составляет ![]() . Тогда
. Тогда ![]() .
.
Искомая вероятность ![]()
![]() .
.
Для заданных значений ![]() ,
,![]()
![]() .
.
Задача 5
В двух партиях ![]() и
и ![]() процентов
доброкачественных изделий соответственно. Наудачу выбирают по одному изделию из
каждой партии. Какова вероятность обнаружить среди них одно доброкачественное и
одно бракованное?
процентов
доброкачественных изделий соответственно. Наудачу выбирают по одному изделию из
каждой партии. Какова вероятность обнаружить среди них одно доброкачественное и
одно бракованное?
Решить задачу при ![]() и
и ![]() .
.
Решение:
Пусть ![]()
![]() – событие обнаружить
доброкачественное изделие из
– событие обнаружить
доброкачественное изделие из ![]() -й партии.
-й партии. ![]() – событие обнаружить
бракованное изделие из
– событие обнаружить
бракованное изделие из ![]() -й партии. Тогда искомая
вероятность
-й партии. Тогда искомая
вероятность ![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() .
.
Для заданных значений ![]() ,
,![]() искомая вероятность
искомая вероятность ![]() .
.
Задача 6
Вероятность того, что цель поражена при одном выстреле первым стрелком – р1, вторым – р2. Первый сделал n1, второй n2 выстрелов. Определить вероятность того, что цель не поражена.
р1 = 0,76; р2 = 0.39; n1 = 2; n2 = 3.
Решение:
Пусть событие А – цель не поражена. Вероятность того, что первый стрелок не попадет в цель при одном выстреле равна (1 – р1). Вероятность того, что первый стрелок не попадет при n1 выстрелах равна (1 – р1)n1, вероятность того, что второй стрелок не попадет в цель при n2 выстрелах равна (1 – р2)n2. Получим
Р(А) = (1 – р1)n1 (1 – р2)n2 =
= 0,242*0,613= 0,013.
Ответ: 0,013.
Задача 7
Урна содержит М
занумерованных шаров от 1 до М. Шары извлекаются по одному без возвращения.
Событие B – хотя бы 1 раз совпадет номер шара
и порядковый номер извлечения. Определить вероятность события С. Найти
предельное значение вероятности при М ![]() .
.
М = 10.
Решение:
Количество совпадений
одного номера шара и порядкового номера извлечения равно ![]() ; количество совпадений
двух номеров –
; количество совпадений
двух номеров – ![]() ; трех номеров –
; трех номеров – ![]() ; … ; М номеров –
; … ; М номеров – ![]() . Общее
количество способов извлечения М шаров равно
. Общее
количество способов извлечения М шаров равно ![]() . Таким образом получаем
вероятность события С:
. Таким образом получаем
вероятность события С:
![]()
![]() .
.
Для М = 10 получим
![]()
Найдем предельное значение вероятности:
![]() 0
0
Задача 8
Дана плотность
распределения р(х) случайной величины ![]() . Найти
. Найти
a)
параметр ![]() ;
;
b)
функцию
распределения ![]() случайной величины
случайной величины![]() ;
;
c)
вероятность
выполнения неравенства ![]() .
.
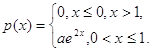 ,
, ![]() .
.
Решение:
a)
найдем значение
параметра из ![]()
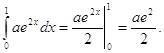
![]()
b)
![]()
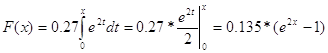 .
. ![]()
c)
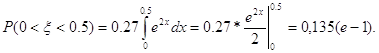
Задача 9
Случайная величина ![]() имеет
плотность распределения
имеет
плотность распределения ![]() . Найти плотность распределения
вероятностей
. Найти плотность распределения
вероятностей ![]() случайной величины
случайной величины ![]()
![]() =
= ![]() ,
, ![]()
Решение:
Найдем ![]() по формуле
по формуле
![]() =
= ![]()
![]() .
.
Найдем ![]()
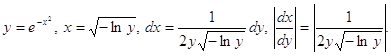
![]() =
= ![]()
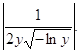
Ответ: ![]() =
= ![]()
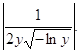
ия
номера шара и порядкового номера извлечения при одном выстреле равна 1 -
р1_________________________________________
ВЫВОДЫ
Корреляция и корреляционные моменты являются достаточно важными понятиями, имеющими применение как в теории вероятностей и ее приложениях, так и в математической статистике.
Многие задачи практики решаются с помощью вычисления коэффициента корреляции или корреляционных моментов. Корреляционный момент – характеристика системы случайных величин, описывающая рассеивания случайных величин и связь между ними. Степень зависимости случайных величин удобнее характеризовать посредством безразмерной величины – коэффициента корреляции.
Обработка статистических данных уже давно применяется в самых разнообразных видах человеческой деятельности. Основными задачами корреляционного анализа являются оценка силы связи и проверка статистических гипотез о наличии и силе корреляционной связи. Корреляционный анализ считается одним из главных методов в маркетинге, наряду с оптимизационными расчетами, а также математическим и графическим моделированием.
СПИСОК ЛИТЕРАТУРЫ
1. Ивашев-Мусатов О.С. Теория вероятностей и математическая
статистика., М.: Наука, 1979.
2. Вентцель Е.С., Овчаров Л.А. Теория вероятностей.–М.:Наука, 1969.
3. В.А. Колемаев, О.В. Староверов, В.Б. Турундаевский. Теория
вероятностей и математическая сатистика. М., 1991.
4. «Теория Статистики» под редакцией Р.А. Шмойловой/ «ФиС», 1998.
5. А.А. Френкель, Е.В. Адамова «Корреляционно регрессионный анализ в экономических приложениях»/ М., 1987.
6. И.Д.Одинцов «Теория статистики»/ М., 1998.
© 2010 Интернет База Рефератов