Курсовая работа: Решение систем нелинейных уравнений методом Бройдена

Федеральное агентство по образованию

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

Факультет автоматики и электромеханики

Кафедра «Автоматизированные и вычислительные системы»

Специальность «Вычислительные машины, комплексы, системы и сети»

КУРСОВАЯ РАБОТА

по дисциплине «Вычислительная математика»

Тема работы «Решение систем нелинейных уравнений методом Бройдена»

Воронеж 2009

РЕФЕРАТ

Пояснительная записка 26 с., 14 рисунка, 2 источника. Ключевые слова: МЕТОД БРОЙДЕНА, РЕШЕНИЕ СИСТЕМ МЕТОДОМ БРОЙДЕНА, РЕШЕНИЕ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ.

Объект исследования или разработки – решение систем нелинейных уравнений методом Бройдена.

Цель работы – создать программу, иллюстрирующую решение систем нелинейных уравнений методом Бройдена и исследовать результат ее работы.

Полученные результаты – листинг полученный программы, проверка соответствия найденных решений точным решениям заданной системы нелинейных уравнений.

Основные конструктивные, технологические и технико-эксплуатационные характеристики - персональная ЭВМ.

Содержание

Реферат

Введение

1. Алгоритм бройдена

1.1 Входные данные для алгоритма Бройдена

1.2 Содержание алгоритма Бройдена

1.3 Метод исключения Гаусса для решения СЛАУ

1.4 Вывод формулы пересчета Бройдена

2. Разработка программы и иследование результата ее работы

Заключение

Список литературы

Приложение

ВВЕДЕНИЕ

Необходимость в решении систем нелинейных уравнений возникает как самостоятельная задача при моделировании нелинейных объектов, а также как промежуточный этап при решении ряда других задач, например, при решении систем обыкновенных дифференциальных уравнений неявными методами или при решении нелинейных краевых задач.

В общем виде задача решения системы нелинейных уравнений ставится так: найти вектор , превращающий систему уравнений

где - нелинейные функции от , в тождество.

Все численные методы решения нелинейного уравнения исходят из того, что решение либо единственно во всей области, либо требуемое решение лежит в известной области. При решении практических задач такая информация обычно поступает от постановщика задачи, который может примерно характеризовать область предполагаемого решения.

Для большинства практических задач отсутствует аналитическое выражение для функции , а значит, и для . В этом случае приходится прибегать к аппроксимации якобиана. Одним из способов такой аппроксимация является метод Бройдена [1].

В курсовой работе будет рассматриваться метод решения Бройдена для систем нелинейных уравнений.

1. АЛГОРИТМ БРОЙДЕНА.

1.1 Входные данные для алгоритма Бройдена

Входными данными для алгоритма Бройдена являются вектор начального решения, начальная матрица Якоби и заданная точность.

1.2 Содержание алгоритма Бройдена

Пусть необходимо решить систему уравнений с начальным вектором . Основной сложностью при использовании метода Бройдена является выбор начальной аппроксимации матрицы Якоби. На практике для обеспечения хорошего начала итерационного процесса один единственный раз используют конечно-разностную аппроксимацию производных, а на следующих шагах матрица аппроксимируется по методу Бройдена.

Для начального вектора формируется матрица Якоби на основе конечно-разностной аппроксимации производных и аналогично методу Ньютона находится вектор очередного приближения из решения системы уравнений. . На следующих шагах поиска матрица Якоби рассчитывается по формуле пересчета Бройдена

где . И весь процесс поиска решения повторяем по той же самой схеме до тех пор, пока не будет получено решение c заданной точностью [1].

Поскольку необходимо решить линейное уравнение, то рассмотрим метод решения Гаусса.

1.3 Метод исключения Гаусса для решения СЛАУ

Суть всех методов исключения состоит в приведении исходной системы уравнений к системе более простого вида, для которой легко найти решение. К этим методам можно отнести метод исключения Гаусса, который имеет много вычислительных схем и, как показали исследования, является идеальным алгоритмом для решения СЛАУ.

Рассмотрим сначала самую простую схему – схему единственного деления. Применение схемы единственного деления продемонстрируем на примере СЛАУ 4- го порядка

Разделив первое уравнение системы на , получим

Из второго уравнения системы вычтем первое, умноженное на коэффициент при , то есть на . В результате получаем:

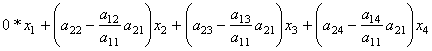
Поступая таким же образом с третьим и последующими уравнениями системы, получим

;

К выделенной системе применим тот же алгоритм, что и к исходной. В результате получаем

Прямой ход метода Гаусса закончен. Из полученной треугольной системы линейных алгебраических уравнений обратным ходом Гаусса отыскиваем вектор решения по следующим формулам

, , .

1.4 Вывод формулы пересчета Бройдена

В процессе построения методов Ньютона и секущих решения нелинейного скалярного уравнения
функция f(x) в окрестности текущей точки подменяется линейной функцией (аффинной моделью)

. Приравнивание к нулю последней, т.е. решение линейного уравнения , порождает итерационную формулу для вычисления приближений к корню уравнения.

Если потребовать, чтобы заменяющая функцию f(x) вблизи точки аффинная модель имела в этой точке одинаковую с ней производную, то, дифференцируя, получаем значение коэффициента , подстановка которого в приводит к известному методу Ньютона. Если же исходить из того, что наряду с равенством должно иметь место совпадение функций f(x) и в предшествующей точке т.е. из равенства , , получаем коэффициент , превращающий в известную формулу секущих.

Равенство , переписанное в виде , называют соотношением секущих в Оно легко обобщается на n -мерный случай и лежит в основе вывода метода Бройдена. Опишем этот вывод.

В n-мерном векторном пространстве соотношение секущих представляется равенством

где - известные n-мерные векторы, - данное нелинейное отображение, а - некоторая матрица линейного преобразования в . С обозначениями , соотношение секущих в обретает более короткую запись . Аналогично одномерному случаю, а именно, по аналогии с формулой , будем искать приближения к решению векторного уравнения по формуле . Обратимую n x n-матрицу в ней нужно подобрать так, чтобы она удовлетворяла соотношению секущих . Но это соотношение не определяет однозначно матрицу : глядя на равенство , легко понять, что при n>1 существует множество матриц , преобразующих заданный n-мерный вектор в другой заданный вектор (отсюда - ясность в понимании того, что могут быть различные обобщения одномерного метода секущих).

При формировании матрицы будем рассуждать следующим образом. Переходя от имеющейся в точке аффинной модели функции F(x) к такой же модели в точке мы не имеем о матрице линейного преобразования никаких сведений, кроме соотношения секущих . Поэтому исходим из того, что при этом переходе изменения в модели должны быть минимальными. Эти изменения характеризует разность . Вычтем из равенства определяющее равенство и преобразуем результат, привлекая соотношение секущих . Имеем:

Представим вектор в виде линейной комбинации фиксированного вектора определенного в , и некоторого вектора t, ему ортогонального: ,

Подстановкой этого представления вектора в разность получаем другой ее вид

Анализируя выражение , замечаем, что первое слагаемое в нем не может быть изменено, поскольку - фиксированный вектор при фиксированном k. Поэтому минимальному изменению аффинной модели будет отвечать случай, когда второе слагаемое в будет нуль-вектором при всяких векторах t, ортогональных векторам , т.е. следует находить из условия

Непосредственной проверкой убеждаемся, что условие будет выполнено, если матричную поправку взять в виде одноранговой nхn-матрицы .

Таким образом, приходим к так называемой формуле пересчета С. Бройдена

2. РАЗРАБОТКА ПРОГРАММЫ И ИСЛЕДОВВАНИЕ РЕЗУЛЬТАТА ЕЕ РАБОТЫ

Задача. Разработать программу, реализующую метод Бройдена.

Структура программы. Программа была разработана в интегрированной среде разработке приложений Microsoft Visual Studio 2008 на языке программирования C#, проект программы Console Application. В ходные данные программы начальный вектор решения, начальная матрица Якоби и удовлетворяющая погрешность. Программа решает систему уравнений 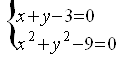. Если программа не находит решения удовлетворяющего требуемой точности за 10 итераций, то поиск решения прекращается, а так же если процесс расходится (в соответствии с приложением А).

Введем матрицу Якоби , погрешность 0,3 начальное решение является точным решение. На 1 итерации получаем результат решения (рисунок 1).

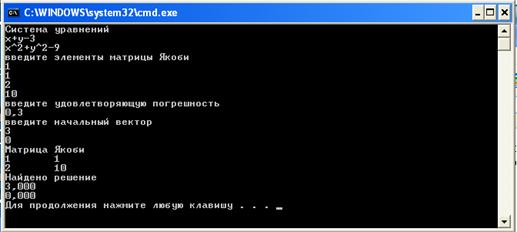
Рисунок 1 – Первый пример работы программы

Результат точное решение на 1 шаге. Попробуем задать начальное решение отличное от точного (рисунок 2).

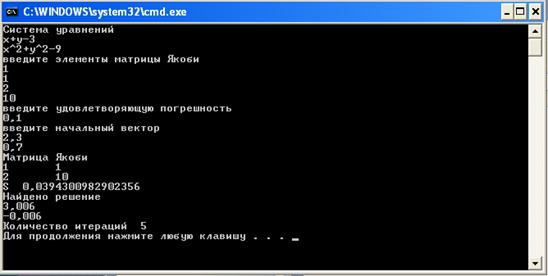
Рисунок 2 – второй пример работы программы

Получили близко решение к точному решению. Попробуем уменьшить погрешность (рисунок 3).

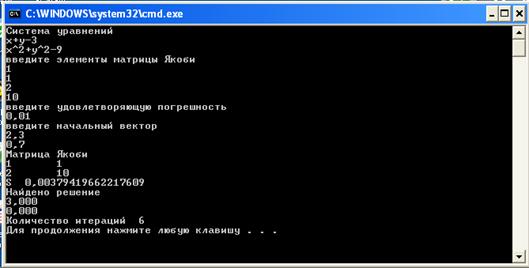
Рисунок 3 – третий пример работы программы

Получили точное решение. Попробуем сильнее отойти в начальном решении от точного (рисунок 4).

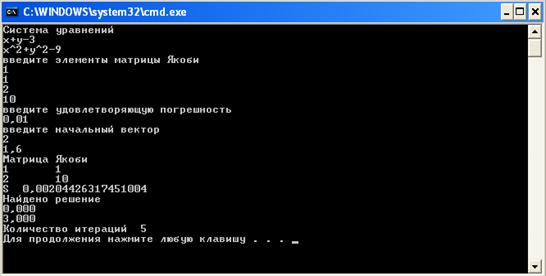
Рисунок 4 – Четвертый пример работы программы

Получаем точное решение. Уменьшим погрешность и сильнее отойдем от точного решения. Теперь начальное решение произвольное (рисунок 5).

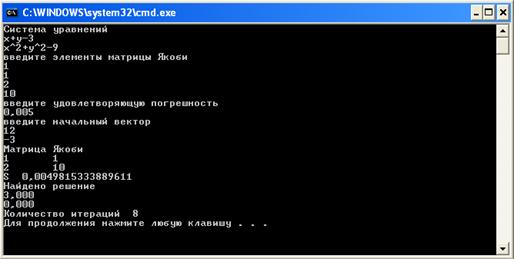
Рисунок 5 – Пятый пример работы программы

Видим увеличение количества итераций. Решение получили точное. Немного изменим начальную матрицу Якоби (рисунок 6).

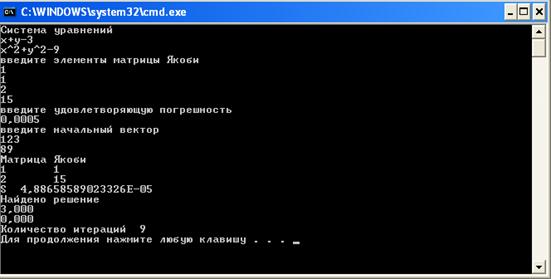
Рисунок 6 – Шестой пример работы программы

Увеличение количества итераций. Решение точное. Теперь возьмем другую матрицу Якоби (рисунок 7).

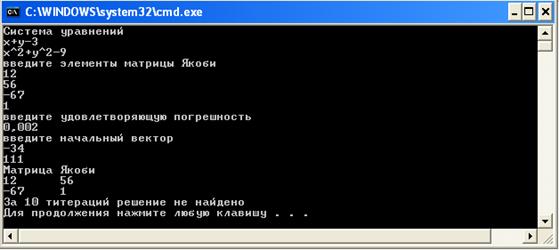
Рисунок 7 – Седьмой пример работы программы

Получили плохой результат решения. Попробуем выяснить из-за чего. Или матрица Якоби в начале исследования была близка к расчетной матрицы Якоби на основе конечно разностной аппроксимации производных или при таком начальном решении требуется слишком много итераций.

Попробуем с начальной матрицей Якоби. Процесс решения стал расходится. Делаем вывод, что не смогли найти решения из-за начального решения (рисунок 8).

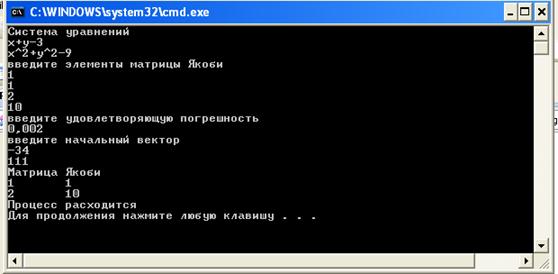
Рисунок 8 – Восьмой пример работы программы

На основе рисунка 9, рисунка 10 и рисунка 11 видим, что наша первая матрица Якоби была удачно выбрана.

Матрица Якоби близка к первой матрице Якоби (рисунок 12).

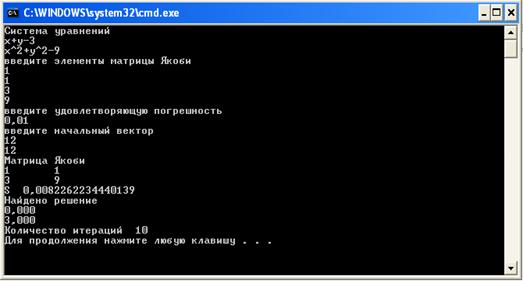
Рисунок 9 – Девятый пример работы программы

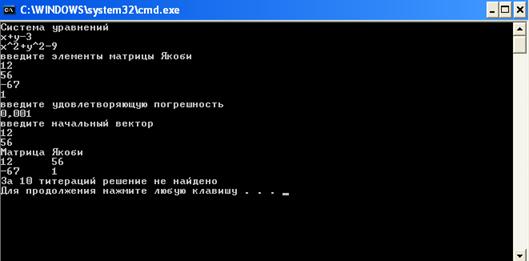
Рисунок 10 – Десятый пример работы программы

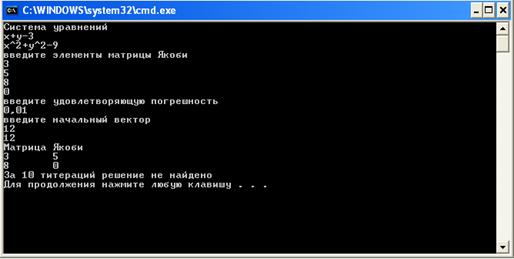
Рисунок 11 – Одиннадцатый пример работы программы

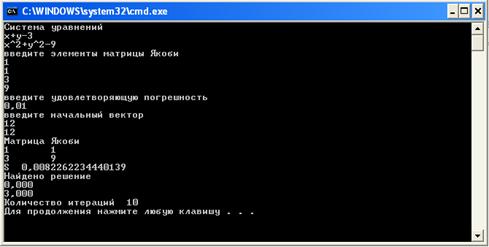
Рисунок 12 – Двенадцатый пример работы программы

Попробуем изменить систему уравнений, решаемую программой и посмотрим на результаты работы программы (рисунок 13,14).

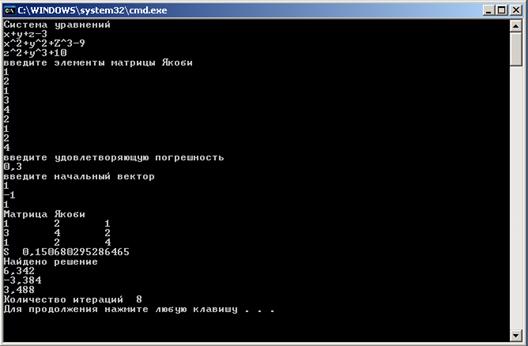
Рисунок 13 – Тринадцатый пример работы программы

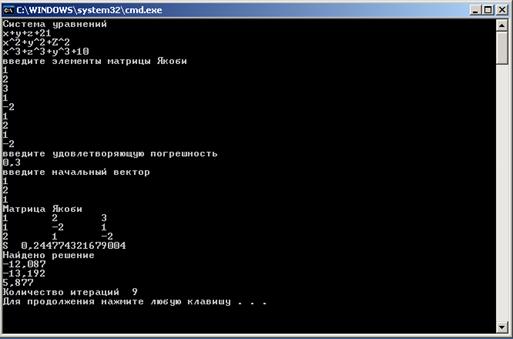
Рисунок 14 – Четырнадцатый пример работы программы

ЗАКЛЮЧЕНИЕ

Если начальное приближение выбрано достаточно близко к решению и если начальная аппроксимация матрицы Якоби достаточно точна, то метод Бройдена обладает сверхлинейной сходимостью, но не квадратичной, как метод Ньютона.

Данная курсовая работа выполнена в полном объеме. В курсовой работе был рассмотрен метод Бройдена, написана программа реализующая его.

СПИСОК ЛИТЕРАТУРЫ

1. С.Л. Подвальный, Л.В. Холопкина. Вычислительная математика- учебное пособие ВГТУ, 2004 - 147 с.

2. Методы решения систем нелинейных уравнений. Метод Ньютона. Его реализации и модификации. - Электрон. дан. – Режим доступа: www.exponenta.ru/educat/referat/XVkonkurs/15/index.asp.

ПРИЛОЖЕНИЕ

Текст программы

/*программа предназначена для решения системы нелинейных уравнений.

Программа выполнена 1 ноября 2009 года. Обем необходимой памяти для работы составляет 124 КБ. Версия программы №1.Автор Харитонова Яна Андреевна.*/

using System;

using System.Collections.Generic;

using System.Linq;

using System.Text;

namespace Broiden

{

class Program

{

static void Main(string[] args)

{

int N = 2;

Console.WriteLine("Система уравнений");

Console.WriteLine("x+y-3" + "\n" + "x^2+y^2-9");

double[,] yakob = new double[N, N];

Console.WriteLine("введите элементы матрицы Якоби");

for (int i = 0; i < N; i++)

{

for (int j = 0; j < N; j++)

{

yakob[i, j] = Convert.ToDouble(Console.ReadLine());

}

double[] V = new double[N];

double[] B = new double[N];

double[] Bnach = new double[N];

double e;

Console.WriteLine("введите удовлетворяющую погрешность ");

e = Convert.ToDouble(Console.ReadLine());

Console.WriteLine("введите начальный вектор");

for (int i = 0; i < N; i++)

{

[i] = Convert.ToDouble(Console.ReadLine());

}

int maunI = 0;

int naid = 0;

int stop = 0;

double S=0;

Console.WriteLine("Матрица Якоби");

for (int i = 0; i < N; i++)

{

for (int j = 0; j < N; j++)

{

Console.Write(yakob[i, j] + "\t");

}

Console.WriteLine();

}

while ((maunI != 10) && (naid != 1) && (stop != 1))

{

maunI++;

Bnach[0] = V[0] + V[1] - 3;

Bnach[1] = V[0] * V[0] + V[1] * V[1] - 9;

int iter = 0;

double[,] A = new double[N, N];

for (int i = 0; i < N; i++)

{

for (int j = 0; j < N; j++)

{

A[i, j] = yakob[i, j];

}

while (iter != N - 1)

{

for (int h = 0; h < N; h++) { B[h] = Bnach[h] * (-1); }

double pomny = A[iter, iter];

for (int j = iter; j < N; j++)

{

A[iter, j] = A[iter, j] / pomny;

}

B[iter] = B[iter] / pomny;

for (int i = iter + 1; i < N; i++)

{

double zap = A[i, iter];

for (int j = iter; j < N; j++)

{

A[i, j] = A[i, j] - A[iter, j] * zap;

}

B[i] = B[i] - B[iter] * zap;

}

iter++;

}

double[] X = new double[N];

if (A[N - 1, N - 1] != 0)

{ X[N - 1] = B[N - 1] / A[N - 1, N - 1]; }

else X[N - 1] = 0;

double SYM = 0;

int l = N - 2;

for (int i = N - 2; i >= 0; i--)

{

SYM = 0;

for (int j = i + 1; j <= N - 1; j++)

{

SYM = SYM + A[i, j] * X[j];

}

if (A[i, l] != 0)

{ X[i] = (B[i] - SYM) / A[i, l]; }

else X[i] = 0;

l--;

}

double[] XJ = new double[N];

double promq = 0; double mq = 0; double nq = 0;

S = 0;

for (int i = 0; i < N; i++)

{

XJ[i] = V[i] + X[i];

if (X[i] >= 0)

{ promq = X[i] + promq; }

else {promq = -X[i] + promq; }

if (V[i] >= 0)

{ mq = mq + V[i]; }

else

{ mq = mq - V[i]; }

if (XJ[i] >= 0)

{ nq = nq + XJ[i]; }

else { nq = nq - XJ[i]; }

}

if (mq != 0) { S = promq / mq; }

else { S = promq / nq; }

if (S < 0) { S = -S; }

if (S < e)

{

Console.WriteLine("S "+S);

naid = 1;

Console.WriteLine("Найдено решение");

for (int i = 0; i < N; i++)

{

Console.WriteLine("{0:n3}", XJ[i]);

}

Console.WriteLine("Количество итераций " + maunI);

}

else

{

if (S > 20) { Console.WriteLine("Процесс расходится"); stop = 1; }

else

{

if (maunI = 10) { Console.WriteLine("За 10 титераций решение не найдено"); }

else

{

double[] Y = new double[N];

Y[0] = (XJ[0] + XJ[1] - 3) - Bnach[0];

Y[1] = (XJ[0] * XJ[0] + XJ[1] * XJ[1] - 9) - Bnach[1];

double[,] J = new double[N, N];

for (int i = 0; i < N; i++)

{

for (int j = 0; j < N; j++)

{

J[i, j] = yakob[i, j];

yakob[i, j] = 0;

}

double[] ymnMAS = new double[N]; double[] PRMAS = new double[N];

for (int i = 0; i < N; i++)

{

double Ymn = 0;

for (int j = 0; j < N; j++)

{

Ymn = Ymn + J[i, j] * X[j];

}

ymnMAS[i] = Ymn;

PRMAS[i] = Y[i] - ymnMAS[i];

}

double del = 0;

for (int i = 0; i < N; i++) { del = del + X[i] * X[i]; }

for (int i = 0; i < N; i++)

{

for (int j = 0; j < N; j++)

{

yakob[i, j] = J[i, j] + ((PRMAS[i] * X[j]) / del);

}

for (int i = 0; i < N; i++)

{ V[i] = XJ[i]; }

}