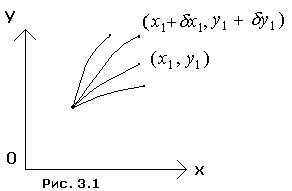Курсовая работа: Вариации при исчислении

Курсовая работа: Вариации при исчислении

1. Элементы вариационного исчисления

1.1 Понятие функционала и оператора

В курсе высшей математики вводилось понятие функции. Если некоторому числу x из области D ставится в соответствие по определенному правилу или закону число y, то говорят, что задана функция y = f(x). Область D называют областью определения функции f(x).

Если же функции y(x) ставится в соответствие по определенному правилу или закону число J, то говорят, что задан функционал J = J(y). Примером функционала может быть определенный интеграл от функции y(x) или от некоторого выражения, зависящего от y(x),

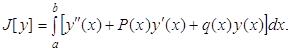
Если теперь функции y(x) ставится в соответствие по определенному правилу или закону вновь функция z(x), то говорят, что задан оператор z = L(y), или z = Ly.

Примерами дифференциальных операторов могут служить:

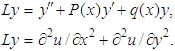
Дадим более строгое определение функционала. Пусть A множество элементов произвольной природы, и пусть каждому элементу u є A приведено в соответствие одно и только одно число J(u). В этом случае говорят, что на множестве A задан функционал J. Множество A называется областью определения функционала J и обозначается через D(J); число J(u) называется значением функционала J на элементе u. Функционал J называется вещественным, если все его значения вещественны. Функционал J называется линейным, если его область определения есть линейное множество и если

J (αu + βv) = αJ(u) + βJ(v).

1.2 Задачи, приводящие к экстремуму функционала

Задача о брахистохроне

Зарождение вариационного исчисления относят обычно к 1696 г., когда И. Бернулли поставил так называемую задачу о брахистохроне: точки А (0,0) и В (а, b) расположены в вертикальной плоскости (xy) (рис. 1). Какова должна быть кривая, лежащая в плоскости (xy) и соединяющая точки А и В, чтобы материальная точка, двигаясь без трения, скатывалась по этой кривой из точки А в точку В в кратчайшее время?

Искомая кривая и была названа брахистохроной.

Пусть уравнение кривой АВ есть y = u(x). Рассмотрим некоторый момент времени t, и пусть в этот момент движущаяся точка находится на расстоянии y от оси x. Тогда , где v скорость движущейся точки, g ускорение силы тяжести. В то же время

Отсюда

.

Обозначим через Т время, в течение которого материальная точка достигает точки В. Интегрируя, находим

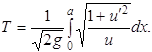                                                                         (1.1)

Задача сводится к следующему: надо найти функцию y = u(x), удовлетворяющую условию

u(0) = 0; u(а) = b (1.2)

и сообщающую интегралу (1.1) наименьшее значение. Условия (1.2) означают, что искомая кривая должна проходить через заданные точки А и В. Такого типа условия принято называть граничными, или краевыми, так как они относятся к концам промежутка, на котором должна быть определена искомая функция.

Примером применения кривой в виде брахистохроны служит образующая цилиндрических поверхностей, используемых на детских площадках, в аттракционах для спуска с возвышения, на трамплинах.

Задача о наибольшей площади

Сформулируем эту задачу так: среди всех плоских кривых, имеющих данную длину  и оканчивающихся в точках А (а, 0) и В (b, 0), найти кривую, ограничивающую вместе с отрезком [а, b] оси x область с наибольшей площадью.

Пусть уравнение кривой будет y = u(x). Задача заключается в том, чтобы найти функцию u(x), удовлетворяющую краевым условиям

u(а) = u(b) = 0     (1.3)

и тождеству

                                                                                   (1.4)

и сообщающую интегралу

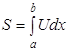                                                                                          (1.5)

наибольшее значение.

Общим для рассмотренных задач является то, что каждый раз ищется функция, удовлетворяющая тем или иным поставленным условиям и сообщающая экстремальное значение заданному функционалу.

Приведенные здесь задачи относятся к ветви математического анализа, называемой вариационным исчислением.

1.3 Постановка задачи вариационного исчисления

Задача вариационного исчисления состоит в следующем: дан функционал J с областью определения D(J); требуется найти элемент u0 є D(J), сообщающий функционалу либо минимальное значение

,                                                                             (1.6)

либо максимальное значение

.                                                                             (1.7)

Задача о максимуме функционала J тождественна с задачей о минимуме функционала – J, поэтому в дальнейшем будем рассматривать только задачу о минимуме функционала J.

В приведенной общей формулировке задачу вариационного исчисления решить вряд ли возможно, поэтому наложим на функционал J некоторые ограничения.

Будем считать, что D(J) есть часть некоторого пространства Х. Чтобы сформулировать дальнейшие ограничения, введем понятие линейного многообразия. Пусть М – линейное множество элементов пространства Х и ū – некоторый фиксированный элемент этого пространства. Линейным многообразием в пространстве Х назовем совокупность элементов, каждый из которых можно представить в виде

u = ū + η, ηєМ.    (1.8)

Если ūєМ, то, очевидно, так определенное линейное многообразие совпадает с М.

Требование 1. Область определения D(J) функционала J есть линейное многообразие.

Будем считать также, что пространство Х бесконечномерно. Тогда в Х линейное множество М также бесконечномерно и, следовательно, из него можно выделить конечномерное подпространство.

Требование 2. Если η пробегает любое конечномерное подпространство, содержащееся в М, то на этом подпространстве функционал J(u) = J (ū + η) непрерывно дифференцируем достаточное число раз.

Введем понятие об абсолютном и относительном минимуме функционала. Функционал J достигает на элементе u0 є D(J) абсолютного минимума, если неравенство

J(u0) = J(u) (1.9)

Справедливо для любого элемента u є D(J). Тот же функционал достигает на элементе u0 относительного минимума, если неравенство (9) справедливо для элементов u є D(J), достаточно близких к u0.

Абсолютный минимум называют еще сильным минимумом, а относительный – слабым.

Существует аналогия между нахождением минимума функции и минимума функционала. При нахождении минимума функции первая производная функции приравнивается к нулю и находится точка, подозрительная на экстремум. Затем с помощью второй производной проверяется достаточное условие экстремума. При нахождении минимума функционала находится первая вариация функционала и приравнивается к нулю. В результате получаем необходимое условие экстремума функционала. Для проверки достаточного условия экстремума функционала находится вторая вариация функционала.

1.4 Первая вариация и градиент функционала

Будем рассматривать функционал J, подчиненный требованиям 1, 2. Возьмем произвольный элемент u є D(J) и произвольный элемент η М. Обозначим через α произвольное вещественное число. Нетрудно видеть, что элемент

u + αη є D(J).       (1.10)

Составим выражение J (u + αη). В силу требования 2 J (u + αη) есть непрерывно дифференцируемая функция от α. Вычислим ее производную и возьмем значение этой производной при α = 0

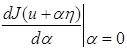.                                                                             (1.11)

В результате получим число, которое можно рассматривать как значение функционала (11), зависящего от двух элементов u и η.

Определение. Функционал

называется первой вариацией функционала J на элементе u и обозначается символом δJ (u, η):

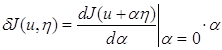.                                                          (1.12)

При этом разность двух функций u є D(J) и u1 D(J) называют вариацией функции u и обозначают δu = u(х) – u1 (х).

Пример. Найти первую вариацию функционала

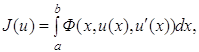                                                                (1.13)

область определения которого D(J) состоит из функций, удовлетворяющих следующим условиям: uС(1) [a, b] и

u(а) = А, u(b) = В,        (1.14)

где А и В-заданные постоянные. Условия (14) означают, что кривые у = u(х), где uD(J), проходят через две фиксированные точки (а, А) и (b, В).

Несложно показать, что функционал (13) удовлетворяет оговоренным выше двум требованиям, кроме того, он удовлетворяет требованию 3.

Требование 3. Вариация δJ (u, η) – не только однородный, но и аддитивный функционал от η.

Составим вариацию функционала (1.13)

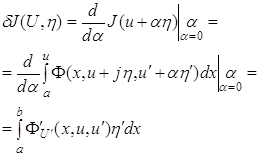                                                    (1.15)

Можно показать, что интеграл:

                                                                                (1.16)

есть ограниченный функционал от η, при этом считаем, что η(х) непрерывно дифференцируема и удовлетворяет условиям:

η(а) = η(b) = 0.    (1.17)

В этом случае интеграл (1.16) можно взять по частям

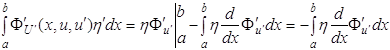
Таким образом, интеграл (1.15) можно записать в виде

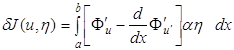.                                                        (1.18)

Здесь u + αη – u = αη = δu u можно записать

                                                             (1.19)

Вариацию δJ (u, η) можно записать в виде

δJ (u, η) = (Рu, η).         (1.20)

Определение. Оператор Р, определенный формулой (1.20), называется градиентом функционала J(u) и обозначается символом

Р = grad J.

Если uD(Р), то вариацию функционала J(u) можно записать в виде

δJ (u, η) = (grad J(u), η)          (1.21)

Здесь взяли α = 1, чтобы не загромождать запись. В выражении (1.18)

.

1.5 Необходимое условие минимума функционала

Пусть функционал J достигает на некотором элементе u0 относительного минимума. Возьмем произвольный элемент ηМ и произвольное вещественное число α. По определению относительного минимума при достаточно малых значениях α

J(u0 + αη)J(u0)   (1.22)

Это неравенство означает, что функция одной вещественной переменной α, равная J(u0 + αη), имеет при α0 = 0 относительный минимум. Но тогда необходимо

или, что то же

δJ(u0, η) = 0         (1.23)

Если функционал в некоторой точке достигает минимума, то в этой точке первая вариация функционала равна нулю. В этом заключается необходимое условие экстремума функционала.

1.6 Уравнение Эйлера. Связь между вариационной и краевой задачами

Рассмотрим основную лемму вариационного исчисления.

Лемма Лагранжа.

Пусть f (х, у) – функция, непрерывная в области D с контуром Г. Если

η (х, у) dxdy = 0                                                           (1.24)

для любой функции η (х, у), непрерывной в области D вместе со своими частнымы производными до n-го порядка включительно и обращающейся в нуль на границе Г (η (х, у)|Г = 0), то

f (х, у) = 0.

Для примера, рассмотренного в 1.4, было получено в точке минимума функционала (1.13) условие

                                                       (1.25)

Исходя из леммы Лагранжа, можем записать

.                                                                               (1.26)

Если условие (1.25) записать в виде

,

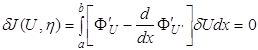то очевидно, что δu (вариация искомой функции) функция неравная нулю на отрезке (а, b), поэтому должно выполняться условие (1.26).

Уравнение (1.26) можно еще записать в виде

Уравнение (1.26) называют уравнением Эйлера. Если предположить существование непрерывной второй производной от u(х), то уравнение (1.26) можно записать в виде

.

Таким образом, условие минимума функционала (1.13) при условии (1.14) приводит к краевой задаче для уравнения Эйлера (1.26) при тех же условиях (1.14), т.е. Существует тесная связь между вариационной задачей о минимуме функционала и краевой задачей для уравнения Эйлера для этого функционала.

Решения уравнения Эйлера (1.26), удовлетворяющие условиям (1.14) называют экстремалями функционала (1.13).

1.7 Пути решения вариационных задач

Один из путей решения вариационной задачи, т.е. задачи нахождения минимума некоторого функционала J(u) при заданных краевых условиях, состоит в сведении этой задачи к краевой задаче для дифференциального уравнения при тех же краевых условиях, которое является уравнением Эйлера для этого функционала, с последующим решением этой задачи.

Второй путь решения вариационной задачи состоит в применении вариационных методов, которые позволяют приближенно найти функцию u0, дающую минимум функционалу J(u), и удовлетворяющую заданным краевым условиям.

Рассмотрим несколько примеров решения задач вариационного исчисления, основанных на нахождении уравнений Эйлера с последующим их решением.

Пример 1.

Найти функцию у = u(х), удовлетворяющую условию

u(0) = u(1) = 0     (1.27)

и дающую минимум функционалу

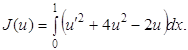                                                                  (1.28)

Будем считать, что функция u(х) непрерывна и имеет непрерывные производные до второго порядка включительно.

Уравнение Эйлера для функционала (28) будет иметь вид

                                                                                          (1.29)

Таким образом, получили краевую задачу для линейного дифференциального уравнения второго порядка с постоянными коэффициентами. Общее решение уравнения (1.29) будет иметь вид

.

Для нахождения произвольных постоянных с1 и с2 воспользуемся краевыми условиями (1.27). В результате получим

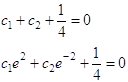
Откуда

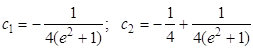
Следовательно, функция, дающая минимум функционалу (1.28) при условии (1.27), будет иметь вид

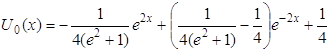.                                     (1.30)

Пример 2.

В качестве второго примера рассмотрим задачу о брахистохроне.

Как было показано ранее (см. 1.2.1), задача состоит в том, чтобы найти функцию у = u(х), удовлетворяющую условиям:

u(0) = 0, u(а) = b

и сообщающую минимум функционалу

.

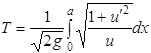В этом случае

.                                                                        (1.31)

Функция (31) при u = 0 терпит разрыв. Путем несложных рассуждений показывается, что все-таки можно воспользоваться уравнением Эйлера в виде (1.26).

Уравнение (1.26) приводится к виду

                                                                            (1.32)

Отсюда

.

Положим . Тогда .

Дифференцируя это выражение, получим . Замена  дает дифференциальное уравнение относительно

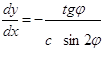
Далее

.

Положив , получим

.

Таким образом, если решение задачи о брахистохроне имеет решение, то это решение есть циклоида.

1.8 Вторая вариация функционала. Достаточное условие минимума функционала

Рассмотрим функцию  от вещественной переменной , считая  и фиксированными.

Эту функцию разложим в ряд Тейлора:

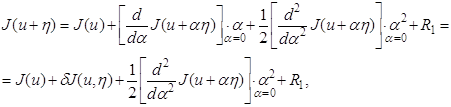             (1.34)

где R1 – остаточный член ряда.

Выражение

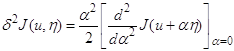
называется второй вариацией функционала J на элементе u.

Разложение (1.34) можно записать в виде

.                                  (1.36)

Пусть функционал J достигает минимума, относительного или абсолютного на элементе u0. Тогда , и формула (1.36) дает

.                                                     (1.37)

Из этого соотношения вытекает достаточное условие того, что элемент u0, удовлетворяющий уравнению Эйлера (экстремаль), сообщает функционалу минимальное значение. Для абсолютного минимума это условие имеет вид (учитывая, что

                                                           (1.38)

для относительного минимума оно состоит в том, что неравенство (1.38) выполняется, когда элемент  достаточно мал по норме.

Условие (1.38) в конкретных задачах трудно проверить, потому что величина  обычно неизвестна, и непосредственно им, как правило, воспользоваться не удается.

Поэтому для проверки достаточного условия экстремума функционала пользуются более простыми условиями.

Запишем вторую вариацию для функционала (1.13)

пользуясь определением второй вариации (1.35)

,

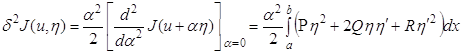где .

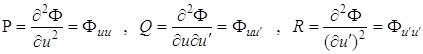Так как , то, предполагая наличие соответствующих производных у Ф, интегрируя по частям и принимая во внимание, что , получим

,                                                                 (1.39)

где .

Считаем, что необходимое условие экстремума выполнено, т.е.  и для определенности будем говорить о минимуме функционала (1.13). Функция , как функция переменной  при должна иметь минимум, следовательно, необходимым условием минимума является тот факт, чтобы  при любом выборе . Можно показать, что отсюда непосредственно вытекает, что вдоль экстремали должно иметь место равенство .

Условие

называют условием Лежандра.

Более сильное условие

называют усиленным условием Лежандра.

Рассмотрим интеграл, входящий в формулу (1.39), заменяя букву  буквой , получим

.

Уравнение Эйлера для этого интеграла будет иметь вид

,                                                                      (1.40)

причем, в этом уравнении есть коэффициент при  и в силу условия , деля обе части уравнения на R, получим уравнение вида

с непрерывными в [a, b] коэффициентами p(x) и q(x). Уравнение (1.40) называют уравнением Якоби.

Пусть - решение уравнения (1.40), удовлетворяющее начальным условиям

.

Существенным для дальнейшего будет тот факт, имеет ли решение  корни внутри промежутка [a, b]. Оказывается, что если такие корни имеются, то исследуемая экстремаль не может давать минимум функционалу (1.13).

Если при a < x < b, то говорят, что экстремаль u(x) в промежутке (a, b) удовлетворяет условию Якоби, а если  при , то говорят, что экстремаль u(x) удовлетворяет усиленному условию Якоби. Следует заметить, что коэффициенты S и R уравнения (1.40) зависят от экстремали u(x) и, следовательно, высказанные выше условия являются условиями, накладываемыми на экстремаль u(x).

Имеет место следующая теорема. Усиленные условия Лежандра и Якоби достаточны для того, чтобы экстремаль давала слабый (местный) экстремум функционалу (1.13).

Можно показать, что если выполнены усиленные условия Лежандра и Якоби и, кроме того,  положительно для всякого конечного p в некоторой области, содержащей экстремаль u(x) внутри, то эта экстремаль дает сильный (абсолютный) минимум.

Пример. Докажем, что экстремаль (1.30) (см Пример 1 в 1.8) дает функционалу (1.28) сильный минимум. Из (1.28) имеем

, , ,

Уравнение (1.40) принимает вид

его решение при условии ,  имеет вид

.

Функция  на отрезке  удовлетворяет усиленному условию Якоби, так как на этом отрезке она положительна. Так как 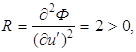 то и усиленное условие Лежандра выполняется. Следовательно, экстремаль (1.30) даёт функционалу (1.28) сильный (абсолютный) минимум.

1.9 Изопериметрическая задача

Изопериметрическая задача ставится следующим образом: Даны функционалы и постоянные ; среди элементов области определения D(J) функционала J, удовлетворяющего уравнениям

                                                                    (1.41)

требуется найти элемент, доставляющий функционалу J наименьшее значение.

Считается, что область

не пуста.

Частным случаем изопериметрической задачи является задача о наибольшей площади, поставленная в 2.2.

Здесь n=1.

                                          (1.42)

За D(J) можно принять множество тех функций из С [a, b], которые обращаются в нуль при x=a и x=b (условие 3), а за  – множество функций из С[1] [a, b], удовлетворяющих тем же условиям (1.3). Очевидно  пересечение не пусто. Будем считать, что функционалы удовлетворяют требованиям 1,2,3. Пересечение линейных многообразий само есть линейное многообразие, поэтому существует элемент  и линейное многообразие  такое, что любой элемент  имеет вид .

Будем считать, что множество  плотно в рассматриваемом пространстве.

Справедлива теорема, принадлежащая Эйлеру и известная под названием правила множителей для изопериметрической задачи.

Теорема Эйлера: Пусть элемент  решает изопериметрическую задачу. Если существуют такие элементы , что определитель

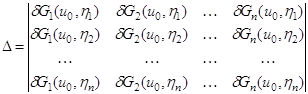                                          (1.43)

отличен от нуля, то найдутся такие постоянные , что

                                                           (1.44)

Рассмотренная теорема дает только необходимое условие минимума для изопериметрической задачи.

Техника решения изопериметрической задачи такова: составляя функционал

,                                                                                  (1.45)

где  – неизвестные постоянные, и составляем для этого функционала уравнение Эйлера. Оно содержит в качестве неизвестных элемент u0 и постоянные . Эти неизвестные определяются из уравнения Эйлера (1.41) и изопериметрических равенств (1.41).

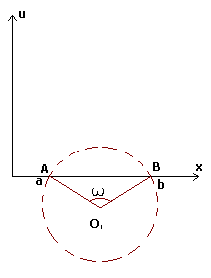
В качестве примера рассмотрим задачу о наибольшей площади (см. 2.2). В соответствии с теоремой Эйлера введем постоянный множитель  и составим функционал

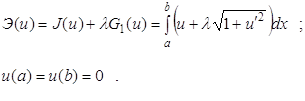
Уравнение Эйлера для функционала Э примет вид

Интегрирование дает

.

Отсюда

.

Интегрируя еще раз, придем к уравнению окружности радиуса

.                                                                      (1.46)

Таким образом, если решение существует, то это – дуга окружности. Для определения ее радиуса  и центра  имеем три уравнения

.

Пусть  будет угол, под которым виден отрезок AB из центра окружности (рис. 2):

.

Для определения  имеем уравнение

,

решение которого всегда возможно при указанном выше условии. Подставляя условия (1.3) в уравнение (1.46) находим . Найдя  из уравнения (1.46) найдем .

1.10 Минимизирующая последовательность

Пусть J-произвольный ограниченный снизу функционал. В этом случае существует нижняя грань его значений

.

Последовательность  элементов из D(J) называется минимизирующей для функционала J, если существует предел J(un), равный m.

Теорема 1: Функционал, ограниченный снизу, имеет по крайней мере одну минимизирующую последовательность.

Из определения нижней грани следует, что: 1) для любого элемента  справедливо равенство ; 2) для любого  существует такой элемент  из D(J), что . Положим  и обозначим 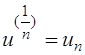. Тогда 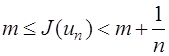, откуда следует, что .

Теорема 2: Пусть D(J) – линейное многообразие некоторого банахова пространства X. Если функционал J непрерывен в D(J) и существует предел минимизирующей последовательности , то элемент сообщает функционалу J минимальное значение.

Доказательство вытекает из непрерывности функционала

.

Теоремы 1, 2 создают возможность решать задачу о минимуме функционала, минуя уравнение Эйлера. Для этого надо прежде всего погрузить множество D(J) в такое банахово пространство X, в котором функционал J был бы непрерывен. Далее следует построить минимизирующую последовательность. Если она сходится, то ее предел решает вариационную задачу.

На этом построены численные вариационные методы (см 15) и обоснование их сходимости.

1.11 Функционал от функций, нескольких независимых переменных

Рассмотрим конечную область  в m-мерном Евклидовом пространстве. Будем считать, что граница Г области  состоит из конечного числа кусочно-гладких (m-1) – мерных поверхностей.

Рассмотрим функционал

                                                         (1.47)

при условии , где g(x) – заданная непрерывная функция на поверхности Г. Считаем, что выполнены требования 1, 2, 3.

Найдем первую вариацию функционала (1.47)

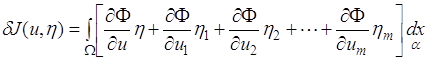                  (1.48)

Здесь обозначено

.

Пусть функция  такова, что существуют обобщенные производные

.

Тогда имеем

и, следовательно

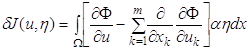                                                      (1.49)

В этом случае уравнение Эйлера для функционала (1.47) принимает вид

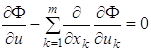,                                                           (1.50)

и называется уравнением Остроградского.

Пример.

Найти уравнение Эйлера для функционала

при краевом условии .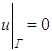

Пусть функция  подчиняется всем оговоренным выше условиям, тогда уравнение (1.50) принимает вид

.                                                                    (1.51)

1.12 Функционал от функций, имеющих производные высших порядков

Рассмотрим функционал вида

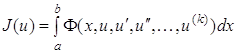.                                                       (1.52)

Будем считать, что функция  определена в области

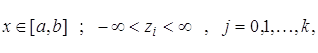
и в этой области k раз непрерывно дифференцируема.

Функционал (1.52) зададим на функциях , удовлетворяющих краевым условиям

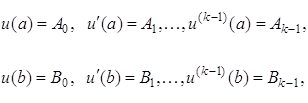                                          (1.53)

где Ai, Bi заданные постоянные. Возьмем функцию  в виде , чтобы удовлетворялись требования 1,2,3 и составим функционал

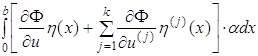                                                    (1.54)

Пусть функция такова, что  имеет обобщенную производную j-го порядка, тогда

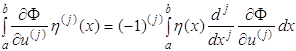
и, следовательно,

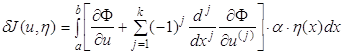                                   (1.55)

Откуда получим уравнение Эйлера

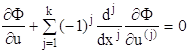                                                                  (1.56)

с краевыми условиями (1.53).

Сказанное выше переносится на случай функции многих независимых переменных. Для функционала

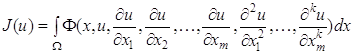                                 (1.57)

при краевых условиях

                                   (1.58)

где  – нормаль к Г.

Уравнение Остроградского будет иметь вид

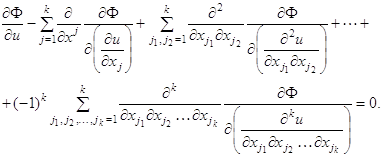                           (1.59)

Это уравнение должно решаться при краевых условиях (1.58)

Пример.

Выражение полной энергии деформации жесткой пластинки (плиты) при малых перемещениях, находящейся под действием поперечной нагрузки , представляет собой функционал вида

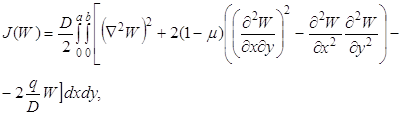                       (1.60)

где W (x, y) – прогиб пластинки; ;

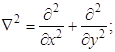 E,  – механические характеристики материала пластинки; h толщина пластинки.

Функция W (x, y) является непрерывной функцией, имеющую непрерывную производную до четвертого порядка включительно и все требования 1,2,3 будут выполнены.

При шарнирно-неподвижном закреплении краев пластинки должны выполняться условия

При x=0, x=a

                                                                            (1.61)

При y=0, y=b

                                                                            (1.62)

Получим уравнение Эйлера(Остроградского) для функционала (1.60) при краевых условиях (1.61), (1.62). Так как

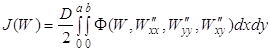
то уравнение Остроградского принимает вид

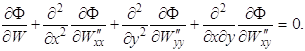                                          (1.63)

При этом

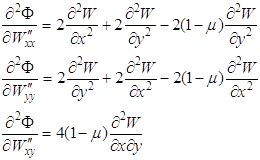
Поставив эти выражения в (1.63), получим уравнение Остроградского для функционала (1.60)

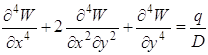.                                                             (1.64)

Уравнение (1.64) является уравнением равновесия рассматриваемой пластины и должно решаться при граничных условиях (1.61), (1.62).

1.13 Функционалы, зависящие от нескольких функций

Рассмотрим функционал

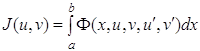                                                               (1.65)

Зададим его на парах  функций из  (непрерывных вместе со своей первой производной), удовлетворяющих краевым условиям

                                   (1.66)

где  – постоянные. Множество таких пар обозначим через D(J). Каждую такую пару будем называть вектором. За  и  возьмем функции из , удовлетворяющие условиям

Множество векторов , очевидно линейное, и D(J) есть линейное многообразие. Таким образом функционал (1.65) удовлетворяет требованиям 1,2,3.

Строим две функции, близкие к u(x) и v(x):

 и .

Подставив их в функционал (1.65), получим функцию  от  и . Найдем частные производные от  по  и  при :

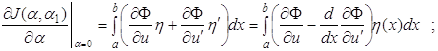
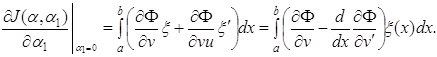
Первая вариация функционала (1.65) выражается формулой

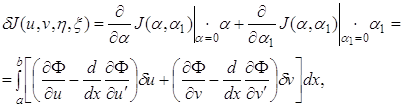
где .

Откуда получаем уравнения Эйлера для функционала (1.65) в виде системы двух дифференциальных уравнений

;                                                     (1.67)

Эти уравнения должны решаться при краевых условиях (1.66).

2. Вариационные задачи с подвижными границами

2.1 Простейшая задача с подвижными границами

В гл. 1 при исследовании функционала

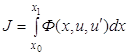
предополагается, что граничные точки  заданы.

Предположим теперь, что одна или обе граничные точки могут перемещаться, тогда класс допустимых кривых расширяется. Поэтому, если на какой-нибудь кривой  достигается экстремум в задаче с подвижными граничными точками, то экстремум тем более достигается по отношению к более узкому классу кривых, имеющих общие граничные точки с кривой , и, следовательно, должно быть выполнено основное, необходимое для достижения экстремума в задаче с неподвижными границами условие – функция  должна быть решением уравнения Эйлера:

.

Итак, кривые , на которых реализуется экстремум в задаче с подвижными границами, должны быть экстремалями.

Общее решение уравнения Эйлера содержит две произвольные постоянные, для определения которых необходимо иметь два условия. В задаче с неподвижными граничными точками такими условиями были

, .

В задаче с подвижными границами одно или оба эти условия отсутствуют и недостающие условия для определения произвольных постоянных общего решения уравнения Эйлера должны быть получены из основного необходимого условия экстремума , так как в задаче с подвижными границами экстремум достигается лишь на решениях  уравнения Эйлера, то в дальнейшем можно рассматривать значение функционала лишь на функциях этого семейства. При этом функционал  превращается в функцию параметров  и  и пределов интегрирования , , а вариация функционала совпадает с дифференциалом этой функции. Для упрощения будем считать, что одна из этих точек, например , закреплена, а другая  может перемещаться и переходить в точку , или, как обычно обозначают в вариационном исчислении, .

Допустимые кривые  и  будем считать близкими, если модули вариаций  и  малы и малы модули приращений  и .

Экстремали, проходящие через точку , образуют пучок экстремалей . Функционал  на кривых этого пучка превращается в функцию  и . Если кривые пучка не пересекаются, то этот функционал можно рассматривать как однозначную функцию  и  (рис. 3.1).

2.2 Условие трансверсальности

Вычислим вариацию функционала  на экстремалях пучка  при перемещении граничной точки из положения  в положение . Так как функционал  на кривых пучка превратился в функцию  и , то его вариация совпадает с дифференциалом этой функции. Выделим из приращения главную линейную по отношению к  и  часть:

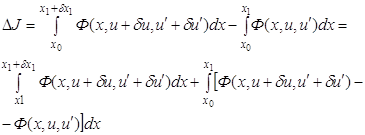  (3.1)

Первое слагаемое правой части преобразует с помощью теоремы о среднем значении:

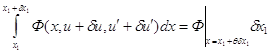, где .

В силу непрерывности функции  будем иметь:

,

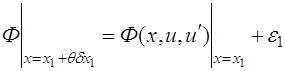где  при , .

Итак,

.

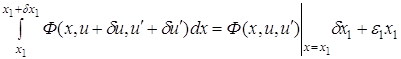Второе слагаемое (3.1) преобразуем путем разложения подинтегральной функции по формуле Тейлора

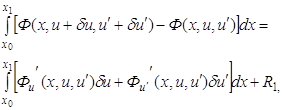
где  является бесконечно малой более высокого порядка, чем  или . В свою очередь линейная часть

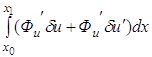
может быть преобразована путем интегрирования по частям второго слагаемого подинтегральной функции к виду

.

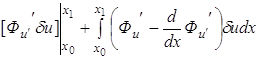Значение функционала берется лишь на экстремалях, следовательно

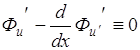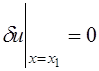. Так как граничная точка  закреплена, то . Следовательно,

.

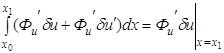Итак, окончательно имеем:

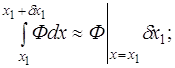
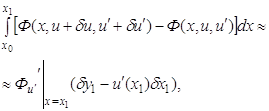
где приближенные равенства также справедливы с точностью до членов порядка выше первого относительно  и .

Таким образом

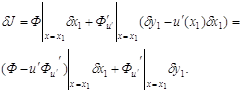
Основное необходимое условие экстремума  приобретает вид

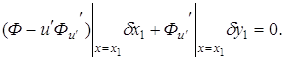                                               (3.2)

Если вариации  и  независимы, то получаем

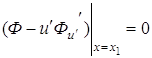 и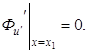

Однако чаще всего вариации  и  бывают зависимы. Пусть, например, правая граничная точка  может перемещаться по некоторой кривой

Тогда  и условие (3.2) принимает вид

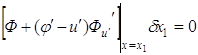
или, так как  изменяется произвольно, то

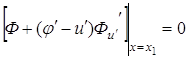.                                                                 (3.3)

Это условие устанавливает зависимость между угловыми коэффициентами  и  в граничной точке. Оно называется условием трансверсальности.

Условие трансверсальности совместно с условием  позволяет определить одну или несколько экстремалей пучка , на которых может достигаться экстремум.

Пример. Найти условие трансверсальности для функционалов вида

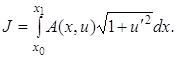
Условие трансверсальности (3.3) имеет в данном случае вид

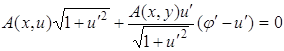
или

Полагая, что  в граничной точке, получим

или

.

Условие трансверсальности в данном случае свелось к условию ортогональности.

2.3 Задача с подвижными границами для функционалов от нескольких функций

Если при исследовании на экстремум функционала

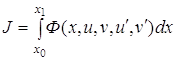                                                                     (3.4)

одна из граничных точек, например  перемещается (, ), а другая, , неподвижна, то экстремум может достигаться лишь на интегральных кривых системы уравнений Эйлера

,                                                 (3.5)

Общее решение системы уравнений Эйлера содержит четыре произвольные постоянные. Зная координаты граничной точки , которую считаем неподвижной, можно исключить две произвольные постоянные. Для определения двух других произвольных постоянных необходимо иметь еще два уравнения, которые могут быть получены из условия , при условии, что функционал задается лишь на решениях системы уравнений Эйлера (3.5). При этом функционал превращается в функцию координат  точки и вариация функционала превращается в дифференциал этой функции. Если экстремали пучка с центром в точке  не пересекаются, то эта функция будет однозначной.

Вычисление вариации  проводится аналогично тому, как это делалось в 3.2:

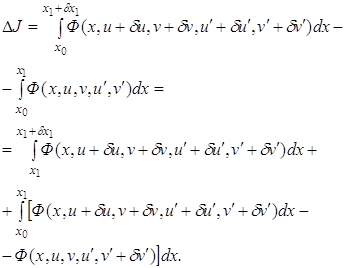
Применяя теорему о среднем значении к первому интегралу и учитывая непрерывность функции , выделив главную линейную часть с помощью формулы Тейлора во втором интеграле и используя равенства (3.5), получим

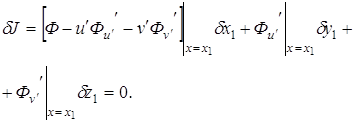                                 (3.6)

Откуда, учитывая зависимость , , , получим

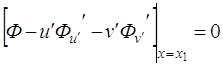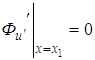,  и .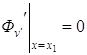

Если граничная точка  может перемещаться по некоторой кривой , , то

, , и условие  (3.6)

переходит в условие (считая  произвольным).

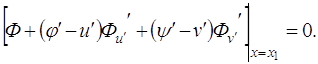                                        (3.7)

Это условие носит название условия трансверсальности в задаче об исследовании на экстремум функционала (3.4).

Условие (3.7) совместно с уравнениями ,  дает недостающие уравнения для определения произвольных постоянных в общем решении системы уравнений Эйлера.

Если граничная точка  может перемещаться по некоторой поверхности , то , причем вариации  и  произвольны. Следовательно, условие (3.6) в силу независимости  и  дает

,

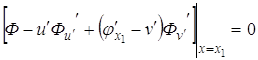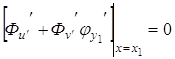                                                                     (3.8)

Если рассматривать функционал

,

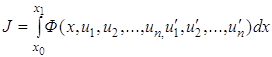то в случае одной подвижной точки  в этой точке

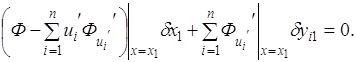
Пример. Найти условие трансверсальности для функционала

,

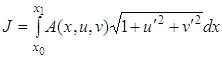если .

Условия трансверсальности (3.8) в данном случае имеют вид

 и  при  или  при  т.е. являются условиями параллельности вектора касательной  к искомой экстремали в точке  и вектора нормали  к поверхности  в той же точке. Следовательно, усливие трансверсальности становится в данном случае условием ортоганальности экстремали к поверхности .

1. Найти экстремаль функционала  при заданных краевых условиях на концах отрезка . Считается, что .

Пример 1.

, , .

Решение:

Вычислим первую вариацию функционала

.

После преобразования этого функционала получим

.

Произвольные функции  и удовлетворяют условию .

В точке  предполагаемого экстремума функционала  должно выполняться необходимое условие , поэтому уравнение Эйлера будет иметь вид

Это уравнение приводится к виду

и должно решаться при условии , .

Имеем

, , , ;

, ,

, , .

откуда , .

Таким образом, получаем решение .

Исследовать функционал , заданный на отрезке , на экстремум. При заданных краевых условиях считается, что .

Пример 2.

, , .

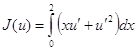Решение. Найдем первую вариацию функционала

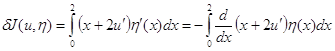
Необходимое условие экстремума функционала в точке  даёт уравнение Эйлера

.

Это уравнение при краевых условиях ,  дает решение

.

Так как в данном примере

, то

, , ,

и усиленное условие Лежандра

 выполняется.

Уравнение Эйлера для интеграла (1.39) (см. 1.8.) будет иметь вид (после замены  на )

или

Откуда

, .

Для нахождения ,  имеем условия , .

Откуда

, .

Проверим условие Якоби. Решение  на интервале  положительно. Следовательно, усиленное условие Якоби выполняется. Отсюда делаем заключение, что экстремаль  дает функционалу

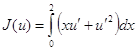
сильный (абсолютный) минимум.

1.  Гельфанд И.М., Фомин С.В. Вариационное исчисление. М.: Наука. 1961.

2.  Коршунов Ю.М., «Математические основы кибернетики», Москва, 1987 г.;

3.  Таха Х., «Введение в исследование операций», Москва, 1985 г.;

4.  Д. Сю., А. Мейер, «Современная теория автоматического управления и её применение», Машиностроение, 1972 г.;