
Рефераты по сексологии
Рефераты по информатике программированию
Рефераты по биологии
Рефераты по экономике
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Рефераты по авиации и космонавтике
Рефераты по административному праву
Рефераты по безопасности жизнедеятельности
Рефераты по арбитражному процессу
Рефераты по архитектуре
Рефераты по астрономии
Рефераты по банковскому делу
Рефераты по биржевому делу
Рефераты по ботанике и сельскому хозяйству
Рефераты по бухгалтерскому учету и аудиту
Рефераты по валютным отношениям
Рефераты по ветеринарии
Рефераты для военной кафедры
Рефераты по географии
Рефераты по геодезии
Рефераты по геологии
Рефераты по геополитике
Рефераты по государству и праву
Рефераты по гражданскому праву и процессу
Рефераты по делопроизводству
Рефераты по кредитованию
Рефераты по естествознанию
Рефераты по истории техники
Рефераты по журналистике
Рефераты по зоологии
Рефераты по инвестициям
Рефераты по информатике
Исторические личности
Рефераты по кибернетике
Рефераты по коммуникации и связи
Реферат: Динамическое программирование и вариационное исчисление
Реферат: Динамическое программирование и вариационное исчисление
Министерство образования РФ
Южно-Уральский государственный университет
Кафедра Автоматики и управления
Реферат
по математическим основам теории систем
на тему
Динамическое программирование и вариационное исчисление
Выполнил:
Группа: ПС-263
Проверил: Разнополов О. А.
Челябинск
2003
1. Динамические задачи оптимизации управления
1.1. Постановка задачи динамического программирования
Среди разнообразных задач кибернетики значительное место занимают задачи, в которых объект управления находится в состоянии непрерывного движения и изменения под воздействием различных внешних и внутренних факторов. Задачи управления такими объектами относятся к классу динамических задач управления.
Объект называется управляемым, если среди действующих на него разнообразных факторов имеются такие, распоряжаясь которыми, можно изменять характер его движения. Такие целенаправленные воздействия называются управлениями и обозначаются u(t).
Характер движения объекта управления определяется системой дифференциальных уравнений, которую удобно сокращенно записывать в векторной форме в виде одного дифференциального уравнения:
x(t)=g(x,u), x(0)=c.
Управление u(t) входит в уравнение, так что это уравнение определяет не просто конкретное движение объекта, а лишь его технические возможности, которые могут быть реализованы путем использования того или иного управления из пространства допустимых управлений U.
Оценить, насколько при том или ином способе управления достигаются поставленные цели, можно, как и раньше, путем введения целевой функции, которую в данном случае удобно записать в виде
J=J[x(t),x(t),u(t),t].
Так, если u(t) - мгновенный расход топлива, а x(t) - мгновенная скорость самолета, то с точки зрения расхода топлива качество управления в любой момент времени может быть охарактеризовано величиной J(t)=u(t)/x(t) (мгновенный расход топлива на единицу пути), которая, естественно, будет зависеть от состояния природы, т.е. от совокупности внешних факторов, определяющих условия полета.
Целевая функция в виде, записанном выше, используется редко, так как она дает оценку лишь мгновенных значений управляемого процесса, тогда как в большинстве задач бывает необходимо оценить процессы в объекте управления на протяжении всего времени управления от 0 до Т.
Во
многих случаях целевую функцию удается подобрать так, что оценку процесса в
объекте управления можно произвести путем интегрирования целевой функции за все
время управления, т.е. за критерий качества управления принять функционал J(u)=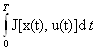 .
.
Так, если целевая функция имеет физический смысл потерь, то можно определяет суммарные потери за весь процесс управления.
Иногда в качестве цели управления удается задать желаемый ход процесса z(t). При этом в качестве целевой функции можно взять квадрат или абсолютное значение отклонения процесса x(t) от желаемого:
J=[x(t)-z(t)]2, J=| x(t)-z(t)| .
В этих случаях критерий качества управления будет определять полную квадратичную или абсолютную ошибку.
В динамических задачах управления наряду с ограничениями, определяющими пространство допусхидшх. управлений U, приходится иметь дело с интегральными ограничениями вида
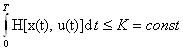 .
.
Весьма часто, например, приходится сталкиваться с необходимостью ограничения пределов изменения мгновенного значения некоторого параметра а(х,u) в процессе управления. Обозначим через a0 то значение параметра а, превышение которого является нежелательным. Если подынтегральную функцию H(х, u), называемую в данном случае функцией штрафа, определить из соотношения
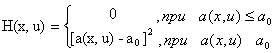
то интегральное ограничение будет выражать требование, чтобы мгновенное параметра а могло превышать а0 лишь кратковременно и на незначительную величину. Это условие будет выполняться тем жестче, чем меньше К. так, при К=0 ограничение вообще не будет допускать превышениен а над а0.
Такие ограничения возникают также тогда, когда приходится иметь дело с ограниченными ресурсами: может быть ограничено находящееся в распоряжении количество энергии, топлива,если речь идет о траекториях, и т.п.
Приведенные соотношения позволяют дать следующее определение оптимального управления в динамических системах. Оптимальным называется управление u*(t), выбираемое из прастранства допустимых управлений U, такое, которое для объекта, описываемого дифференциальным уравнением, минимизирует критерий качества при заданных ограничениях на используемые ресурсы.
1.2. Многошаговые процессы управления
1.2.1. Поведение динамической системы как функция начального состояния
Нахождение оптимального управления в динамических системах во многих случаях существенно облегчается, если процесс управления удается разбить естественным или искусственным путем на отдельные шаги или этапы. Для того чтобы вести рассмотрение в общем виде, будем считать, что состояние объекта описывается многомерной переменной х={x1,...,хn).
Предполагая, что процесс является неуправляемым и неопределенность в состоянии природы отсутствует, дифференциальное уравнение, определяющее движение объекта, запишем в виде: x(t)=g(x), x(0)=c.
Решение этого уравнения записывают обычно как х=х(t), чем подчеркивается зависимость решения от времени. Однако не менее важно то, что решение уравнения зависит от начального состояния с. Поэтому более строгой является такая форма записи, которая показывает явную зависимость решения х как от времени, так и начального состояния: х=х(c, t)=х[x(0), t].
Такая форма записи позволяет рассматривать состояние системы в произвольный момент времени t как некоторое преобразование начального состояния х(0)=с на интервале t.
Рассмотрим движение объекта на интервале от 0 до t2, который промежуточной точкой t1 разобьем на два интервала длительностью t1 и τ=t2-t1.
Рассмотрим три состояния объекта управления:
начальное состояние х(о) =с;
состояние х(с, t1) в промежуточный момент t1 ;
состояние х(с, t2) в конечный момент t2;
К описанию последнего состояния можно подойти двояким образом. Это состояние можно рассматривать или как преобразование начального состояния х(о)=с на интервале t2=t1+ τ: х(с, t2)= х(с, t1 + τ) или как преобразование состояния х(с, t1) на интервале τ: х(с, t2)= х[x(с, t1), τ].
Так как оба выражения описывают одно и то же состояние, то, приравнивая их, получаем соотношение: х(с, t1 + τ)=х[x(с, t1), τ].
1.2.2. Представление динамического процесса в виде последовательности преобразований
Предположим, что динамический процесс х(с, t) на интервале от 0 до tf может быть естественным или искусственным образом представлен как многошаговый, и найдем подходящий способ описания такого процесса. Для того чтобы получить многошаговый процесс, интервал от 0 до tf следует разбить на n последовательных шагов, длительности которых примем равными τ1,τ2,..., τn. Обозначим через tk(k=0,...,n) моменты окончания k-го шага так, что tk+1= tk+τk+1, а через xk - состояние объекта в момент tk: xk=x(c,tk).
Рассмотрим состояние xk+1=x(c,tk+1)=x(c,tk+τk+1). Это выражение в можно представить в виде: xk+1=x[x(c,tk),τk+1]=x(xk,τk+1).
Это соотношение представляет состояние объекта xk+1 как результат преобразования состояния xk на (k+1)-м шаге.
Введем в рассмотрение оператор Т, который будет означать преобразование состояния процесса за один шаг:
Т (xk) = x(xk, τk+1), k = 0,n-1. Тогда получим: xk+1=Т (xk).
Полагая k=0,n-1, можем описать весь динамический процесс в виде последовательности преобразований
x0=c , x1=Т (x0), , xn=Т (xn-1).
1.2.3. Многошаговый процесс управления
Динамический процесс, описываемый преобразованием xk+1=Т(xk), является неуправляемым. Для получения управляемого многошагового процесса необходимо иметь возможность на каждом шаге осуществлять не одно преобразование Т(хk), а одно из множества преобразований Тi(хk).
Удобно считать, что конкретный вид преобразования будет зависеть от параметра uk, который на k-м шаге может принимать одно из множества значений Uk. Параметр uk будем называть управлением, а множество Uk - пространством допустимых управлений на k-м шаге. Преобразование, осуществляемое на k-м шаге, теперь можно записать в виде
xk+1=Т(xk, uk), uk![]() Uk .
Uk .
Если в этом соотношении положить последовательно tk=0,n-1 и учесть начальное состояние х0, то получим описание всего управляемого многошагового процесса:
xk+1=Т(xk, uk), uk![]() Uk , tk=0,n-1, х0=x(0)=c.
Uk , tk=0,n-1, х0=x(0)=c.
Данное соотношение, называемое разностным уравнением объекта управления, аналогично дифференциальному уравнению, дающему описание непрерывного динамического процесса.
2. Оптимальное управление как вариационная задача
2.1. Математическая формулировка задачи оптимального управления
Характерной тенденцией в построении современных систем автоматического управления является стремление получать системы, которые в некотором смысле являются наилучшими. При управлении технологическими процессами это стремление выражается в том, чтобы улучать максимальное количество продукции высокого качества при ограниченном использовании ресурсов (сырья, энергии и т.п.). В системах управления кораблями, самолетами, ракетами стремятся минимизировать время, по истечении которого объект выходит в заданную точку или на заданную траекторию при ограничении угла отклонения рулей, количества расходуемого топлива и т. п. В следящих и стабилизирующих системах представляет интерес достижение максимальной точности при наличии всевозможных ограничений, накладываемых на координаты регулируемого объекта, исполнительные элементы и регулятор. Во всех этих примерах задачи управления сводятся к нахождению наилучшего в определенном смысле слова процесса из множества возможных процессов, т.е. относятся к классу динамических задач управления.
Как было
показано ранее, математическая формулировка динамических задач оптимального
управления сводится к следующему. Имеется объект управления, состояние которого
характеризуется многомерной переменной х={х1,…,xn}. Характер процессов в объекте управления можно изменять,
используя то или иное упвление u из
пространства допустимых правлений U. В общем случае управление u![]() U может быть также многомерной величиной u={u1,...,um}.
Характер движения объекта управления описывается системой дифференциальных
уравнений х=g (х, u), х (0)=с.
U может быть также многомерной величиной u={u1,...,um}.
Характер движения объекта управления описывается системой дифференциальных
уравнений х=g (х, u), х (0)=с.
За критерий качества управления принимается интегральная оценка вида
J(u)=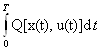 ,имеющая физический смысл потерь, где Т- время
протекания процесса управления, a Q[x(t), u(t)]=q(t) - мгновенные потери в момент t при состоянии системы x(t) и управлении u(t). Добавочными ограничениями могут
быть ограничения, накладываемые на количество ресурсов или пределы изменения
некоторых параметров, выражающиеся математически соотношением
,имеющая физический смысл потерь, где Т- время
протекания процесса управления, a Q[x(t), u(t)]=q(t) - мгновенные потери в момент t при состоянии системы x(t) и управлении u(t). Добавочными ограничениями могут
быть ограничения, накладываемые на количество ресурсов или пределы изменения
некоторых параметров, выражающиеся математически соотношением
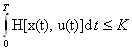 .
.
Как было установлено ранее, оптимальным называется такое управление u* из множества допустимых управлений U, при котором для объекта, описываемого дифференциальным уравнением, и заданных ограничениях на используемые ресурсы критерий качества управления принимает минимальное (максимальное) значение.
Сформулированная подобным образом задача оптимального управления относится к классу вариационных задач, решением которых занимается раздел математики, получивший название вариационного исчисления. Величина J(u) получила название функционала. В отличие от функции, например, f(x), численные значения которой задаются на множестве значений аргумента х, численные значения функционала J(u) задаются на множестве всевозможных управлений u(t). Задача нахождения оптимального управления сводится к тому, чтобы из множества допустимых управлений U выбрать такое, при котором функционал J(t) принимает минимальное численное значение.
2.2. Постановка вариационной задачи
Обычно задачи, требующие минимизации функционала, подчиненного дифференциальному соотношению, при наличии интегрального ограничения заменяются минимизацией нового функционала
J(u)=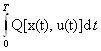 + λ
+ λ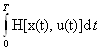 ,
,
подчиненного только дифференциальному соотношению. Параметр λ, в функционале, получивший название множителя Лагранжа, в задачах оптимизации управления играет роль «цены» ограниченных ресурсов. Его значение находится из граничных условий вариационной задачи.
Возможность упрощения вариационной задачи с интегральными ограничениями посредством введения множителей Лагранжа вытекает из следующей теоремы.
Теорема
1. Если u(t)-оптимальное управление, при котором функционал J(u)=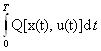 +λ
+λ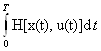 достигает абсолютного минимума и выполняется
ограничение
достигает абсолютного минимума и выполняется
ограничение 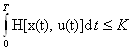 , тогда при u(t) достигается
абсолютный минимум функционала J(u)=
, тогда при u(t) достигается
абсолютный минимум функционала J(u)=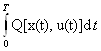 , подчиненного ограничению
, подчиненного ограничению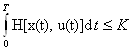 .
.
Доказательство:
следует от противного. Пусть v(t)-другое управление, отличное от u(t), причем такое, что 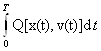 <
<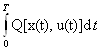
и
выполнено условие 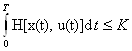 .
.
Тогда 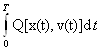 +λ
+λ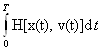 ≤
≤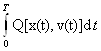 +λK<
+λK<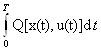 +λK=
+λK=
= +λ
+λ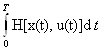 , что противоречит предположению, что u(t) обращает J(u)=
, что противоречит предположению, что u(t) обращает J(u)=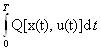 +λ
+λ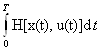 в минимум.
в минимум.
Важнейшим понятием вариационного исчисления является понятие вариации функции, которое при исследовании функционалов играет такую же роль, как дифференциал при исследовании функций.
Пусть f(x) – функция, непрерывная на интервале [a,b]. Рассмотрим внутреннюю точку х этого интервала и некоторое фиксированное значение дифференциала аргумента функции ∆x=dx. Разность f(x+∆x)-f(x)=df(x)=f(x)∆x называется дифференциалом функции f(x) в точке х. Как известно, условие df(x)=0 является необходимым условием минимума (максимума) функции f(x) в точке х.
Получим аналогичные соотношения в вариационноми исчислении.
Рассмотрим задачу с закреплёнными концами при фиксированном времени.
Пусть задана некоторая целевая функция
J=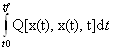 à min,
при условиях x(t0)=x0 , x(tf)=xf , t
à min,
при условиях x(t0)=x0 , x(tf)=xf , t ![]() [t0,tf], x(t)
[t0,tf], x(t)![]() Rn, причём x(t) непрерывна, и дифференцируема.
Rn, причём x(t) непрерывна, и дифференцируема.
Пусть у нас имеется оптимальное решение x(t)=x*(t).
Проведём
сдвиг от этого решения: выберем произвольную функцию η(t),
такую, что η(t0)=η(tf)=0, η(t)![]() Rn ,причём η(t) непрерывна, и дифференцируема.
Rn ,причём η(t) непрерывна, и дифференцируема.
Тогда наше решение запишется как
x(t)=x*(t)+εη(t) и
соответственно x(t)=x*(t)+εη(t), где ε=[ε1,…,εn]T , ε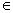 Rn, εi=const.
Rn, εi=const.
Таким образов выражение εη(t) есть не что иное, как ∆x для функции f(x), εη(t) называется вариацией функционала.
При фиксированных x(t) и η(t), наша целевая функция буде функцией от ε:
J(ε)=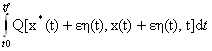 à min,
à min,
Решение этого уравнение известно, т.к. это будет достигаться при ε=0,x(t)=x*(t).
Разложим функцию J(ε) в ряд Тейлора в точке ε=0n:
J(ε)=J(0n)+![]() J(ε)ε +
J(ε)ε +![]()
![]() 2J(ε)ε2 + o(∆x).
2J(ε)ε2 + o(∆x).
Необходимое условие минимума J(ε)-J(0n) ≥0, тогда получим
J(ε)-J(0n)=![]() J(ε)ε +
J(ε)ε +![]()
![]() 2J(ε)ε2 + o(∆x) ≥0.
2J(ε)ε2 + o(∆x) ≥0.
Для того, чтобы неравенство выполнялось первое слагаемое должно равняттся нулю (т.к. оно может принимать как положительные, так и отрицательные значения):
![]() J(ε)=δJ=0
I необходимое условие экстремума
функционала.
J(ε)=δJ=0
I необходимое условие экстремума
функционала.
Если это условие выполняется, то получим
J(ε)-J(0n)=![]()
![]() 2J(ε)ε2 + o(∆x) ≥0,
2J(ε)ε2 + o(∆x) ≥0,
отбросим члены малости больше 2.
![]() 2J(ε)= δ2 J ( ≥ 0, ≤ 0)
2J(ε)= δ2 J ( ≥ 0, ≤ 0)
– второе необходимое условие экстремума функционала.
В вариационном исчислении условие δJ=0 используется для получения так называемого дифференциального уравнения Эйлера, среди множества решений которого и определяется затем управление u(t), обращающее в минимум функционал.
Применим выше изложенные рассуждения для вывода дифференциального уравнения Эйлера.
Воспользуемся
I необходимое условие экстремума
функционала![]() J(ε)=δJ=0.
J(ε)=δJ=0.
δJ=![]() J(ε)=
J(ε)=
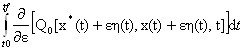 =
=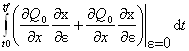 =
=
=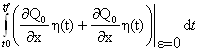 =
=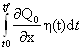 +
+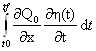 =| 2-й интеграл по частям |=
=| 2-й интеграл по частям |=
= 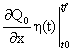 +
+ 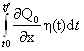 –
– 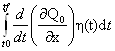 =
= 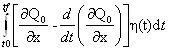 ≡ 0.
≡ 0.
Т.е.
получим δJ=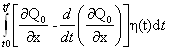 ≡ 0.
≡ 0.
По
основной лемме вариационного исчисления: если есть функции r(t) и g(t), при t![]() [t0,tf], причём
[t0,tf], причём
g(t0)=g(tf)=0 и =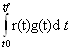 ≡ 0 , то r(t) ≡ 0 для
любых t
≡ 0 , то r(t) ≡ 0 для
любых t![]() [t0,tf].
[t0,tf].
Значит для
δJ=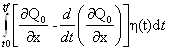 ≡ 0
получим, что
≡ 0
получим, что 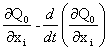 ≡0, i=1,n.
≡0, i=1,n.
Полученное уравнение называется уравнением Эйлера (оно выражает 1-е необходимое условие экстремума функционала).
2.3. Трудности, связанные с решением вариационной задачи
При отыскании оптимального управления вариационными методами приходится сталкиваться с трудностями, ряд которых носит принципиальный характер:
1. Вариационные методы дают возможность находить только относительные максимумы и минимумы функционала J(u), тогда как интерес представляет нахождение абсолютного максимума или минимума.
2. Уравнения Эйлера для многих технических задач оказываются нелинейными, что часто не дает возможности получить решение вариационной задачи в явном виде.
3. На значения управляющих сигналов обычно бывают наложены ограничения, делающие невозможным поиск оптимального управления вариационными методами.
Поскольку последнее обстоятельство имело решающее значение для развития новых идей в области оптимального управления, остановимся на нем более подробно.
Обычными ограничениями, накладываемыми на сигналы управления, являются ограничения вида |ui(t)|≤ Mi.
Означающие необходимость ограничения по величине сигналов, подводимых к органам управления. Так, ограниченными являются предельное напряжение, подводимое к якорю электродвигателя, предельный угол поворота руля самолета, предельная температура в камере эрания реактивного двигателя и т.п. При этом получение оптимальных процессов требует, как правило, поддержания сигналов управления на предельных значениях, что соответствует наиболее быстрому и эффективному протеканию процессов в объекте управления. Типичный для этих случаев характер изменения управления u(t) при оптимальном процессе приведен на рис.1.
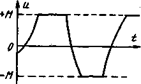
Рис.1. Характерный вид оптимального управляющего сигнала
Однако предельные значения управления u(t) лежат на границах области допустимых управлений U и, следовательно, не являются внутренними точками этой области, для которых только и применимы вариационные
Один из подходов к вычислению оптимальных процессов получил название динамического программирования. Метод динамического программировании дает в руки инженера эффективную вычислительную процедуру решения задачи оптимизации управления, хорошо приспособленную к использованию ЭВМ. Этот метод мы рассмотрим более подробно.
2.4. Метод динамического программирования
2.4.1. Дискретная форма вариационной задачи
Преодоление рассмотренных трудностей решения вариационной задачи лежит на путях использования эффективных вычислительных методов, одним из которых является метод динамического программирования. Этот метод дает возможность находить оптимальное управление в многошаговых задачах. Однако он может применяться и для решения вариационных задач, если их представить в дискретной форме.
Воспользовавшись теоремой, сформулируем вариационную задачу в следующем виде: для объекта, описываемого дифференциальным уравнением, x(t)=g(x,u), x(0)=c, найти управление u(t) из области допустимых управления U, которое минимизирует функционал
J(u)=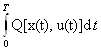 , где Q(x,u)=Q1(x,u)+λH(x,u).
, где Q(x,u)=Q1(x,u)+λH(x,u).
Дискретную форму записи этой задачи получим, если выбор управления u(t) будем производить только в дискретные моменты t=kδ, k=0,n-1, где δ=Т/n, При этом вместо функции x(t) и u(t) будем рассматривать последовательности
xk=x(t)|t=kδ , uk=u(t)|t=kδ .
Заменяя производную x=dx/dt на отношение приращений (xk+1-xk)/δ, вместо дифференциального уравнения получаем уравнение в конечных разностях:
![]() g(xk,uk)
g(xk,uk)
Обычно это уравнение записывают в более удобной форме, разрешая его относительно хk+1: xk+1=xk+ g(xk,uk) δ, k=0,n-1, x0=c.
При этом интеграл
J(u)=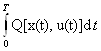
заменится суммой
Jn(u)= ![]() ,
,
где под u понимается последовательность используемых управлений u=(u0,…,un-1)
Теперь задача заключается в выборе таких управлений ui, которые обеспечивают минимальное значение суммы.
Во многих задачах управления оказывается целесообразным считать δ=1. В частности, это удобно делать в тех случаях, когда процесс естественным образом разбивается на отдельные шаги, причем в пределах каждого шага управление u(t) остается неизменным. При этом мы приходим к многошаговому процессу управления, рассмотренному ранее, в котором xk и uk означают состояние объекта и применяемое управление в начале каждого шага.
2.4.2.Рекуррентное соотношение метода динамического программирования
Оптимизация управления n-шагового процесса состоит в том, чтобы найти такую последовательность управлений ui, при которой критерий качества Jn(u) принимает минимальное значение. Это минимальное значение критерия качества управления n-шагового процесса будет зависеть только от начального состояния x0 и его можно обозначать fn(x0). По определению имеем:
fn(x0)=min min … min [Q(x0,u0)+ Q(x1,u1)+…+ Q(xn-1,un-1)].
Заметим, что первое слагаемое этого выражения Q(x0,u0) зависит только от управления u0, тогда как остальные слагаемые зависят как от u0, так и от управлений на других шагах. Так, Q(x1,u1) зависит от u1, но оно зависит и от u0, так как x1 =T(x0,u0). Аналогично обстоит дело и с остальными слагаемыми. Поэтому выражение можно записать в виде
fn(x0)=min {Q(x0,u0)+ min … min [Q(x1,u1)+…+ Q(xn-1,un-1)]}.
Заметим далее, что выражение min … min [Q(x1,u1)+…+ Q(xn-1,un-1)] представляет собой минимальное значение критерия качествa управления (n-1)-шагового процесса, имеющего начальное состояние х1. В соответствии с определением эту величину можем обозначить через fn-1(x1). Таким образом, получаем: fn(x0)=min {Q(x0,u0)+ fn-1(x1)}.
Эти рассуждения можно повторить, если рассмотреть (n-1)-шаговый процесс, начинающийся с начального состояния x1. Минимальное значение критерия качества управления для этого случая fn-1(x1)=min {Q(x1,u1)+ fn-2(x2)}.
Продолжая эти рассуждения, получаем аналогичное выражение для (n -k) -шагового процесса, начинающегося с состояния xk:
fn-k(xk)=min {Q(xk,uk)+ fn-(k+1)(xk+1)}.
Последнее уравнение, называемое часто уравнением Беллмана, представляет собой рекуррентное соотношение, позволяющее последовательно определять оптимальное управление на каждом шаге управляемого процесса.
Сама идея оптимизации управления на каждом шаге отдельно, если трудно оптимизировать сразу весь процесс в целом, не является оригинальной и широко используется на практике. Однако при этом часто не принимают во внимание, что оптимизация каждого шага еще не означает оптимизацию всего процесса в целом.
Особенностью метода динамического программирования является то, что оно совмещает простоту решения задачи оптимизации управления на отдельном шаге с дальновидностью, заключающейся в учете самых отдаленных последствий этого шага.
В методе динамического программирования выбор управления на отдельном шаге производится не с точки зрения интересов данного шага, выражающихся в минимизации потерь на данном шаге, т.е. величины Q(xk,uk), а с точки зрения интересов всего процесса в целом, выражающихся в минимизации суммарных потерь Q(xk,uk)+ fn-(k+1)(xk+1) на всех последующих шагах. Отсюда следует основное свойство оптимального процесса, заключающееся в том, что каковы бы ни были начальное состояние и начальное управление, последующие управления должны быть оптимальными относительно состояния, являющегося результатом применения первого управления.
Из основного свойства оптимального управления следует, что оптимизация управления для произвольной стадии многошагового процесса заключается в выборе только последующих управлений. Поэтому бывает удобно учитывать не те шаги, которые уже были пройдены, а те, которые осталось проделать, для того чтобы привести процесс в конечное состояние.
2.5. Вариационная задача условной минимизации для условий в виде равенств
Рассматриваемая задача состоит в определении управляющих воздействий u(t) минимизирующих (или максимизирующих) показатель качества J.
Объект управления описывается уравнениями: x=q(x,u,t),
y=g(x,t).
Составляющие q, g предполагаются непрерывными по х и u и непрерывно дифференцируемыми по х. Объект управления предполагается управляемым и наблюдаемым, т.е. все переменные состояния доступны измерению и возбуждается любое из состояний управляемого объекта.
Если переменные функции не являются независимыми, а подчинены ограничениям типа равенств, т. е. f(x)=0, то необходимые условия экстремума определяются методом множителей Лагранжа.
Пусть целевая функция имеет вид:
J=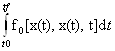 à min,
при условиях x(t0)=x0 , x(tf)=xf , t
à min,
при условиях x(t0)=x0 , x(tf)=xf , t ![]() [t0,tf], x(t)
[t0,tf], x(t)![]() Rn,
Rn,
при ограничениях fi(x(t),x(t),t)=0, i=1,m.
Задача решается методом множителей Лагранжа:
запишем лагранжиан
J=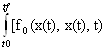 +
+![]() λi(t)fi(x(t),x(t),t)] dt àmin по x(t), λ(t).
λi(t)fi(x(t),x(t),t)] dt àmin по x(t), λ(t).
Запишем более в компактном виде:
J= =
=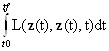 àmin по z(t), где z(t)=
àmin по z(t), где z(t)=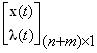 .
.
Первым необходимым условием экстремума функционала J является δJ=0.
Производя рассуждения аналогичные вышеизложенным получаем уравнение:
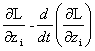 =0, i=1,n+m.
=0, i=1,n+m.
Это уравнение называется уравнением Эйлера-Лагранжа.
© 2010 Интернет База Рефератов