
Рефераты по сексологии
Рефераты по информатике программированию
Рефераты по биологии
Рефераты по экономике
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Рефераты по авиации и космонавтике
Рефераты по административному праву
Рефераты по безопасности жизнедеятельности
Рефераты по арбитражному процессу
Рефераты по архитектуре
Рефераты по астрономии
Рефераты по банковскому делу
Рефераты по биржевому делу
Рефераты по ботанике и сельскому хозяйству
Рефераты по бухгалтерскому учету и аудиту
Рефераты по валютным отношениям
Рефераты по ветеринарии
Рефераты для военной кафедры
Рефераты по географии
Рефераты по геодезии
Рефераты по геологии
Рефераты по геополитике
Рефераты по государству и праву
Рефераты по гражданскому праву и процессу
Рефераты по делопроизводству
Рефераты по кредитованию
Рефераты по естествознанию
Рефераты по истории техники
Рефераты по журналистике
Рефераты по зоологии
Рефераты по инвестициям
Рефераты по информатике
Исторические личности
Рефераты по кибернетике
Рефераты по коммуникации и связи
Реферат: Прикладная математика
Реферат: Прикладная математика
УДК
Методические указания к выполнению курсовой работы по дисциплине ” Прикладная математика” /Сост.: Колемаев В.А., Карандаев И.С. и др. ГУУ, М.:2000.
СоставителиКолемаев В.А. – профессор, доктор экономических наук
§15.
Карандаев И.С. - доцент. § § 2, 4-10
приложения I, III, IX.
Малыхин В.И. - профессор, доктор физико-математических наук
§ § 11-14, приложения V, VII, VIII.
Гатауллин Т.М. - доцент, кандидат физико-математических наук
§ § 1, 3, приложение IV.
Прохоров Ю.Г. - доцент, кандидат физико-математических наук
Приложение VI.
Юнисов Х.Х. – старший преподаватель, приложение II.
Ответственный редактор
заведующий кафедрой прикладной математики
доктор экономических наук, профессор
Колемаев В.А.
Рецензент
кандидат экономических наук, доцент
кафедры экономической кибернетики
Васильева Л.Н.
© Государственный университет управления, 2000
ПредисловиеУчебными планами всех специальностей ГУУ предусмотрено выполнение курсового проекта по дисциплине ² Прикладная математика² . Как указано в программе этой дисциплины, прикладная математика состоит из двух основных разделов: теории вероятностей и ее приложений и математических методов исследования операций, которые включают также финансовую математику, что особенно важно для студентов-заочников, специализирующихся в области финансового и банковского менеджмента. Программой предусмотрено также изучение основных вопросов линейной алгебры.
Рекомендуется изучить основы теории систем линейных алгебраических уравнений по учебнику [1]. Напомним, что в задачах линейной оптимизации приходится в основном рассматривать системы линейных алгебраических уравнений в предпочитаемой форме, когда каждое уравнение системы содержит неизвестную, входящую только в это уравнение, причем с коэффициентом +1, а поиск оптимального решения сводится к направленному перебору базисных неотрицательных решений. Поэтому студент должен иметь ввиду, что нет смысла приступать к рассмотрению линейной производственной задачи курсовой работы, пока не изучены основы теории систем линейных алгебраических уравнений, изложенные в §§ 1, 2 главы 1 учебника [1].
Краткое и сжатое изложение основных вопросов исследования операций дано в работе [7], а разбор задач - в пособии [16]. При этом полезно предварительно ознакомиться с работой [11], где некоторые важнейшие вопросы программы изложены весьма подробно и доходчиво. Специальные вопросы исследования операций изложены в работах [6], [8] и [25].
Финансовая математика может быть изучена по работам [20], [23]. Необходимый для этого материал по теории вероятностей и математической статистике рекомендуется изучить по учебнику [2].
§ 1. ЦЕЛИ И ЗАДАЧИ КУРСОВОГО ПРОЕКТАВыполнение курсового проекта по прикладной математике направлено на усиление связи обучения студентов с практикой совершенствования управления, организации современного производства, всего механизма хозяйствования.
В процессе работы над курсовым проектом студент не только закрепляет и углубляет теоретические знания, полученные на лекциях и на практических занятиях, но и учится применять методы исследования операций при постановке и решении конкретных экономических задач.
Цель курсового проекта - подготовить студента к самостоятельному проведению операционного исследования, основными этапами которого являются построение математической модели, решение управленческой задачи при помощи модели и анализ полученных результатов.
§ 2. Задание на курсовОЙ ПрОЕКТ Сформулировать линейную производственную задачу и составить ее математическую модель, взяв исходные данные из приложения 1, где технологическая матрица А затрат различных ресурсов на единицу каждой продукции, вектор объемов ресурсов В и вектор удельной прибыли С при возможном выпуске четырех видов продукции с использованием трех видов ресурсов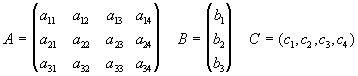
компактно записаны в виде
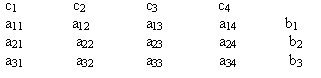
Преобразовать данную задачу к виду основной задачи линейного программирования, решить ее методом направленного перебора базисных допустимых решений, обосновывая каждый шаг процесса, найти оптимальную производственную программу, максимальную прибыль, остатки ресурсов различных видов и указать ² узкие места² производства.
В последней симплексной таблице указать обращенный базис Q-1, соответствующий оптимальному набору базисных неизвестных. Проверить выполнение соотношения
H = Q-1B
Если по оптимальной производственной программе какие-то два вида продукции не должны выпускаться, то в таблице исходных данных вычеркнуть соответствующие два столбца, составить математическую модель задачи оптимизации производственной программы с двумя оставшимися переменными, сохранив прежнюю нумерацию переменных и решить графически.
2. Сформулировать задачу, двойственную линейной производственной задаче, как задачу определения расчетных оценок ресурсов, и найти ее решение, пользуясь второй основной теоремой двойственности (о дополняющей нежесткости). Указать оценку единицы каждого ресурса, минимальную суммарную оценку всех ресурсов, оценки технологий.
Применить найденные двойственные оценки ресурсов к решению следующей задачи.
Сформулировать задачу о "расшивке узких мест производства" и составить математическую модель. Определить область устойчивости двойственных оценок, где сохраняется структура программы производства. Решить задачу о ² расшивке узких мест производства² при условии, что дополнительно можно получить от поставщиков не более одной трети первоначально выделенного объема ресурса любого вида (если задача окажется с двумя переменными, то только графически); найти план приобретения дополнительных объемов ресурсов, дополнительную возможную прибыль.
По пунктам 1, 2, 3 составить сводку результатов [10, c. 21].
3. Составить математическую модель транспортной задачи по исходным данным из
приложения 2, где вектор объемов производства А(a1,..., am),
потребления - В (b1,..., bn) и матрица транспортных издержек
С=(сij), i =![]() ; j =
; j = ![]() кратко записаны в виде
кратко записаны в виде
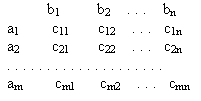
Если полученная модель окажется открытой, то свести ее к замкнутой и найти оптимальное решение транспортной задачи методом потенциалов.
4. Методом динамического программирования решить задачу распределения капитальных вложений между четырьмя предприятиями производственного объединения, располагающего суммой в 700 тыс. руб., по исходным данным, приведенным в приложении 3 (выделяемые суммы кратны 100 тыс.).
5. Рассмотреть динамическую задачу управления производством и запасами. Решить конкретную задачу по исходным данным, приведенным в приложении 4.
6. Рассмотреть матричную игру как модель сотрудничества и конкуренции, взяв исходные данные из приложения 5. Найти графически решение игры. Указать, как проявляется конкуренция между игроками и сотрудничество между ними.
7. Рассмотреть задачу о максимальном потоке в сети. Решить конкретную задачу на сети с 8-9 вершинами, предложив исходные данные самостоятельно.
Рассмотреть задачу о кратчайшем пути. Решить конкретную задачу, предложив исходные данные самостоятельно. Рассмотреть задачу о назначениях. Решить конкретную задачу, предложив исходные данные самостоятельно. Методом ветвей и границ найти целочисленное решение задачи о "расшивке узких мест производства", рассмотренной в пункте 2. Если же все компоненты плана "расшивки" были целочисленными, то в условии17. Рассмотреть задачу принятия решений в условиях неопределенности, взяв исходные данные из приложения 7. По номеру ![]() берете строки с номерами
берете строки с номерами ![]() . Например, при
. Например, при ![]() :
:
1. (2,1/2)(0,1/4)(14,1/8))(6,1/8) 2. (2,1/2)(4,1/4)(18,1/8))(8,1/8)
3. (4,1/4)(0,1/4)(6,1/3))(12,1/6) 4. (6,1/4)(2,1/4)(14,1/3))(4,1/6)
В этих строках опускаете дроби и получаете:
1. (2,0,14,6) 2.(2,4,18,8) 3. (4,0,6,12) 4.(6,2,14,4)
Полученные строки объединяете в матрицу, аналогичную матрице ![]() . Вероятности состояний берете из строки с номером
. Вероятности состояний берете из строки с номером ![]() , оставляя в ней только дроби: 1.(2,1/2)(0,1/4)(14,1/8)(6,1/8), т. е. получаете (1/2,1/4,1/8,1/8). Затем:
, оставляя в ней только дроби: 1.(2,1/2)(0,1/4)(14,1/8)(6,1/8), т. е. получаете (1/2,1/4,1/8,1/8). Затем:
а) Найдите матрицу рисков.
б) Найдите решения, рекомендуемые правилами Вальда, Сэвиджа, Гурвица (l задайте сами).
в) При данных вероятностях состояний проанализируйте имеющееся семейство из 4-х операций: каждая операция имеет две характеристики – средний ожидаемый доход и средний ожидаемый риск, нанесите для каждой операции эти характеристики на плоскую систему координат и выявите операции, оптимальные по Парето.
г) Затем найдите выпуклую оболочку множества полученных точек и дайте интерпретацию точек полученной выпуклой оболочки.
д) Придумайте пробную операцию, которая значительно сместит распределение вероятностей, и определите максимально оправданную стоимость пробной операции, используя какой-нибудь подходящий критерий эффективности операций (например, средний ожидаемый доход).
е) Выберите какие-нибудь две операции, предположите, что они независимы друг от друга и найдите операцию, являющуюся их линейной комбинацией и более хорошую, чем какая-либо из имеющихся.
ж) Придумайте взвешивающую формулу (ее придется объяснить при защите курсовой работы!) и найдите по ней худшую и лучшую операции.
Произвести математико-статистический анализ за T лет Xt, Kt, Lt (t = 1, …, T) о выпуске продукции (в стоимостном виде), ОПФ и числе занятых исследуемого производственного экономического объекта:а) найти прогноз выпуска, фондов и занятых на 1, 2, 3 года вперед
![]()
по выявленному линейному или квадратичному тренду;
б) найти прогноз выпуска на 1, 2, 3 года вперед
![]()
с помощью построенной мультипликативной производственной функции
![]()
в) на основе результатов расчетов сделать выводы о состоянии и перспективах развития исследуемого экономического объекта.
§3. Организация выполнения курсовоГО ПрОЕКТАСтудент выполняет 5-8 пунктов задания в любом наборе в соответствии со своей специальностью и своими интересами по согласованию с руководителем, при этом пункты 1, 2, 4, 6 являются обязательными для студентов любых специальностей. Номера задач из приложений выбираются либо по номеру студента в списке, либо по начальной букве своей фамилии по схеме:
Начальная буква А Б В Г Д Е Ж З И, Й Ка-Кл Км-Кр
Номер задания 1 2 3 4 5 6 7 8 9 10 11
Кс-Кя Л М Н О П Р С Т У Ф Х Ц,Ч Ш,Щ,Ы Э,Ю,Я
12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
Курсовая работа выполняется аккуратно на одной стороне листа стандартного формата. Графики строятся черными или цветными карандашами средней твердости на обычной или миллиметровой бумаге. Листы с текстом курсовой работы и графики должны быть сшиты.
Текст работы должен содержать все необходимые расчеты и пояснения. В случае применения ЭВМ в работе должны содержаться блок-схема решения задачи, распечатка программы и результатов с необходимыми пояснениями.
В курсовом проекте обязательны оглавление и сквозная нумерация всех листов. Образец титульного листа содержится в приложении 9.
Курсовая работа сдается преподавателю до защиты для проверки. При защите курсовой работы студент должен показать знание теоретического курcа и умение математически ставить, решать и анализировать конкретные экономические задачи.
§4. Линейная производственная задачаЗадача о рациональном использовании производственных мощностей является одной из первых задач, для решения которой были применены методы линейного программирования. В общем виде математическая модель задачи об использовании производственных мощностей может быть получена следующим образом.
Предположим, что предприятие или цех выпускает n видов изделий, имея m групп оборудования. Известны нормы времени на обработку каждого изделия на каждой группе оборудования, например, в минутах или часах и фонд времени работы каждой группы оборудования. Пусть, кроме того, известно, что из всех n видов изделий наибольшим спросом пользуются k видов. Требуется составить план производства, при котором выпуск дефицитных изделий будет наибольшим возможным.
Примем следующие обозначения:
i – номер группы оборудования (i=1,2, … , m);
j – номер вида изделия (j=1,2, … , n);
aij – норма времени на обработку единицы i-го изделия на j-ой группе оборудования;
bi– действительный фонд времени работы i-й группы оборудования;
xi–планируемое количество единиц j-го изделия;
(x1, x2, … , xn)–искомый план производства.
Какова бы ни была производственная программа (x1, x2, … , xn), ее компоненты должны удовлетворять условию, что суммарное время обработки всех изделий на данной группе оборудования не должно превышать фонда времени работы этой группы оборудования. На обработку x1 единиц первого изделия на i-й группе оборудования будет затрачено ai1x1 единиц времени, на обработку x2 единиц второго изделия на той же группе оборудования будет затрачено ai2x2 единиц времени и т.д. Необходимое время на обработку всех x1, x2, … , xn изделий на i-й группе оборудования будет равно сумме
![]()
Эта сумма не может превышать фонд времени работы i-й группы оборудования, т.е. должна быть £ bi. Выписывая такие условия для всех m групп оборудования, получаем:
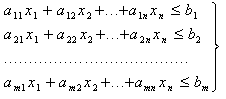 (1)
(1)
Так как компоненты плана суть количество изделий и, следовательно, не могут быть выражены отрицательными числами, то естественным образом добавляются условия:
x1 ³ 0, x2,³ 0,…, xn³ 0. (2)
Обозначим через сj прибыль на единицу j-го изделия. При плане производства (х1, х2, …, хn) прибыль предприятия будет равна:
z = c1x1 + c2x2 + … + cnxn.(3)
Мы хотим составить производственную программу (х1, х2, …, хn) так, чтобы функция (3) приняла наибольшее значение при выполнении всех других условий.
Система линейных неравенств (1), (2) и линейная форма (3) образуют математическую модель задачи о рациональном использовании производственных мощностей. Среди всех решений системы линейных неравенств (1), удовлетворяющих условию неотрицательности (2), необходимо найти такое решение, при котором линейная форма (3) принимает наибольшее возможное значение. Это – задача линейного программирования.
Исходные параметры задачи могут быть представлены в виде технологической матрицы A затрат ресурсов на единицу продукции каждого вида, вектора B объемов ресурсов и вектора C удельной прибыли:
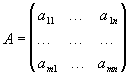 ,
,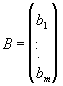 ,C=(c1, …, cn)
,C=(c1, …, cn)![]()
В качестве примера рассмотрим задачу оптимизации производственной программы цеха, который может выпускать два вида изделий, имея четыре группы производственного оборудования. Пусть
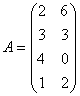 ,
, 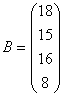 ,
, ![]() , или кратко
, или кратко 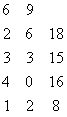
Задача состоит в том, чтобы найти производственную программу, максимизирующую прибыль:
![]() (4)
(4)
при условиях:
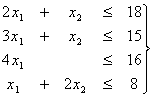 (5)
(5)
![]() (6)
(6)
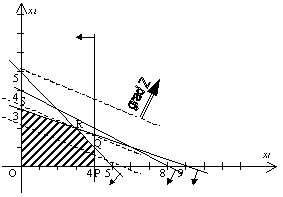
Полученную задачу линейного программирования с двумя переменными можно решить графически. Система линейных неравенств (5), (6) определяет выпуклый многоугольник OPQRS допустимых решений. Линии уровня функции Z перпендикулярны вектору-градиенту grad Z=(6,9) и образуют семейство параллельных прямых (градиент указывает направление возрастания функции). Наибольшего значения функция Z достигает в точке R. Координаты этой точки определяют оптимальный план производства x1=3, x2=2, а максимальная прибыль будет равна 36.
Последовательное улучшение производственной программыПредположим теперь, что предприятие может выпускать четыре вида продукции, используя для этого три вида ресурсов. Известна технологическая матрица А затрат любого ресурса на единицу каждой продукции, вектор В объемов ресурсов и вектор С удельной прибыли
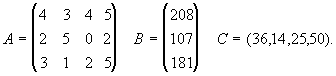 (7)
(7)
Требуется составить производственную программу, обеспечивающую предприятию наибольшую прибыль при имеющихся ограниченных ресурсах
Математическая модель задачи:
найти производственную программу
(x1, x2, x3, x4)
максимизирующую прибыль
z = 36x1+ 14x2 + 25x3 + 50x4 (8)
при ограничениях по ресурсам
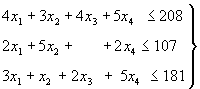 (9)
(9)
где по смыслу задачи
x1 ³ 0, x2 ³ 0, x3 ³ 0, x4 ³ 0. (10)
Получили задачу на условный экстремум. Для ее решения систему неравенств (9) при помощи дополнительных неотрицательных неизвестных х5, х6, х7 заменим системой линейных алгебраических уравнений
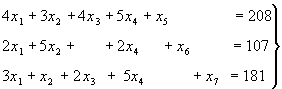 (11)
(11)
где дополнительные переменные имеют смысл остатков соответствующих ресурсов. Среди всех решений системы уравнений (11), удовлетворяющих условию неотрицательности
х1³ 0, х2³ 0, … , х5³ 0, … , х7³ 0.(12)
надо найти то решение, при котором функция (8) примет наибольшее значение.
Воспользуемся тем, что правые части всех уравнений системы (11) неотрицательны, а сама система имеет предпочитаемый вид – дополнительные переменные являются базисными. Приравняв к нулю свободные переменные х1, х2, х3, х4, получаем базисное неотрицательное решение
x1=0, x2=0, x3=0, x4=0, x5=208, x6=107, x7=181(13)
первые четыре компоненты которого определяют производственную программу
x1=0, x2=0, x3=0, x4=0(14)
по которой мы пока ничего не производим.
Из выражения (8) видно, что наиболее выгодно начинать производить продукцию четвертого вида, так как прибыль на единицу продукции здесь наибольшая. Чем больше выпуск в этой продукции, тем больше прибыль. Выясним, до каких пор наши ресурсы позволяют увеличить выпуск этой продукции. Для этого придется записать для системы уравнений (11) общее решение
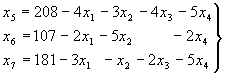 (15)
(15)
Мы пока сохраняем в общем решении х1=х2=х3=0 и увеличиваем только х4. При этом значения базисных переменных должны оставаться неотрицательными, что приводит к системе неравенств
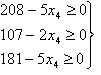 или
или 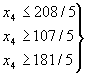 т.е.0 £
х4 £
т.е.0 £
х4 £
![]()
Дадим х4 наибольшее значение х4 =181/5, которое она может принять при нулевых значениях других свободных неизвестных, и подставим его в (15). Получаем для системы уравнений (11) частное неотрицательное решение
х1=0, х2=0, х3=0, х4=![]() ; x5=27; x6=
; x5=27; x6=![]() ; x7=0(16)
; x7=0(16)
Нетрудно убедиться, что это решение является новым базисным неотрицательным решением системы линейных алгебраических уравнений (11), для получения которого достаточно было принять в системе (11) неизвестную х4 за разрешающую и перейти к новому предпочитаемому виду этой системы, сохранив правые части уравнений неотрицательными, для чего за разрешающее уравнение мы обязаны принять третье, так как
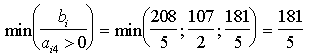
а разрешающим элементом будет а34=5. Применив известные формулы исключения, получаем для системы уравнений (11) новый предпочитаемый эквивалент
x1 + 2x2 + 2x3 + x5 - x7 = 27
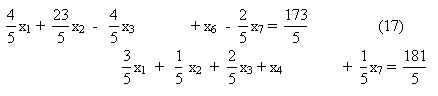
Приравняв к нулю свободные переменные х1, х2, х3, х7, получаем базисное неотрицательное решение, совпадающее с (16), причем первые четыре компоненты его определяют новую производственную программу
х1=0, х2=0, х3=0, х4=![]() . (18)
. (18)
Исследуем, является ли эта программа наилучшей, т.е. обеспечивает ли она наибольшую прибыль. Для этого выразим функцию прибыли (8) через новые свободные переменные х1, х2, х3, х7.
Из последнего уравнения системы (17) выражаем базисную переменную х4 через свободные и подставляем в (8). Получаем
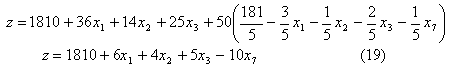
Видим, что программа (18) не является наилучшей, так как прибыль будет расти, если мы начнем производить или первую, или вторую, или третью продукцию, но наиболее быстро функция z растет при возрастании х1. Поэтому принимаем х1 в системе (17) за разрешающую неизвестную, находим разрешающее уравнение по
![]() (20)
(20)
и исключаем х1 из всех уравнений системы (17), кроме первого уравнения. Получим следующий предпочитаемый эквивалент системы условий, который определит для системы (11) новое базисное неотрицательное решение и уже третью производственную программу, для исследования которого нам придется выразить функцию (19) через новые свободные переменные, удалив оттуда переменную х1, ставшую базисной. Мы видели выше, как это делается (удаляли х4 из (8)).
Важно обратить внимание на то, что эти удаления можно выполнить очень просто. Представим соотношение (8) в виде уравнения
-36х1 - 14х2 - 25х3 - 50х4 = 0 – z(21)
и припишем его к системе (11). Получается вспомогательная система уравнений
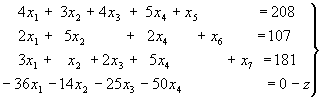 (22)
(22)
Напомним, что разрешающую неизвестную в системе (11) мы выбрали х4. Этой переменной в последнем уравнении системы (22) отвечает наименьший отрицательный коэффициент D 4=-50. Затем мы нашли разрешающий элемент а34=5 и исключили неизвестную х4 из всех уравнений системы (11), кроме третьего. Далее нам пришлось х4 исключать и из функции (8). Теперь это можно сделать очень просто, если посмотреть на систему уравнений (22). Очевидно, достаточно умножить третье уравнение системы (22) на 10 и прибавить к четвертому; получим
-6х1 - 4х2 - 5х3 - 10х4 = 1810 – z(23)
Таким образом, мы преобразовывали вспомогательную систему уравнений (22) к виду
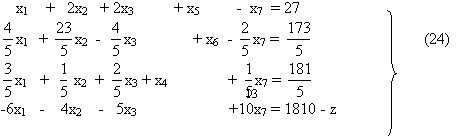
Первые три уравнения этой системы представляют некоторый предпочитаемый эквивалент (17) системы уравнений (11) и определяют базисное неотрицательное решение (16) и производственную программу (18), а из последнего уравнения системы (24) получается выражение (19) функции цели через свободные переменные. Очевидно, если имеется хотя бы один отрицательный коэффициент D j при какой-нибудь переменной xj в последнем уравнении системы (24), то производственная программа не является наилучшей и можно далее продолжать процесс ее улучшения. С помощью (19) мы выяснили, что следует начинать производить продукцию первого вида, т.е. фактически мы нашли в последнем уравнении системы (24) наименьший отрицательный коэффициент
min(D j<0) = min(-6, -4, -5) = -6 = D 1
и решили перевести свободную переменную х1 в число базисных, для чего, согласно (20)определили разрешающее уравнение и указали разрешающий элемент а11=1.
Учитывая сказанное выше, теперь мы будем преобразовывать не систему (17), а всю вспомогательную систему (24), по формулам исключения. Эта система преобразуется к виду
x1 + 2x2 + 2x3 + x5 - x7 = 27
3x2 - ![]() x3 -
x3 - ![]() x5 + x6 +
x5 + x6 + ![]() x7 = 13 (25)
x7 = 13 (25)
- x2 - ![]() x3 + x4 -
x3 + x4 - ![]() x5 +
x5 + ![]() x7 = 20
x7 = 20
8x2 + 7x3 + 6x5 + 4x7 = 1972 - z
Первые три уравнения системы (25) представляют некоторый предпочитаемый эквивалент системы уравнений (11) и определяют базисное неотрицательное решение системы условий рассматриваемой задачи
x1=27, x2=0, x3=0, x4=20, x5=0, x6=13, x7=0(26)
т.е. определяют производственную программу
x1=27, x2=0, x3=0, x4=20(27)
и остатки ресурсов:
первого видах5=0
второго видах6=13(28)
третьего видах7=0
В последнем уравнении системы (25) среди коэффициентов при неизвестных в левой части уравнения нет ни одного отрицательного. Если из этого уравнения выразить функцию цели z через остальные неотрицательные переменные
z = 1972 - 8х2 - 7х3 - 6х5 - 4х7(29)
то становится совершенно очевидным (в силу того, что все xj³ 0), что прибыль будет наибольшей тогда, когда
x2=0, x3=0, x5=0, x7=0(30)
Это означает, что производственная программа (27) является наилучшей и обеспечивает предприятию наибольшую прибыль
zmax = 1972(31)
Итак, организовав направленный перебор базисных неотрицательных решений системы условий задачи, мы пришли к оптимальной производственной программе и указали остатки ресурсов, а также максимальную прибыль.
Остается заметить, что процесс решения обычно записывается в виде некоторой таблицы 1.
Таблица 1
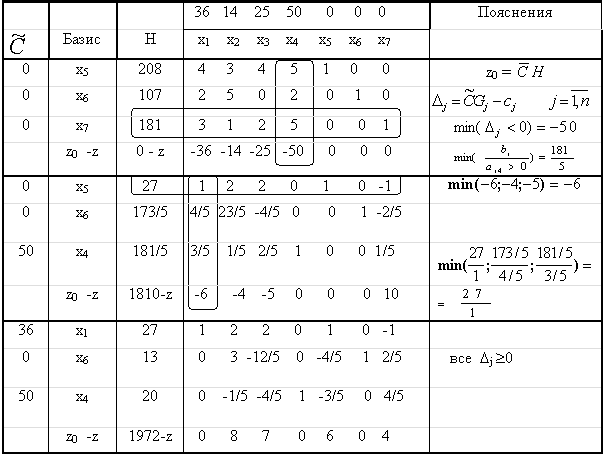
где представлены расширенные матрицы вспомогательных систем уравнений (22) ® (24) ® (25). Эти таблицы принято называть симплексными.
Следует обратить внимание на экономический смысл элементов последней строки последней симплексной таблицы. Например, коэффициент D 3=7 при переменной х3 показывает, что если произвести одну единицу продукции третьего вида (она не входит в оптимальную производственную программу), то прибыль уменьшится на 7 единиц.
В заключение заметим, что в рассматриваемом простейшем примере линейной производственной задачи возможна самопроверка результата.
Воспользуемся тем, что в оптимальной производственной программе х2=0, х3=0. Предположим, что вторую и третью продукции мы не намеревались выпускать с самого начала. Рассмотрим задачу с оставшимися двумя переменными, сохранив их нумерацию. Математическая модель задачи будет выглядеть следующим образом:
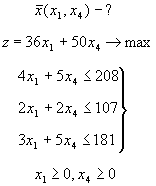
Студенту не составит труда решить эту задачу графически и убедиться, что результаты совпадают.
Следует при этом обратить внимание на то, что последовательное улучшение производственной программы
(x1=0, x4=0) ®
(x1=0, x4=![]() ) ®
(x1=27, x4=20)
) ®
(x1=27, x4=20)
на графике означает движение от одной вершины многогранника допустимых решений к другой вершине по связывающей их стороне многоугольника (в случае трех переменных это будет "езда" по ребрам многогранника допустимых решений от одной вершины к другой до достижения оптимальной вершины).
§5. Двойственная задачаРанее мы рассмотрели конкретную линейную производственную задачу по выпуску четырех видов продукции с использованием трех видов ресурсов по заданным технологиям.
Теперь представим себе, что возникла новая ситуация. Знакомый предприниматель П (Петров), занимающийся производством каких-то других видов продукции, но с использованием трех таких же видов ресурсов, какие имеются у нас, предлагает нам "уступить" по определенным ценам все имеющиеся у нас ресурсы и обещает платить у1 рублей за каждую единицу первого ресурса, у2 руб – второго, у3 руб – третьего. Возникает вопрос: при каких ценах у1, у2, у3 мы можем согласиться с предложением П.
Величины у1, у2, у3 принято называть расчетными, или двойственными, оценками ресурсов. Они прямо зависят от условий, в которых действует наше предприятие.
Напомним, что в нашей задаче технологическая матрица А, вектор объемов ресурсов В и вектор удельной прибыли С имели вид
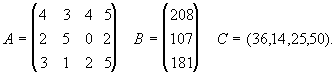
Для производства единицы продукции первого вида мы должны затратить, как видно из матрицы А, 4 единицы ресурса первого вида, 2 единицы ресурса второго вида и 3 единицы третьего (элементы первого столбца матрицы). В ценах у1, у2, у3 наши затраты составят 4у1 + 2у2 + 3у3, т.е. столько заплатит предприниматель П за все ресурсы, идущие на производство единицы первой продукции. На рынке за единицу первой продукции мы получили бы прибыль 36 руб. Следовательно, мы можем согласиться с предложением П только в том случае, если он заплатит не меньше
4у1 + 2у2 + 3у3 ³ 36.
Аналогично, во втором столбце матрицы А указаны затраты различных ресурсов на производство единицы продукции второго вида. В ценах П эти затраты составят 3у1 + 5у2 + у3, а на рынке за единицу продукции второго вида мы получили бы прибыль 14 рублей. Поэтому перед предпринимателем П мы ставим условие
3у1 + 5у2 + у3 ³ 14
и т.д. по всем видам продукции.
Учтем, что за все имеющиеся у нас ресурсы нам должны заплатить 208у1 + 107у2 + 181у3 рублей. При поставленных нами условиях предприниматель П будет искать такие значения величин у1, у2, у3, чтобы эта сумма была как можно меньше. Подчеркнем, что здесь речь идет не о ценах, по которым мы когда-то приобретали эти ресурсы, а об этих ценах, которые существенно зависят от применяемых нами технологий, объемов ресурсов и от ситуации на рынке.
Таким образом, проблема определения расчетных оценок ресурсов приводит к задаче линейного программирования: найти вектор двойственных оценок
у(у1, y2, y3)
минимизирующий общую оценку всех ресурсов
f = 208y1 + 107y2 +181y3 (1)
при условии, что по каждому виду продукции суммарная оценка всех ресурсов, затрачиваемых на производство единицы продукции, не меньше прибыли, получаемой от реализации единицы этой продукции
4y1 + 2y2 + 3y3 ³ 36
3y1 + 5y2 + y3 ³ 14
4y1 + 2y3 ³ 25
5y1 + 2y2 + 5y3 ³ 50
причем оценки ресурсов не могут быть отрицательными
y1![]() 0, y2
0, y2![]() 0,
y3
0,
y3![]() 0. (3)
0. (3)
Решение полученной задачи легко найти с помощью второй основной теоремы двойственности, согласно которой для оптимальных решений ![]() (х1, х2, х3, х4) и
(х1, х2, х3, х4) и ![]() (y1, y2, y3) пары двойственных задач необходимо и достаточно выполнение условий
(y1, y2, y3) пары двойственных задач необходимо и достаточно выполнение условий
x 1 (4y1 + 2y2 + 3y3 - 36) = 0y1 (4x1 +3x2 + 4x3 + 5x4 - 208) = 0
x 2 (3y1 + 5y2 + y3 - 14) = 0y2 (2x1 +5x2 + 2x4 - 107) = 0
x 3 (4y1 + 2y3 - 25) = 0y3 (3x1 + x2 + 2x3 + 5x4 - 181) = 0 .
x 4(5y1 + 2y2 + 5y3 - 50) = 0
Ранее было найдено, что в решении исходной задачи х1>0, x4>0. Поэтому
4y1 + 2y2 + 3y3 - 36 = 0
5y1 + 2y2 + 5y3 - 50 = 0
Если же учесть, что второй ресурс был избыточным и, согласно той же теореме двойственности, ее двойственная оценка равна нулю
у2=0,
то приходим к системе уравнений
4y1 + 3y3 - 36 = 0
5y1 + 5y3 - 50 = 0
откуда следует
у1=6, у3=4.
Таким образом, получили двойственные оценки ресурсов
у1=6; у2=0; у3=4, (4)
причем общая оценка всех ресурсов равна 1972.
Заметим, что решение (4) содержалось в последней строке последней симплексной таблицы исходной задачи. Важен экономический смысл двойственных оценок. Например, двойственная оценка третьего ресурса у3=4 показывает, что добавление одной единицы третьего ресурса обеспечит прирост прибыли в 4 единицы.
§ 6. Задача о " расшивке узких мест производства"При выполнении оптимальной производственной программы первый и третий ресурсы используются полностью, т.е. образуют ² узкие места производства² . Будем их заказывать дополнительно. Пусть T(t1,t2,t3)- вектор дополнительных объемов ресурсов. Так как мы будем использовать найденные двойственные оценки ресурсов, то должно выполняться условие
H + Q-1T ![]() 0.
0.
Задача состоит в том, чтобы найти вектор
T (t1, 0, t3),
максимизирующий суммарный прирост прибыли
W = 6t1 + 4t3 (1)
при условии сохранения двойственных оценок ресурсов (и, следовательно, структуры производственной программы)
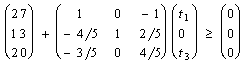 (2)
(2)
предполагая, что можно надеяться получить дополнительно не более 1/3 первоначального объема ресурса каждого вида
![]()
![]()
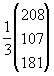 (3)
(3)
причем по смыслу задачи
t1 ![]() 0, t3
0, t3 ![]() 0. (4)
0. (4)
Переписав неравенства (2) и (3) в виде:
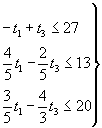 (5)
(5)
![]() (6)
(6)
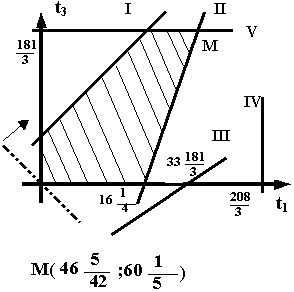
приходим к задаче ЛП: максимизировать (1) при условиях (5), (6) и (4).
Эту задачу легко решить графически: см. рис. 1. Программа ² расшивки² имеет вид
t1=![]() , t2=0, t3=
, t2=0, t3=![]()
и прирост прибыли составит 519![]() .
.
Сводка результатов приведена в таблице
Таблица 1
|
сj |
36 |
14 |
25 |
50 |
b |
x4+i |
yi |
ti |
|
4 |
3 |
4 |
5 |
208 |
0 |
6 |
46 5/12 |
|
|
aij |
2 |
5 |
0 |
2 |
107 |
13 |
0 |
0 |
|
3 |
1 |
2 |
5 |
181 |
0 |
4 |
60 1/3 |
|
|
xj |
27 |
0 |
0 |
20 |
1972 |
519 2/3 |
||
|
D j |
0 |
8 |
7 |
0 |
Транспортная задача формулируется следующим образом. Однородный продукт, сосредоточенный в m пунктах производства (хранения) в количествах а1, а2,..., аm единиц, необходимо распределить между n пунктами потребления, которым необходимо соответственно b1, b2,..., bn единиц. Стоимость перевозки единицы продукта из i-го пункта отправления в j-ый пункт назначения равна сij и известна для всех маршрутов. Необходимо составить план перевозок, при котором запросы всех пунктов потребления были бы удовлетворены за счет имеющихся продуктов в пунктах производства и общие транспортные расходы по доставке продуктов были минимальными.
Обозначим через хij количество груза, планируемого к перевозке от i-го поставщика j-му потребителю. При наличии баланса производства и потребления
![]() (1)
(1)
математическая модель транспортной задачи будет выглядеть так:
найти план перевозок
Х = (хij), i = 1,m; j = 1,n
минимизирующий общую стоимость всех перевозок
![]() (2)
(2)
при условии, что из любого пункта производства вывозится весь продукт
![]() (3)
(3)
и любому потребителю доставляется необходимое количество груза
![]() (4)
(4)
причем по смыслу задачи
х11 > 0 ,. . . ., xmn > 0. (5)
Для решения транспортной задачи чаще всего применяется метод потенциалов. Пусть исходные данные задачи имеют вид
А(а1, а2, а3) = (54; 60; 63); В(b1, b2, b3, b4) = (41; 50; 44; 30); С = ![]()
![]()
![]()
![]()
![]()
Общий объем производства å аi = 55+60+63 = 178 больше, требуется всем потребителям å bi = 42+50+44+30 = 166, т.е. имеем открытую модель транспортной задачи. Для превращения ее в закрытую вводим фиктивный пункт потребления с объемом потребления 178-166 = 12 единиц, причем тарифы на перевозку в этот пункт условимся считать равными нулю, помня, что переменные, добавляемые к левым частям неравенств для превращения их в уравнения, входят в функцию цели с нулевыми коэффициентами.
Первое базисное допустимое решение легко построить по правилу ² северо-западного угла² .
|
Потребление |
b1 =41 |
b2 =50 |
b3 =44 |
b4 =30 |
b5 =12 |
|
|
Производство |
||||||
|
а1 =54 |
41 |
13 |
p1 =0 |
|||
|
a2 =60 |
37 |
23 |
p2 = |
|||
|
a3 =63 |
* |
21 |
30 |
12 |
p3 = |
|
|
q1 = |
q2 = |
q3 = |
q4 = |
q5 = |
||
Следует иметь в виду, что по любой транспортной таблице можно восстановить соответствующий предпочитаемый эквивалент системы уравнений (3), (4), а в таблице записаны лишь правые части уравнений, причем номер клетки показывает, какая неизвестная в соответствующем уравнении является базисной. Так как в системе (3), (4) ровно m + n - 1 линейно независимых уравнений, то в любой транспортной таблице должно быть m + n - 1 занятых клеток.
Обозначим через
m
![]() )
)
вектор симплексных множителей или потенциалов. Тогда
D ij = m Aij - сij i = 1,m; j = 1,n
откуда следует
D ij = pi + qj - cij i = 1,m; j = 1,n(6)
Один из потенциалов можно выбрать произвольно, так как в системе (3), (4) одно уравнение линейно зависит от остальных. Положим, что р1 = 0. Остальные потенциалы находим из условия, что для базисных клеток ![]() . В данном случае получаем
. В данном случае получаем
D 11 = 0, p1 + q1 - c11 = 0,0+q1 -1 = 0,q1 = 1
D 12 = 0, p1 + q2 - c12 = 0,0+q2 -4 = 0,q2 = 4
D 22 = 0, p2 + q2 - c22 = 0,р2 +4-6 = 0,р2 = 2
и т.д., получим: q3=0, p3=6, q4= 1, q5= -6.
Затем по формуле (6) вычисляем оценки всех свободных клеток:
D 21 = p2 + q5 - c21 = 2+1-3 = 0
D 31 = p3 + q1 - c31 = 6+1-2 = 5
D 32 = 5; D 13 = -3; D 14 = -1; D 24 = -2; D 15 = -6; D 25 = -4.
Находим наибольшую положительную оценку
max (![]() ) = 5 =
) = 5 = ![]()
Для найденной свободной клетки 31 строим цикл пересчета - замкнутую ломаную линию, соседние звенья которой взаимно перпендикулярны, сами звенья параллельны строкам и столбцам таблицы, одна из вершин находится в данной свободной клетке, а все остальные - в занятых клетках. Это будет 31-11-12-22-23-33. Производим перераспределение поставок вдоль цикла пересчета
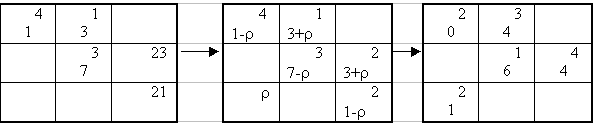
![]() = 21
= 21
Получаем второе базисное допустимое решение:
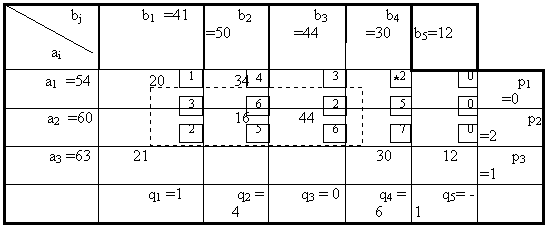
Находим новые потенциалы, новые оценки. Наибольшую положительную оценку будет иметь свободная клетка 14. Для нее строим цикл пересчета 14-11-31-34 производим перераспределение
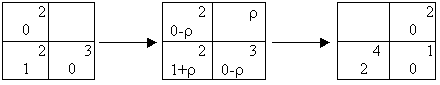
r max = 20
и получаем третье базисное допустимое решение. Продолжаем процесс до те пор, пока не придем к таблице, для которой все
D ij £ 0 i = 1,m; j = 1,n
Читателю не составит труда проверить, что будет оптимальным базисное допустимое решение
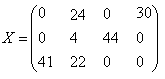
Динамическое программирование - это вычислительный метод для решения задач управления определенной структуры. Данная задача с n переменными представляется как многошаговый процесс принятия решений. На каждом шаге определяется экстремум функции только от одной переменной.
Знакомство с методом динамического программирования проще всего начать с рассмотрения нелинейной задачи распределения ресурсов между предприятиями одного производственного объединения или отрасли. Для определенности можно считать, что речь идет о распределении капитальных вложений.
Предположим, что указано n пунктов, где требуется построить или реконструировать предприятия одной отрасли, для чего выделено b рублей. Обозначим через fi(xi) прирост мощности или прибыли на j-м предприятии, если оно получит xi рублей капитальных вложений. Требуется найти такое распределение (x1,x2, ... , xn) капитальных вложений между предприятиями, которое максимизирует суммарный прирост мощности или прибыли
z = f1(x1) + f2(х2) + ... + fn(xn)
при ограничении по общей сумме капитальных вложений
x1 + x2 + ... + xn = b
причем будем считать, что все переменные xj принимают только целые неотрицательные значения
xj = 0, или 1, или 2, или 3, ...
Функции fj(xj) мы считаем заданными, заметив, что их определение - довольно трудоемкая экономическая задача.
Воспользуемся методом динамического программирования для решения этой задачи.
Введем параметр состояния и определим функцию состояния. За параметр состояния x примем количество рублей, выделяемых нескольким предприятиям, а функцию состояния Fk(x ) определим как максимальную прибыль на первых k предприятиях, если они вместе получают x рублей. Параметр x может изменяться от 0 до b. Если из x рублей k-е предприятие получит xk рублей, то каково бы ни было это значение, остальные x - xk рублей естественно распределить между предприятиями от первого до (К-1)-го так, чтобы была получена максимальная прибыль Fk-1(x - xk). Тогда прибыль k предприятий будет равна fk(xk) + Fk-1(x - xk). Надо выбрать такое значение xk между 0 и x , чтобы эта сумма была максимальной, и мы приходим к рекуррентному соотношению
Fk(x )=max{fk(xk) + Fk-1(x -xk)}
0 £ xk £ x
для k = 2, 3, 4, ... , n . Если же k=1, то
F1(x ) = f1(x )
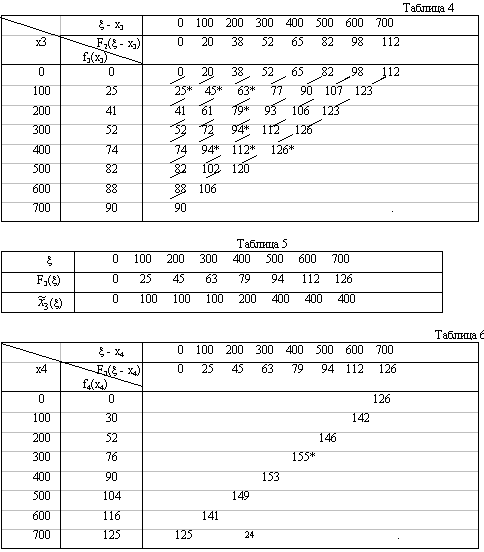
Рассмотрим конкретный пример. Пусть производственное объединение состоит из четырех предприятий (n=4). Общая сумма капитальных вложений равна 700 тыс. рублей (b=700), выделяемые предприятиям суммы кратны 100 тыс. рублей. Значения функций fj(xj) приведены в таблице 1, где, например, число 88 означает, что если третье предприятие получит 600 тыс. руб. капитальных вложений, то прирост прибыли на этом предприятии составит 88 тыс. руб.
Таблица I
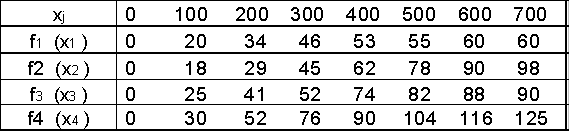
Прежде всего заполняем табл. 2. Значения f2(x2) складываем со значениями F1(x
- x2) = f1(x
- x2) и на каждой северо-восточной диагонали находим наибольшее число, которое отмечаем звездочкой и указываем соответствующее значение ![]() . Заполняем таблицу 3.
. Заполняем таблицу 3.
Продолжая процесс, табулируем функции F3(x
), ![]() (x
) и т.д. В табл. 6 заполняем только одну диагональ для значения x
= 700. Наибольшее число на этой диагонали:
(x
) и т.д. В табл. 6 заполняем только одну диагональ для значения x
= 700. Наибольшее число на этой диагонали:
Zmax = 155 тыс. руб.,
причем четвертому предприятию должно быть выделено
х*4 = ![]() 4 (700) = 300 тыс. руб.
4 (700) = 300 тыс. руб.
На долю остальных трех предприятий остается 400 тыс. руб. Из табл. 5 видно, что третьему предприятию должно быть выделено
x*3 = ![]() 3 (700-x*4) =
3 (700-x*4) = ![]() 3 (400) = 200 тыс. руб.
3 (400) = 200 тыс. руб.
Продолжая обратный процесс, находим
x*2 = ![]() 2 (700 - x*4 - x*3) =
2 (700 - x*4 - x*3) = ![]() 2 (200) = 100 тыс. руб.
2 (200) = 100 тыс. руб.
На долю первого предприятия остается
x*1 = 700 - x*4 - x*3 - x*2 = 100 тыс. руб.
Таким образом, наилучшим является следующее распределение капитальных вложений по предприятиям:
x*1 =100; x*2 =100; x*3 = 200; x*4 = 300.
Оно обеспечивает производственному объединению наибольший воможный прирост прибыли 155 тыс. руб.
Студенту рекомендуется проверить выполнение равенства
f1(x*1) + f2(x*2) + f3(x*3) + f4(x*4) = z max
Таблица 2
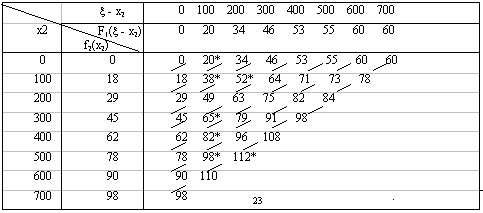
Таблица 3
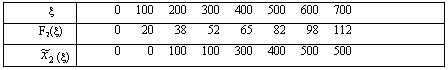
 § 9. Динамическая задача управления производством >и запасами
§ 9. Динамическая задача управления производством >и запасами
Предприятие производит партиями некоторые изделия. Предположим, что оно получило заказы на n месяцев. Размеры заказов значительно меняются от месяца к месяцу. Поэтому иногда лучше выполнять одной партией заказы нескольких месяцев, а затем хранить изделия, пока они не потребуются, чем выполнять заказ в тот именно месяц, когда этот заказ должен быть отправлен. Необходимо составить план производства на указанные n месяцев с учетом затрат на производство и хранение изделий. Обозначим:
xj - число изделий, производимых в j -й месяц;
yj - величина запаса к началу j го месяца (это число не содержит изделий, произведенных в j -м месяце);
dj - число изделий, которые должны быть отгружены в j -й месяц;
fj (xj,yj+1) - затраты на хранение и производство изделий в j -м месяце.
Будем считать, что величины запасов к началу первого месяца y1 и к концу последнего yn+1 заданы.
Задача состоит в том, чтобы найти план производства
(x1, x2, ..., xn)(1)
компоненты которого удовлетворяют условиям материального баланса
xj + yj - dj = yj+1j = 1,n(2)
и минимизируют суммарные затраты за весь планируемый период
![]() (3)
(3)
причем по смыслу задачи
xj ³ 0, yj ³ 0, j = 1,n(4)
Прежде чем приступить к решению поставленной задачи, заметим, что для любого месяца j величина yj+1 запаса к концу месяца должна удовлетворять ограничениям
0 £ yj+1 £ dj+1 + dj+2 + ... + dn(5)
т.е. объем производимой продукции xj на этапе j может быть настолько велик, что запас yj+1 удовлетворяет спрос на всех последующих этапах, но не
имеет смысла иметь yj+1 больше суммарного спроса на всех последующих этапах. Кроме того, из соотношений (2) и (4) непосредственно следует, что переменная xj должна удовлетворять ограничениям
0 £ xj £ dj + yj+1 (6)
Следует также заметить, что переменные xj, yj могут принимать только целые неотрицательные значения, т.е. мы получили задачу целочисленного нелинейного программирования.
Будем решать задачу (1)-(6) методом динамического программирования.
Введем параметр состояния и составим функцию состояния.
За параметр состояния x примем наличный запас в конце k -го месяца
x = yk+1(7)
а функцию состояния Fk(x ) определим как минимальные затраты за первые k месяцев при выполнении условия (5)
![]() (8)
(8)
где минимум берется по неотрицательным целым значениям x1,...,xk, удовлетворяющим условиям
xj + yj - dj = yj+1j = 1, k-1 (9)
xk + yk - dk = x (10)
Учитывая, что
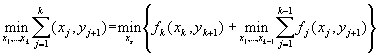 (11)
(11)
и величина запаса yk к концу (k-1) периода, как видно из уравнения (10), равна
yk = x + dk - xk (12)
приходим к рекуррентному соотношению
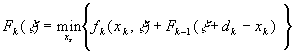 (13)
(13)
где минимум берется по единственной переменной xk, которая, согласно (6) может изменяться в пределах
0 £ xk £ dk + x (14)
принимая целые значения, причем верхняя граница зависит от значений параметра состояния, изменяющегося в пределах
0 £ x £ dk+1 + dk+2 + ... + dn(15)
а индекс k может принимать значения
k = 2, 3, 4, ... , n (16)
Если k=1, то
![]() (17)
(17)
где
x1 = x + d1 - y1(18)
0£ x £ d2 + d3 + ... + dn(19)
т.е. на начальном этапе при фиксированном уровне y1 исходного запаса каждому значению параметра x отвечает только одно значение переменной x1, что несколько уменьшает объем вычислений.
Применив известную вычислительную процедуру динамического программирования, на последнем шаге (при k = n) находим значение последней компоненты xn* оптимального решения, а остальные компоненты определяем как
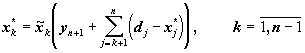 (20)
(20)
Рассмотрим более подробно функции затрат fj(xj, yj+1) и рекуррентные соотношения. Пусть
j j(xj) = axj2 + bxj + c
j j (xj) - затраты на производство (закупку) xj единиц продукции на этапе j;
hj - затраты на хранение единицы запаса, переходящей из этапа j в этап j+1.
Тогда затраты на производство и хранение на этапе j равны
fj(xj, yj+1) = j j(xj) + hj yj+1 = axj2 + bxj + c + hj yj+1.(21)
Выведенные ранее рекуррентные соотношения динамического программирования для решения задачи управления производством и запасами в нашем случае принимают вид:
![]() (22)
(22)
где
k = 2, 3, ... , n(23)
0 £ yk+1 £ dk+1 + dk+1 + ... + dn (24)
0 £ xk £ dk + yk+1(25)
yk = yk+1 + dk - xk(26)
Если же k=1, то
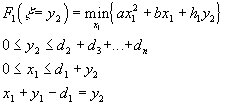
Остается заметить, что полезно обозначить выражение в фигурных скобках через
W k(xk, yk+1) = axj2 + bxj + c + hkyk+1 + Fk-1(yk)(31)
и записать рекуррентное соотношение (22) в виде
![]() (32)
(32)
где минимум берется по целочисленной переменной xk, удовлетворяющей условию (25).
Пример. Рассмотрим трехэтапную систему управления запасами с дискретной продукцией и динамическим детерминированным спросом.
Пусть спрос (заявки) потребителей на нашу продукцию составляют: на первый этап d1=3 единицы, на второй – d2=2, на третий - d3=4 единицы. К началу первого этапа на складе имеется только 2 единицы продукции, т.е. начальный уровень запаса равен y1=2. Затраты на хранение единицы продукции на разных этапах различны и составляют соответственно h1=1, h2=3, h3=2. Затраты на производство xj единиц продукции на j-м этапе определяются функцией
j
j(xj) = xj2 + 5xj + 2 ![]() (33)
(33)
т.е. а=1; b=5; с=2. Требуется указать, сколько единиц продукции на отдельных этапах следует производить, чтобы заявки потребителей были удовлетворены, а наши общие затраты на производство и хранение за все три этапа были наименьшими.
Исходные данные задачи можно кратко записать одной строкой:
d1 d2 d3 a b c h1 h2 h3y1
1 2 4 15 2 1 3 22
Воспользовавшись рекуррентными соотношениями, последовательно вычисляем
F1 (x
= y2), F2 (x
= y3), ..., Fk (x
= yk+1), ... и соответственно находим ![]() 1 (x
= y2),
1 (x
= y2), ![]() 2 (x
= y3 ), ..., `
2 (x
= y3 ), ..., `
![]() k (x
= yk+1), ...
k (x
= yk+1), ...
Положим k = 1. Согласно (27) имеем
![]() (34)
(34)
Учтем, что согласно (28) параметр состояния x = у2 может принимать целые значения на отрезке
0 ![]() у2
у2 ![]() d2 + d3
d2 + d3
0 ![]() y2
y2 ![]() 2 + 4
2 + 4
т.е.
у2 = 0, 1, 2, 3, 4, 5, 6.
При этом, вообще говоря, каждому значению параметра состояния должна отвечать определенная область изменения переменной x1, характеризуемая условием (29)
0 ![]() х1
х1 ![]() 3 + у2
3 + у2
Однако, на первом этапе объем производства х1 не может быть меньше единицы, так как спрос d1 = 3, а исходный запас у1 = 2. Более того, из балансового уравнения
х1 + у1 - d1 = у2
непосредственно следует, что объем производства связан со значением параметра состояния x = у2 соотношением
x1 = y2 + d1 - y1 = y2 + 3 - 2 = y2 +1(35)
В этом и состоит особенность первого этапа. Если задан уровень запаса к началу первого этапа, то каждому значению у2 отвечает единственное значение х1 и потому
F1(x = y2) = W 1 (x1, y2)
Придавая у2 различные целые значения от 0 до 6 и учитывая (35), находим
y2 = 0,x1 = 0+1 = 1,W 1 (1;0) = 12 + 5× 1 + 2 + 1× 0 = 8
y2 = 1, x1 = 1+1 = 2,W 1 (2;1) = 22 + 5× 2 + 2 + 1× 1 = 17
и т.д. Значения функции состояния F1(x ) представлены в табл. 1
Таблица 1
|
x = y2 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
F1 (x = y2) |
8 |
17 |
28 |
41 |
56 |
73 |
92 |
|
x1(x =y2) |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
Переходим ко второму этапу. Полагаем k = 2 и табулируем функцию
F2(x = y3) с помощью соотношения (32)
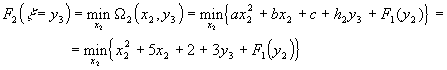 (37)
(37)
Здесь минимум берется по единственной переменной х2, которая может изменяться, согласно (25), в пределах
0 £ x2 £ d2 + y3 или 0 £ x2 £ 2 + y3(38)
где верхняя граница зависит от параметра состояния x = у3, который, согласно (15), принимает значения на отрезке
0 £ y3 £ d3 , т.е. 0 £ y3 £ 4(39)
а аргумент у2 в последнем слагаемом справа в соотношении (37) связан с х2 и у3 балансовым уравнением
x2 + y2 - d2 = y3
откуда следует
y2 = y3 + d2 - x2 = y3 + 2 - x2(40)
Придавая параметру состояния различные значения от 0 до 4, будем последовательно вычислять W
2 (x2, x
), а затем определять F2(x
) и ![]() 2(x
).
2(x
).
Положим, например x = у3 = 2. Тогда, согласно (38),
0 £ x2 £ 4,
т.е. переменная х2 может принимать значения: 0, 1, 2, 3, 4, а каждому значению х2 отвечает определенное значение у2, вычисляемое по формуле (40):
у2 = 4 - х2
Последовательно находим:
если x2 = 0, то y2 = 4-0 = 4,W 2 (0,2) = 02 + 5× 0 + 2 + 3× 2 + F1(4) = 8 + 56 = 64,
x2 = 1, y2 = 4-1 = 3, W 2 (1,2) = 12 + 5× 1 + 2 + 3× 2 + F1(3) = 14 + 41 = 55,
x2 = 2, y2 = 4-2 =2, W 2 (2,2) = 22 + 5× 2 + 2 + 3× 2 + F1(2) = 22 + 28 = 50,
x2 = 3, y2 = 4-3 = 1, W 2 (3,2) = 32 + 5× 3 + 2 + 3× 2 + F1(1) = 32 + 17 = 49*,
x2 = 4, y2 = 4-4 = 0, W 2 (3,2) = 42 + 5× 4 + 2 + 3× 2 + F1(0) = 44 + 8 = 52.
Наименьшее из полученных значений W 2 есть F2 (2), т.е.
причем минимум достигается при значении х2, равном
`
![]() 2 (x
= y3 = 2) = 3
2 (x
= y3 = 2) = 3
Аналогично для значения параметра x = у3 = 3, проведя необходимые вычисления, найдем
F2 (x
= y3 = 3) = 63;`
![]() 2 (x
= y3 = 3) = 3.
2 (x
= y3 = 3) = 3.
Процесс табулирования функции F2 (x = y3) приведен в табл. 2, а результаты табулирования сведены в табл. 3.
Таблица 3
|
x = у3 |
0 |
1 |
2 |
3 |
4 |
|
F2 (x = y3) |
24 |
36 |
49 |
63 |
78 |
|
|
2 |
2 |
3 |
3 |
4 |
Переходим к следующему этапу. Полагаем k=3 и табулируем функцию F3 (x = y4):
![]()
Вычисляем значение функции состояния только для одного значения аргумента x = у4 = 0, так как не хотим оставлять продукцию в запас в конце исследуемого периода. Процесс вычислений приведен в табл. 4. Получаем
![]()
причем минимум достигается при двух значениях переменной х3, равных
`
![]() 3 (x
= y4 = 0) = 3 или `
3 (x
= y4 = 0) = 3 или `
![]() 3 (x
= y4 = 0) = 4.
3 (x
= y4 = 0) = 4.
Таким образом, мы получили не только минимальные общие затраты на производство и хранение продукции, но и последнюю компоненту оптимального решения. Она равна
![]() = 3 или
= 3 или ![]() = 4.
= 4.
Рассмотрим случай, когда на последнем этапе планируем выпускать три единицы продукции
![]() = 3.
= 3.
Остальные компоненты оптимального решения найдем по обычным правилам метода динамического программирования. Чтобы найти предпоследнюю компоненту, учтем, что
х3 + у3 - d3 = y4
или
3 + у3 - 4 = 0,
откуда
у3 = 1.
Из таблицы (3) значений ![]() находим
находим
![]()
Аналогично, продолжая двигаться в обратном направлении и учтя, что
х2 + у2 - d2 = y3
|
|
|
|
xk |
yk = yk+1 + dk - xk |
W k(xk, yk+1) =j k(xk) + hkyk+1 + Fk-1(yk) |
|
0 £ y3 £ d3 |
x = y3 |
0 £ x2 £ d2 + y3 |
x2 |
y2 = y3 + d2 - x2 |
W
2(x2, y3) = a |
|
0 £ y3 £ 4 |
x = y3 |
0 £ x2 £ 2 + y3 |
x2 |
y2 = y3 + 3 - x2 |
|
|
y3 = 0 |
0 £ x2 £ 2 |
x2 = 0 x2 = 1 x2 = 2 |
y2 = 2-0 = 2 y2 = 2- 1 = 1 y2 = 2-2 = 0 |
W 2(0;0) = 02 + 5× 0 + 2 + 3× 0 + F1(2) =2+28 =30 W 2(1;0) = 12 + 5× 1 + 2 +3× 0 + F1(1)=8+17 =25 W 2(2;0) = 22 +5× 2 + 2 + 3× 0 +F1(0) =16+8=24* |
|
|
y3 = 1 |
0 £ x2 £ 3 |
x2 = 0 x2 = 1 x2 = 2 x2 = 3 |
y2 = 3 - 0 = 3 y2 = 3-1 = 2 y2 = 3-2 = 1 y2 = 3-3 = 0 |
W 2(0;1) = 02 + 5× 0 + 2 + 3× 1 + F1(3) = 5+41=46 W 2(1;1) = 12 + 5× 1 + 2 + 3× 1 + F1(2) =11+28 =39 W 2(2;1) = 22 + 5× 2 + 2 + 3× 1 + F1(1)=19+17 =36* W 2(3;1) = 32 + 5× 3 + 2 + 3× 1 + F1(0)=29+8 =37 |
|
|
y3 = 2 |
....................... |
........ |
............................ |
............................................................. |
|
|
y3 = 3 |
0 £ x2 £ 5 |
x2 = 0 x2 = 1 x2 = 2 x2 = 3 x2 = 4 x2 = 5 |
y2 = 5 - 0 = 5 y2 = 5 - 1 = 4 y2 = 5 - 2 = 3 y2 = 5 - 3 = 2 y2 = 5 - 4 = 1 y2 = 5 - 5 = 0 |
W 2(0;3) = 02 + 5× 0 + 2 + 3× 3 + F1(5) = 11+73=84 W 2(1;3) = 12 + 5× 1 + 2 + 3× 3 + F1(4) =17+56 =73 W 2(2;3) = 22 + 5× 2 + 2 + 3× 3 + F1(3)=25+41 =66 W 2(3;3) = 32 + 5× 3 + 2 + 3× 3 + F1(2)=35+28 =63* W 2(4;3) = 42 + 5× 4 + 2 + 3× 3 + F1(1)=47+17 =64 W 2(5;3) = 52 + 5× 5 + 2 + 3× 3 + F1(0)=61+8 =69 |
|
|
y3 = 4 |
0 £ x2 £ 6 |
x2 = 0 x2 = 1 x2 = 2 x2 = 3 x2 = 4 x2 = 5 x2 = 6 |
y2 = 6 - 0 = 6 y2 = 6 - 1 = 5 y2 = 6 - 2 = 4 y2 = 6 - 3 = 3 y2 = 6 - 4 = 2 y2 = 6 - 5 = 1 y2 = 6 - 6 = 0 |
W 2(0;4) = 02 + 5× 0 + 2 + 3× 4 + F1(6) = 14+92=106 W 2(1;4) = 12 + 5× 1 + 2 + 3× 4 + F1(5) =20+73 =93 W 2(2;4) = 22 + 5× 2 + 2 + 3× 4 + F1(4)=28+56 =84 W 2(3;4) = 32 + 5× 3 + 2 + 3× 4 + F1(3)=38+41 =79 W 2(4;4) = 42 + 5× 4 + 2 + 3× 4 + F1(2)=50+28 =78* W 2(5;4) = 52 + 5× 5 + 2 + 3× 4 + F1(1)=64+17 =81 W 2(6;4) = 62 + 5× 6 + 2 + 3× 4 + F1(0)=80+8 =88 |
|
|
|
|
xk |
yk = yk+1 + dk - xk |
W k(xk, yk+1) = j k(xk) + hkyk+1 + Fk-1(yk) |
|
0 £ y4 £ 0 |
x = y4 |
0 £ x3 £ d3 + y4 |
x3 |
y3 = y4 + d3 - x3 |
W 3(x3, y4) = a1+ bx3 + c + h3y4 + F2(y3) |
|
y4 = 0 |
x = y4 |
0 £ x3 £ 4 |
x3 |
y3 = y4 + 4 - x3 |
|
|
y4 = 0 |
0 £ x3 £ 4 |
x3 = 0 x3 = 1 x3 = 2 x3 = 3 x3 = 4 |
y3 = 4-0 = 4 y3 = 4- 1 = 3 y3 = 4-2 = 2 y3 = 4-3 = 1 y3 = 4-4 = 0 |
W 3(0;0) = 02 + 5× 0 + 2 + 2× 0 + F2(4)=2+78=80 W 3(1;0) = 12 + 5× 1 + 2 + 2× 0 + F2(3)=8+63=71 W 3(2;0) = 22 + 5× 2 + 2 + 2× 0 + F2(2)=16+49=65 W 3(3;0) = 32 + 5× 3 + 2 + 2× 0 + F2(1)=26+36=62* W 3(4;0) = 42 + 5× 4 + 2 + 2× 0 + F2(0)=38+24=62* |
Самопроверка результатов Таблица 5
|
Этапы |
январь |
февраль |
март |
Итого за 3 месяца |
|
Имеем продукции к началу месяца, шт. |
у1 = 2 |
у2 = 1 |
у3 = 1 |
у1 = 2 |
|
Производим в течение месяца, шт. |
х1 = 2 |
х2 = 2 |
х3 = 3 |
х1+ х2+ х3 = 7 |
|
Отпускаем заказчикам, шт. |
d1 = 3 |
d2 = 2 |
d3 = 4 |
d1+ d2+ d3 = 9 |
|
Остаток к концу месяца (храним в течение текущего месяца), шт. |
у2 = 1 |
у3 = 1 |
у4 = 0 |
|
|
Затраты на производство, руб. |
j (х1)=16 |
j (х2)=16 |
j (х3)=26 |
j (х1) + j (х2) + j (х3) = 58 |
|
Затраты на хранение, руб. |
h1у2 = 1 |
h2у3 = 3 |
0 |
h1у2 + h2у3 = 4 |
или
2 + у2 - 2 = 1,
получаем
у2 = 1;
из таблицы (2) значений х1(x ) находим
![]() .
.
Итак, оптимальный план производства имеет вид
х1 = 2
х2 = 3
х3 = 3,
а минимальные общие затраты составляют 62 единицы.
Полезна самопроверка полученного результата. Для этого по исходным данным и найденному плану производства заполняем таблицу 5 и убеждаемся, что заявки потребителей на каждом этапе выполняются
у1 + х1 ³ d1у2 + х2 ³ d2у3 + х3 ³ d3
2 + 2 ³ 31 + 2 ³ 21 + 3 ³ 4
и что суммарный объем производства и имевшегося к началу первого этапа запаса продукции равен суммарной потребности
у1 + х1 + х2 + х3 = d1 + d2 + d3
2 + 2 + 2 + 3 = 3 + 2 + 4
причем это достигается при наименьших возможных затратах на производство и хранение продукции
j (х1) + j (х2) + j (х3) + h1у2 + h2у3 = F3(y4=0)
16 + 16 + 26 + 1 + 4 = 62
Студенту рекомендуется найти другой вариант оптимальной производственной программы, когда на последнем этапе предполагается произвести 4 единицы продукции, и так же выполнить самопроверку.
§10. Матричная модель производственной программы предприятияПредприятие состоит из n цехов. Каждый цех выпускает только один вид продукции. Пусть j-й цех выпускает xj единиц продукции, из которых yj единиц отправляет за пределы предприятия как товарную продукцию, а остающаяся часть используется другими цехами предприятия.
Пусть ajk – кол-во продукции j-го цеха, расходуемое на производство единицы продукции k-го цеха. Числа aij образуют матрицу А коэффициентов прямых затрат, называемую структурной. Производственная программа предприятия представляется вектором X(x1, … , xn), а выпуск товарной продукции – вектором У(у1, … , уn). Очевидно,
(Е - А)Х = У или Х = (Е - А)-1У.
Элементы любого столбца матрицы (Е - А)-1, называемой матрицей коэффициентов полных затрат, показывают затраты всех цехов, необходимые для обеспечения выпуска единицы товарного продукта того цеха, номер которого совпадает с номером данного столбца.
При заданном векторе У выпуска товарной продукции легко определить производственную программу Х и наоборот.
Дополним структурную матрицу А матрицей В коэффициентов прямых затрат, получаемых со стороны сырья, полуфабрикатов и т.п. Очевидно, затраты получаемых со стороны материалов определяются элементами матрицы S, где
В = (Е - А)-1У = S
Зная закупочные цены сырья и рыночные цены готовой продукции, можно подсчитать прибыль.
§11. Матричная игра как модель конкуренции и сотрудничестваПусть игроки – Первый и Второй, играют в матричную игру с матрицей ![]() . Пусть стратегия Первого есть
. Пусть стратегия Первого есть ![]() , а Второго –
, а Второго – ![]() . Тогда выигрыш Первого есть случайная величина (с.в.)
. Тогда выигрыш Первого есть случайная величина (с.в.) ![]() с рядом распределения:
с рядом распределения:
|
|
a1j |
… |
|
… |
|
||||
|
|
… |
|
… |
|
Математическое ожидание этой с.в., т.е. ![]() есть средний выигрыш Первого. Пусть
есть средний выигрыш Первого. Пусть ![]() есть дисперсия этой с.в. Естественно назвать среднее квадратическое отклонение с.в.
есть дисперсия этой с.в. Естественно назвать среднее квадратическое отклонение с.в. ![]() , т.е.
, т.е. ![]() риском для Первого при игре со стратегиями
риском для Первого при игре со стратегиями ![]() . Поскольку выигрыш Первого есть проигрыш для Второго, то
. Поскольку выигрыш Первого есть проигрыш для Второго, то ![]() есть случайный проигрыш Второго и
есть случайный проигрыш Второго и ![]() вполне естественно можно назвать риском игры с такими стратегиями и для Второго.
вполне естественно можно назвать риском игры с такими стратегиями и для Второго.
Предположим сначала, что игроки озабочены только максимизацией среднего дохода за партию игры – обычная цель в таких играх. Тогда игроки будут играть со своими оптимальными стратегиями: ![]() – Первый игрок и
– Первый игрок и ![]() – Второй.
– Второй.
Математическое ожидание с. в. ![]() называется ценой игры, обозначим ее
называется ценой игры, обозначим ее ![]() .
.
Но что же назвать риском всей игры?
Вычислим дисперсию выигрыша Первого при оптимальных стратегиях игроков.
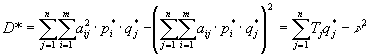 .
.
Так как ![]() , а через
, а через ![]() сумма обозначена
сумма обозначена ![]() .
.
Заметим, что в сумме ![]() можно оставить лишь те слагаемые, у которых
можно оставить лишь те слагаемые, у которых ![]()
Заметим теперь, что если Первый играет со стратегией ![]() , а Второй отвечает
, а Второй отвечает ![]() -й чистой стратегией, то выигрыш первого есть с.в. с рядом распределения:
-й чистой стратегией, то выигрыш первого есть с.в. с рядом распределения:
|
|
a1j |
… |
|
… |
|
||||
|
|
… |
|
… |
|
Если ![]() есть оптимальная стратегия Первого, а
есть оптимальная стратегия Первого, а ![]() , то из теории матричных игр с нулевой суммой известно, что выигрыш Первого при таких стратегиях по-прежнему равен цене игры
, то из теории матричных игр с нулевой суммой известно, что выигрыш Первого при таких стратегиях по-прежнему равен цене игры ![]() , а дисперсия выигрыша Первого при этом равна
, а дисперсия выигрыша Первого при этом равна ![]() , то есть равна
, то есть равна ![]() . Таким образом, что происходит с риском выигрыша Первого, можно понять, сравнив дисперсию при оптимальных стратегиях
. Таким образом, что происходит с риском выигрыша Первого, можно понять, сравнив дисперсию при оптимальных стратегиях ![]() и дисперсию
и дисперсию ![]() или величины
или величины ![]() и
и ![]() . Пусть
. Пусть ![]() Как легко понять, если среди
Как легко понять, если среди ![]() есть разные числа, то
есть разные числа, то ![]()
Теперь можно сделать следующий вывод:
Чуть-чуть отойдя от своей оптимальной стратегии (смотрите ниже Пример) и таким образом почти не уменьшив свой выигрыш, Первый может значительно уменьшить свой риск. При этом уменьшается и риск Второго, что отвечает и его интересам.
Чисто математически можно сказать, что в описанной ситуации риск выигрыша Первого не зависит от его стратегии непрерывно.
Рассмотрим подробно пример матричной игры с матрицей ![]() . Как известно, общий случай в окрестности оптимальных стратегий игроков сводится к анализу такой игры.
. Как известно, общий случай в окрестности оптимальных стратегий игроков сводится к анализу такой игры.
Пример. Пусть матрица игры есть ![]() .
Графическое решение этой игры показано на рисунке 1.
.
Графическое решение этой игры показано на рисунке 1.
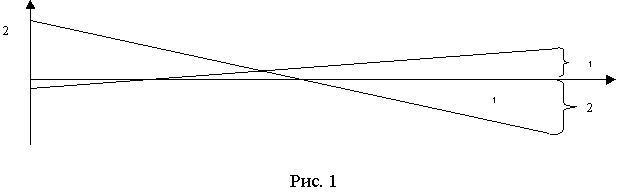
Цена игры ![]() , оптимальные стратегии игроков есть
, оптимальные стратегии игроков есть ![]() ,
, ![]() . Дисперсия выигрыша Первого при оптимальных стратегиях
. Дисперсия выигрыша Первого при оптимальных стратегиях ![]() , т. е. риск игры равен примерно 1. Далее вычисления дают
, т. е. риск игры равен примерно 1. Далее вычисления дают ![]() ,
, ![]() ;
; ![]() ,
,![]() Примерная, но достаточно точная зависимость риска Первого в малой окрестности его оптимальной стратегии показана на рис. 2.
Примерная, но достаточно точная зависимость риска Первого в малой окрестности его оптимальной стратегии показана на рис. 2.
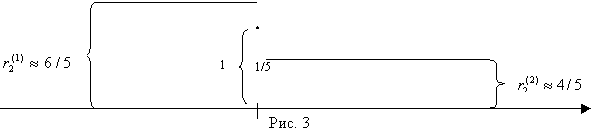
Как видно из рис. 2 при отходе Первого от своей оптимальной стратегии вправо, т. е. при увеличении вероятности x выбора им 1-й строки. Второй начинает отвечать 1-й чистой стратегией и риск Первого скачком увеличивается до ![]() , а при отходе Первого от своей оптимальной стратегии влево Второй переходит на свою 2-ю чистую стратегию и риск Первого скачком снижается до
, а при отходе Первого от своей оптимальной стратегии влево Второй переходит на свою 2-ю чистую стратегию и риск Первого скачком снижается до ![]()
Аналогичное верно и в отношении Второго. Кратко повторим. Примерная, но достаточно точная зависимость риска Второго в малой окрестности его оптимальной стратегии показана на рис. 3. Как видно из рис. 3 при отходе второго от своей оптимальной стратегии вправо, т. е. при увеличении вероятности у выбора им 1-й строки Первый начинает отвечать 2-й чистой стратегией и риск Второго скачком уменьшается до ![]() , а при отходе второго от своей оптимальной стратегии влево Первый переходит на свою 1-ю чистую стратегию и риск Второго скачком увеличивается до
, а при отходе второго от своей оптимальной стратегии влево Первый переходит на свою 1-ю чистую стратегию и риск Второго скачком увеличивается до ![]()
Пусть ![]() . Эту величину и можно назвать риском всей игры. Однако играть с таким риском можно лишь при согласии обеих сторон. Для анализируемой игры
. Эту величину и можно назвать риском всей игры. Однако играть с таким риском можно лишь при согласии обеих сторон. Для анализируемой игры ![]() и игроки для достижения такого риска должны играть так: Первый играет со своей оптимальной стратегией
и игроки для достижения такого риска должны играть так: Первый играет со своей оптимальной стратегией ![]() 3,5), а Второй должен использовать 2-ю чистую стратегию.
3,5), а Второй должен использовать 2-ю чистую стратегию.
Финансовой называется операция, начальное и конечное состояния которой имеют денежную оценку и цель проведения которой заключается в максимизации дохода - разности между конечной и начальной оценками.
Почти всегда финансовые операции проводятся в условиях неопределенности и потому их результат невозможно предсказать заранее. Поэтому финансовые операции рискованны, т.е. при их проведении возможны как прибыль так и убыток (или не очень большая прибыль по сравнению с той, на что надеялись проводившие эту операцию).
Как оценить операцию с точки зрения ее доходности и риска?
Существует несколько разных способов. Наиболее распространенным является представление дохода операции как случайной величины и оценка риска операции как среднего квадратического отклонения этого случайного дохода.
Рассмотрим какую-нибудь операцию, доход которой есть случайная величина Q. Средний ожидаемый доход `
Q - это математическое ожидание с.в. Q: ![]() , где pi есть вероятность получить доход qi. А среднее квадратическое отклонение (СКО)
, где pi есть вероятность получить доход qi. А среднее квадратическое отклонение (СКО) ![]() - это мера разбросанности возможных значений дохода вокруг среднего ожидаемого дохода. Вполне разумно считать s
количественной мерой риска операции и обозначить r. Напомним, что дисперсия
- это мера разбросанности возможных значений дохода вокруг среднего ожидаемого дохода. Вполне разумно считать s
количественной мерой риска операции и обозначить r. Напомним, что дисперсия
D[Q] = M [(Q - ` Q)2] = M [Q2] - ` Q2.
Рассмотрим четыре операции Q1, Q2, Q3, Q,4. Найдем средние ожидаемые доходы ` Qi и риски ri операций.
Ряды распределения, средние ожидаемые доходы и риски:
|
Q1 |
: |
5 |
2 |
8 |
4 |
` Q1 = 29/6 » 4.81 |
r1 » 1.77 |
|
1/2 |
1/6 |
1/6 |
1/6 |
||||
|
Q2 |
: |
2 |
3 |
4 |
12 |
` Q2 = 25/6 » 4.16 |
r2 » 3.57 |
|
1/2 |
1/6 |
1/6 |
1/6 |
||||
|
Q3 |
: |
8 |
5 |
3 |
10 |
` Q3 = 7 |
r3 » 2.30 |
|
1/2 |
1/6 |
1/6 |
1/6 |
||||
|
Q4 |
: |
1 |
4 |
2 |
8 |
` Q4 = 17/6 » 2.81 |
r4 » 2.54 |
|
1/2 |
1/6 |
1/6 |
1/6 |
Напомним, как находить Q и r.
![]()
r1 = M [Q21 ] - (Q1)2; M [Q21] = 25*1/2+4*1/6+64*1/6+16*1/6=159/6;
Q21 = 841/36; D [Q1] = (159*6-841)/36 = 113/36; ![]()
Нанесем средние ожидаемые доходы ` Q и риски r на плоскость - доход откладываем по горизонтали, а риски по вертикали (см. рис.):
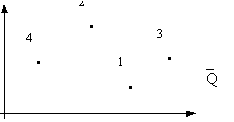
Получили 4 точки. Чем правее точка (` Q, r), тем более доходная операция, чем точка выше - тем более она рисковая. Значит, нужно выбирать точку правее и ниже. Точка (` Q¢ , r¢ ) доминирует точку (` Q, r) если ` Q¢ ³ ` Q и r¢ £ r. В нашем случае 1-я операция доминирует 2-ю, 3-я доминирует 2-ю и 3-я доминирует 4-ю. Но 1-я и 3-я операции несравнимы - доходность 3-й больше, но и риск ее тоже больше.
Точка, не доминируемая никакой другой называется оптимальной по Парето, а множество всех таких точек называется множеством оптимальности по Парето. Легко видеть, что если из рассмотренных операций надо выбирать лучшую, то ее обязательно надо выбрать из операций, оптимальных по Парето.
Для нахождения лучшей операции иногда применяют подходящую взвешивающую формулу, которая для пар (` Q, r) дает одно число, по которому и определяют лучшую операцию. Например, пусть взвешивающая формула есть j (Q)= 2× Q - r . Тогда получаем:
j (Q1)= 2*4.81-1.77 = 7.85; j (Q2)= 4.75; j (Q3)= 11.70; j (Q4)= 3.08
Видно, что 3-я операция - лучшая, а 4-я - худшая.
§ 13. Задача формирования оптимального портфеля ценных бумаг.На финансовом рынке обращается, как правило, множество ценных бумаг: государственные ценные бумаги, акции частных фирм, векселя и т.п. Ценная бумага удостоверяет возможность получения некоторого дохода. В общем случае владелец получит некоторый случайный доход.
Из характеристик ценных бумаг наиболее значимы две: эффективность и рискованность. Эффективность E есть некоторый обобщенный показатель дохода или прибыли. Будем считать E случайной величиной, ее математическое ожидание есть mЕ.
При исследовании финансового рынка дисперсию обычно называют вариацией V и рискованность обычно отождествляется со Средним Квадратическим Отклонением. Таким образом, V=D[E]= M[( E- mЕ )2 ] и s
=![]() .
.
Рассмотрим общую задачу распределения капитала, который участник рынка хочет потратить на покупку ценных бумаг, по различным видам ценных бумаг.
Пусть xi - доля капитала, потраченная на закупку ценных бумаг i-го вида. Пусть Ei - эффективность (можно считать, доход за некоторый период времени) ценных бумаг i-го вида, стоящих одну денежную единицу. Через Vij будем обозначать ковариацию ценных бумаг i-го и j -го видов (или корреляционный момент Kij). Пусть mi - математическое ожидание эффективности Ei и s
i = ![]() , где Vii - вариация или дисперсия этой эффективности Ei . Рискованность ценной бумаги i-го вида отождествим со средним квадратическим отклонением s
i.
, где Vii - вариация или дисперсия этой эффективности Ei . Рискованность ценной бумаги i-го вида отождествим со средним квадратическим отклонением s
i.
Набор ценных бумаг, находящихся у участника рынка, называется его портфелем. Эффективность портфеля ( в простейшем случае это доход, приносимый ценными бумагами портфеля за какой-нибудь промежуток времени), вообще говоря, есть случайная величина, обозначим ее через Ep, тогда ожидаемое значение этой эффективности mp =M[Ep]=![]() . Дисперсия портфеля есть D[Ep ]=
. Дисперсия портфеля есть D[Ep ]= ![]() . Величина
. Величина ![]() может быть названа риском портфеля. Обычно D[Ep] обозначается Vp. Итак, мы выразили эффективность и риск портфеля через эффективности составляющих его ценных бумаг и их ковариации.
может быть названа риском портфеля. Обычно D[Ep] обозначается Vp. Итак, мы выразили эффективность и риск портфеля через эффективности составляющих его ценных бумаг и их ковариации.
Каждый владелец портфеля ценных бумаг сталкивается с дилеммой: хочется иметь эффективность побольше, а риск поменьше. Однако поскольку "нельзя поймать двух зайцев сразу", необходимо сделать определенный выбор между эффективностью и риском.
Математическая формализация задачи формирования оптимального портфеля такова:
Найти xi, минимизирующие вариацию эффективности портфеля
Vp = ![]() ,
,
при условии, что обеспечивается заданное значение ожидаемой эффективности портфеля mp, т.е.
mp =![]() .
.
поскольку xi - доли, то в сумме они должны составлять единицу:
![]() =1 .
=1 .
Решение (оптимальное) этой задачи обозначим *. Если x*i >0 , то это означает рекомендацию вложить долю x*i наличного капитала в ценные бумаги i-го вида. Если же x*i <0 , то содержательно это означает провести операцию "short sale". Если такие операции невозможны, значит необходимо ввести ограничения xi ³ 0 . Что такое операция "short sale" ?
Если x*i < 0 , то инвестор, формирующий портфель, обязуется через какое-то время поставить ценные бумаги i-го вида (вместе с доходом, какой они бы принесли их владельцу за это время). За это сейчас он получает их денежный эквивалент. На эти деньги он покупает более доходные ценные бумаги и получает по ним доход и оказывается в выигрыше!
Если на рынке есть безрисковые бумаги (к таким можно с некоторой натяжкой отнести государственные ценные бумаги), то решение задачи об оптимальном портфеле сильно упрощается и приобретает замечательное новое качество.
Пусть m0 - эффективность безрисковых бумаг, а x0 - доля капитала в них вложенного. Пусть mr - средняя ожидаемая эффективность и Vr, s r - вариация (дисперсия), СКО эффективности рисковой части портфеля, в рисковую часть портфеля вложено (1-x0) часть всего капитала. Тогда ожидаемая эффективность всего портфеля mp =x0 m0 +(1-x0 )mr, вариация портфеля Vp =(1-x0 )2 Vr и риск портфеля s p =(1-x0 ) s r (считается, что безрисковые бумаги некоррелированы с остальными). Исключая x0, получим
mp = m0 +s p (m -m0 )/ s r ,
т.е. ожидаемая эффективность портфеля линейно зависит от его риска.
Рассмотрим задачу об оптимальном портфеле в этом случае. Рисковые виды ценных бумаг будем нумеровать числами от 1 до n .
![]()
x0 m0 + ![]() = mp
= mp
x0 + ![]() = 1
= 1
Изложим теперь окончательное решение этой задачи.
Пусть V - матрица ковариаций рисковых видов ценных бумаг, X=(xi), M=(mi) - векторы-столбцы долей xi капитала, вкладываемых в i-й вид рисковых ценных бумаг и ожидаемых эффективностей этого вида, i=1,.., n. Пусть также I - n-мерный вектор-столбец, компоненты которого есть 1. Тогда оптимальное значение долей xi есть
![]() .
.
Здесь V-1 - матрица, обратная к V . В числителе дроби стоит число, в знаменателе, если выполнить все действия (верхний индекс Т означает транспонирование вектора-столбца), тоже получится число, причем константа, определяемая рынком и не зависящая от инвестора, V-1(M-m0I) - вектор-столбец размерности n . Видно, что этот вектор не зависит от эффективности портфеля mp. Таким образом, вектор долей рисковых видов ценных бумаг пропорциональный этому вектору также не зависит от mp. Следовательно, структура рисковой части портфеля не зависит от mp. Однако сумма компонент вектора X* зависит от mp, именно, компоненты вектора X* пропорционально увеличиваются с ростом mp, поэтому доля x0 безрисковых вложений будет при этом сокращаться.
Пример. Сформировать оптимальный портфель заданной эффективности из трех видов ценных бумаг: безрисковых эффективности 2 и некоррелированных рисковых ожидаемой эффективности 4 и 10 и рисками 2 и 4 . Как устроена рисковая часть оптимального портфеля? При какой ожидаемой эффективности портфеля возникает необходимость в операции "short sale" и с какими ценными бумагами?
Решение. Итак, m0 =2, M=![]() , V=
, V=![]() . Зададимся эффективностью портфеля mp. Теперь надо найти обратную матрицу к матрице V . Это просто: V-1 =
. Зададимся эффективностью портфеля mp. Теперь надо найти обратную матрицу к матрице V . Это просто: V-1 = ![]() . Вычислим знаменатель:
. Вычислим знаменатель:
![]() .
.
Итак, вектор долей рисковых бумаг есть X* =((mз-2)/5)![]() . Таким образом, рисковые доли должны быть одинаковы и каждая из них равна (mз-2)/10 . Следовательно, x*0 =1-(mр-2)/5 . Понятно, что необходимость в операции "short sale" возникнет, если x*0 < 0, т.е. когда mр > 7 .
. Таким образом, рисковые доли должны быть одинаковы и каждая из них равна (mз-2)/10 . Следовательно, x*0 =1-(mр-2)/5 . Понятно, что необходимость в операции "short sale" возникнет, если x*0 < 0, т.е. когда mр > 7 .
Можно доказать, что риск оптимального портфеля в зависимости от его доходности при наличии безрисковых бумаг равен ![]() , где
, где ![]()
Постановку задачи формирования оптимального портфеля (1) можно словами сформулировать так:
Сформировать портфель минимального риска из всех имеющих эффективность не менее заданной.
Но столь же естественна и задача формирования портфеля максимальной эффективности из всех имеющих риск не более заданного, т.е. найти ![]() , максимизирующие ожидаемую эффективность портфеля
, максимизирующие ожидаемую эффективность портфеля
![]()
при условии, что обеспечивается значение риска портфеля не более заданного, т.е.
![]()
поскольку ![]() – доли, то в сумме они должны составлять единицу:
– доли, то в сумме они должны составлять единицу: ![]()
Если на рынке есть безрисковые бумаги, то в такой постановке задача формирования такого оптимального портфеля имеет решение, очень похожее на (2): Оптимальное значение долей ![]() рисковых бумаг есть
рисковых бумаг есть
![]() (3)
(3)
Можно доказать, что эффективность портфеля максимальной эффективности в зависимости от заданного его риска ![]() равна
равна ![]() .
.
Предположим, что ЛПР (Лицо, Принимающее Решения) рассматривает несколько возможных
решений i=1,..m. Ситуация неопределенна, понятно лишь, что наличествует
какой-то из вариантов ![]() . Если будет
принято
. Если будет
принято ![]() -e решение, а ситуация есть
-e решение, а ситуация есть
![]() -я , то фирма, возглавляемая ЛПР,
получит доход
-я , то фирма, возглавляемая ЛПР,
получит доход ![]() . Матрица
. Матрица ![]() называется матрицей последствий (возможных решений). Какое же решение нужно
принять ЛПР? В этой ситуации полной неопределенности могут быть высказаны лишь
некоторые рекомендации предварительного характера. Они не обязательно будут
приняты ЛПР. Многое будет зависеть, например, от его склонности к риску. Но
как оценить риск в данной схеме?
называется матрицей последствий (возможных решений). Какое же решение нужно
принять ЛПР? В этой ситуации полной неопределенности могут быть высказаны лишь
некоторые рекомендации предварительного характера. Они не обязательно будут
приняты ЛПР. Многое будет зависеть, например, от его склонности к риску. Но
как оценить риск в данной схеме?
Допустим, мы хотим оценить риск, который несет i-e решение. Нам неизвестна
реальная ситуация. Но если бы ее знали, то выбрали бы наилучшее решение, т.е.
приносящее наибольший доход. Т.е. если ситуация есть ![]() -я
, то было бы принято решение, дающее доход
-я
, то было бы принято решение, дающее доход ![]() .
.
Значит, принимая ![]() -e решение мы рискуем получить не
-e решение мы рискуем получить не ![]() , а только
, а только ![]() , значит принятие
, значит принятие ![]() -го решения несет риск недобрать
-го решения несет риск недобрать ![]() . Матрица
. Матрица ![]() называется матрицей рисков.
называется матрицей рисков.
Пример 1. Пусть матрица последствий есть 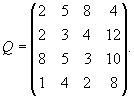
Составим матрицу рисков. Имеем ![]() Следовательно, матрица рисков есть
Следовательно, матрица рисков есть
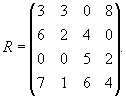
А. Принятие решений в условиях полной неопределенности.
Не все случайное можно "измерить" вероятностью. Неопределенность – более широкое понятие. Неопределенность того, какой цифрой вверх ляжет игральный кубик отличается от неопределенности того, каково будет состояние российской экономики через 15 лет. Кратко говоря, уникальные единичные случайные явления связаны с неопределенностью, массовые случайные явления обязательно допускают некоторые закономерности вероятностного характера.
Ситуация полной неопределенности характеризуется отсутствием какой бы то ни было дополнительной информации. Какие же существуют правила-рекомендации по принятию решений в этой ситуации?
Правило Вальда (правило крайнего пессимизма). Рассматривая ![]() -e решение будем полагать, что на самом деле ситуация складывается самая плохая, т.е. приносящая самый малый доход
-e решение будем полагать, что на самом деле ситуация складывается самая плохая, т.е. приносящая самый малый доход ![]() .
.
Но теперь уж выберем решение ![]() с наибольшим
с наибольшим ![]() . Итак, правило Вальда рекомендует принять решение
. Итак, правило Вальда рекомендует принять решение ![]() , такое что
, такое что
![]()
Так, в вышеуказанном примере, имеем ![]() Теперь из чисел 2,2,3,1 находим максимальное. Это – 3 . Значит, правило Вальда рекомендует принять 3-е решение.
Теперь из чисел 2,2,3,1 находим максимальное. Это – 3 . Значит, правило Вальда рекомендует принять 3-е решение.
Правило Сэвиджа (правило минимального риска). При применении этого правила анализируется матрица рисков ![]() . Рассматривая
. Рассматривая ![]() -e решение будем полагать, что на самом деле складывается ситуация максимального риска
-e решение будем полагать, что на самом деле складывается ситуация максимального риска ![]()
Но теперь уж выберем решение ![]() с наименьшим
с наименьшим ![]() . Итак, правило Сэвиджа рекомендует принять решение
. Итак, правило Сэвиджа рекомендует принять решение ![]() , такое что
, такое что
![]()
Так, в вышеуказанном примере, имеем ![]() Теперь из чисел 8,6,5,7 находим минимальное. Это – 5. Значит правило Сэвиджа рекомендует принять 3-е решение.
Теперь из чисел 8,6,5,7 находим минимальное. Это – 5. Значит правило Сэвиджа рекомендует принять 3-е решение.
Правило Гурвица (взвешивающее пессимистический и оптимистический подходы к ситуации). Принимается решение ![]() , на котором достигается максимум
, на котором достигается максимум
![]()
где ![]() . Значение
. Значение ![]() выбирается из субъективных соображений. Если
выбирается из субъективных соображений. Если ![]() приближается к 1, то правило Гурвица приближается к правилу Вальда, при приближении
приближается к 1, то правило Гурвица приближается к правилу Вальда, при приближении ![]() к 0, правило Гурвица приближается к правилу "розового оптимизма" (догадайтесь сами, что это значит). В вышеуказанном примере при
к 0, правило Гурвица приближается к правилу "розового оптимизма" (догадайтесь сами, что это значит). В вышеуказанном примере при ![]() правило Гурвица рекомендует 2-е решение.
правило Гурвица рекомендует 2-е решение.
В. Принятие решений в условиях частичной неопределенности.
Предположим, что в рассматриваемой схеме известны вероятности ![]() того, что реальная ситуация развивается по варианту
того, что реальная ситуация развивается по варианту ![]() . Именно такое положение называется частичной неопределенностью. Как здесь принимать решение? Можно выбрать одно из следующих правил.
. Именно такое положение называется частичной неопределенностью. Как здесь принимать решение? Можно выбрать одно из следующих правил.
Правило максимизации среднего ожидаемого дохода. Доход, получаемый фирмой при реализации ![]() -го решения, является случайной величиной
-го решения, является случайной величиной ![]() с рядом распределения
с рядом распределения
|
|
… |
|
||
|
|
… |
|
Математическое ожидание ![]() и есть средний ожидаемый доход, обозначаемый также
и есть средний ожидаемый доход, обозначаемый также ![]() . Итак, правило рекомендует принять решение, приносящее максимальный средний ожидаемый доход.
. Итак, правило рекомендует принять решение, приносящее максимальный средний ожидаемый доход.
Предположим, что в схеме из предыдущего п. вероятности есть (1/2, 1/6, 1/6, 1/6). Тогда ![]()
Максимальный средний ожидаемый доход равен 7, соответствует 3-у решению.
Правило минимизации среднего ожидаемого риска. Риск фирмы при реализации ![]() -го решения, является случайной величиной
-го решения, является случайной величиной ![]() с рядом распределения
с рядом распределения
|
|
… |
|
||
|
|
… |
|
Математическое ожидание ![]() и есть средний ожидаемый риск, обозначаемый также
и есть средний ожидаемый риск, обозначаемый также ![]() . Правило рекомендует принять решение, влекущее минимальный средний ожидаемый риск.
. Правило рекомендует принять решение, влекущее минимальный средний ожидаемый риск.
Вычислим средние ожидаемые риски при указанных выше вероятностях. Получаем ![]() Минимальный средний ожидаемый риск равен 7/6, соответствует 3-у решению.
Минимальный средний ожидаемый риск равен 7/6, соответствует 3-у решению.
Нанесем средние ожидаемые доходы ![]() и средние ожидаемые риски
и средние ожидаемые риски ![]() на плоскость – доход откладываем по вертикали, а риски по горизонтали (см.рис.):
на плоскость – доход откладываем по вертикали, а риски по горизонтали (см.рис.):
Получили 4 точки. Чем выше точка ![]() :
:![]() ,
тем более доходная операция, .Q3 чем точка правее – тем более она
рисковая. Значит, нужно выбирать точку выше и левее. Точка
,
тем более доходная операция, .Q3 чем точка правее – тем более она
рисковая. Значит, нужно выбирать точку выше и левее. Точка ![]() Q1 доминирует точку
Q1 доминирует точку ![]() ,
если
,
если ![]() Q2 и
Q2 и ![]() и хотя бы одно из этих .Q4 неравенств строгое. В нашем случае 3-я
операция доминирует все остальные.
и хотя бы одно из этих .Q4 неравенств строгое. В нашем случае 3-я
операция доминирует все остальные.
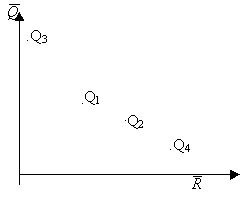
Точка, не доминируемая никакой другой называется оптимальной по Парето, а множество всех таких точек называется множеством оптимальности по Парето. Легко видеть, что если из рассмотренных операций надо выбрать лучшую, то ее обязательно надо выбрать из операций, оптимальных по Парето. В нашем случае, множество Парето, т.е. оптимальных по Парето операций, состоит только из одной 3-й операции.
Для нахождения лучшей операции иногда применяют подходящую взвешивающую формулу, которая для пар ![]() дает одно число, по которому и определяют лучшую операцию. Например, пусть взвешивающая формула есть
дает одно число, по которому и определяют лучшую операцию. Например, пусть взвешивающая формула есть ![]() . Тогда получаем:
. Тогда получаем: ![]()
![]() . Видно, что 3-я операция – лучшая, а 4-я – худшая.
. Видно, что 3-я операция – лучшая, а 4-я – худшая.
С. Правило Лапласа.
Иногда в условиях полной неопределенности применяют правило Лапласа равновозможности, когда все вероятности ![]() считают равными. После этого можно выбрать какое-нибудь из двух приведенных выше правил-рекомендаций принятия решений.
считают равными. После этого можно выбрать какое-нибудь из двух приведенных выше правил-рекомендаций принятия решений.
Цель математико-статистического анализа данных, характеризующих поведение исследуемого экономического объекта, состоит в том, чтобы выявить тенденции изменения выпуска продукции и используемых ресурсов, установить зависимость между выпуском и затратами ресурсов и по этим тенденциям и зависимостям найти прогнозы выпуска на ближайшую перспективу.
Выявление тенденций и установление зависимостей между выпуском и ресурсами осуществляется с помощью методов экстраполяции временных рядов и регрессионного анализа, изучаемых в курсе "Теория вероятностей и математическая статистика" [ ].
Расчеты по регрессионным моделям целесообразно выполнять на персональных ЭВМ с помощью пакетов прикладных программ, имеющих в своем составе программы множественной линейной регрессии (например, Statistica for Windows, Statgraf, SAS), однако возможно их выполнение на научном калькуляторе по формулам регрессионного анализа, приведенным в [ ].
Технику проведения расчетов и получения прогнозов покажем на примере исследования экономики США. Исходные данные для расчетов, взятые из следующих источников: Economic Report of the President, 1995,Wash,1995; Statistical Abstract of the USA, 1995, Wash, 1995, приведены в следующей таблице.
Валовой внутренний продукт, (в ценах 1987 г.), основные производственные фонды (в ценах 1987 г.) и число занятых в США в 1960-1995 г.г.
|
№ п.п. |
Год |
ВВП (млрд. долл.) Xt |
ОПФ (млрд. долл.) Kt |
Число занятых (млрд. чел.) Lt |
|
1 |
1960 |
1986,9 |
5596,9 |
65,8 |
|
2 |
1961 |
2035,7 |
5685,6 |
65,7 |
|
3 |
1962 |
2140,5 |
5849,8 |
66,7 |
|
4 |
1963 |
2234,2 |
6098,9 |
67,8 |
|
5 |
1964 |
2357,4 |
6336,1 |
69,3 |
|
6 |
1965 |
2493,3 |
6621,5 |
71,1 |
|
7 |
1966 |
2635,7 |
6921,8 |
72,9 |
|
8 |
1967 |
2705,6 |
7237,0 |
74,4 |
|
9 |
1968 |
2816,0 |
7434,0 |
75,9 |
|
10 |
1969 |
2891,0 |
8062,0 |
77,9 |
|
11 |
1970 |
2889,5 |
8416,8 |
78,7 |
|
12 |
1971 |
2978,2 |
8596,7 |
79,4 |
|
13 |
1972 |
3133,2 |
9533,6 |
82,2 |
|
14 |
1973 |
3298,5 |
9718,1 |
85,1 |
|
15 |
1974 |
3283,5 |
9455,7 |
86,8 |
|
16 |
1975 |
3250,2 |
9493,2 |
85,8 |
|
17 |
1976 |
3414,0 |
9620,9 |
88,8 |
|
18 |
1977 |
3568,2 |
9755,9 |
92,0 |
|
19 |
1978 |
3738,8 |
11217,1 |
96,0 |
|
20 |
1979 |
3848,6 |
12117,0 |
98,8 |
|
21 |
1980 |
3824,4 |
11691,4 |
99,3 |
|
22 |
1981 |
3883,1 |
11987,8 |
100,4 |
|
23 |
1982 |
3794,5 |
10717,1 |
99,5 |
|
24 |
1983 |
3938,5 |
10849,2 |
100,8 |
|
25 |
1984 |
4177,5 |
11989,2 |
105,0 |
|
28 |
1987 |
4544,5 |
13063,7 |
112,4 |
|
29 |
1988 |
4724,0 |
13382,5 |
115,0 |
|
30 |
1989 |
4854,2 |
13838,9 |
117,3 |
|
31 |
1990 |
5002,5 |
15411,8 |
117,9 |
|
32 |
1991 |
4881,6 |
14295,5 |
116,9 |
|
33 |
1992 |
4984,1 |
14252,1 |
117,6 |
|
34 |
1993 |
5139,9 |
14412,5 |
119,3 |
|
35 |
1994 |
5372,0 |
15319,8 |
123,1 |
|
36 |
1995 |
5604,1 |
15939,2 |
126,7 |
а) Анализ тенденций изменения и прогнозирование ВВП, ОПФ и числа занятых.
Анализ тенденции изменения и прогнозирование покажем на примере ВВП. Если имеет место линейный тренд, то модель изменения ВВП принимает вид
![]() ,
,
где
![]() - линейный (относительно времени) тренд,
- линейный (относительно времени) тренд,
![]() - среднее значение ВВП (значение тренда) при t=0 (
- среднее значение ВВП (значение тренда) при t=0 (![]() »
x1 -
»
x1 - ![]() ),
),
![]() - среднегодовой прирост ВВП,
- среднегодовой прирост ВВП,
e t – отклонение фактического значения ВВП от тренда.
Оценки коэффициентов тренда приведены в [ ] и имеют вид
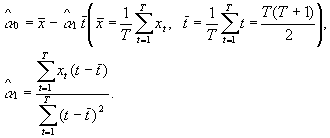
Выполнив расчеты на ЭВМ с помощью указанных ППП, либо непосредственно подставив значения временного ряда ВВП (взятые из таблицы) в последние две формулы, получаем оценки коэффициентов тренда
![]() = 1854,1 – оценка среднего значения ВВП в 1959 г. (млрд. долл.)
= 1854,1 – оценка среднего значения ВВП в 1959 г. (млрд. долл.)
![]() = 96,66 – оценка среднегодового
прироста ВВП (млрд. долл.), тем самым и оценки тренда
= 96,66 – оценка среднегодового
прироста ВВП (млрд. долл.), тем самым и оценки тренда
Хt = 1854,1 + 96,66× t.
Прогноз осуществляем по следующей формуле (подставляем будущие значения времени в уравнение тренда)
![]()
в частности,
(1996)![]() = 1854,1 + 96,66×
37 = 5430,6;
= 1854,1 + 96,66×
37 = 5430,6;
(1997) ![]() = 5527,3;
= 5527,3;
(1998) ![]() = 5623,9.
= 5623,9.
Точно так же находим оценки трендов и прогнозируемые значения ОПФ и числа занятых
![]() = 5071,7 + 290,05t;
= 5071,7 + 290,05t;
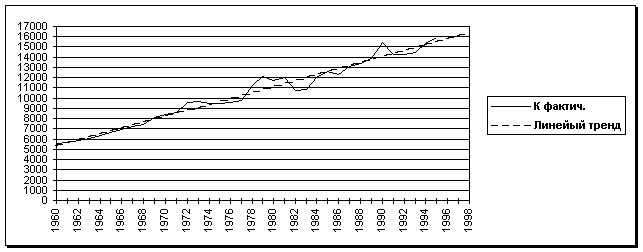
(1996) ![]() = 5071,7 + 290,05×
37 = 15803,6;
= 5071,7 + 290,05×
37 = 15803,6;
(1997) ![]() = 16093,6;
= 16093,6;
(1998) ![]() = 16383,7;
= 16383,7;
![]() = 60,36 + 1,796t;
= 60,36 + 1,796t;
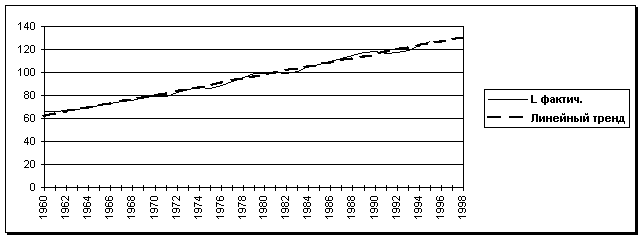
(1996) ![]() = 60,36 + 1,796×
37 = 126,8;
= 60,36 + 1,796×
37 = 126,8;
(1997) ![]() = 128,6;
= 128,6;
(1998) ![]() = 130,4.
= 130,4.
Замечание. Полученные прогнозы основаны на данных 1960 – 1995 г.г. К настоящему времени уже известны фактические данные за 1996 – 1998 г.г., поэтому есть возможность сравнить прогнозируемые значения с фактическими.
На приводимых ниже рисунках показаны фактические, расчетные (по линейному тренду) и прогнозируемые значения.
Прогноз ОПФ на 1996 – 1998 г.г. (млрд. долл.)
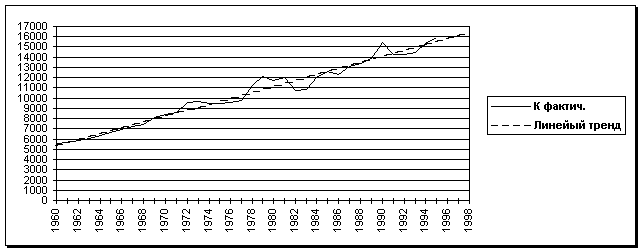
Прогноз числа занятых на 1996-1998 г.г. (млн. чел.)
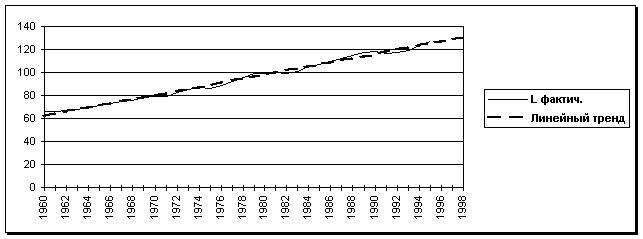
б) Установление зависимости ВВП от ресурсов (ОПФ и числа занятых) и прогнозирование ВВП с помощью найденной зависимости.
Зависимость ВВП от ОПФ и числа занятых постулируем в форме мультипликативной функции
![]() ,
,
где
А – коэффициент нейтрального технического прогресса,
a K, a L – коэффициенты эластичности по фондам и по труду.
При наложении этой гипотетической зависимости на реальные данные приходим к следующей модели
![]()
![]() - корректировочный коэффициент, который приводит расчетные (по модели) данные к фактическим.
- корректировочный коэффициент, который приводит расчетные (по модели) данные к фактическим.
В логарифмах эта модель приобретает вид уравнения регрессии с двумя независимыми переменными
![]() .
.
Вводя в программу линейной множественной регрессии в качестве значений зависимой переменной логарифмы ВВП (ln Xt, t = 1,…,T), а в качестве значений двух переменных логарифмы ОПФ (ln Kt, t = 1,…,T) и числа занятых (ln Lt, t = 1,…,T), получаем в результате работы программы оценки параметров регрессии
![]() .
.
Так расчеты на ЭВМ с помощью ППП " Statistica for Windows" по логарифмам походных данных дали следующие результаты
![]() ,
,
поэтому (![]() = 2,248)
= 2,248)
![]() .
.
Используя прогнозируемые значения ресурсов, получаем прогноз ВВП с помощью найденной зависимости от ресурсов
(1996) ![]()
(1997) ![]() = 5576,7;
= 5576,7;
(1998) ![]() = 5680,1.
= 5680,1.
На приводимом ниже рисунке показаны фактические, расчетные (по линейному тренду и по мультипликативной функции) значения ВВП.
Прогноз ВВП на 1996-1998 г.г.(млрд. долл.)
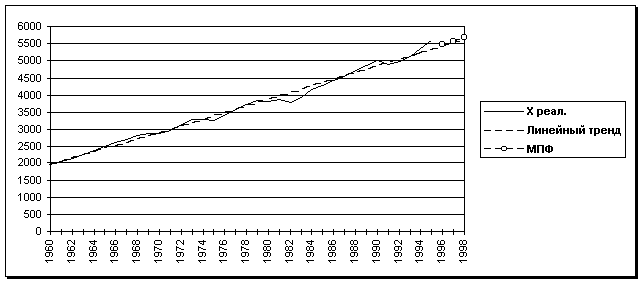
в) Выводы из результатов расчетов.
Как видно из таблицы исходных данных экономика США в 1960-1995 г.г. находилась в состоянии экономического роста, прерываемого в 1960-1961 г.г., 1969-1970 г.г., 1974-1975 г.г., 1980-1982 г.г., 1990-1992 г.г. кризисами и спадами производства.
Этот экономический рост характеризуется среднегодовыми приростами: ВВП – на 96,7 млрд. долл., ОПФ – на 290,1 млрд. долл., числа занятых – на 1,8 млн. чел. Увеличение ОПФ на 1% приводит к увеличению ВВП на 0,404%, а увеличение числа занятых на 1% - на 0,803%, т.е. экономический рост являлся фондосберегающим.
Если бы тенденции сохранились, то к концу 1998 г. ОПФ составили бы 16383,7 млрд. долл. (рост по сравнению с 1995 г. на 2,8%), ВВП достиг бы в 1998 г. значений: при прогнозе по линейному тренду – 5623,9 млрд. долл. (рост на 0,35%), при прогнозе на мультипликативной зависимости – 5680,1 (рост на 1,4%).
© 2010 Интернет База Рефератов