Реферат: Вклад Л.Эйлера в развитие математического анализа

План

Введение

1 Понятие математического анализа. Исторический очерк

2 Вклад Л.Эйлера в развитие математического анализа

3 Дальнейшее развитие математического анализа

Заключение

Список литературы

Введение

Л. Эйлер - самый продуктивный математик в истории, автор более чем 800 работ по математическому анализу, дифференциальной геометрии, теории чисел, приближённым вычислениям, небесной механике, математической физике, оптике, баллистике, кораблестроению, теории музыки и др. Многие его работы оказали значительное влияние на развитие науки.

Почти полжизни Эйлер провёл в России, где энергично помогал создавать российскую науку. В 1726 году он был приглашён работать в Санкт-Петербург. В 1731—1741 и начиная с 1766 года был академиком Петербургской Академии Наук (в 1741-1766 годах работал в Берлине, оставаясь почётным членом Петербургской Академии). Хорошо знал русский язык, часть своих сочинений (особенно учебники) публиковал на русском. Первые русские академики по математике (С. К. Котельников), и по астрономии (С. Я. Румовский) были учениками Эйлера. Некоторые из его потомков до сих пор живут в России.

Л.Эйлер внес очень большой вклад в развитие математического анализа.

Цель реферата – изучить историю развития математического анализа в XVIII веке.

1 Понятие математического анализа. Исторический очерк

Математический анализ - совокупность разделов математики, посвящённых исследованию функций и их обобщений методами дифференциального и интегрального исчислений. При столь общей трактовке к анализу следует отнести и функциональный анализ вместе с теорией интеграла Лебега, комплексный анализ (ТФКП), изучающий функции, заданные на комплексной плоскости, нестандартный анализ, изучающий бесконечно малые и бесконечно большие числа, а также вариационное исчисление.

В учебном процессе к анализу относят

· дифференциальное и интегральное исчисление

· теорию рядов (функциональных, степенных и Фурье) и многомерных интегралов

· векторный анализ.

При этом элементы функционального анализа и теории интеграла Лебега даются факультативно, а ТФКП, вариационное исчисление, теория дифференциальных уравнений читаются отдельными курсами. Строгость изложения следует образцам конца XIX века и в частности использует наивную теорию множеств.

Предшественниками математического анализа были античный метод исчерпывания и метод неделимых. Все три направления, включая анализ, роднит общая исходная идея: разложение на бесконечно малые элементы, природа которых, впрочем, представлялась авторам идеи довольно туманно. Алгебраический подход (исчисление бесконечно малых) начинает появляться у Валлиса, Джеймса Грегори и Барроу. В полной мере новое исчисление как систему создал Ньютон, который, однако, долгое время не публиковал свои открытия.[1]

Официальной датой рождения дифференциального исчисления можно считать май 1684, когда Лейбниц опубликовал первую статью «Новый метод максимумов и минимумов…»[2]. Эта статья в сжатой и малодоступной форме излагала принципы нового метода, названного дифференциальным исчислением.

В конце XVII века вокруг Лейбница возникает кружок, виднейшими представителями которого были братья Бернулли, Якоб и Иоганн, и Лопиталь. В 1696, используя лекции И. Бернулли, Лопиталь написал первый учебник[3], излагавший новый метод в применении к теории плоских кривых. Он назвал его «Анализ бесконечно малых», дав тем самым и одно из названий новому разделу математики. В основу изложения положено понятие переменных величин, между которыми имеется некоторая связь, из-за которой изменение одной влечёт изменение другой. У Лопиталя эта связь даётся при помощи плоских кривых: если M - подвижная точка плоской кривой, то её декартовы координаты x и y, именуемые диаметром и ординатой кривой, суть переменные, причём изменение x влечёт изменение y. Понятие функции отсутствует: желая сказать, что зависимость переменных задана, Лопиталь говорит, что «известна природа кривой». Понятие дифференциала вводится так:

«Бесконечно малая часть, на которую непрерывно увеличивается или уменьшается переменная величина, называется ее дифференциалом… Для обозначения дифференциала переменной величины, которая сама выражается одной буквой, мы будем пользоваться знаком или символом d.[4]http://ru.wikipedia.org/wiki/%D0%9C%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B9_%D0%B0%D0%BD%D0%B0%D0%BB%D0%B8%D0%B7 - cite_note-4#cite_note-4 … Бесконечно малая часть, на которую непрерывно увеличивается или уменьшается дифференциал переменной величины, называется … вторым дифференциалом».[5]

Эти определения поясняются геометрически, при этом на рисунке бесконечно малые приращения изображены конечными. Рассмотрение опирается на два требования (аксиомы). Первое:

Требуется, чтобы две величины, отличающиеся друг от друга лишь на бесконечно малую величину, можно было брать безразлично одну вместо другой. [6]

Отсюда получается x + dx = x, далее

dxy = (x + dx)(y + dy) − xy = xdy + ydx + dxdy = (x + dx)dy + ydx = xdy + ydx

и проч. правила дифференцирования. Второе требование гласит:

Требуется, чтобы можно было рассматривать кривую линию как совокупность бесконечного множества бесконечно малых прямых линий.

Продолжение каждой такой линии называется касательной к кривой.[7] Исследуя касательную, проходящую через точку M = (x,y), Лопиталь придаёт большое значение величине

$y\frac{dx}{dy}-x$ ,

достигающее экстремальных значений в точках перегиба кривой, отношению же dy к dx не придаётся никакого особого значения.

Примечательно нахождение точек экстремума. Если при непрерывном увеличении диаметра x ордината y сначала возрастает, а затем убывает, то дифференциал dy сначала положителен по сравнению с dx, а потом отрицателен.

Но всякая непрерывно возрастающая или убывающая величина не может превратиться из положительной в отрицательную, не проходя через бесконечность или нуль… Отсюда следует, что дифференциал наибольшей и наименьшей величины должен равняться нулю или бесконечности.

Вероятно, эта формулировка не безупречна, если вспомнить о первом требовании: пусть, скажем, y = x2, тогда в силу первого требования

2xdx + dx2 = 2xdx;

в нуле правая часть равна нулю, а левая нет. Видимо следовало сказать, что dy можно преобразовать в соответствии с первым требованием так, чтобы в точке максимума dy = 0. В примерах все само собой понятно, и лишь в теории точек перегиба Лопиталь пишет, что dy равен нулю в точке максимума, будучи разделён на dx[8]

Далее, при помощи одних дифференциалов формулируются условия экстремума и рассмотрено большое число сложных задач, относящихся в основном к дифференциальной геометрии на плоскости. В конце книги, в гл. 10, изложено то, что теперь называют правилом Лопиталя, хотя и в не совсем обычной форме. Пусть величина ординаты y кривой выражена дробью, числитель и знаменатель которой обращаются в нуль при x = a. Тогда точка кривой с x = a имеет ординату y, равную отношению дифференциала числителя к дифференциалу знаменателя, взятому при x = a.

По замыслу Лопиталя написанное им составляло первую часть «Анализа», вторая же должна была содержать интегральное исчисление, то есть способ отыскания связи переменных по известной связи их дифференциалов. Первое его изложение дано Иоганном Бернулли в его «Математических лекциях о методе интеграла»[9]. Здесь дан способ взятия большинства элементарных интегралов и указаны методы решения многих дифференциальных уравнений первого порядка.

2 Вклад Л.Эйлера в развитие математического анализа

Леонард Эйлер (Euler, Leonhard) (1707–1783) входит в первую пятерку величайших математиков всех времен и народов. Родился в Базеле (Швейцария) 15 апреля 1707 в семье пастора и провел детство в близлежащем селении, где его отец получил приход. Здесь на лоне сельской природы, в благочестивой обстановке скромного пасторского дома Леонард получил начальное воспитание, наложившее глубокий отпечаток на всю его последующую жизнь и мировоззрение. Обучение в гимназии в те времена было непродолжительным. Осенью 1720 тринадцатилетний Эйлер поступил в Базельский университет, через три года окончил низший – философский факультет и записался, по желанию отца, на теологический факультет. Летом 1724 на годичном университетском акте он прочел по-латыни речь о сравнении картезианской и ньютонианской философии. Проявив интерес к математике, он привлек к себе внимание Иоганна Бернулли. Профессор стал лично руководить самостоятельными занятиями юноши и вскоре публично признал, что от проницательности и остроты ума юного Эйлера он ожидает самых больших успехов.

Еще в 1725 Леонард Эйлер выразил желание сопровождать сыновей своего учителя в Россию, куда они были приглашены в открывавшуюся тогда – по воле Петра Великого – Петербургскую Академию наук. На следующий год получил приглашение и сам. Покинул Базель весной 1727 и после семинедельного путешествия прибыл в Петербург. Здесь он был зачислен сначала адъюнктом по кафедре высшей математики, в 1731 стал академиком (профессором), получив кафедру теоретической и экспериментальной физики, а затем (1733) кафедру высшей математики.

Сразу же по приезде в Петербург он полностью погрузился в научную работу и тогда же поразил всех плодотворностью своей деятельности. Многочисленные его статьи в академических ежегодниках, первоначально посвященные преимущественно задачам механики, скоро принесли ему всемирную известность, а позже способствовали и славе петербургских академических изданий в Западной Европе. Непрерывный поток сочинений Эйлера печатался с тех пор в трудах Академии в течение целого века.

Наряду с теоретическими исследованиями, Эйлер уделял много времени и практической деятельности, исполняя многочисленные поручения Академии наук. Так, он обследовал разнообразные приборы и механизмы, участвовал в обсуждении способов подъема большого колокола в Московском кремле и т.п. Одновременно он читал лекции в академической гимназии, работал в астрономической обсерватории, сотрудничал в издании Санкт-Петербургских ведомостей, вел большую редакционную работу в академических изданиях и пр. В 1735 Эйлер принял участие в работе Географического департамента Академии, внеся большой вклад в развитие картографии России. Неутомимая работоспособность Эйлера не была прервана даже полной потерей правого глаза, постигшей его в результате болезни в 1738.

Осенью 1740 внутренняя обстановка в России осложнилась. Это побудило Эйлера принять приглашение прусского короля, и летом 1741 он переехал в Берлин, где вскоре возглавил математический класс в реорганизованной Берлинской Академии наук и словесности. Годы, проведенные Эйлером в Берлине, были наиболее плодотворными в его научной деятельности. На этот период падает и его участие в ряде острых философско-научных дискуссий, в том числе о принципе наименьшего действия. Переезд в Берлин не прервал, однако, тесных связей Эйлера с Петербургской Академией наук. Он по-прежнему регулярно посылал в Россию свои сочинения, участвовал во всякого рода экспертизах, обучал посланных к нему из России учеников, подбирал ученых на замещение вакантных должностей в Академии и выполнял много других поручений.

Религиозность и характер Эйлера не соответствовали окружению «вольнодумного» Фридриха Великого. Это привело к постепенному осложнению отношений между Эйлером и королем, который при этом отлично понимал, что Эйлер является гордостью Королевской Академии. В последние годы своей берлинской жизни Эйлер исполнял фактически обязанности президента Академии, но должности этой так и не получил. В итоге летом 1766, несмотря на сопротивление короля, Эйлер принял приглашение Екатерины Великой и вернулся в Петербург, где оставался затем до конца своей жизни.

В том же 1766 Эйлер почти полностью потерял зрение и на левый глаз. Однако это не помешало продолжению его деятельности. С помощью нескольких учеников, писавших под его диктовку и оформлявших его труды, полуслепой Эйлер подготовил в последние годы своей жизни еще несколько сотен научных работ.

В начале сентября 1783 Эйлер почувствовал легкое недомогание. 18 сентября он еще занимался математическими исследованиями, но неожиданно потерял сознание и, по меткому выражению панегириста, «прекратил вычислять и жить».

Похоронен на Смоленском лютеранском кладбище в Петербурге, откуда его прах перенесен осенью 1956 в некрополь Александро-Невской лавры.

Научное наследие Леонарда Эйлера колоссально. Ему принадлежат классические результаты в математическом анализе. Он продвинул его обоснование, существенно развил интегральное исчисление, методы интегрирования обыкновенных дифференциальных уравнений и уравнений в частных производных. Эйлеру принадлежит знаменитый шеститомный курс математического анализа, включающий «Введение в анализ бесконечно малых», «Дифференциальное исчисление» и «Интегральное исчисление» (1748–1770). На этой «аналитической трилогии» учились многие поколения математиков всего мира.

Эйлер получил основные уравнения вариационного исчисления и определил пути дальнейшего его развития, подведя главные итоги своих исследований в этой области в монографии «Метод нахождения кривых линий, обладающих свойствами максимума или минимума» (1744). Значительны заслуги Эйлера в развитии теории функций, дифференциальной геометрии, вычислительной математики, теории чисел. Двухтомный курс Эйлера «Полное руководство по алгебре» (1770) выдержал около 30 изданий на шести европейских языках.

Фундаментальные результаты принадлежат Леонарду Эйлеру в рациональной механике. Он впервые дал последовательно аналитическое изложение механики материальной точки, рассмотрев в своей двухтомной «Механике» (1736) движение свободной и несвободной точки в пустоте и в сопротивляющейся среде. Позже Эйлер заложил основы кинематики и динамики твердого тела, получив соответствующие общие уравнения. Итоги этих исследований Эйлера собраны в его «Теории движения твердых тел» (1765). Совокупность уравнений динамики, представляющих законы количества движения и момента количества движения, крупнейший историк механики Клиффорд Трусделл предложил называть «Эйлеровыми законами механики».

В 1752 была опубликована статья Эйлера «Открытие нового принципа механики», в которой он сформулировал в общем виде ньютоновы уравнения движения в неподвижной системе координат, открыв путь для изучения механики сплошных сред. На этой основе он дал вывод классических уравнений гидродинамики идеальной жидкости, найдя и ряд их первых интегралов. Значительны также его работы по акустике. При этом ему принадлежит введение как «эйлеровых» (связанных с системой отсчета наблюдателя), так и «лагранжевых» (в сопутствующей движущемуся объекту системе отсчета) координат.

Замечательны многочисленные работы Эйлера по небесной механике, среди которых наиболее известна его «Новая теория движения Луны» (1772), существенно продвинувшая важнейший для мореходства того времени раздел небесной механики.

Наряду с общетеоретическими исследованиями, Эйлеру принадлежит ряд важных работ по прикладным наукам. Среди них первое место занимает теория корабля. Вопросы плавучести, остойчивости корабля и других его мореходных качеств были разработаны Эйлером в его двухтомной «Корабельной науке» (1749), а некоторые вопросы строительной механики корабля – в последующих работах. Более доступное изложение теории корабля он дал в «Полной теории строения и вождения кораблей» (1773), которая использовалась в качестве практического руководства не только в России.

Значительный успех имели комментарии Эйлера к «Новым началам артиллерии» Б.Робинса (1745), содержавшие, наряду с другими его сочинениями, важные элементы внешней баллистики, а также разъяснение гидродинамического «парадокса Даламбера». Эйлер заложил теорию гидравлических турбин, толчком для развития которой явилось изобретение реактивного «сегнерова колеса». Ему принадлежит и создание теории устойчивости стержней при продольном нагружении, приобретшей особую важность спустя столетие.

Много работ Эйлера посвящено различным вопросам физики, главным образом геометрической оптике. Особого упоминания заслуживают изданные Эйлером три тома «Писем к немецкой принцессе о разных предметах физики и философии» (1768–1772), выдержавшие впоследствии около 40 изданий на девяти европейских языках. Эти «Письма» были своего рода учебным руководством по основам науки того времени, хотя собственно философская сторона их и не соответствовала духу эпохи Просвещения.

Современная пятитомная «Математическая энциклопедия» указывает двадцать математических объектов (уравнений, формул, методов), которые носят сейчас имя Эйлера. Его имя носит и ряд фундаментальных уравнений гидродинамики и механики твердого тела.

Наряду с многочисленными собственно научными результатами, Эйлеру принадлежит историческая заслуга создания современного научного языка. Он является единственным автором середины XVIII в., труды которого читаются даже сегодня без всякого труда.

Петербургский архив Российской Академии наук хранит, кроме того, тысячи страниц неопубликованных исследований Эйлера, преимущественно в области механики, большое число его технических экспертиз, математические «записные книжки» и колоссальную научную корреспонденцию.

Его научный авторитет при жизни был безграничен. Он состоял почетным членом всех крупнейших академий и ученых обществ мира. Влияние его трудов было весьма значительным и в XIX в. В 1849 Карл Гаусс писал, что «изучение всех работ Эйлера останется навсегда лучшей, ничем не заменимой, школой в различных областях математики».

Общий объем сочинений Эйлера громаден. Свыше 800 его опубликованных научных работ составляют около 30 000 печатных страниц и складываются в основном из следующего: 600 статей в изданиях Петербургской Академии наук, 130 статей, опубликованных в Берлине, 30 статей в разных журналах Европы, 15 мемуаров, удостоенных премий и поощрений Парижской Академии наук, и 40 книг отдельных сочинений. Все это составит 72 тома близкого к завершению «Полного собрания трудов» (Opera omnia) Эйлера, издаваемого в Швейцарии с 1911. Все работы печатаются здесь на том языке, на котором они были первоначально опубликованы (т.е. на латинском и французском языках, которые были в середине XVIII в. основными рабочими языками, соответственно, Петербургской и Берлинской академий). К этому добавится еще 10 томов его Научной переписки, к изданию которой приступили в 1975.

Надо отметить особое значение Эйлера для Петербургской Академии наук, с которой он был тесно связан на протяжении свыше полувека. «Вместе с Петром I и Ломоносовым, – писал академик С.И.Вавилов, – Эйлер стал добрым гением нашей Академии, определившим ее славу, ее крепость, ее продуктивность». Можно добавить еще, что дела Петербургской академии велись в течение почти целого века под руководством потомков и учеников Эйлера: непременными секретарями Академии с 1769 до 1855 были последовательно его сын, зять сына и правнук.

Он вырастил трех сыновей. Старший из них был петербургским академиком по кафедре физики, второй придворным врачом, а младший – артиллерист дослужился до чина генерал-лейтенанта. Почти все потомки Эйлера приняли в XIX в. российское подданство. Среди них были высшие офицеры российской армии и флота, а также государственные деятели и ученые. Лишь в смутное время начала XX в. многие из них вынуждены были эмигрировать. Сегодня прямые потомки Эйлера, носящие его фамилию, все еще живут в России и Швейцарии.

Перемены в математическом анализе отражены в обширном трактате Эйлера. Изложение анализа открывает двухтомное «Введение», где собраны изыскания о различных представлениях элементарных функций. Термин «функция» впервые появляется лишь в 1692 у Лейбница, однако на первые роли его выдвинул именно Эйлер. Изначальная трактовка понятия функции состояла в том, что функция — это выражение для счёта (нем. Rechnungsausdrϋck) или аналитическое выражение.[10]

Функция переменного количества есть аналитическое выражение, составленное каким-либо образом из этой переменного количества и чисел или постоянных количеств.[11]

Подчёркивая, что «основное различие функций лежит в способе составления их из переменного и постоянных», Эйлер перечисляет действия, «посредством которых количества могут друг с другом сочетаться и перемешиваться; действиями этими являются: сложение и вычитание, умножение и деление, возведение в степень и извлечение корней; сюда же следует отнести также решение алгебраических уравнений. Кроме этих действий, называемых алгебраическими, существует много других, трансцендентных, как-то: показательные, логарифмические и бесчисленные другие, доставляемые интегральным исчислением».[12] Такая трактовка позволяла без труда обращаться с многозначными функциями и не требовала пояснения, над каким полем рассматривается функция: выражение для счёта определено для комплексных значений переменных даже тогда, когда для рассматриваемой задачи это не нужно.

Операции в выражении допускались лишь в конечном числе, а трансцендентное проникало при помощи бесконечно большого числа $\infty$ . В выражениях это число используется наряду с натуральными числами. Напр., считается допустимым такое выражение для экспоненты

$e^x=\left(1+\frac{x}{\infty}\right)^\infty$ ,

в котором лишь поздние авторы видели предельный переход. С аналитическими выражениями производились разнообразные преобразования, позволившие Эйлеру найти представления для элементарных функций в виде рядов, бесконечных произведений и т. д. Эйлер преобразует выражения для счёта так, как это делают в алгебре, не обращая внимания на возможность вычислить значение функции в точке по каждой из написанных формул.

В отличие от Лопиталя Эйлер подробно рассматривает трансцендентные функции и в особенности два наиболее изученные их классы — показательные и тригонометрические. Он обнаруживает, что все элементарные функции могут быть выражены при помощи арифметических действий и двух операций — взятия логарифма и экспоненты[13].

Сам ход доказательства прекрасно демонстрирует технику использования бесконечно большого. Определив синус и косинус при помощи тригонометрического круга, Эйлер выводит из формул сложения следующее:

$(\cos x + \sqrt{-1}\sin x)(\cos y + \sqrt{-1}\sin y)=\cos{(x+y)}+ \sqrt{-1} \sin{(x+y)},$

а отсюда

$2\cos nx =(\cos x + \sqrt{-1}\sin x)^n+(\cos x - \sqrt{-1}\sin x)^n$

Полагая $n=\infty$ и z = nx, он получает

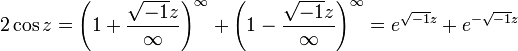$2\cos z =\left (1 + \frac{\sqrt{-1} z}{\infty}\right)^\infty+\left (1 - \frac{\sqrt{-1}z}{\infty}\right)^\infty=e^{\sqrt{-1}z}+e^{-\sqrt{-1}z}$ ,

отбрасывая бесконечно малые величины большего порядка. Используя это и аналогичное выражение, Эйлер получает и свою знаменитую формулу

$e^{\sqrt{-1}x}=\cos{x}+\sqrt{-1}\sin{x}$ .

Указав различные выражения для функций, которые теперь называют элементарными, Эйлер переходит к рассмотрению кривых на плоскости, начертанным свободным движением руки. По его мнению, не для всякой такой кривой можно отыскать единое аналитическое выражение. В XIX веке с подачи Казорати[14] это утверждение считалось ошибочным: по теореме Вейерштрасса всякая непрерывная в современном смысле кривая может быть приближенно описана полиномами. На самом деле Эйлера это едва ли убедило, ведь нужно ещё переписать предельный переход при помощи символа $\infty$ .

Изложение дифференциального исчисления Эйлер начинает с теории конечных разностей, за ним в третьей главе следует философское разъяснение о том, что «бесконечно малое количество есть точно нуль», более всего не устроившее современников Эйлера. Затем из конечных разностей при бесконечно малом приращении образуются дифференциалы, а из интерполяционной формулу Ньютона - формула Тейлора. Этот метод в существенном восходит к работам Тейлора (1715 г.). При этом у Эйлера появляется устойчивое отношение $\frac{d^ky}{dx^k}$ , которое, однако, рассматривается как отношение двух бесконечно малых. Последние главы посвящены приближенному вычислению при помощи рядов.

В трёхтомном интегральном исчислении Эйлер трактует понятие интеграла так:

«Та функция, дифференциал которой = Xdx, называется его интегралом и обозначается знаком S, поставленным спереди».[15]

В целом же эта часть трактата Эйлера посвящена более общей с современной точки зрения задаче об интегрировании дифференциальных уравнений. При этом Эйлер находит ряд интегралов и дифференциальных уравнений, которые приводят к новым функциям, напр., Γ-функции, эллиптические функции и т. д. Строгое доказательство их неэлементарности было дано в 1830-х годах Якоби для эллиптических функций и Лиувиллем.

3 Дальнейшее развитие математического анализа

Следующим крупным произведением, сыгравшим значительную роль в развитии концепции анализа, явилась «Теория аналитических функций»[16] Лагранжа и обширный пересказ работ Лагранжа, выполненный Лакруа[17] в несколько эклектической манере.

Желая избавиться от бесконечно малого вовсе, Лагранж обратил связь между производными и рядом Тейлора. Под аналитической функцией Лагранж понимал произвольную функцию, исследуемую методами анализа. Саму функцию он обозначил как f(x), дав графический способ записи зависимости - ранее же Эйлер обходился одними переменными. Для применения методов анализа по мнению Лагранжа необходимо, чтобы функция разлагалась в ряд

$f(x+h)=f(x)+ph+qh^2+\dots$ ,

коэффициенты которого будут новыми функциями x. Остаётся назвать p производной (дифференциальным коэффициентом) и обозначить его как f'(x). Таким образом, понятие производной вводится на второй странице трактата и без помощи бесконечно малых. Остаётся заметить, что

$f'(x+h)=p+2qh+\dots$ ,

поэтому коэффициент q является удвоенной производной производной f(x), то есть

$q=\frac{1}{2!}f''(x)$ и т. д.[24]

Такой подход к трактовке понятия производной используется в современной алгебре и послужил основой для создания теории аналитических функций Вейерштрасса.

Лагранж оперировал такими рядами как формальными и получил ряд замечательных теорем. В частности, впервые и вполне строго доказал разрешимость начальной задачи для обыкновенных дифференциальных уравнений в формальных степенных рядах.

Вопрос об оценке точности приближений, доставляемых частными суммами ряда Тейлора, впервые был поставлен именно Лагранжем: в конце Теории аналитических функций он вывел то, что теперь называют формулой Тейлора с остаточным членом в форме Лагранжа.[18] Однако, в противоположность современным авторам, Лагранж не видел нужды в употреблении этого результата для обоснования сходимости ряда Тейлора.

Вопрос о том, действительно ли функции, употребимые в анализе, могут быть разложены в степенной ряд, впоследствии стал предметом дискуссии. Конечно, Лагранжу было известно, что в некоторых точках элементарные функции могут не разлагаться в степенной ряд, однако в этих точка они и недифференцируемы ни в каком смысле. Коши в своём Алгебраическом анализе привёл в качестве контрпримера функцию

$f(x)=e^{-1/x^2},$

доопределённую нулём в нуле. Эта функция всюду гладкая на вещественной оси и в нуле имеет нулевой ряд Маклорена, который, следовательно, не сходится к значению f(x). Против этого примера Пуассон возразил, что Лагранж определял функцию как единое аналитическое выражение, в примере Коши же функция задана по разному в нуле, и при $x\not=0$ . Лишь в конце XIX века Прингсхейм[19] доказал, что существует бесконечно дифференцируемая функция, заданная единым выражением, ряд Маклорена для которой расходится. Пример такой функцией доставляет выражение

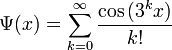$\Psi(x)=\sum \limits_{k=0}^\infty \frac{\cos{(3^kx)}}{k!}$ .

В XVIII веке были разработаны и практически применены такие разделы анализа, как вариационное исчисление, обыкновенные дифференциальные уравнения и дифференциальные уравнения в частных производных, преобразования Фурье и производящие функции. На фундаменте анализа возникла математическая физика, аналитические методы глубоко проникли в геометрию и даже в теорию чисел.

В XIX веке Коши первым дал анализу твёрдое логическое обоснование, введя понятие предела последовательности, он же открыл новую страницу комплексного анализа. Пуассон, Лиувилль, Фурье и другие изучали дифференциальные уравнения в частных производных и гармонический анализ.

В последней трети XIX века Вейерштрасс произвёл арифметизацию анализа, полагая геометрическое обоснование недостаточным, и предложил классическое определение предела через ε-δ-язык. Он же создал первую строгую теорию множества вещественных чисел. В это же время попытки усовершенствования теоремы об интегрируемости по Риману привели к созданию классификации разрывности вещественных функций. Также были открыты «патологические» примеры (нигде не дифференцируемые непрерывные функции, заполняющие пространство кривые). В связи с этим Жордан разработал теорию меры, а Кантор - теорию множеств, и в начале XX века математический анализ был формализован с их помощью. Другим важным событием XX века стала разработка нестандартного анализа как альтернативного подхода к обоснованию анализа.

Заключение

Завершая работу над рефератом можно прийти к выводу, что математический анализ – это совокупность разделов математики, посвященных исследованию функций и их обобщений методами дифференциального и интегрального исчислений. В него также входят теории функций действительного и комплексного переменного, теория дифференциальных уравнений, вариационное исчисление ряд других математических дисциплин.

Большой вклад в развитие математического анализа внес Л.Эйлер. Он принадлежит к числу гениев, чь творчество стало достоянием всего человечества. До сих пор школьники всех стран изучают тригонометрию и логарифмы в том виде, какой придал им Эйлер. Студенты проходят высшую математику по руководствам, первыми образцами которых явились классические монографии Эйлера. Он был прежде всего математиком, но он знал, что почвой, на которой расцветает математика, является практическая деятельность. Он оставил важнейшие труды по самым различным отраслям математики, механики, физики, астрономии и по ряду прикладных наук. Трудно даже перечислить все отрасли, в которых трудился великий учёный.

Список литературы

1. Артемьева Т. В. Леонард Эйлер как философ // Философия в Петербургской Академии наук XVIII века. - СПб.: 1999. - 182 с.

2. Гиндикин С. Г. Рассказы о физиках и математиках. - 3-е изд., расш. - М.: МЦНМО, 2001. - 465 с.

3. Делоне Б. Н. Леонард Эйлер // Квант. - 1974. - № 5.

4. К 250-летию со дня рождения Л. Эйлера: Сборник. - Изд-во АН СССР, 1958.

5. Летопись Российской Академии наук. Том 1. 1724-1802. - М.: Наука, 2000.

6. Математика XVIII столетия / Под редакцией А. П. Юшкевича. - М.: Наука, 1972. - Т. 3. - (История математики в 3-х томах).

7. Полякова Т. С. Леонард Эйлер и математическое образование в России. - КомКнига, 2007. - 184 с.

8. Прудников В. Е. Русские педагоги-математики XVIII-XIX веков. - 1956.

9. Юшкевич А. П. История математики в России. - М.: Наука, 1968.

[1] Ньютон И. Математические работы. M, 1937.

[2] Leibniz //Acta Eroditorum, 1684. L.M.S., т. V, c. 220—226. Рус. пер.: Успехи Мат. Наук, т. 3, в. 1 (23), с. 166—173.

[3] Лопиталь. Анализ бесконечно малых. М.-Л.:ГТТИ, 1935.

[4] Там же. Гл.1, опр.2

[5] Там же. Гл.4, опр.1.

[6] Лопиталь. Анализ бесконечно малых. М.-Л.:ГТТИ, 1935. гл.1, требование 1.

[7] Там же. Гл.2. опр.

[8] Лопиталь. Анализ бесконечно малых. М.-Л.:ГТТИ, 1935 § 46.

[9] Bernulli, Johann. Die erste Integrelrechnunug. Leipzig-Berlin, 1914

[10] См. Маркушевич А. И. Элементы теории аналитических функций, Учпедгиз, 1944. С. 21 и сл.; Koenig F. Kommentierender Anhang zu Funktionentheorie von F. Klein. Leipzig: Teubner, 1987;

[11] Эйлер. Введение в анализ. Т. 1. Гл. 1, § 4

[12] Эйлер. Введение в анализ. Т. 1. Гл. 1, § 6

[13] Там же. Гл.8.

[14] Casorati F. Teorica delle funzioni di variabili complesse. Pavia, 1868. P. 191

[15] Эйлер. Интегральное исчисление. Т. 1, опр. 2

[16] Lagrange. OEvres. Vol. 9

[17] Lacroix. Traite du calcul differentiel et du calcul integral. Vol. 1-3. 1 ed., 1798. (Большой Лакруа)// http://gallica.bnf.fr

[18] См. также: История математики, т. 3., с. 297—300

[19] Pringssheim A.// Math. Ann. Bd. 43 (1893); см. также: Маркушевич А. И. Элементы теории аналитических функций. М., 1944. C. 16-17.