Шпаргалка: Основные понятия математического анализа

Шпаргалка: Основные понятия математического анализа

1. Определение неопред. интеграла. Если ф-ия F(x) – первообр для ф-ии f(x) на промежутке [a,b], то мн-о ф-ий F(x)+C, где С =const, назыв неопред интегр от ф-и f(x) на этом промежутке: ∫f(x)dx=F(x)+C При этом ф-я f(x) назыв подынтегр ф-ей, f(x)dx – подынтегр выр-ем, х переменной интегр-я.

2. Опред-ие первообр от непрерыв ф-ии. Ф-ия F(x) назыв первообр для ф-ии f(x) на промежутке [a,b], если для всех значений х из этого промежутка вып- я F’(x)=f(x). Если ф-ия f(x), хЄ[a,b] – непрерыв, то для нее сущ-ет первообразная (неопред. Интеграл)

4. Выр-ие (∫f(x)dx). Производная неопред интеграла = подынтегр ф-ии. (∫f(x)dx)’=f(x). Док-во: (∫f(x)dx)’= =(F(x)+C)’= F’(x)= f(x)dx

5. Выр. ∫dF(x) Неопред интеграл от дифф-ла некоторой ф-ии = сумме этой ф-ии и произвольной постоянной ∫dF(x)=F(x)+C.Так как ∫dF(x)= F’(x)dx, то ∫F’(x)dx=F(x)+C. Теорема: Если ф-я F(x) является первообр ф-ии f(x) на отрезке [a,b], то мн-во всех первообр ф-ии f(x) задается формулой F(x)+C, С=const.

Док-во: F(x)+C – первообр, тогда (F(x)+C)’= F’(x)+C’= F’(x)=f(x) Ф(х) – -тоже первообразная: Ф’(х)=f(x), xЄ[a,b]. (Ф(х)-F(x))’= Ф’(х)-F’(x)=f(x)- f(x)=0 =>Ф(х)-F(x)=C, С-const. Таким образом Ф(х)=F(x)+С. Ф-ия, производ которой на некотором промежутке Х равна 0, постоянна на этом промежут-ке. φ’(x)=0 => φ(x)=C, для каждого хЄ[a,b], тогда для каждого х1,х2 Є [a,b], х1<х2. По теореме Лангранжа: φ(x2)- φ(x1)=0, φ(x)=С

6. Если k-const, ненулевое число, то ∫kf(x)dx=k∫f(x)dx –k можно вынести из-под знака интеграла. Пусть F(x) – первообр для ф-ии f(x), т.е. F’(x)=f(x), тогда kF(x)-первообр для ф-ии kf(x): (kF(x))’=kF’(x)=kf(x). èk∫f(x)dx=k[C+(x)F]=kF(x)+C1=∫kf(x)dx, где С1=kC         7. Если ∫f(x)dx=F(x)+C, то и ∫f(u)du= F(u)+C, u=φ(x) – произвольная ф-ия, непрерывн, дифферен-я. f(x)-непрерыв. => ∫f(x)dx=F(x)+C, u=φ(x)-непрерыв. дифферен.ф-я. F(u)=F(φ(x)) –согласно инвариантности первого дифф-ла. Инвариантность первого дифф-ла: y=f(x) dy=f’(x)dx y=f(u), u=φ(x)– непрерыв, диф-я dy=f’(x)du dF(u)=F’(u)du= =f(u)du ∫f(u)du=∫d(F(u))=F(u)+C

8. Выражение d(∫f(x)dx)=f(x)dx - Дифференциал от неопред интегр = подынтегр выр-ю. d(∫f(x)dx)=d(F(x)+C) =dF(x)+dC=F’(x)dx+0=f(x)dx

9. Интеграл ∫[f(x)±g(x)]dx= ∫f(x)dx±∫g(x)dx –неопред интеграл от алгебраической суммы двух ф-ий равен алгебраической суммe интегр от этих

ф-ий в отдельности: Пусть F(x) и G(x) – первообразные для ф-ий f(x) и g(x): ∫[f(x)+g(x)]dx=∫(F’(x)+G’(x))dx=∫(F(x)+G(x))’dx=∫d(F(x)+G(x))= F(x)+G(x)+C= F(x)+G(x)+C1+C2=F(x)+C1+G(x)+C2 =∫f(x)dx+∫g(x)dx.

10. Вывод формулы замены переменного в неопред интегр (подстановка). Пусть ф-я x=φ(t) опред-на и диф-ма на некотором промежутке Т и Х-мн-во значений этой ф-ии, на кот. определена ф-я f(x). Тогда, если на мн-е Х ф-я f(x) имеет первообр, то на мн-ве Т справедлива фор-ла: ∫f(x)dx= ∫f[φ(t)]φ’(t)dt Док:Пусть F(x)-первообр для f(x) на мн-ве Х. Рассмотрим на мн-ве Т сложную ф-ю F[φ(t)]: (F[φ(t)])’= Fx’[φ(t)]φ’(t) =f[φ(t)]φ’(t), т.е. ф-я f[φ(t)]φ’(t) имеет на мн-ве Т первообр F[φ(t)] >∫f[φ(t)]φ’(t)dt=F[φ(t)]+C,Замечая что F[φ(t)]+C=F(x)+C= ∫f(x)dx, => получаем ∫f(x)dx= ∫f[φ(t)]φ’(t)dt.

Дарбу: Mn=sup (f(x)); mn=inf (f(x)), xÎ(xi-1; xi) Sρ=å Mn∆xi верхний; Sρ=å mn ∆xi- нижний; СВ-ВА:

1, "верхняя сумма >=нижней; 2, при изменеии разбиения верхняя не увел, нижняя не умень.; 3, измельчение разбиения-добовлене нескольких точек 0=< Sρ-I<e -для верх и ниж - Лемма.

11. Вывод формулы интегрир по частям. Пусть ф-ии u(x) и v(x) определены и диф-мы нанекотором пром-ке Х и пусть ф-я u’(x)v(x) имеет первообр на этом пром-ке. Тогда на пром-ке Х ф-я u(x)v’(x) также имеет перво-ю и справедлива формула: ∫u(x)v’(x)dx=u(x)v(x)-∫v(x)u’(x)dx. Док-во: [u(x)v(x)]’= u’(x)v(x)+u(x)v’(x) è u(x)v’(x)=[u(x)v(x)]’-u’(x)v(x)Первообр ф-ии [u(x)v(x)]’ на пром-ке Х является ф-я u(x)v(x). Ф-я u’(x)v(x) имеет первообр на Х по условию теор. è, и ф-я u(x)v’(x) имеет пер-ю на Х.Интегр-уя последнее рав-во получаем: ∫u(x)v’(x)dx=u(x)v(x)-∫v(x)u’(x)dx. Так как v’(x)dx=dv,u’(x)dx=du, то ее можно записать в виде: ∫udv=uv-∫vdu По лекциям: d(uv)=udv+vdu;∫d(uv)= ∫udv+vdu => ∫udv=∫d(uv)-∫vdu=uv-∫vdu Теорема о существовании конечного.

12. Определение дробно рациональной ф-ии. Понятие правильной и неправильной рациональной фун-ии. Простейшие дроби вида 1-4. Фун-ия вида Pn(x)=anxn+ an-1xn-1 +…+ a1x1+ a0, n – натуральное число. ai, i=0, n=const называется мн-ном n-ой степени.

Определение: Дробно рацион фун-й (рациональной дробью) назыв фун-ия равная отношению 2-х мн-нов: f(x)= Pm(x)/ Qn(x), Pm(x)-мн-eн степени m, Qn(x)-многочлен степени n. Рацион дробь назыв правильной, если m<n. Иначе неправильной. P(x)/Q(x)= S(x)+R(x)/Q(x).Пример(деление дроби). Простейшие дроби 4 вида

1) A/(x-a)

2) A/(x-a)k k>=2 целое

3) (Mx+n)/(x2+px+q) x2+px+q=0, D<0

4) (Mx+n)/(x2+px+q)k k>=2

предела интегральных сумм для непрерывных ф-ий: Пусть сущ f.

13. Если х=а – действит корень кратности k знамен-ля Qn(x) прав-ой рацион дроби, т.е. Qn(x)=(х-а)k Õn-k(x) Тогда дробь будет представляться в виде суммы 2 правильных дробей: Pm(x)/Qn(x)=A/(х-а)k+Rs(x)/(х-а)k-1Õn-k(x) A-некоторая постоянная, s<n-1 Док-во: Pm(x)/Qn(x)=[A Õn-k(x)+ Pm(x)-A Qn-k(x)]/[(х-а)k Õn-k(x)]=[ A Õn-k(x)]/ [(х-а)k Õn-k(x)]+[ Pm(x)-A Qn-k(x)]/ [(х-а)k Õn-k(x)]=A/(х-а)k +[Pm(x)-A Qn-k(x)]/ [(х-а)k Õn-k(x)], для каждого А. х=а – корень ура-я Pm(x)- A Õn-k(x)=0; Pm(а)- A Õn-k(а)=0; Pm(а)≠0 и A Õn-k(а)≠0; A= Pm(а)/A Õn-k(а); Pm(x)- A Õn-k(x)=(x-a) Rs(x); Pm(x)/Qn(x)= A/(х-а)k +[(x-a) Rs(x)]/[(x-a) Õn-k(x)]= A/(х-а)k + Rs(x)/[(х-а)k-1 Õn-k(x)]; A= Pm(а)/Õn-1(а).

14. Если Qn(x)= (x2+px+q)µ Тn-µ(x), где p2-4q<0, Тn-µ(x) мн-ен не делится на x2+px+q, то правильную рацион дробь Pm(x)/Qn(x) можно представить в виде суммы 2 правильных: Pm(x)/Qn(x) =(Mx+N)/ (x2+px+q)µ +Фs(x)/[ (x2+px+q)µ-1. Тn-µ(x)],µ,N-нек постоянные, s<n-1 Док-во: Pm(x)/Qn(x) =[(Mx+N) Тn-µ(x)+ Pm(x)-(Mx+N) Тn-µ(x)]//(x2+px+q)µ Тn-µ(x)]= (Mx+N)/(x2+px+q)µ+ [Pm(x)-(Mx +N) Тn-µ(x)]/[ (x2+px+q)µ Тn-µ(x)] для люб µ и N. x2+px+q=0, D<0, x12=α±iβ, µ и N: Pm (α+iβ)-[ µ (α+iβ)+N]*T n-µ(α+iβ)=0. µ (α+iβ)+N=[ Pm (α+iβ)] /[ T n-µ(α+iβ)]=k+il. Система{ µ α+N =k=> N=k- α(L/b) µb=L=> m=L/b Pm(x)/Qn(x)=(Mx+N)/(x2+px+q)µ +Фs(x)/[ (x2+px+q)µ-1Тn-µ(x)] конечному пределу при ранге разбиения à 0.

15. Разложение рацион дроби на простейшие. Если рацион ф-я R(x)/Q(x) имеет степень мн-на в числ-ле < степени мн-на в знамен-ле, а мн-н Q(x) представлен в виде Q(x)= A(x-a)r(x-b)s…(x2+2px+q)t(x2+2ux+v)z …, где a,b,.., p,q,u,v,…-вещественные числа, то эту ф-ю можно единств образом представить в виде:R(x)/Q(x) =A1/(x-a)+A2/(x-a)2+…. An/(x-a)n+…. (M1x+N1) / (x2+2px+q)+ (M2x+N2)/ /(x2+2px+q)2+…+(Mkx+Nk)/(x2+2px+q)k +, где А1,А2,.М1..N1-вещест числа

16. Определение дробно рацион фун-ии. Понятие правильной и неправ-ной рациональной фун-ии. Простейшие дроби вида 1-4. Фун-ия вида Pn(x)=anxn+ an-1xn-1 ++ a1x1+ a0, n – натуральное число. ai, i=0, n=const называется мн-ном n-ой степени.

Определение: Дробно рацион фун-uей (рациональной дробью) назыв фун-ия равная отн-ю 2-х мн-нов: f(x)= Pm(x)/ Qn(x), Pm(x)-мн-eн степени m, Qn(x)-многочлен степени n. Рацион дробь назыв правильной, если m<n. Иначе неправильной. P(x)/Q(x)= S(x)+R(x)/Q(x).Пример(деление дроби). Простейшие дроби 4 вида

1)A/(x-a) 2)A/(x-a)k k>=2 целое

3)(Mx+n)/(x2+px+q) x2+px+q=0, D<0

4) (Mx+n)/(x2+px+q)k k>=2

17. Вычисление интегралов от тригонометрических ф-ий.

1) ∫R(sinx, cosx)dx Замена перем-ных tg(x/2)=t (универ. тригонометр замена) sinx=2t/(1+t2) cosx=(1-t2)/ /(1+t2) dx=2/(1+t2)dt;∫R(2t/(1+t2), (1-t2)/ /(1+t2)) 2/(1+t2)dt=∫Ř(t)dt

2)∫R(sinx) cosxdx=|sinx=t, cosxdx=dt|=∫R(t)dt

3)∫R sinx(cosx)dx=|cosx=t, -sinxdx=dt|=-∫R(t)dt

4) ∫R(tgx)dx=|t=tgx, x=arctgt, dx=dt/(1+t2)|= ∫R(t)dt/(1+t2)  5) R(sinx, cosx)= R(-sinx, -cosx)

∫R(sinx, cosx)dx=|t=tgx, dx = dt/(1+ t2)| =∫Ř(t)dt

6) ∫sin m x cos n xdx

a)m=2k+1 ∫sin 2k x cos n x sinxdx=∫(1-cos 2 x)k cos n x sinxdx=|t=cosx, dt=-sinxdx|=-∫(1-t 2)k t n dt

b)n=2k+1 ∫sin m x cos 2k x cosxdx= ∫sin m x (1-sin 2 x)k dsinx

7) ∫sin 2p x cos 2a xdx sin2x=(1-cos2x)/2

cos2x=(1+cos2x)/2 sinxcosx=(1/2)sin2x

8) m=-µ n=-ν замена t=tgx

1/ sin2x=1+ ctg2x 1/ cos2x=1+tg2x

9) ∫tg m x dx; ∫ctg m x dx, m-целое >0ое tg2x=1/ cos2x-1

сtg2x=1/ sin2x-1

10) ∫sinmxcosnxdx ∫sinmxsinnxdx

∫cosmxcosnxdx sinmxcosnx=(1/2)(sin(m+n)x+sin(m-n)x)

sinmxsinnx=(1/2)(cos(m-n)x-cos(m+n)x)

Теорема о существовании конечного предела интегральных сумм для непрерывных ф-ий

Пусть существует f определенная на замкнутом интервале [a,b] => ее интегр суммы стремяться к конечному пределу при ранге разбиения à 0.

ax2+bx+c=a(x+b/2a)+(4ac-b2)/(4a2) x+b/2a=t; (ax+b)/(cx+d)=tk=>

ax+b= cx tk+ dtk=>x=…; dx=(…)dt

Замена переменной: ∫f(x)dx=|x= φ(t); t=g(x); dx= φ’(t)dt |=∫f(φ(t)) φ’(t)dt

Поднесение по знак дифф-ла: Если ∫f(x)dx=F(x)+C, то ∫f(n)dx=F(n)+C

интегрир по частям: ∫udv=uv-∫vdu

∫x sin x dx=|u=x; du=dx; dv=sin x dx; v= -cos x|=-xcos x-∫-cos xdx= -xcos x+sin x.

Ф-цию вида R(x,mÖ(ax+b)/(cx+d) –называют дробно линейной ирр-тью. С помощью замены t=mÖ(ax+b)/(cx+d) рационализируем интеграл. tm= (ax+b)/(cx+d); x=(b-dtm)/(ctm-a) –рацион ф-ция от t; dx=(mtm-1(ad-bc)dt)/(ctm-a)² Þ òR(x,mÖ(ax+b)/ (cx+d))dx=òR((b-dtm)/ (ctm-a),t) (mtm-1(ad-bc)dt)/(ctm-a)²= òR1(t)dt. R1(t)-рацион-ая. Вида òR(x,Öax²+bx+c)dx, -квадр-ая ирр-ть где а, b, c=const. Если трёхчлен ax²+bx+c имеет действит корни х1 х2 то ax²+bx+c=a(x-x1)(x-x2) и R(x,Öax²+bx+c)=R(x,(x-x1)Ö(x-x2)a/(x-x1)=R1(x,Ö(x-x2)/(x-x1); пусть ax²+bx+c не имеет действит корней и а>0. Тогда подстановка (Эйлера) t=Ö(ax²+bx+c) +xÖa Þax²+bx+c=t²-2xtÖa+ax²; x=(t²-c)/2t(Öa)+b –рацион функ-ция от t Ч.Т.Д; Если а<0 с>0 (ax²+bx+c)>=0) то можно сделать замену Öax²+bx+c=xt+Öc {}{} Опред интеграл. Ограниченность интегрируемой ф-ии. {O}Разбиением t[a,b] называется произвольное мн-во точек xi, I=0,1,…,it удовлетворяющее условию x0=a<x1<x2<…<xit-1<xit{} Каждый из отрезков [xi-1,xi] назыв отрезком разбиения t{} Пусть ф-ция y=f(x) определена на [a,b] и t произвольное разбиение этого отрезка, в каждом отрезке разбиения в произвольном образе выберем (.) xiÎ[xi-1,xi] I=1,..,it и рассмотрим сумму st(f,x1,…,xit)= åI=1ixf(xI)Dx; -интегральная сумма {Определение} Число I –называется опред ò ф-ции y=f(x) на отр[a;b] и обозначается aòbf(x)dx Если " E >0 $dE=d(E)>0 | при любом разбиении s мелкости |t|<dE и любом выборе (.) xiÎ[xi-1,xi], I=1,…,it | åI=1itf(xi)Dx-I | <E При этом пишут I=limst |t|®0. {T}Если ф-ция интегрируема на отр. [a,b] то она ограничина на этом отрезке {Док-во} Пусть ф-ция y=f(x) интегрируема на [a,b] но не является ограниченным. на этом отрезке. На этом отрезке рассмотрим произвольное разбиение t отрезка [a,b] то она ограничена хотя бы на одном на одном отр. разбиения. Пусть это будет отр.[xj0-1,xj0] Тогда на этом отрезке существует последов-ть точек $ {xnjo}>0 | limn®¥f(xnjo)=¥ Рассмотрим сумму st=åI=1itf(xI)Dxi=f(xio)Dxjo +åI=1itf(x)Dxi=f(xjo)Dxjo+B Зафиксируем произвольным образом xiÎ[xi-1,xi] i¹jo limst(f,x1,…,x0n,..,xit) =lim(f(xjo)Dxjo+B)=¥ m>0 существует n0 | st(f,x1,…,xjo(n),…,xit)>m Отсюда Þ, что интегр сумма при мелкости разбеения |t|®0 не могут стремится ни к какому конечному результату. Предположим, что $ I=lim|t|®0stÞ "E>0 $dE>0 | "t, |t|<dE и любой выбор точек xi вып-ся нер-во |dt-I|<EÞ|dt|=|dt-I+I|<|dt-I|+|I| <E+|I|; M=E+|I| при любом разбиении t в частности при при |t|<dE можно выбрать точки x1,..,xit такие, что |st|>M Þф-ция не может быть не ограничена на отр[a,b]. Ч.Т.Д. Ф-ла Ньтона-Лейбница aòbf(x)dx=Ф(b)-Ф(а)=Ф(х)|аb –(1) {T} (основная теорема интегрального исчисления) Пусть ф-ция y=f(x) непрерывна на [a,b] и Ф(х)-какая либо из её первообразных. Þ (1) {Док-во} F(x)= aòxf(t)dt тогда ф-ции F(x) и Ф(x) первообразные для f(x) на [a,b] $ F(x)=Ф(х)+С; aòxf(t)dt=Ф(х)+С Если x=a то aòаf(t)dt=0 Þ 0=Ф(а)+СÞ С=-Ф(а)Þ aòxf(t)dt=Ф(х)-Ф(а) Поллагая в равенстве x=b приходим к вормуле (1) Ч.Т.Д.

18. Равномерная сх-сть ф-ых послед-стей и рядов. Признак Вейерштрасса. Ф-циональную посл-сть {fn)x)} x Î E наз. равномерно сходящейся ф-цией f на м-ж Е, если для Î e >0, сущ номер N, такой, что для " т х Î E и " n >N вып-ся: |fn(x)-f(x)|<e. Если м-ж {fn)x)} равномерно сх-ся на м-ж Е, то она и просто сх-ся в ф-ции f на м-ж. Е тогда пишут: fn à f.

наз. равномерно сх-ся рядом, если на м-ж Е равномерно сх-ся посл-сть его частичной суммы., т. е. равномерная сх-сть ряда означает:Sn(x) à f(x) Не всякий сходящийся ряд является равномерно сх-ся, но всякий равномерно сх-ся – есть сх-ся Т. (Признак Вейерштрасса равномерной сх-ти ряда): Если числовой ряд: (7), где a >=0 сх-ся и для " x Î E и " n = 1,2… если выполняется нер-во un(x)|<=an(8), ряд (9) наз абс-но и равномерно сх-ся на м-ж Е.

Док-ва:

Абсолютная сх-сть в каждой т. х следует из неравенства (8) и сх-ти ряда (7). Пусть S(x) – сумма ряда (9), а Sn(x) – его частичная сумма.

Зафиксируем произвольное e >0 В силу сх-ти ряда (7) сущ. номера N, " n >N и вып. нерво . Следовательно: |S(x)-Sn(x)| = . Это означает, что Sn(x) à S(x) что означает равномерную сх-сть ряда..

19. Степенные ряды. Теорема Абеля. Степенным рядом наз ф-ный ряд вида: a0+a1x+a2x2+… + anxn =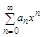 (1) xÎR членами которого Степенным рядом наз также ряд: a0+a1(x-x0)+a2(x-x0)2… + an(x-x0)n = 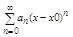(2) Степенной ряд (1) сх-ся абс-но по крайней мере в т. х = 0, а ряд (2) в т х = х0, т.е в этих случаях все кроме 1 равны 0. являются степенные ф-ции. Числа an Î R, наз коэффициентами ряда(1). Ряд (2) сводится к ряду (1) по ф-ле у = х-х0.Т Абеля: 1Если степенной ряд (1) сх-ся в т. х0 ¹ 0, то он сх-ся абсолютно при любом х, для которого |x|<|x0|, Если степеннгой ряд (1) расх-ся в т. х0, то он расх-ся в любой т. х, для которой |x|>|x0|

20. Радиус сх-ти и интервал сх-ти степенного ряда. Рассмотрим степенной ряд: (1) Число (конечное или бесконечное) R>=0 наз радиусом сх-ти ряда (1) если для любого х такого, что |x|<R ряд (1) сх-ся, а для " х таких. что |x|>R ряд расх-ся интервалом сх-ти. Т1 Для всякого степенного ряда (1) сущ-ет радиус сх-ти R 0<=R<=+¥ при этом, если |x|<R, то в этой т. х ряд сх-ся абс-но. Если вместо х взять у = х-х0, то получится: интервал сх-ти: |x-x0<R| будет: (x0-R, x0+R)При этом если |x-x0|<R, то ряд сх-ся в т. x абс-но иначе расх-ся. На концах интервала, т. е. при x = -R, x=+R для ряда (1) или x = x0-R, x=x0+R для ряда (3) вопрос о сх-ти решается индивидуально. У некоторых рядов интервал сх-ти может охватывать всю числовую прямую при R = +¥ или вырождаться в одну точку при R=0. Интервал на числовой оси состоящий из т. х для которых |x|<R, т. е. (-R, +R) наз. Т2 Если для степенного ряда (1) сущ-ет предел (конечный или бесконечный): , то радиус сх-ти будет равен этому пределу. Если сущ-ет предел степенного ряда, то радиус сх-ти равен 1/пределот ряда Если степенной ряд (1) имеет радиус сх-ти R>0, то на любом отрезке действительной оси вида |[-r,r] целиком лежащем внутри интервала сх-ти ряд (1) сх-ся равномерно.

На любом отрезке |x-x0|<=r сумма степенного ряда является непрерывной ф-цией.

Если ф-ция f(x) на интервале (x0-R, x0+R) является суммой ряда, то она дифференцируема на этом интервале и е производная f’(x) находится дифференцированием ряда. Степенной ряд можно почленно интегрировать на любом отрезке целиком принадлежащем интервалу сходимости при этом полученный степенной ряд имеет тот же радиус сходимости что и исходный ряд.

21. Разложение ф-ций в степенные ряды. Ряды Тейлора и Маклорена.

Пусть(1) сх-ся при |x-x0|<R а его сумма является ф-лой f(x)= (2) В этом случае говорят, что ф-ция f(x) разложена в степенной ряд. (1). Т1 Если ф-ция f распространяется в некоторой окрестности т. х0 f(x)= , то  и справедлива формула: (15) Если в некоторой окрестности заданной точки ф-ция распадается в степенной ряд, то это разложение единственно.

Пусть дествит. ф-ция f определена в некоторой окрестности т. х0 и имеет в этой точке производные всех порядков, тогда ряд:(6) наз рядом Тейлора ф-ции f в т, х0        При х0=0 ряд Тейлора принимает вид:

(6’) и называется ряд Маклорена.

Ряд Тейлора может:

1 Расх-ся всюду, кроме х=х0

2 Сх-ся, но не к исходной ф-ции f(x), а к какой-нибудь другой.

3 Сх-ся к исходной ф-ции f(x)

Бесконечная дифференцируемость ф-ции f(x) в какой-то т. х0 является необходимым условием разложимости ф-ции в ряд Тейлора, но не является достаточным. Для введения доп-ных условий треб. ф-ла Тейлора.

Т2 Если ф-ция f(x) (n+1) дифф-ма на интервале (x0-h, x0+h) h>0, то для всех x Î (x0-h, x0+h) имеет место ф-ла Тейлора:

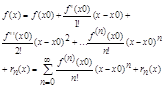
где остаток rn(x) можно записать:

(8)

(9)

Формула (8) наз остаточным членом ф-лы Тейлора в интегральной форме. Ф-ла (9) – формулой Лагранжа.

Преобразуя ф-лу Тейлора при х0 = 0 получаем ф-лу Маклорена.

Т3 Если ф-ция f(x) имеет в окрестности т х0 производные любого порядка и все они ограниченны одним и тем же числом С, т е " x Î U(x0) |f(n)(x)|<=C, то ряд Тейлора этой ф-ции сх-ся в ф-ции f(x) для всех х из этой окрестности.

22. Разложение элементарных ф-ций в ряд Тейлора (Маклорена). 1 Разложение ф-ции ех  ряд Маклорена. радиус сх-ти: R=¥ следовательно ряд абсолютно сх-ся на всей числовой прямой. Разложение sinx и cosx В степенной ряд Маклорена  сх-ся на всей числовой оси,  сх-ся на всей числовой оси, f(x) = (1+x)a 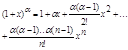 наз. биномиальный ряд с показ-ем a.

Разложение ф-ции ln(1+x)

сх-ся при 1<x<=1

5 Разложение arctgx в степенной ряд Маклорена

сх-ся при -1<=x<=1.