
Рефераты по сексологии
Рефераты по информатике программированию
Рефераты по биологии
Рефераты по экономике
Рефераты по москвоведению
Рефераты по экологии
Краткое содержание произведений
Рефераты по физкультуре и спорту
Топики по английскому языку
Рефераты по математике
Рефераты по музыке
Остальные рефераты
Рефераты по авиации и космонавтике
Рефераты по административному праву
Рефераты по безопасности жизнедеятельности
Рефераты по арбитражному процессу
Рефераты по архитектуре
Рефераты по астрономии
Рефераты по банковскому делу
Рефераты по биржевому делу
Рефераты по ботанике и сельскому хозяйству
Рефераты по бухгалтерскому учету и аудиту
Рефераты по валютным отношениям
Рефераты по ветеринарии
Рефераты для военной кафедры
Рефераты по географии
Рефераты по геодезии
Рефераты по геологии
Рефераты по геополитике
Рефераты по государству и праву
Рефераты по гражданскому праву и процессу
Рефераты по делопроизводству
Рефераты по кредитованию
Рефераты по естествознанию
Рефераты по истории техники
Рефераты по журналистике
Рефераты по зоологии
Рефераты по инвестициям
Рефераты по информатике
Исторические личности
Рефераты по кибернетике
Рефераты по коммуникации и связи
Шпаргалка: Шпаргалка по математике
Шпаргалка: Шпаргалка по математике
Формулы сокр. умножения и разложения на множители :
(a±b)²=a²±2ab+b²
(a±b)³=a³±3a²b+3ab²±b³
a²-b²=(a+b)(a-b)
a³±b³=(a±b)(a²∓ab+b²),
(a+b)³=a³+b³+3ab(a+b)
(a-b)³=a³-b³-3ab(a-b)
xn-an=(x-a)(xn-1+axn-2+a²xn-3+...+an-1)
ax²+bx+c=a(x-x1)(x-x2)
где x1 и x2 — корни уравнения
ax²+bx+c=0
Степени и корни :
ap·ag = ap+g
ap:ag=a p-g
(ap)g=a pg
ap /bp = (a/b)p
ap×bp = abp
a0=1; a1=a
a-p = 1/a
pÖa =b => bp=a
pÖapÖb = pÖab
Öa ; a = 0
____
/ __ _
pÖ gÖa = pgÖa
___ __
pkÖagk = pÖag
p ____
/ a pÖa
/ ¾¾ = ¾¾¾¾
Ö b pÖb
a 1/p = pÖa
pÖag = ag/p
Квадратное уравнение
ax²+bx+c=0; (a¹0)
x1,2= (-b±ÖD)/2a; D=b² -4ac
D>0® x1¹x2 ;D=0® x1=x2
D<0, корней нет.
Теорема Виета:
x1+x2 = -b/a
x1× x2 = c/a
Приведенное кв. Уравнение:
x² + px+q =0
x1+x2 = -p
x1×x2 = q
Если p=2k (p-четн.)
и x²+2kx+q=0, то x1,2 = -k±Ö(k²-q)
Нахождение длинны отр-ка
по его координатам
Ö((x2-x1)²-(y2-y1)²)
Логарифмы:
loga x = b => ab = x; a>0,a¹0
a loga x = x, logaa =1; loga 1 = 0
loga x = b; x = ab
loga b = 1/(log b a)
logaxy = logax + loga y
loga x/y = loga x - loga y
loga xk =k loga x (x >0)
logak x =1/k loga x
loga x = (logc x)/( logca); c>0,c¹1
logbx = (logax)/(logab)
Прогрессии
Арифметическая
an = a1 +d(n-1)
Sn = ((2a1+d(n-1))/2)n
Геометрическая
bn = bn-1 × q
b2n = bn-1× bn+1
bn = b1×qn-1
Sn = b1 (1- qn)/(1-q)
S= b1/(1-q)
Тригонометрия.
sin x = a/c
cos x = b/c
tg x = a/b=sinx/cos x
ctg x = b/a = cos x/sin x
sin (p-a) = sin a
sin (p/2 -a) = cos a
cos (p/2 -a) = sin a
cos (a + 2pk) = cos a
sin (a + 2pk) = sin a
tg (a + pk) = tg a
ctg (a + pk) = ctg a
sin² a + cos² a =1
ctg a = cosa / sina , a ¹ pn, nÎZ
tga × ctga = 1, a ¹ (pn)/2, nÎZ
1+tg²a = 1/cos²a , a¹p(2n+1)/2
1+ ctg²a =1/sin²a , a¹ pn
Формулы сложения:
sin(x+y) = sin x cos y + cos x sin y
sin (x-y) = sin x cos y - cos x sin y
cos (x+y) = cos x cos y - sin x sin y
cos (x-y) = cos x cos y + sin x sin y
tg(x+y) = (tg x + tg y)/ (1-tg x tg y )
x, y, x + y ¹ p/2 + pn
tg(x-y) = (tg x - tg y)/ (1+tg x tg y)
x, y, x - y ¹ p/2 + pn
Формулы двойного аргумента.
sin 2a = 2sin a cos a
cos 2a = cos² a - sin² a = 2 cos² a - 1 =
= 1-2 sin²a
tg 2a = (2 tga)/ (1-tg²a)
1+ cos a = 2 cos² a/2
1-cosa = 2 sin² a/2
tga = (2 tg (a/2))/(1-tg²(a/2))
Ф-лы половинного аргумента.
sin² a/2 = (1 - cos a)/2
cos²a/2 = (1 + cosa)/2
tg a/2 = sina/(1 + cosa ) = (1-cos a)/sin a
a¹ p + 2pn, n ÎZ
Ф-лы преобразования суммы в произв.
sin x + sin y = 2 sin ((x+y)/2) cos ((x-y)/2)
sin x - sin y = 2 cos ((x+y)/2) sin ((x-y)/2)
cos x + cos y = 2cos (x+y)/2 cos (x-y)/2
cos x - cos y = -2sin (x+y)/2 sin (x-y)/2
sin (x+y)
tg x + tg y = —————
cos x cos y
sin (x - y)
tg x - tgy = —————
cos x cos y
Формулы преобр. произв. в сумму
sin x sin y = Ѕ(cos (x-y) - cos (x+y))
cos x cos y = Ѕ(cos (x-y)+ cos (x+y))
sin x cos y = Ѕ(sin (x-y)+ sin (x+y))
Соотнош. между ф-ями
sin x = (2 tg x/2)/(1+tg2x/2)
cos x = (1-tg2 2/x)/ (1+ tg² x/2)
sin2x = (2tgx)/(1+tg2x)
sin²a = 1/(1+ctg²a) = tg²a/(1+tg²a)
cos²a = 1/(1+tg²a) = ctg²a / (1+ctg²a)
ctg2a = (ctg²a-1)/ 2ctga
sin3a = 3sina -4sin³a = 3cos²asina-sin³a
cos3a = 4cos³a-3 cosa=
= cos³a-3cosasin²a
tg3a = (3tga-tg³a)/(1-3tg²a)
ctg3a = (ctg³a-3ctga)/(3ctg²a-1)
sin a/2 = ±Ö((1-cosa)/2)
cos a/2 = ±Ö((1+cosa)/2)
tga/2 = ±Ö((1-cosa)/(1+cosa))=
sina/(1+cosa)=(1-cosa)/sina
ctga/2 = ±Ö((1+cosa)/(1-cosa))=
sina/(1-cosa)= (1+cosa)/sina
sin(arcsin a) = a
cos( arccos a) = a
tg ( arctg a) = a
ctg ( arcctg a) = a
arcsin (sina) = a ; aÎ [-p/2 ; p/2]
arccos(cos a) = a ; a Î [0 ; p]
arctg (tg a) = a ; a Î[-p/2 ; p/2]
arcctg (ctg a) = a ; a Î [ 0 ; p]
arcsin(sina)=
1)a - 2pk; aÎ[-p/2 +2pk;p/2+2pk]
2) (2k+1)p - a; aÎ[p/2+2pk;3p/2+2pk]
arccos (cosa) =
1) a-2pk ; aÎ[2pk;(2k+1)p]
2) 2pk-a ; aÎ[(2k-1)p; 2pk]
arctg(tga)= a-pk
aÎ(-p/2 +pk;p/2+pk)
arcctg(ctga) = a -pk
aÎ(pk; (k+1)p)
arcsina = -arcsin (-a)= p/2-arccosa =
= arctg a/Ö(1-a²)
arccosa = p-arccos(-a)=p/2-arcsin a=
= arc ctga/Ö(1-a²)
arctga =-arctg(-a) = p/2 -arcctga =
= arcsin a/Ö(1+a²)
arc ctg a = p-arc cctg(-a) =
= arc cos a/Ö(1-a²)
arctg a = arc ctg1/a =
= arcsin a/Ö(1+a²)= arccos1/Ö(1+a²)
arcsin a + arccos = p/2
arcctg a + arctga = p/2
Тригонометрические уравнения
sin x = m ; |m| = 1
x = (-1)n arcsin m + pk, kÎ Z
sin x =1 sin x = 0
x = p/2 + 2pk x = pk
sin x = -1
x = -p/2 + 2 pk
cos x = m; |m| = 1
x = ± arccos m + 2pk
cos x = 1 cos x = 0
x = 2pk x = p/2+pk
cos x = -1
x = p+ 2pk
tg x = m
x = arctg m + pk
ctg x = m
x = arcctg m +pk
sin x/2 = 2t/(1+t2); t - tg
cos x/2 = (1-t²)/(1+t²)
Показательные уравнения.
Неравенства: Если af(x)>(<) aа(ч)
1) a>1, то знак не меняеться.
2) a<1, то знак меняется.
Логарифмы : неравенства:
logaf(x) >(<) log a j(x)
1. a>1, то : f(x) >0
j(x)>0
f(x)>j(x)
2. 0<a<1, то: f(x) >0
j(x)>0
f(x)<j(x)
3. log f(x) j(x) = a
ОДЗ: j(x) > 0
f(x) >0
f(x ) ¹ 1
Тригонометрия:
1. Разложение на множители:
sin 2x - Ö3 cos x = 0
2sin x cos x -Ö3 cos x = 0
cos x(2 sin x - Ö3) = 0
....
2. Решения заменой ....
3.
sin² x - sin 2x + 3 cos² x =2
sin² x - 2 sin x cos x + 3 cos ² x = 2 sin² x + cos² x
Дальше пишеться если sin x = 0, то и cos x = 0,
а такое невозможно, => можно поделить на cos x
Тригонометрические нер-ва :
sin a ³ m
2pk+a1 = a = a2+ 2pk
2pk+a2 = a= (a1+2p)+ 2pk
Пример:
I cos (p/8+x) < Ö3/2
pk+ 5p/6< p/8 +x< 7p/6 + 2pk
2pk+ 17p/24 < x< p/24+2pk;;;;
II sin a = 1/2
2pk +5p/6 =a= 13p/6 + 2pk
cos a ³(=) m
2pk + a1 < a< a2+2 pk
2pk+a2< a< (a1+2p) + 2pk
cos a ³ - Ö2/2
2pk+5p/4 =a= 11p/4 +2pk
tg a³(=) m
pk+ arctg m =a= arctg m + pk
ctg ³(=) m
pk+arcctg m < a< p+pk
Производная:
(xn)’ = n× xn-1
(ax)’ = ax× ln a
(lg ax )’= 1/(x×ln a)
(sin x)’ = cos x
(cos x)’ = -sin x
(tg x)’ = 1/cos² x
(ctg x)’ = - 1/sin²x
(arcsin x)’ = 1/ Ö(1-x²)
(arccos x)’ = - 1/ Ö(1-x²)
(arctg x)’ = 1/ Ö(1+x²)
(arcctg x)’ = - 1/ Ö(1+x²)
Св-ва:
(u × v)’ = u’×v + u×v’
(u/v)’ = (u’v - uv’)/ v²
Уравнение касательной к граф.
y = f(x0)+ f ’(x0)(x-x0)
уравнение к касательной к графику в точке x
1. Найти производную
2. Угловой коофициент k =
= производная в данной точке x
3. Подставим X0, f(x0), f ‘ (x0), выразим х
Интегралы :
ò xn dx = xn+1/(n+1) + c
ò ax dx = ax/ln a + c
ò ex dx = ex + c
ò cos x dx = sin x + cos
ò sin x dx = - cos x + c
ò 1/x dx = ln|x| + c
ò 1/cos² x = tg x + c
ò 1/sin² x = - ctg x + c
ò 1/Ö(1-x²) dx = arcsin x +c
ò 1/Ö(1-x²) dx = - arccos x +c
ò 1/1+ x² dx = arctg x + c
ò 1/1+ x² dx = - arcctg x + c
Площадь криволенейной трапеции.
Геометрия
Треугольники
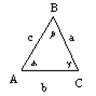
a + b + g =180
Теорема синусов
a² = b²+c² - 2bc cos a
b² = a²+c² - 2ac cos b
c² = a² + b² - 2ab cos g
Медиана дели треуг. на два равновеликих. Медиана делит
противопол. сторону напополам.
Биссектриса - угол.
Высота падает на пр. сторону
под прямым углом.
Формула Герона :
p=Ѕ(a+b+c)
_____________
S = Öp(p-a)(p-b)(p-c)
S = Ѕab sin a
Sравн.=(a²Ö3)/4
S = bh/2
S=abc/4R
S=pr
Трапеция.
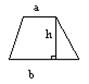
S = (a+b)/2× h
Круг
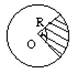
S= pR²
Sсектора=(pR²a)/360
Стереометрия
Параллепипед
V=Sосн×Р
Прямоугольный
V=abc
Пирамида
V =1/3Sосн.×H
Sполн.= Sбок.+ Sосн.
Усеченная :
H . _____
V = 3 (S1+S2+ÖS1S2)
S1 и S2 — площади осн.
Sполн.=Sбок.+S1+S2
Конус
V=1/3 pR²H
Sбок. =pRl
Sбок.= pR(R+1)
Усеченный
Sбок.= pl(R1+R2)
V=1/3pH(R12+R1R2+R22)
Призма
V=Sосн.×H
прямая: Sбок.=Pосн.×H
Sполн.=Sбок+2Sосн.
наклонная :
Sбок.=Pпс×a
V = Sпс×a, а -бок. ребро.
Pпс — периметр
Sпс пл. перпенд. сечения
Цилиндр.
V=pR²H ; Sбок.= 2pRH
Sполн.=2pR(H+R)
Sбок.= 2pRH
Сфера и шар .
V = 4/3 pR³ - шар
S = 4pR³ - сфера
Шаровой сектор
V = 2/3 pR³H
H - высота сегм.
Шаровой сегмент
V=pH²(R-H/3)
S=2pRH
| град | 0° | 30° | 45° | 60° | 90° | 120° | 135° | 180° | |||||
| a | -p/2 | -p/3 | -p/4 | -p/6 | 0 | p/6 | p/4 | p/3 | p/2 | 2p/3 | 3p/4 | 3p/6 | p |
| sina | -1 | -Ö3/2 | -Ö2/2 | - Ѕ | 0 | Ѕ | Ö2/2 | Ö3/2 | 1 | - Ѕ | 0 | ||
| cosa | 1 | Ö3/2 | Ö2/2 | Ѕ | 0 | - Ѕ | -Ö2/2 | - Ö3/2 | -1 | ||||
| tga | Ï | -Ö3 | -1 | -1/Ö3 | 0 | 1/Ö3 | 1 | Ö3 | Î | -Ö3 | -1 | 0 | |
| ctga | --- | Ö3 | 1 | 1/Ö3 | 0 | -1/Ö3 | -1 | -- |
| n | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 2 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 |
| 3 | 8 | 27 | 64 | 125 | 216 | 343 | 512 | 729 |
| 4 | 16 | 81 | 256 | 625 | 1296 | 2401 | 4096 | 6561 |
| 5 | 32 | 243 | 1024 | 3125 | 7776 | 16807 | 32768 | 59049 |
| 6 | 64 | 729 | 4096 | 15625 | 46656 |
|
||
| 7 | 128 | 2181 |
|
|||||
| 8 | 256 | 6561 |
|
|||||
| -a | p-a | p+a | p/2-a | p/2+a | 3p/2 - a | 3p/2+a | |
| sin | -sina | sina | -sina | cosa | cosa | -cosa | -cosa |
| cos | cosa | -cosa | -cosa | sina | -sina | -sina | sina |
| tg | -tga | -tga | tga | ctga | -ctga | ctga | -ctga |
| ctg | -ctga | -ctga | ctga | tga | -tga | tga | -tga |
© 2010 Интернет База Рефератов